朱小楼中学2007年高二直线平面几何体单元检测题 2007
2007年高考“立体几何”题
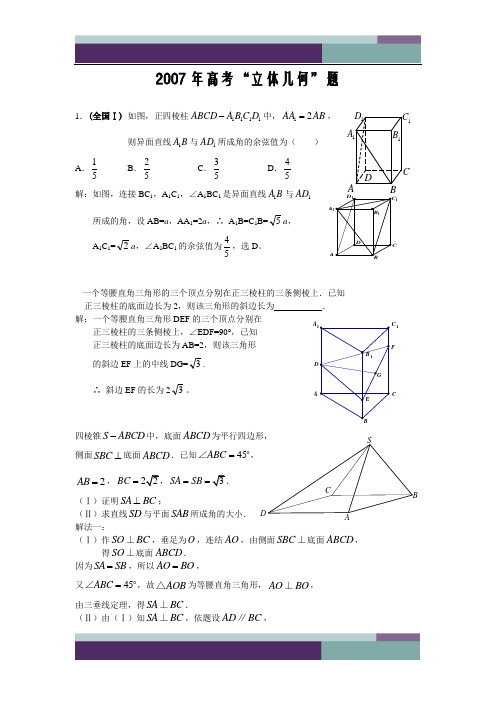
2007年高考“立体几何”题1.(全国Ⅰ) 如图,正四棱柱1111ABCD A BC D -中,12AA AB =,则异面直线1A B 与1AD 所成角的余弦值为( )A .15B .25C .35D .45解:如图,连接BC 1,A 1C 1,∠A 1BC 1是异面直线1A B 与1AD所成的角,设AB=a ,AA 1=2a ,∴ A 1B=C 1B=5a , A 1C 1=2a ,∠A 1BC 1的余弦值为45,选D 。
一个等腰直角三角形的三个顶点分别在正三棱柱的三条侧棱上.已知 正三棱柱的底面边长为2,则该三角形的斜边长为 . 解:一个等腰直角三角形DEF 的三个顶点分别在 正三棱柱的三条侧棱上,∠EDF=90°,已知 正三棱柱的底面边长为AB=2,则该三角形的斜边EF 上的中线DG=3. ∴ 斜边EF 的长为23。
四棱锥S ABCD -中,底面ABCD 为平行四边形, 侧面SBC ⊥底面ABCD .已知45ABC =∠,2AB =,BC =SA SB ==(Ⅰ)证明SA BC ⊥;(Ⅱ)求直线SD 与平面SAB 所成角的大小. 解法一:(Ⅰ)作SO BC ⊥,垂足为O ,连结AO ,由侧面SBC ⊥底面ABCD ,得SO ⊥底面ABCD . 因为SA SB =,所以AO BO =,又45ABC =∠,故AOB △为等腰直角三角形,AO BO ⊥, 由三垂线定理,得SA BC ⊥.(Ⅱ)由(Ⅰ)知SA BC ⊥,依题设AD BC ∥,1A AB1B1A1D1C C DC 1A CFAD BCS故SA AD ⊥,由AD BC ==,SA =AO , 得1SO =,SD =.SAB △的面积211122S ABSA ⎛=-= ⎝连结DB ,得DAB △的面积21sin13522S AB AD == 设D 到平面SAB 的距离为h ,由于D SAB S ABD V V --=, 得121133h S SO S =,解得h = 设SD 与平面SAB 所成角为α,则sin 11h SD α===. 所以,直线SD 与平面SBC 所成的我为. 解法二:(Ⅰ)作SO BC ⊥,垂足为O ,连结AO ,由侧面SBC ⊥底面ABCD ,得SO ⊥平面ABCD . 因为SA SB =,所以AO BO =.又45ABC =∠,AOB △为等腰直角三角形,AO OB ⊥. 如图,以O 为坐标原点,OA 为x 0)A ,,(0B ,(0C ,(001)S ,,,(2,(0CB =,0SA CB =,所以SA BC ⊥.(Ⅱ)取AB 中点E ,0E ⎫⎪⎪⎝⎭,连结SE ,取SE 中点G ,连结OG ,12G ⎫⎪⎪⎝⎭,. 12OG ⎫=⎪⎪⎝⎭,,1SE ⎫=⎪⎪⎝⎭,(AB =. 0SE OG =,0AB OG =,OG 与平面SAB 内两条相交直线SE ,AB 垂直.所以OG ⊥平面SAB ,OG 与DS 的夹角记为α,SD 与平面SAB 所成的角记为β,OD BCAS则α与β互余.D,(DS =. 22cos 11OG DS OG DSα==,sin 11β=所以,直线SD 与平面SAB 所成的角为arcsin 11.2.(全国II) 已知正三棱柱111ABC A B C -的侧棱长与底面边长相等,则1AB 与侧面11ACC A 所成角的正弦值等于()ABC .2D 解:已知正三棱柱ABC -A 1B 1C 1的侧棱长与底面边长相等,取A 1C 1的中点D 1,连接BD 1,AD 1,∠B 1AD 1是AB 1与侧面ACC 1A 1所成的角,11sin 4B AD ∠==,选A 。
高二数学下第9章《直线平面简单几何体》复习测试2及答案.

高二数学下第9章《直线、平面、简单几何体》复习测试2及答案一:选择题(本大题共10小题,每小题5分,共50分,在每小题的四个选项中,只有一项符合要求) 1.若a 、b 是异面直线,直线c ∥a ,那么b c 与 ( ) (A)一定是异面直线 (B)一定是相交直线 (C) 不可能是相交直线 (D)不可能是平行直线2.两两互相平行的直线a 、b 、c 可以确定平面的个数是( ) (A ).1或3 (B ).1 (C ).3 (D ).4 3. 右图用符号语言可表述为( ) (A) m =βα ,α⊂n ,m A ⊂,n A ⊂ (B) m =βα ,α∈n ,A n m = (C) m =βα ,α⊂n ,A n m = (D) m =βα ,α∈n ,m A ∈,n A ∈4.一个水平放置的三角形用斜二测法画出的直观图是一个边长为4的正三角形,则原三角形的面积为( ).A 34 .B 8 .C 38 .D 685.已知在空间四边形ABCD 中,=⋅+⋅+⋅( ).A 1 .B 2 .C 0 .D 不能确定6. 已知平面α与β所成的二面角为80°,P 为α、β外一定点,过点P 的一条直线与α、β所成的角都是30°,则这样的直线有且仅有( )(A )1条 (B )2条 (C )3条 (D )4条 7. 在下列关于直线l 、m 与平面α、β的命题中,真命题是( ) (A)若l ⊂β且α⊥β,则l ⊥α. (B) 若l ⊥β且α∥β,则l ⊥α.(C) 若l ⊥β且α⊥β,则l ∥α. (D) 若α∩β=m 且l ∥m,则l ∥α.8. 一个平面与一个正方体的十二条棱所在的直线都成相等的角,则这个角的余弦值为( ) A.22 B. 33 C. 36D. 19 . 已知点M 在平面ABC 内,并且对空间任一点O ,OC OB OA x OM 3121++= 则x 的值为( ) (A)61 (B)31 (C) 21(D)0 10. 如图,在棱长为2的正方体1111D C B A ABCD -中, O 是底面ABCD 的中心,E 、F 分别是1CC 、AD 的中点。
高中直线、平面、简单几何体测试题

B、
C、l至多与a,b中一条相交D、l至少与a,b中一条相交
2.三条直线a,b,c中,已知b,c是异面直线,则这三条直线所能确定的平面个数为()
A、0;B、2 C、0或2 D、0或1或2
3.线段AB,CD所在直线是异面直线,线段AB,CD的中点分别为M,N,连结AC,BD,且线段AC,BD的中点分别为P,Q,则直线MN,PQ的位置关系是()
5.如果把两条异面直线看成是一对,那么在正方体的12条棱中,共有________对异面直线.
6.正方体ABCD- 中,M是 的中点,则与AM成异面直线的棱共有条.
7.直线a,b是异面直线,直线a,c也是异面直线,则直线b,c的位置关系是_________.
8.给出下列命题:①直线a∥AB,b∥BC,则a、b所成的角为θ;②若直线a、b与c所成的角相等,则a∥b;③若直线a∥b,且b与c所成的角为θ,则a与c所成的角也是θ;④若直线a、b与直线c所成的角不相等,则a与b不平行.其中正确命题的题号为.
A、 ,M,O三点共线
B、 ,M,O,C四点共面
C、 ,O, ,M四点共面
D、 ,D,O,M四点共面
3.下列说法正确的是()
A、如果一条直线和两条直线都相交,那么这三条直线可确定一个平面
B、三点确定一个平面
C、四边相等的四边形是菱形
D、分别在两个相交平面内的两条直线如果相交,那么交点一定在两个平面的交线上
§9.1平面(一)
一、选择题
1.下列命题中正确的个数为()
(1)书桌面是平面
(2)
(2)8个平面重叠起来要比4个平面重叠起开厚
(3)一个平面长为50m,宽为20m
(4)
高中数学高二会考复习(直线、平面、简单几何体)试卷,复习资料

高二会考复习(直线、平面、简单几何体)班级: 姓名:一.选择题:1.空间四点A 、B 、C 、D 共面但不共线,则下列结论成立的是( )A.四点中必有三点共线B.四点中有三点不共线C.AB 、BC 、CD 、DA 四条直线中有两条平行D.直线AB 与CD 相交2.P 为△ABC 所在平面外一点,连结PA 、PB 、PC 后,则这六条棱所在的直线中,异面直线对数共有( )A.2对B.3对C.4对D.6对3.若直线a b 、都与直线l 垂直,则直线a b 、的位置关系是( )A.平行B.相交C.异面D.以上都可能4.在棱长为a 的正方体1111ABCD A B C D -中,与AD 异面且距离等于a 的棱共有( )A.4条B.5条C.6条D.7条5.在正方体1111ABCD A B C D -中,与1AD 所成60°的面对角线共有( )A.4条B.6条C.8条D.10条6.直线与平面平行的充要条件是这条直线与平面内的( )A.一条直线不相交B.两条直线不相交C .任意一条直线不相交 D.无数条直线不相交7.已知直线a ∥平面α,直线b α⊆,则a b 与的关系为( ) A.相交 B.平行 C.异面 D.平行或异面8.四面体ABCD 中E 、F 分别是AC 与BD 的中点,若CD=2AB=2,EF ⊥AB ,则EF 与CD 所成角为( )A.90°B.45°C.60°D.30°9.若直线a ⊥直线b ,且a ⊥平面α,则有( )A.b α∥B.b α⊆C.b α⊥D.b α∥或b α⊆10.斜线AB 交平面α于B ,AB 与平面α成60°角,BC α⊆,则∠ABC 的取值范围为( )A.(0,)3πB.[,]32ππC.2[,]33ππD.[,]3ππ 11.若(2,1,3),(1,2,9)a x b y ==-,如果a b ∥,则( )A.1,1x y ==B.11,22x y ==- C.13,62x y ==- D.13,62x y =-=12.在棱长为1的正方体1111ABCD A B C D -中,M 、N 分别为11A B 和1BB 的中点,那么直线AM 与CN 所成角的余弦值为( )C.35D.2513.已知过球面上A 、B 、C 三点的截面和球心的距离等于球半径的一半,且AB=BC=CA=2,则球面面积( )A.169πB.83πC.4πD.649π 二.填空题:14.正方体的全面积是2a ,它的顶点都在球面上,这个球的表面积是15.正方形ABCD 所在平面与正方形ABEF 所在平面成60°的二面角,则异面直线AD 与BF 所成角的余弦值为 16.已知向量,a b 的夹角为30°,且||3,||4a b ==,则(2)()a b a b +⋅-=17.已知A 、B 两点到平面α的距离是3,5cm cm 。
2007年高考试题分类汇编(立体几何)

2007年高考试题分类汇编(立体几何)考点1空间中点、线、面的位置关系1.(2007·重庆卷·文科)垂直于同一平面的两条直线A .平行B .垂直C .相交D .异面 2.(2007·浙江卷·理科)若P 两条异面直线l ,m 外的任意一点,则 A .过点P 有且仅有一条直线与l ,m 都平行 B .过点P 有且仅有一条直线与l ,m 都垂直 C .过点P 有且仅有一条直线与l ,m 都相交 D .过点P 有且仅有一条直线与l ,m 都异面3.(2007·重庆卷·理科)若三个平面两两相交,且三条交线互相平行,则这三个平面把空间分成A .5部分B .6部分C .7部分D .8部分 4.(2007·安徽卷·文理科)设l ,m ,n 均为直线,其中m ,n 在平面α内,“l α⊥”是“l m ⊥且l n ⊥”的A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件5.(2007·安徽卷·理科)在正方体上任意选择4个顶点,它们可能是如下各种几何形体的4个顶点,这些几何形体是 (写出所有正确结论的编.号.). ①矩形;②不是矩形的平行四边形;③有三个面为等腰直角三角形,有一个面为等边三角形的四面体; ④每个面都是等边三角形的四面体; ⑤每个面都是直角三角形的四面体.6.(2007·北京卷·文理科)平面α∥平面β的一个充分条件是 A .存在一条直线a ,使a α∥,a β∥ B .存在一条直线a ,使a α⊂,a β∥ C .存在两条平行直线a ,b ,使b β⊂,b α∥ D .存在两条异面直线a ,b ,使a α⊂,a β∥,b α∥7.(2007·福建卷·文理科)已知m ,n 为两条不同的直线,α,β为两个不同的平面,则下列命题中正确的是A .m α⊂,n α⊂,m ∥β,n ∥β⇒α∥βB .m α⊥,m n ⊥⇒n ∥αC .α∥β,m α⊂,n α⊂⇒m ∥nD .m ∥n ,n α⊥⇒m α⊥ 8.(2007·广东卷·文科)已知l ,m ,n 是互不相同的空间直线,α,β是不重合的平面,则下列命题中为真命题的是A .α∥β,l α⊂,n β⊂,l ∥nB .αβ⊥,l α⊂,则l β⊥C .l n ⊥,m n ⊥,则l ∥mD .l α⊥,l ∥β,则αβ⊥ 9.(2007·辽宁卷·文理科)若m ,n 是两条不同的直线,α,β,γ是三个不同的平面,则下列命题中的真命题是 A .若m β⊂,αβ⊥,则m α⊥ B .若m αγ=,n βγ=,m n ∥,则αβ∥ C .若m β⊥,m α∥,则αβ⊥ D .若αγ⊥,αβ⊥,则βγ⊥10.(2007·天津卷·文理科)设a ,b 为两条直线,α,β为两个平面,下列四个命题中,正确的命题是A .若a ,b 与α所成的角相等,则a b ∥B .若a α∥,b β∥,αβ∥,则a b ∥C .若a α⊂,b β⊂,a b ∥,则αβ∥D .若a α⊥,b β⊥,αβ⊥,则a b ⊥ 11.(2007·湖北卷·理科)平面α外有两条直线m 和n ,如果m 和n 在平面α内的射影分别是m '和n ',给出下列四个命题:①m n m n ''⊥⇒⊥; ②m n m n ''⊥⇒⊥;③m '与n '相交⇒m 与n 相交或重合; ④m '与n '平行⇒m 与n 平行或重合. 其中不正确的命题个数是A .1B .2C .3D .4 12.(2007·广东卷·理科)如果一个凸多面体是n 棱锥,那么这个凸多面体的所有顶点所确定的直线共有 条.这些直线中共有)(n f 对异面直线,则)4(f = ;)(n f = .(答案用数字或n 的解析式表示)13.(2007·湖南卷·文科)如图1,在正四棱柱1111ABCD A B C D -中,E 、F 分别是1AB ,1BC 的中点,则以下结论中不成立的是:A .EF 与1BB 垂直 B .EF 与BD 垂直C .EF 与CD D .EF 与11A C 异面14.(2007·江西卷·理科)如图,正方体1AC 的棱长为1,过点A 作平面1A BD 的垂线,垂足为点H ,则以下命题中,错误..的命题是 A .点H 是1A BD ∆的垂心 B .AH 垂直平面11CB D C .AH 的延长线经过点1C D .直线AH 和1BB 所成角为4515.(2007·江西卷·文科)如图,正方体1AC 的棱长为1,过点A 作平面1A BD 的垂线,垂足为点H ,则有下列四个命题 A .点H 是1A BD ∆的垂心 B .AH 垂直平面11CB DC .二面角111C BD C --D .点H 到平面1111A B C D 的距离为34其中真命题的代号是 .(写出所有真命题的代号)16.(2007·宁夏卷·理科)一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱.这个四棱锥的底面为正方形,且底面边长与各侧棱长相等,这个三棱锥的底面边长与各侧棱长也都相等.设四棱锥、三棱锥、三棱柱的高分别为1h ,2h ,h ,则12::h h h =ABCDE FA 1B 1C 1D 11111AB2:2 C2:217.(2007·全国卷Ⅰ·理科)一个等腰直角三角形的三个顶点分别在正三棱柱的三条侧棱上.已知正三棱柱的底面边长为2,则该三角形的斜边长为 . 18.(2007·陕西卷·文科)已知P 为平面α外一点,直线l α⊂,点Q l ∈,点P 到平面α的距离为a ,点P 到直线l 的距离为b ,点P 、Q 之间的距离为c ,则 A .a b c ≤≤ B .c a b ≤≤ C .a c b ≤≤ D .b c a ≤≤19.(2007·四川卷·理科)如图,1111ABCD A B C D -为正方体,下面结论错误..的是A.//BD 平面11CB DB.1AC BD ⊥C.1AC ⊥平面11CB DD.异面直线AD 与1CB 所成的角为6020.(2007·安徽卷·文科)在正方体上任意选择两条棱,则这两条棱相互平行的概率为 .考点2空间中点、线、面的度量关系考法1与球有关的组合体1.(2007·安徽卷·理科)半径为1的球面上的四点A ,B ,C ,D 是正四面体的顶点,则A 与B 两点间的球面距离为 A.arccos( B.arccos( C .1arccos()3- D .1arccos()4- 2.(2007的正方形ABCD 沿对角线AC 折成直二面角,折成直二面角后,在A ,B ,C ,D 四点所在的球面上,B 与D 两点之间的球面距离为A2 B .π C .2π D .3πABCDA 1B 1C 1D 13.(2007·福建卷·理科)顶点在同一球面上的正四棱柱1111ABCD A B C D -中,1AB =,1AA =,则A 、C 两点间的球面距离为 A .4π B .2πC.4 D.24.(2007·江西卷·理科)四面体ABCD 的外接球球心在CD 上,且2CD =,AB =A ,B 间的球面距离是A .π6B .π3C .2π3D .5π65.(2007·四川卷·理科)设球O 的半径是1,A 、B 、C 是球面上三点,已知A到B 、C 两点的球面距离都是2π,且二面角B OA C --的大小是3π,则从A 点沿球面经B 、C 两点再回到A 点的最短距离是A .76πB .54πC .43πD .32π考法2表面积与体积1.(2007·湖南卷·理科)棱长为1的正方体1111ABCD A B C D -的8个顶点都在球O 的表面上,E F ,分别是棱1AA ,1DD 的中点,则直线EF 被球O 截得的线段长为 A.2 B .1 C.12+ D2.(2007·辽宁卷·文理科)若一个底面边长为的正六棱柱的所有顶点都在一个球面上,则此球的体积为 .3.(2007·宁夏卷·文科)已知三棱锥S ABC -的各顶点都在一个半径为r 的球面上,球心O 在AB 上,SO ⊥底面ABC,AC =,则球的体积与三棱锥体积之比是ABC OA .πB .2πC .3πD .4π4.(2007·全国卷Ⅰ·文科)正四棱锥S ABCD -的底面边长和各侧棱长都为,点S ,A ,B ,C ,D 都在同一个球面上,则该球的体积为 .5.(2007·全国卷Ⅱ·文理科)一个正四棱柱的各个顶点在一个直径为2cm 的球面上.如果正四棱柱的底面边长为1cm ,那么该棱柱的表面积为 2cm . 6.(2007·陕西卷·理科)一个正三棱锥的四个顶点都在半径为1的球面上,其中底面的三个顶点在该球的一个大圆上,则该正三棱锥的体积是 A7.(2007·陕西卷·文科)Rt ABC ∆的三个顶点在半径为13的球面上,两直角边的长分别为6和8,则球心到平面ABC 的距离是A .5B .6C .10D .128.(2007·天津卷·文科)一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为 . 9.(2007·福建卷·文科)如图在正方体1111ABCD A B C D -中,E 、F 、G 、H 分别是1AA 、AB 、1BB 、11B C 的中点,则异面直线EF 与GH 所成的角等于 A .45 B .60 C .90 D .12010.(2007·湖北卷·文科)在棱长为1的正方体1111ABCD A B C D -中,E ,F 分别为棱1AA ,1BB 的中点,G 为棱11A B 上的一点,且11A G A B λ=(01λ≤≤).则点G 到平面1D EF 的距离为 AB.2C.3DABC1BD1A1C1D EFGH2007年高考试题分类汇编(立体几何) 第7 页 共 16 页7.(2007·全国卷Ⅰ·文理科)如图,正四棱柱1111ABCD A B C D -中,12AA AB =,则异面直线1A B 与1AD 所成角的余弦值为A .15B .25C .35D .457.(2007·全国卷Ⅱ·理科)已知正三棱柱111ABC A B C -的侧棱长与底面边长相等,则1AB 与侧面11ACC A 所成角的正弦值等于 A .2 D 7.(2007·全国卷Ⅱ·文科)已知三棱锥的侧棱长的底面边长的2倍,则侧棱与底面所成角的余弦值等于 A B C D 14.(2007·四川卷·理科)在正三棱柱111ABC A B C -,底面三角形的边长为1,则1BC 与侧面11ACC A 所成的角是 .考点3解答题1.(2007·安徽卷·理科)如图,在六面体1111ABCD A B C D -中,四边形ABCD 是边长为2的正方形,四边形1111A B C D 是边长为1的正方形,1DD ⊥平面1111A B C D ,1DD ⊥平面ABCD ,12DD =.ABCD A 1B 1C 1D 1 A BC DEFG A 1B 1C 1D 1(Ⅰ)求证:11A C 与AC 共面,11B D 与BD 共面; (Ⅱ)求证:平面11AA C C ⊥平面11B BDD ;(Ⅲ)求二面角11A B B C --的大小(用反三角函数值表示).2.(2007·北京卷·理科)如图,在Rt AOB ∆中,π6OAB ∠=,斜边4AB =. Rt AOC ∆可以通过Rt AOB ∆以直线AO 为轴旋转得到,且二面角B AO C --是直二面角.动点D 的斜边AB 上. (Ⅰ)求证:平面COD ⊥平面AOB ;(Ⅱ)当D 为AB 的中点时,求异面直线AO 与CD 所成角的大小; (Ⅲ)求CD 与平面AOB 所成角的最大值.3.(2007·北京卷·文科)如图,在Rt AOB ∆中,π6OAB ∠=,斜边4AB =. Rt AOC ∆可以通过Rt AOB ∆以直线AO 为轴旋转得到,且二面角B AO C --是直二面角,D 是AB 的中点.(Ⅰ)求证:平面COD ⊥平面AOB ; (Ⅱ)求异面直线AO 与CD 所成角的大小.ABDA 1B 1C 1D 1ABCDO4.(2007·福建卷·理科)如图,正三棱柱111ABC A B C -的所有棱长都为2,D 为1CC 中点.(Ⅰ)求证:1AB ⊥面1A BD ; (Ⅱ)求二面角1A A D B --的大小; (Ⅲ)求点C 到平面1A BD 的距离.5.(2007·福建卷·文科)如图,正三棱柱111ABC A B C -的所有棱长都为2,D 为1CC 中点.(Ⅰ)求证:1AB ⊥面1A BD ; (Ⅱ)求二面角1A A D B --的大小;ABCODABCDB 1C 1A 1ABCDB 1C 1A 16.(2007·广东卷·理科)如图所示,等腰ABC ∆的底边BC =高3CD =,点E 是线段BD 上异于点B 、D 的动点.点F 在BC 边上,且EF AB ⊥.现沿EF 将BEF ∆折起到PEF ∆的位置,使PE AE ⊥.记BE x =,()V x 表示四棱锥P ACFE -的体积.(Ⅰ)求()V x 的表达式;(Ⅱ)当x 为何值时,()V x 取得最大值?(Ⅲ)当()V x 取得最大值时,求异面直线AC 与PF 所成角的余弦值.7.(2007·湖北卷·理科)如图,在三棱锥V ABC -中,VC ⊥底面ABC ,AC BC ⊥,D 是AB 的中点,且AC BC a ==,VDC θ∠=(π02θ<<). (Ⅰ)求证:平面VAB ⊥VCD ;(Ⅱ)当解θ变化时,求直线BC 与平面VAB 所成的角的取值范围.8.(2007·湖北卷·文科)如图,在三棱锥V ABC -中,VC ⊥底面ABC ,AC BC ⊥,D 是AB 的中点,且AC BC a ==,VDC θ∠=(π02θ<<). (Ⅰ)求证:平面VAB ⊥VCD ;(Ⅱ)试确定角θ的值,使得直线BC 与平面VAB 所成的角为π6. PBEFACD VADC9.(2007·辽宁卷·文理科)如图,在直三棱柱111ABC A B C -中,90ACB ∠=,AC BC a ==,D ,E 分别为棱AB ,BC 的中点,M 为棱1AA 上的点,二面角M DE A --为30. (Ⅰ)证明:111A B C D ⊥;(Ⅱ)求MA 的长,并求点C 到平面MDE 的距离.10.(2007·江西卷·理科)右图是一个直三棱柱(以111A B C 为底面)被一平面所截得到的几何体,截面为ABC .已知11111A B B C ==,11190A B C ∠=,14AA =,12BB =,13CC =.(Ⅰ)设点O 是AB 的中点,证明:OC ∥平面111A B C ; (Ⅱ)求二面角1B AC A --的大小; (Ⅲ)求此几何体的体积.VADCABECDMA 1B 1C 1ACOBA 1B 1C 111.(2007·江西卷·文科)右图是一个直三棱柱(以111A B C 为底面)被一平面所截得到的几何体,截面为ABC .已知11111A B B C ==,11190A B C ∠=,14AA =,12BB =,13CC =.(Ⅰ)设点O 是AB 的中点,证明:OC ∥平面111A B C ; (Ⅱ)求AB 与平面11AAC C 所成的角的大小; (Ⅲ)求此几何体的体积.12.(2007·宁夏卷·理科)如图,在三棱锥S ABC -中,侧面SAB 与侧面SAC 均为等边三角形,90BAC ∠=°,O 为BC 中点. (Ⅰ)证明:SO ⊥平面ABC ; (Ⅱ)求二面角A SC B --的余弦值.13.(2007·全国卷Ⅰ·理科)四棱锥S ABCD -中,底面ABCD 为平行四边形,侧面SBC ⊥底面ABCD .已知45ABC =∠,2AB =,BC =SA SB == (Ⅰ)证明SA BC ⊥;(Ⅱ)求直线SD 与平面SAB 所成角的大小.ACOBA 1B 1C 1ABCSO14.(2007·全国卷Ⅱ·文理科)如图,在四棱锥S ABCD -中,底面ABCD 为正方形,侧棱SD ⊥底面ABCD ,E ,F 分别为AB ,SC 的中点. (Ⅰ)证明EF ∥平面SAD ;(Ⅱ)设2SD DC =,求二面角A EF D --的大小.15.(2007·山东卷·理科)如图,在直四棱柱1111ABCD A B C D -中,已知122DC DD AD AB ===,AD DC ⊥,AB ∥DC .(Ⅰ)设E 是DC 的中点,求证:1D E ∥平面1A BD ; (Ⅱ)求二面角11A BD C --的余弦值.ACBDSAEBCFSD ABCD EA 1B 1C 1D 116.(2007·山东卷·文科)如图,在直四棱柱1111ABCD A B C D -中,已知122DC DD AD AB ===,AD DC ⊥,AB ∥DC .(Ⅰ)求证:11D C AC ⊥;(Ⅱ)设E 是DC 上一点,试确定E 的位置,使1D E ∥平面1A BD ,并说明理由.17.(2007·陕西卷·理科)如图,在底面为直角梯形的四棱锥P ABCD -中,//AD BC ,90ABC ∠=,PA ⊥平面ABCD ,4PA =,2AD =,AB =6BC =. (Ⅰ)求证:BD ⊥平面PAC ; (Ⅱ)求二面角A PC D --的大小.18.(2007·陕西卷·文科)如图,在底面为直角梯形的四棱锥P ABCD -中,//AD BC ,90ABC ∠=,PA ⊥平面ABCD ,3PA =,2AD =,AB =6BC =. (Ⅰ)求证:BD ⊥平面PAC ; (Ⅱ)求二面角P BD A --的大小.A BCDEA 1B 1C 1D 1ABCDPEABADPE19.(2007·四川卷·理科)如图,PCBM 是直角梯形,90PCB ∠=,PM ∥BC ,1PM =,2BC =,又1AC =,120ACB ∠=,AB ⊥PC ,直线AM 与直线PC 所成的角为60.(Ⅰ)求证:平面PAC ⊥平面ABC ; (Ⅱ)求二面角B AC M --的大小; (Ⅲ)求三棱锥MAC P -的体积.20.(2007·四川卷·理科)如图,在四棱锥P ABCD -中,PA ⊥底面ABCD ,AB AD ⊥,AC CD ⊥,60ABC ∠=,PA AB BC ==,E 是PC 的中点. (Ⅰ)证明:CD AE ⊥; (Ⅱ)证明:PD ⊥平面ABE ; (Ⅲ)求二面角A PD C --的大小.21.(2007·四川卷·文科)如图,在四棱锥P ABCD -中,PA ⊥底面ABCD ,AB AD ⊥,AC CD ⊥,ABC ∠=60,PA AB BC ==,E 是PC 的中点. (Ⅰ)求PB 和平面PAD 所成的角的大小; (Ⅱ)证明AE ⊥平面PCD ; (Ⅲ)求二面角A PD C --的大小.ABCMPABCDEP22.(2007·重庆卷·理科)如右图,在直三棱柱111C B A ABC -中,12AA =,1AB =,90ABC ∠=;点D 、E 分别在1BB ,1A D 上,且D A E B 11⊥,四棱锥1ABDA C -与直三棱柱的体积之比为5:3.(Ⅰ)求异面直线DE 与11C B 的距离;(Ⅱ)若2=BC ,求二面角B DC A --的平面角的正切值.23.(2007111C B A ABC -中,90ABC ∠=,1AB =,12AA =,32BC =,点D 在1BB 上,且113BD BB =,11BB A D ⊥,垂足为E ,求:(Ⅰ)求异面直线1A D 与11C B 的距离; (Ⅱ)求四棱锥C ABDE -的体积.ABCDEPEDA 1B 1C 1CBA。
朱小楼中学2007年高二直线平面几何体

朱小楼中学2007年高二直线平面几何体单元检测题2007-4-13命题人:程浩 学号________. 姓名________.一.选择题 (每小题5分,共50分)1.已知向量)2,0,1(),0,1,1(-==,且k +与-2互相垂直,则k 的值是 A.1 B.51 C.53 D.57 2.棱长为a 的正方体中,连结相邻面的中心,以这些线段为棱的八面体的体积为12D. 6C. 4B. 3.A 3333a a a a 3.设O 、A 、B 、C 是不共面的四点,对于空间一点P ,使四点P 、A 、B 、C 共面的条件是 R)z y,x, OC z y B. R)z y,x, OC z y x .A ∈++=∈++=((OC 21OB 41OA 41OP D. OC 21OB 21OA OP .C ++=++=4.5.6.如图,正方体AC 1中,M 是棱D 1D 的中点,O 是正方形ABCD 的中心,则异面直线OA 1与AM 所成的角是A. 90B. 60C. 45D. 30 7. x , b a )31x,(-1, b ),21,3,2( a 的值为则且若⊥==D.1 5-C. 92-B. 1811.A 8.正方体ABCD –A 1B 1C 1D 1中,E 、F 分别是AA 1与CC 1的中点,则直线ED 与直线D 1F 所成角为A.51arccosB.31arccosC.3πD.6π9.设三点A (1,1,0),B (1,0,1),C (0,1,1),则△ABC 的形状为 A.直角三角形 B.等边三角形 C.等腰三角形 D.等腰直角三角形 10.在侧棱长为a 的正四棱锥中,棱锥的体积最大时底面边长为 A.332 a B.3a C.33a D.a 第Ⅱ卷(非选择题 共5道填空题6道解答题) 请将你认为正确的答案代号填在下表中 1 2 3 4 5 6 7 8 9 10二.简答题 (每小题5分,共25分)11.把函数)32cos(π+=x y 的图象沿向量a 平移后得到函数32cos +=x y 的图象,则向量a 可以是__________12.已知平面α⊥β, βα⋂=l ,P 是空间一点,且P 到α、β的距离分别是1、2,则点P 到l 的距离为。
高二数学下学期测试卷直线、平面、简单几何体. 试题

中学高二下学期数学测试卷制卷人:歐陽文化、歐陽理複;制卷時間:二O 二二年二月七日直线、平面、简单几何体班级: 姓名:一、选择题:在每一小题给出的四个选项里面,只有一项是哪一项符合题目要求的,请把正确答案的代号填在题后的括号内〔本大题一一共10个小题,每一小题5分,一共50分〕.1.正方体ABCD —A 1B 1C 1D 1中,P 、Q 、R 分别是AB 、AD 、B 1C 1的中点。
那么,正方体的过P 、Q 、R 的截面图形是A .三角形B .四边形C .五边形D .六边形2.正方体ABCD —A 1B 1C 1D 1中,以顶点A 、C 、B 1、D 1为顶点的正四面体的全面积为AB .2C .4D .3.对于任意的直线a 与平面α,在平面α内必有直线b ,使直线b 与aA .平行B .相交C .垂直D .互为异面直线 4.α、β为两个互相垂直的平面,m 、n 为一对异面直线,以下条件:①m //α、n β⊂;②m ⊥α、n β//;③m ⊥α、n β⊥;④m //α、n β//且m 与α的间隔 等于n 与β的间隔 ,其中是m ⊥n 的充分条件的有 A .①④ B .① C .③ D .②③5.直线m ⊥平面α,直线n ⊂平面β,那么以下命题正确的选项是A .假设n m ⊥,则βα//B .假设n m //,则βα⊥C .假设βα//,则n m ⊥D .假设βαα////,则n6.设a ,b ,c 是空间三条直线,α,β是空间两个平面,那么以下命题中,逆命题不成立的是A .当c ⊥α时,假设c ⊥β,那么α∥βB .当α⊂b 时,假设b ⊥β,那么βα⊥C .当α⊂b ,且c 是a 在α内的射影时,假设b ⊥c ,那么a ⊥bD .当α⊂b ,且α⊄c 时,假设c ∥α,那么b ∥c7.正三棱锥P ABC -的高为2,侧棱与底面ABC 所成角为45,那么点A 到侧面PBC 的距是A .3B .230 C .22D 8.设m 、n 是两条不同的直线,α、β是两个不同的平面.考察以下命题,其中正确的命题是A .βαβα⊥⇒⊥⊂⊥n m n m ,,B .n m n m ⊥⇒⊥βαβα//,,//C.n m n m ⊥⇒⊥⊥βαβα//,,D .ββαβα⊥⇒⊥=⊥n m n m ,,9.两条直线,m n ,两个平面,αβ,给出下面四个命题:①//,m n m n αα⊥⇒⊥ ②//,,//m n m n αβαβ⊂⊂⇒ ③//,////m n m n αα⇒ ④//,//,m n m n αβαβ⊥⇒⊥ 其中正确命题的序号是〔 〕A .①、③B .②、④C .①、④D .②、③10.假设m n ,是两条不同的直线,αβγ,,是三个不同的平面,那么以下命题中的真命题...是 A .假设m βαβ⊂⊥,,那么m α⊥B .假设m αγ=n βγ=,m n ∥,那么αβ∥C .假设m β⊥,m α∥,那么αβ⊥D .假设αγ⊥,αβ⊥,那么βγ⊥一、 选择题答案二、填空题:请把答案填在题中横线上〔本大题一一共5个小题,每一小题5分,一共25分〕.11.直三棱柱111C B A ABC -中,11===BB BC AC ,31=AB .那么三棱锥C AB A 11-的体积为12.在三棱锥O ABC -中,三条棱,,OA OB OC 两两互相垂直,且,OA OB OC M ==是AB 边的中点,那么OM 与平面ABC 所成角的大小是________________〔用反三角函数表示〕13.等边三角形ABC与正方形ABDE有一公一共边AB,二面角C AB D--的M N,分别是AC BC,的中点,那么EM AN,所成角的余弦值等于.14.将正方形ABCD沿对角线BD折成直二面角,给出以下四个结论:①AC⊥BD;②AB,CD所成角为60°;③△ADC为等边三角形;④AB与平面BCD所成角为60°。
二)-2007年高考数学试题汇编——立体几何(

2007年高考数学试题汇编—-立体几何(二)二、填空题19.(全国Ⅰ?理?16题)一个等腰直角三角形的三个顶点分别在正三棱柱的三条侧棱上.已知正三棱柱的底面边长为2,则该三角形的斜边长为.【解答】一个等腰直角三角形DEF的三个顶点分别在正三棱柱的三条侧棱上,∠EDF=90°,已知正三棱柱的底面边长为AB=2,则该三角形的斜边EF上的中线DG=,∴斜边EF的长为2。
20.(全国Ⅱ?理?15题)一个正四棱柱的各个顶点在一个直径为2cm的球面上。
如果正四棱柱的底面边长为1cm,那么该棱柱的表面积为 cm2。
【解答】一个正四棱柱的各个顶点在一个直径为2cm的球面上.正四棱柱的对角线的长为球的直径,现正四棱柱底面边长为1cm,设正四棱柱的高为h,∴2R=2=,解得h=,那么该棱柱的表面积为2+4cm2。
21.(安徽?理?15题)在正方体上任意选择4个顶点,它们可能是如下各种几何形体的4个顶点,这些几何形体是(写出所有正确结论的编号)。
①矩形;②不是矩形的平行四边形;③有三个面为等腰直角三角形,有一个面为等边三角形的四面体;④每个面都是等边三角形的四面体;⑤每个面都是直角三角形的四面体。
【解答】在正方体ABCD-A1B1C1D1上任意选择4个顶点,它们可能是如下各种几何形体的4个顶点,这些几何形体是①矩形如ACC1A1;.③有三个面为等腰直角三角形,有一个面为等边三角形的四面体,如A-A1BD;④每个面都是等边三角形的四面体,如ACB1D1;⑤每个面都是直角三角形的四面体,如AA1DC,所以填①③④⑤。
22.(江苏?理?14题)正三棱锥高为2,侧棱与底面所成角为,则点侧面的距离是.【解答】设P在底面ABC上的射影为O,则PO=2,且O是三角形ABC的中心,设底长为a,则设侧棱为b则斜高 .面积法求到侧面的距离23.(辽宁?理?15题)若一个底面边长为,棱长为的正六棱柱的所有顶点都一个平面上,则此球的体积为.【解答】根据条件正六棱柱的最长的对角线为球的直径,由得R=,球体积为24.(上海?理?10题)平面内两直线有三种位置关系:相交,平行与重合。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
朱小楼中学2007年高二直线平面几何体单元检测题2007-4-13命题人:程浩 学号________. 姓名________.一.选择题 (每小题5分,共50分)1. 已知向量)2,0,1(),0,1,1(-==b a ,且b a k +与b a -2互相垂直,则k 的值是 A.1 B.51 C.53 D.57 2. 棱长为a 的正方体中,连结相邻面的中心,以这些线段为棱的八面体的体积为12D. 6C. 4B. 3.A 3333a a a a 3. 设O 、A 、B 、C 是不共面的四点,对于空间一点P ,使四点P 、A 、B 、C 共面的条件是R)z y,x, OC z OB y OA OP B. R)z y,x, OC z OB y OA x OP .A ∈++=∈++=((OC 21OB 41OA 41OP D. OC 21OB 21OA OP .C ++=++=4.5.6. 如图,正方体AC 1中,M 是棱D 1D 的中点,O 是正方形ABCD 的中心,则异面直线OA 1与AM 所成的角是 A. 90 B. 60 C. 45 D. 30 7. x , b a )31x,(-1, b ),21,3,2( a 的值为则且若⊥==D.1 5-C. 92-B. 1811.A8. 正方体ABCD –A 1B 1C 1D 1中,E 、F 分别是AA 1与CC 1的中点,则直线ED 与直线D 1F 所成角为A.51arccosB.31arccos C.3π D.6π9. 设三点A (1,1,0),B (1,0,1),C (0,1,1),则△ABC 的形状为 A.直角三角形 B.等边三角形 C.等腰三角形 D.等腰直角三角形 10. 在侧棱长为a 的正四棱锥中,棱锥的体积最大时底面边长为 A.332 a B.3a C.33a D.a 二.简答题 (每小题5分,共25分)11. 把函数)32cos(π+=x y 的图象沿向量a 平移后得到函数32cos +=x y 的图象,则向量a 可以是__________12. 已知平面α⊥β, βα⋂=l ,P 是空间一点,且P 到α、β的距离分别是1、2,则点P 到l 的距离为 。
13. 与)1,0,2( --=a 共线且满足方程10 -=⋅b a 的向量= b __________14. 某地球仪上北纬30纬线的长度为12πcm ,该地球仪的半径是__________cm ,表面积MOCC1D1B1A1ABD是______________cm 2.15. 设A(1,2,-1),B(0,3,1),C(-2,1,2)是平行四边形的三个顶点,则此平行四边形的面积为__________________. 三.解答题 (共75分)16. 下面的一组图形为某一四棱锥S —ABCD 的侧面与底面; (1)请画出四棱锥S —ABCD 的示意图. 是否存在一条侧棱垂直于底面?如果存在,请给出证明;(2)若SA ⊥面ABCD ,E 为AB 中点,求二面角E —SC —D 的大小; (3)求点D 到面SEC 的距离.17. 如图,已知正四棱柱ABCD —A 1B 1C 1D 1中,底面边长AB=2,侧棱BB 1的长为4,过点B 作B 1C 的垂线交侧棱CC 1于点E ,交B 1C 于点F. ⑴求证:A 1C ⊥平面BED ;⑵求A 1B 与平面BDE 所成的角的正弦值.18. 如图正三棱柱,棱都相等,D 是BC 上一点,AD ⊥C 1D. (1)求证:截面ADC 1⊥侧面BCC 1B 1. (2)求二面角CAC 1D 的大小.(3)若AB =2,求A 1B 与截面ADC 1的距离.ABD C A 1B 1D 1 C 1EF19. 在四棱锥V-ABCD 中,底面ABCD 是正方形,侧面VAD 是正三角形,平面VAD ⊥底面ABCD. (Ⅰ)证明AB ⊥平面VAD ;(Ⅱ)求面VAD 与面VDB 所成的二面角的大小.20. 如图,某建筑物的基本单元可近似地按以下方法构作:先在地平面α内作菱形ABCD ,其边长为1,∠BAD =60°,再在平面α的上侧,分别以△ABD 与△CBD 为底面安装上相同的正三棱锥P -ABD 与Q -CBD ,∠APB =90°。
⑴求证:PQ ⊥BD ;⑵求二面角P -BD -Q 的大小; ⑶求点P 到平面QBD 的距离。
21. 已知正三棱柱ABC -A 1B 1C 1的侧棱长为2,底面边长为1,M 是BC 中点。
在直线CC 1上求一点N ,使MN ⊥AB 1。
(直线平面几何体)单元检测题参考答案(仅供参考)A B CP QD1 234 5 6 7 8 9 10 DCDD D DA A BA6. 如图,正方体AC 1中,M 是棱D 1D 的中点,O 是正方形ABCD 的中心,则异面直线OA 1与AM 所成的角是 A. 90 B. 60 C. 45 D. 30 8. 连B 1F ,则B 1F ∥DE ,所以∠D 1FB 为异面直线ED 与D 1F 所成的角.令正方体棱长为2,则51=F B ,51=F A ,811=D B ,∴5152855cos 1=⨯-+=∠FB D ,∴51arccos 1=∠FB D ,故选A.二.简答题答案: 11. )3,6(π12.513. )2,0,4(; 14. 43 192π15. 52三.解答题答案:16. (1)存在一条侧棱SA ⊥面ABCD.……2分 SAB ∆在 中有AD SA SAD AB SA ⊥∆⊥中有,,⊥∴SA 面ABCD.……………………4分(2)取SD 中点F ,SC 的中点G , 连AF 、FG 、EG ,.////21//21//GE AF AE FG DC AE DC FG ====⇒⇒⎪⎪⎭⎪⎪⎬⎫ .SAD CD AD CD DC SA ABCD SA 面又面又⊥⇒⎭⎬⎫⊥⊥⇒⊥ ……………………………6分⎭⎬⎫⊥⊥⇒SD AF AF CD 又∴二面角E —SC —D 的平面角为90°.………………………………………………9分(3).SEC DH SEC SCD H SC DH D 面面面于作过⊥⇒⎭⎬⎫⊥⊥∴DH 为点D 到面SEC 的距离 ∴DH ·SC=SD ·DCa aa a DH 3632=⋅=∴. MOCC1D1B1A1ABDSCD SEC SCDEG FG AF SCD AF 面面面又面⊥⇒⊥⇒⎭⎬⎫⊥⇒//……8分17. ⑴解法(一)(1)以D 为原点,DA 、DC 、DD 1所在直线分别为x 、y 、z 轴建立空间直角坐标系0-xyz ,则D (0,0,0),A (2,0,0),C (0,2,0),B (2,2,0), A 1(2,0,4),D 1(0,0,4),C 1(0,2,4),B 1(2,2,4), 设E (0,2,t ),则∵),4,0,2(),,0,2(,11--=-=⊥C B t BE C B BE,1,04041=∴=-+=⋅∴t t C B BE404),0,2,2(),4,2,2(),1,0,2(),1,2,0(11=-+=⋅∴=--=-=∴BE C A DB C A BE E 又 且,00441=++-=⋅DB C A,11BE C A DB C A ⊥⊥∴且BDE C A BE C A DB C A 平面且⊥∴⊥⊥∴111,(2)设A 1C ∩平面BDE=K , 设A 1C ∩平面BDE=K ,),4,22,22(),,22,2(),,22,2()1,2,0()0,2,2(1-+-=∴+∴+=+=⋅+⋅=n n m m K A n n m m K n n m m n m DEn DB m DK 设 0120)22(2)22(211=-+⇒=++-=⋅⇒⊥n m n m m DB K A DB K A …①同理有045404)22(211=-+⇒=-++=⋅⇒⊥n m n n m DE K A DE K A …② 由①,②联立解得),310,35,35(,32,611--=∴==K A n m,52||,365||11==∴B A K A 又易知,63052635||||sin 111===∠∴B A K A BK A 即所求角的正弦值是630解法(二)(1)证明:连AC 交BD 于点O ,由正四棱柱性质可知AA 1⊥底面ABCD ,AC⊥BD ,∴A 1C ⊥BD又∵A 1B ⊥侧面BC 1且B 1C ⊥BE , ∴A 1C ⊥BE , ∵BD ∩BE=B , ∴A 1C ⊥平面BDE(2)解:设A 1C 交平面BDE 于点K ,连BK , 则∠A 1BK 为A 1B 与平面BDE 所成的角,∵在侧面BC 1中BE ⊥B 1C ,∴△BCE ∽△B 1BC ,1,4,2,11=∴===∴CE BB BC BB BCBC CE 又 连结OE ,则OE 为平面ACC 1A 1与平面DBE 的交线,122,12,2,223,126,33OEAC K Rt ECO CO AC AB OE CO EC OE CK EC CO CK ∴=∆===∴=+=⨯⋅=⋅∴==在中又A BD CA 1B 1D 1C 1E F KyxzABDCA 1B 1D 1 C 1E FKO3653662,62121221=-=∴=++=K A AA BC AB C A63042635sin 221111=+==∠∆∴BA KA BK A BK A Rt 中在即为A 1B 与平面BDE 所成的角的正弦值.18. (1)证明:易证AD ⊥面BB 1C 1C ∴面ADC 1⊥面BB 1C 1C552)3(,510)2(arcsin19. 证明:(Ⅰ)作AD 的中点O ,则VO ⊥底面ABCD.…………………………1分 建立如图空间直角坐标系,并设正方形边长为1,…………………………2分则A (12,0,0),B (12,1,0),C (-12,1,0),D (-12,0,0),V (0,0,32), ∴13(0,1,0),(1,0,0),(,0,)22AB AD AV ===-………………………………3分由(0,1,0)(1,0,0)0AB AD AB AD ⋅=⋅=⇒⊥……………………………………4分13(0,1,0)(,0,)022AB AV AB AV ⋅=⋅-=⇒⊥……………………………………5分又AB ∩AV=A ∴AB ⊥平面V AD …………………………………………6分(Ⅱ)由(Ⅰ)得(0,1,0)AB =是面V AD 的法向量………………………………7分 设(1,,)n y z =是面VDB 的法向量,则11303(1,,)(,1,)0(1,1,)22330(1,,)(1,1,0)03x n VB y z n z n BD y z =-⎧⎧⎧⋅=⋅--=⎪⎪⎪⇒⇒⇒=-⎨⎨⎨=-⋅=⎪⎪⎪⎩⋅--=⎩⎩……9分 ∴3(0,1,0)(1,1,)213cos ,72113AB n ⋅-<>==-⨯,……………………………………11分 又由题意知,面V AD 与面VDB 所成的二面角,所以其大小为21arccos 7…………12分20. ∵P -ABD ,Q -CBD 是相同的正三棱锥,∴△这BD 与△QBD 是全等的等腰三角形, 取BD 中点E ,连结PE ,QE ,则BD ⊥PE ,BD ⊥QE ∴BD ⊥平面PQE ,从而PQ ⊥BD 。
