华东师大初中数学九年级下册397568二次函数y=ax^2+bx+c(a≠0)的图象与性质—知识讲解(基础)
初三华东师大版数学下二次函数的图象与性质知识点

初三华东师大版数学下二次函数的图象与性质
知识点
在二次函数的题中,我们经常会遇到一次函数与二次函数
相交的境况。
查字典数学网为大家整理了二次函数的图象与性质知识点,希望对大家有帮助!知识点一般地,自变量x和因变量y之间存在如下关系:函数图像y=ax^2+bx+c(a,b,c为常数,a≠0,且a决定函数的开口方向, a>0时,开口方向
向上, a0时,抛物线向上开口;当a0),对称轴在y轴左;当
a与b异号时(即ab0时,抛物线与x轴有2个交点。
Δ= b方-4ac=0时,抛物线与x轴有1个交点。
Δ= b方-4ac0时,
y=a(x-h)^2的图象可由抛物线y=ax^2向右平行移动h个单位得到,当h0,k>0时,将抛物线y=ax^2向右平行移动h个单位,再向上移动k个单位,就可以得到y=a(x-h)^2 +k的图象;当h>0,k0时,将抛物线向左平行移动|h|个单位,再向上移动k个单位可得到y=a(x-h)^2+k的图象;当h0时,开口向上,
当a0,当x ≤ -b/2a时,y随x的增大而减小;当x ≥ -
b/2a时,y随x的增大而增大.若a0,图象与x轴交于两点
A(x₁,0)和B(x₂,0),其中的x1,x2是一元二次方程
ax^2+bx+c=0(a≠0)的两根.这两点间的距离AB=|x₂-x₁|当
△=0.图象与x轴只有一个交点;当△0时,图象落在x轴的上方,x为任何实数时,都有y>0;当a0(a。
初三下数学课件(华东师大)-二次函数

自我诊断 3. 在半径为 5cm 的圆面上,挖去一个半径为 xcm 的圆面,剩下的
圆环的面积为 ycm2,则 y 与 x 的函数关系式为( D )
A.y=πx2-5
B.y=π(5-x)2
C.y=-(对于二次函数 y=-x2-3x+2,正确的是( C )
A.a=0,b=3,c=2
26.1 二次函数
二次函数的概念 一般地,形如 y=ax2+bx+c (a、b、c 是常数,a≠0)的函数叫做二次 函数,其中 x 是自变量,a、b、c 分别是函数解析式的 二次 项系数、 一次 项系数和 一次 项.
自我诊断 1. 下列函数关系中,一定为二次函数的是( C )
A.y=3x-1
B.y=ax2+bx+c
.
11.已知二次函数 y=ax2+bx-5.当 x=-1 时,y=-6;当 x=1 时,y= -2. (1)求 a、b 的值; (2)求当 x=2 时,y 的值.
解:(1)将 x=-1 时,y=-6;x=1 时,y=-2 代入二次函数解析式中得,
-6=a-b-5 -2=a+b-5
,解得ab= =12
C.y=2t2-2t+1
D.y=x2+1x
自我诊断 2. 若 y=(a-1)x2-ax+6 是关于 x 的二次函数,则 a 的取值范围
是( B ) A.a≠0
B.a≠1
C.a≠1 且 a≠0
D.无法确定
列二次函数关系式
列二次函数关系式要着眼于三个方面:(1)找准实际问题中的 等量关系 ;(2)
根据等量关系列出方程或等式;(3)将方程或等式整理成二次函数的一般式 .
解:根据二次函数的定义,可知其最高次数为 2,且二次项系数不为 0,得
m2-3m+2=2
华东师大版初三数学下册二次函数单元知识点总结

华东师大版初三数学下册二次函数单元知识点
总结
一般式y=ax2+bx+c(其中a,b,c为常数,且a 0)中含有三个待定的系数a ,b ,c.求二次函数的一般式时,必须要有三个独立的定量条件。
初中频道为大家整理了二次函数单元知识点,希望对大家有帮助!
一、二次函数
二次函数的概念:
一般地,y=ax^2+bx+c(a,b,c为常数,a 0),则称y为x的二次函数。
二次函数的结构特征:
一般地,y=ax^2+bx+c,
⑴等号左边是函数,右边是关于自变量x的二次式,x的最高次数是2.
⑵a,b,c是常数,
二、二次函数的图象与性质
一般地,自变量x和因变量y之间存在如下关系:
函数图像
y=ax^2+bx+c
(a,b,c为常数,a 0,且a决定函数的开口方向,a 0时,开口方向向上,a 0时,开口方向向下,IaI还可以决定开口大小,IaI越大开口就越小,IaI越小开口就越大.) 则称y为x的二次函数。
二次函数表达式的右边通常为二次三项式。
三、实践与探索
1、任务型教学重在沟通信息,不强调语言形式。
2、任务型教学重在解决某些问题。
3、任务型教学是老师设置的活动。
4、任务型教学重在如何完成任务。
5、任务型教学评价的标准看任务完成的情况。
二次函数单元知识点的全部内容就是这些,不知道大家是否已经都掌握了呢?预祝大家可以更好的学习,取得优异的成绩。
九年级数学下册27.2二次函数的图象与性质2.2二次函数y=ax2bxc的图象与性质第2课时课件华东师大版

4.函数 y 1 x 32的图象是由 y 1 x2 的图象向____平移____
2
2
个单位得到的,顶点坐标是_______.当x____时,函数值y随x的增
大而减小;当x____时,函数值y随x的增大而增大;当x____时,函
数取得____值,其值为______.
【解析】函数 y 1 的x 图3象2 是由
抛物线y=a(x-h)2与y=ax2的平移 【例1】已知抛物线y=a(x-h)2向左平移2个单位后,所得抛物线 为y=-2(x+5)2,试求a,h的值. 【解题探究】 (1)抛物线左右平移对a的值有影响吗?a的值为多少? 答:抛物线左右平移对a的值没有影响,a=-2.
(2)对于抛物线平移的问题可以(填“可以”或“不可以”)转化 为抛物线顶点的平移. (3)y=a(x-h)2的顶点坐标为(h,0),y=-2(x+5)2的顶点坐标为 (-5,0),将点(h,0)向左平移2个单位后为(h-2,0),所以h-2=-5, 得h=-3. (4)综上可知a=-2,h=-3.
【规范解答】 (1)函数y=6(x+4)2的顶点坐标为(-4,0),对称轴为直线x=-4; ………………………………………………………………2分 (2)向右平移3个单位后的关系式为y=6(x+1)2,顶点坐标为 (-1,0),对称轴为直线x=-1;………………………………4分 (3)因为函数y=6(x+1)2的图象开口向上,所以当x≥-1时,y随x的 增大而增大;当x≤-1时,y随x的增大而减小.……………6分
函数y=a(x-h)2的图象和性质 【例2】(6分)已知函数y=6(x+4)2, (1)直接写出它的顶点坐标及对称轴; (2)直接写出向右平移3个单位后的关系式、顶点坐标及对称 轴; (3)平移后当x取何值时,y随x的增大而增大?当x取何值时,y随x 的增大而减小? 特别提醒:左右平移时注意h值的增减变化.
九年级数学下册27.2二次函数的图象与性质2.5二次函数y=ax2bxc的图象与性质第5课时课件华东师大版

2.某广场有一喷水池,水从地面喷出,
如图,以水平地面为x轴,出水点为原
点,建立平面直角坐标系,水在空中
划出的曲线是抛物线y=-x2+4x(单位:
米)的一部分,则水喷出的最大高米 (D)1米
【解析】选A.直接根据二次函数的顶点坐标公式计算即可,最
大高度为 4ac b2 4 (1) 0 42 4.
2.实际问题中确定最值 【问题】某网店以每件60元的价格购进一批商品,若以单价80 元销售,每月可售出300件.调查表明:单价每上涨1元,该商品 每月的销售量就减少10件. (1)请写出每月销售该商品的利润y(元)与单价上涨x(元)间的函 数关系式; (2)单价定为多少元时,每月销售商品的利润最大?最大利润为 多少?
图象过点(10,300),(12,240),
即可得
10k 12k
b b
解30得0,
240,
……kb …60…300,,……………2分
∴y=-30x+600.………………………………………………3分
当x=14时,y=180;当x=16时,y=120,
即点(14,180),(16,120)均在函数y=-30x+600的图象上,
第5课时
1.求二次函数最值的方法 (1)配方法:y=ax2+bx+c化为y=a_(_x_-_h_)_2_+_k_的形式,当自变量x=_h_ 时,函数y最大(小)=_k_.如二次函数y=3x2+6x+4可化为 y=3_(_x_+_1_)_2+_1_,因为a=3_>_0,所以函数y有最_小__值,所以当 x=_-_1_时,y的最_小__值为_1_.
4.如图,在△ABC中,∠B=90°,AB=8 cm,BC=6 cm,点P从点A 开始沿AB向B以2 cm/s的速度移动,点Q从点B开始沿BC向C点以 1 cm/s的速度移动,如果P,Q分别从A,B同时出发,当△PBQ的 面积最大时,运动时间t为_____ s.
2019华东师大初中数学九年级下册二次函数y=ax__(a≠0)的图象与性质—知识讲解(基础)

二次函数y=ax2(a≠0)的图象与性质—知识讲解(基础)【学习目标】1.经历探索二次函数y=ax2和y=ax2+c的图象的作法和性质的过程,进一步获得将表格、表达式、图象三者联系起来的经验.2.会作出y=ax2和y=ax2+c的图象,并能比较它们与y=x2的异同,理解a与c对二次函数图象的影响.3.能说出y=ax2+c与y=ax2图象的开口方向、对称轴和顶点坐标.4.体会二次函数是某些实际问题的数学模型.【要点梳理】要点一、二次函数y=ax2(a≠0)的图象与性质1.二次函数y=ax2(a≠0)的图象二次函数y=ax2的图象(如图),是一条关于y轴对称的曲线,这样的曲线叫做抛物线.抛物线y=ax2(a≠0)的对称轴是y轴,它的顶点是坐标原点.当a> 0时,抛物线的开口向上,顶点是它的最低点;当a<0时,抛物线的开口向下,顶点是它的最高点.2.二次函数y=ax2(a≠0)的图象的画法——描点法描点法画图的基本步骤:列表、描点、连线.(1)列表:选择自变量取值范围内的一些适当的x的值,求出相应的y值,填入表中.(自变量x 的值写在第一行,其值从左到右,从小到大.)(2)描点:以表中每对x和y的值为坐标,在坐标平面内准确描出相应的点.一般地,点取的越多,图象就越准确.(3)连线:按照自变量的值由小到大的顺序,把所描的点用平滑的曲线连结起来.要点诠释:(1)用描点法画二次函数y=ax2(a≠0)的图象时,应在顶点的左、右两侧对称地选取自变量x的值,然后计算出对应的y值.(2)二次函数y=ax2(a≠0)的图象,是轴对称图形,对称轴是y轴.y=ax2(a≠0)是最简单的二次函数.(3)画草图时应抓住以下几点:开口方向,对称轴,顶点,与x轴的交点,与y轴的交点.3.二次函数y=ax 2(a ≠0)的图象的性质二次函数y=ax 2(a≠0)的图象的性质,见下表:要点诠释:顶点决定抛物线的位置.几个不同的二次函数,如果二次项系数a 相同,那么抛物线的开口方向、开口大小完全相同,只是顶点的位置不同. │a │相同,抛物线的开口大小、形状相同.│a │越大,开口越小,图象两边越靠近y 轴,│a │越小,开口越大,图象两边越靠近x 轴. 要点二、二次函数y=ax 2+c(a ≠0)的图象与性质 1.二次函数y=ax 2+c(a ≠0)的图象 (1)0a >(()0c c +>()0c c +<2.二次函数y=ax 2+c(a ≠0)的图象的性质关于二次函数2(0)y ax c a =+≠的性质,主要从抛物线的开口方向、顶点、对称轴、函数值的增减性以及函数的最大值或最小值等方面来研究.下面结合图象,将其性质列表归纳如下:【典型例题】类型一、二次函数y=ax 2(a ≠0)的图象与性质1.(2014秋•青海校级月考)二次函数y=ax 2与直线y=2x ﹣1的图象交于点P (1,m ) (1)求a ,m 的值;(2)写出二次函数的表达式,并指出x 取何值时该表达式y 随x 的增大而增大? (3)写出该抛物线的顶点坐标和对称轴.【思路点拨】(1)把点P (1,m )分别代入二次函数y=ax 2与直线y=2x ﹣1即可求出未知数的值;(2)把a 代入二次函数y=ax 2与即可求出二次函数表达式; 根据二次函数的对称轴及增减性判断出x 的取值. (3)根据二次函数的性质直接写出即可.【答案与解析】解:(1)点P (1,m )在y=2x ﹣1的图象上∴m=2×1﹣1=1代入y=ax 2∴a=1(2)二次函数表达式:y=x 2因为函数y=x 2的开口向上,对称轴为y 轴,当x >0时,y 随x 的增大而增大;(3)y=x 2的顶点坐标为(0,0),对称轴为y 轴.【总结升华】本题考查了用待定系数法求函数解析式的方法,及二次函数的增减性. 举一反三:【变式1】二次函数2y ax =与22y x =-的形状相同,开口大小一样,开口方向相反,则a = . 【答案】2.【变式2】(2015•山西模拟)抛物线y=﹣x 2不具有的性质是( ). A.开口向上 B. 对称轴是y 轴 C. 在对称轴的左侧,y 随x 的增大而增大 D. 最高点是原点 【答案】A.2.已知y=(m+1)x 2m m+是二次函数且其图象开口向上,求m 的值和函数解析式.【思路点拨】根据二次函数的定义以及函数y=ax 2(a≠0)的图象性质来解答. 【答案与解析】由题意,2210m m m ⎧+=⎨+⎩>,解得m=1,∴二次函数的解析式为:y=22x .【总结升华】本题中二次函数还应该有m+1≠0的限制条件,但当10m +>时,一定存在m+1≠0,所以就不再考虑了.类型二、二次函数y=ax 2+c(a ≠0)的图象与性质3.(2016•安徽模拟)在同一坐标系中,一次函数y=ax +b 与二次函数y=ax 2﹣b 的图象可能是( )A .B .C .D .【思路点拨】先由一次函数y=ax +b 图象得到字母a 、b 的正负,再与二次函数y=ax 2﹣b 的图象相比较看是否一致. 【答案与解析】解:A 、由直线y=ax +b 的图象经过第二、三、四象限可知:a <0,b <0,二次函数y=ax 2﹣b 的图象开口向上,∴a >0,A 不正确;B 、由直线y=ax +b 的图象经过第一、二、三象限可知:a >0,b >0,二次函数y=ax 2﹣b 的图象开口向下, ∴a <0,B 不正确;C 、由直线y=ax +b 的图象经过第一、二、四象限可知:a <0,b >0,二次函数y=ax 2﹣b 的图象开口向上, ∴a >0,C 不正确;D 、由直线y=ax +b 的图象经过第一、二、三象限可知:a >0,b >0,二次函数y=ax 2﹣b 的图象开口向上,顶点在y 轴负半轴,∴a >0,b >0,D 正确. 故选D .【总结升华】本题考查了一次函数的图象以及二次函数的图象,解题的关键是根据函数图象逐条分析四个选项中a 、b 的正负.本题属于基础题,难度不大,解决该题型题目时,根据一次函数的图象找出其系数的正负,再与二次函数图象进行比较即可得出结论.4.求下列抛物线的解析式: (1)与抛物线2132y x =-+形状相同,开口方向相反,顶点坐标是(0,-5)的抛物线; (2)顶点为(0,1),经过点(3,-2)并且关于y 轴对称的抛物线.【思路点拨】抛物线形状相同则||a 相同,再由开口方向可确定a 的符号,由顶点坐标可确定c 的值,从而确定抛物线的解析式2y ax c =+. 【答案与解析】(1)由于待求抛物线2132y x =-+形状相同,开口方向相反,可知二次项系数为12, 又顶点坐标是(0,-5),故常数项5k =-,所以所求抛物线为2152y x =-. (2)因为抛物线的顶点为(0,1),所以其解析式可设为21y ax =+,又∵该抛物线过点(3,-2),∴912a +=-,解得13a =-. ∴所求抛物线为2113y x =-+. 【总结升华】本题考察函数2(0)y ax c a =+≠的基本性质,并考察待定系数法求简单函数的解析式.5.在同一直角坐标系中,画出2y x =-和21y x =-+的图象,并根据图象回答下列问题.(1)抛物线21y x =-+向________平移________个单位得到抛物线2y x =-;(2)抛物线21y x =-+开口方向是________,对称轴为________,顶点坐标为________;(3)抛物线21y x =-+,当x________时,随x 的增大而减小;当x________时,函数y 有最________值,其最________值是________.【思路点拨】利用描点法画出函数图象,根据图象进行解答. 【答案与解析】函数2y x =-与21y x =-+的图象如图所示:(1)下; l ; (2)向下; y 轴; (0,1); (3)>0; =0; 大; 大 ; 1. 【总结升华】本例题把函数21y x =-+与函数2y x =-的图象放在同一直角坐标系中进行对比,易得出二次函数2(0)y ax c a =+≠与2(0)y ax a =≠的图象形状相同,只是位置上下平移的结论.2(0)y ax c a =+≠可以看作是把2(0)y ax a =≠的图象向上(0)k >或向下(0)k <平移||k 个单位得到的. 举一反三:【变式】函数23y x =可以由231y x =-怎样平移得到?【答案】向上平移1个单位.。
华师版九年级下册数学第26章二次函数第2节二次函数的图象与性质第1课时二次函数y=ax2的图象与性质

26.2 二次函数的图象与性质
26.2.1 二次函数y=ax2的 图象与性质
学习目标
1 课时讲解 二次函数y=ax2的图象的画法
二次函数y=ax2的图象与性质
2 课时流程
逐点 导讲练
课堂 小结
作业 提升
感悟新知
知识点 1 二次函数y=ax2的图象的画法
知1-讲
1. 抛物线 二次函数y=ax2的图象是一条曲线,这条曲线 叫做抛物线 y=ax2. 抛物线的顶点:抛物线是轴对称图形,抛物线与其对称 轴的交点叫做抛物线的顶点,顶点是抛物线的最低点或 最高点.
感悟新知
2. 用描点法画函数y=ax2(a ≠ 0)的图象的一般步骤
知1-讲
(1)列表:自变量 x的取值应有一定的代表性,并且所
对应的函数值不能太大也不能太小,以便于描点和全面反
映图象情况 .
(2)描点:点取得越多、越密集,画出的图象就越准确 .
(3)连线:按自变量由小到大(或由大到小)的顺序,依
感悟新知
(1)比较a,b,c,d的大小;
知2-练
解 :由抛物线的开口方向,知a>0,b>0,c<0,d<0.
由抛物线的开口大小,知|a|>|b|,|c|>|d|,
∴ a>b,c<d. ∴ a>b>d>c.
开口越大,二次项系数的绝 对值越小
感悟新知
(2)说明a与c,b与d的数量关系. 解 :∵①与③,②与④分别关于x轴对称, ∴①与③,②与④的开口大小相同,方向相反. ∴ a+c=0,b+d=0.
感悟新知
知2-练
3-1. 已知二次函数y=(2-a)xa2-14, 在其图象对称轴的左
九年级数学二次函数的概念华东师大版
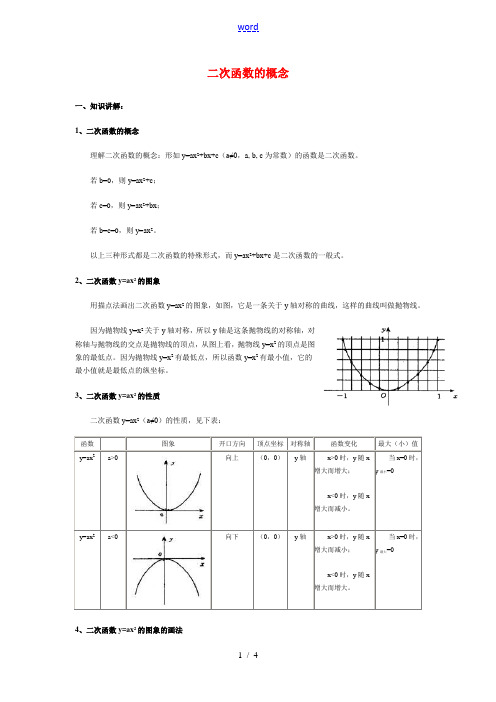
二次函数的概念一、知识讲解:1、二次函数的概念理解二次函数的概念:形如y=ax2+bx+c(a≠0,a, b, c为常数)的函数是二次函数。
若b=0,则y=ax2+c;若c=0,则y=ax2+bx;若b=c=0,则y=ax2。
以上三种形式都是二次函数的特殊形式,而y=ax2+bx+c是二次函数的一般式。
2、二次函数y=ax2的图象用描点法画出二次函数y=ax2的图象,如图,它是一条关于y轴对称的曲线,这样的曲线叫做抛物线。
因为抛物线y=x2关于y轴对称,所以y轴是这条抛物线的对称轴,对称轴与抛物线的交点是抛物线的顶点,从图上看,抛物线y=x2的顶点是图象的最低点。
因为抛物线y=x2有最低点,所以函数y=x2有最小值,它的最小值就是最低点的纵坐标。
3、二次函数y=ax2的性质二次函数y=ax2(a≠0)的性质,见下表:函数图象开口方向顶点坐标对称轴函数变化最大(小)值y=ax2a>0 向上(0,0)y轴x>0时,y随x增大而增大;x<0时,y随x增大而减小。
当x=0时,y最小=0y=ax2a<0 向下(0,0)y轴x>0时,y随x增大而减小;x<0时,y随x增大而增大。
当x=0时,y最大=04、二次函数y=ax2的图象的画法用描点法画二次函数y=ax2的图象时,应在顶点的左、右两侧对称地选取自变量x的值,然后计算出对应的y值,这样的对应值选取越密集,描出的图象越准确。
[例题分析]例1、(1) 若是二次函数,求m的值。
(2)已知函数的图象是开口向下的抛物线,求m的值。
(1)分析:根据二次函数的定义,只要满足m2+m≠0且m2-m=2,就是二次函数。
解:故若是二次函数,则m的值等于2。
(2)分析:抛物线开口向下,二次项系数小于零。
解:∵函数的图象是开口向下的抛物线,∴此函数是二次函数,∴∴m=-2.例2、函数y=ax2(a≠0)与直线y=2x-3交于点(1,b),求(1)a和b的值;(2)求抛物线y=ax2的解析式,并求顶点坐标和对称轴;(3)x取何值时,二次函数y=ax2中的y随着x的增大而增大;(4)求抛物线与直线y=-2的两交点及顶点所构成的三角形的面积。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二次函数y=ax 2+bx+c(a ≠0)的图象与性质—知识讲解(基础)【学习目标】1. 会用描点法画二次函数2(0)y ax bx c a =++≠的图象;会用配方法将二次函数2y ax bx c =++的解析式写成2()y a x h k =-+的形式;2.通过图象能熟练地掌握二次函数2y ax bx c =++的性质;3.经历探索2y ax bx c =++与2()y a x h k =-+的图象及性质紧密联系的过程,能运用二次函数的图象和性质解决简单的实际问题,深刻理解数学建模思想以及数形结合的思想.【要点梳理】要点一、二次函数2(0)y ax bx c a =++≠与=-+≠2()(0)y a x h k a 之间的相互关系 1.顶点式化成一般式从函数解析式2()y a x h k =-+我们可以直接得到抛物线的顶点(h ,k),所以我们称2()y a x h k =-+为顶点式,将顶点式2()y a x h k =-+去括号,合并同类项就可化成一般式2y ax bx c =++.2.一般式化成顶点式2222222b b b b y ax bx c a x x c a x x c a a a a ⎡⎤⎛⎫⎛⎫⎛⎫=++=++=++-+⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦22424b ac b a x a a -⎛⎫=++⎪⎝⎭. 对照2()y a x h k =-+,可知2bh a=-,244ac b k a -=.∴ 抛物线2y ax bx c =++的对称轴是直线2b x a =-,顶点坐标是24,24b ac b a a ⎛⎫-- ⎪⎝⎭.要点诠释:1.抛物线2y ax bx c =++的对称轴是直线2bx a =-,顶点坐标是24,24b ac b a a ⎛⎫-- ⎪⎝⎭,可以当作公式加以记忆和运用.2.求抛物线2y ax bx c =++的对称轴和顶点坐标通常用三种方法:配方法、公式法、代入法,这三种方法都有各自的优缺点,应根据实际灵活选择和运用. 要点二、二次函数2(0)y ax bx c a =++≠的图象的画法1.一般方法:列表、描点、连线;2.简易画法:五点定形法. 其步骤为:(1)先根据函数解析式,求出顶点坐标和对称轴,在直角坐标系中描出顶点M ,并用虚线画出对称轴. (2)求抛物线2y ax bx c =++与坐标轴的交点,当抛物线与x 轴有两个交点时,描出这两个交点A 、B 及抛物线与y 轴的交点C ,再找到点C 关于对称轴的对称点D ,将A 、B 、C 、D 及M 这五个点按从左到右的顺序用平滑曲线连结起来. 要点诠释:当抛物线与x 轴只有一个交点或无交点时,描出抛物线与y 轴的交点C 及对称点D ,由C 、M 、D 三点可粗略地画出二次函数图象的草图;如果需要画出比较精确的图象,可再描出一对对称点A 、B ,然后顺次用平滑曲线连结五点,画出二次函数的图象, 要点三、二次函数2(0)y ax bx c a =++≠的图象与性质 1.二次函数20()y ax bx c a =++≠图象与性质2.二次函数20()y ax bx c a =++≠图象的特征与a 、b 、c 及b 2-4ac 的符号之间的关系要点四、求二次函数2(0)y ax bx c a =++≠的最大(小)值的方法如果自变量的取值范围是全体实数,那么函数在顶点处取得最大(或最小)值,即当2bx a=-时,244ac b y a-=最值.要点诠释:如果自变量的取值范围是x 1≤x ≤x 2,那么首先要看2ba-是否在自变量的取值范围x 1≤x ≤x 2内,若在此范围内,则当2bx a=-时,244ac b y a -=最值,若不在此范围内,则需要考虑函数在x 1≤x ≤x 2范围内的增减性,如果在此范围内,y 随x 的增大而增大,则当x =x 2时,222y ax bx c =++最大值;当x =x 1时,211y ax bx c =++最小值,如果在此范围内,y 随x 的增大而减小,则当x =x 1时,211=ax +bx +y c 最大值;当x =x 2时,222=ax +bx +y c 最小值,如果在此范围内,y 值有增有减,则需考察x =x 1,x =x 2,2b x a=-时y 值的情况.【典型例题】类型一、二次函数2(0)y ax bx c a =++≠的图象与性质1.求抛物线2142y x x =-+-的对称轴和顶点坐标. 【答案与解析】解法1(配方法):2221114(2)4(211)4222y x x x x x x =-+-=---=--+-- 211(1)422x =--+-217(1)22x =---.∴ 顶点坐标为71,2⎛⎫- ⎪⎝⎭,对称轴为直线1x =.解法2(公式法):∵ 12a =-,1b =,4c =-,∴ 11122()2b x a=-=-=⨯-,2214(4)147214242ac b a ⎛⎫⨯-⨯-- ⎪-⎝⎭==-⎛⎫⨯- ⎪⎝⎭.∴ 顶点坐标为71,2⎛⎫- ⎪⎝⎭,对称轴为直线1x =.解法3(代入法):∵ 12a =-,1b =,4c =-, ∴ 111222b x a =-=-=⎛⎫⨯- ⎪⎝⎭. 将1x =代入解析式中得,21711422y =-⨯+-=-.∴ 顶点坐标为71,2⎛⎫- ⎪⎝⎭,对称轴为直线1x =.【总结升华】所给二次函数关系是一般式,求此类抛物线的顶点有三种方法:(1)利用配方法将一般式化成顶点式;(2)用顶点公式24,24b ac b aa ⎛⎫-- ⎪⎝⎭直接代入求解;(3)利用公式先求顶点的横坐标,然后代入解析式求出纵坐标.这三种方法都有各自的优缺点,应根据实际灵活选择和运用.举一反三:【高清课程名称:二次函数2(0)y ax bx c a =++≠的图象与性质 高清ID 号: 392790 关联的位置名称(播放点名称):例题1】 【变式】把一般式2286y x x =-+-化为顶点式.(1)写出其开口方向、对称轴和顶点D 的坐标;(2)分别求出它与y 轴的交点C ,与x 轴的交点A 、B 的坐标. 【答案】(1)向下;x=2;D (2,2). (2)C (0,-6);A (1,0);B (3,0).2.(2016•泰安)二次函数y=ax 2+bx+c 的图象如图所示,那么一次函数y=ax+b 的图象大致是( )A .B .C .D .【思路点拨】由y=ax 2+bx+c 的图象判断出a >0,b >0,于是得到一次函数y=ax+b 的图象经过一,二,四象限,即可得到结论. 【答案】A .【解析】解:∵y=ax 2+bx+c 的图象的开口向上, ∴a >0,∵对称轴在y 轴的左侧, ∴b >0,∴一次函数y=ax+b 的图象经过一,二,三象限. 故选A .【总结升华】本题考查了二次函数和一次函数的图象,解题的关键是明确二次函数的性质,由函数图象可以判断a 、b 的取值范围.类型二、二次函数2(0)y ax bx c a =++≠的最值3.求二次函数211322y x x =++的最小值. 【答案与解析】解法1(配方法):∵ 2221111(6)(639)2222y x x x x =++=++-+ 21(3)42x =+-,∴ 当x =-3时,4y =-最小.解法2(公式法):∵ 102a =>,b =3,12c = ∴ 当331222b x a =-=-=-⨯时,22114341922414242ac b y a ⨯⨯---====-⨯最小.解法3(判别式法):∵ 211322y x x =++,∴ 26(12)0x x y ++-=.∵ x 是实数,∴ △=62-4(1-2y)≥0,∴ y ≥-4.∴ y 有最小值-4,此时2690x x ++=,即x =-3.【总结升华】在求二次函数最值时,可以从配方法、公式法、判别式法三个角度考虑,根据个人熟练程度灵活去选择.举一反三:【高清课程名称:二次函数2(0)y ax bx c a =++≠的图象与性质 高清ID 号: 392790 关联的位置名称(播放点名称):例题2】【变式】用总长60m 的篱笆围成矩形场地.矩形面积S 随矩形一边长L 的变化而变化.当L 是多少时,矩形场地的面积S 最大?【答案】(30)S L L =-2(30)L L =-- 2(15)225L =--+(0<L <30).15L ∴=(m )时,场地的面积S 最大,为225m 2.类型三、二次函数2(0)y ax bx c a =++≠性质的综合应用4.已知二次函数21y x bx c =+++的图象过点P(2,1). (1)求证:24c b =--; (2)求bc 的最大值. 【答案与解析】(1)∵ 21y x bx c =+++的图象过点P(2,1),∴ 1=4+2b+c+1,∴ c=-2b-4.(2)22(24)2(2)2(1)2bc b b b b b =--=-+=-++.∴ 当1b =-时,bc 有最大值.最大值为2.【总结升华】(1)将点P(2,1)代入函数关系式,建立b 、c 的关系即可.(2)利用(1)中b 与c 的关系,用b 表示bc ,利用函数性质求解.举一反三:【变式】(2015•咸宁)如图是二次函数y=ax 2+bx+c 的图象,下列结论: ①二次三项式ax 2+bx+c 的最大值为4; ②4a+2b+c<0;③一元二次方程ax 2+bx+c=1的两根之和为﹣1; ④使y≤3成立的x 的取值范围是x≥0. 其中正确的个数有( )A. 1个B.2个C.3个D.4个 【答案】B.提示:∵抛物线的顶点坐标为(﹣1,4),∴二次三项式ax 2+bx+c 的最大值为4,①正确;∵x=2时,y <0,∴4a+2b+c<0,②正确;根据抛物线的对称性可知,一元二次方程ax 2+bx+c=1的两根之和为﹣2,③错误; 使y≤3成立的x 的取值范围是x≥0或x≤﹣2,④错误, 故选:B .。
