初二几何证明题1
初二几何证明题

初二上证明题011.如图,DE ∥BC ,∠D +∠B =180°.求证:AB ∥CD . 2. 3. 4. 5.6.如图,AB ∥CD ,GH 分别与AB 、CD 相交于点E 、F ,EM 平分∠AEG ,FN 平分∠CFG . 求证:EM ∥FN .7.如图,OB =BC ,OC 平分∠AOB .求证:AO ∥BC . 8. 9. 10. 11. 12. 13.14.B 如图,AB ∥CD ,∠A +∠E =∠AME .求证:AB ∥EF .15.B 如图,E 为AC 上的一点,∠1=∠B ,∠2=∠D ,BE ⊥DE .求证:AB∥CD .16.B 已知:在图中,∠A =∠F ,∠C =∠D =65°试求∠CBD 和∠CED 的度数.初二上几何证明00217.B 如图:已知在四边形ABCD 中,AD ∥BC ,AB ∥CD ,∠B 是∠A 的5倍。
BCD EAHGCDEA BNM F ABCO求∠C 和∠D 的度数.18.B 如图:已知AB ∥CD ,问∠B +∠E +∠D 等于多少度?19.B 如图,AB ∥CD ,∠B =130°,∠BPC =65°.试求∠C 的度数. 20.B 如图,已知AB ∥CD ∥EF ,且∠ABC =50°,∠CEF =150°,求∠BCE 的度数.21.B 如图,AB ∥EF ,AB ⊥AC ,AB ⊥BD ,∠E =∠F =120°,求∠DBF 与∠CAE的度数.22.B 如图,∠ABC 、∠ACB 的平分线交于点O ,DE 过点O ,且DE ∥BC ,求证:DE=BD+CE . 初二上几何证明题00323.B 如图:已知在四边形ABCD 中,AD ∥BC ,AB ∥CD ,∠B 是∠A 的5倍。
求∠C 和∠D 的度数.24.B 如图:已知AB ∥CD ,问∠B +∠E +∠D 等于多少度?25.B 如图,AB ∥CD ,∠B =130°,∠BPC =65°.试求∠C 的度数. 26.B 如图,已知AB ∥CD ∥EF ,且∠ABC =50°,∠CEF =150°,求∠BCE 的度数.27.B 如图,AB ∥EF ,AB ⊥AC ,AB ⊥BD ,∠E =∠F =120°,求∠DBF 与∠CAE的度数.28.B 如图,∠ABC 、∠ACB 的平分线交于点O ,DE 过点O ,且DE ∥BC ,求证:DE=BD+CE . 初二上几何证明题00429.C 如图,BD 是△ABC 的一条角平分线,AE ∥BD ,交CB 的延长线于点E ,F为AE 的中点.OE D A BCED C BAA B CDP FED C B A OE D A BCED C BAA B CDP求证:BD ⊥BF .30.C 如图,在四边形ABCD 中,AB =AD ,BC =DC .求证:AC 垂直平分BD .31. 32. 33. 34. 35.36.C 如图,已知AE ∥BF ,AE =BF ,AC =BD .你能判断ED 与CF 相等吗?请说明你的理由.37. 38. 39. 40.41.C 如图,AB =CD ,AE =FD ,BF =EC .求证:AF =ED . 42. 43.44. 45. 46. 47. 48.49.C 如图,PA =PB ,PC 是△PAB 的中线,∠A =55°,求:∠B 的度数. 50.AC PA BCD EFAB C DFEAB CD51.C 如图:在△ABC 中,AD =AE ,点D 、E 在BC 上,CE =BD ,写出AB =AC 的说理过程. 52. 53. 54. 55. 56.初二上几何证明题00557.如图,∠1=∠2,∠3=∠4,求证:(1)△ADE ≌△ABE ;(2)∠DCA =∠BCA . 58.59. 60. 61. 62. 63.64.如图,∠1=∠2,∠3=∠4.求证:EA 平分∠DEC . 65.如图:已知△ABC 是等腰三角形,AB =AC ,BD ⊥AC 于点D ,CE ⊥AB 于点E ,求证:BD =CE .66.如图,在等腰△ABC 中,两条腰上的高BD 和CE 相交于O ,求证:△BOC是等腰三角形.67.如图在△ABC 中,AB =AC ,BD 、CE 分别平分∠ABC 和∠ACB ,写出△ABD ≌△ACE 的理由. 68.DEB CA4321ED CBAEOABCDEABCDBD CE A O 34ABCDE 1269. 70. 71.72.如图,在△ABC 中,BE =CD ,∠1=∠2.求证:AB =AC . 初二上几何证明题00673.C 如图,在△ABC 中,BF 、CE 相交于点O ,AE =AF ,AO 平分∠BAC .求证:AB =AC . 74.75. 76. 77. 78.79.C 如图,AD =AE ,∠D =∠E ,∠1=∠2,BE 、CD 相交于点O .求证:OB=OC . 80. 81. 82. 83. 84.85.C 如图,AC 、BD 相交于点O ,AB=CD ,∠BAD=∠ADC ,求证:△ABO ≌△DCO .86.C 如图,B 、C 是线段AD 上的两点,AB =CD ,∠A =∠D ,AE =DF .87.求证:⑴∠E =∠F ;⑵OB =OC .21AB CDEODC B AA B C DEFOA B C FOEA B CDOE12H E A 88.C 如图:已知AD =BC ,AC =BD ,求证:∠1=∠2.89.C 如图:已知AC 、BD 的交点O 平分AC 、BD ,过点O 引直线EF 交AB 、DC 于点E 、F , 90.求证:OE=OF . 91. 92. 93.初二上几何证明题00794.如图,已知AB =AC ,D 是AB 上一点,DE ⊥BC 于E ,ED 的延长线交CA 的延长线于F ,求证:△ADF 是等腰三角形.95.C 已知:如图DC ⊥CA ,EA ⊥CA ,CD =AB ,CB =AE ,说明BD ⊥BE 的理由.96.C 已知:如图,在△ABC 中,∠ABC =45°,AD ⊥BC ,BE ⊥AC .求证:BH =AC .97. 98. 99.100.C 如图,△ABC 的两条高AD 、BE 相交于H ,且AD =BD .试说明下列结论成立的理由.⑴∠DBH =∠DAC ;⑵△BDH ≌△ADC .101.C 已知,如图,△ABC 的两条高BD 和CE 相交于F ,CF=AB ,求证:DB=DC .102.C 如图,在△ABC 中,AB =AC ,∠BAC =90°,BD 平分∠ABC 交AC 于点OF E DCB A ABCDE H FAD BE CD ,CE ⊥BD 交BD 延长线于点E .求证:BD =2CE .初二上几何证明题008103.C 已知:如图,在△ABC 中,BE 、CF 分别是边AC 、AB 上的高,BP=AC ,CQ=AB ,求证:AP=AQ . 104.C 如图,已知∠BDA =∠CEA ,CE 与BD 交于点P ,PB=PC ,求证:AB=AC . 105.106.C 如图,在△ABC 中,AB =AC ,BD 与CE 相交于点O ,BO =CO .求证:∠B =∠C .107.如图,已知:E 是∠AOB 的平分线上一点,EC ⊥OB ,ED ⊥OA ,C 、D 是垂足,连接CD ,108.求证:⑴OD =OC ;⑵∠ECD =∠EDC ;⑶OE 是CD 的中垂线.109.C 如图,在∠MON 的两边分别截取OA=OB ,OC=OD ,如果连结AD 、BC 相交于点P ;110.求证:OP 平分∠MON .111.C 如图:已知,AB=AD ,∠ABC =∠ADC ,求证:△ABC ≌△ADC . 112. 113.114.初二上几何证明题009115.C 如图,已知AB =AC ,DB =DC .说明∠B =∠C 的理由.116. 117.118.C 如图,在四边形ABCD 中,AB =CD ,AD =BC .求证:∠B =∠D .PEDCB AP ONMCDBAQF ABCPEDC BAAB CD119.C 如图,在△ABC 中,∠C =90°,AC =BC ,D 为AB 上一点,AD =AC ,ED ⊥AB 于点D ,120.求证:BD =DE =CE .121.C 如图,在△ABC 中,∠BAC =90°,AB =AC ,D 为BC 的中点,DE ⊥DF ,E 、F 分别在AB 、AC 上,求证:DE =DF .122.123.C 如图,在△ABC 中,∠ACB =90°,AC =BC ,AE ⊥BE 于点E ,AE =12BD .求证:BD 平分∠ABC . 124.125.C 如上图,在上题其他条件不变的情况下,即在△ABC 中,∠ACB =90°,AC =BC ,AE ⊥BE 于点E ,能否由条件“BD 平分∠ABC ”得到结论“AE =12BD ”? 126. 127.初二上几何证明题010128.C 如图,在△ABC 中,AB =2AC ,AD 平分∠BAC ,AD =BD .求证:CD ⊥AC . 129. 130. 131.132.C 如图,已知D 为等边△ABC 内一点,P 为等边△ABC 外一点,BD =DA ,BP =AB ,∠DBP =∠DBC .求证:∠P =30°.ABCDEFAB CD E A BCABCDP133.C 如图:AD ∥BC ,∠1=∠2,∠3=∠4,直线DC 过点E 交AD 于点D ,交BC 于点C ,134.求证:AD +BC =AB .135.C 如图,点E 在△ABC 外部,点D 在BC 边上,DE 交AC 于点F ,若∠1=∠2=∠3,AC =AE ,试说明,△ABC ≌△ADE 的理由. 136.C 如图,△ABC 是等边三角形,点D 、E 分别在AC 、AB 上,且AD =BE .求证:∠A =∠1.137.C 如图,△ABC 是等边三角形,D 是AC 上的一点,∠1=∠2,BD =CE .求证:△ADE 是等边三角形初二上几何证明题011138.C 如图,已知△ABC 和△ADE 都是等边三角形,点B 、C 、D 在一直线上,试说明: 139.(1)∠ECD =60°;(2)CE =AC +DC . 140.141.C 如图所示,在等边三角形ABC 的边BC 上任取一点D ,以CD 为边向外作等边三角形CDE ,连结AD 、BE .求∠BAD +∠CBE 的度数(要有说理的过程). 142. 143. 144.145.如图,C 为AB 上的一点,△ACD 和△BCE 都是等边三角形,AE 交DC 于点M ,BD 交EC 于点N . 求证:⑴AE =BD ;⑵CM =CN .123AB CD F EAB CD EABCD E146.C 如图,已知C 是线段AB 上一点,分别以AC 、BC 为边在AB 同侧作等边△ACD 和等边△BCE ,AE 交CD 于点G ,BD 交CE 于点H .求证:GH ∥AB .147. 148. 149.150.C 如图,在四边形ABCD 中,AD ∥BC ,E 是CD 边上的一点,AE 平分∠BAD ,BE 平分∠ABC .151.求证:DE =EC .152.C 如上图,在四边形ABCD 中,AD ∥BC ,E 是CD 的中点,AD +BC =AB . 153.求证:(1)BE 平分∠ABC ;(2)AE ⊥BE . 154. 155.初二上几何证明题012156.D 如图,已知△ABC 中,AB=AC ,D 是AC 上一点,E 是AB 延长线上一点,CD=BE ,连结DE 交BC 于点P ,求证:DP=EP .157.D 如图,在△ABC 中,点D 在AB 边上,点E 在AC 边的延长线上,CE =BD ,DG =GE .158.求证:AB =AC .159. 160.161.D 如图:在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于点F ,求证:AF=EF .CB DAEHG EDCBAFEC BADABGD EC162.163.D 如图,在△ABC 中,M 为BC 的中点,过点M 作∠BAC 的平分线AD 的平行线交AB 于点E ,交CA 的延长线于点F .求证:BE =CF .164.D 如图:已知EC 与AD 相交于点B ,∠AEC =∠A +∠C ,EB =BC .求证:AB =BD+DC .165.C 如图:在△ABC 中,AD ⊥BC 于点D ,∠B =2∠C ,求证:AB +BD =DC . 初二几何证明题013166.C 如图,在△ABC 中,AD ⊥BC 于点D ,AB +BD =DC .求证:∠B =2∠C .167.C 如图:已知AP 是∠BAC 的平分线,AB +BP =AC ,求证:∠B =2∠C . 168. 169. 170. 171.172.C 如图,已知在△ABC 中,∠A =2∠B ,CD 平分∠ACB ,试猜想BC 、AD 、AC 三线段之间有着怎样的数量关系,并加以证明. 173.174. 175. 176.177.C 如图,在△ABC 中,BE =CE ,AD =2AE ,AC 平分∠EAD .求证:CD =AB . 178.D CB AABCDADBE C179.C 如图,在△ABC 中,BC =2AB ,AD 为BC 边上的中线,AE 为△ABD 的中线.求证:AC =2AE . 180.181.D 如图,在△ABC 中,AB =AC ,D 是CB 延长线上的一点,∠D =60°,E是AD 上的一点,DE =DB . 求证:AE =BE +BC .初二上几何证明题014182.C 如图,已知点D 在∠BAC 内,求证:∠BDC =∠BAC +∠B +∠C . 183. 184. 185. 186. 187.188.D 如图,AD 平分∠BAC ,CD ⊥AD ,D 为垂足,AB >AC ,求证:∠2=∠1+∠B .189.C 如图,在△ABC 中,BC =10,D 是BC 上的一点,且BD =4,求ABD S V ∶A DC S V 的值.190.C 如图:点D 是△ABC 的边BC 上的一点,且23BD DC ∶∶,若ABD S V =8㎝2,求:△ADC 的面积.ABCDE ABECDDCB A 2A B CD 1DC B ADCBA191.C 如图,点D 是△ABC 的边BC 的中点,点E 是AD 的中点,当△ABE 的面积是4㎝2时,192.求:(1)△ABD 的面积,(2)△ABC 的面积. 193. 194.D 如图,△ABC 是等腰三角形,AB=AC ,把△ABC 绕着点B 旋转后得△A ′BC ′,若旋转角的度数正好是底角度数的一半,且C ′在腰AC 上,AC ′=BC ′,求证:△A ′MB 是等腰三角形.195. 196.初二上几何证明题015197.D 如图所示:∠ABC 的平分线BF 与△ABC 中∠ACB 的相邻外角的平分线CF 相交于点F ,过F 作DF ∥BC ,交AB 于D ,交AC 于E ,则:(1)图中有几个等腰三角形?为什么?(2)BD 、CE 、DE 之间存在着什么关系?请说明理由. 198.如图,在△ABC 中,BP 平分∠ABC ,CP 是△ABC 的外角平分线,求证:2∠P =∠A .199.C 如图所示,在△ABC 中,∠A =α,△ABC 的内角平分线或外角平分线交于点P ,且∠P =β,试探求下各图中α与β的关系,并对图(2)(3)加以说明.ABC DE MC 'A'CB A ABFDECAB C DPABC EF(2)(1)ABCE(3)PABCP200.C 我们知道:平面图形的运动有________、_______、_______等三种形式;如图:△ABD 和△BCE 都是等边三角形,试用运动的思想说明AE 等于DC ,且它们的夹角为60°. 201.202.D 如图中的①,AB ⊥BD ,ED ⊥BD ,C 为BD 上的一点,AB =CD ,BC =DE . (1)求证:AC ⊥CE .(2)若将CD 沿CB 方向平移得到图②、③、④、⑤的情形,其余条件不变,结论AC ⊥CE 还成立吗?请说明理由.初二上几何证明题016203.D 已知,在△ABC 中,AB =AC .(本题9分) (1)如图⑴,如果∠BAD =40°,AD 是△ABC 的中线,AD =AE ,则∠EDC = ;(2)如图⑵,如果∠BAD =70°,AD 是△ABC 的中线,AD =AE ,则∠EDC = ;(3)思考,通过以上两题,你发现∠BAD 与∠EDC 数量之间有什么关系?请用式子表示 ;(4)如图⑶,如果AD 不是△ABC 的中线,AD =AE ,是否仍有上述关系?请说OGFECDBAB(C')C'ACDE ABCDE E D CBA③②①CC'C'AB D EAB C D E⑤④ABCDEAB CD EAB CD E明理由. (5) (6) (7) (8) (9)(10)(1)(2)(3)204.D 如图(1),已知∠BAC =90°,AB=AC ,AE 是过点A 的一条直线,且B 、C 在AE 的异侧,BD ⊥AE 于点D ,CE ⊥AE 于点E ,205.求证:(1)BD=DE +CE ;206.(2)若直线AE 绕点A 旋转到图(2)位置时,其余条件不变,问BD 与DE 、CE 的关系如何?请予以证明;207.(3)若直线AE 绕点A 旋转到图(3)位置时,其余条件不变,则BD 与DE 、CE 的关系如何?请予以证明.208. 209. 210. 211. 212. 213.214.(1)(2)(3)215.D 如图,已知点C 是AB 上一点,△ACM 、△CBN 都是等边三角形. (1)说明AN =MB ;AB CDEADECBACDE B(2)将△ACM 绕点C 按逆时针旋转180°,使A 点落在CB 上,请对照原题图在备用图上画出符合要求的图形;(3)在(2)所得到的图形中,结论“AN =BM ”是否成立?若成立,请说明理由;若不成立,也请说明理由;(4)在(2)所得到的图形中,设MA 的延长线与BN 相交于点D ,请你判断△ABD 的形状,并说明你的理由.(5)(6) (7) (8) (9)NMCBAA BC MN。
初中数学几何证明经典试题(含答案)【范本模板】
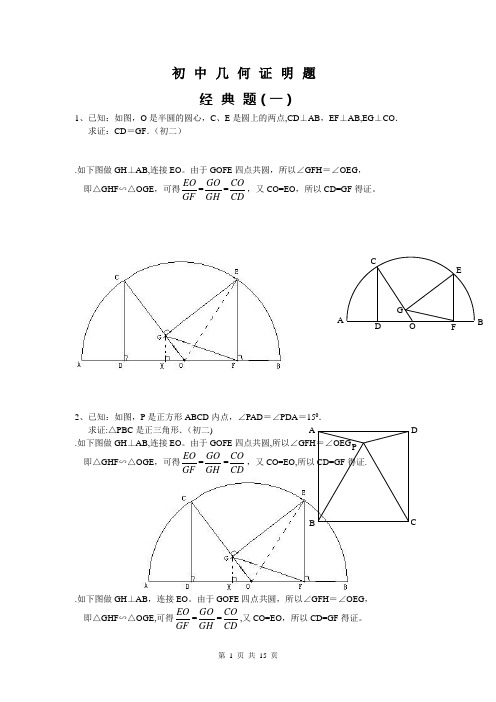
初中几何证明题经典题(一)1、已知:如图,O是半圆的圆心,C、E是圆上的两点,CD⊥AB,EF⊥AB,EG⊥CO.求证:CD=GF.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE ,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
2、已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=150.求证:△PBC是正三角形.(初二).如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证..如下图做GH⊥AB,连接EO。
由于GOFE四点共圆,所以∠GFH=∠OEG,即△GHF∽△OGE,可得EOGF=GOGH=COCD,又CO=EO,所以CD=GF得证。
APCDBAFGCEBOD3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)D 2 C 2B 2 A 2D 1 C 1 B 1 C B DA A 1 A N FE CDMB · A HEOF2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 引圆的两条直线,交圆于B 、C 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .求证:CE =CF .(初二)2、如图,四边形ABCD 为正方形,DE ∥AC ,且CE =CA ,直线EC 交DA 延长线于F .求证:AE =AF .(初二)3、设P 是正方形ABCD 一边求证:PA =PF .(初二)4、如图,PC 切圆O 于C ,AC 为圆的直径,PEFB 、D .求证:AB =DC ,BC =AD.(初三)经典 1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC 求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD .(初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P,且 AE =CF .求证:∠DPA =∠DPC .(初二)经典难题(五)1、 设P 是边长为1的正△ABC 内任一点,L =PA +PB +PC ,求证:≤L <2.2、已知:P 是边长为1的正方形ABCD 内的一点,求PA +PB +PC 的最小值.3、P 为正方形ABCD 内的一点,并且PA =a ,PB =2a ,PC =3a ,求正方形的边长.C BD A F PD E CB A APCBACPDA CBPD4、如图,△ABC中,∠ABC=∠ACB=800,D、E分别是AB、AC上的点,∠DCA=300,∠EBA=200,求∠BED的度数.经典题(一)1.如下图做GH⊥AB,连接EO。
初二数学压轴几何证明题(含答案)

1.四边形ABCD是正方形,△BEF是等腰直角三角形,∠BEF=90°,BE=EF,连接DF,G 为DF的中点,连接EG,CG,EC.ﻫ(1)如图1,若点E在CB边的延长线上,直接写出EG与GC 的位置关系及的值;ﻫ(2)将图1中的△BEF绕点B顺时针旋转至图2所示位置,请问(1)中所得的结论是否仍然成立?若成立,请写出证明过程;若不成立,请说明理由;(3)将图1中的△BEF绕点B顺时针旋转α(0°<α<90°),若BE=1,AB=,当E,F,D三点共线时,求DF的长及tan∠ABF的值.解:(1)EG⊥CG,=,ﻫ理由是:过G作GH⊥EC于H,ﻫ∵∠FEB=∠DCB=90°,∴EF∥GH∥DC,ﻫ∵G为DF中点,ﻫ∴H为EC中点,ﻫ∴EG=GC,GH=(EF+DC)=(EB+BC),ﻫ即GH=EH=HC,ﻫ∴∠EGC=90°,即△EGC是等腰直角三角形,∴=;ﻫ(2)ﻫ解:结论还成立,ﻫ理由是:如图2,延长EG到H,使EG=GH,连接CH、EC,过E作BC的垂线EM,延长CD,∵在△EFG和△HDG中ﻫ∴△EFG≌△HDG(SAS),∴DH=EF=BE,∠FEG=∠DHG,∴EF∥DH,ﻫ∴∠1=∠2=90°-∠3=∠4,ﻫ∴∠EBC=180°-∠4=180°-∠1=∠HDC,在△EBC和△HDC中ﻫ∴△EBC≌△HDC.ﻫ∴CE=CH,∠BCE=∠DCH,∴∠ECH=∠DCH+∠ECD=∠BCE+∠ECD=∠BCD=90°,∴△ECH是等腰直角三角形,ﻫ∵G为EH的中点,ﻫ∴EG⊥GC,=,ﻫ即(1)中的结论仍然成立;ﻫﻫ(3)ﻫ解:连接BD,∵AB=,正方形ABCD,ﻫ∴BD=2,ﻫ∴cos∠DBE==,∴∠DBE=60°,ﻫ∴∠ABE=∠DBE-∠ABD=15°,ﻫ∴∠ABF=45°-15°=30°,∴tan∠ABF=,∴DE=BE=,∴DF=DE-EF=-1.解析: (1)过G作GH⊥EC于H,推出EF∥GH∥DC,求出H为EC中点,根据梯形的中位线求出EG=GC,GH=(EF+DC)=(EB+BC),推出GH=EH=BC,根据直角三角形的判定推出△EGC是等腰直角三角形即可;ﻫ(2)延长EG到H,使EG=GH,连接CH、EC,过E作BC的垂线EM,延长CD,证△EFG≌△HDG,推出DH=EF=BE,∠FEG=∠DHG,求出∠EBC=∠HDC,证出△EBC≌△HDC,推出CE=CH,∠BCE=∠DCH,求出△ECH是等腰直角三角形,即可得出答案;3(ﻫ)连接BD,求出cos∠DBE==,推出∠DBE=60°,求出∠ABF=30°,解直角三角形求出即可.2.已知正方形ABCD和等腰直角三角形BEF,BE=EF,∠BEF=90°,按图1放置,使点E在BC上,取DF的中点G,连接EG,CG.(1)延长EG交DC于H,试说明:DH=BE.ﻫ(2)将图1中△BEF绕B点逆时针旋转45°,连接DF,取DF中点G(如图2),莎莎同学发现:EG=CG且EG⊥CG.在设法证明时他发现:若连接BD,则D,E,B三点共线.你能写出结论“EG=CG且EG⊥CG”的完整理由吗?请写出来.ﻫ(3)将图1中△BEF绕B点转动任意角度α(0<α<90°),再连接DF,取DF的中点G(如图3),第2问中的结论是否成立?若成立,试说明你的结论;若不成立,也请说明理由.(1)证明:∵∠BEF=90°,∴EF∥DH,ﻫ∴∠EFG=∠GDH,ﻫ而∠EGF=∠DGH,GF=GD,ﻫ∴△GEF≌△GHD,ﻫ∴EF=DH,而BE=EF,ﻫ∴DH=BE;ﻫ(2)连接DB,如图,ﻫ∵△BEF为等腰直角三角形,∴∠EBF=45°,ﻫ而四边形ABCD为正方形,∴∠DBC=45°,ﻫ∴D,E,B三点共线.ﻫ而∠BEF=90°,∴△FED为直角三角形,ﻫ而G为DF的中点,∴EG=GD=GC,∴∠EGC=2∠EDC=90°,∴EG=CG且EG⊥CG;ﻫﻫ(3)第2问中的结论成立.理由如下:连接AC、BD相交于点O,取BF的中点M,连接OG、EM、MG,如图,ﻫ∵G为DF的中点,O为BD的中点,M为BF的中点,ﻫ∴OG∥BF,GM∥OB,ﻫ∴四边形OGMB为平行四边形,∴OG=BM,GM=OB,而EM=BM,OC=OB,∴EM=OG,MG=OC,∵∠DOG=∠GMF,而∠DOC=∠EMF=90°,∴∠EMG=∠GOC,ﻫ∴△MEG≌△OGC,∴EG=CG,∠EGM=∠OCG,ﻫ又∵∠MGF=∠BDF,∠FGC=∠GDC+∠GCD,∴∠EGC=∠EGM+∠MGF+∠FGC=∠BDF+∠GDC+∠GCD+∠OCG=45°+45°=90°,ﻫ∴EG=CG且EG⊥CG.解析:(1)由∠BEF=90°,得到EF∥DH,而GF=GD,易证得△GEF≌△GHD,得EF=DH,而BE=EF,即可得到结论.ﻫ(2)连接DB,如图2,由△BEF为等腰直角三角形,得∠EBF=45°,而四边形ABCD为正方形,得∠DBC=45°,得到D,E,B三点共线,而G为DF的中点,根据直角三角形斜边上的中线等于斜边的一半得到EG=GD=GC,于是∠EGC=2∠EDC=90°,即得到结论.ﻫ(3)连接AC、BD相交于点O,取BF的中点M,连接OG、EM、MG,由G为DF的中点,O为BD的中点,M为BF的中点,根据三角形中位线的性质得OG∥BF,GM∥OB,得到OG=BM,GM=OB,而EM=BM,OC=OB,得到EM=OG,MG=OC,又∠DOG=∠GMF,而∠DOC=∠EMF =90°,得∠EMG=∠GOC,则△MEG≌△OGC,得到EG=CG,∠EGM=∠OCG,而∠MGF=∠BD F,∠FGC=∠GDC+∠GCD,所以有∠EGC=∠EGM+∠MGF+∠FGC=∠BDF+∠GDC+∠GCD+∠OCG=45°+45°=90°.3.已知正方形ABCD和等腰Rt△BEF,BE=EF,∠BEF=90°,按图①放置,使点F在BC上,取DF的中点G,连接EG、CG.ﻫ(1)探索EG、CG的数量关系和位置关系并证明;ﻫ(2)将图①中△BEF绕B点顺时针旋转45°,再连接DF,取DF中点G(如图②),问(1)中的结论是否仍然成立.证明你的结论;(3)将图①中△BEF绕B点转动任意角度(旋转角在0°到90°之间),再连接DF,取DF的中点G(如图③),问(1)中的结论是否仍然成立,证明你的结论.ﻫ解:(1)EG=CG且EG⊥CG.ﻫ证明如下:如图①,连接BD.∵正方形ABCD和等腰Rt△BEF,∴∠EBF=∠DBC=45°.∴B、E、D三点共线.ﻫ∵∠DEF=90°,G为DF的中点,∠DCB=90°,∴EG=DG=GF=CG.ﻫ∴∠EGF=2∠EDG,∠CGF=2∠CDG.ﻫ∴∠EGF+∠CGF=2∠ED C=90°,ﻫ即∠EGC=90°,∴EG⊥CG.ﻫﻫ(2)仍然成立,证明如下:如图②,延长EG交CD于点H.ﻫ∵BE⊥EF,∴EF∥CD,∴∠1=∠2.ﻫ又∵∠3=∠4,FG=DG,ﻫ∴△FEG≌△DHG,∴EF=DH,EG=GH.∵△BEF为等腰直角三角形,∴BE=EF,∴BE=DH.ﻫ∵CD=BC,∴CE=CH.∴△ECH为等腰直角三角形.又∵EG=GH,∴EG=CG且EG⊥CG.ﻫ(3)仍然成立.证明如下:如图③,延长CG至H,使GH=CG,连接HF交BC于M,连接EH、EC.∵GF=GD,∠HGF=∠CGD,HG=CG,ﻫ∴△HFG≌△CDG,ﻫ∴HF=CD,∠GHF=∠GCD,∴HF∥CD.∵正方形ABCD,∴HF=BC,HF⊥BC.∵△BEF是等腰直角三角形,∴BE=EF,∠EBC=∠HFE,∴△BEC≌△FEH,ﻫ∴HE=EC,∠BEC=∠FEH,ﻫ∴∠BEF=∠HEC=90°,ﻫ∴△ECH为等腰直角三角形.又∵CG=GH,∴EG =CG 且EG ⊥C G.解析:(1)首先证明B 、E、D三点共线,根据直角三角形斜边上的中线等于斜边的一半,即可证明EG=DG=GF=CG,得到∠EGF=2∠EDG ,∠CGF=2∠CDG,从而证得∠EGC=90°;ﻫ(2)首先证明△FE G≌△DHG,然后证明△ECH 为等腰直角三角形.可以证得:EG=CG 且EG ⊥C G.ﻫ(3)首先证明:△BEC ≌△FEH,即可证得:△ECH 为等腰直角三角形,从而得到:EG=C G且EG ⊥CG.已知,正方形A BCD 中,△BEF 为等腰直角三角形,且BF 为底,取DF 的中点G,连接EG 、C G.ﻫ(1)如图1,若△B EF 的底边B F在BC 上,猜想E G和CG 的数量关系为______;ﻫ(2)如图2,若△B EF 的直角边BE 在BC 上,则(1)中的结论是否还成立?请说明理由;(3)如图3,若△B EF 的直角边BE 在∠DB C内,则(1)中的结论是否还成立?说明理由. 解:(1)GC=EG,(1分)理由如下:ﻫ∵△BEF 为等腰直角三角形,ﻫ∴∠DEF=90°,又G为斜边DF 的中点, ∴EG= DF,∵A BCD 为正方形,ﻫ∴∠BCD=90°,又G为斜边DF 的中点,∴CG= DF,ﻫ∴G C=EG;ﻫ(2)成立.如图,延长EG 交CD 于M,D,∵∠BEF =∠FEC=∠BCD=90°,∴EF ∥C1 2 1 2∴∠EFG=∠MD G,ﻫ又∠E GF=∠DGM ,D G=FG ,∴△G EF ≌△GMD,ﻫ∴EG=MG,即G 为EM 的中点.∴CG为直角△EC M的斜边上的中线,ﻫ∴CG=G E= EM;(3)成立.ﻫ取BF 的中点H,连接EH ,GH ,取BD 的中点O,连接O G,OC . ∵CB=CD,∠DCB=90°,∴C O= BD .ﻫ∵DG=G F,ﻫ∴GH ∥BD ,且GH= BD ,ﻫOG ∥BF,且OG= B F,ﻫ∴CO =GH .∵△BEF 为等腰直角三角形. B F∴EH=∴EH=OG . ∵四边形O BHG 为平行四边形, ∴∠BOG =∠BH G.∵∠B OC=∠BH E=90°. ∴∠GOC=∠EHG .ﻫ∴△GOC ≌△E HG .ﻫ∴EG=GC .此题考查了正方形的性质,以及全等三角形的判定与性质.要求学生掌握直角三角形斜边上的中线等于斜边的一半,以及三角形的中位线与第三边平行且等于第三边的一半.掌握这些性质,熟练运用全等知识是解本题的关键.解析:(1)E G=CG,理由为:根据三角形BEF 为等腰直角三角形,得到∠DEF 为直角,又G 为DF 中点,根据在直角三角形中,斜边上的中线等于斜边的一半,得到EG 为DF 的一半,同理在直角三角形DC F中,得到CG 也等于DF 的一半,利用等量代换得证;ﻫ(2)成立.理由为:延长EG 交CD 于M,如图所示,根据“A SA ”得到三角形E FG 与三角形GDM 全等,由全等三角形的对应边相等得到EG 与MG 相等,即G 为EM 中点,根据直角三角形斜边上的中线等于斜边的一半得到E G与CG相等都1212 1 2 1 2。
(完整版)初中几何证明题五大经典(含答案)
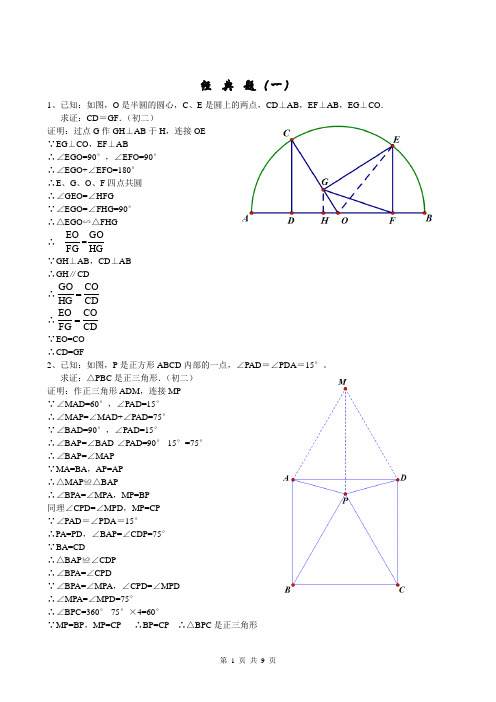
经典题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)证明:过点G 作GH ⊥AB 于H ,连接OE ∵EG ⊥CO ,EF ⊥AB∴∠EGO=90°,∠EFO=90° ∴∠EGO+∠EFO=180° ∴E 、G 、O 、F 四点共圆 ∴∠GEO=∠HFG∵∠EGO=∠FHG=90° ∴△EGO ∽△FHG ∴FG EO =HGGO∵GH ⊥AB ,CD ⊥AB ∴GH ∥CD∴CD COHG GO =∴CDCO FG EO = ∵EO=CO ∴CD=GF2、已知:如图,P 是正方形ABCD 内部的一点,∠PAD =∠PDA =15°。
求证:△PBC 是正三角形.(初二) 证明:作正三角形ADM ,连接MP ∵∠MAD=60°,∠PAD=15° ∴∠MAP=∠MAD+∠PAD=75° ∵∠BAD=90°,∠PAD=15°∴∠BAP=∠BAD-∠PAD=90°-15°=75° ∴∠BAP=∠MAP ∵MA=BA ,AP=AP ∴△MAP ≌△BAP∴∠BPA=∠MPA ,MP=BP 同理∠CPD=∠MPD ,MP=CP ∵∠PAD =∠PDA =15°∴PA=PD ,∠BAP=∠CDP=75° ∵BA=CD∴△BAP ≌∠CDP ∴∠BPA=∠CPD∵∠BPA=∠MPA ,∠CPD=∠MPD ∴∠MPA=∠MPD=75°∴∠BPC=360°-75°×4=60°∵MP=BP ,MP=CP ∴BP=CP ∴△BPC 是正三角形3、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC 的延长线交MN于E 、F .求证:∠DEN =∠F .证明:连接AC ,取AC 的中点G ,连接NG 、MG ∵CN=DN ,CG=DG ∴GN ∥AD ,GN=21AD ∴∠DEN=∠GNM ∵AM=BM ,AG=CG ∴GM ∥BC ,GM=21BC ∴∠F=∠GMN ∵AD=BC ∴GN=GM∴∠GMN=∠GNM ∴∠DEN=∠F经典题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O 为外心,且OM ⊥BC 于M . (1)求证:AH =2OM ;(2)若∠BAC =600,求证:AH =AO .(初二) 证明:(1)延长AD 交圆于F ,连接BF ,过点O 作OG ⊥AD 于G ∵OG ⊥AF ∴AG=FG ∵AB⌒ =AB ⌒ ∴∠F=∠ACB又AD ⊥BC ,BE ⊥AC ∴∠BHD+∠DBH=90° ∠ACB+∠DBH=90° ∴∠ACB=∠BHD ∴∠F=∠BHD∴BH=BF 又AD ⊥BC ∴DH=DF∴AH=AG+GH=FG+GH=GH+DH+DF+GH=2GH+2DH=2(GH+DH )=2GD 又AD ⊥BC ,OM ⊥BC ,OG ⊥AD ∴四边形OMDG 是矩形 ∴OM=GD ∴AH=2OM (2)连接OB 、OC∵∠BAC=60∴∠BOC=120° ∵OB=OC ,OM ⊥BC ∴∠BOM=21∠BOC=60°∴∠OBM=30° ∴BO=2OM由(1)知AH=2OM ∴AH=BO=AO2、设MN 是圆O 外一条直线,过O 作OA ⊥MN 于A ,自A 引圆的两条割线交圆O 于B 、C 及D 、E ,连接CD 并延长交MN 于Q ,连接EB 并延长交MN 于P. 求证:AP =AQ .证明:作点E 关于AG 的对称点F ,连接AF 、CF 、QF ∵AG ⊥PQ ∴∠PAG=∠QAG=90°又∠GAE=∠GAF ∴∠PAG+∠GAE=∠QAG+∠GAF 即∠PAE=∠QAF∵E 、F 、C 、D 四点共圆 ∴∠AEF+∠FCQ=180° ∵EF ⊥AG ,PQ ⊥AG ∴EF ∥PQ∴∠PAF=∠AFE ∵AF=AE∴∠AFE=∠AEF ∴∠AEF=∠PAF ∵∠PAF+∠QAF=180° ∴∠FCQ=∠QAF ∴F 、C 、A 、Q 四点共圆 ∴∠AFQ=∠ACQ 又∠AEP=∠ACQ ∴∠AFQ=∠AEP3、设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)证明:作OF ⊥CD 于F ,OG ⊥BE 于G ,连接OP 、OQ 、OA 、AF 、AG ∵C 、D 、B 、E 四点共圆 ∴∠B=∠D ,∠E=∠C ∴△ABE ∽△ADC ∴DFBGFD 2BG 2DC BE AD AB === ∴△ABG ∽△ADF ∴∠AGB=∠AFD ∴∠AGE=∠AFC ∵AM=AN , ∴OA ⊥MN 又OG ⊥BE ,∴∠OAQ+∠OGQ=180° ∴O 、A 、Q 、E 四点共圆 ∴∠AOQ=∠AGE 同理∠AOP=∠AFC ∴∠AOQ=∠AOP又∠OAQ=∠OAP=90°,OA=OA ∴△OAQ ≌△OAP ∴AP=AQ 在△AEP 和△AFQ 中 ∠AFQ=∠AEP AF=AE ∠QAF=∠PAE ∴△AEP ≌△AFQ ∴AP=AQ4、如图,分别以△ABC 的AB 和AC 为一边,在△ABC 的外侧作正方形ABFG 和正方形ACDE ,点O 是DF 的中点,OP ⊥BC求证:BC=2OP (初二)证明:分别过F 、A 、D 作直线BC 的垂线,垂足分别是L 、M 、N ∵OF=OD ,DN ∥OP ∥FL ∴PN=PL∴OP 是梯形DFLN 的中位线 ∴DN+FL=2OP ∵ABFG 是正方形∴∠ABM+∠FBL=90° 又∠BFL+∠FBL=90° ∴∠ABM=∠BFL又∠FLB=∠BMA=90°,BF=AB ∴△BFL ≌△ABM ∴FL=BM同理△AMC ≌△CND ∴CM=DN∴BM+CN=FL+DN ∴BC=FL+DN=2OP经典题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F . 求证:CE =CF .(初二)证明:连接BD 交AC 于O 。
初二证明题练习题

初二证明题练习题题目一:证明下列几何题中的等式。
1. 证明ABCD是一个正方形。
解答:首先,我们已知AD = BC (对边相等)和∠ADB = ∠CBA(直角相等)。
因此,根据SSS三边相等定理,我们可以得出AD = BC,AB = DC 和∠DAC = ∠CBA。
同时,我们还知道∠DAC + ∠CAB = 90°(补角定理)。
由于∠DAC = ∠CBA,我们可以得知∠CDA = 90°。
根据两组对边相等且对角线垂直的条件,我们可以得出ABCD是一个正方形。
2. 证明三角形ABC中,如果∠B = ∠C,那么AB = AC。
解答:已知∠B = ∠C,我们可以知道△ABC是一个等腰三角形(两个边相等)。
由等腰三角形的性质,我们可以得知AB = AC。
题目二:根据已知条件,给出相关结论的证明。
1. 已知x > 0,y > 0,证明2xy < x^2 + y^2。
解答:我们可以根据多种方法来证明这个不等式,其中一种方法如下:由于x > 0和y > 0,我们可以将不等式两边同时除以xy,得到:2 < (x^2 + y^2) / xy。
我们进一步将右边的分数展开,得到:2 < (x/y) + (y/x)。
根据调和平均数不等式,我们知道(x/y) + (y/x) >= 2,且等号只在x = y时取得。
因此,我们得出结论2 < (x/y) + (y/x) <= (x^2 + y^2) / xy。
2. 已知三角形ABC中,AB = AC,∠B > ∠C,证明BC > BA。
解答:由于∠B > ∠C和AB = AC,我们可以推知∠A > 90°。
因此,在△ABC中,我们可以根据余弦定理得到:BC^2 = AB^2 + AC^2 - 2AB * AC * cosA。
由于∠A > 90°,cosA < 0。
几何证明练习题带答案

几何证明练习题带答案一、选择题1. 已知三角形ABC中,AB=AC,点D在BC上,且BD=DC。
求证:∠BAD=∠CAD。
A. 利用等腰三角形性质B. 利用角平分线定理C. 利用等边三角形性质D. 利用相似三角形性质答案:B2. 已知线段AB和CD平行,且M是线段AB上的一点,N是线段CD上的一点,MN与AB、CD不平行。
求证:∠AMN≠∠CNM。
A. 利用平行线性质B. 利用内错角定理C. 利用同位角定理D. 利用补角定理答案:A二、填空题1. 在三角形ABC中,若∠A=90°,AB=AC,那么∠B=∠C=______。
答案:45°2. 已知三角形ABC中,AB=5,AC=7,BC=6,根据勾股定理可知这是一个______三角形。
答案:直角三、简答题1. 如何证明三角形内角和定理?答案:在三角形ABC中,延长BC至点D,根据外角定理,∠ACD=∠A+∠B。
又因为∠ACD+∠C=180°,所以∠A+∠B+∠C=180°,证明了三角形内角和为180°。
2. 如何证明圆内接四边形的对角互补?答案:设圆内接四边形ABCD,连接对角线AC和BD,由于AC和BD 都是圆的直径,根据圆周角定理,∠A+∠C=90°,∠B+∠D=90°。
因此,对角互补。
四、证明题1. 已知三角形ABC中,AB=AC,点D在BC上,且BD=DC。
证明∠BAD=∠CAD。
证明:由于AB=AC,根据等腰三角形性质,∠ABC=∠ACB。
又因为BD=DC,根据等边三角形性质,∠ABD=∠ACD。
因此,∠BAD=∠ABC-∠ABD=∠ACB-∠ACD=∠CAD。
2. 已知圆O中,弦AB和CD相交于点P,PA=PB,PC=PD。
证明:OP垂直于AB和CD。
证明:由于PA=PB,根据圆周角定理,∠APB=∠PBA。
同理,∠CPD=∠PDC。
因为∠APB+∠CPD=180°,所以∠OPB+∠OPD=90°。
几何证明题及其答案1

例1:如图2-4-27,四边形ABCD 是正方形,△ECF 是等 腰直角三角形,其中CE=CF ,G 是CD 与EF 的交点. (1)求证:△BCF ≌△DCE .(2)若BC=5,CF=3,∠BFC=900,求DG :GC 的值.例2:已知如图2-4-28,BE 是⊙O 的走私过圆上一点作⊙O 的切线交EB 的延长线于P .过E 点作ED ∥AP 交⊙O 于D ,连结DB 并延长交PA 于C ,连结AB 、AD .(1)求证:2AB PB BD = .(2)若PA=10,PB=5,求AB 和CD 的长.例3:如图2-4-29,⊙1O 和⊙2O 相交于A 、B 两点,圆心1O 在⊙2O 上,连心线1O 2O 与⊙1O 交于点C 、D ,与⊙2O 交于点E ,与AB 交于点H ,连结AE .(1)求证:AE 为⊙1O 的切线.(2)若⊙1O 的半径r=1,⊙2O 的半径32R =,求公共弦AB 的长. (3)取HB 的中点F ,连结1O F ,并延长与⊙2O 相交于点G ,连结EG ,求EG 的长.例4 如图2-4-30,A 为⊙O 的弦EF 上的一点,OB 是和这条弦垂直的半径,垂足为H,BA 的延长线交⊙O 于点C ,过点C 作⊙O 的切线与EF 的延长线交于点D . (1)求证:DA=DC图2-4-27GFED CB A 图2-4-28C 321OEPB A O 2O 1H G F ED B CA 图2-4-28(2)当DF :EF=1:8且DF=2时,求AB AC 的值.(3)将图2-4-30中的EF 所在的直线往上平移到⊙O 外,如图2-4-31,使EF 与OB 的延长线交⊙O 于点C ,过点C 作⊙O 的切线交EF 于点D .试猜想DA=DC 是否仍然成立,并证明你的结论.【提高训练】1.如图2-4-32,已知在△ABC 中,AB=AC ,D 、E 分别是AB 和BC 上的点,连结DE 并延长与AC 的延长线相交于点F .若DE=EF ,求证:BD=CF .2.点O 是△ABC 所在平面内一动点,连结OB 、OC ,并将AB 、OB 、OC 、AC 的中点D 、E 、F 、G 依次连结,如果DEFG 能构成四边形.(1)如图2-4-33,当O 点在△ABC 内时,求证四边形DEFG 是平行四边形.(2)当点O 移动到△ABC 外时,(1)中的结论是否成立?画出图形,并说明理由.(3)若四边形DEFG 为矩形,O 点所在位置应满足什么条件?试说明理由.图2-4-30H FE D O C B A K 图2-4-30HF E DO CBA 图2-4-32F EDC B A 图2-4-33O GF E D CB A3.如图2-4-35,等腰梯形ABCD中,AD∥BC,∠DBC=450.翻折梯形ABCD,使点B重合于点D,折痕分别交边AB、BC于点F、E.若AD=2,BC=8,求:(1)BE的长.(2)∠CDE的正切值.4.如图2-4-35,四边形ABCD内接于⊙O,已知直径AD=2,∠ABC=1200,∠ACB=450,连结OB交AC于点E.(1)求AC的长.(2)求CE:AE的值.(3)在CB的延长上取一点P,使PB=2BC,试判断直线PA和⊙O的位置关系,并加以证明你的结论.5.如图2-4-36,已知AB是⊙O的直径,BC、CD分别是⊙O的切线,切点分别为B、D,E 是BA和CD的延长线的交点.(1)猜想AD与OC的位置关系,并另以证明.(2)设A DO C的值为S,⊙O的半径为r,试探究S与r的关系.(3)当r=2,1sin3E∠=时,求AD和OC的长.图2-4-34FEDC BAO图2-4-35PEDCBA图2-4-36OEDCBA答案例1.分析与解答 (1)∵四边形 ABCD 是正方形,∴∠BCF+∠FCD=900,BC=CD .∵△ECF 是等腰直角三角形,CF=CE .∴∠ECD+∠FCD=900.∴∠BCF=∠ECD .∴△BCF ≌△DCE(2)在△BFC 中,BC=5,CF=3,∠BFC=900. ∴BF=2222534BC CF -=-=.∵△BCF ≌△DCE ,∴DE=BF=4,∠BFC=∠DEC=∠FCE=900. ∴DE ∥FC .∴△DGE ∽△CGF .∴DG :GC=DE :CF=4:3.例2.分析与解答 (1)证明:∵PA 是⊙O 的切线,∴∠1=∠2. ∵ED ∥AP ,∴∠P=∠PED .而∠3=∠BED ,∴∠3=∠P .∴△ABD ∽△PBA .∴2AB PB BD =. (2)连结OA 、AE .由切割线定理得,2PA PB BD = .即2105(5)BE =⨯+, ∴BE=15.又∴△PAE ∽△PBA ,∴2AE PAAB PB==,即AE=2AB . 在Rt △EBA 中,22215(2)AB AB =+,∴35AB =.将AB 、PB 代入2AB PB BD = ,得BD=9. 又∵∠BDE=900,ED ∥AP , ∴DC ⊥PA .∴BC ∥OA .∴BC PBOA PO=. ∴515315252BC =⨯=+.∴CD=12 例3.分析与解答 (1)连结A 1O .∵1O E 为⊙2O 的直径,∴∠1O AE=900. 又∵1O A 为⊙1O 的半径,∴AE 为⊙1O 的切线.(2)∵1O A=r=1,1O E=2R=3,△A 1O E 为Rt △,AB ⊥1O E , ∴△A 1O E ∽△H 1O A .∴2111O A O H O E = . ∴113O H =.2242223AB AH OA OH ==-=. (3)∵F 为HB 的中点,∴HF=1243HF AB ==, ∴221133O F O H HF =+=.∵11HO F GO E ∠=∠. ∴Rt △1O HF ∽Rt △1OGE .∴11O F HFO E EG=. ∴11HF O EEG O F = ,即233623EG ⨯==. 例4.分析与解答 (1)连结OC ,则OC ⊥DC ,∴∠DCA=900-∠ACO=900-∠B .又∠DAC=∠BAE=900-∠B ,∴∠DAC=∠DCA .∴DA=DC .(2)∵DF :EF=1:8,2DF =,∴EF=8DF=82, 又DC 为⊙O 的切线,∴229218DC DF DE ==⨯= . ∴1832DC ==.∴32AD DC ==,32222AF AD DF =-=-=, 822262AE EF AF =-=-=. ∴622224AB AC AE AF ==⨯= .(3)结论DA=DC 仍然成立.理由如下:如图2-4-31,延长BO 交⊙O 于K ,连结CK ,则∠KCB=900.又DC 是⊙O 的切线,∴∠DCA=∠CKB=900-∠CBK .又∠CBK=∠HBA ,∴∠BAH=900-∠HBA=900-∠CBK . ∴∠DCA=∠BAH .∴DA=DC . 提高部分:【答案】 1.过D 作DG ∥AC 交BC 于G ,证明△DGE ≌△FCE 2.(1)证明DG ∥EF 即可(2)结论仍然成立,证明略(3)O 点应在过A 点且垂直于BC 的直线上(A 点除外),说理略. 3.(1)BE=5 (2)3tan 5CDE ∠=4.(1)3AC = (2)1:2CE AE =(3)∵1:2CE AE =,PB=2BC ,∴CE :AE=CB :PB . ∴BE ∥AP .∴AO ⊥AP .∴PA 为⊙O 的切线5.(1)AD ∥OC ,证明略(2)连结BD ,在△ABD 和△OCB 中,∵AB 是直径,∴∠ADB=∠OBC=900. 又∵∠OCB=∠BAD ,∴Rt △ABD ∽Rt △OCB .∴AD ABOB OC=.222S AD OC AB OB r r r ==== , ∴22S r = (3)433AD =,23OC =.。
初二数学 几何证明初步经典练习题 含答案

几何证明初步练习题1、三角形的内角和定理:三角形的内角和等于180°.推理过程:○1 作CM ∥AB ,则∠A= ,∠B= ,∵∠ACB +∠1+∠2=1800( ,∴∠A+∠B+∠ACB=1800. ○2 作MN ∥BC ,则∠2= ,∠3= ,∵∠1+∠2+∠3=1800,∴∠BAC+∠B+∠C=1800. 2.求证:在一个三角形中,至少有一个内角大于或者等于60°。
3、.如图,在△ABC 中,∠C >∠B,求证:AB >AC 。
4. 已知,如图,AE5. 已知:如图,EF ∥AD ,∠1 =∠2. 求证:∠AGD +∠BAC = 180°.反证法经典例题6.求证:两条直线相交有且只有一个交点.7.如图,在平面内,AB 是L 的斜线,CD 是L 的垂线。
求证:AB 与CD 必定相交。
8.2一.角平分线--轴对称9、已知在ΔABC 中,E为BC的中点,AD 平分BAC ∠,BD ⊥AD 于D .AB =9,AC=13求DE的长第9题图 第10题图 第11题图分析:延长BD交AC于F.可得ΔABD ≌ΔAFD .则BD =DF .又BE =EC ,即D E为ΔBCF 的中位线.∴DE=12FC=12(AC-AB)=2. 10、已知在ΔABC 中,108A ∠=,AB =AC ,BD 平分ABC ∠.求证:BC =AB +CD . 分析:在BC上截取BE=BA,连接DE.可得ΔBAD ≌ΔBED .由已知可得:18ABD DBE ∠=∠=,108A BED ∠=∠=,36C ABC ∠=∠=.∴72DEC EDC ∠=∠=,∴CD=CE ,∴BC =AB +CD .11、如图,ΔABC 中,E是BC 边上的中点,DE ⊥BC 于E ,交BAC ∠的平分线AD 于D ,过D 作DM ⊥AB 于M,作DN ⊥AC 于N .求证:BM =CN .分析:连接DB 与DC .∵DE 垂直平分BC ,∴DB =DC .易证ΔAMD ≌ΔAND .∴有DM =DN .∴ΔBMD ≌ΔCND (HL).∴BM =CN .二、旋转12、如图,已知在正方形ABCD 中,E在BC 上,F在DC 上,BE +DF=EF .求证:45EAF ∠=. C B ADE F D A B C B A E D NM B D A C分析:将ΔADF 绕A顺时针旋转90得ABG .∴GAB FAD ∠=∠.易证ΔAGE ≌ΔAFE .∴ 1452FAE GAE FAG ∠=∠=∠= 13、如图,点E 在ΔABC 外部,D 在边BC 上,DE 交AC 于F .若123∠=∠=∠,AC=AE.求证:ΔABC ≌ΔADE .分析:若ΔABC ≌ΔADE ,则ΔADE 可视为ΔABC 绕A逆时针旋转1∠所得.则有B ADE ∠=∠.∵12B ADE ∠+∠=∠+∠,且12∠=∠.∴B ADE ∠=∠.又∵13∠=∠.∴BAC DAE ∠=∠.再∵AC=AE.∴ΔABC ≌ΔADE .14、如图,点E为正方形ABCD的边CD上一点,点F为CB的延长线上的一点,且EA⊥AF.求证:DE=BF.分析:将ΔABF 视为ΔADE 绕A顺时针旋转90即可.∵90FAB BAE EAD BAE ∠+∠=∠+∠=.∴FBA EDA ∠=∠. 又∵90FBA EDA ∠=∠=,AB=AD.∴ΔABF ≌ΔADE .(ASA)∴DE=DF. 平移第14题图 第15题图 第16题图 第17题图三、平移15、如图,在梯形ABCD 中,BD ⊥AC ,AC =8,BD =15.求梯形ABCD 的中位线长. 分析:延长DC到E使得CE=AB.连接BE.可得ACEB .可视为将AC平移到BE.AB平移到CE.由勾股定理可得DE=17.∴梯形ABCD中位线长为8.5.16、已知在ΔABC 中,AB =AC ,D 为AB 上一点,E为AC 延长线一点,且BD =CE .求证:DM =EM 分析:作DF∥AC交BC于F.易证DF=BD=CE.则DF可视为CE平移所得.∴四边形DCEF为DCEF .∴DM=EM.线段中点的常见技巧 --倍长四、倍长17、已知,AD为ABC 的中线.求证:AB+AC>2AD.分析:延长AD到E使得AE=2AD.连接BE易证ΔBDE ≌ΔCDA .∴BE=AC.∴AB+AC>2AD.18、如图,AD 为ΔABC 的角平分线且BD =CD .求证:AB =AC . 分析:延长AD到E使得AD=ED.易证ΔABD ≌ΔECD .∴EC=AB. ∵BAD CAD ∠=∠.∴E CAD ∠=∠.∴AC=EC=AB. 19、已知在等边三角形ABC中,D和E分别为BC与AC上的点,且AE=CD.连接AD与BE交于点P,作BQ⊥AD于Q.求证:BP=2PQ.分析:延长PD到F使得FQ=PQ.在等边三角形ABC中AB=BC=AC,60ABD C ∠=∠=.又∵AE=CD,∴BD=CE.∴ΔABD ≌ΔBCE .∴CBE BAD ∠=∠.∴60BPQ PBA PAB PBA DBP ∠=∠+∠=∠+∠=.易证ΔBPQ ≌ΔBFQ .得BP=BF,又60BPD ∠=.∴ΔBPF 为等边三角形.∴BP=2PQ.中位线五、中位线、中线:20、已知在梯形ABCD 中,AD ∥BC ,E和F分别为BD 与AC 的中点, 求证:1()2EF BC AD =-. 分析:取DC中点G,连接EG与FG.则EG为ΔBCD 中位线,FG为ΔACD 的中位线. ∴EG∥=12BC ,FG ∥=12AD .∵AD ∥BC .∴过一点G有且只有一条直线平行于已知直线BC,即E、F、G共线.∴1()2EF BC AD =-. 直角三角形斜边上的中线等于斜边的一半21、已知,在ABCD 中BD AB 21=.E为OA的中点,F为OD中点,G为BC中点. 求证:EF=EG.分析:连接BE .∵BD AB 21=,AE=O E.∴BE⊥CE,∵BG=CG. ∴BD EG 21=.又EF为ΔAOD 的中位线.∴AD EF 21=.∴EF=EG. 22、在ΔABC 中,AD是高,CE是中线,DC=BE,DG⊥CE于G.求证:(1)CG=EG.(2)2B BCE ∠=∠.分析:(1)连接DE.则有DE=BE=DC.∴Rt ΔCDG ≌Rt ΔEDG (HL).∴EG=CG.∵DE=BE.∴B BDE DEC BCE ∠=∠=∠+∠.∵DE=CD.∴DEC BCE ∠=∠.∴2B BCE ∠=∠.几何证明初步测验题(1)一、选择题(每空3 分,共36 分)1、使两个直角三角形全等的条件是( )A 、一组锐角对应相等B 、两组锐角分别对应相等C 、一组直角边对应相等D 、两组直角边分别对应相等2、如图,已知AB ∥CD ,∠A =50°,∠C =∠E .则∠C =( )A .20°B .25°C .30°D .40°第2题图 第4题图 第6题图 第7题图3、用反证法证明命题“一个三角形中不能有两个角是直角”,应先假设这个三角形中( )A .有两个角是直角B .有两个角是钝角C .有两个角是锐角D .一个角是钝角,一个角是直角4、如图,直线AB 、CD 相交于点O ,∠BOE=90°,OF 平分∠AOE ,∠1=15°30’,则下列结论不正确的是( ) A D B E F OC B E F ED G AA.∠2=45° B.∠1=∠3 C.∠AOD+∠1=180° D.∠EOD=75°30’5、下列说法中,正确的个数为()①三角形的三条高都在三角形内,且都相交于一点②三角形的中线都是过三角形的某一个顶点,且平分对边的直线③在△ABC中,若∠A=12∠B=13∠C,则△ABC是直角三角形④一个三角形的两边长分别是8和10,那么它的最短边的取值范围是2<b<18A.1个 B.2个 C.3个 D.4个6、如图,在AB=AC的△ABC中,D是BC边上任意一点,DF⊥AC于F,E在AB边上,使ED⊥BC于D,∠AED=155°,则∠EDF等于()A、50°B、65°C、70°D、75°7、如图,已知△ABC是等腰直角三角形,∠A=90°,BD是∠ABC的平分线,DE⊥BC于E,若BC=10cm,则△DEC的周长为()A.8cm B.10cm C.12cm D.14cm8、如图,已知△ABC中,∠ABC=45°,AC=4,H是高AD和BE的交点,则线段BH的长度为()A. B.9、如图,正方形ABCD内有两条相交线段MN、EF,M、N、E、F分别在边AB、CD、AD、BC上.小明认为:若MN = EF,则MN⊥EF;小亮认为: 若MN⊥EF,则MN = EF.你认为()A.仅小明对 B.仅小亮对 C.两人都对 D.两人都对第9题图第10题图第11题图第12题图10、如图,△ABC为等边三角形,AQ=PQ,PR=PS,PR⊥AB于R,PS⊥AC于S,•则四个结论正确的是().①点P在∠A的平分线上; ②AS=AR; ③QP∥AR; ④△BRP≌△QSP.A.全部正确; B.仅①和②正确; C.仅②③正确; D.仅①和③正确11、如图,△ABC中,CD⊥AB于D,一定能确定△ABC为直角三角形的条件的个数是()①∠1=∠②③∠+∠2=90°④=3:4:5 ⑤A.1 B.2 C.3 D.412、如图,过边长为1的等边△ABC的边AB上一点P,作PE⊥AC于E,Q为BC延长线上一点,当PA=CQ时,连PQ交AC边于D,则DE的长为()A.13B.12C.23D.不能确定二、填空题(每空3 分,共15 分)13、命题“对顶角相等”中的题设是_________ ,结论是___________ 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
O B M A B
E F
C
D 练习1
1、已知x ∶y ∶z =3∶4∶5,且x +y -z =6,则z y x 232+-=
2、四边形ABCD ∽四边形A′B′C′D′,∠A=70°,∠B′=108°,∠C′=92°,则∠D=______
3、已知两个相似多边形的一组对应边分别是15cm 和23cm ,它们的周长差40cm ,则其中较大三角形的周长是 cm
4、△ABC 中,D 、E 分别在AB 、AC 上,并且AD :DB=2:1,AE :EC=1:2,则S △ADE :S △ABC = 。
5、如图3,要测量A 、B 两点间距离,在O 点打桩,取OA 的中点 C ,OB 的中点D ,测得
CD =30米,则AB =______米
6、如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与ABC △相似的是
7、如图,路灯距地面
1.6米的小明从距离灯的底部(点O )20米的点A 处,沿OA 所在的直线行走14米到点B 时,人影的长度 A.增大1.5米 B.减小1.5米 C.增大3.5米 D.减小3.5米
(第7题图)
8、 一个△ABC 的面积被平行于它的一边BC 的两条线段三等分,如果BC=12 cm ,则这两条线段中较长的一条是
9、如图,△ABC 中,D 是边AC 上的一点,且∠DBC=∠A ,BC=6,AC=3,则CD 的长是
10、如图,已知:△ABC 中,AD 是∠BAC 的平分线,AD 的垂直平分线交AD 于E,交BC 的延长线于
F.求证:FD 2
=FB.FC.
11、已知ABC △,延长BC 到D ,使CD BC =.取AB 的中点F ,连结FD 交AC 于点E .
(1)求AE
AC
的值; (2)若AB a FB EC ==,,求AC 的长.
12、如图:已知△ABC 中,AB=5,BC=3,AC=4,PQ ∥AB ,P 点在AC 上(与A 、C 不重合),Q 在BC 上.
(1) 当△PQC 的面积等于四边形PABQ 面积的
3
1
,求CP 的长. (2)当△PQC 的周长与四边形PABQ 的周长相等时,求CP 的长.
(3)试问:在AB 上是否存在一点M ,使得△PQM 为等腰直角三角形,若不存在,请简要说明理由:若存在,请求出PQ 的长.
13、阅读以下文字并解答问题:
在“测量物体的高度” 活动中,某数学兴趣小组的4名同学选择了测量学校里的四棵树的高度.在同一时刻的阳光下,他们分别做了以下工作:
小芳:测得一根长为1米的竹竿的影长为0.8米,甲树的影长为4.08米(如图1). 小华:发现乙树的影子不全落在地面上,有一部分影子落在教学楼的墙壁上(如图2),墙壁上的影长为1.2米,落在地面上的影长为2.4米.
小丽:测量的丙树的影子除落在地面上外,还有一部分落在教学楼的第一级台阶上(如图3),测得此影子长为0.2米,一级台阶高为0.3米,落在地面上的影长为4.4米.
小明:测得丁树落在地面上的影长为2.4米,落在坡面上影长为3.2米(如图4).身高是1.6m 的小明站在坡面上,影子也都落坡面上,小芳测得他的影长为2m .
(1)在横线上直接填写甲树的高度为 米. (2)求出乙树的高度(画出示意图).
(3)请选择丙树的高度为 A 、6.5米 B 、5.75米 C 、6.05米 D 、7.25米 (4)你能计算出丁树的高度吗?试试看.
无锡市格致中学阶段性反馈2010.5
初二数学参考答案
一、填空题
1、cm 4;
2、12;
3、ο90;
4、18.6;
5、115;
6、9:2;
7、7500:1;
8、
60;9、5
192⨯;10、1
3418,24,18-⎪
⎭
⎫
⎝⎛⨯n
二、选择题
11、B;12、A;13、D;14、D;15、C;16、A;17、D;18、D;19、C;20、C 三、作图题
21、直接利用 X 型形似作图 四、解答题
22、分两种情况讨论CBA Δ∽CPQ Δ,CBA Δ∽CQP Δ,可以求出时间分别是
11
1656或
23、连接FA,证明FAC Δ∽FBA Δ,由于FD FA =,命题获证。
24、法一:连接AD FC ,;法二:过F E 或者 做平行线,命题获证,在命题获证的基础上第二问求出。
25、(1)用相似CPQ Δ∽CAB Δ
(2)设出x PC = 表示出CQ ,利用周长列出方程,求出PC
(3)当∠PQM=90°时(画图)
过P作PN⊥AB于N
设PQ=QM=PN=MN=a
∠QMB=∠ANP=90°
∠B=90°-∠A=∠APN
∴△MQB∽△NAP∽△CAB
∴AN:PN=AC:BC,BM:QM=BC:BC
∴MB=3/4a,AN=4/3a
∵AB=AN+NM+MB
∴3/4a+4/3a+a=5
∴PQ=a=60/37
当∠QPM=90°时
同理有PQ=60/37
当∠PMQ=90°时
过P作PN⊥AB于N,过Q作QR⊥AB于R,过M作MS⊥PQ于S
设PN=QR=a
则PQ=MN=2a
类似前两种情况可得△RQB∽△NAP∽△CAB
∴RB=3/4a,AN=4/3a
∵AB=AN+NM+MB
∴3/4a+4/3a+2a=5
∴a=60/49 ∴PQ=2a=120/49
26、(1)1 ::0.8=X :4.08 求出甲树高X=5.1米
(2)先求墙壁上的影长展开在地上的距离 1 :0.8=1.2:X 求出X=0.96米得出落在地面上的影长一共为0.96+2.4=3.36米则 1:0.8=X:3.36 求出乙树高
X=4.2米
(3)台阶高0.3米投影到地面则影长为1:0.8=0.3:X 求出X=0.24 则在水平面上的总影长为0.24+0.2+4.4=4.84米则1:0.8=X:4.84求出丙树高X=6.05米
(4)1.6:2=X:3.2求出X=2.56米则1:0.8=2.56:X 求出斜面上的影子落在水平面上的影长X=2.048米则丁树在水平面上的总影长为2.048+2.4=4.448 则1:0.8=X:4.448 求出丁树高X=5.56米。
