人教版六年级数学上册第四单元第五课时_圆的面积(例1)
《圆的面积》说课稿

人教版六年级数学(上册)《圆的面积》说课稿麦积区渭南中心学校刘慧贤一、教材的地位和作用圆的面积是六年级上册第四单元的内容,本单元是在学生掌握了直线图形的周长和面积,并且对圆已有初步认识的基础上进行学习的。
从认识圆入手,到圆的周长和面积,与直线图形的学习顺序是一致的。
但是,学习圆是从学习直线图形到学习曲线图形,无论是内容本身,还是研究问题的方法都有所变化。
教材通过对圆的研究,使学生初步认识研究曲线图形的基本方法——“化曲为直"、“化圆为方”,同时也渗透了曲线图形与直线图形的内在联系。
在本单元中,本节内容安排在“认识圆,圆的周长"之后,这样可以让学生借鉴在学习圆周长时的经验来研究圆的面积;有利于让学生感悟学习平面图形的规律和方法。
通过对圆面积的研究,使学生初步掌握研究曲线图形的基本方法,为以后学习圆柱、圆锥的表面积及体积打基础。
二、学情分析学生对圆的特征,多边形面积的计算已基本掌握,但对于像圆这样的曲线图形的面积,学生是第一次接触,如何把圆转化成直线图形具有一定的难度.学生对探究学习并不陌生,但在探究学习过程中,往往是盲目探究,因此,组织学习素材,让学生形成合理猜想,进行有方向的探究也是教学中关注的问题。
三、说教法、学法1、发展迁移原则运用迁移规律,注意从旧到新、引导学生在整理旧知的基础上学习新知,体现“温故知新”的教学思想。
2、学生为主体,教师为主导的教学原则针对几何知识教学的特点、本节课的教学内容以及小学生以形象思维为主,我打算主要采用动手操作,自主探索,合作交流的学习方式,通过课件演示和实践操作,以激发学生的学习兴趣,调动学生的学习积极性.通过学生动手操作、观察、实验得出结论,体现了教学以学生为主体、老师为主导的教学原则。
3、反馈教学法为了体现学生的主体性和创新性,在教学中,采用反馈教学法进行教学,给学生提供一个参与圆面积公式形成和运用的机会,使学生不仅“学会”而且“会学"。
人教版六年级数学《圆的面积》教学设计(优秀7篇)

人教版六年级数学《圆的面积》教学设计(优秀7篇)圆的面积教案篇一教学目标1、使学生理解圆面积公式的推导过程,掌握求圆面积的方法并能正确计算;2、培养学生动手操作的能力,启发思维,开阔思路;3、渗透初步的辩证唯物主义思想。
教学重点和难点圆面积公式的推导方法。
教学过程设计(一)复习准备我们已经学习了圆的认识和圆的周长,谁能说说圆周长、直径和半径三者之间的关系?已知半径,圆周长的一半怎么求?(出示一个整圆)哪部分是圆的面积?(指名用手指一指。
)这节课我们一起来学习圆的面积怎么计算。
(板书课题:圆的面积)(二)学习新课1、我们以前学过的三角形、平行四边形和梯形的面积公式,都是转化成已知学过的图形推导出来的,怎样计算圆的面积呢?我们也要把圆转化成已学过的图形,然后推导出圆面积的计算公式。
决定圆的大小的是什么?(半径)所以,分割圆时要保留这个数据,沿半径把圆分成若干等份。
展示曲变直的变化图。
2、动手操作学具,推导圆面积公式。
为了研究方便,我们把圆等分成16份。
圆周部分近似看作线段,其用自己的学具(等分成16份的圆)拼摆成一个你熟悉的、学过的平面图形。
思考:(1)你摆的是什么图形?(2)所摆的图形面积与圆面积有什么关系?(3)图形的各部分相当于圆的什么?(4)你如何推导出圆的面积?(学生开始动手摆,小组讨论。
)指名发言。
(在幻灯前边说边摆。
)①拼出长方形,学生叙述,老师板书:②还能不能拼出其它图形?学生可以拼出:刚才,我们用不同思路都能推导出圆面积的公式是:S=r2。
这几种思路的共同特点都是将圆转化成已学过的图形,并根据转化后的图形与圆面积的关系推导出面积公式。
例1 一个圆的半径是4厘米,它的面积是多少平方厘米?S=r2=3.1442=3.1416=50.24(平方厘米)答:它的面积是50.24平方厘米。
想一想;求圆面积S应知道什么?如果给d和C,又怎样求圆面积?圆的面积课堂教学设计篇二教学目标:⑴让学生经历探索圆面积公式的过程,能正确计算圆的面积,并能应用公式解决相关的简单实际问题。
六年级数学上册教案34:圆:圆的面积-人教版

3.圆的面积第1课时圆的面积▶教学内容教科书P67~68例1及“做一做”第1题,完成教科书P71“练习十五”中第2题。
▶教学目标1.经历操作、观察、验证、讨论和归纳等过程,探索并掌握圆的面积计算公式,能正确计算圆的面积,能应用圆的面积公式解决相关的简单实际问题。
2.运用转化的数学思想方法解决问题,提升问题解决能力,感悟极限和模型思想,增强空间观念,发展数学思维。
3.进一步体验数学与生活的联系,提高学生学习数学的兴趣。
▶教学重点理解并掌握圆的面积计算公式,能正确地计算圆的面积。
▶教学难点理解圆的面积计算公式的推导过程。
▶教学准备课件,圆规,剪刀。
▶教学过程课前三分钟准备,安全教育一、激趣导入,揭示课题1激趣导入。
师:大家看,一匹马被拴在木桩上。
马在它活动的最大范围内走一圈。
(出示课件)师:那马最多能吃多大面积的草呢?【学情预设】由于这里没有给出具体的数据,不能直接用数据回答。
学生可能不知道怎么表述,如果没有学生回答,也不要强求。
师:马在它活动的最大范围内走一圈的长指的是图中的哪一部分?马最多能吃到的草的部分是圆的什么?【学情预设】学生说出马在它活动的最大范围内走一圈的长是图中圆的周长,马最多能吃到的草的部分是圆的面积。
【设计意图】没有给出具体的数据,主要是借助具体的情境,让学生体会周长和面积的区别,初步感受面积的意义。
2.明确圆面积的含义,揭示课题。
师:你能用自己的话说说什么是圆的面积吗?引导学生表述:圆所占平面的大小就是圆的面积。
师:老师这里有两个圆,哪个圆的面积大一些?为什么?(出示课件)【学情预设】学生都知道左边的圆的面积大一些。
因为在圆的认识中已经知道半径决定圆的大小,这里学生都应该知道左边圆的半径大一些,所以面积大一些。
师:同学们都认为圆的面积大小与它的半径有关,那么圆的面积和半径究竟有怎样的关系呢?这就是我们这节课要研究的问题。
(板书课题:圆的面积)【设计意图】用动画情境引入学习内容,既可以激起学生学习的兴趣,又可以让学生在课堂上涉猎生活中的数学问题,让学生体验到数学个大小不同的圆,初步感知圆的面积大小与圆的半径有关,为后面研究圆的面积的知识奠定基础。
第五单元《圆的面积》(教案)六年级上册数学人教版

第五单元《圆的面积》(教案)
一、教学目标
1.理解圆的基本概念,包括圆心、半径、直径等;
2.掌握计算圆的面积的相关公式和方法;
3.运用所学知识解决实际问题。
二、教学重点
1.圆的基本概念的理解;
2.圆的面积公式和计算方法的掌握。
三、教学难点
1.圆的面积公式的理解和应用;
2.复杂问题的解决方法。
四、教学过程
A. 导入新知识
1.引入课题,带领学生观察一张圆形图案,让学生自己提出与圆形有关的概念。
2.解决学生提出的问题,讲解圆的相关概念,包括圆心、半径、直径等。
B. 讲解新知识
1.介绍圆的面积公式,并通过例题演示如何计算圆的面积。
2.引导学生理解并掌握圆的面积公式,以及运用该公式计算圆的面积的方法。
C. 练习和巩固
1.分组练习计算圆的面积,可以使用实际物品来帮助学生进行计算,如橡皮、盘子等。
2.课堂练习,将学生分成小组通过抢答的方式来巩固所学内容,加深记忆。
D. 拓展和应用
1.引入实际问题,让学生运用所学知识计算圆形物品的面积,并提出相关解决方法。
2.带领学生进行小组讨论,分享各自的解决方法,并从中发现问题、总结经验。
五、课程总结
通过本节课的学习,学生掌握了圆的基本概念和计算圆的面积的相关公式和方法,能够运用所学知识解决实际问题。
此外,在课堂的练习中,还锻炼了学生的思维能力和团队协作能力。
六、板书设计
圆
定义✅圆心
✅半径
✅直径
面积公式πr²。
人教版六年级数学上册第五单元(4) 圆的面积

第4课时圆的面积(1)教学目标1, 使学生理解圆的面积公式推导过程,掌握求圆的面积的方法并正确计算。
2, 激发学生参与整个课堂教学活动的学习兴趣,培养学生的分析、观察和概括能力,发展学生的空间观念。
重点:1、理解圆的面积公式的推导过程。
2、掌握圆的面积的计算公式,能够正确地计算圆的面积。
难点:理解圆的面积公式的推导过程。
导学过程:知识回顾1、什么是面积?2、还记得这些平面图形的面积计算公式吗?写出公式3、平行四边形的面积公式推导过程还记得吗?(我们是通过剪拼的方法把它转化成长方形的。
)新知探究:(一)、定义:请你摸一摸哪里是圆的面积?(圆所占平面的大小就是圆的面积。
)(二)引导学生操作:(拿出一个圆片)提问:我们怎么剪?圆的大小是由什么决定的?。
(沿直径或半径剪。
)我们要把圆通过剪成多份并用拼的方法转化成学过的规则图形,为了计算上的方便,我们把圆平均分成多份。
将一个圆分别平均分成2份、4分、8分、16份……分别罗列排观察几组图提问:随着等分份数的不断增加,你有什么发现吗?A:随着等分份数的不断增加,曲线越来越直。
B:随着等分份数的不断增加,每一小份越来越接近三角形。
(三)拼摆推导面积公式。
学生操作把圆转化成了什么图形?。
我们来试一试,展示学生的作品。
提问:转化后的图形面积与圆的面积有什么关系?。
1、拼摆:课件演示:把圆等分成不同等份时的图形的趋势。
2、推导面积公式:小组讨论:长方形各部份相当于圆的什么?。
请你推导圆的面积公式。
学生汇报:(说推导过程)3,读圆面积公式(S=πγ2)。
并说说圆面积的大小与什么有关?给直径怎么办?。
给出周长呢?。
知识梳理:本节课学习了什么知识?。
随堂练习:1、根据下面所给的条件,求圆的面积。
(1)、半径2分米(2)、直径10厘米(3)、周长25.12cm2、计算:①公园草地上一个自动旋转喷灌装置的射程市10m,它能喷灌的面积是多少?②一个圆的周长是125.6cm,它的面积是多少平方厘米?3、判断:(1)圆的半径越大,圆所占的面积也越大。
六年级上册数学教案-第5单元3圆的面积人教版(1)

六年级上册数学教案第5单元 3 圆的面积人教版 (1)作为一名经验丰富的教师,我对于本节课的教学内容、教学目标、教学难点与重点、教具与学具准备、教学过程、板书设计、作业设计以及课后反思都有着深思熟虑的规划和准备。
一、教学内容本节课的教学内容选自人教版六年级上册第5单元《圆的面积》。
我们将学习圆的面积的计算方法,以及如何将圆等分成若干份来推导出圆的面积公式。
二、教学目标通过本节课的学习,我希望学生们能够掌握圆的面积的计算方法,理解圆的面积公式的推导过程,并能运用圆的面积公式解决实际问题。
三、教学难点与重点本节课的重点是圆的面积公式的推导和应用,难点是理解圆的面积公式的推导过程。
四、教具与学具准备为了更好地进行课堂教学,我准备了PPT、圆的面积公式的黑板板书、圆的模型、以及练习题。
五、教学过程1. 实践情景引入:我会通过展示一些生活中的圆形物体,如圆桌、圆形的操场等,让学生们观察并思考这些物体的面积如何计算。
2. 讲解圆的面积公式:我会用PPT展示圆的面积公式的推导过程,同时用黑板板书进行详细讲解,让学生们理解并掌握圆的面积公式。
3. 例题讲解:我会选取一些典型的例题进行讲解,让学生们通过实例来理解和运用圆的面积公式。
4. 随堂练习:我会给出一些练习题,让学生们在课堂上进行练习,巩固他们对圆的面积公式的理解和运用。
5. 作业布置:我会布置一些有关圆的面积的练习题,让学生们课后进行巩固练习。
六、板书设计板书设计主要包括圆的面积公式和推导过程,以及一些关键的步骤和要点。
七、作业设计答案:半径为5cm的圆面积为78.5cm²,半径为8cm的圆面积为200.96cm²,半径为10cm的圆面积为314cm²。
2. 一辆自行车轮胎的直径为70cm,求轮胎的面积。
答案:轮胎的半径为35cm,面积为3848.45cm²。
八、课后反思及拓展延伸课后,我会对课堂教学进行反思,看学生们是否掌握了圆的面积公式,以及对例题的理解和运用情况。
2022-2023学年六年级数学上册典型例题系列之第五单元圆的面积基础篇(解析版)人教版

2022-2023学年六年级数学上册典型例题系列之第五单元圆的面积基础篇(解析版)编者的话:《2022-2023学年六年级数学上册典型例题系列》是基于教材知识点和常年考点考题总结与编辑而成的,该系列主要包含典型例题、专项练习、分层试卷三大部分。
典型例题部分是按照单元顺序进行编辑,主要分为计算和应用两大部分,其优点在于考题典型,考点丰富,变式多样。
专项练习部分是从常考题和期末真题中选取对应练习,其优点在于选题经典,题型多样,题量适中。
分层试卷部分是根据试题难度和掌握水平,主要分为基础卷、提高卷、拓展卷三大部分,其优点在于考点广泛,分层明显,适应性广。
本专题是第五单元圆的面积基础篇。
本部分内容考察圆面积的计算公式及实际应用,部分考点和题型难度稍大,建议作为本章重点内容进行讲解,一共划分为十五个考点,欢迎使用。
【考点一】圆与长方形的拼切转化问题。
【方法点拨】把一个圆割成一个近似的长方形,割拼成的长方形的长相当于圆周长的一半,用字母πr表示,宽相当于圆的半径,用字母r表示,因为长方形的面积=长×宽,所以圆的面积=πr2。
【典型例题】把一个圆平均分成若干个小扇形,再拼成一个近似的长方形,这个长方形的长是9.42厘米,周长是24.84厘米,这个圆的周长是()厘米,面积是()厘米2。
解析:圆的半径:9.42÷3.14=3(厘米)圆的周长:9.42×2=18.84(厘米)圆的面积:3.14×32=3.14×9=28.26(平方厘米)【对应练习1】在学习圆的面积计算公式时,是通过转化的思想,把圆转化成长方形后推导出来的。
小明把一个圆转化成近似长方形后,发现圆的周长比长方形周长少8厘米,如图,那么原来圆的面积是( )平方厘米。
解析:圆的半径:82=4÷(厘米)圆的面积:20324.4⨯(平方厘米).14=5所以圆的面积是:50.24(平方厘米)【对应练习2】把一个圆形硬纸片剪拼成一个近似的长方形后,周长比原来增加了8dm,这个圆的半径是( )dm,近似长方形的面积是( )dm²。
人教版 六年级上册 第五单元《圆》单元作业设计
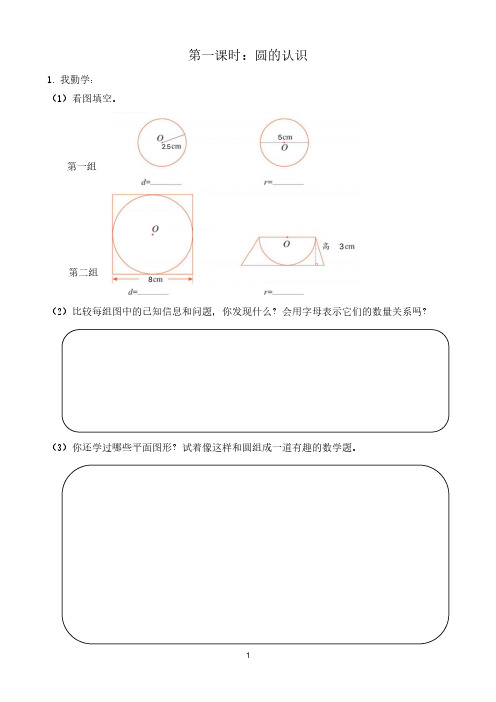
8
4.我尝试: 用一根绳子在操场上围出一块地,你有几种围法?怎样围面积最大? (1)你觉得选择多长的绳子方便操作,说说你的想法。
(2)你学过哪些平面图形,有几种围法?分别画出示意图,并计算每种图形的面积,说说你 的理由。
(3)如果在这块地上,摆放直径为1m的圆形桌子,最多可以放几张,请你结合生活实际画图 说理。
2.我能行: 体育课上,同学们正在进行抢球比赛。老师把球筐放在操场中间,要求同学们围在一起比赛 ,想一想,要如何站位才公平呢?说说你的想法,并试着在方框里画出示意图。
示意图
3,我尝试: (1)怎样才能画出一个半径2米的圆,你有什么好办法?先试着画个示意图,再实践体验, 并与大家分享你的收获。
示意图
(2)
减去
得到
外圆面积 —
内圆面积 = 圆环面积
用字母表示 (
)— (
)=(
)
2.我善思:
在研究圆环面积的计算方法时,我们学会运用“外圆面积-内圆面积=圆环面积”的方法。观
察上图,你能借助研究圆的面积计算公式的方法,把圆环也平均分成若干份吗?试着拼成一
个近似的平行四边形,这时平行四边形的底是( ),平行四边形的面积是(
示意图
3.收获乐园: 收获乐园
用你喜欢的方式(如画图、列表、写提纲等),把当天的学习内容整理记录下来。
4.成长乐园:
我勤学
能基本完成 ☆
有实践精神 ☆☆
有突破和协作 ☆☆☆
精神
自评
○ 满意
他评
○ 满意
师评
○ 满意
送给自己一句话:
我反思 我善思 ☆ ☆☆ ☆☆☆
我成长 我能行 ☆ ☆☆ ☆☆☆
我尝试 ☆ ☆☆ ☆☆☆
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
宽 =半径
长 = 圆周长的一半
长方形面积 = 长
×
宽
r
圆面积 = 周长一半 × 半径 C S = × r 2 1 2πr = × r 2 =πr×r
1
r
C 2
=πr2
S = πr2
复习:
r
r = 2分米
小明发现这个半径2分米的圆,它的周长和直径是一样的。
求周长:2×3.14×2 =3.14×4 =12.56(分米) 求面积: 3.14×22
=3.14×102 =3.14×100 =314 (m2)
3、小刚量得一棵树干的周长是125.6cm。这棵树干 的横截面的面积是多少?
(1)树干横截面的半径: 125.6÷3.14÷2 = 40÷2
综合列式:
3.14×(125.6÷3.14÷2)2 = 3.14×202 = 3.14×400 = 1256 (cm2)
求面积:
( 原 来 平 行 四 边 形 的 高 )
长 方 形 的 宽 长方形的长 (原来平行四边形的底)
将圆转化成什么样的图形来推导它的面积计算公式呢?
分成4份
分成4份
分成8份ቤተ መጻሕፍቲ ባይዱ
分成8份
分成16份
分成16份
分成32份
1、观察你拼成的图形,和同桌说一说: 长方形的长是圆的( ) 长方形的宽是圆的( )
=πr2
谢谢同学们的努力! 再见
= 20(cm)
(2)树干横截面的面积:
3.14×20
2
=3.14×400 =1256 (cm2)
答:它的面积是1256平方厘米.
知道哪些条件就可 求圆的面积?
(知道半径、直径或是周长)
1
:知道直径
第3题:知道周长
3.14×(125.6÷3.14÷2)2 = 3.14×202 = 3.14×400 = 1256 (cm2) S=π(d÷2)2
3.14×102
=3.14×100
=314 (m2)
答:它能喷灌的面积是314平方米。
*知识拓展*
三角形的底是
4 c = c ,高是4r 16 4
根据三角形面积公式可得:
c 1 × × 4r 4 2 2πr 1 × 4r × = 4 2
=πr2
*知识拓展*
5 3 ,高是2r 梯形的上底是 C ,下底是 C 16 16 根据梯形面积公式可得: 5 1 3 C+ ×( ) C 16 16 2 1 c × × 2r = 2 2 1 = × πr × 2r 2 × 2r
=3.14×4 =12.56(平方分米)
除了转化为长方形,还能转化为什么 图形呢?
1
圆形花坛的直径是20m,它的面积是多少平方米?
(1)花坛的半径: 20÷2=10(m) (2)花坛的面积: 3.14×102 =3.14×100 =314 (m2) 答:它的面积是314平方米。
综合列式: 3.14×(20÷2)2
人教版六年级数学上册第四单元
圆的 面积
马郎小学 陈伟
复习:什么叫平面图形的面积? 下列图形的面积是如何计算的? a a h a a h b h a
S=a2
S=ah
S=ah÷2
S=(a+b)h÷2
b
a
S=ab
圆所占平面的大小叫做圆的面积。
复习:
r
r = 2分米
求周长:2×3.14×2 =3.14×4 =12.56(分米)
3.14×(20÷2)2 =3.14×102 =3.14×100
=314 (m2)
S=π(d÷2)2
圆的面积公式: 用S表示圆的面积
知道半径:
知道直径: 知道周长:
S=πr2
d2 S=π( ) 2
S=π(d÷2)2
S=π(C÷π÷2)2
2、公园草地上一个自动旋转喷灌装置的射程是10m, 它能喷灌的面积是多少?
