2012中考数学试题及答案分类汇编:平面几何基础
2012年全国中考数学试题分类解析汇编专题52:平面几何的综合
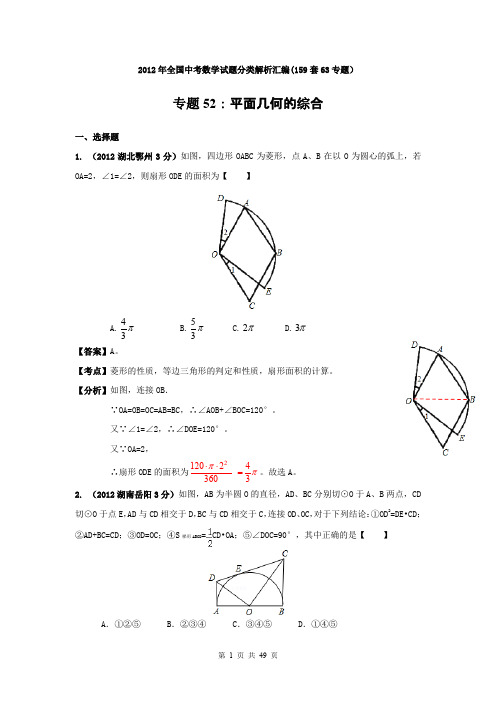
2012年全国中考数学试题分类解析汇编(159套63专题)专题52:平面几何的综合一、选择题1. (2012湖北鄂州3分)如图,四边形OABC 为菱形,点A 、B 在以O 为圆心的弧上,若OA=2,∠1=∠2,则扇形ODE 的面积为【 】A.π34B.π35C.π2D.π3【答案】A 。
【考点】菱形的性质,等边三角形的判定和性质,扇形面积的计算。
【分析】如图,连接OB .∵OA=OB=OC=AB=BC,∴∠AOB+∠BOC=120°。
又∵∠1=∠2,∴∠DOE=120°。
又∵OA=2,∴扇形ODE 的面积为21202 4 3603ππ⋅⋅=。
故选A 。
2. (2012湖南岳阳3分)如图,AB 为半圆O 的直径,AD 、BC 分别切⊙O 于A 、B 两点,CD 切⊙O 于点E ,AD 与CD 相交于D ,BC 与CD 相交于C ,连接OD 、OC ,对于下列结论:①OD 2=DE•CD; ②AD+BC=CD;③OD=OC;④S 梯形ABCD =CD•OA;⑤∠DOC=90°,其中正确的是【 】A .①②⑤ B.②③④ C.③④⑤ D.①④⑤【答案】A 。
【考点】切线的性质,切线长定理,相似三角形的判定与性质。
1052629【分析】如图,连接OE ,∵AD 与圆O 相切,DC 与圆O 相切,BC 与圆O 相切,∴∠DAO=∠DEO=∠OBC=90°,∴DA=DE,CE=CB ,AD∥BC。
∴CD=DE+EC=AD+BC。
结论②正确。
在Rt△ADO 和Rt△EDO 中,OD=OD ,DA=DE ,∴Rt△ADO≌Rt△EDO(HL )∴∠AOD=∠EOD。
同理Rt△CEO≌Rt△CBO,∴∠EOC=∠BOC。
又∠AOD+∠DOE+∠EOC+∠COB=180°,∴2(∠DOE+∠EOC)=180°,即∠DOC=90°。
结论⑤正确。
∴∠DOC=∠DEO=90°。
福建省各市2012年中考数学试题分类解析汇编 专题8 平面几何基础

福建省各市2012年中考数学试题分类解析汇编专题8:平面几何基础一、选择题1. (2012福建龙岩4分)下列命题中,为真命题的是【 】A .对顶角相等B .同位角相等C .若22=a b ,则=a bD .若a >b ,则22a >b -- 【答案】A 。
【考点】真命题,对顶角的性质,同位角的定义,平方根的意义,不等式的性质。
【分析】根据对顶角的性质,同位角的定义,平方根的意义,不等式的性质分别作出判断:A .对顶角相等,命题正确,是真命题;B .两平行线被第三条直线所截,同位角才相等,命题不正确,不是真命题;C .若22=a b ,则=a b ±,命题不正确,不是真命题;D .若a >b ,则22a <b --,命题不正确,不是真命题。
故选A 。
2. (2012福建龙岩4分)下列几何图形中,既是轴对称图形又是中心对称图形的是【 】A .等边三角形B .矩形C . 平行四边形D .等腰梯形【答案】B 。
【考点】轴对称图形和中心对称图形。
【分析】根据轴对称图形与中心对称图形的概念,轴对称图形两部分沿对称轴折叠后可重合;中心对称图形是图形沿对称中心旋转180度后与原图重合。
因此,只有矩形既是轴对称图形又是中心对称图形。
故选B 。
3. (2012福建南平4分)正多边形的一个外角等于30°.则这个多边形的边数为【 】A .6B .9C .12D .15【答案】C 。
【考点】多边形的外角性质。
【分析】正多边形的一个外角等于30°,而多边形的外角和为360°,则:多边形边数=多边形外角和÷一个外角度数=360°÷30°=12。
故选C 。
4. (2012福建宁德4分)下列两个电子数字成中心对称的是【 】【答案】A 。
【考点】中心对称图形。
【分析】根据轴中心对称图形的概念,中心对称图形是图形沿对称中心旋转180度后与原图重合。
2002-2012上海中考数学试题分类解析汇编专题7-平面几何基础

2002年-2012年上海市中考数学试题分类解析汇编专题7:平面几何基础和向量一、选择题1.(上海市2002年3分)下列命题中,正确的是【 】 (A )正多边形都是轴对称图形;(B )正多边形一个内角的大小与边数成正比例; (C )正多边形一个外角的大小随边数的增加而减少; (D )边数大于3的正多边形的对角线长相等. 【答案】A ,C 。
【考点】正多边形和圆,命题与定理。
【分析】根据正多边形的性质,以及正多边形的内角和.外角和的计算方法即可求解:A 、所有的正多边形都是轴对称图形,故正确;B 、正多边形一个内角的大小=(n -2)×180n ,不符合正比例的关系式,故错误;C 、正多边形的外角和为360°,每个外角=0360n,随着n 的增大,度数将变小,故正确;D 、正五边形的对角线就不相等,故错误。
故选A ,C 。
2.(上海市2008年Ⅱ组4分)计算32a a -的结果是【 】 A .aB .aC .a -D .a -【答案】B 。
【考点】向量的计算。
【分析】根据向量计算的法则直接计算即可:32=a a a -。
故选B 。
3.(上海市2008年Ⅱ组4分)如图,在平行四边形ABCD 中,如果AB a =,AD b =,那么a b +等于【 】A .BDB .ACC .DBD .CA【答案】B 。
【考点】向量的几何意义。
【分析】根据向量的意义,=a b AC +。
故选B 。
4.(上海市2009年4分)下列正多边形中,中心角等于内角的是【 】 A .正六边形 B .正五边形C .正四边形C .正三边形【答案】C 。
【考点】多边形内角与外角。
【分析】正n 边形的内角和可以表示成02180n -⋅(),则它的内角是等于02180n n-⋅(),n 边形的中心角等于0360n,根据中心角等于内角就可以得到一个关于n 的方程:002180360n n n-⋅=(),解这个方程得n =4,即这个多边形是正四边形。
广东省2012年中考数学试题分类解析汇编 专题8 平面几何基础

某某2012年中考数学试题分类解析汇编专题8:平面几何基础一、选择题1. (2012某某省3分)已知三角形两边的长分别是4和10,则此三角形第三边的长可能是【】A. 5 B.6 C.11 D.16【答案】C。
【考点】三角形三边关系。
【分析】设此三角形第三边的长为x,则根据三角形两边之和大于第三边,两边之差小于第三边的构成条件,得10﹣4<x<10+4,即6<x<14,四个选项中只有11符合条件。
故选C。
2. (2012某某某某3分)下列图形中,既是轴对称图形又是中心对称图形的是【】【答案】B。
【考点】轴对称图和中心称对形。
【分析】根据轴对称图形与中心对称图形的概念,轴对称图形两部分沿对称轴折叠后可重合;中心对称图形是图形沿对称中心旋转180度后与原图重合。
因为圆既是轴对称图形又是中心对称图形,故选B。
3. (2012某某某某3分)下列图形中是轴对称图形的是【】A.B.C.D.【答案】C。
【考点】轴对称图形。
【分析】根据轴对称图形的概念,轴对称图形两部分沿对称轴折叠后可重合,对各选项分析判断后利用排除法求解:A、不是轴对称图形,故本选项错误;B、不是轴对称图形,故本选项错误;C、是轴对称图形,故本选项正确;D、不是轴对称图形,故本选项错误。
故选C。
4. (2012某某某某4分)下列平面图形,既是中心对称图形,又是轴对称图形的是【】A.等腰三角形 B.正五边形 C.平行四边形 D.矩形【答案】D。
【考点】中心对称图形,轴对称图形。
【分析】根据轴对称图形与中心对称图形的概念,轴对称图形两部分沿对称轴折叠后可重合;中心对称图形是图形沿对称中心旋转180度后与原图重合。
因此,A、∵等腰三角形不是中心对称图形,是轴对称图形,故此选项错误;B、∵正五边形形不是中心对称图形,是轴对称图形,故此选项错误;C、平行四边形图形是中心对称图形,但不是轴对称图形,故此选项错误;D、∵矩形既是中心对称图形,又是轴对称图形,故此选项正确。
浙江省温州市2001-2012年中考数学试题分类解析 专题8 平面几何基础

2001-2012年浙江温州中考数学试题分类解析汇编(12专题)专题8:平面几何基础一、选择题1. (2001年浙江温州3分)如图,正方体ABCD-A1B1C1D1中,与平面A1C1平行的平面是【】A.平面AB1 B.平面AC C.平面A1D D.平面C1D【答案】B。
【考点】认识立体图形。
【分析】根据正方体的概念和特性,相对的面互相平行,因此,和平面A1C1相对的面是平面AC,那么这两个面平行。
故选B。
2. (2002年浙江温州4分)如图,立方体 ABCD—A1B1C1D1中,与棱AD垂直的平面是【】A.平面A1B,平面CD1 B.平面A1D,平面BC1C.平面AC,平面A1C1 D.平面BD,平面AD1【答案】A。
【考点】认识立体图形。
【分析】根据正方体的概念和特性,与棱AD垂直的平面是:平面A1B和平面CD1。
故选A。
3. (2003年浙江温州4分)如图,长方体ABCD-A1B1C1D1中,与平面AC平行的平面是【】A.平面AD1 B.平面A1C1 C.平面BC l D.平面A1B【答案】B。
【考点】认识立体图形。
【分析】根据正方体的概念和特性,相对的面互相平行,因此,和平面AC相对的面是平面A1C1,那么这两个面平行。
故选B。
4. (2004年浙江温州4分)下面给出的四条线段中,最长的是【】(A) a (B) b (C) c (D) d【答案】D。
【考点】比较线段的长短。
【分析】通过观察比较:d线段长度最长。
故选D。
5. (2004年浙江温州4分)高斯用直尺和圆规作出了正十七边形,如图, 正十七边形的中心角∠AOB的度数近似于【】(A) 11° (B) 17° (C) 21° (D) 25°【答案】C。
【考点】正多边形和圆。
【分析】正多边形一定有外接圆,且每条边所对的中心角相等,因此360°÷17≈21°。
故选C。
6. (2005年浙江温州4分)如图,正方体ABCD-A1B1C1D1中,与平面A1C1平行的平面是【】A、平面AB1B、平面ACC、平面A1DD、平面C1D【答案】B。
湖南各市2012年中考数学试题分类解析汇编专题8:平面几何基础

湖南各市2012年中考数学试题分类解析汇编专题8:平面几何基础一、选择题1. (2012湖南长沙3分)下列平面图形中,既是轴对称图形,又是中心对称图形的是【】A.B.C.D.【答案】A。
【考点】轴对称图形和中心对称。
【分析】根据轴对称图形与中心对称图形的概念,轴对称图形两部分沿对称轴折叠后可重合;中心对称图形是图形沿对称中心旋转180度后与原图重合。
因此,A、是轴对称图形,也是中心对称图形,故本选项正确;B、是轴对称图形,不是中心对称图形,故本选项错误;C、不是轴对称图形,是中心对称图形,故本选项错误;D、是轴对称图形,不是中心对称图形,故本选项错误。
故选A。
2. (2012湖南长沙3分)下列四个角中,最有可能与70°角互补的是【】A.B.C.D.【答案】D。
【考点】补角。
【分析】根据互补的两个角的和等于180°求出70°角的补角,然后结合各选项即可选择:70°角的补角=180°﹣70°=110°,是钝角,结合各选项,只有D选项是钝角,所以,最有可能与70°角互补的是D选项的角。
故选D。
3. (2012湖南长沙3分)现有3cm,4cm,7cm,9cm长的四根木棒,任取其中三根组成一个三角形,那么可以组成的三角形的个数是【】A.1个B.2个C.3个D.4个【答案】B。
【考点】构成三角形的三边的条件。
【分析】四条木棒的所有组合:3,4,7和3,4,9和3,7,9和4,7,9,根据三角形两边之和大于第三边,两边之差小于第三边的构成条件,只有3,7,9和4,7,9能组成三角形。
故选B。
4. (2012湖南益阳4分)下列图案中是中心对称图形但不是轴对称图形的是【】A.B.C.D.5. (2012湖南益阳4分)下列命题是假命题的是【】A.中心投影下,物高与影长成正比B.平移不改变图形的形状和大小C.三角形的中位线平行于第三边D.圆的切线垂直于过切点的半径【答案】A。
【中考12年】江苏省泰州市2001-2012年中考数学试题分类解析 专题8 平面几何基础

2001-2012年某某某某中考数学试题分类解析汇编(12专题)专题8:平面几何基础一、选择题2.(2001某某某某4分)①若不等式()a 2x 2a <--的解集为x 1>-,则a 2<。
②若α、β+3+2αβαβ--,则以α、β为根的一元二次方程为2x +3x+2=0。
③方程(x+3x 3=0-的解为x=3±。
④用反证法证明“三角形中至少有一个内角不小于600”。
第一步应假设三角形中三个内角都小于600。
以上4条解答,正确的条数为【 】。
A.0B. 1C. 2D.3【答案】C 。
【考点】解不等式,非负数的性质,一元二次方程的根,解无理方程,反证法。
【分析】根据相关知识逐一判断:①当a 2<时,原不等式化为2a x a 2>--,即x 1>-;当a 2>时,原不等式化为2a x a 2<--,即x 1<-。
∴若不等式()a 2x 2a <--的解集为x 1>-,则a 2<。
∴结论正确。
②∵α、β为实数,且+3+2=0αβαβ--,∴+3=02=0αβαβ-- ,,即+=3=2αβαβ ,。
∴根据一元二次方程根与系数的关系知,以α、β为根的一元二次方程为2x 3x+2=0-。
∴结论错误。
③∵当x=3-时,方程()x+3x 3=0-无意义,∴结论错误。
④结论正确。
∴正确的条数为2条。
故选C 。
3.(某某省某某市2002年4分)等腰三角形一边长为4,一边长9,它的周长是【 】A 、17B 、22C 、17或22D 、13【答案】B 。
【考点】等腰三角形的性质,三角形的构成条件。
【分析】分底边是4和底边是两种情况讨论:当底边是4时:三边是4,9,9,则周长是22;当底边是9时:三边是:4,4,9,因为4+4<9不能构成三角形。
∴等腰三角形的周长为22。
故选B 。
4.(某某省某某市2002年4分)下列图形中是中心对称图形的是【 】A 、B 、C 、D 、【答案】C 。
辽宁省各市2012年中考数学分类解析 专题8 平面几何基础

某某各市2012年中考数学试题分类解析汇编专题8:平面几何基础一、选择题1. (2012某某某某3分)下列图形是中心对称图形的是【 】A .B .C .D .【答案】C 。
【考点】中心对称图形。
【分析】根据中心对称图形的概念,中心对称图形是图形沿对称中心旋转180度后与原图重合。
因此,根据中心对称图形的定义可知:只有C 选项旋转180°后能和原来的图形重合。
故选C 。
2. (2012某某某某3分)如图,C 、D 分别EA 、EB 为的中点,∠E=300,∠1=1100,则∠2的度数为【 】A.080B. 090C. 0100D. 0110【答案】A 。
【考点】三角形中位线定理,平行线的性质,三角形外角性质。
【分析】∵C、D 分别EA 、EB 为的中点,∴CD∥AB。
∴∠ECD=∠2。
∵∠1是△ECD 的外角,∴∠E+∠ECD=∠1。
∵∠E=300,∠1=1100,∴∠ECD=1100-300=800。
故选A 。
3. (2012某某某某3分)下列图形中,既是轴对称图形又是中心对称图形的是【 】【答案】A。
【考点】轴对称图形和中心对称图形。
【分析】根据轴对称图形与中心对称图形的概念,轴对称图形两部分沿对称轴折叠后可重合;中心对称图形是图形沿对称中心旋转180度后与原图重合。
因此,A. 既是轴对称图形又是中心对称图形,选项正确;B. 是轴对称图形不是中心对称图形,选项错误;C. 是中心对称图形不是轴对称图形,选项错误;D. 是轴对称图形不是中心对称图形,选项错误。
故选A。
4. (2012某某某某3分)下列交通标志是轴对称图形的是【】A. B. C. D.【答案】A。
【考点】轴对称图形。
【分析】根据轴对称图形与,轴对称图形两部分沿对称轴折叠后可重合。
因此,只有选项A 符合。
故选择A。
5. (2012某某某某3分)下列各图,不是轴对称图形的是【】【答案】A。
【考点】轴对称图形。
【分析】根据轴对称图形的概念,轴对称图形两部分沿对称轴折叠后可重合,因此,选项A 不是轴对称图形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2012中考数学试题及答案分类汇编:
平面几何基础
一、选择题
1.(河北省2分)如图,∠1+∠2等于
A 、60°
B 、90°
C 、110°
D 、180°
【答案】B 。
【考点】平角的定义。
【分析】根据平角的定义得到∠1+90°+∠2=180°,即由∠1+∠2=90°。
故选B 。
2.(河北省3分)已知三角形三边长分别为2,x ,13,若x 为正整数 则这样的三角形个数为
A 、2
B 、3
C 、5
D 、13
【答案】B 。
【考点】一元一次方程组的应用,三角形三边关系。
【分析】根据三角形的三边关系:三角形两边之和大于第三边,两边差小于第三边,得
213132x >x <+⎧⎨+⎩
,解得,11<x <15,所以,x 为12、13、14。
故选B 。
3.(山西省2分)如图所示,∠AOB 的两边.OA 、OB 均为平面反光镜,
∠AOB=35°,在OB 上有一点E ,从E 点射出一束光线经OA 上的点D 反射后,反射光线DC 恰好与OB 平行,则∠DEB 的度数是
A .35°
B .70°
C .110°
D .120°
【答案】B 。
【考点】平行线的性质,入射角与反射角的关系,三角形内角和定理,等腰三角形的性质。
【分析】过点D 作DF ⊥AO 交OB 于点F ,则DF 是法线,根据入射角等
于反射角的关系,得∠1=∠3,
∵CD ∥OB ,∴∠1=∠2(两直线平行,内错角相等)。
∴∠2=∠3(等量代换);
在Rt △DOF 中,∠ODF=90°,∠AOB=35°,
∴∠2=55°;∴在△DEF 中,∠DEB=180°-2∠2=70°。
故选B 。
4.(山西省2分)一个正多边形,它的每一个外角都等于45°,则该正多边形是
A .正六边形
B .正七边形
C .正八边形
D .正九边形
【答案】C 。
【考点】多边形内角与外角。
【分析】多边形的外角和是360度,因为是正多边形,所以每一个外角都是45°,即可得到外角的个数,从而确定多边形的边数:∵360÷45=8,∴这个正多边形是正八边形。
故选C 。
5.(内蒙古巴彦淖尔、赤峰3分)下列图形中,∠1一定大于∠2的是
A 、D C
B A 21
22112
1O
【答案】C 。
【考点】对顶角的性质,内错角的性质,三角形外角定理,圆周角定理。
【分析】根据对顶角的性质,内错角的性质,三角形外角定理,圆周角定理逐一作出判断:
A.∠1和∠2是对顶角,根据对顶角相等的性质,∠1=∠2,选项错误;
B.∠1和∠2是内错角,当两条直线平行时∠1=∠2,选项错误;
C.根据三角形的外角等于和它不相邻的两内角之和的性质,得∠1>∠2,选项正确;
D.根据同弧所对圆周角相等的性质,∠1=∠2,选项错误。
故选C。
6.(内蒙古包头3分)已知下列命题:
①若a=b,则a2=b2;
②若x>0,则|x|=x;
③一组对边平行且对角线相等的四边形是矩形;
④一组对边平行且不相等的四边形是梯形.
其中原命题与逆命题均为真命题的个数是
A、1个
B、2个
C、3个
D、4个
【答案】A。
【考点】命题与定理,原命题和逆命题,有理数的乘方,绝对值,矩形的判定,梯形的判定。
【分析】根据真假命题的定义,逐个选项进行分析即可得出答案:
①若a=b,则a2=b2,其逆命题为若a2=b2,则a=b,逆命题错误,故本选项错误,
②若x>0,则|x|=x,其逆命题为若|x|=x,则x>0,逆命题错误,故本选项错误,
③例如等腰梯形,满足一组对边平行且两条对角线相等,但它不是矩形,故本选项错误,
④一组对边平行且不相等的四边形是梯形,其逆命题为若四边形是梯形,则它的对边平行且不相等,原命题和逆命题都正确,故本选项正确。
所以,原命题与逆命题均为真命题的个数为1个。
故选A。
7.(内蒙古乌兰察布3分)下列图形既是轴对称图形,又是中心对称图形的是
【答案】D。
【考点】中心对称和轴对称图形。
【分析】根据轴对称图形与中心对称图形的概念,轴对称图形两部分沿对称轴折叠后可重合;中心对称图形是图形沿对称中心旋转180度后与原图重合。
只有选项D符合。
故选D。
8.(内蒙古乌兰察布3分)如图,已知矩形ABCD ,一条直线将该矩形ABCD 分割成两个多边形,若这两个多边形的内角和分别为M 和N ,则M + N
不可能是
A . 3600
B . 5400
C 7200
D . 6300
【答案】D。
【考点】图形的分割,三角形和多边形内角和定理。
【分析】条直线将该矩形ABCD 分割成两个多边形,可能有三种情况:①分割线经过两个顶点,多边形被分成两个三角形,根据三角形内角和定理,得M + N=3600;②分割线只经过一个顶点,多边形被分成一个三角形和一个四边形,根据三角形和多边形内
角和定理,得M + N=5400;③分割线不经过顶点,多边形被分成两个四边形,根据多边形内角和定理,得M + N=7200。
因此,M + N 不可能是6300。
故选D 。
二、填空题
1. (天津3分)如图,六边形ABCDEF 的六个内角都相等.若AB=1,BC=CD=3,
DE=2,则这个六边形的周长等于 ▲ 。
【答案】15。
【考点】多边形内角和定理,补角定义,正三角形的判定和性质。
【分析】如图,把AF ,BC ,DE 分别向两边延长,分别交于点G ,H ,I 。
∵六边形ABCDEF 的六个内角都相等,
∴根据多边形内角和定理,得六边形的每个内角都是
()0
62180=1206-。
∴△ABG ,△CDH ,△EFI 的每个内角都是600。
∴△ABG ,△CDH ,△EFI 和△GHI 都是正三角形。
∵AB=1,BC=CD=3,DE=2,
∴GH=GB +BC +CH=AB +BC +CD=1+3+3=7。
EF=EI=HI -HD -DE=GH -CD -DE=7-3-2=2。
AF=GI -GA -FI=GH -AB -EF=7-1-2=4。
∴六边形的周长=AB +BC +CD +DE +EF +AF=1+3+3+2+2+4=15。
2.(内蒙古呼伦贝尔3分)正n 边形的一个外角是30°,则n= ▲ 。
【答案】12。
【考点】多边形内角和定理,平角定义。
【分析】由正n边形的一个外角是30°,根据平角定义,它的每个内角是1500。
根据多边形内角和定理,得,(n-2)×1800=n×1500,解得,n=12。
三、解答题
1.(山西省9分)如图,△ABC是直角三角形,∠ACB=90°.
(1)实践与操作利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法).
①作△ABC的外接圆,圆心为O;
②以线段AC为一边,在AC的右侧作等边△ACD;
③连接BD,交⊙O于点F,连接AE,
(2)综合与运用在你所作的图中,若AB=4,BC=2,则:
①AD与⊙O的位置关系是______.(2分)
②线段AE的长为__________.(2分)
【答案】解:(1)作图如下:
(2)①相切。
②4
21
7。
【考点】尺规作图,直线与圆的位置关系,勾股定理。
【分析】(1)①以AB为直径作圆O即可。
②分别以A、B为半径作弧交于点D连接AD,CD即可。
③根据题意连接,找到交点即可。
(2)①可证∠BAD=90°,由切线的判定得出AD 与⊙O 的位置关系:
∵AB=4,BC=2,△ACD 是等边三角形。
∴∠BAD=∠BAC+∠CAD=30°+60°=90°。
∴AD 与⊙O 的位置关系是相切。
②根据三角形的面积公式即可求出线段AE 的长:
∵AB=4,BC=2,∴AD=AC=224223-=,BD=()2222AB AD 423
27+=+=。
∵11
AB AD AE BD 22⋅=⋅,即11 423AE 2722⋅⋅=⋅⋅,∴4AE 217=。
