轴心受力构件计算表
轴心受力构件
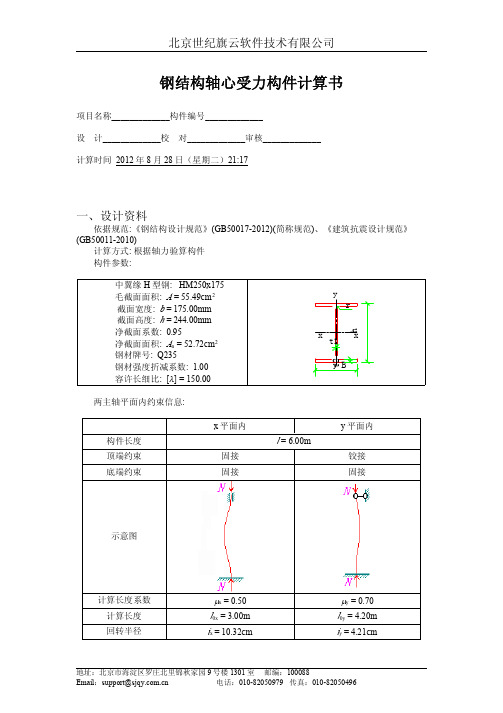
第4章 轴心受力构件4.1 概述轴心受力构件广泛地应用于钢结构承重构件中，如钢屋架、网架、网壳、塔架等杆系结构的杆件，平台结构的支柱等。
这类构件，在节点处往往做成铰接连接，节点的转动刚度在确定杆件计算长度时予以适当考虑，一般只承受节点荷载。
根据杆件承受的轴心力的性质可分为轴心受拉构件和轴心受压构件。
一些非承重构件，如支撑、缀条等，也常常由轴心受力构件组成。
轴心受力构件的截面形式有三种：第一种是热轧型钢截面，如图4-1(a )中的工字钢、H 型钢、槽钢、角钢、T 型钢、圆钢、圆管、方管等；第二种是冷弯薄壁型钢截面，如图4-1(b )中冷弯角钢、槽钢和冷弯方管等；第三种是用型钢和钢板或钢板和钢板连接而成的组合截面，如图4-1(c )所示的实腹式组合截面和图4-1(d ) 所示的格构式组合截面。
轴心受力构件的截面必须满足强度、刚度要求，且制作简单、便于连接、施工方便。
因此，一般要求截面宽大而壁厚较薄，能提供较大的刚度，尤其对于轴心受压构件，承载力一般由整体稳定控制，宽大的截面因稳定性能好从而用料经济，但此时应注意板件的局部屈曲问题，板件的局部屈曲势必影响构件的承载力。
4.2 轴心受力构件的强度轴心受力构件的强度计算是以构件的净截面达到屈服应力为限ynf A N ==σ根据概率极限状态设计法，N 取设计值（标准值乘以荷载分项系数），yf 也去设计值（除以抗力分项系数087.1=Rγ）即f，钢材设计强度见附表1.1，P313。
表达式为fA N n≤ （4.1）nA 为轴心受力构件的净截面面积。
在螺栓连接轴心受力构件中，需要特别注意。
4.3 轴心受力构件的刚度为满足正常使用要求，受拉构件（包括轴心受拉、拉弯构件）、受压构件（轴心受压构件、压弯构件）不宜过分细长，否则刚度过小，制作、运输、安装过程中易弯曲（P118列出四种不利影响）。
受拉和受压构件的刚度通过长细比λ控制][),max(max λλλλ≤=y x （4.4） 式中x x x i l /0=λ，yy y i l /0=λ；][λ为容许长细比，见表4.1，4.2。
钢结构轴心受力构件计算书GB50017-2012
地址：北京市海淀区罗庄北里锦秋家园 9 号楼 1301 室 邮编：100088
Email：support@
电话：010-82050979 传真：010-82050496
北京世纪旗云软件技术有限公司
荷载参数: N = 200.00kN
受力状态: 轴心受压
二、强度验算
构件截面的最大厚度为 11.00mm, 根据《钢结构设计规范》(GB50017-2012)表 5.4.1, f = 215.00N/mm2 , fy =235.00N/mm2 , fu =370.00N/mm2
t2 h
y r
x t1 x yB
两主轴平面内约束信息:
构件长度 顶端约束 底端约束
x 平面内
固接 固接
l = 6.00m
y 平面内
铰接 固接
示意图
计算长度系数 计算长度 回转半径
µx = 0.50 l0x = 3.00m ix = 10.32cm
µy = 0.70 l0y = 4.20m iy = 4.21cm
235
235
腹板净高 h0 与其厚度 tw 之比:
h0 = 200.00 = 28.57 <= min [ 21
235 + 0.42λ , 7
tw 7.00
235.00
式中, λ-------两主轴方向长细比的较大值; 根据规范 8.3.1-1, 腹板高厚比满足
235 + 50 ] = 62.90 235.00
2. 腹板高厚比验算
地址：北京市海淀区罗庄北里锦秋家园 9 号楼 1301 室 邮编：100088
Email：support@
电话：010-82050979 传真：010-82050496
钢筋混凝土轴心受力构件承载力计算
图5.3
5.2.2 轴心受拉构件承载力计算
5.2.2.1 截面形式
轴心受压柱以方形为主，也可选用矩形、圆形或 正多边形截面；柱截面尺寸一般不宜小于 250mm×250mm，构件长细比应控制在l0/b≤30、 l0/h≤25、l0/d≤25。
此处l0为柱的计算长度，b为柱的短边，h为柱的 长边，d为圆形柱的直径。
l0 垂直排架方向 有柱间支撑 无柱间支撑
1.2H
1.0H
1.0H
1.2H
有吊车房屋 柱
上柱 下柱
2.0Hu 1.0Hl
1.25Hu 0.8Hl
1.5Hu 1.0Hl
露天吊车柱和栈桥柱
2.0Hl
1.0Hl
—
表5.3 框架结构各层柱的计算长度
楼盖类型 现浇楼盖 装配式楼盖
柱的类别 底层柱
其余各层柱 底层柱
图5.5 柱中箍筋的构造要求
5.2.3 配有普通箍筋轴心受压柱的承载力计算
根据构件的长细比（构件的计算长度l0与构件截 面回转半径i之比）的不同，轴心受压构件可分为短柱 （对矩形截面l0/b≤8,b为截面宽度）和长柱。
5.2.3.1 试验研究分析
钢筋混凝土短柱经试验表明：在整个加载过程 中，由于纵向钢筋与混凝土粘结在一起，两者变形 相同，当混凝土的极限压应变达到混凝土棱柱体的 极限压应变ε0=0.002时，构件处于承载力极限状态， 稍再增加荷载，柱四周出现明显的纵向裂缝，箍筋 间的纵筋向外凸出，最后中部混凝土被压碎而宣告 破坏（图5.6）。因此在轴心受压柱中钢筋的最大压 应变为0.002，故不宜采用高强钢筋，对抗压强度高 于400N/mm2者，只能取400N/mm2
【例5.2】某现浇多层钢筋混凝土框架结构，底层中柱按轴
钢结构原理-第4章轴心受力构件
存在，且都是变量，再 加上材料的弹塑性，轴 压构件属于极值点失稳， 其极限承载力Nu很难用 解析法计算，只能借助 计算机采用数值法求解。
《钢结构原理》 第4章 轴心受力构件
缺陷通常只考虑影响最大的残余应力和初弯曲（l/1000）。 采用数值法可以计算出轴压构件在某个方向（绕 x 或 y 轴）的 柱子曲线，如下图，纵坐标为截面平均应力与屈服强度的比值， 横坐标为正则化长细比。
《钢结构原理》 第4章 轴心受力构件
4.1 概述
4.1.1 定义：构件只承受轴心力的作用。 承受轴心压力时称为轴心受压构件。 承受轴心拉力时称为轴心受拉构件。
N
N
N
N
《钢结构原理》 第4章 轴心受力构件
4.1.2 轴心受力构件的应用 平面及空间桁架（钢屋架、管桁架、塔桅、网架等）； 工业及民用建筑结构中的一些柱； 支撑系统；等等。
(a) N
(b) N
Hale Waihona Puke (c) NNN
N
《钢结构原理》 第4章 轴心受力构件
4.4.3 理想轴心受压构件的弯曲屈曲 4.4.3.1 弹性弯曲屈曲
取隔离体，建立平衡微分方程
EyIN y0
用数学方法解得：N 的最 小值即分岔屈曲荷载 Ncr，又称 为欧拉荷载 NE 。
Ncr2EI/l2
对应的临界应力为：
《钢结构原理》 第4章 轴心受力构件
4.4 轴心受压构件的整体稳定
概念：在压力作用下，构件的外力必须和内力相平衡。 平衡有稳定、不稳定之分。当为不稳定平衡时，轻微的扰 动就会使构件产生很大的变形而最后丧失承载能力，这种 现象称为丧失稳定性，简称失稳，也称屈曲。 特点：与强度破坏不同，构件整体失稳时会导致完全 丧失承载能力，甚至整体结构倒塌。失稳属于承载能力极 限状态。与混凝土构件相比，钢构件截面尺寸小、构件细 长，稳定问题非常突出。只有受压才有稳定问题。
轴心受力构件
第4章 轴心受力构件例题 4.1 某焊接组合工字形截面轴心受压构件的截面尺寸如图4-13所示，承受轴心压力设计值(包括构件自重)N ＝2000kN ，计算长度l 0y ＝6m ，l 0x ＝3m ，翼缘钢板为火焰切割边，钢材为Q345，截面无削弱。
要求验算该轴心受压构件的整体稳定性是否满足设计要求，并计算整体稳定承载力。
图4—13 焊接工字形截面解 （1）截面及构件几何特性计算A =250×12×2+250×8=8000mm 2I y =(250×2743-242×2503)/12=1.1345×108 mm 4 I x =(12×2503×2+250×83)/12=3.126×107 mm 41.1198000/101345.1/8=⨯==A I i y y mm5.628000/10126.3/7=⨯==A I i x x mmλy =l 0y /i y =6000/119.1=50.4 λx =l 0x /i x =3000/62.5=48.0 (2)整体稳定性验算查表4－5，截面关于x 轴和y 轴都属于b 类，λy >λx1.61235/3454.50235/==y y f λ查附表7得φ=0.80169.31180008016.01020003=⨯⨯=A N ϕN/mm 2≈f =310N/ mm 2 故可认为整体稳定性满足要求。
（3）整体稳定承载力计算φAf =0.8016×8000×310=1.988×106N=1988kN 该轴心受压构件的整体稳定承载力为1988kN 。
例题4.2 某焊接T 形截面轴心受压构件截面尺寸如图4—14所示。
承受轴心压力设计值(包括构件自重)N ＝2000kN ，计算长度l 0x ＝l 0y ＝3m ，翼缘钢板为火焰切割边，钢材为Q345，截面无削弱。
轴心受力构件计算
ห้องสมุดไป่ตู้
f y / 235
图4.21 我国的柱子曲线
4.3.5 轴心受压构件的整体稳定计算
轴心压杆临界应力σ cr确定之后，构件的整体稳定计 算，其稳定计算式应为：
cr cr f y N f A R fy R
2)扭转屈曲：绕纵轴扭转; 3)弯扭屈曲：即有弯曲变形也有扭转变形。
图4.11 轴心压杆的屈曲变形
(a)弯曲屈曲；(b)扭转屈曲；(c)弯扭屈曲
弯曲屈曲：双轴对称截面，单轴对称截面绕非对称轴； 扭转屈曲：十字形截面； 弯扭屈曲：单轴对称截面（槽钢，等边角钢）。
4.3.2理想轴心压杆弯曲屈曲临界应力
— 构件计算长度
i--截面的回转半径
表4.2 受拉构件的容许长细比 承受静力荷载或间接承受动力荷载的结构 构件名称 一般建筑结构 桁架的杆件 吊车梁或吊车桁架以 下的柱间支撑 350 300 400 有重级工作制吊车的厂房 250 200 350 直接承受动力 荷载的结构 250 — —
其他拉杆、支撑、系 杆(张紧的圆钢除外)
2
cr
fy
图4.24 轴心受压构件的局部失稳(c)
由此确定宽厚比限值 b / t
（1）翼缘（三边简支一边自由）
图4.21
轴心受压构件的翼缘失稳
b 235 (10 0.1 ) t fy
λ- 两方向长细比的较大值
不满足此条件时 加大厚度 t
当λ小于30时，取30；当λ大于100时，取100
注：残余应力对弱轴的影响大于对强轴的影响
轴心受力构件部分公式及例题
N c = ϕAf = 0.802 × 8000 × 315 = 2020000 N = 2020 kN
钢结构原理 Principles of Steel Structure
第四章
轴心受力构件
某焊接T形截面轴心受压构件的截面尺寸如右图所示 形截面轴心受压构件的截面尺寸如右图所示， 例4.2 某焊接 形截面轴心受压构件的截面尺寸如右图所示， 承受轴心压力设计值（包括自重） 承受轴心压力设计值（包括自重）N=2000kN，计算长度 ， l0x=l0y=3m，翼缘钢板为火焰切割边，钢材为 ，翼缘钢板为火焰切割边，钢材为Q345， ， f=315N/mm2，截面无削弱，试计算该轴心受压构件的整体 截面无削弱， 稳定性。 稳定性。
(
)
λz =
=
Iω
2 Ai0 2 lω + I t 25.7
y
-250×8 ×
80 × 180.7 = 45.2 2 536500 300 + 28.7 25.7
x
x
λz < λ y，λx
故该构件由弯曲屈曲控制设计。 故该构件由弯曲屈曲控制设计。
钢结构原理 Principles of Steel Structure
-250×8 ×
x
x
y -250×12 ×
钢结构原理 Principles of Steel Structure
第四章 1、截面及构件几何性质计算 、
截面面积 惯性矩： 惯性矩：
轴心受力构件
A = 250 × 12 × 2 + 250 × 8 = 8000mm 2 1 I x = ( 250 × 2743 − 242 × 2503 ) = 1.1345 × 108 mm 4 12 1 I y = (12 × 2503 × 2 + 250 × 83 ) = 3.126 × 107 mm 4 y 12
轴心受力构件
轴心受力构件设计轴心受拉构件时需进行强度和刚度的验算，设计轴心受压构件时需进行强度、整体稳定、局部稳定和刚度的验算。
一、轴心受力构件的强度和刚度1．轴心受力构件的强度计算轴心受力构件的强度是以截面的平均应力达到钢材的屈服点为承载力极限状态f A N n ≤=σ (1) 式中 N ——构件的轴心拉力或压力设计值；n A ——构件的净截面面积；f ——钢材的抗拉强度设计值。
采用高强度螺栓摩擦型连接的构件，验算最外列螺栓处危险截面的强度时，按下式计算：f A N n≤='σ (2) 'N =)5.01(1n n N - (3)式中 n ——连接一侧的高强度螺栓总数；1n ——计算截面(最外列螺栓处)上的高强度螺栓数；0.5——孔前传力系数。
采用高强度螺栓摩擦型连接的拉杆，除按式(2)验算净截面强度外，还应按下式验算毛截面强度f A N ≤=σ (4)2．轴心受力构件的刚度计算轴心受力构件的刚度是以限制其长细比保证][λλ≤ (5) 式中 λ——构件的最大长细比；[λ]——构件的容许长细比。
二、 轴心受压构件的整体稳定1．理想轴心受压构件的屈曲形式理想轴心受压构件可能以三种屈曲形式丧失稳定：①弯曲屈曲 双轴对称截面构件最常见的屈曲形式。
②扭转屈曲 长度较小的十字形截面构件可能发生的扭转屈曲。
③弯扭屈曲 单轴对称截面杆件绕对称轴屈曲时发生弯扭屈曲。
2．理想轴心受压构件的弯曲屈曲临界力若只考虑弯曲变形，临界力公式即为著名的欧拉临界力公式，表达式为N E =22l EI π=22λπEA (6) 3．初始缺陷对轴心受压构件承载力的影响实际工程中的构件不可避免地存在初弯曲、荷载初偏心和残余应力等初始缺陷，这些缺陷会降低轴心受压构件的稳定承载力。
1）残余应力的影响当轴心受压构件截面的平均应力p f >σ时，杆件截面内将出现部分塑性区和部分弹性区。
由于截面塑性区应力不可能再增加，能够产生抵抗力矩的只是截面的弹性区，此时的临界力和临界应力应为：N cr =22l EI e π=22lEI π·I I e (7) cr σ=22λπE ·I I e (8) 式中 I e ——弹性区的截面惯性矩(或有效惯性矩)；I ——全截面的惯性矩。
轴心受力构件和拉弯、压弯构件的计算
v v1 v2
v''
1
M
x
/ EI
x
Nv / EI x
dv2 dz
1V
1
dM dz
x
1Nv '
v2'' 1Nv''
其中 1 ——单位剪力作用下剪切角变形
v'' v1'' v2'' Nv / EI x 1Nv''
v''
N
v 0
EIx (1 1N )
稳定平衡方程的解
Ncr
2EIx
框架柱的计算长度
第5.3.4条：单厂阶形柱的计算长度
考虑折减——荷载较大的柱失稳时会受到低荷载柱的支承作用； ——考虑厂房的空间作用； ——对多跨厂房，如刚性屋盖或设屋盖纵向水平支撑――则将柱顶视作不动铰支座。
单阶柱
（1）下段柱的计算长度系数 2 ：
当柱上端和横梁铰接时，按柱上端为自由的单阶柱的数值乘以折减系数（整体作用）
1、受压时保证单构件稳定 2、受拉是保证均匀传力 3、分支距离近，填板刚度大，
可视作实腹截面
轴压构件的抗剪验算
第5.1.6条：
第5.1.7条：
1.此时如按柱剪力验算支撑，不十 分恰当，因为该剪力可视作轴压构 件的偶然剪力。
当撑杆的作用是支撑一系列柱 时，就完全不对了 2.原理：带支撑压杆的挠度增量及 支撑构件的轴向变形，根据变形协 调条件推导其轴力； 3.此支撑力不与其他作用产生的轴 力叠加，而是取较大值； 4.一道支撑架在同一方向所支撑的 柱不宜超过8根。
λ
多条柱子曲线 （200多条）
影响因素： 截面形式、尺寸 残余应力分布 初偏心、初弯曲、初扭曲
钢结构设计轴心受力构件截面强度计算
钢结构设计轴心受力构件截面强度计算7.1.1 轴心受拉构件，当端部连接及中部拼接处组成截面的各板件都由连接件直接传力时，其截面强度计算应符合下列规定：1 除采用高强度螺栓摩擦型连接者外，其截面强度应采用下列公式计算：2 采用高强度螺栓摩擦型连接的构件，其毛截面强度计算应采用式（7.1.1-1），净截面断裂应按下式计算：3 当构件为沿全长都有排列较密螺栓的组合构件时，其截面强度应按下式计算：式中：N——所计算截面处的拉力设计值(N)；f——钢材的抗拉强度设计值(N／mm2)；A——构件的毛截面面积(mm2；A n——构件的净截面面积，当构件多个截面有孔时，取最不利的截面(mm2)；f u——钢材的抗拉强度最小值(N／mm2)；n——在节点或拼接处，构件一端连接的高强度螺栓数目；n1——所计算截面(最外列螺栓处)高强度螺栓数目。
7.1.2 轴心受压构件，当端部连接及中部拼接处组成截面的各板件都由连接件直接传力时，截面强度应按本标准式(7.1.1-1)计算。
但含有虚孔的构件尚需在孔心所在截面按本标准式(7.1.1-2)计算。
7.1.3 轴心受拉构件和轴心受压构件，当其组成板件在节点或拼接处并非全部直接传力时，应将危险截面的面积乘以有效截面系数η，不同构件截面形式和连接方式的η值应符合表7.1.3的规定。
表7.1.3 轴心受力构件节点或拼接处危险截面有效截面系数条文说明7.1.1 原规范在条文说明中给出了式(7.1.1-1)和式(7.1.1-2)，并指出“如果今后采用屈强比更大的钢材，宜用这两个公式来计算，以确保安全”。
当前，屈强比高于0.8的Q460钢已开始采用，为此，用这两个公式取代了净截面屈服的计算公式。
对于Q235和Q345钢，用这两个公式可以节约钢材。
当沿构件长度有排列较密的螺栓孔时，应由净截面屈服控制，以免变形过大。
7.1.2 轴压构件孔洞有螺栓填充者，不必验算净截面强度。
7.1.3 有效截面系数是考虑了杆端非全部直接传力造成的剪切滞后和截面上正应力分布不均匀的影响。
角钢,工字钢、槽钢、圆钢规格重量及构件受力计算表格含附页
X轴截面强度验算 57.53 63.75 kN/cm2 kN/cm2
Y轴截面强度验算 57.53 280.75 kN/cm2 kN/cm2
s强度= (1-0.5n1/n)*N/An = s稳定= N/(An*j) =
4 轴心受压构件计算剪力 V = (A*f/85)*(fy/235)6505 795
kN cm
M [钢件最大弯矩值] Ao [钢件的截面面积]
0 113.08
kN-cm cm2
16 21.5 12.5 10.2 21.5
mm mm mm mm mm
NbHFV
NbHWV[腹板摩擦型高强螺栓抗剪承载力设计值] 3 钢构件截面特性 钢构件截面特性 构件截面类别 I [相应轴截面慣性矩] 1876 20.37 39.03 0.9023 1.05 X轴截面特性 b 46909
B.
轴心受力构件计算书 H500x200x10.2x16-12.5 1 构件信息 N [钢件的轴力值] L [ 钢件的计算长度] 截面信息 B [钢件截面宽度] 200 mm tFb [钢件翼缘厚] dFb [翼缘螺孔径] r H [钢件截面高度] 500 mm [内圆弧半径] tWb [钢件腹板厚] dWb [腹板螺孔径] 2 钢构件材质信息 f fv fy [钢材抗拉、抗压、抗弯强度设计值] [钢材抗剪强度设计值] [钢材屈服强度设计值] [翼缘摩擦型高强螺栓抗剪承载力设计值] 21.5 12.5 23.5 83.8 83.8 kN/cm2 kN/cm2 kN/cm2 KN KN Y轴截面特性 X轴截面 cm
焊接H型钢截面特征 H 几何特征 500 mm Ix 截面特性 46909 cm4 B 200 mm Wx 1876 cm3 tw 10.2 mm Iy 2137 cm4 tf 16 mm Wy 214 cm3 r 12.5 mm 截面面积 113.08 cm2 每米重量 88.8 kg/m 外表面积 1.76 m2/m
第四章 轴心受力构件 -公式整理
( 4 27b )
B、等边双角钢截面，图（b）
b
y
b
当 b t 0.58 l 0 y b时：
4 0 . 475 b yz y 1 2 2 l0 y t 当 b t 0.58 l 0 y b时：
y
（b）
( 4 28a )
yz
a x
1 分肢对最小刚度轴 1 1的长细比, 1 l 01 i1 ；
l 01 分肢计算长度，焊接时 ，取相邻缀板间净距 离；螺栓连接时，取相 邻两缀板边缘螺栓的 距离。
1
x
3、缀材的设计
计算证明，在常用的常细比范围内 85 235 f y ，
l
z
N
因此平行于缀材面的最大柱剪力：
当 b1 t 0.56 l 0 y b 1 时：
2 2 l b1 0yt 3 .7 1 t 52.7b14
( 4 30a )
yz
( 4 30b )
④、单轴对称的轴心受压构件在绕非对称轴以外的任意轴失稳时 ，应按弯扭屈曲计算其稳定性。
当计算等边角钢构件绕平行轴（u轴)稳 定时，可按下式计算换算长细比，并按b类 截面确定 值：
热 扎 剖 分T 形 钢 ：
自由边受拉时：
h0 235 15 0 .2 tw fy
h0 235 13 0 .17 tw fy
( 4 46 )
tw
( 4 47 )
h0
tw
h0
焊 接T形 钢 ：
t
( 4 48 )
D
3、圆管截面
D 235 100 t fy
( 4 52 )
建筑结构——轴心受力构件计算
求出初选截面面积及回转 ixT和iyT 。
A N
f
ixT
l0 x
（21.9） (21.10)
ixT
l0 x
（21.11）
b.根据 A，ixT和iyT 在型钢表中选一适当的型钢截面。
(2) 组合截面 如果在型钢表中不能够找到比较适当的规格时，可采用组合截面。
a. 初定截面轮廓尺寸 h ixT
1
b iyT
表21.1
表21.2
（4）屈曲分析 a. 如（图21.7）所示两 端 铰支的理想细长压杆，当N力较小时，杆件只有
轴心压缩变形，杆轴保持平直。这时如有外力F干扰，使它微弯，当F力撤去 后，杆件又恢复原来的直线状态，这时杆件处于稳定的平衡状态。
b. 随着N力逐渐加大到某一数值时，如有外力F干扰，杆件微弯，撤除 F力后，杆件仍保持微弯状态，不再恢复到原来的直线状态。这种平衡状态 叫随遇平衡。
l0
2EI l
l0 l , 称为计算长度系数。其值见表21.3
（21.5）
表21.3
1.实际轴心受压构件的实用计算方法
（1）柱子曲线
轴心受压杆件失稳时临界应力与cr 长细比
之间的关系曲线称为
柱子曲线，《钢结构设计规范》将柱子曲线归纳为a,b,c,d四组。 详见表21.4
（本表只列出常用的a、b、c三种类型）。
2C1.3 轴心受力构件
1.轴心受力构件的强度 （1）概述
承载能力是以截面的平均应力达到钢材的屈服强度为极限状态。当构 件截面有削弱时，截面的应力分布不再是均匀的，如图（21.4a）
图21.4 有孔洞拉杆的截面应力分布
构件孔洞附近有应力集中现象。但最后截面上各点的应力均可达到屈服强度，如
受拉构件的承载力计算—轴心受拉构件
E'c=0.5Ec
c= ftk,
又 s E c
s = 2Eftk
故开裂轴力：
Ncr = Ac ftk + 2Eftk As
（3）混凝土开裂后： 混凝土退出工作，应力全部由钢筋承担，钢筋应力急剧增加。 配筋率增大，裂缝间距减小，最大裂缝宽度减小，反之亦然， 当然裂缝间距及裂缝宽度也和钢筋直径有关。
（4）破坏阶段： 受拉钢筋屈服，整个截面裂缝全部裂通。
Nu= fyAs
2.轴心受拉构件承载力计算
N Nu= fyAs
N ––– 轴向拉力的设计值; N u ––– 轴向受拉构件的极限承载力; As ––– 纵向受拉钢筋截面面积; fy ––– 钢筋抗拉设计强度值. 注意 ： 轴心受拉构件的钢筋用量并不是由强度要求确定的， 裂缝宽度验算对纵筋用量起决定作用。
轴心受拉构件正截面承载力计算 （建筑规范）
1.轴心受拉构件受力特点
（1）混凝土开裂前：
N Ncr
•钢筋与混凝土共同承担拉力
cftk
s = c c = Ec c s = Es s
sAs
2Eftk
s
Es Ec
c
E c
其时： •混凝土应力等于其开裂强度，并且进入了塑性发展阶段， 其变形模量降低为：
钢结构轴心受力构件计算
钢结构轴心受力构件计算3.1 轴心受力构件概述在钢结构中，轴心受力构件的应用十分广泛，如桁架、塔架和网架、网壳等杆件体系。
这类结构的节点通常假设为铰接，当无节间荷载作用时，杆件只受轴向力（轴向拉力或轴向压力）的作用，称为轴心受力构件（轴心受拉构件或轴心受压构件）。
图3-1所示为轴心受力构件在工程上应用的一些实例。
图3-1 轴心受力构件在工程中的应用（a）桁架；（b）塔架；（c）网架轴心受力构件常用的截面形式可分为实腹式和格构式两大类。
（1）实腹式构件制作简单，与其他构件的连接也比较方便，常用的截面形式很多，可直接选用轧制型钢截面，如圆钢、钢管、角钢、工字钢、H 型钢、T 型钢等[图3-2（a）]；也可选用由型钢或钢板组成的组合截面[图3-2（b）]；在轻型结构中则可采用冷弯薄壁型钢截面[图3-2（c）]。
以上这些截面中，截面紧凑（如圆钢）或对两主轴刚度相差悬殊者（如单槽钢、工字钢），一般适用于轴心受拉构件，而受压构件通常采用较为开展、组成板件宽而薄的截面。
（2）格构式构件[图3-2（d）]容易使压杆实现两主轴方向的稳定性。
这种构件的刚度大、抗扭性好，用料较省。
格构式截面一般由两个或多个型钢肢件组成，肢件之间采用缀条或缀板连成整体，缀条和缀板统称为缀材。
图3-2 轴心受力杆件的截面形式（a）轧制型钢截面；（b）焊接实腹式组合截面；（c）冷弯薄壁型钢截面；（d）格构式截面3.2 轴心受力构件的强度及刚度轴心受拉构件的设计除根据结构用途、构件受力大小和材料供应情况选用合理的截面形式外，还要对所选截面进行强度和刚度验算。
强度要求就是使构件截面上的最大正应力不超过钢材的强度设计值，刚度要求就是使构件的长细比不超过容许长细比。
轴心受压构件在设计时，除使所选截面满足强度和刚度要求外，还应使其满足构件整体稳定性和局部稳定性的要求。
整体稳定性要求是使构件在设计荷载作用下不致发生屈曲而丧失承载能力；局部稳定性要求一般是使组成构件的板件宽厚比不超过规定限值，以保证板件不会屈曲，或者使格构式构件的分肢不发生屈曲。
轴心受力构件的强度和刚度计算
轴心受力构件的强度和刚度计算1．轴心受力构件的强度计算轴心受力构件的强度是以截面的平均应力达到钢材的屈服应力为承载力极限状态。
轴心受力构件的强度计算公式为f A Nn≤=σ （4-1） 式中： N ——构件的轴心拉力或压力设计值；n A ——构件的净截面面积；f ——钢材的抗拉强度设计值。
对于采用高强度螺栓摩擦型连接的构件，验算净截面强度时一部分剪力已由孔前接触面传递。
因此，验算最外列螺栓处危险截面的强度时，应按下式计算：f A N n≤='σ （4-2）'N =)5.01(1nn N - （4-3）式中： n ——连接一侧的高强度螺栓总数；1n ——计算截面（最外列螺栓处）上的高强度螺栓数； 0.5——孔前传力系数。
采用高强度螺栓摩擦型连接的拉杆，除按式（4-2）验算净截面强度外，还应按下式验算毛截面强度f AN≤=σ （4-4）式中： A ——构件的毛截面面积。
2．轴心受力构件的刚度计算为满足结构的正常使用要求，轴心受力构件应具有一定的刚度，以保证构件不会在运输和安装过程中产生弯曲或过大的变形，以及使用期间因自重产生明显下挠，还有在动力荷载作用下发生较大的振动。
轴心受力构件的刚度是以限制其长细比来保证的，即][λλ≤ （4-5）式中： λ——构件的最大长细比；[λ]——构件的容许长细比。
3. 轴心受压构件的整体稳定计算《规范》对轴心受压构件的整体稳定计算采用下列形式：f AN≤ϕ （4-25）式中：ϕ——轴心受压构件的整体稳定系数，ycrf σϕ=。
整体稳定系数ϕ值应根据构件的截面分类和构件的长细比查表得到。
构件长细比λ应按照下列规定确定： （1）截面为双轴对称或极对称的构件⎭⎬⎫==y y y x x x i l i l //00λλ（4-26）式中：x l 0，y l 0——构件对主轴x 和y 的计算长度；x i ，y i ——构件截面对主轴x 和y 的回转半径。
双轴对称十字形截面构件，x λ或y λ取值不得小于5.07b/t （其中b/t 为悬伸板件宽厚比）。