静电场习题课
静电场习题优秀课件

设经过S1、S2旳电场强度通量分别为1、2,经过整个
球面旳电场强度通量为3,则
[]
(A)1>2,3=q/0 (B)1<2,3=2q/0 (C)1=2,3=q/0; (D)1<2,3=q/0;
q
o
S2
图1-4
2q
o
X
S12a
答:[ D ]
1-14(a) 点电荷q位于边长为a旳正立方体旳中心,经 过此立方体旳每一面旳电通量各是多少?
(b) 若电荷移至正方体旳一种顶点上,则经过每个面 旳电通量又各是多少?
解: (a) 因为6个全等旳正方形构成一种封闭
面, 所以 q 6 0
(b) 该顶点可视为边长等于2a 旳大立方 q
体旳中心, 经过每个大面旳电通量为 每个小立方体中不经过该顶点旳
6 0
三个小面上旳电通量为
q
24 0
而经过该顶点旳另三个 小面旳电通量为0.
s
E
dS
4r
2E
q内
0
(1) E1 = 0
(2)E2
q1
4 0r22
9
109
1.0 108 (0.2)2
q1 q2
2.25 103 v / m
(3)
E3
q1 q2
4 0r32
9
109
(1.0
1.5) (0.5)2
108
9 102 v / m
E不是r旳连续函数, 在两个球面处有跃变.
1-16 (1)设地球表面附近旳场强约为200v·m-1,方向指向 地球中心,试求地球所带旳总电量。 (2) 在离地面 1400m高处,场强降为20v·m-1,方向仍指向地球中心, 试计算在1400m下大气层里旳平均电荷密度.
静电场习题课

2
(2)两离子初速度分别为 v、v/,则
L 2v L qE n m
L 2v l′ + qE = v m
L 2m Δt=t-t′ = (v v ) vv qE
L 2m 0 要使 Δt=0,则须 vv qE 2mvv 所以:E= qL
7.如图所示,同一竖直平面内固定着两水平绝缘细杆 AB、CD,长 均为 L,两杆间竖直距离为 h,BD 两端以光滑绝缘的半圆形细杆 相连,半圆形细杆与 AB、CD 在同一竖直面内,且 AB、CD 恰为半 圆形圆弧在 B、D 两处的切线,O 为 AD、BC 连线的交点,在 O 点 固定一电量为 Q 的正点电荷.质量为 m 的小球 P 带正电荷,电量 为 q,穿在细杆上,从 A 以一定初速度出发,沿杆滑动,最后可 到达 C 点.已知小球与两水平杆之间动摩擦因数为μ ,小球所受 库仑力始终小于小球重力.求: (1) P 在水平细杆上滑动时受摩擦力的极大值和极小值; (2) P 从 A 点出发时初速度的最小值.
1 2 -mgh-2mg·2L=0- 2 mv0 ,
得 v0= 2 gh(h 2L) .
8.一个质量为m,带有电荷-q的小物体,可在倾角 为θ 的绝缘斜面上运动,斜面底端有一与斜面垂 直的固定绝缘挡板,斜面顶端距底端的高度为h, 整个斜面置于匀强电场中,场强大小为E,方向水 平向右,如图所示.小物体与斜面的动摩擦因数 为μ ,且小物体与档板碰撞时不损失机械能。求: (1) 为使小物体能从静止开始沿斜面下滑,μ 、q、 E、θ 各量间必须满足的关系。 (2) 小物体自斜面顶端从静止开始沿斜面下滑到 停止运动所通过的总路程。
6.飞行时间质谱仪可通过测量离子飞行时间得到离子的荷质比 q/m,如 图 1。 带正电的离子经电压为 U 的电场加速后进入长度为 L 的真空管 AB, 可测得离子飞越 AB 所用时间 t1。改进以上方法,如图 2,让离子飞越 AB 后进入场强为 E(方向如图)的匀强电场区域 BC,在电场的作用下 离子返回 B 端,此时,测得离子从 A 出发后飞行的总时间 t2, (不计离 子重力) ⑴忽略离子源中离子的初速度, ①用 t1 计算荷质比; ②用 t2 计算荷质比。
第一章(5)习题课

∴
E
0,
( r R)
E的方向垂直轴线沿径向, > 0则背离轴线;
R ˆ, ( r R ) r 0r
< 0则指向轴线。
11、无限大的均匀带电平面,电荷面密度为,P点与 平面的垂直距离为d,若取平面的电势为零,则P点的 电势 V p d / 2 0 ,若在P点由静止释放一个电子(其 质量为m,电量绝对值为e)则电子到达平面的速率为:
3、一均匀静电场,场强 E (400i 600 j )V m 1 , 则点a(3、2)和点b(1、0)之间的电势差为 Vab 2000V
解 : E 400i 600 j
b b a a
dl dxi dyj
Vab E dl (400i 600 j ) (dxi dyj )
侧 面 EdS E 侧 面 dS 2πrhE
(1) r < R时,
qi 0 ,
qi 由高斯定理 Φ ε0
即 2πrhE 0, 得 E 0 (2) r > R时, q i 2πRhσ ,
qi 由高斯定理 Φ ε0
σR 即 2πrhE 2πRhσ / ε0 , 得 E ε0 r
2
10.( 第一章习题二 .9) 无限长均匀带电圆柱面,电荷 面密度为,半径为R,求圆柱面内外的场强分布。
解:作一半径为r,高为h的同轴圆柱面
R r
E
为高斯面, 根据对称性分析,圆柱面 侧面上任一点的场强大小相等, 方向
h E
S
ˆ r
沿矢径方向。 Φ S E dS 上底 E dS 下底 E dS 侧面 E dS
14静电场习题课

X
由于左右半圆环电荷分布的对称性,合场强的y分量抵消 由于左右半圆环电荷分布的对称性,合场强的y
λ dl + )=- dEx=dEcos( π φ 2cos φ 4ππR 0 λR 0 2 =- d 2cosφ φ 4ππR 0
λ0 2π 2 Ex=- ∫ cos φd φ 4πε R 0 0 λ0 2π 1-cos 2φ =- dφ ∫ 0 4πε R 2 0 λ0 =- 4ε0 R
2
d
•
⇒ E = 0 试指出其错误。 试指出其错误。
答:所选球面上场强的大小不处处相等,不能用: 所选球面上场强的大小不处处相等,不能用:
E • dS = E • 4πr ∫∫
S
2
〔例5〕已知空间电场强度分布为 〕 求(1)通过图示立方体的电通量, )通过图示立方体的电通量, (2)该立方体内的总电荷是多少? )该立方体内的总电荷是多少? 解:(1) :( )
q ∴U 0= =U球 4πε r 0
〔例14〕正电荷均匀分布在半径为R的球形体积内,电荷体 〕正电荷均匀分布在半径为R的球形体积内, 密度为ρ,求球内a点与球外b点的电势差时, ρ,求球内 密度为ρ,求球内a点与球外b点的电势差时,得出结果
R O
σ
x
X
σ -σ x E= i + 〔1- i〕 2 2 2ε 2ε R +x 0 0 σ x = i 2 2 2ε R +x 0
U= E •d l ∫Ecos π = -E(-dx) = dl ∫ ∫
0 x 0 x 0 x
σ 0 x 注意符号变换! 注意符号变换! dx = ∫ 2 x 2 2ε R +x 0 -1 σ 01 2 2 = ∫(R +x ) 2d(R 2+x2) x 2ε 2 0 σ 1 (R +x )2 0 σ = 〔 • 〕 = 〔R- R 2+x2〕 x 1 2ε 2 2ε 0 0 2
静电场习题课

e ES cos
闭合曲面外法线方向(自内向外)为正
s
穿进闭合面的电场线对该闭合面提供负通量; 穿出闭合面的电场线对该闭合面提供正通量 C.有时利用高斯定理求电通量非常方便
利用高斯定理求电通量 例1: 点电荷q位于正立方体中 q 心,则通过侧面abcd的电通量 e 6
4 0
(A)
0
(B)
(C)
(D)
8 0
2. 如图所示,两个“无限长”的共轴圆柱面, 半径分别为R1和R2,其上均匀带电,沿轴线 方向单位长度上所带电荷分别为1和2 ,则 在两圆柱面之间、距离轴线为r的P点处的场 [ A ] 强大小E为: 1 1 1 2 2 (A) 2 π r (B) (C) 2 R r (D) 2 0 r R1 0 2 2 0 r 0
UP
i
E
3、 先求 V,再求 E 。 E gradV
V V V gradV x i y j z k
4 0 r 带电体
dq
2
r
0
4 0 ri
dq 4 0 r
qi
U
带电体
先求 E 再求 U 。
pe q
q2 F q 2 0 2 0 s
Sd S
•电偶极子在均匀外电场中所受到的力和力矩 =p e e E F=0 M •力偶矩 力图使电偶极子的偶极矩 转到与外电场
一致方向上来
八、电势、电势差与电势能 零电势点 1. 电势: U E dl ( = E dl ) a
底
2 E DS d DS / 0
静电场场强习题课

常见旳电量分布旳对称性:
球对称
柱对称
面对称
均 球体 匀 带 球面
无限长柱体 柱面
电 (点电荷) 旳
带电 线
n
r
n
无限大平板 平面
S
S
n
E
2 0 r
E
2 0
7
例:无限大带电平面旳电场叠加问题
σ
σ
E
E
E
E
σ
σ
ε0
0
ε0
0
0
0
8
例8-11 电荷分布:无限长、均匀、圆柱形轴对称,
设单位长度上旳电荷为,圆柱半径R.求距轴心
E内 0
2)电荷在柱体内均匀分布:
右边: q (s内) i
0
1
0
r 2h R 2 h
h
1
0
r2 R2
h
E内 2rh
r2
0R2
h
E内 2R2 0 r
方向沿半径向外
10
均匀带电柱面 电场图示
E
2 0 R
O
R
均匀带电柱体 电场图示
E
2 0 R
O
R
r 1
r
r 1
r
11
例: 均匀带电球体场强旳 分布 ( 解:分析知场强球对称E Er
E
Q
4 0 R 2
O
R
r 2
r
r 2
r
13
例. 求均匀带电球体空腔部分旳电场。球半径为R, 在球内挖去一种半径为r(r<R)旳球体。
试证:空腔部分旳电场为匀强电场,并求出该电场。
证明: 用补缺法证明。设空腔内P点场强为E
将空腔补上,实心球p点场强为 E1
05静电场——习题课
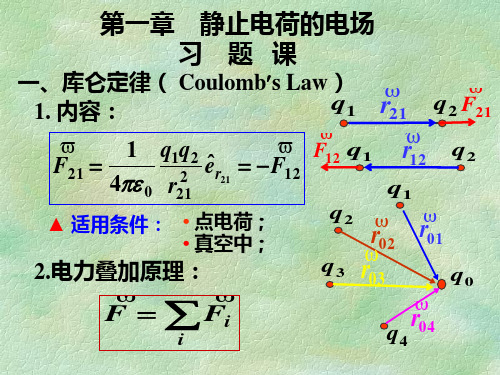
1.14(1)点电荷 位于边长为 的正立方体的中心, ( )点电荷q位于边长为 的正立方体的中心, 位于边长为a 通过此立方体的每一面的电通量各是多少? 通过此立方体的每一面的电通量各是多少? (2)若电荷移至正方体的一个顶点上,那么通过每 )若电荷移至正方体的一个顶点上, 个面的电通量又各是多少? 个面的电通量又各是多少? q 解: 1)由于立方体的 6 个侧面对于其 ( ) ● 中心对称, 则由Gauss定理知,通过各 定理知, 中心对称, 则由 定理知 个面的电通量都相等。 个面的电通量都相等。且等于整个闭合 q ● 高斯面电能量的六分之一, 高斯面电能量的六分之一,所以每个面 通过的电通量应为 q / (6ε0)。 。 填空题1039 (本题 分)在边长为 的正 本题3分 在边长为a的正 填空题 a 方形平面的中垂线上,距中心o点 方形平面的中垂线上,距中心 点a/2 处 q 有一电量q的正电荷,则通过该平面的电 有一电量 的正电荷, 的正电荷 ● a a/2 场强度通量为 q / (6ε0) 。 为边长作一个正六面体。 解:以a 为边长作一个正六面体。
ε0
E = 0 (r < a ) r > a , q int = 2π al σ , E 在筒外, 在筒外, δa (r ≥ a ) E = ε 0r o E-r 曲线如图。 曲线如图。
E∝1 r
a
r
1.18 两个无限长同轴圆筒半径分别为R1和R2,单位长 两个无限长同轴圆筒半径分别为 度带电量分别为+λ和 。求内筒内、 度带电量分别为 和-λ。求内筒内、两筒间及外筒外的 电场分布。 电场分布。 根据电场分布的轴对称性, 解:根据电场分布的轴对称性,可以选与圆筒同轴的圆 柱面(上下封顶 作高斯面。再根据高斯定律即可得出: 上下封顶)作高斯面 柱面 上下封顶 作高斯面。再根据高斯定律即可得出: 在筒内, 在筒内,r < R1 : E = 0 在筒间, 在筒间, R1 < r < R2 :
静电习题课

xdq dE 2 2 3/ 2 4 0 ( r x )
哈尔滨工程大学理学院
静电场习题课
y
dl R r O x R x R x
y
r
O dE
r R sin ,
x R cos ,
dl Rd
E
/2
0
2R 3 sin cos d 3 4 0 40 R
哈尔滨工程大学理学院
静电场习题课 2. 一锥顶角为θ的圆台,上下底面半径分别为R1和R2 , 在它的侧面上均匀带电,电荷面密度σ,求:顶角O的 电势。(以无穷远处电势为零点)
R1
R2
哈尔滨工程大学理学院
静电场习题课 1、判断带电体类型(均匀的连续面分布) 2、选坐标 3、找微元
dq ds
4 r q U 4 r
i 1 0
i
连续分布的带电体 场无对称性
U
dq 4 r
0
场有对称性
哈尔滨工程大学理学院
U P E dl
P
静电场习题课
F
定理
D ds q
0
qq ˆ r 4 r 1
1 2 2
i
有源场
s
静 电 学
方向沿x正方向
电荷元在球面电荷电场中具有电势能: dW = (qdx) / (40 x) 整个线电荷在电场中具有电势能:
q W 4 0
哈尔滨工程大学理学院
r0 l r0
r0 l dx q ln x 4 0 r0
静电场习题课 8.一电容器由两个很长的同轴薄圆筒组成,内、外圆筒半 径分别为R1 = 2 cm,R2 = 5 cm,其间充满相对介电常量 为r 的各向同性、均匀电介质.电容器接在电压U = 32 V 的电源上,(如图所示),试求距离轴线R = 3.5 cm处的A点 的电场强度和A点与外筒间的电势差.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
静 电 场 习 题 课 (数学表达式中字母为黑体者表示矢量)壹 内容提要一、电荷守恒定律(略) .二、库仑定律 : F=q 1q 2r /(4πε0r 3) .三、电场强度E :1. 定义:E=F /q 0 (F 为试验电荷q 0在电场E 中所受作用力);2. 电场叠加原理 i E E ∑= (矢量叠加);点电荷系激发的电场:)4/(30r q i πεi r E ∑=;连续带电体激发的电场: E=∫ q r d q /(4πε0r 3) .四、高斯定理:1.电场线(略);2.电场强度通量 Фe =∫S E∙d S (计算电场强度通量时注意曲面S 的法线正方向);3.高斯定理:真空中0d iSe qΦ∑=⋅=⎰S E (过闭合曲面的电场强度通量) ;介质中iSq0d ∑=⋅⎰S D ;4.库仑电场为有源场.五、环路定理: 1. 表达式⎰=⋅l 0d l E ;2. 静电场为保守场.六、电势V : 1.定义式 (场强与电势的积分关系):⎰⋅=)0(d pV l E (p 表示场点,(0) 表示电势零点);2. 电势差 ⎰⋅=-=B Al E d B A AB V V V ;3. 电势叠加原理 V V i∑=(标量叠加);点电荷系激发的电势:)4/(0r q V iπε∑=;连续带电体激发的电势:()[]⎰=qr q V 04d πε;4.静电场力的功 W AB =qV AB ;5. 场强与电势的微分关系 E=-grad V=-[(∂V/∂x )i+(∂V/∂y )j+(∂V/∂z )k ] .七、电偶极子:1.定义(略);2.电矩 P e =q l ;3.激发的电场:延长线上 E=[1/(4πε0)] (2P e /r 3);中垂线上E=[1/(4πε0)] (-P e /r 3);4. 激发的电势 V =P e ·r / (4πε0r 3) ;5.在均匀电场中受力矩 M= P e ×E .八、导体:1.静电平衡条件 导体内E=0, 导体表面附近外E 垂直表面;2.推论 (1) 导体为等势体,导体表面为等势面,(2) 导体表面曲率半径小处面电荷密度大, (3) 导体表面外附近电场E=σ/ε0, 3.静电屏蔽(1) 空腔导体内的物体不受腔外电场的影响,(2)接地空腔导体外的物体不受腔内电场的影响.九、电介质:1.有极分子取向极化,无极分子位移极化;2.极化强度 P=∑p e /ΔV ,在各向同性介质中P=χε0E ;3.电位移矢量 D=ε0E+P ,在各向同性介质中D=ε0εr E=εE ,εr =1+χ.十、电容:1.定义式 C=Q/U=Q /(V 1-V 2);2.几种电容器的电容 (1) 平行板电容器C=εS/d ,(2) 圆柱形电容器C=2πεl/ln(R 2/R 1),(3) 球形电容器C=4πεR 2R 1 /(R 2-R 1),(4)孤立导体球C=4πεR ;3.并联C=C 1+C 2+C 3+…;4串联1/C=1/C 1+1/C 2+1/C 3+….十一、静电场的能量:1.点电荷系的相互作用能W e = (1/2)∑q i V i ;2.连续带电体的能量W e = (1/2)∫q V d q ;3.电容器的电能W e = (1/2)qU= (1/2)CU 2= q 2/(2C );4.静电场的能量密度w e =(1/2)D ·E ,W e =∫V w e d V=(1/2)∫V D ·E d V .十二、几种特殊带电体激发电场:1.无限长均匀带电直线激发电场的场强E =λr /(2πε0r 2);2.均匀带电园环轴线上的场强与电势E=Qx/[4πε0 (x 2+R 2)3/2],V= Q/[4πε0 (x 2+R 2)1/2];3. 无限大均匀带电平面激发电场的场强E=σ/(2ε0);4. 均匀带电球面激发电场的场强与电势:球面内E =0,V= Q/(4πε0 R ) ,球面外E = Q r /(4πε0 r 3),V= Q/(4πε0 r );5. 均匀带电球体激发电场的场强与电势:球体内E = Q r /(4πε0 R 3), 球体外E = Q r /(4πε0 r 3),V= Q/(4πε0 r );6. 无限长均匀带电圆柱面激发电场的场强:柱面内E =0,柱面外E =λr /(2πε0r 2); 7. 无限长均匀带电圆柱体激发电场的场强: 柱体内E =λr /(2πε0R 2),柱体外E =λr /(2πε0r 2). 贰 练习一至练习七答案及简短解答练习一 一.C A C D D 二.1) 2qy j /[4πε0 (a 2+y 2)3/2] , ±a/21/2;2) M/ (E sin θ);3)2l sin θ(4πε0mg tg θ)1/2[或者2l θ (4πε0mg θ)1/2 (因θ很小)]。
三.1) 取园弧微元d q=λd l=[Q/(πR )]R d θ=Q d θ/π,d E =d q/(4πε0r 2)=Q d θ/(4π2ε0R 2), d E x =d E cos(θ+π)= -d E cos θ, d E y =d E sin(θ+π)=-d E sin θ, E x =()⎰⎰-=2/32/2024d cos d ππεπθθR Q E x =Q/(2π2ε0R 2),()04d sin d 2/32/202⎰⎰=-==ππεπθθR Q E E y y ,故E=E x =()2022R Q επ,方向x 轴正向(图略)。
2) 取环带微元d q =σd S =σ2π(R sin θ)R d θ=2πσR 2sin θd θ,d E =d qx/[4πε0(r 2+x 2)3/2]=2πσR 2sin θd θ(R cos θ) ÷(4πε0R 3)= σsin θcos θd θ /(2ε0),()()0/204/2d cos sin εσεθθθσπ==⎰E ,方向x 轴正向(图略)。
练习二 一. A D B A D 二. 1) λd/ε0, λd/[πε0(4R 2-d 2)], 沿矢径OP ; 2)-qq 0/(8πε0l ); 3)负,< 。
三.1) (1)取圆柱形高斯面,底面∆S 平行地面(图略),012d ερS/h S E S E ∆=∆+∆-=⋅⎰S E ,ρ=ε0(E 1-E 2)/h=4.43×10-13Cm -3; (2) 取圆柱形高斯面,底面∆S 平行地面,上底在地表外,下底在地内(图略),地内E 0为零,0101d εσS/S E S E S E ∆=∆-=∆+∆-=⋅⎰S E ,σ =-ε0E 1=-8.9× 10-10Cm -2。
2) (1) ()[]()⎰⎰⎰====Vq R r qr r r R qr V Q RR43204d 4d 4d ππππρ;(2)电荷球对称,电场球对称,作同心球形高斯面(图略)。
球内,r <R ,()()404004312d 44d R qr R r qr E r εεπππ===⋅⎰⎰rSS E ,E 1=qr 2/(4πε0R 4), E 1=qr r / (4πε0R 4); 球外,r >R , 0224d επq/E r==⋅⎰SS E ,E 2=q/(4πε0r 2),E 2=q r /(4πε0r 3);(3) 球内电势()()[]⎰⎰⎰⎰∞∞+=⋅+⋅=RR l E l E 20402214d 4d d d r r q R r qr V RrRrπεπε()())()()4030040340312341212R qr R q R q R qr R qR πεπεπεπεπε-=+-=; 球外电势V=()[]()r q r r q V 020244d d πεπε==⋅=⎰⎰∞∞rRl E 。
练习三 一.B C B D D 二.1)电场力作负功,a 点电势高;2)Ed ;3)-2×10-7C 。
三.1) 取微元d x (图略), d q =λ0(x -a )d x ,()()[]⎰⎰===+qx x a -x r q V la a0004)d (4d πελπε()[]()[]{}a l a a -l +=ln 400πελ。
2)在电场中作同中心的扇形环路abcda(图略),ab 与cd 段场强与路径垂直,bc 与da 场强大小不等而路径相等,于是有⎰⎰⎰⎰⎰⎰⎰≠-=⋅+⋅+⋅+⋅=⋅bcadldacdbcabl E l E l E l E l E 0d d d d d d d l E l E ,与静电场的环路定理相矛盾,故此电场不是静电场。
练习四 一.A C D D C 二.1)(U 0/2)+Qd/(4ε0S );2)[λq/(2πε0m )]1/2;3)不变,减小。
三.1)E x =-∂U/∂x=-∂[-(x 2+y 2)1/2+ln x ]/∂x=x/(x 2+y 2)1/2-1/x =0.55V/m ; E y =-∂U/∂y=-∂[-(x 2+y 2)1/2+ln x ]/∂y=x/(x 2+y 2)1/2=0.6V/m ;E z =-∂U/∂z=02)(1)因静电感应, 金属球壳内表面带电-q ,外表面均匀带电q+Q ;(2) 内表电荷在O 产生的电势()[]⎰=qq -a q V 04d πε=-q/(4πε0a ); (3) V O=V q+V-q +V Q+q =q/(4πε0r )-q/(4πε0a )+(q+Q )/(4πε0b ), 或V O =[ q/(4πε0)](1/r -1/a+1/b )+Q/(4πε0b )。
练习五 一.D D B A B 二.1)100V ;2)电位移;3) (图略)。
三.1)求线电荷密度:一法、因场柱对称, 取半径为r (R 1<r <R 2)的同轴高斯面,有⎰⋅SS D d =2πrlD =λl ,D=λ/(2πr ) , E=D /(ε0εr )= λ/(2πε0εr r ) , U =)[]()r/r rd 2121R 0λεπε⎰R = [λ/(2πε0εr)]ln(R 2/R 1),λ= 2πε0εr U/ ln(R 2/R 1); 二法、圆柱形电容器电容 C=2πε0εr L / [ln(R 2/R 1)], 内圆筒带电 q=CU =2πε0εr LU / [ln(R 2/R 1)],λ=(q / L )= 2πε0εr U/ ln(R 2/R 1)。
由高斯定理得A 点场强 E A =λ/ (2πε0εr r ) = U / [R ln(R 2/R 1)]=998V/m , A 点与外筒间的电势差为U '=()]{}⎰⎰=⋅2212ln d d R RR Rl E R R r r U()()122ln ln R R R R U ==12﹒5V 。
