静电场习题课(下)
合集下载
静电场习题课
2.无限长均匀带电平面 已知 无限长均匀带电平面 已知: 求: 解: 沿
σ
Y
dq
b a
d
P
Q 两点的场强
与平面共面) 与平面共面 P 点(与平面共面
Y 方向放置的无限长直线
dy
a
d
X dE
dq dq = σdxdy 线密度: = σdx 线密度:
P
dq 在P点产生的
σdx σdx dE = = 2πε 0r 2πε 0 ( a + b x )
3.无限大平面挖一园孔 无限大平面挖一园孔 已知: 已知
σ
R
O
求:轴线上一点的场强 轴线上一点的场强 σ P点 E1 = + σ + 原电荷 2ε0 圆孔
E
P X
R
σ
P点
x σ E2 = ( 1 ) 2ε0 x2 + R2
σ x E = E1 E2 = 2ε x2 + R2
无限" 三."无限"带电体零电势点的选取 无限 1.求无限长均匀带电直线的电势分布 1.求无限长均匀带电直线的电势分布 场强分布 由定义
R
0
E1 = 0
Eo
r
0′
证明空腔内为均匀电场 0处
+ ρ + 原电荷 ρ 0 处
d
E2ds = E2 4πd 2 = ∫
s
∫ dq
s
ε0
4 3 ρ πr = 3
ε0
3
4 3 ρ πr ρr 3 E2 = 3 2 = 2 4πε 0d 3ε0d
ρr ∴Eo = E2 = 2 3ε0d
O′ 点场强的计算
A: EA > EB > EC ,A > B > C B : EA > EB > EC ,A < B < C C : EA < EB < EC ,A > B > C D : EA < EB < EC ,A < B < C
静电场习题课
2
2
(2)两离子初速度分别为 v、v/，则
L 2v L qE n m
L 2v l′ ＋ qE ＝ v m
L 2m Δt＝t－t′ ＝ (v v ) vv qE
L 2m 0 要使 Δt＝0，则须 vv qE 2mvv 所以：E＝ qL
7.如图所示，同一竖直平面内固定着两水平绝缘细杆 AB、CD，长 均为 L，两杆间竖直距离为 h，BD 两端以光滑绝缘的半圆形细杆 相连，半圆形细杆与 AB、CD 在同一竖直面内，且 AB、CD 恰为半 圆形圆弧在 B、D 两处的切线，O 为 AD、BC 连线的交点，在 O 点 固定一电量为 Q 的正点电荷．质量为 m 的小球 P 带正电荷，电量 为 q，穿在细杆上，从 A 以一定初速度出发，沿杆滑动，最后可 到达 C 点．已知小球与两水平杆之间动摩擦因数为μ ，小球所受 库仑力始终小于小球重力．求： (1) P 在水平细杆上滑动时受摩擦力的极大值和极小值； (2) P 从 A 点出发时初速度的最小值．
1 2 －mgh－2mg·2L=0－ 2 mv0 ，
得 v0= 2 gh(h 2L) ．
8.一个质量为m，带有电荷-q的小物体，可在倾角 为θ 的绝缘斜面上运动，斜面底端有一与斜面垂 直的固定绝缘挡板，斜面顶端距底端的高度为h， 整个斜面置于匀强电场中，场强大小为E，方向水 平向右，如图所示．小物体与斜面的动摩擦因数 为μ ，且小物体与档板碰撞时不损失机械能。求： (1) 为使小物体能从静止开始沿斜面下滑，μ 、q、 E、θ 各量间必须满足的关系。 (2) 小物体自斜面顶端从静止开始沿斜面下滑到 停止运动所通过的总路程。
6.飞行时间质谱仪可通过测量离子飞行时间得到离子的荷质比 q/m，如 图 1。 带正电的离子经电压为 U 的电场加速后进入长度为 L 的真空管 AB， 可测得离子飞越 AB 所用时间 t1。改进以上方法，如图 2，让离子飞越 AB 后进入场强为 E（方向如图）的匀强电场区域 BC，在电场的作用下 离子返回 B 端，此时，测得离子从 A 出发后飞行的总时间 t2， （不计离 子重力） ⑴忽略离子源中离子的初速度， ①用 t1 计算荷质比； ②用 t2 计算荷质比。
2
(2)两离子初速度分别为 v、v/，则
L 2v L qE n m
L 2v l′ ＋ qE ＝ v m
L 2m Δt＝t－t′ ＝ (v v ) vv qE
L 2m 0 要使 Δt＝0，则须 vv qE 2mvv 所以：E＝ qL
7.如图所示，同一竖直平面内固定着两水平绝缘细杆 AB、CD，长 均为 L，两杆间竖直距离为 h，BD 两端以光滑绝缘的半圆形细杆 相连，半圆形细杆与 AB、CD 在同一竖直面内，且 AB、CD 恰为半 圆形圆弧在 B、D 两处的切线，O 为 AD、BC 连线的交点，在 O 点 固定一电量为 Q 的正点电荷．质量为 m 的小球 P 带正电荷，电量 为 q，穿在细杆上，从 A 以一定初速度出发，沿杆滑动，最后可 到达 C 点．已知小球与两水平杆之间动摩擦因数为μ ，小球所受 库仑力始终小于小球重力．求： (1) P 在水平细杆上滑动时受摩擦力的极大值和极小值； (2) P 从 A 点出发时初速度的最小值．
1 2 －mgh－2mg·2L=0－ 2 mv0 ，
得 v0= 2 gh(h 2L) ．
8.一个质量为m，带有电荷-q的小物体，可在倾角 为θ 的绝缘斜面上运动，斜面底端有一与斜面垂 直的固定绝缘挡板，斜面顶端距底端的高度为h， 整个斜面置于匀强电场中，场强大小为E，方向水 平向右，如图所示．小物体与斜面的动摩擦因数 为μ ，且小物体与档板碰撞时不损失机械能。求： (1) 为使小物体能从静止开始沿斜面下滑，μ 、q、 E、θ 各量间必须满足的关系。 (2) 小物体自斜面顶端从静止开始沿斜面下滑到 停止运动所通过的总路程。
6.飞行时间质谱仪可通过测量离子飞行时间得到离子的荷质比 q/m，如 图 1。 带正电的离子经电压为 U 的电场加速后进入长度为 L 的真空管 AB， 可测得离子飞越 AB 所用时间 t1。改进以上方法，如图 2，让离子飞越 AB 后进入场强为 E（方向如图）的匀强电场区域 BC，在电场的作用下 离子返回 B 端，此时，测得离子从 A 出发后飞行的总时间 t2， （不计离 子重力） ⑴忽略离子源中离子的初速度， ①用 t1 计算荷质比； ②用 t2 计算荷质比。
静电场习题课讲稿PPT课件
x
L
第10页/共114页
例 求一均匀带电圆环轴线上任一点 x处的电场。
已知： q 、R 、 x。
dq
y
R
d Ey p
d Ex
x
d Ey
x
dE
第11页/共114页
课堂练习：
1.求均匀带电半圆环圆心处的 E，已知 R、
电荷元dq产生的场
dE
dq
4 0 R2
Y
根据对称性 dEy 0
dq
dEx
r dS E
第41页/共114页
dS
E
r
第42页/共114页
r>R
电通量
e E dS E4r 2
电量
qi q
r
高斯定理
E4r 2 q 0
场强
q
E 4 0r 2
第43页/共114页
E
R
高斯面
均匀带电球体电场强度分布曲线
E
E
R
qr E 40R3
q
ε 40r 2
O
r
O
R
第44页/共114页
E
E
均匀带电球面
E
E
E
dS
R
r
E
第36页/共114页
E
高斯面
E
E
E
E
E
dS
rE
E
高斯面
E
R
E
E
第37页/共114页
rR
e
qi
E2 q
dS E2 dS E2 4r 2
s2
E2 4r 2 q 0
+
+ +
+ R
L
第10页/共114页
例 求一均匀带电圆环轴线上任一点 x处的电场。
已知： q 、R 、 x。
dq
y
R
d Ey p
d Ex
x
d Ey
x
dE
第11页/共114页
课堂练习：
1.求均匀带电半圆环圆心处的 E，已知 R、
电荷元dq产生的场
dE
dq
4 0 R2
Y
根据对称性 dEy 0
dq
dEx
r dS E
第41页/共114页
dS
E
r
第42页/共114页
r>R
电通量
e E dS E4r 2
电量
qi q
r
高斯定理
E4r 2 q 0
场强
q
E 4 0r 2
第43页/共114页
E
R
高斯面
均匀带电球体电场强度分布曲线
E
E
R
qr E 40R3
q
ε 40r 2
O
r
O
R
第44页/共114页
E
E
均匀带电球面
E
E
E
dS
R
r
E
第36页/共114页
E
高斯面
E
E
E
E
E
dS
rE
E
高斯面
E
R
E
E
第37页/共114页
rR
e
qi
E2 q
dS E2 dS E2 4r 2
s2
E2 4r 2 q 0
+
+ +
+ R
大学物理(第四版)课后习题及答案 静电场
电场强度E的方向为带电平板外法线方向。
证2：如图所示，取无限长带电细线为微元，各微元在点P激发的电场强 度dE在Oxy平面内且对x轴对称，因此，电场在y轴和z轴方向上的分量之 和，即Ey、Ez均为零，则点P的电场强度应为
积分得 电场强度E的方向为带电平板外法线方向。 上述讨论表明，虽然微元割取的方法不同，但结果是相同的。
（2）由于正、负电荷分别对称分布在y轴两侧，我们设想在y轴上能 找到一对假想点，如果该带电环对外激发的电场可以被这一对假想点上 等量的点电荷所激发的电场代替，这对假想点就分别称作正、负等效电 荷中心。等效正负电荷中心一定在y轴上并对中心O对称。由电偶极矩p 可求得正、负等效电荷中心的间距，并由对称性求得正、负电荷中心。 解：（1）将圆环沿y轴方向分割为一组相互平行的元电偶极子，每一元 电偶极子带电
行，对电场强度通量贡献为零。整个高斯面的电场强度通量为 由于，圆柱体电荷均匀分布，电荷体密度，处于高斯面内的总电荷 由高斯定理可解得电场强度的分布， 解：取同轴柱面为高斯面，由上述分析得 题7.16：一个内外半径分别R1为R2和的均匀带电球壳，总电荷为Q1，球 壳外同心罩一个半径为 R3的均匀带电球面，球面带电荷为Q2。求电场 分布。电场强度是否是场点与球心的距离r的连续函数？试分析。
题7.16分析：以球心O为原点，球心至场点的距离r为半径，作同心球面 为高斯面。由于电荷呈球对称分布，电场强度也为球对称分布，高斯面 上电场强度沿径矢方向，且大小相等。因而，在确定高斯面内的电荷 后， 利用高斯定理 即可求的电场强度的分布 解：取半径为r的同心球面为高斯面，由上述分析 r < R1，该高斯面内无电荷，，故
E=0 在距离圆孔较远时x>>r，则 上述结果表明，在x>>r时。带电平板上小圆孔对电场分布的影响可以忽 略不计。 题7.15：一无限长、半径为R的圆柱体上电荷均匀分布。圆柱体单位长 度的电荷为，用高斯定理求圆柱体内距轴线距离为r处的电场强度。
证2：如图所示，取无限长带电细线为微元，各微元在点P激发的电场强 度dE在Oxy平面内且对x轴对称，因此，电场在y轴和z轴方向上的分量之 和，即Ey、Ez均为零，则点P的电场强度应为
积分得 电场强度E的方向为带电平板外法线方向。 上述讨论表明，虽然微元割取的方法不同，但结果是相同的。
（2）由于正、负电荷分别对称分布在y轴两侧，我们设想在y轴上能 找到一对假想点，如果该带电环对外激发的电场可以被这一对假想点上 等量的点电荷所激发的电场代替，这对假想点就分别称作正、负等效电 荷中心。等效正负电荷中心一定在y轴上并对中心O对称。由电偶极矩p 可求得正、负等效电荷中心的间距，并由对称性求得正、负电荷中心。 解：（1）将圆环沿y轴方向分割为一组相互平行的元电偶极子，每一元 电偶极子带电
行，对电场强度通量贡献为零。整个高斯面的电场强度通量为 由于，圆柱体电荷均匀分布，电荷体密度，处于高斯面内的总电荷 由高斯定理可解得电场强度的分布， 解：取同轴柱面为高斯面，由上述分析得 题7.16：一个内外半径分别R1为R2和的均匀带电球壳，总电荷为Q1，球 壳外同心罩一个半径为 R3的均匀带电球面，球面带电荷为Q2。求电场 分布。电场强度是否是场点与球心的距离r的连续函数？试分析。
题7.16分析：以球心O为原点，球心至场点的距离r为半径，作同心球面 为高斯面。由于电荷呈球对称分布，电场强度也为球对称分布，高斯面 上电场强度沿径矢方向，且大小相等。因而，在确定高斯面内的电荷 后， 利用高斯定理 即可求的电场强度的分布 解：取半径为r的同心球面为高斯面，由上述分析 r < R1，该高斯面内无电荷，，故
E=0 在距离圆孔较远时x>>r，则 上述结果表明，在x>>r时。带电平板上小圆孔对电场分布的影响可以忽 略不计。 题7.15：一无限长、半径为R的圆柱体上电荷均匀分布。圆柱体单位长 度的电荷为，用高斯定理求圆柱体内距轴线距离为r处的电场强度。
矿大《大学物理》习题解答(下)
=
σ 2ε 0
1 −
a a2 +
R2
由题意,令 E=σ/(4ε0)，得到
From: 理学院
~3~
2018
中国矿业大学（北京）《大学物理》习题
R＝ 3a
*4. 一半径为 R 的半球面，均匀地带有电荷，电荷面密度为 σ，求球心 O 处的电场强 度。
R dθ
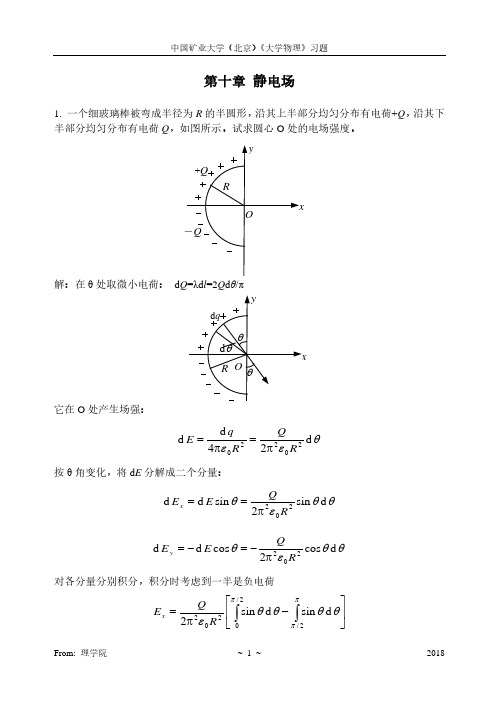
θ
dE
O
x
解：选取坐标轴 Ox 沿半球面的对称轴，如图所示。把半球面分成许多微小宽度的环带， 每一环带之面积：
O 点处的总场强：
∫ σ
E= 2ε 0
π /2
sinθ
0
d(sinθ )
=
σ 2ε 0
sin 2 θ 2
|π0 / 2 =
σ 4ε 0
E = σ i 4ε 0
其中 i 为沿 x 轴正方向的单位矢量。
5. 半径为 R 的均匀带电球体内的电荷体密度为 ρ ,若在球内挖去一块半径为 r ＜ R 的 小球体，如图所示．试求：两球心 O 与 O′ 点的场强，并证明小球空腔内的电场是均匀
E1
=
λ 4πε 0 R
(− i
−
j )
半无限长直线 B∞在 O 点产生的场强 E2 ：
E2
=
λ 4πε 0 R
(− i
+
j学（北京）《大学物理》习题
半圆弧线段在 O 点产生的场强 E3 ：
E3
=
λ 2πε 0 R
i
由场强叠加原理，O 点合场强为：
E = E1 + E2 + E3 = 0
From: 理学院
~4~
2018
的．
中国矿业大学（北京）《大学物理》习题
大学物理第6章真空中的静电场课后习题与答案
第6章真空中的静电场习题及答案1.电荷为q 和2q 的两个点电荷分别置于x1m 和x1m 处。
一试验电荷置于x 轴上何处，它受到的合力等于零？解：根据两个点电荷对试验电荷的库仑力的大小及方向可以断定，只有试验电荷 q 位于点电荷 0q 的右侧，它受到的合力才可能为0，所以2qqqq00224(x 1)4(x1) ππ 00故x3222.电量都是q 的三个点电荷，分别放在正三角形的三个顶点。
试问：(1)在这三角形的中心放 一个什么样的电荷，就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都 为零)?(2)这种平衡与三角形的边长有无关系?解：(1)以A 处点电荷为研究对象，由力平衡知，q 为负电荷，所以2 4 1 π 0 q a 22 cos304 1 π 0 ( q 33qa 2 )3故qq3(2)与三角形边长无关。
3.如图所示，半径为R 、电荷线密度为1的一个均匀带电圆环，在其轴线上放一长为l 、电荷线密度为2的均匀带电直线段，该线段的一端处于圆环中心处。
求该直线段受到的电场力。
解：先求均匀带电圆环在其轴线上产生的场强。
在带电圆环上取dqdl 1，dq 在带电圆环轴 线上x 处产生的场强大小为 dE 4 dq20(xRy2 )根据电荷分布的对称性知，yE0E zdEdEcos x41xdq 1R 3 22 2O(xR) 02xl式中：为dq 到场点的连线与x 轴负向的夹角。
E x4x 220(xR) 3 2dqzx21R R 1 x4x 2R2()3 2 2xR 2( 02 )3 2下面求直线段受到的电场力。
在直线段上取dqdx2，dq受到的电场力大小为Rx12dFxdxEdq32222(xR)0方向沿x轴正方向。
直线段受到的电场力大小为Rlx12FdxdF3202220xR)(11R1121/22R22lR方向沿x轴正方向。
4.一个半径为R的均匀带电半圆环，电荷线密度为。
求：（1）圆心处O点的场强；（2）将此带电半圆环弯成一个整圆后，圆心处O点场强。
14静电场习题课
0
X
由于左右半圆环电荷分布的对称性，合场强的ｙ分量抵消 由于左右半圆环电荷分布的对称性，合场强的ｙ
λ ｄｌ ＋ ）＝－ ｄEｘ＝ｄEｃｏｓ（ π φ 2ｃｏｓ φ 4ππR 0 λR 0 2 ＝－ ｄ 2ｃｏｓφ φ 4ππR 0
λ0 2π 2 Eｘ＝－ ∫ ｃｏｓ φｄ φ 4πε R 0 0 λ0 2π 1－ｃｏｓ 2φ ＝－ ｄφ ∫ 0 4πε R 2 0 λ0 ＝－ 4ε0 R
2
d
•
⇒ E = 0 试指出其错误。 试指出其错误。
答：所选球面上场强的大小不处处相等，不能用： 所选球面上场强的大小不处处相等，不能用：
E • dS = E • 4πr ∫∫
S
2
〔例5〕已知空间电场强度分布为 〕 求（1）通过图示立方体的电通量， ）通过图示立方体的电通量， （2）该立方体内的总电荷是多少？ ）该立方体内的总电荷是多少？ 解：（1） ：（ ）
ｑ ∴U 0＝ ＝U球 4πε ｒ 0
〔例14〕正电荷均匀分布在半径为R的球形体积内，电荷体 〕正电荷均匀分布在半径为R的球形体积内， 密度为ρ,求球内ａ点与球外ｂ点的电势差时， ρ,求球内 密度为ρ,求球内ａ点与球外ｂ点的电势差时，得出结果
R O
σ
x
X
σ －σ ｘ E＝ ｉ ＋ 〔1－ ｉ〕 2 2 2ε 2ε R ＋ｘ 0 0 σ ｘ ＝ ｉ 2 2 2ε R ＋ｘ 0
U＝ E •ｄ ｌ ∫Eｃｏｓ π ＝ －E（－ｄｘ） ＝ ｄｌ ∫ ∫
0 ｘ 0 ｘ 0 ｘ
σ 0 ｘ 注意符号变换！ 注意符号变换！ ｄｘ ＝ ∫ 2 ｘ 2 2ε R ＋ｘ 0 －1 σ 01 2 2 ＝ ∫（R ＋ｘ ） 2ｄ（R 2＋ｘ2） ｘ 2ε 2 0 σ 1 （R ＋ｘ ）2 0 σ ＝ 〔 • 〕 ＝ 〔R－ R 2＋ｘ2〕 ｘ 1 2ε 2 2ε 0 0 2
X
由于左右半圆环电荷分布的对称性，合场强的ｙ分量抵消 由于左右半圆环电荷分布的对称性，合场强的ｙ
λ ｄｌ ＋ ）＝－ ｄEｘ＝ｄEｃｏｓ（ π φ 2ｃｏｓ φ 4ππR 0 λR 0 2 ＝－ ｄ 2ｃｏｓφ φ 4ππR 0
λ0 2π 2 Eｘ＝－ ∫ ｃｏｓ φｄ φ 4πε R 0 0 λ0 2π 1－ｃｏｓ 2φ ＝－ ｄφ ∫ 0 4πε R 2 0 λ0 ＝－ 4ε0 R
2
d
•
⇒ E = 0 试指出其错误。 试指出其错误。
答：所选球面上场强的大小不处处相等，不能用： 所选球面上场强的大小不处处相等，不能用：
E • dS = E • 4πr ∫∫
S
2
〔例5〕已知空间电场强度分布为 〕 求（1）通过图示立方体的电通量， ）通过图示立方体的电通量， （2）该立方体内的总电荷是多少？ ）该立方体内的总电荷是多少？ 解：（1） ：（ ）
ｑ ∴U 0＝ ＝U球 4πε ｒ 0
〔例14〕正电荷均匀分布在半径为R的球形体积内，电荷体 〕正电荷均匀分布在半径为R的球形体积内， 密度为ρ,求球内ａ点与球外ｂ点的电势差时， ρ,求球内 密度为ρ,求球内ａ点与球外ｂ点的电势差时，得出结果
R O
σ
x
X
σ －σ ｘ E＝ ｉ ＋ 〔1－ ｉ〕 2 2 2ε 2ε R ＋ｘ 0 0 σ ｘ ＝ ｉ 2 2 2ε R ＋ｘ 0
U＝ E •ｄ ｌ ∫Eｃｏｓ π ＝ －E（－ｄｘ） ＝ ｄｌ ∫ ∫
0 ｘ 0 ｘ 0 ｘ
σ 0 ｘ 注意符号变换！ 注意符号变换！ ｄｘ ＝ ∫ 2 ｘ 2 2ε R ＋ｘ 0 －1 σ 01 2 2 ＝ ∫（R ＋ｘ ） 2ｄ（R 2＋ｘ2） ｘ 2ε 2 0 σ 1 （R ＋ｘ ）2 0 σ ＝ 〔 • 〕 ＝ 〔R－ R 2＋ｘ2〕 ｘ 1 2ε 2 2ε 0 0 2
静电场中的导体与电介质习题课.ppt
S2
代入上面式子，可求得：
E1
1
r1 0
E2 2 r20
1 S2 E1
- S1 2 E2
D2
D、E 方向均向右。
D1
A d1
d2
B
静电场中的导体和介质习题课
（2）正负两极板A、B的电势差为：
U A U B E1d1 E2d2
d1
1
d2
2
q S
d1
1
d2
2
按电容的定义式：C
q UA UB
d1
S
d2
1 2
上面结果可推广到多层介质的情况。
静电场中的导体和介质习题课
【例题】平行板电容器的极板是边长为 a的正方形，间
距为 d，两板带电±Q。如图所示，把厚度为d、相对介
电常量为εr的电介质板插入一半。试求电介质板所受
电场力的大小及方向。
解：选取坐标系
OX，如图所示。 当介质极插入x 距离时，电容器 的电容为
功等于电容器储能的增量,有
F
W (x) x
( r 20a[a
1)Q2d
(r 1)x]2
静电场中的导体和介质习题课
插入一半时，x=a/2 ,则
F( a ) 2( r 1)Q2d 2 0a3 ( r 1)2
F(a/2)的方向沿图中X轴的正方向。
注释：由结果可知，εr＞1，电场力F是指向电容器内 部的，这是由于在电场中电介质被极化，其表面上产 生束缚电荷。在平行极电容器的边缘，由于边缘效应 ，电场是不均匀的，场强E 对电介质中正负电荷的作 用力都有一个沿板面向右的分量，因此电介质将受到 一个向右的合力，所以电介质板是被吸入的。
E E0
r
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
A．平行板电容器 C 0S ( E )
d
0
2 3
qa qb
S d
B．圆柱形电容器 C 20L
ln R2 R1
C．球形电容器 C 40R1R2
R2 R1
( E ) 2 0 r
( E Q )
4 0 r 2
26．电容器的串联：极板首尾相接
R2 R1 L
特点：A、 有一个公共端，且 公共端上不再引出其它元件。
电学习题课（下）
20.导体的静电 平衡条件:导体内部电场强度处 处为零。即 E内部＝0
21. 导体处于静电平衡状态时的性质：
A.导体是个等势体，导体表面是个等势面。
B. 导体内部各点(宏观点)净余电荷为零；电荷只 能分布在表面。
C. 导体表面附近一点的总电场强度方向
与导体表面垂直;场强大小与导体
表面对应点的电荷面密度成正比。
－q ．把另一电荷为Q(Q＜0 )的点电荷从D
点沿路径DCO移到O点，
C
则电场力所做的功为
l
__-_Q__q_/_(_6___0_l)_____
AO +q
B q
D
2l
13．在匀强电场中，将一负电
B
荷从A移到B，如图所示．则：
E
A
(A) 电场力作正功，负电荷的电势能减少
(B) 电场力作正功，负电荷的电势能增加
C总
Q总 U总
•只要有一个电容增大，则总电容增大
28、电介质对电容的影响
A、两导体板之间均匀充满电介质时，将电容公
式中的 0 改为 即可。
B、 若按等势面分层均匀充满电介质，则：
(1)仍按电容定义式计算电容
d1 d2
1 2
E1
1
E2 2
U E1d1 E2d2
C QU
(2)将两种介质交界面处看成有一个金属薄板,故
E
0
例：静电平衡后，金属板各面所带电
1 2 3 4
荷面密度之间的关系 1 4 , 2 3
• 当两板带等量异号电荷时: 1 4＝0 , 2 3
• 当两板带等量同号电荷时: 1 4 , 2 3 0
22.静电平衡下空腔导体的性质
A.若金属空腔内部无带电体,则空腔内表面不带 任何电荷，空腔内部任一点场强为零。
B.若金属空腔内部有带电体,则空腔内表面有等 量异号感应电荷。 ）
C.导体接地时，(A)若外界无电荷，则外壁上电 荷处处为零，外部空间任一点场强为零; (B)若 外界有电荷，则外壁上一定有异号电荷。
D.腔内电荷(包括内壁上的电荷)对内壁以外空间 任何一点的合场强为零;腔外电荷(包括外壁上的 电荷)对外壁以内空间任何一点的合场强为零。
思考：若断开电源，其 C1 C2
它条件不变，则应选哪
个答案？
［Ａ］
［Ａ］ 思考：
1、电势差如何变化？ 2、若断开电源，其它条件不变，则电荷 和电势差如何变化？
后面为未讲习题
12．如图，A点与B点间距离为2l，OCD是 以B为中心，以l为半径的半圆路径. A、B 两处各放有一点电荷，电荷分别为＋q和
(A) U12减小，E减小，W减小． (B) U12增大，E增大，W增大． (C) U12增大，E不变，W增大． (D)U12减小，E不变，W不变．
［C］
4、C1和C2两空气电容器并联以后接电源充 电．在电源保持联接的情况下，在C1中插入一电 介质板，如图所示, 则 [ ]C (A) C1极板上电荷增加，C2极板上电荷减少 (B) C1极板上电荷减少，C2极板上电荷增加 (C) C1极板上电荷增加，C2极板上电荷不变 (D) C1极板上电荷减少，C2极板上电荷不变
两极板间的电势差为_______2_F_d__/ _C_，极板上的 电荷_____2_F_d_C__．
作业题6.两导体球A、B．半径分别为R1=0.5 m， R2 =1.0 m，中间以导线连接，两球外分别包以 内半径为R =1.2 m的同心导体球壳(与导线绝缘)
并接地，导体间的介质均为空气，如图所示．已
原电容器看成两个电容器的串联。
C1
1S d1
,
C2
2S d2
1 1 1 C C1 C2
d1 1 d2 2
C.电容器的两板之间平行放入一层金属板
d’
d C 0S
d d'
29. 带电电容器所存储的静电能 W Q2 1 CU2
2C 2
外力作功等于静电能的增加。 30.电场的能量密度: w 1 E2
2
➢一个带电系统的静电能就是它在整个空间激
发的电场能量
W 1 E2dV 2 电场空间
1.如图所示，将一正电荷从无穷远处移到一个不 带电的导体附近，则导体内的电场强度_____， 导体的电势_______．(填增大、不变、减小)
(不变, 增大 )
+
2.一空气平行板电容器，电容为C，两极板间距
离为d．充电后，两极板间相互作用力为F．则
B、q1=q2=…=q ；U＝U1＋U2 ＋…＋Un
C、 1 ＝ 1 ＋ 1 ＋＋ 1
C C1 C2
Cn
R2R1
27、电容器的并联：
特点：A、有两个公共端，且在公共端上还引 出导线接其它元件。
B、U1＝U2＝…＝U ; q=q1+q2+…+qn
C、 C＝C1＋C2＋…＋Cn
•讨论：无论是串联还是并联:
知：空气的击穿场强为3×106 V/m，今使A、B两
球所带电荷逐渐增加，计算： (1)此系统何处首先被击穿？这里场强为何值?
(2) 击穿时两球所带的总电荷Q为多少？
(设导线本身不带电，且对电场无影响．)
A R R1
B R2
R
3.一个平行板电容器，充电后与电源断开， 当用绝缘手柄将电容器两极板间距离拉大， 则两极板间的电势差U12、电场强度的大小 E、电场能量W将发生如下变化：
(C) 电场力作负功，负电荷的电势能减少
(D) 电场力作负功，负电荷的电势能增加．Fra bibliotek［］ D
14. 有N个电量均为q的点电荷，以两种方式分布
在相同半径的圆周上：一种是无规则地分布，另
一种是均匀分布．比较这两种情况下在过圆心O并 垂直于圆平面的z轴上任一点P(如图所示)的场强
与电势，则有
(A) 场强相等，电势等．
23. 接地线的存在意味着: A.导体的电势为零;
B.接地线只提供导体与地交换电荷的通道，并不 保证导体腔外壁上的电荷在任何情况下都为零。
例：如图，两导体板分别带qa和
qb当一导体接地时，求两板之间
的场强。E 2 qa
S
0 0s
24. 孤立导体的电容
C q U
25. 电容器电容的定义
C q U
z
P
(B) 场强不等，电势不等．