第十讲非线性规划一运筹学清华大学林谦
非线性规划ppt课件

g3(x) x1 x2 x3 0
;
20
一维搜索方法
目标函数为单变量的非线性
规划问题称为一维搜索问题
min t0 (0ttmax )
其中 t R 。
(t)
➢精确一维搜索方法 0.618法 Newton法
➢非精确一维搜索方法 Goldstein法 Armijo法
;
21
0.618法(近似黄金分割法)
定义 4.1.2 对于非线性规划(MP),若 x* X ,并且存在 x* 的一个
领域 N ( x* ) x Rn x x* ( 0, R) ,使
f (x* ) f (x), x N (x* ) X ,
则称 x* 是(MP)的局部最优解或局部极小点,称 f ( x* ) 是(MP)的局部
函数(t) 称为在[a,b]上是单谷的,如果存在一个 t * [a, b] ,使得(t) 在[a, t * ]上严格递减,且在[t * , b] 上严格递增。区间[a,b]称为(t) 的单 谷区间。
第 1 步 确定单谷区间[a,b],给定最后区间精度 0 ;
第 2 步 计算最初两个探索点
t1 a 0.382(b a) b 0.618(b a)
;
22
0.618法例题
• 例4.3.1 用0.618法求解
min(t) t3 2t 1 t0
(t) 的单谷区间为[0,3], 0.5
解答
例4.3.1解答 • 迭换换代tbtb 过程0311..62..∧✓18可0036145436481由-00下101.2.∧...0✓871110650431表48611 给0-0100.2.∨...0✓1470出2064308168821 --000100...∨...00✓4178376340791868681 01..7140486 a2112a
清华大学-《运筹学》课程教学大纲

清华大学-《运筹学》课程教学大纲《运筹学》课程教学大纲课程名称:运筹学编号.20345144:学时:72 编者姓名:曾鸿能单位:中山大学职称:副教授主审姓名:单位:职称:教授对象:本科生专业:资源与环境规划年级:三年级编写日期:2001年9月一、课程目的与教学基本要求学习本课程后,使学生掌握运筹学有关分支的基本理论和方法,牢固掌握解题算法步骤,培养学生应用规划论、优化技术解决实际问题能力。
为专业课在系统规划、最优设计、参数优选、最优管理与运行等数学方法及计算机算法打下必要的基础。
在已学过微积分、初等集合论和线性代数基础上学习本课程,通过教授、自学、复习、作业练习、辅导、编程上机等教学环节达到上述目的。
学习中要注意到学科系统性,数学概念和逻辑的严密性、准确性和完整性,但不偏重纯数学方法论证。
着重基本概念、基本思路、基本方法、算法步骤、几何直观解析。
了解各种方法特点和实用价值,提高建立模型、分析求解能力和技巧。
应注重实际应用中建立模型,选择可行求解的理论方法,编制算法的计算机程序这三方面训练的有机结合。
二、课程内容(含学时分配)绪言:运筹学简史、性质和特点、工作步骤、模型、分支及应用、运筹学展望(1学时)i.线性规划与目标规划(共30学时)1-1 线性规划问题及其数学模型(2学时)一、应用实例二、线性规划的数学模型三、标准形式1-2 线性规划问题的图解法(1学时)教学要求:1.初步掌握建立线性规划模型方法2.掌握线性规划模型特征;如何化线性规划模型为标准型3.掌握两个变量线性规划问题的图解法重点:通过图解法初步了解基本概念和求解思路1-3 线性规划的基本概念和基本定理(4学时)教学要求:1.掌握可行解、基、凸集、凸组合、顶点的概念2.了解线性规划理论依据---几个基本定理、求解线性规划问题基本思路重点:三个基本定理难点:基本定理的证明1-4 单纯形法(4学时)1.单纯形法求解过程说明2.单纯形表(1)单纯形表的结构和原理(2)换基Ⅰ确定换入变量Ⅱ确定换出变量Ⅲ旋转迭代教学要求:牢固掌握线性规划的单纯形求解方法重点:单纯形方法求解步骤和公式难点:单纯形表构成原理,换基迭代公式推导1-5 单纯形法进一步讨论(2学时)(一)大M单纯形法(二)两阶段法(三)退化问题(四)检验数的几种表示法(五)单纯形法小结教学要求:1.了解引入工人变量目的2.牢固掌握大M法和两阶段法求解过程、判别什么情况下无解3.牢固掌握单纯形法计算框图重点:两阶段法及单纯形法计算框图1-6 改进单纯形法(2学时)教学要求:1.了解改进单纯形方法的思想2.掌握改进单纯形法计算步骤重点:改进单纯形法计算步骤(主要用于计算机计算)难点:新基逆矩阵求解公式及其实质1-7 线性对偶规划(4学时)一、对偶问题提出二、对偶规则三、线性对偶理论四、对偶问题的经济学解释——影子价格五、对偶单纯形法教学要求:1.掌握对偶规则2.了解线性对偶理论、影子价格的意义3.牢固掌握对偶单纯形法重点:对偶单纯形法计算步骤及对偶单纯形法应用范围难点:线性对偶理论的证明1-8 灵敏度分析与参数线性规划(3学时)教学要求:1.掌握系数变化范围的确定及增加新变量、新约束灵敏度分析2.掌握参数连续变化对最优解及最优值的影响重点:灵敏度分析与参数线性规划的应用。
非线性规划

非线性规划(nonlinear programming)1.非线性规划概念非线性规划是具有非线性约束条件或目标函数的数学规划,是运筹学的一个重要分支。
非线性规划研究一个n元实函数在一组等式或不等式的约束条件下的极值问题,且目标函数和约束条件至少有一个是未知量的非线性函数。
目标函数和约束条件都是线性函数的情形则属于线性规划。
2.非线性规划发展史公元前500年古希腊在讨论建筑美学中就已发现了长方形长与宽的最佳比例为0.618,称为黄金分割比。
其倒数至今在优选法中仍得到广泛应用。
在微积分出现以前,已有许多学者开始研究用数学方法解决最优化问题。
例如阿基米德证明:给定周长,圆所包围的面积为最大。
这就是欧洲古代城堡几乎都建成圆形的原因。
但是最优化方法真正形成为科学方法则在17世纪以后。
17世纪,I.牛顿和G.W.莱布尼茨在他们所创建的微积分中,提出求解具有多个自变量的实值函数的最大值和最小值的方法。
以后又进一步讨论具有未知函数的函数极值,从而形成变分法。
这一时期的最优化方法可以称为古典最优化方法。
最优化方法不同类型的最优化问题可以有不同的最优化方法,即使同一类型的问题也可有多种最优化方法。
反之,某些最优化方法可适用于不同类型的模型。
最优化问题的求解方法一般可以分成解析法、直接法、数值计算法和其他方法。
(1)解析法:这种方法只适用于目标函数和约束条件有明显的解析表达式的情况。
求解方法是:先求出最优的必要条件,得到一组方程或不等式,再求解这组方程或不等式,一般是用求导数的方法或变分法求出必要条件,通过必要条件将问题简化,因此也称间接法。
(2)直接法:当目标函数较为复杂或者不能用变量显函数描述时,无法用解析法求必要条件。
此时可采用直接搜索的方法经过若干次迭代搜索到最优点。
这种方法常常根据经验或通过试验得到所需结果。
对于一维搜索(单变量极值问题),主要用消去法或多项式插值法;对于多维搜索问题(多变量极值问题)主要应用爬山法。
第一讲 绪论、线性规划引论(运筹学-清华大学,林谦)

x 0 (自变量约束,食品量不会为负)
j
z c1 x1 a 2 x 2 c n x n min
(目标函数,使购食品费用取最小值) (i=1,2,…,m; j=1,2,…,n)
page 12 25 January 2014
Prof. Wang School of Economics & Management
page 3 25 January 2014
Prof. Wang School of Economics & Management
Operations Research
第一讲
§1.1 运筹学简述 (2)
也许有人怀疑,运筹学是研究从众多方案(甚至无限多个方 案)中选佳的优化技术,那么在当代计算机技术迅速发展的 今天,这种优化技术是否会丧失其重要性?事实正相反,新 型计算机的出现,恰为运筹学的应用开辟了新天地。 假设有70艘油轮向70个港口运货,已知每艘油轮驶向每个港 口的费用,油轮公司需制订出最优运输方案。采用全枚举法 (穷举法)需计算方案数为 70!( 大于 10100 ); IBM 公司当 时生产的大计算机1秒种大约可算出109(即10亿)个方案。 若要逐个算出全部方案,则需调用占有空间为1050个地球一 样大的IBM公司生产的众多大计算机同时计算几百亿年以上。 而在这种大机器上用线性规划的单纯形法计算只需几秒钟 (这是整数规划问题)。 可见,将运筹学与计算机科学及其它科学结合应用,将会产 生更好的效果。
page 4 25 January 2014
Prof. Wang School of Economics & Management
Operations Research
运筹学-非线性规划

Edition,2010 3.吴祈宗,运筹学与最优化方法(第二版),机械工业出版社,
解:显然,目标函数
f
(x)
( x1
3)2 2
( x2
5)2
是凸函数, 且约束条件为线性
函数, 故此规划问题为凸规划.
x2
( 3 ,5)
2
(1, 3)
点x*=(1,3)T是唯一最优解. 由于 f在点(1,3)的梯度为
f (1,3) (1, 4)T ,
从图中可以看出,向量(1, 4)T
1 D1 x x D1是凸集,其中是实数. 2 D1 D2 x y x D1 , y D2 是凸集.D1 D2也是凸集.
3 D1 D2是凸集.
凸函数与凹函数
定义: D为凸集, 若对任意x1,x2D及任意实数a, 0≤a≤1有 f(ax1+(1-a)x2)≤a f(x1)+(1-a)f(x2)
例:投资决策问题
某企业有n个项目可供选择投资, 并且至少要对其中一个项目投资. 已知该企业拥有总资金A元, 投资于第i(i=1,2,…,n)个项目需要花 资金ai 元, 并预计收益为bi元, 试选择最佳投资方案使得总收益和 总投资之比最大.
解:
设投资决策变量为
1, xii 0,
决定投资第 i 个项目 决定不投资第:
f
(
x1
,
清华大学运筹学课件(完整课件)
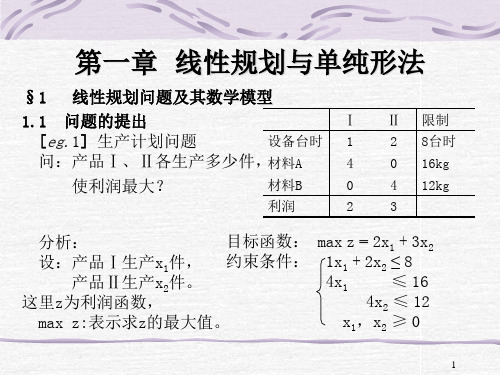
化标准型
max z = x1 + 3x2 + 0x3 + 0x4
x1 + 2x2 + x3 = 3
2x1 + 3x2
+ x4 = 4
x1,x2,x3,x4 ≥ 0
系数矩阵
1 A 2
2 3
1 0
0 1
p1
p2
p3 p4 , 则 B p3 p4
取x3、x4为基变量,令非基变量x1= x2=0 ∴ 初始基可行解:X(0) = (0 0 3 4)T
③
3
z = 2x1 + 4x2,此时表示 目标函数的直线与表示
Q2(4,2)
① *
条件①的直线平行,
o
最优点在线段Q3Q2上。
即存在无穷多最优解。
4 Q1
x1
7
(3)无界解
[eg.5]
max z = 2x1 + 3x2 4x1 ≤ 16 x1,x2 ≥ 0
则x2 → ∞,z → ∞。 即存在无界解。
对于
n
m
max z c j x j cni xni
j 1
i 1
n
aij x j xni bi
i 1, , m
j1
x
j
0
j 1, , n m
设 xni 为基变量可行,i 1,, m
x j为非基变量, j 1,, n
n
xni bi aij x j j 1
代入目标函数
产品Ⅱ生产x2件。
4x1
≤ 16
这里z为利润函数,
4x2 ≤ 12
max z:表示求z的最大值。
《运筹学》全套课件清华大学
运输问题
通过线性规划求解运输问题中 的最优运输方案,使得总运费 最小化。
投资组合
通过线性规划确定最优的投资 组合,使得风险最小化或收益
最大化。
03
整数规划
整数规划问题的数学模型
整数规划问题的定义和分类
介绍整数规划问题的基本概念、分类以及与其 他优化问题的关系。
03
Bellman-Ford算法
适用于存在负权边的图,通过不断松弛边的方式求解最短路。
网络最大流问题
网络最大流问题的定义
给定一个有向带权图,找到从源点到汇点的最大流 量。
增广路算法
通过不断寻找增广路来增加流量,直到没有增广路 为止。
Edmonds-Karp算法
对增广路算法进行优化,使用广度优先搜索寻找增 广路。
整数规划问题的应用
生产计划问题
阐述整数规划在生产计划问题中的应用,如 生产批量计划、生产排程等。
金融投资问题
分析整数规划在金融投资问题中的应用,如 投资组合优化、风险管理等。
物流配送问题
探讨整数规划在物流配送问题中的应用,如 车辆路径问题、设施选址问题等。
其他应用领域
介绍整数规划在其他领域的应用,如计算机 科学、生物医学工程等。
运筹学的应用领域
工业工程
在生产计划、物流管理、设施规划等领域 ,运筹学可以帮助企业提高生产效率、降 低成本、优化资源配置。
其他领域
如金融工程、医疗健康、环境保护等领域 ,运筹学也发挥着重要作用,为各种实际 问题提供有效的解决方法。
交通运输
在交通规划、交通控制、航空运输等领域 ,运筹学可以优化交通网络设计、提高运 输效率、减少交通拥堵等问题。
非线性规划课件
②再固定x₂=x₂ (1): 求以x₁为单变量的目标函数的极值点,
得 X(2)=(x,(2),x₂ (1))T ,S(2)=f(X(2))
此时S(2)优于S(1), 且搜索区间缩短为x₁*∈[x,(2),b,],x₂*∈[x₂ (1),b₂] 第二步:如此交替搜索,直至满足给定精度ε为止
否则,继续缩短区间,
直至满足给定的精度为
①f(x₂)≥f(xq), 取[aq=ao,b,=x,]
X₁ =X2
x'2=b₁-λ(b₁-aq) ②f(x₂)<f(x₁), 取[a=x2,b,=b,]
x=aq+λ(b₁-aq)
10
x₂ =x₁
例 求 解 f(x)=-18x²+72x+28 的极大值点,δ≤0.1,起始搜索区间为[0,3] 解:①用间接法:令 f'(x)=-36x+72=0, 得驻点 x=2
xq*∈[aq,b,],x²*∈[a₂ ,b₂ ],.,x*∈[an,b,]
1、原理: ①从起点 X(0) 出发,沿平行于 x, 轴的方向P(1)进行一维搜索,
求得 f(X) 在该方向P(1)上近似极值点 X(1);
②从点 X(1) 出发,沿平行于 x₂ 轴的方向P(2)进行一维搜索,
求得 f(X) 在该方向P(2)上近似极值点 X(2); ③从点 X(2) 出发,照此交替进行下去,直至满足给定的精度ε为止
六、 寻优方法概述:
1、N.L.P.问题分类
① 无约束条件的NLP问题。 ② 有约束条件的NLP问题。 2、寻优方法
① 间接法(解析法):适应于目标函数有简单明确的数学表达式。
非线性规划
非线性规划非线性规划(Nonlinear Programming ,简记为NP)研究的对象是非线性函数的数值最优化问题,是运筹学的最重要分支之一,20世纪50年代形成一门学科,其理论和应用发展十分迅猛,随着计算机的发展,非线性规划应用越来越广泛,针对不同的问题提出了特别的算法,到目前为止还没有适合于各种非线性规划问题的一般算法,有待人们进一步研究.§1 非线性规划基本概念一、引例例7.1 一容器由圆锥面和圆柱面围成. 表面积为S ,圆锥部分高为h ,h 和圆柱部分高2x 之比为a ,1x 为圆柱底圆半径.求21,x x 使面积最大.解: 由条件 a x h =2/22121231x x x ax V ππ+=21212222112221x x x x a x x S πππ+++⋅⋅=所以,数学模型为:212)311(max x x a V π+=s.t. S x x x x a x x =+++21212222112πππ0,21≥x x例7.2 某高校学生食堂用餐,拟购三种食品,馒头0.3元/个,肉丸子1元/个,青菜0.6/碗.该学生的一顿饭支出不能够超过5元.问如何花费达到最满意?解: 设该学生买入馒头,肉丸子,青菜的数量分别为321,,x x x ; 个人的满意度函数即为效用函数为321321321),,(aaax x Ax x x x u =.于是数学模型为321321321),,(max aaax x Ax x x x u =s.t.56.03.0321≤++x x x 321,,x x x 为非负整数二、数学模型称如下形式的数学模型为数学规划(Mathematical Programming 简称MP ) )(min x f z = (7.1) (MP ) t s . 0)(≥x g i m i ,,1 = (7.2) 0)(=x h j l j ,,1 = (7.3)其中Tn x x x x ),,,(21 =是n 维欧几里得空间nR 中的向量(点),)(x f 为目标函数,0)(,0)(=≥x h x g j i 为约束条件.称满足约束条件的向量x 为(MP )问题的一个可行解,全体可行点组成的集合称为可行域.K ={}l j x h mi x g R x j i n,,2,10)(,,2,10)( ===≤∈如果)(),(),(x h x g x f j i 均为线性函数,就是前面所学的线性规划问题(LP).如果至少有一个为非线性函数称为非线性规划问题.由于等式约束0)(=x h j 等价于下列两个不等式约束 0)(,0)(≥-≥x h x h j j 所以(MP)问题又可表示为 )(min x f z =s.t. 0)(≥x g i m i ,,1 = (7.4) 三、数学基础 1、线性代数知识考虑二次型Az z T ,z 为n 维向量正定的二次型:若对于任意0≠z ,有0>Az z T; 半正定的二次型:若对于任意0≠z ,有0≥Az z T ; 负定的二次型:若对于任意0≠z ,有0<Az z T ; 半负定的二次型:若对于任意0≠z ,有0≤Az z T ;不定二次型:0≠∃z ,有0>Az z T,又0≠∃z ,有0<Az z T.二次型Az z T 为正定的充要条件是它的矩阵A 的左上角各阶主子式都大于零. 二次型Az z T 为负定的充要条件是它的矩阵A 的左上角各阶主子式负正相间.2、分析数学知识(1)方向导数和梯度(二维为例)考虑函数),(21x x f Z =,及方向j i lϕϕsin cos +=梯度:Tx f x f j x f i x f x x f ),(),(212121∂∂∂∂=∂∂+∂∂=∇ ; 方向导数:⎪⎪⎭⎫⎝⎛∂∂∂∂=∂∂+∂∂=∂∂ϕϕϕϕsin cos ),(sin cos 2121x f x f x f x f l f )),,(cos(||),(||),(),(21212121l x x gardf x x gardf lx x gardf lx x f T=⋅=⋅∇=考虑等值线00201),(c x x f =上一点),(0201x x 梯度方向 ),(0201x x gardf 即为法线方向n.如果)(x f 二次可微,称⎪⎪⎪⎪⎪⎭⎫⎝⎛=)()()()()()()()()()(212222111211x h x h x h x h x h x h x h x h x h x H nn n n n n为)(x f 在点 x 处的Hesse 矩阵.(2)多元函数泰勒公式:若)(,),(0x f R S x x f u n⊆∈=在点0x 处的某个领域具有二阶连续偏导数,则有x x x f x x x f x f x x f T T∆∆+∇∆+∆∇+=∆+)(21)()()(02000θ 10≤≤θ )||(||)(21)()(||)(||)()(2020000x x x f x x x f x f x x x f x f T TT ∆+∆∇∆+∆∇+=∆+∆∇+=οο 四、最优解的类型定义7.1 (MP)问题的一个可行点*x 被称为整体极小点,如果对于任意的可行点K x ∈,都有不等式)()(*x f x f ≥成立.如果对于任意可行点*,x x K x ≠∈均有)()(*x f x f >,称点*x 是)(x f 的可行解集K上的严格整体极小点.定义7.2 问题(MP)的一个可行点*x 被称为一个局部极小点,如果存在一个正数ε使得对于所有满足关系式ε<-*x x 的可行点x 都有)()(*≥x f x f 成立.如果对任意的可行点K x ∈,*≠x x ,存在一个正数ε使得对于所有满足关系式ε<-*x x 的可行点x 都有)()(*>x f x f 成立.则称*x 是)(x f 在K 上的一个局部严格极小点.显然整体极小点一定是局部极小点,反之不然. 五、凸规划定义7.3 集合K 被称为nR 中的一个凸集,如果对于K 中任意两点21,x x 和任一实数]1,0[∈λ,点K x x ∈-+21)1(λλ.几何解释:当一个集合是凸集时,连接此集合中任意两点的线段也一定包含在此集合内,规定φ空集是凸集.定义7.4 凸函数:)(x f 是凸集K 上的实值函数,如果对于K 中任意两点21,x x 和任意实数]1,0[∈λ有不等式)()1()())1((2121x f x f x x f λλλλ-+≤-+成立.严格凸函数:)(x f 是凸集K 上的实值函数,如果对于K 中任意两点21,x x ,21x x ≠和任意实数)1,0(∈λ,有不等式)()1()())1((2121x f x f x x f λλλλ-+<-+成立.定义7.5 )(x f 是定义在凸集K 上的实值函数,如果)(x f -是K 上凸函数,称)(x f 是凹函数.定理7.1 设)(x f 是凸集K 上的凸函数,则)(x f 在K 中的任一局部极小点都是它的整体极小点.证明: 设*x 是一局部极小点而非整体极小点,则必存在可行点K x ∈(可行域))()(*x f x f <∍.对任一]1,0[∈λ,由于)(x f 的凸性,有 )()()1()())1((***x f x f x f x x f ≤-+≤-+λλλλ当0→λ时,*)1(x x λλ-+与*x 充分接近,与*x 是局部极小矛盾. 证毕. 定义7.6 设有(MP)问题)(min x f kx ∈,若可行域K 是凸集,)(x f 是K 上的凸函数,则称此规划问题为凸规划.定理7.2 凸规划的任一局部极小解为整体极小解. 六、非线性规划问题的求解方法 考虑(MP)问题:lj x h m i x g t s x f j i ,,10)(,,10)(.)(min ===≥ (7.5) 一般来说,MP 问题难以求得整体极小点,只能求得局部极小点.以后我们说求(MP)问题,指的是求局部极小点.1、无约束极小化问题(UMP ) )(min x f nRx ∈ (7.6) 这里)(x f 是定义在n R 上的一个实值函数定理7.3(一阶必要条件)如果)(x f 是可微函数.*x 是上述无约束问题(UMP )的一个局部极小点或局部极大点的必要条件是:0)(*=∇x f .满足0)(=∇x f 的点称为平稳点或驻点.定理7.4 设)(x f 为定义在n R 上的二阶连续可微函数,如果*x 是)(x f 的一个局部极小点,必有nT Ry y x H y x f ∈∀≥=∇0)(0)(**这里)(*x H 表示)(x f 在*x 处的Hesse 矩阵.证明:nE y ∈∀,根据)(x f 在点*x 处的展开式有)()(21)()(2*2**λολλ++=+y x H y x f y x f T)0)((*=∇x f若0)(,*<∍∈∃y x H y R y T n ,当λ充分小时,有 )()(21|2*2λολ>y x H y T∴有)()(**x f y x f <+λ.这和*x 是)(x f 的极小矛盾.定理7.5 设)(x f 是定义在nR 上的二阶连续可微函数,如果点*x 满足0)(*=∇x f ,而且存在*x 的一个邻域0)(),(,),(*≥∈∀∈∀∍*y x H y x x R y x T n 有 ,则*x 是)(x f 的一个局部极小点.在高等数学中求解极值点方法先求出满足0)(=∇x f 的点及不可导点.在这些点判断)(x f 是否取得极小值.2、等式约束的极小化问题考虑 )(min x fl j x h t s j ,,10)(. == (7.7)定义7.7 如果)(,),(),(21x h x h x h l ∇∇∇ 在点x 处线性无关,则称点x 是此约束条件的一个正则点.Langrange 乘子法:引进拉格朗日函数 ∑=-=lj jj x h u x f u x L 1)()(),(其中Tl u u u u ),,,(21 =被称为拉格朗日乘子向量.定理7.6 设l j x h x f j ,,1),(),( =是连续可微函数,*x 是)(x f 在可行集中的一个局 部极小点.在*x 是正则点的假定下必存在一个拉格朗日乘子向量u ,使得),(*u x 满足方程组)(0)()(*1**==∇-∇∑=x h x h u x f lj j j对等式约束,用拉格朗日乘子法求解出平稳点,判断是否极值点.用上述解析法求解无约束和等式约束极值问题的平稳点,再判断是否为极值点.该方法有一定的局限性:(1)它们要求函数是连续的,可微的,实际问题中不一定满足这一条件; (2)上述求平稳点的方程组求解比较困难,有些解不出来; (3)实际问题中有大量的不等式约束.因此求解非线性规划应有更好的新方法.实际应用中一般用迭代法来求解非线性规划问题,即求近似最优解的方法.3、非线性规划问题的求解方法—迭代法迭代法一般过程为:在(MP)问题的可行域K 内选择初始点0:,0=k x ,确定某一方向k p ,使目标函数)(x f 从k x 出发,沿k p 方向使目标函数值下降,即)0(,>∈+=λλK p x x k ,有)()(0x f x f <,进一步确定kλ,使)(m i n )(0k k k k k p x f p x f λλλ+=+>,令k k k k p x x λ+=+1.如果1+k x 已满足某终止条件,1+k x 为近似最优解.否则,从1+k x 出发找一个方向1+k p ,确定步长1+k λ,使K p x x k k k k ∈+=++++1112λ,有)(min )(1102++>++=k k k p x f x f λλ.如此继续,将得到点列{}kx .显然有 >>>>)()()(1kx f x f x f ,即点列{}kx 相对应的目标函数是一个单调下降的数列.当{}kx 是有穷点列时,希望最后一个点是(MP)问题的某种意义下的最优解.当{}kx 为无穷点列时,它有极限点,其极限点是(MP)的某种意义下的最优解(此时称该方法是收敛的).迭代法求解(MP)的注意点:该方法构造的点列{}kx ,其极限点应是近似最优解,即该算法必须是收敛的.迭代法一般步骤:①. 选取初始点0x ,0:=k ②. 构造搜索方向kp ③. 根据kp 方向确定k λ ④. 令k k k k p x xλ+=+1⑤. 若1+k x已满足某终止条件,停止迭代,输出近似最优解1+k x.否则令1:+=k k ,转向第②步.计算终止条件在上述迭代中有:若1+k x满足某终止条件则停止计算,输出近似最优解1+k x.这里满足某终止条件即到达某精确度要求.常用的计算终止条件有以下几个:(1)自变量的改变量充分小时,11||||ε<-+k k x x,或21||||||||ε<-+kk k x x x ,停止计算. (2)当函数值的下降量充分小时,31)()(ε<-+k kx f x f ,或41|)(|)()(ε<-+k k k x f x f x f , 停止计算.(3)在无约束最优化中,当函数梯度的模充分小时51||)(||ε<∇+k x f ,停止计算.迭代法的关键:① 如何构造每一轮的搜索方向kp ② 确定步长k λ关于k λ,前面是以)(min kk p x f λλ+产生的,也有些算法k λ取为一个固定值,这要根据具体问题来确定.关于kp 的选择,在无约束极值问题中只要是使目标函数值下降的方向就可以了,对于约束极值问题则必需为可行下降方向.定义7.8 设0,,:1≠∈→p R x R R f nn,若存在0>δ使),0(δλ∈∀,)()(x f p x f <+λ则称向量p 是函数)(x f 在点x 处的下降方向.定义7.9 设0,,,≠∈∈∈p R p K x R K nn,若存在0>λ使得K p x ∈+λ,称向量p 是点x 处关于K 的可行方向. 若一个向量p 既是目标函数f 在点x 处的下降方向,又是该点处关于可行域K 的可行方向,则称p 为函数f 在点x 处关于区域K 的可行下降方向.根据不同原理产生了不同的kp 和k λ的选择方法,就产生了各种算法. 在以后的讨论中,一维极值的优化问题是讨论求解步长k λ.无约束极值中讨论的最速下降法,共轭方向法,坐标轮换法,牛顿法,变尺度法及有约束极值中讨论的可行方向法都是根据不同的原理选择kp 得到的迭代算法.七、迭代算法的收敛性定义7.10 设有一算法A ,若对任一初始点(可行点),通过A 进行迭代时,或在有限步后停止得到满足要求的点;或得到一个无穷点列,它的任何一个聚点均是满足要求的点,则称此算法A 具有全局收敛性.定义7.11 设(UMP )问题的目标函数Px Qx x x f T+=21)(,Q 为对称半正定矩阵, 若由算法A 进行迭代时,不论初始点0x 如何选择,必能在有限步后停止迭代,得到所要求的点,则称此算法A 有二次有限终止性.定义7.12 设序列{}kr收敛于*r,定义满足∞<=--≤**+∞−→−βhkk k rr r r 1______lim0的非负数h 的上确界为{}k r 的收敛级.若序列的收敛级为h ,就称序列是h 级收敛的.若1=h 且1<β就称序列是以收敛比β线性收敛的. 若1>h 或1=h 且0=β就称序列是超线性收敛的. 如何判别算法的收敛性和收敛速度问题本书不讨论.本书给出的算法中,最速下降法具有全局收敛性、是线性收敛的;改进牛顿法具有全局收敛性、二次有限终止性、是二阶线性收敛的;变尺度法和共轭方向法具有全局收敛性和二次有限终止性、是超线性收敛的;Zoutenddijk 法不具有全局收敛性、改进的T-V 法具有全局收敛性;制约函数法具有全局收敛性.关于这些算法的收敛性的讨论和证明有兴趣的读者可参考其他文献.§2 一维极值问题的优化方法前面讨论迭代算法时,从kx 出发确定沿k p 方向的步长k λ是这样求解的),(min 0k k p x f λλ+>这里k x ,k p 已知.所以,若记)()(λλg p x f k k =+,则为求解)(min 0λλg >的过程.于是我们考虑如下形式的极值问题.)(min x f bx a ≤≤ (7.8)b a R x ,,1∈为任意实数很显然可应用高等数学中学过的解析法,即令0)('=x f 求出平稳点,但如前面所述如果该方程解不出来,怎么办?可用下述迭代算法—0.618法.定义7.13 )(x f 定义在],[b a 上,若存在点∍∈],[*b a x 当*x y x ≤<,有)()(y f x f >,当*x y x ≥>时,)()(y f x f >,称)(x f 在],[b a 中为单峰函数(单谷函数).显然满足定义要求的点*x 是)(x f 在],[b a 中的极小点.在],[b a 中任选两点21,x x ,且b x x a <<<21,根据)(x f 的单峰性,若)()(21x f x f <,则*x 必然位于],[2x a 内,如果)()(21x f x f >,则*x 必然位于],[1b x 内.如果)()(21x f x f =,则*x 必然位于],[21x x ,记此区间为],[11b a .如此继续,得闭区间套⊃⊃⊃⊃],[],[],[11n n b a b a b a .显然 ,1,0],,[*=∈i b a x i i ,又0→-i i a b .由闭区间套性质, *x 为极小值点.闭区间套的选择方法不同,求得的*x 的快慢及求解过程的计算量是不一样的,有一个常用的方法是0.618法.0.618法: 取],[],[b a =βα① 在],[βα中选取1λ和2λ,)(618.0),(382.021αβαλαβαλ-+=-+=,求出)(1λf 和)(2λf 进入②.② 若)()(21λλf f <,取],[],[2λαβα=,若αλ-2已足够小,停止,否则进入③.若)()(21λλf f >,取],[],[1βλβα=,若1λβ-已足够小,停止,否则进入④. 若)()(21λλf f =,取],[],[21λλβα=,若12λλ-已足够小,停止,否则进入①. ③ 取上一步中的1λ为2λ,显然有)(618.02αβαλ-+=,令)(382.01αβαλ-+=,求出)(1λf ,返回②.④ 取上一步的2λ为1λ,则有)(382.01αβαλ-+=,令)(618.02αβαλ-+=,求出)(2λf 返回②.设初始区间为],[b a ,用0.618法,经过k 次迭代后],[βα的长度ka b 618.1)(-=-αβ,只要k 充分大αβ-可以小于任何给定的正数.例7.3 用0.618法求解λλλ2)(min 2+=f单峰区间为[-3,5],2.0=ε解:[α,β]=[-3,5]1λ=-3+0.382×8=0.056 )(1λf =0.1152λ=-3+0.618×8=1.944 )(2λf =7.667由于)(1λf <)(2λf 所以新的不定区间为[α,β] =[-3,1.944] 由于β-α=4.944>0.22λ:=1λ=0.056 )(2λf :=)(1λf =0.115 1λ=-3+0.382×4.944=-1.112 )(1λf =-0.987如此反复得下表7-1:在进行8次迭代后,2.0112.1936.0<+-=-αβ取中间值024.1*-=λ或032.12-=λ作为近似最优解.显然真正极小点是-1.0.一维收索方法很多,如函数逼近法、牛顿法等可参考其他文献.§3 无约束极值的优化方法考虑无约束最优化问题(UMP ))(min x f nR x ∈ (7.9) 前面已经讨论过,求解此无约束优化问题,可以求出平稳点及不可导点的方法.令0)(*=∇x f ,求出平稳点.如果)(*2x f ∇是正定的,则*x 是UMP 的严格局部最优解.若)(x f 在n R 上是凸函数,则是整体最优解.在求解0)(*=∇x f 这n 维方程组比较困难时,就用最优化算法——迭代法.本节将介绍最速下降法,牛顿法,共轭方向法,坐标轮换法,变尺度法.这些算法就是用不同的方法来选择搜索方向k p 而得到的.当然kp 必须是下降方向.定理7.7 设R R f n→:,在点x 处可微,若存在nR p ∈,使0)(<∇p x f T,则向量p是f 在x 处的下降方向.证明:)(x f 可微(在x 处),由泰勒展开式,有 ||)(||)()()(p p x f x f p x f Tλολλ+∇+=+ ,0,0)(><∇λp x f T0)(<∇∴p x f Tλ),(当δλδ0∈∃∴时,有0||)(||)(<+∇p p x f Tλολ),0()()(δλλ∈∀<+∴x f p x fp ∴是)(x f 在点x 的下降方向. 证毕.一、最速下降法最速下降法又称梯度法,选择负梯度方向作为目标函数值下降的方向,是比较古老的一种算法,其它的方法是它的变形或受它的启发而得到的,因此它是最优化方法的基础. 基本思想:迭代法求解无约束最优化(5.9)问题的关键是求下降方向kp .显然最容易想到的是使目标函数值下降速度最快的方向.从当前点kx 出发,什么方向是使)(x f 下降速度最快呢? 由泰勒展开知:||)(||)()()(k k T k k k k p p x f p x f x f λολλ+∇-=+-略去λ的高阶无穷小项,取)(kkx f p -∇=时,函数值下降最多.而)(kx f ∇为)(x f 在kx 处的梯度,所以下降方向kp 取为负梯度方向时,目标函数值下降最快.最速下降法:①. 取初始点0x ,允许误差0>ε,令0:=k ②. 计算)(kkx f p -∇=③. 若ε<||||k p ,停止,点k x 为近似最优解.否则进入④.④. 求 k λ,使)(min )(0kk k k k p x f p x f λλλ+=+≥ ⑤. 令kk k k p x xλ+=+1,1:+=k k ,返回②例7.4 用最速下降法求解下列无约束优化问题1222121225),(m in x x x x x f -+=取初始点Tx )2,2(0= 终止误差 610-=ε解:很显然,该问题的整体最优解为Tx )0,1(*=⎪⎪⎭⎫⎝⎛-=∇215022)(x x x f ,令0,10)(21==⇒=∇x x x f易验证)(*2x f ∇是正定的, ∴是整体最优解. 下面用最速下降法求解T T x x x f x f x f )50,22(),()(2121-=∂∂∂∂=∇ T x )2,2(0=T x f )100,2()(0=∇∴取Tp )100,2(0-=由⎪⎪⎭⎫⎝⎛--=⎪⎪⎭⎫ ⎝⎛--+⎪⎪⎭⎫ ⎝⎛=+λλλλ10022210022200p x4)22(2)1002(25)22()(2200+---+-=+λλλλp x f得0)1002(5000)22(4=----=λλλd df020007679.0500008100080==⇒λ⎪⎪⎭⎫⎝⎛-=⎪⎪⎭⎫ ⎝⎛--+⎪⎪⎭⎫ ⎝⎛=+=0007679.0959984642.11002020007679.0220001p x x λ重复上述过程得 Tx )01824717.0,009122542.1(2=789850288.0)(,078282.0)(,100)(21-=-==x f x f x f图7-1从图7-1可知,{}kx 随着迭代次数的增加,越来越接近与最优解)0,1(,同时也看到,随着迭代次数的增加,收敛速度越来越慢.极小点附近沿着一种锯齿形前进,即产生“拉锯”现象:{}kx沿相互正交的方向小步拐进,趋于最优解的过程非常缓慢.这种现象怎样解释?如何克服?在求k λ时,由于)()(kkp x f λλϕ+=,求导得0)('=λϕ,k λ是)(λϕ的极小点.故有0)()('=⋅+∇=k T k k k k p p x f λλϕ,即0)(=⋅+∇kk k k p p x f λ,又)(11++-∇=k k x f p,即0)(1=⋅+k T k p p 或0)()(1=∇⋅∇+k T k x f x f .也就是最速下降法相邻两个搜索方向是彼此正交的.因此最速下降法是局部下降最快,但不一定是整体下降最快的.在实际应用中一般开始几步用最速下降法,后来用下面介绍的牛顿法.这样两个算法结合起来,求解速度较快.二、牛顿法 基本思想:考虑无约束优化问题(5.9))(min x f nRx ∈ 由前面的讨论知,若能解出方程组0)(=∇x f ,求出平稳点*x ,则可验证*x 是否为极值点.由于0)(=∇x f 难以求解.如果)(x f 具有连续的二阶偏导数,则考虑用)(x f 在点*x 二阶泰勒展开式条件替代)(x f ∇,即由22||)(||))(()(21)()()()(k k k T k k T k k x x x x x f x x x x x f x f x f -+-∇-+-∇+=ο))(()(21)()()()()(2kk T k k T k k x x x f x x x x x f x f x g x f -∇-+-∇+=≈⇒令0))(()()()(2=-∇+∇=∇≈∇kk k x x x f x f x g x f)())((121k k k k x f x f x x ∇∇-=⇒-+即从kx 出发,搜索方向为)())((12kkkx f x f p ∇∇-=-,步长恒为1,得到下一个迭代点1+k x.牛顿法:①. 选取初始点0,0=:k x ,精度0>ε ②. 计算)(kx f ∇,如果ε≤∇||)(||kx f ,计算终止.否则计算)(2kx f ∇,求出搜索方向)())((12kk k x f x f p ∇∇-=-. ③. 令1:,1+=+=+k k p x x k k k ,返回②.例7.5 考虑无约束问题22122214)(m in x x x x x f -+=试分别取初始点(1)T x )1,1(0=,(2)T x )4,3(0=(3)Tx )0,2(0=,取精度要求310-=ε,用牛顿法求解.解:⎪⎪⎭⎫ ⎝⎛--=∇212211228)(x x x x x x f ⎪⎪⎭⎫⎝⎛---=∇22228)(1122x x x x f (1) 取Tx )1,1(0=有Tx f )1,6()(0=∇ ε>=∇0828.6||)(||0x f⎪⎪⎭⎫⎝⎛--=∇2226)(02x fT x f x f p )2500.2,7500.1()())((01020--=∇⋅∇-=-Tp x x )2500.1,7500.0(01--=+= 重复计算结果得表7-2.ε<=0||)(||4x f T x )0,0(4=∴为近似最优解.实际上,该问题最优解为**)0,0(=x(2) 取Tx )4,3(0=,同上计算,得TT x x x )4,8284.2(,)4,8333.2(),4,3(21===有ε<=∇=∇=∇0||)(||,1667.0||)(||,1||)(||210x f x f x f ,这一迭代结果收敛到)(x f 的鞍点T)4,22(.(3) 取Tx )0,2(0=T x f )4,16()(0-=∇ ⎪⎪⎭⎫⎝⎛--=∇2448)(02x f0)(02=∇x f , 即)(02x f ∇不可逆,所以无法求得点1x .牛顿法的主要缺点:(1) 该法的某次迭代反而使目标函数值增大(见上例).(2) 初始点0x 距极小点*x 较远时,产生的点列{}kx可能不收敛,还会出现)(*2x f ∇的奇异情况.(3) )(*2x f ∇的逆矩阵计算量大. 牛顿迭代法的主要优点:当目标函数)(x f 满足一定条件,初始点0x 充分接近极小点*x 时,由牛顿法产生的点列{}kx 不仅能够收敛到*x,而且收敛速度非常快.实际应用中常将最速下降法和牛顿法结合起来使用.牛顿法的改进:上面介绍的牛顿法中,kx 处的搜索方向为)())((12kkkx f x f p ∇∇-=-,步长恒为 1.若通过一维搜索来取最优步长k λ,可防止在迭代中步长恒为1时标目标函数值增大的可能. 改进的牛顿法:①. 取初始点nR x ∈0,允许误差0:,0=>k ε.②. 检验是否满足ε<∇||)(||kx f ,若是,迭代停止,得到k x 为近似最优解.否则进入③.③. 令)())((12kk k x f x f p ∇∇-=-.④. 求k λ,使)()(min kk k k k p x f p x f λλλ+=+. ⑤. 令k k k k p x x λ+=+1,令1+=k k :转②.三、坐标轮换法既然求解非线性规划问题的迭代法是给出初始点0x ,求出一个方向kp ,根据kp 确定步长k λ,使k k k k p x xλ+=+1,如果1+k x 满足某精度要求则停止,否则继续找方向1+k p .显然构造出搜索方向有一定的困难,能否按既定的搜索方向寻找最优解,省去找搜索方向kp 呢?在最速下降法中我们看到相邻两个搜索方向kp 和1+k p是正交的.我们知道在n 维欧氏空间中坐标轴向量n εεε,,,21 是正交的,可否选坐标轴向量为搜索方向kp 为呢?回答是肯定的,这样我们得到了坐标轮换法.基本思想:从1x 出发,取11ε=p ,沿1p 进行一维搜索得到1112p x x λ+=.若2x 满足精度要求,则停止.否则取22ε=p ,2223p x x λ+=.如此继续,, 取n n n n n n p x x p λε+==+1,,若1+n x 满足精度要求,则停止.否则令11ε=+n p ,1112+++++=n n n n p x x λ,如此反复连续,可以求出近似最优解.坐标轮换法的缺点是收敛速度较慢,搜索效率较低,但基本思想简单,沿坐标轴的方向进行搜索.四、共轭方向法和共轭梯度法共轭方向法是一类方法的总称,它原来是为求解目标函数为二次函数的问题而设计的.这类方法的特点是:方法中的搜索方向是与二次函数的系数矩阵Q 有关的所谓共轭方向,用这类方法求解n 元二次函数的极小化问题最多进行n 次一维搜索便可以得到极小点.由于可微的非二次函数在极小点附近的性态近似于二次函数,因此这类方法也用于求可微的非二次函数的UMP 问题.定义7.14 设Q 为n n ⨯对称正定矩阵,如果0=Qy x T称n 维向量x 和y 关于Q 共轭.定义7.15 设k p p p ,,,21 为nR 中一组向量, Q 是一个n n ⨯对称正定矩阵.如果k j i j i Qp p Qp p i T i j T i ,,2,1,,,0,0 =≠≠=,称k p p p ,,,21 为Q 共轭向量组,也称它们为一组Q 共轭方向.当E Q =(单位矩阵)时,为正交方向.定理7.8 若k p p p ,,,21 为矩阵Q 共轭向量组,则它们必线性无关. 证明: 若存在k l l l ,,,21 ,使011=++k k p l p l ,则对任一k j ,,2,1 =,由 0)(11===∑∑==j T j j ki j T j iki iiT jQp p l Qp pl p l Q p又0>j Tj Qp p , 0=∴j l∴ k p p p ,,,21 线性无关. 证毕.由高等代数知识可知, Q 共轭向量组中最多包含n 个向量, n 是向量的维数.反之,可以证明,由n 维空间的任一组基出发可以构造出一组Q 共轭方向11,,,-n pp p .前面我们已经讲述了坐标轮换法,在n 维欧几里德空间中, n εεε,,,21 是一组线性无关的正交向量.从0x 出发,依次使用n εεε,,,21 作为下降方向进行一维精确搜索来确定n x x x ,,,21 ,重复进行得点列{}k x ,最终求得满足精度要求的最优解.刚才我们引进了共轭向量组11,,,-n p p p ,又证明了它们的线性无关性,那么是否可以用这共轭向量组像坐标轮换法一样,从0x 出发依次用11,,,-n pp p 作为下降方向来确定{}kx,最终求得近似最优解?回答是肯定的.这个方法称为共轭方向法.共轭方向法适合任何可微凸函数,且对于二次函数极值)(min x f x p Qx x T T+=21特 别有效.下面的定理告诉我们用共轭方向法求解二次函数的极值,经过n 次迭代就能求得最优解.定理7.9 设Q 为n n ⨯对称正定矩阵,函数x p Qx x x f T T+=21)(,又设 110,,,-n p p p 为一组Q 共轭向量组,且每个i p 是(下面形成的)i x 点处的下降方向.则由任一点0x 出发,按如下迭代至多n 步后收敛,k k k k p x xλ+=+1,这里k λ满足)(m i n )(0k k k k k p x f p x f λλλ+=+>.证明: 欲证至多n 步收敛,即证0)(=∇nx f .下证)(nx f ∇和11,,,-n pp p 正交.p Qx x f +=∇)( p Qx x f kk+=∇∴)( p p x Q p Qx xf k k k k k ++=+=∇++)()(11λkk k k k k Qp x f p Qp Qx λλ+∇=++=)( =+∇=∇---111)()(n n n n Qpx f x f λ 11111)(--++++++∇=n n k k k Qp Qp xf λλQ p Q p x f x f Tn n T k k T k T n )()()()(11111--++++++∇=∇λλkT n n k T k k k T k k T n Qp p Qp p p x f p x f )()()()(11111--++++++∇=∇λλ000+++= )2,,2,1,0(-=n k 又0)(1=∇-n Tn px f0)(=∇∴kT n p x f )1,,1,0(-=n k)(nx f ∇∴和11,,,-n pp p 正交, 又110,,,-n pp p 线性无关.0)(=∇∴nx fnx ∴是问题的最优解. 证毕. 共轭方向法具有二次有限终止性. 由于共轭方向组11,,,-n p p p 的取法有很大的随意性,用不同方式产生一组共轭方向就得到不同的共轭方向法.如果利用迭代点处的负梯度向量为基础产生一组共轭方向,这样的方法叫共轭梯度法.下面对二次函数讨论形成Q 共轭梯度方向的一般方法,然后引到求解无约束化问题上.任取初始点n R x ∈0,若0)(0≠∇x f ,取)(0x f p -∇=,从0x 点沿方向0p 进行一维搜索 ,求得0λ.令0001p x x λ+=,若0)(1=∇x f ,则已获得最优解1*x x =.否则,取0011)(p x f p υ+-∇=,其中0υ的选择要使1p 和0p 关于Q 共轭,由0)(01=Qp p T ,得0100)()()(Qp p x f Q p T T ∇=υ一般地,若已获得Q 共轭方向kp p p ,,,1和依次沿它们进行一维搜索的得到的点列110,,,+k x x x ,若0)(1=∇+k x f ,则最优解为1*+=k x x ,否则∑=+++-∇=ki i i k k p xf p011)(α为使1+k p 和11,,,-k pp p 是共轭,可证0110====-k ααα所以有 k k k k p x f pυ+-∇=++)(11又1+k p和kp 是Q 共轭的.有0)(1=+k Tk Qp p,得kT k k T k k Qpp x f Q p )()()(1+∇=υ 2,,2,1,0-=n k 进一步可得k υ221||)(||||)(||k k x f x f ∇∇=+ 2,,1,0-=n k综合起来得 Fletcher-Reeves 公式2)21110||(||||)(||)()(k k k k k k k x f x f p x f px f p ∇∇=+-∇=-∇=+++υυ 2,,2,1,0-=n k (7.10)共轭梯度法: ①. 选取初始点0x ,给定终止误差0>ε. ②. 计算)(0x f ∇,若ε≤∇||)(||0x f ,停止迭代,输出0x .否则进行③.③. 取)(0x f p -∇=,令0:=k④. 求k λ,)(min )(0kkkk kp x f p x f λλλ+=+≥,令k k k k p x xλ+=+1⑤. 计算)(1+∇k xf ,若ε≤∇+||)(||1k x f ,停止迭代,1*+=k x x 为最优解.否则转⑥.⑥. 若n k =+1,令nx x =:0,转③(已经完成一组共轭方向的迭代,进入下一轮)否则转⑦ ⑦. 取kk k k p xf pυ+-∇=++)(11,其中221||)(||||)(||k k k x f x f ∇∇=+υ,令1:+=k k ,转④当)(x f 是二次函数时上述共轭梯度法至多进行n 步可求得最优解.当)(x f 不是二次函数,共轭梯度法也可以构造11,,,-n p p p ,但已不具有有限步收敛的性质,于是和坐标轮换法一样经过一轮迭代后,采用重新开始的技巧.上述共轭梯度法就是带有再开始技巧的F-R 法.例7.6 用F-R 法求下面问题 2212121252),(m in x x x x x f +-=取初始点T x )2,2(0=,终止误差为610-=ε解:在例7.4中已得Tx f p )100,2()(0-=-∇= Tx )0007679.0,959984642.1(1-= Tx f )038395.0,919969284.1()(1-=∇000368628.010004687756228.3||)(||||)(||20210==∇∇=x f x f υ ⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫ ⎝⎛--+⎪⎪⎭⎫ ⎝⎛-=+-∇=0015322.092070654.11002000368628.0038395.0919969284.1)(0011p x f p υ⎪⎪⎭⎫ ⎝⎛+--=+0015322.00007679.092070654.1959984642.111λλλp x0378228399.7687703443.3)(11=+-=+λλλd p x df499808794.01=∴λ⎪⎪⎭⎫ ⎝⎛≈⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫⎝⎛⨯+--⨯+=+=010********.0999998622.00015322.0499808794.00007679.0)92070654.1(499808794.0959984642.11112p x x λε<=∇0||)(||2x f , ∴最优解⎪⎪⎭⎫⎝⎛==012*x x .五、变尺度法当初始点为)(x f 的其极值点附近时牛顿法收敛速度很快,但缺点是需计算)(2kx f ∇的逆矩阵,在实际问题中目标函数往往相当复杂,计算二阶导数的工作量或者太大或者不可能,在x 的维数很高时,计算逆矩阵也相当费事.如果能设法构造另一个矩阵kH ,用它来逼近二阶导数矩阵的逆矩阵12))((-∇kx f 则可避免上述问题.下面就来研究如何构造12))((-∇kx f 的近似矩阵kH .我们希望:每一步都能以现有的信息来确定下一个搜索方向,每做一次迭代,目标函数值均有所下降,这些近似矩阵最后应收敛于最优解处的海赛矩阵的逆矩阵12))((-∇kx f .p Qx x f xp Qx x x f T T+=∇+=)(21)(考虑于是 )]()([)()()(11111k k k k k k k k x f x f Q x x x x Q x f xf ∇-∇=-⇒-=∇-∇+-+++当)(x f 是非二次函数时,令)]()([111k k k k k x f x f H x x ∇-∇=-+++ (7.11)称为拟牛顿条件.显然,我们构造出来的近似矩阵k H 必须满足上述拟牛顿条件及递推性:k k k H H H ∆+=+1,这里k H ∆称为矫正矩阵.记 k k k kk k x x x x f x f G -=∆∇-∇=∆++11)()( 有 kk k k k k G H H G H x ∆∆+=∆=∆+)(1 .变尺度法即DEP 法是由Davidon 首先提出,后来又被Fletcher 和Powell 改进的算法.记kk T k kT k k k k T k T k k k k kk T k kT k k k k T k T k k kG H G HG G H x G x x H H G H G H G G H x G x x H ∆∆∆∆-∆∆∆∆+=∆∆∆∆-∆∆∆∆=∆+)()()()()()()()(1 (7.12)容易验证1+k H 满足拟牛顿条件,称上式为DEP 公式.变尺度方法计算步骤:(1) 给出初始点nR x ∈0,允许误差0>ε.(2) 若ε<∇||)(||0x f ,停止,0x 为近似最优解;否则转下一步.(3) 取I H =0(单位矩阵),0=:k . (4) )(kk k x f H p ∇-=(5) 求k λ,使)(min )(0kk k k k p x f p x f λλλ+=+≥. (6) 令kk k k p x xλ+=+1(7) 若ε<∇+||)(||1k xf ,1+k x 为最优解,停止;否则当1-=n k 时,令n x x =:0转(3).(即迭代一轮n 次仍没求得最优解,以新的0x 为起点重新开始一轮新的迭代).k k k k k kx x x x f xf G n k -=∆∇-∇=∆-<++11),()(1时,令当.计算kk T k kT k k k k T k T k k kk G H G H G G H x G x x H H∆∆∆∆-∆∆∆∆+=+)()()()(1,令1+=k k :,转(4). §4 约束极值的最优化方法考虑(MP)问题:0)(0)(..)(min =≥x H x g t s x f (7.13)其中Tl T m x h x h x h x g x g x g ))(,),(()(,))(,),(()(11 ==是向量函数.显然 0)(0)(0)(≥-≥⇔=x h x h x h , 于是(MP )问题可以写为:Tm x g x g x g x g t s x f ))(,),(()(0)(..)(min 1 =≥ (7.14)一、积极约束设0x 是(MP )问题(5.14)的一个可行解.对0)(0≥x g i 来说,在点0x 有两种情况:或者0)(0>x g i ,或者0)(0=x g i .0)(0>x g i 时,则0x 不在0)(0=x g i 形成的边界上,称这一约束为0x 的非积极约束;0)(0=x g i 时,0x 处于由0)(0≥x g i 这个约束条件形成的可行域边界上,当0x 有变化时就不满足0)(0=x g i 的条件,所以称为积极约束,记为:{}()|()0,1i I x i g x i m ==≤≤.定义7.16 设x 满足约束条件0)(0≥x g i ),,1(m i =,0)(|{)(==x g i x I i ,}m i ≤≤1,如果)(x g i ∇,)(x I i ∈线性无关,则称点x 是约束条件的一个正则点.二、可行方向、下降方向的代数条件前面我们已经给出可行方向和下降方向的定义,下面给出其代数条件.可行方向:设K 是(MP )问题(5.14)的可行域,K x ∈,0,≠∈p R p n.若存在00>λ使得],0[0λλ∈时有K p x ∈+λ,称p 为x 点处的一个可行方向.由泰勒公式:||)(||)()()(p p x g x g p x g T i i i λολλ+∇+=+当x 为)(x g i 的积极约束时,有0)(=x g i .只要0>λ足够小,)(p x g i λ+和p x g T i )(∇λ同号,于是当0)(>∇p x g T i 时有0)(≥+p x g i λ )(x I i ∈.当x 为)(x g i 的非积极约束时,有0)(>x g i .由)(x g i 的连续性,当0>λ足够小时,由保号性知 0)(≥+p x g i λ )(x I i ∉.所以只要 0)(>∇p x g T i ,)(x I i ∈就可保证0)(≥+p x g i λ,于是p 为x 点处的一个可行方向.称0)(>∇p x g T i ,)(x I i ∈ 为p 在点x 处是可行方向的代数条件.下降方向:设K 是(MP )问题的可行域,K x ∈,0,≠∈p R p n.若存在00>λ使得],0[0λλ∈时,有)()(x f p x f <+λ,称p 为x 点处的一个下降方向.由泰勒公式:||)(||)()()(p p x f x f p x f Tλολλ+∇+=+.当λ足够小时,只要0)(<∇p x f T,有)()(x f p x f <+λ. 称0)(<∇p x f T为p 在x 点处的一个下降方向的代数条件.三、可行下降方向设K 为(MP )问题(5.14)的可行域,K x ∈,若存在0,≠∈p R p n,p 既是x 点处的下降方向又是可行方向,则称p 为点x 处的可行下降方向.定理7.10 考虑非线性规划问题(5.14),K x ∈,),,1)()(m i x g x f i =(和在x点处可微,若*x 是局部极小点,则x 点处必不存在可行下降方向,即不存在p 同时满足:⎪⎩⎪⎨⎧∈>∇<∇)(0)(0)(x I i p x g p x f Ti T证明:反证法,设局部极小点x 处存在可行下降方向p ,于是1λ∃,当],0[1λλ∈时有)()(x f p x f <+λ,又p 为可行方向.2λ∃∴当],0[2λλ∈时K p x ∈+λ,这与x 是。
2024版清华大学运筹学完整学习教案
案例分析:资源分配问题优化
案例背景
资源分配问题是一类典型的优化问题,涉及到如何 将有限的资源分配给不同的项目或任务,以使得整 体效益最大化。
求解过程
根据问题的特点选择合适的求解方法进行求解,如 动态规划、整数规划或启发式算法等。在求解过程 中需要注意对算法进行调试和优化,以提高求解效 率和准确性。
Floyd算法
适用于求解任意两点间最短路径问题,通过逐步构建 中间点集合,将问题分解为更小的子问题求解。
比较分析
从算法思想、时间复杂度、空间复杂度等方面 对两种算法进行比较分析。
最大流问题及其在网络中应用
最大流问题定义
01
给定一个有向图,其中每最大流量。
Ford-Fulkerson算法
一款数学计算软件,提供丰富的数学 函数库和强大的计算能力,可用于进 行复杂的运筹学建模和求解。
CPLEX
一款高性能的数学规划求解器,适用 于大规模线性规划、整数规划、混合 整数规划等问题的求解。
Gurobi
另一款高效的数学规划求解器,提供 多种算法和并行计算功能,适用于解 决复杂的优化问题。
实验设计思路和数据收集方法
图论是研究图的结构和性质的数学分支,通常 用节点和边表示图中的对象及其相互关系。
图的分类
根据边是否有向、是否加权等性质,图可分为 无向图、有向图、加权图等。
图的基本性质
介绍图的连通性、度、路径、回路等基本概念和性质。
最短路径问题求解方法比较
Dijkstra算法
适用于求解带权有向图中单源最短路径问题, 通过逐步确定已知最短路径的节点集合,不断 向外扩展求解。
发展历程
运筹学起源于20世纪30年代末,在第二次世界大 战期间得到广泛应用。战后,运筹学得到进一步发 展,广泛应用于军事、经济、工程等领域。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
·凸函数:定义在凸集上的函数f(X)称为凸函数,条件是 对于每一对x1,x2及每一个a,0≤a≤1存在:
f(ax1+(1-a)x2)≤a f(x1)+1(1-a)f(x2)
上式中,若≤变为<,则称为严格凸函数。
page 12 3 August 2019
Prof. Wang School of Economics & Management
B) 对于所有d,则dT▽2 f(X*)·d≥0
ii)判断极小点的充分条件
命题(二阶充分条件——无约束):设f(X)C2 是定义在 以X*为内点的一个区域上的函数,若
A) ▽f(X*)=0 B) Hess阵H(X*)正定(或负定)
则X*是f(X)的严格极小点(或极大点)
page 11 3 August 2019
目标函数 约束条件
page 3 3 August 2019
max:f(X) =30x1+450x2
0.5x1+2x2+0.25x22≤800
x1≥0,x2≥0
Prof. Wang School of Economics & Management
Operations Research
第二十一讲
§2 非线性规划的数学模型及 特点 (1)
page 15 3 August 2019
Prof. Wang School of Economics & Management
Operations Research
第二十一讲
§4 非线性规划求解方法分类(1)
1.一维最优化 ①斐波那契(Fibonacci)法 ②黄金分割法(0.618法) ③牛顿法(切线法) ④抛物线逼近法 ⑤成功和失败法
个函数。若X*是f( X)在上的一个相对极小点。则对于任 一X*处的可行方向dEn有:
A) ▽f(X*)·d≥0 B) ▽f(X*)·d=0,则必有dT·▽2 f(X*)·d≥0
▽2 f( X)表示f( X)的第二阶梯度或二阶导数,又称Hess或海 森阵,亦可用H或F表示。
page 10 3 August 2019
非线性规划的数学模型通常表示成以下形式。
min f(X) hi(X)=0 i=1,2,…,m gj(X)≥0 j=1,2,…,l
[例4-3]求解下述非线性规划 min f(X)=(x1-2)2+(x2-2)2 h(X)=x1+x2-6=0
page 4 3 August 2019
Prof. Wang School of Economics & Management
Operations Research
第二十一讲
§3 解和算法的基本性质 (9)
④凸规划定义:已知非线性规划: min f(X) gj(X)≥0
若f(X)为凸函数,gj(X)为凹函数,则称该规划为凸规划。 凸规划的局部极值点即为全局极值点。 线性规划为凸规划。 2.下降算法的收敛性问题(定性分析)(略)
ii)点X* Q,如果对于所有X Q成立f(X)≥f(X*),则称X* 为f在Q上的全局极小点。同样,若对于所有X Q, X≠X*时,存在f(X)>f(X*),则称X*为f在Q上的严格全局极 小点。
尽管问题的提法往往求全局极小点,然而,无论从 理论上或从计算观点看,实践现实性表明我们必须以很 多情形上满足一个相对极小点。当然,对于凸规划,这 二者是统一的。
Prof. Wang School of Economics & Management
Operations Research
第二十一讲
§1 非线性规划问题的现实来 源-问题的提出 (2)
[解]设公司应经营销售第一、二种设备数额分别为x1件和x2 件,追求的目标为最大销售额,即:
目标函数f(X)=30x1+450x2取极大 由于营业时间有限,必须满足:0.5x1+(2+0.25x2)x2≤800 当然,销售设备数不会为负数,即:x1≥0,x2≥0 综合得出该问题数学模型为:
Operations Research
第二十一讲
§3 解和算法的基本性质 (1)
1.极小点、凸集及其关系 ①极小点定义
i) 对于X* Q,如果存在一个 >0,使所有与X*的距离 小于 的X Q(即X Q,且|X-X*|<)都满足不等式
f(X)≥f(X*),则称X*为f在Q上的一个相对极小点或局部极
page 19 3 August 2019
Prof. Wang School of Economics & Management
Operations Research
第二十一讲
第十讲 非线性规划(二)
§1 一维最优化方法 §2 多维无约束寻优方法(使用导数)
page 20 3 August 2019
[例4-1]某公司经营两种设备。第一种设备每件售价为30元, 第二种设备每件售价为450元。且知,售出第一、二种设 备分别需时为每件约0.5小时和(2+0.25x2)小时,其中x2 为第二种设备售出数量。公司的总营业时间为800小时。
求:公司为获取最大营业额(销售额)的最优营业计划。
page 2 3 August 2019
Prof. Wang School of Economics & Management
Operations Research
第二十一讲
§3 解和算法的基本性质 (6)
iii)极小点的充分必要条件——无约束情形。(略)
③凸函数与凹函数
i)定义:
·凸集:若在X集合中,任意两点之联线都落在该集合 内,则称该集合为X的凸集。(a)源自(b)(c)严格凸 x
page 13 3 August 2019
凸x 图 4-2
非凸 x
Prof. Wang School of Economics & Management
Operations Research
第二十一讲
§3 解和算法的基本性质 (8)
ii)有关性质(凸函数性质)
·设f1(X),f2(X)是凸集上的凸函数,则函数f1(X)+f2(X)在
page 5 3 August 2019
Prof. Wang School of Economics & Management
Operations Research
第二十一讲
§2 非线性规划的数学模型及 特点 (3)
[例4-4]非线性规划为
min f(X)=(x1-2)2+(x2-2)2 h(X)=x1+x2-6≤0
Prof. Wang School of Economics & Management
Operations Research
第二十一讲
§3 解和算法的基本性质 (5)
命题3 (二阶必要条件——无约束情况):设X*是集合 的内点,且X*是函数f(X)C2在上一个相对极小点。则:
A) ▽f(X*)=0
page 17 3 August 2019
Prof. Wang School of Economics & Management
Operations Research
第二十一讲
§4 非线性规划求解方法分类(3)
(ii) 不采用导数: (a)直接法(模式搜索法) (b)可变多面体法 (c)鲍威尔法 (d)随机搜索法
Operations Research
第二十一讲
§2 非线性规划的数学模型及 特点 (2)
显然,与直线AB相切的点必 为最优解。
图 4-1(a) 中 的 D 点 即 为 最 优 点,此时目标函数值为:
f(X*)=2,x1*=x*2=3
x1 6
A
f(X)=4
3
D
2C
f(X)=2
B
0 23
6 x2
图4-1 (a)
上也是凸函数。
·设f(X)是凸集上的凸函数,则对任意的a≥0,函数af(X)是
凸的。
·设f(X)是凸集上的凸函数,对每一个实数C,则集合 C={x:x,f(X)C}是凸集。
iii) 凸函数的判定(略)
page 14 3 August 2019
Prof. Wang School of Economics & Management
小点。若对于所有X Q,X≠X*且与X*距离小于 ,有
f(X)>f(X*),则称X*为f在Q上的一个严格相对极小点。
page 7 3 August 2019
Prof. Wang School of Economics & Management
Operations Research
第二十一讲
§3 解和算法的基本性质 (2)
Prof. Wang School of Economics & Management
Operations Research
第二十一讲
§1 一维最优化方法 (1)
目前常用的一些方法有: ·斐波那契( Fibonacci)法——序贯试验法 ·黄金分割法(0.618法) ·牛顿切线法 ·抛物线逼近法 ·成功与失败试探法 下面将着重介绍斐波那契与黄金分割法的主要思路及步 骤。
page 18 3 August 2019
Prof. Wang School of Economics & Management
Operations Research
第二十一讲
§4 非线性规划求解方法分类(4)
②有约束情形 (i)线性逼近法 (ii)可行方向法 (iii)罚函数法 (iv)可变容差法 非线性规划的求解方法很多,上面列出的仅是一些常用的 方法。后面将简单介绍几个最基本解法的思路和步骤。
