《组合数学》第五版 第6章解答.
组合数学第五版答案

组合数学第五版答案简介《组合数学第五版答案》是对组合数学第五版的习题答案进行整理和解答的参考资料。
组合数学是一门研究集合之间的组合方式和规律的数学科学。
它广泛应用于计算机科学、统计学、运筹学等领域,在算法设计、图论分析等方面有着重要的应用价值。
本文档包含了《组合数学第五版》中各章节的习题答案,主要内容涵盖了排列组合、图论、生成函数、递推关系、容斥原理等多个重要主题。
通过对这些习题的解答,可以帮助读者更好地理解组合数学的基本概念、方法和应用。
目录•第一章:基本概念和方法•第二章:排列组合•第三章:图论•第四章:生成函数•第五章:递推关系•第六章:容斥原理第一章:基本概念和方法1.习题1:证明排列的总数为n! (阶乘)。
2.习题2:计算组合数C(n, m)的值。
3.习题3:探究组合数的性质并给出证明。
第二章:排列组合1.习题1:计算排列数P(n, m)的值。
2.习题2:解决带有限制条件的排列问题。
第三章:图论1.习题1:证明图论中的握手定理。
2.习题2:解决图的着色问题。
第四章:生成函数1.习题1:利用生成函数求解递推关系。
2.习题2:应用生成函数解决组合数学问题。
第五章:递推关系1.习题1:求解递推关系的通项公式。
2.习题2:应用递推关系解决实际问题。
第六章:容斥原理1.习题1:理解容斥原理的基本思想并给出证明。
2.习题2:应用容斥原理解决计数问题。
结论通过对《组合数学第五版答案》中的习题进行解答,读者可以更好地掌握组合数学的基本概念和方法。
组合数学在计算机科学、统计学、运筹学等领域具有广泛的应用,通过学习和理解组合数学,读者可以提高解决实际问题的能力,并为进一步深入研究相关领域打下坚实的基础。
注:本文档中的习题答案仅供参考,请读者在独立思考和解答问题时加以思考和验证,以深入理解组合数学的核心概念和方法。
组合数学 第6章
观察规律
固定k, 令S={1,…, k}.
circ(n) : S的长为n的圆排列个数.
per(d) : S的周期为d的线排列数.
line(n) : S的长为n的线排列数(=kn, circ(n)n).
周期1: 1111, 2222,
per(1)=2
固定k, 令S={1,…, k}. circ(n) : S的长为n的圆排列个数. per(d) : S的周期为d的线排列数. line(n) : S的长为n的线排列数(=kn, circ(n)n).
kn line(n) per(d ) -------(1)
d|n
circ(n) 1 per(d ) -------(2) d|n d 先由(1)解出per(n), 再带入(2)解出circ(n)
1
k
推论(C102,E165)
定理: 设A1, A2,…, An是有限集合, 则
n
|A1A2…An| = | Ai | | Ai Aj |
i 1
1i jn
| Ai Aj Ak |
1i jkn
+(-1)n-1|A1A2…An|
欧拉函数(n) (ex32,C122,E196)
(n)是1~n中与n互素的数的个数.
n! 3!
n! n!
n!
1
1 1!
1 2!
1 3!
n1!
错排的递推关系(C109,E176)
定理: Dn = (n-1) Dn-2 + (n-1) Dn-1. 证明: 对错排i1…in, (1) i1有n-1种取值, 设i1 = k; (2) 或(2a) ik=1; 或(2b) ik1. 将i1,ik互换则有
组合数学习题解答
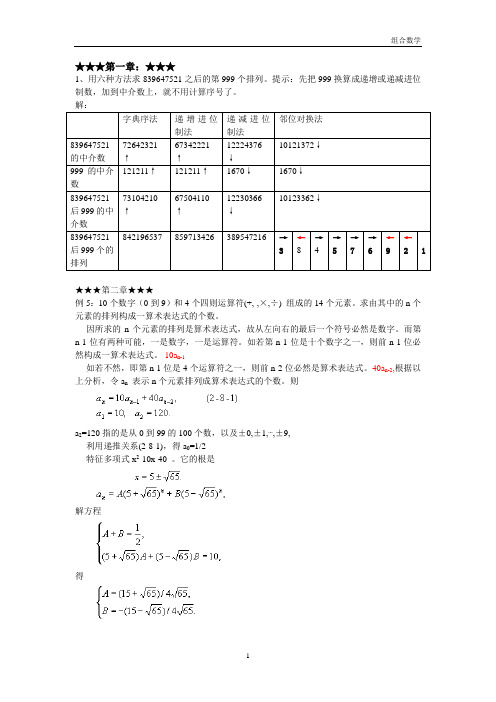
★★★第一章:★★★1、用六种方法求839647521之后的第999个排列。
提示:先把999换算成递增或递减进位制数,加到中介数上,就不用计算序号了。
解:字典序法递增进位制法递减进位制法邻位对换法839647521的中介数72642321↑67342221↑12224376↓10121372↓999的中介数121211↑121211↑1670↓1670↓839647521后999的中介数73104210↑67504110↑12230366↓10123362↓839647521后999个的排列842196537 859713426 389547216 →3←8→4→5→7→6←9←21★★★第二章★★★例5:10个数字(0到9)和4个四则运算符(+,-,×,÷) 组成的14个元素。
求由其中的n个元素的排列构成一算术表达式的个数。
因所求的n个元素的排列是算术表达式,故从左向右的最后一个符号必然是数字。
而第n-1位有两种可能,一是数字,一是运算符。
如若第n-1位是十个数字之一,则前n-1位必然构成一算术表达式。
10a n-1如若不然,即第n-1位是4个运算符之一,则前n-2位必然是算术表达式。
40a n-2,根据以上分析,令a n表示n个元素排列成算术表达式的个数。
则a2=120指的是从0到99的100个数,以及±0,±1,...,±9,利用递推关系(2-8-1),得a0=1/2特征多项式x2-10x-40 。
它的根是解方程得例7:平面上有一点P,它是n个域D1,D2,...,D n的共同交界点,见图2-8-4现取k种颜色对这n个域进行着色,要求相邻两个域着的颜色不同。
试求着色的方案数。
令a n表示这n个域的着色方案数。
无非有两种情况(1)D1和D n-1有相同的颜色;(2)D1和D n-1所着颜色不同。
第一种情形,域有k-1种颜色可用,即D1D n-1域所用颜色除外;而且从D1到D n-2的着色方案,和n-2个域的着色方案一一对应。
组合数学课后习题答案

第一章答案1.(a) 45 ( {1,6},{2,7},{3,8},…,{45,50} )(b) 45⨯5+(4+3+2+1) = 235( 1→2~6, 2→3~7, 3→4~8, …,45→46~50, 46→47~50, 47→48~50, 49→50 ) 2.(a) 5!8!(b) 7! P(8,5) (c) 2 P(5,3) 8! 3. (a) n!P(n+1, m) (b) n!(m+1)!(c) 2!((m+n-2)+1)! 4. 2 P(24,5) 20!5. 2⨯5⨯P(8,2)+3⨯4⨯P(8,2)6. (n+1)!-17. 用数学归纳法易证。
8. 41⨯319. 设 n=p 1n 1p 2n 2…p kn k , 则n 2的除数个数为 ( 2p 1+1) (2p 2+1) …(2p k+1).10.1)用数学归纳法可证n 能表示成题中表达式的形式;2)如果某n 可以表示成题中表达式的形式,则等式两端除以2取余数,可以确定a 1;再对等式两端的商除以3取余数,又可得a 2;对等式两端的商除以4取余数,又可得a 3;…;这说明表达式是唯一的。
11.易用C(m,n)=m!/(n!(m-n)!)验证等式成立。
组合意义:右:从n 个不同元素中任取r+1个出来,再从这r+1个中取一个的全体组合的个数;左:上述组合中,先从n 个不同元素中任取1个出来,每一个相同的组合要生复 C(n-1,r) 次。
12.考虑,)1(,)1(101-=-=+=+=∑∑n nk k k n nnk kknx n x kC x x C 求导数后有令x=1, 即知.210-==∑n nk kn n kC13. 设此n 个不同的数由小到大排列后为a 1, a 2, …, a n 。
当第二组最大数为a k 时,第二组共有2k-1种不同的可能,第一组有2n-k -1种不同的可能。
故符合要求的不同分组共有12)2()12(21111+-=-----=∑n k n k n k n 种。
《组合数学》第五版 第6章答案.pdf

set size
justification
S
13 4
13 = 14 − 5 + 5 − 1
Ai
8 4
13 − 5 = 8
Ai ∩ Aj 0 13 − 5 − 5 = 3 < 4
By inclusion/exclusion
13
8
|A1 ∩ A2 ∩ A3 ∩ A4 ∩ A5| =
4
− 5 = 365. 4
set size
justification
S
17 3
17 = 14 + 4 − 1
Ai
8 3
17 − 9 = 8
Ai ∩ Aj 0 17 − 9 − 9 = −1 < 3
By inclusion/exclusion
17
8
|A1 ∩ A2 ∩ A3 ∩ A4| =
3
− 4 = 456. 3
8. Let S denote the set of positive integral solutions for x1 + x2 + x3 + x4 + x5 = 14. For 1 ≤ i ≤ 5 let Ai denote the set of elements in S with xi ≥ 6. We seek |A1 ∩A2 ∩A3 ∩A4 ∩A5|. We have
X∩Y ∩Z
0
15 − 5 − 4 − 5 = 1 < 3
X∩Y ∩W 0
15 − 5 − 4 − 6 = 0 < 3
X ∩Z ∩W
0 15 − 5 − 5 − 6 = −1 < 3
Y ∩Z∩W
0
组合数学课后习题答案

组合数学课后习题答案问题1求解以下组合数:(a)C(5, 2)(b)C(7, 3)(c)C(10, 5)解答:(a)C(5, 2) 表示从5个不同元素中选取2个的组合数。
根据组合数的定义,我们可以使用公式 C(n, k) = n! / (k! * (n-k)!) 来计算组合数。
计算 C(5, 2): C(5, 2) = 5! / (2! * (5-2)!) = 5! / (2! * 3!) = (5 * 4 * 3!) / (2! * 3!) = (5 * 4) / 2 = 10所以 C(5, 2) = 10。
(b)C(7, 3) 表示从7个不同元素中选取3个的组合数。
计算 C(7, 3): C(7, 3) = 7! / (3! * (7-3)!) = 7! / (3! * 4!) = (7 * 6 * 5 * 4!) / (3! * 4!) = (7 * 6 * 5) / 3 = 35 * 2 = 70所以 C(7, 3) = 70。
(c)C(10, 5) 表示从10个不同元素中选取5个的组合数。
计算 C(10, 5): C(10, 5) = 10! / (5! * (10-5)!) = 10! / (5! * 5!) = (10 * 9 * 8 * 7 * 6 * 5!) / (5! * 5!) = (10 * 9 * 8 * 7 * 6) / (5 * 4 * 3 * 2 * 1) = 252所以 C(10, 5) = 252。
问题2在一个集合 {a, b, c, d, e} 中,求解以下问题:(a)有多少种不同的3个元素的子集?(b)有多少种不同的4个元素的子集?(c)有多少种不同的空集合?(a)在一个集合 {a, b, c, d, e} 中选取3个元素的子集。
子集的元素个数为3,所以我们需要从5个元素中选取3个。
利用组合数的公式 C(n, k) = n! / (k! * (n-k)!),我们可以计算组合数。
高等数学(同济第五版)课后答案 第六章
=(3p 2
y−
1 2
y2
−
1 6p
y3)
p −3
p
= 16 3
p2
.
5. 求由下列各曲线 所围成的图形的面积;
(1)ρ=2acosθ ; 解:
所求的面积为
A=
1 2
π
∫−2π 2
(2acosθ )2dθ
π
=
4a
2
∫2
0
cos2θdθ
=πa2.
(2)x=acos3t, y=asin3t; 解
a
a
z 20. 利用题 19 和结论, 计算曲线 y=sin x(0≤x≤π)和 x 轴所围
成的图形绕 y 轴旋转所得旋转体的体积.
∫ ∫ .3 解
V = 2π π xsin xdx = −2π π xd cosx = 2π (−xcosx +sin x)π = 2π 2 .
0
0
0
w 21. 计算曲线 y=ln x 上相应于 3 ≤ x≤ 8 的一段弧的长度.
o 解 设弦的倾角为 α. 由图可以看出, 抛物线与过焦点的弦所围成的图形的面积为
.c A= A0+ A1.
e 显然当α
=π 2
时,
A1=0;
当α <π 2
时,
A1>0.
因此, 抛物线与过焦点的弦所围成的图形的面积的最小值为
h a ∫ z A0 =2 0
2axdx = 8 3
a
x3 a = 8 a2 . 03
曲线 ρ = 2 sinθ 与 ρ 2 =cos 2θ 的交点 M 的极坐标为 M ( 2 , π ) . 所求的面积为 26
A
组合数学习题解答ex5
Байду номын сангаас
5.
max z=3x1+x2+x3+2x4 3x1+2x2+4x3+2x4=2 4x1+x2-3x3+x4+x5= -1 x1-3x2+x3+3x4+x6=3 2x1+x2+x3+3x4+x7=5 x1, x2, x3, x4…x7≥0 min z=2x1-3x2+6xx+x4-2x5 2x1-3x2+x3+3x4-x5=3 x1+x2-2x3+9x4=4 x1, x2, x3, x4, x5≥0 min z=x1+x1 8x1+ 5x2≥1 -7x1+4x2≤7 3x1+8x2≤12 5x1+2x2≤10 4x1+5x2≤10 x1,x2≥0
组合数学6章作业答案
第6章 容斥原理及应用6.7 练习题3、求出从1到10000既不是完全平方数也不是完全立方数的整数个数。
解:∵100001002=,9261213=,10648223=∴从1到10000,共有100个平方数,21个立方数 又∵409646=,1562556=∴从1到10000,共有4个6次方数,也就是共有4个数既是平方数又是立方数 计算:10000-100-21+4=9883∴从1到10000既不是完全平方数也不是完全立方数的整数有9883个□4、确定多重集{}d c b a S ⋅⋅⋅⋅=5,4,34,的12-组合的个数。
解:设T :{}d c b a S ⋅∞⋅∞⋅∞⋅∞=,,,*的所有12-组合 1A :a 的个数大于4的12-组合2A :b 的个数大于3的12-组合 3A :c 的个数大于4的12-组合4A :d 的个数大于5的12-组合要求的是:4321A A A A ⋂⋂⋂ = T )(4321A A A A +++-)(434232413121A A A A A A A A A A A A ⋂+⋂+⋂+⋂+⋂+⋂+ )(432431421321A A A A A A A A A A A A ⋂⋂+⋂⋂+⋂⋂+⋂⋂- )(4321A A A A ⋂⋂⋂+T =⎪⎪⎭⎫ ⎝⎛-+121412=4551A =⎪⎪⎭⎫ ⎝⎛-+7147=120 2A =⎪⎪⎭⎫ ⎝⎛-+8148=165 3A =⎪⎪⎭⎫ ⎝⎛-+7147=120 4A =⎪⎪⎭⎫⎝⎛-+6146=8421A A ⋂=⎪⎪⎭⎫ ⎝⎛-+3143=20 31A A ⋂=⎪⎪⎭⎫ ⎝⎛-+2142=10 41A A ⋂=⎪⎪⎭⎫⎝⎛-+1141=432A A ⋂=⎪⎪⎭⎫ ⎝⎛-+3143=20 42A A ⋂=⎪⎪⎭⎫ ⎝⎛-+2142=10 43A A ⋂=⎪⎪⎭⎫⎝⎛-+1141=4321A A A ⋂⋂=421A A A ⋂⋂=431A A A ⋂⋂=432A A A ⋂⋂=4321A A A A ⋂⋂⋂=0 455-(120+165+120+84)+(20+10+4+20+10+4)=34∴多重集{}d c b a S ⋅⋅⋅⋅=5,4,34,的12-组合的个数是34 □9、确定方程204321=+++x x x x满足611≤≤x ,702≤≤x ,843≤≤x ,624≤≤x的整数解的个数。
组合数学(第6章6.1)
σx(A1∩A2)= σx(S)−σx(A1)− σx(A2)+σx(A1∩A2)
— —
S
A1A1∩A2 A2
| A1 ∩ A2 |=| S | − | A1 | − | A2 | + | A1 ∩ A2 |
一般情形:容斥原理计数
定理6.1.1 集合S不具有性质P1,P2,…,Pm的物 体的个数:
注意到:
—
—
|A1∩A2|=∑ σx(A1∩A2)
x∈S
—
—
—
—
S中的元素可分为4种情况: 1)x不属于A1和A2; 左边 右边 −0−0+0=1 左边=1; 右边=1− − 2)x属于A1且不属于A2;
左边=0; 右边 −1−0+0=0 右边=1− − 左边
3)x属于A2, 不属于A1; 左边 右边 −0−1+0=0 左边=0;右边 右边=1− − 4)x属于A1, 又属于A2; 左边=0;右边 −1−1+1=0 左边 右边=1− − 右边
2 (−1)k mαk+…+ k
3 (−1)mαm
应 用
例. 从0到99999中有多少含有数字2, 5和8的整数。 解:设A1,A2 和A3分别是不包含数字2, 5和8的集合, 需要计算 | A I A2 I A3 | 1 0到99999的整数个数:α0=105 α1=|A1|=|A2|=|A3|=95 α2=|A1∩A2|=85 α3=|A1∩A2 ∩A3|=75 因此,答案为:105−3×95+3×85-75
6.1 容斥原理— 一个简单的例子
例. 计算1到600中不能被6整除的整数个数。 解:1到600中能被6整除的整数个数为600/6 =100个。因此,1到600中不能被6整除的 整数个数是600−100=500个。
