求一棵二叉树的深度和双分支结点的个数
中国农业大学_821数据结构_《数据结构》习题(6)

第6章 二叉树与树一、回答题1. 图6-1所示的树的叶子结点、非中端结点、每个结点的度及树的深度各是多少?图6-1 树2. 已知一棵树边的集合表示为:{ ( L, N ), ( G, K ), ( G, L ), ( G, M ), ( B, E ), ( B, F ), ( D, G ), ( D, H ), ( D, I ), ( D, J ), ( A, B ), ( A, C ), ( A, D ) },画出这棵树,并回答以下问题:(1) 树的根结点是哪个?哪些是叶子结点?哪些是非终端结点? (2) 树的度是多少?各个结点的度是多少? (3) 树的深度是多少?各个结点的层数是多少?(4) 对于结点G ,它的双亲结点、祖先结点、孩子结点、子孙结点、兄弟和堂兄弟分别是哪些结点?3. 如果一棵度为m 的树中,度为1的结点数为n 1,度为2的结点数为n 2,……,度为m 的结点数为n m ,那么该树中含有多少个叶子结点?有多少个非终端结点?ABECDFGHJI4. 任意一棵有n 个结点的二叉树,已知有m 个叶子结点,能否证明度为2结点有m-1个?5. 已知在一棵含有n 个结点的树中,只有度为k 的分支结点和度为0的叶子结点,那么该树含有的叶子结点的数目是多少?6. 一棵含有n 个结点的k 叉树,可能达到的最大深度和最小深度各为多少?7. 对于3个结点A 、B 、C ,可以过程多少种不同形态的二叉树?8. 深度为5的二叉树至多有多少个结点?9. 任何一棵二叉树的叶子结点在先序、中序和后序遍历中的相对次序是发生改变?不发生改变?不能确定?10. 设n 、m 为一棵二叉树上的两个结点,在中序遍历时,n 在m 前的条件是什么? 11. 已知某二叉树的后续遍历序列是dabec ,中序遍历序列是debac ,那么它的前序遍历序列是什么?12. 对一棵满二叉树,m 个树叶,n 个结点,深度为h ,则n 、m 和h 之间的关系是什么? 13. 对图6-2(a)和(b)所示的二叉树,它们的经过先序、中序和后序遍历后得到的结点序列分别是什么?画出它们的先序线索二叉树和后序线索二叉树。
数据结构二叉树实验报告
一 、实验目的和要求(1)掌握树的相关概念,包括树、节点的度、树的度、分支节点、叶子节点、孩子节点、双亲节 点、树的深度、森林等定义。
(2)掌握树的表示,包括树形表示法、文氏图表示法、凹入表示法和括号表示法等。
(3)掌握二叉树的概念,包括二叉树、满二叉树和完全二叉树的定义。
(4)掌握二叉树的性质。
(5)重点掌握二叉树的存储结构,包括二叉树顺序存储结构和链式存储结构。
(6)重点掌握二叉树的基本运算和各种遍历算法的实现。
(7)掌握线索二叉树的概念和相关算法的实现。
(8)掌握哈夫曼树的定义、哈夫曼树的构造过程和哈夫曼编码的产生方法。
(9)掌握并查集的相关概念和算法。
(10)灵活运用二叉树这种数据结构解决一些综合应用问题。
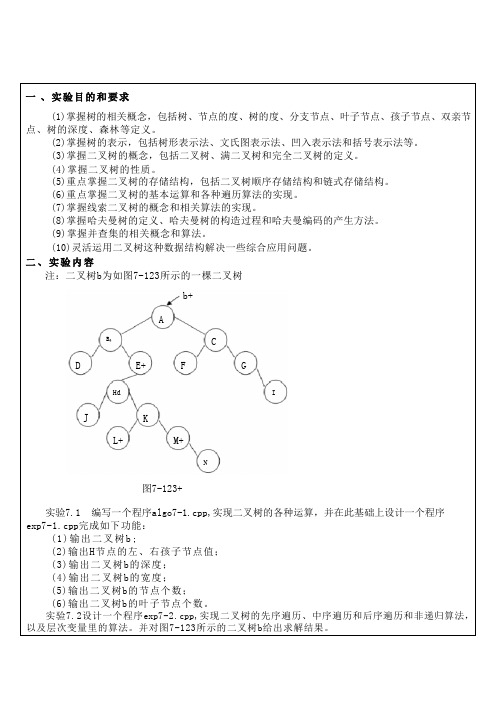
二、实验内容注:二叉树b 为如图7-123所示的一棵二叉树图7-123+实验7.1 编写一个程序algo7-1.cpp,实现二叉树的各种运算,并在此基础上设计一个程序exp7-1.cpp 完成如下功能:(1)输出二叉树b ;(2)输出H 节点的左、右孩子节点值; (3)输出二叉树b 的深度; (4)输出二叉树b 的宽度; (5)输出二叉树b 的节点个数;(6)输出二叉树b 的叶子节点个数。
实验7.2设计一个程序exp7-2.cpp,实现二叉树的先序遍历、中序遍历和后序遍历和非递归算法, 以及层次变量里的算法。
并对图7-123所示的二叉树b 给出求解结果。
b+ACF GIKL+NM+E+HdJD₄B臣1607-1.CPPif(b?-HULL)re3P4+;Qu[rear]-p-b;Qu[rear].1no=1;while(reart=front){Front++;b=Qu[front]-P;lnum-Qu[front].1no;if(b->Ichildt=NULL)rpar+t;Qu[rear]-p=b->1child;Qu[rear].Ino-lnun+1;if(D->rch11d?=NULL)1/根结点指针入队//根结点的层次编号为1 1/队列不为空1/队头出队1/左孩子入队1/右孩子入队redr+t;qu[rear]-p=b->rchild;Qu[rear].1no-lnun*1;}}nax-0;lnun-1;i-1;uhile(i<=rear){n=0;whdle(i<=rear ge Qu[1].1no==1num)n+t;it+;Inun-Qu[i].1n0;if(n>max)nax=n;}return max;田1607-1.CPPreturn max;}elsereturn o;口×int Modes(BTNode *D) //求二叉树D的结点个数int nun1,nun2;if(b==NULL)returng,else if(b->ichild==NULL&D->rchild==NULL)return 1;else{num1-Hodes(b->Ichild);num2=Nodes(b->rchild);return(num1+nun2+1);LeafNodes(BINode *D) //求二叉树p的叶子结点个数int num1,num2;1f(D==NULL)return 0;else if(b->1chi1d==NULLc& b->rch11d==NULL)return 1;else{num1-LeafModes(b->lchild);num2=LeafNodes(b->rchild);return(nun1+nun2);int程序执行结果如下:xCProrn FlslirosfViu l SudiollyPrjecslro7 LJebuglFoj7 ex<1)输出二叉树:A<B<D,E<H<J,K<L,M<,N>>>>),C<F,G<,I>>)<2)'H’结点:左孩子为J石孩子为K(3)二叉树b的深度:7<4)二叉树b的宽度:4(5)二叉树b的结点个数:14(6)二叉树b的叶子结点个数:6<?>释放二叉树bPress any key to continue实验7 . 2程序exp7-2.cpp设计如下:坠eTPT-2.EPP#include<stdio.h》winclude<malloc.h>deFn Masie 00typde chr ElemTyetypede sruct nde{ElemType data;stuc node *lclldstruct node rchild;》BTHode;extern vod reaeBNodeBTNode extrn void DispBTHode(BTNodeuoid ProrderBTNode *b)if(b?-NULL)- 回1 / 数据元素1 / 指向左孩子1 / 指向右孩子*eb car *str)xb1 / 先序遍历的递归算法1 / 访问根结点/ / 递归访问左子树1 7 递归访问右子树/ / 根结点入栈//栈不为空时循环/ / 退栈并访问该结点/ / 右孩子入栈{》v oidprintf(*c“,b->data); Preorder(b->lchild); Pre0rder(b->rchild);Preorder1(BTNode *b)BTNode xSt[Maxsize],*p;int top=-1;if(b!-HULL)top++;St[top]-b;uhle (op>-)p-St[top];top--;printf("%c“,p->data);if(p->rchild?-HULL)A约e程p7-2.CPPprintF(”后序逅历序列:\n");printf(" 递归算法=");Postorder(b);printf("\n");printf(“非递归算法:“);Postorder1(b);printf("\n");序执行结果如下:xCAPrograFleicsoftVisal SudlyrjecsProj 2Debuzlroj72ex"二叉树b:A(B(D,ECH<J,K(L,M<,N)>))),C(F,GC.I>))层次遍历序列:A B C D E F G H I J K L M N先序遍历序列:递归算法:A B D E H J K L M N C F G I非归算法:A B D E H J K L M N C F G I中序遍历序列:递归算法: D B J H L K M N E A F C G I非递归算法:D B J H L K M N E A F C G I后序遍历序列:递归算法: D J L N M K H E B F I G C A非递归算法:D J L N H K H E B F I G C APress any key to continue臼p7-3.CPP15Pp a t h[p a t h l e n]-b->d a t a;//将当前结点放入路径中p a t h l e n t+;/7路任长度培1Al1Path1(b->ichild,patn,pathlen);1/递归扫描左子树Al1Path1(b->rchild,path,pathlen); //递归扫描右子树pathlen-- ; //恢复环境uoid Longpath(BTNode *b,Elemtype path[1,int pathlen,Elemtype longpath[],int elongpatnien) int i;1f(b==NULL){if(pathlen>longpatnlen) //若当前路径更长,将路径保存在1ongpatn中for(i-pathlen-1;i>-8;i--)longpath[i]=path[1];longpathlen-pathlen;elsepath[pathlen]=b->data; pathlen4; //将当前结点放入路径中//路径长度增1iongPath(b->lchild,path₇pathlen,langpath,longpathien);//递归扫描左子树LongPath(b->rchiid,path,pathien,longpath,longpathien);//递归扫描石子树pathlen--; /7饮其环境oid DispLeaf(BTNode xb)- 口凶uoid DispLeaf(BTNode xb)iE(D!=NULL){ if(b->1child--HULL B& b->rchild--HULL)printf("3c“,b->data);elsepispLeaf(b->ichild);DispLeaf(b->rchild);oid nain()8TNodexb;ElenType patn[Maxsize],longpath[Maxsize];int i.longpathien-U;CreateBTNode(b,"A(B(D,E(H(J,K(L,H(,N))))),C(F,G(,I)))");printf("\n二灾树b:");DispBTNode(b);printf("\n\n*);printf(”b的叶子结点:");DispLeaf(b);printf("\n\n");printf("A11Path:");A11Path(b);printf("m");printf("AiiPath1:n");AliPath1(b.path.);printf("");LongPath(b,path,8,longpath,longpathlen);printf(”第一条量长路径长度=d\n”,longpathlen);printf(”"第一茶最长路径:");for(i=longpathlen;i>=0;i--)printf("c",longpatn[1]);printf("\n\n");。
树和二叉树习题集与答案解析

一、填空题1. 不相交的树的聚集称之为森林。
2. 从概念上讲,树与二叉树是两种不同的数据结构,将树转化为二叉树的基本目的是_树可采用孩子-兄弟链表(二叉链表)做存储结构,目的是利用二叉树的已有算法解决树的有关问题。
3. 深度为k的完全二叉树至少有2 k-1个结点。
至多有2 k-1个结点,若按自上而下,从左到右次序给结点编号(从1开始),则编号最小的叶子结点的编号是2 k-2+1。
4. 在一棵二叉树中,度为零的结点的个数为n 0,度为2的结点的个数为n 2,则有n0= n2+1。
5. 一棵二叉树的第i(i≥1)层最多有2 i-1个结点;一棵有n(n>0)个结点的满二叉树共有(n+1)/2个叶子和(n-1)/2个非终端结点。
6.现有按中序遍历二叉树的结果为abc,问有5种不同形态的二叉树可以得到这一遍历结果。
7. 哈夫曼树是带权路径最小的二叉树。
8. 前缀编码是指任一个字符的编码都不是另一个字符编码的前缀的一种编码方法,是设计不等长编码的前提。
9. 以给定的数据集合{4,5,6,7,10,12,18}为结点权值构造的Huffman 树的加权路径长度是165 。
10. 树被定义为连通而不具有回路的(无向)图。
11. 若一棵根树的每个结点最多只有两个孩子,且孩子又有左、右之分,次序不能颠倒,则称此根树为二叉树。
12. 高度为k,且有个结点的二叉树称为二叉树。
2k-1 满13. 带权路径长度最小的二叉树称为最优二叉树,它又被称为树。
Huffman14. 在一棵根树中,树根是为零的结点,而为零的结点是结点。
入度出度树叶15. Huffman树中,结点的带权路径长度是指由到之间的路径长度与结点权值的乘积。
结点树根16. 满二叉树是指高度为k,且有个结点的二叉树。
二叉树的每一层i上,最多有个结点。
2k-1 2i-1二、单选题1. 具有10个叶结点的二叉树中有(B) 个度为2的结点。
(A)8 (B)9 (C)10 (D)112.对二叉树的结点从1开始进行连续编号,要求每个结点的编号大于其左右孩子的编号,同一结点的左右孩子中,其左孩子的编号小于其右孩子的编号,则可采用_(3)次序的遍历实现编号。
树结构习题及答案

第5章 树【例5-1】写出如图5-1所示的树的叶子结点、非终端结点、每个结点的度及树深度。
解:(1)叶子结点有:B 、D 、F 、G、H 、I 、J 。
(2)非终端结点有:A 、C 、E 。
(3)每个结点的度分别就是:A 的度为4,C 的度为2,E 的度为3,其余结点的度为0。
(4)树的深度为3。
【例5-2】一棵度为2的树与一棵二叉树有什么区别?解:度为2的树有两个分支,但分支没有左右之分;一棵二叉树也有两个分支,但有左右之分,左右子树的次序不能交换。
【例5-3】树与二叉树有什么区别?解:区别有两点:(1)二叉树的一个结点至多有两个子树,树则不然;(2)二叉树的一个结点的子树有左右之分,而树的子树没有次序。
: :空树或者任一结点均无左孩子的非空二叉树;:空树或者任一结点均无右孩子的非空二叉树;:空树或仅有一个结点的二叉树。
【例5-7】如图5-5所示的二叉树,要求: (1)写出按先序、中序、后序遍历得到的结点序列。
(2)画出该二叉树的后序线索二叉树。
解:bac def图5-5A B C D EF G H I J 图5-1图5-4(1) 先序遍历序列:ABDEFC中序遍历序列:DEFBAC后序遍历序列:FEDBCA(2)其后序线索二叉树如图5-6所示。
C、D、的结点图5-13第六步: 30 27 43A、4B、5C、6D、72、假设在一棵二叉树中,双分支结点数为15,单分支结点数为30个,则叶子结点数为(2、B )个。
A、15B、16C、17D、473、假定一棵三叉树的结点数为50,则它的最小高度为(3、C )。
A、3B、4C、5D、64、在一棵二叉树上第4层的结点数最多为( 4、D)。
A、2B、4C、6D、85、用顺序存储的方法将完全二叉树中的所有结点逐层存放在数组中R[1、、n],结点R[i]若有左孩子,其左孩子的编号为结点(5、B)。
A、 R[2i+1]B、 R[2i]C、 R[i/2]D、 R[2i-1]6、由权值分别为3,8,6,2,5的叶子结点生成一棵哈夫曼树,它的带权路径长度为(6、D )。
数据结构-树习题

数据结构-树习题第六章树⼀、选择题1、⼆叉树的深度为k,则⼆叉树最多有( C )个结点。
A. 2kB. 2k-1C. 2k-1D. 2k-12、⽤顺序存储的⽅法,将完全⼆叉树中所有结点按层逐个从左到右的顺序存放在⼀维数组R[1..N]中,若结点R[i]有右孩⼦,则其右孩⼦是(B )。
A. R[2i-1]B. R[2i+1]C. R[2i]D. R[2/i]3、设a,b为⼀棵⼆叉树上的两个结点,在中序遍历时,a在b前⾯的条件是( B )。
A. a在b的右⽅B. a在b的左⽅C. a是b的祖先D. a是b的⼦孙4、设⼀棵⼆叉树的中序遍历序列:badce,后序遍历序列:bdeca,则⼆叉树先序遍历序列为()。
A. adbceB. decabC. debacD. abcde5、在⼀棵具有5层的满⼆叉树中结点总数为(A)。
A. 31B. 32C. 33D. 166、由⼆叉树的前序和后序遍历序列( B )惟⼀确定这棵⼆叉树。
A. 能B. 不能7、某⼆叉树的中序序列为ABCDEFG,后序序列为BDCAFGE,则其左⼦树中结点数⽬为( C )。
A. 3B. 2C. 4D. 58、若以{4,5,6,7,8}作为权值构造哈夫曼树,则该树的带权路径长度为( C )。
A. 67B. 68C. 69D. 709、将⼀棵有100个结点的完全⼆叉树从根这⼀层开始,每⼀层上从左到右依次对结点进⾏编号,根结点的编号为1,则编号为49的结点的左孩⼦编号为( A )。
A. 98B. 99C. 50D. 4810、表达式a*(b+c)-d的后缀表达式是( B )。
A. abcd+-B. abc+*d-C. abc*+d-D. -+*abcd11、对某⼆叉树进⾏先序遍历的结果为ABDEFC,中序遍历的结果为DBFEAC,则后序遍历的结果是( B )。
A. DBFEACB. DFEBCAC. BDFECAD. BDEFAC12、树最适合⽤来表⽰( C )。
数据结构之二叉树(BinaryTree)

数据结构之⼆叉树(BinaryTree)⽬录导读 ⼆叉树是⼀种很常见的数据结构,但要注意的是,⼆叉树并不是树的特殊情况,⼆叉树与树是两种不⼀样的数据结构。
⽬录 ⼀、⼆叉树的定义 ⼆、⼆叉树为何不是特殊的树 三、⼆叉树的五种基本形态 四、⼆叉树相关术语 五、⼆叉树的主要性质(6个) 六、⼆叉树的存储结构(2种) 七、⼆叉树的遍历算法(4种) ⼋、⼆叉树的基本应⽤:⼆叉排序树、平衡⼆叉树、赫夫曼树及赫夫曼编码⼀、⼆叉树的定义 如果你知道树的定义(有限个结点组成的具有层次关系的集合),那么就很好理解⼆叉树了。
定义:⼆叉树是n(n≥0)个结点的有限集,⼆叉树是每个结点最多有两个⼦树的树结构,它由⼀个根结点及左⼦树和右⼦树组成。
(这⾥的左⼦树和右⼦树也是⼆叉树)。
值得注意的是,⼆叉树和“度⾄多为2的有序树”⼏乎⼀样,但,⼆叉树不是树的特殊情形。
具体分析如下⼆、⼆叉树为何不是特殊的树 1、⼆叉树与⽆序树不同 ⼆叉树的⼦树有左右之分,不能颠倒。
⽆序树的⼦树⽆左右之分。
2、⼆叉树与有序树也不同(关键) 当有序树有两个⼦树时,确实可以看做⼀颗⼆叉树,但当只有⼀个⼦树时,就没有了左右之分,如图所⽰:三、⼆叉树的五种基本状态四、⼆叉树相关术语是满⼆叉树;⽽国际定义为,不存在度为1的结点,即结点的度要么为2要么为0,这样的⼆叉树就称为满⼆叉树。
这两种概念完全不同,既然在国内,我们就默认第⼀种定义就好)。
完全⼆叉树:如果将⼀颗深度为K的⼆叉树按从上到下、从左到右的顺序进⾏编号,如果各结点的编号与深度为K的满⼆叉树相同位置的编号完全对应,那么这就是⼀颗完全⼆叉树。
如图所⽰:五、⼆叉树的主要性质 ⼆叉树的性质是基于它的结构⽽得来的,这些性质不必死记,使⽤到再查询或者⾃⼰根据⼆叉树结构进⾏推理即可。
性质1:⾮空⼆叉树的叶⼦结点数等于双分⽀结点数加1。
证明:设⼆叉树的叶⼦结点数为X,单分⽀结点数为Y,双分⽀结点数为Z。
形考作业三及答案

形考作业三及答案本部分作业覆盖教材第6-7章的内容)一、单项选择题1.假定一棵二叉树中,双分支结点数为15,单分支结点数为30,则叶子结点数为()。
A.15 B.16 C.17 D.472.二叉树第k层上最多有()个结点。
A.2k B.2k-1C.2k-1 D.2k-13.二叉树的深度为k,则二叉树最多有()个结点。
A.2k B.2k-1C.2k-1 D.2k-14. 设某一二叉树先序遍历为abdec,中序遍历为dbeac,则该二叉树后序遍历的顺序是()。
A.abdec B.debac C.debca D.abedc5.将含有150个结点的完全二叉树从根这一层开始,每一层从左到右依次对结点进行编号,根结点的编号为1,则编号为69的结点的双亲结点的编号为()。
A.33 B.34 C.35 D.366.如果将给定的一组数据作为叶子数值,所构造出的二叉树的带权路径长度最小,则该树称为()。
A.哈夫曼树 B.平衡二叉树C.二叉树 D.完全二叉树7.下列有关二叉树的说法正确的是()。
A.二叉树中度为0的结点的个数等于度为2的结点的个数加1B.二叉树中结点个数必大于0C.完全二叉树中,任何一个结点的度,或者为0或者为2D.二叉树的度是28.在一棵度为3的树中,度为3的结点个数为2,度为2的结点个数为1,则度为0的结点个数为()。
A.4 B.5 C.6 D.79.在一棵度具有5层的满二叉树中结点总数为()。
A.31 B.32 C.33 D.1610. 利用n个值作为叶结点的权生成的哈夫曼树中共包含有( )个结点。
A. nB. n+1C. 2*nD. 2*n-111. 利用3、6、8、12这四个值作为叶子结点的权,生成一棵哈夫曼树,该树中所有叶子的最长带权路径长度为( )。
A. 18B. 16C. 12D. 3012.在一棵树中,()没有前驱结点。
A.分支结点 B.叶结点 C.树根结点 D.空结点13.在一棵二叉树中,若编号为i的结点存在右孩子,则右孩子的顺序编号为()。
数据结构本科期末综合练习二填空与判断题剖析

数据结构〔本科〕期末综合练习二〔填空与判断题〕填空题数据是__信息__的载体,它能够被计算机程序识别、存储和加工处理。
数据结构包括逻辑结构、__存储结构__和数据的运算三个方面。
数据结构的逻辑结构包括线性结构和__非线性__结构两大类。
数据结构的存储结构包括顺序、__链接___、索引和散列等四种。
5. 根本数据类型是计算机已经实现了的_数据结构__。
抽象数据类型的特点是__数据封装__、信息隐蔽、使用与实现别离。
算法的一个特性是__有穷性__,即算法必须执行有限步就结束。
面向对象的特征应包括对象、类、__继承__、消息通信。
属性与效劳相同的对象构成类,类中的每个对象称为该类的__实例__。
对象的私有状态只能通过该对象的__操作〔或效劳〕_才能改变。
模板类是一种数据抽象,它把__数据类型_当作参数,可以实现类的复用。
1 2.在类的继承结构中,位于上层的类叫做基类,其下层的类那么叫做__派生〔或子〕__类。
1 3.一维数组所占用的空间是连续的。
但数组元素不一定顺序存取,通常是按元素的__下标〔或顺序号〕__存取的。
在程序运行过程中不能扩充的数组是__静态__分配的数组。
这种数组在声明它时必须指定它的大小。
在程序运行过程中可以扩充的数组是__动态___分配的数组。
这种数组在声明它时需要使用数组指针。
16. 二维数组是一种非线性结构,其中的每一个数组元素最多有__两个__个直接前驱〔或直接后继〕。
17. 假设设一个nn的矩阵A的开始存储地址LOC(0,0) 及元素所占存储单元数d,按行存储时其任意一个矩阵元素a[i][j] 的存储地址为__LOC(0,0)+(i*n+j)*d __。
118.对称矩阵的行数与列数__相等_且以主对角线为对称轴,aij=aji,因此只存储它的上三角局部或下三角局部即可。
将一个n阶对称矩阵的上三角局部或下三角局部压缩存放于一个一维数组中,那么一维数组需要存储__n(n+1)/2_个矩阵元素。
