2格林公式及其应用
格林公式的讨论及其应用

格林公式的讨论及其应用目录一、引言 (2)二、牛顿-莱布尼兹(Newton-Leibniz)公式的应用 (3)(一)牛顿-莱布尼兹公式简介 (3)(二)牛顿-莱布尼兹公式的物理意义 (3)(三)牛顿-莱布尼兹公式在生活中应用 (3)三、格林(Green)公式的应用 (4)(一)格林公式的简介 (4)(二)格林公式的物理原型 (4)1、物理原型 (4)2、计算方法 (4)(三)格林公式在生活中的应用 (5)1.曲线积分计算平面区域面积 (5)2.GPS面积测量仪的数学原理 (6)四、高斯(Gauss)公式的应用 (7)(一)高斯公式的简介 (7)(二)保守场 (8)(三)高斯公式在电场中的运用 (8)(四)高斯定理在万有引力场中的应用 (11)五、斯托克斯(Stokes)公式的应用 (12)(一)斯托克斯公式简介 (12)(二)Stokes公式中P、Q、R的物理意义 (13)(四)旋度与环流量 (14)(五)旋度的应用 (14)六、结语 (16)参考文献............................................................................................................................... 错误!未定义书签。
致谢................................................................................................................................. 错误!未定义书签。
摘要牛顿-莱布尼兹(Newton-Leibniz)公式、格林(Green)公式、高斯(Gauss)公式和斯托克斯(Stokes)公式是积分学中的几个非常重要的公式,分别建立了原函数与定积分、曲线积分与二重积分、曲线积分与三重积分、曲线积分和曲面积分之间的联系,它们除了在数学上用来计算多元函数的积分有很大用处之外,在其他的领域也有很多重要的应用。
格林公式的讨论及其应用

格林公式的讨论及其应用目录一、引言 (2)二、牛顿-莱布尼兹(Newton-Leibniz)公式的应用 (3)(一)牛顿-莱布尼兹公式简介 (3)(二)牛顿-莱布尼兹公式的物理意义 (3)(三)牛顿-莱布尼兹公式在生活中应用 (3)三、格林(Green)公式的应用 (4)(一)格林公式的简介 (4)(二)格林公式的物理原型 (4)1、物理原型 (4)2、计算方法 (4)(三)格林公式在生活中的应用 (5)1.曲线积分计算平面区域面积 (5)2.GPS面积测量仪的数学原理 (6)四、高斯(Gauss)公式的应用 (7)(一)高斯公式的简介 (7)(二)保守场 (8)(三)高斯公式在电场中的运用 (8)(四)高斯定理在万有引力场中的应用 (11)五、斯托克斯(Stokes)公式的应用 (12)(一)斯托克斯公式简介 (12)(二)Stokes公式中P、Q、R的物理意义 (13)(四)旋度与环流量 (14)(五)旋度的应用 (14)六、结语 (16)参考文献............................................................................................................................... 错误!未定义书签。
致谢................................................................................................................................. 错误!未定义书签。
摘要牛顿-莱布尼兹(Newton-Leibniz)公式、格林(Green)公式、高斯(Gauss)公式和斯托克斯(Stokes)公式是积分学中的几个非常重要的公式,分别建立了原函数与定积分、曲线积分与二重积分、曲线积分与三重积分、曲线积分和曲面积分之间的联系,它们除了在数学上用来计算多元函数的积分有很大用处之外,在其他的领域也有很多重要的应用。
3.2格林公式及其应用

P Q R d ( Pnx Qny Rnz )dS . x y z
*格林第一公式
1 2 u u ( x , y , z ), v v ( x , y , z ) C ( ) C (), 设 , v v v 记 P u , Q u , R u , 由高斯公式,可得 x y z
于是
1 u(M 0 ) 2 4 a
a
udS .
注 如果 u C() ,则定理可包含与边界相切的球面。
3.极值原理
*物理背景:稳定温度场在动态平衡下,温度分布在 内部不可能有最高点或最低点。
*数学角度证明 定理2.3(极值原理) 对不恒等于常数的调和函数 u ( x, y, z ) ,其在区域 的任何内点上的值不可能达到 它在 上的上界或下界。 证 用反证法证明。设调和函数 u ( x, y, z ) 不恒等于 常数,且在区域 上的上界为m (注:只需证明有上界 情况即可,相反情况,定理自然成立),而 u ( x, y, z ) 在 内某点 M 0 取值 m ,我们来引出矛盾。
y
x
其中 K 表示 中以 M 0 为球心,以 为半径的 小球,边界记 。
1 1 u F )dS dV . 令u F , 则 (u n r r n r \ K
1 1 1 1 1 2 2, 在球面 上,由于 n n r r r r r
4. 第一边值问题解的唯一性及稳定性
u 0, 定理2.4 狄利克雷内问题 的解如果存在, u f
必是唯一的,而且连续地依赖于所给的边界条件 f 。 证 假设有两个调和函数 u1 ( x, y, z) 和 u2 ( x, y, z),它们
格林公式及其应用

Pdx Qdy Pdx Qdy
L2
Pdx Qdy Pdx Qdy 0,
L1 L1 ( L2 ) L2
Pdx Qdy 0
此时L1 ( L2 )为有向闭曲线,故结论成立, 反之也成立.
3、定理2
设区域G是一个单连通域,函数P( x, y )、Q( x, y ) 在G内具有一阶连续偏导数,则曲线积分 Pdx Qdy
Q y2 x2 P 2 2 2 x ( x y ) y 则
L
xdy ydx x y
2 2
0
(2) 原点在D内时
选取适当小的r 0, 作位于D内的圆周l x2 y2 r 2 记L与l所围的闭区域为D1;
即D1为复连通区域,
l的方向取逆时针方向 有 , xdy ydx x y
P 因 连续,故第一式左边 y 2 ( x ) P ( x, y ) P b dy dx y dxdy a 1 ( x ) y D a Px, 2 ( x) Px,1 ( x)dx
b
第一式右边 Pdx Pdx Pdx
第三节
格林公式及其应用
一、格林公式
二、平面上曲线积分与路径 无关的条件 三、二元函数的全微分求积
一、 格林公式
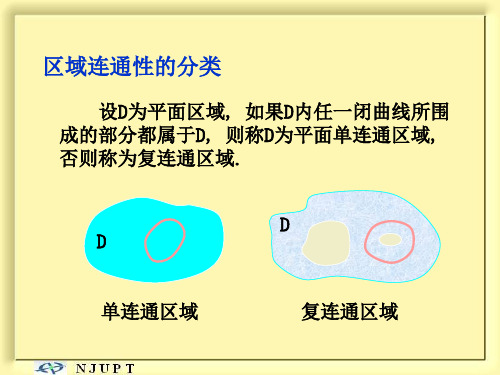
平面单连通区域: 设D为平面区域,如果D内任一闭曲线所围的部
分都属于D,则称D为平面单连通区域,否则称为复连
通区域.
通俗的说,平面单连通区域是不含有“洞”的区
域.
例如 圆形区域: x, y ) x 2 y 2 1} {(
Pdx Qdy
ABPA
Q P x y dxdy Pdx Qdy D3 BCNB
格林公式(公开教学用)

B
x
b
y
E
xd 1( y)
nD
c
C
o
m
x 2( y)
x
y 型区域
按照 y 型区域考虑
Q dxdy
d
[
2 ( y) Q(x, y)dx]dy
D x
c 1( y)
x
d
c Q( 2 ( y), y) Q(1( y), y)dy
Q(x, y)dy Q(x, y)dy Q(x, y)dy
3)平面曲线 L 的正向:当人(观
察者)沿L的方向行走时,D内在靠近人
Hale Waihona Puke 的一侧始终在人的左侧。L
L
D
D l洞
外圈是逆时针方向;内圈是顺时针方向。
2、格林(Green)公式(定理1)
(1)D 是由分段光滑 (或光滑)的有向
闭曲线 L 围成; (2)函数 P(x, y),Q(x, y) 在D上具有一
阶连续偏导数;
y2 x2 x2 y2
2
,
补充定理:
1) 设P,Q 在 D 内具有一阶连续偏导数
2)
在
D
内恒有
Q x
P y
3) L1, L2 为D内任意两条同向闭曲线;
4) L1,L2 各自所围的区域中有相同的不
属于D的点,则
D
Pdx Qdy Pdx Qdy
L1
L2
L1 L2
解:当 (0,0利) 用D格林公式,结论为0.
(3)L要求取正向.(若不是正向 ? )
(4)二重积分的被积函数必须是 Q P .
x y
同学们思考一下,说明的第(2) 条其实是可以修改的,应该改成什么?
格林公式及其应用格林公式

格林公式及其应用格林公式格林公式是向量分析中的一个重要定理,也被称为格林-斯托克斯定理。
它是由爱尔兰数学家乔治·格林在19世纪提出的,用于计算一个曲线或曲面上的环流和散度之间的关系。
格林公式的应用非常广泛,可以用来求解流体力学、电磁学和热力学等领域的问题。
下面将介绍格林公式的表达形式,以及它在常见问题中的具体应用。
1.格林公式的表达形式格林公式有两种常见的表达形式,一种是针对平面区域的格林公式,另一种是针对空间曲线的格林公式。
下面将分别介绍这两种格林公式的表达形式。
1.1平面区域的格林公式若D是一个紧致的平面区域,边界为C(C是一个简单、逐段光滑的曲线),向量函数F(x,y)=(P(x,y),Q(x,y))在区域D中具有二阶连续偏导数,则有如下格林公式:∬D(∂Q/∂x-∂P/∂y)dxdy=∮C(Pdx+Qdy)其中,∂P/∂y和∂Q/∂x分别表示P和Q对y和x的偏导数,dxdy表示在D中的面积元素,Pdx+Qdy表示沿着边界C的曲线元素。
1.2空间曲线的格林公式若S是一个有向光滑曲面,它的边界为C(C是一个简单、光滑的曲线),向量函数F(x,y,z)=(P(x,y,z),Q(x,y,z),R(x,y,z))在曲面S内具有连续偏导数,则有如下格林公式:∯S(∂R/∂y-Q)dydz+(∂P/∂z-R)dzdx+(∂Q/∂x-P)dxdy=∮C(Pdx+Qdy+Rdz)其中,∂P/∂z、∂Q/∂x和∂R/∂y分别表示P、Q和R对z、x和y的偏导数,dydz、dzdx和dxdy表示在S内的面积元素,Pdx+Qdy+Rdz表示沿着边界C的曲线元素。
2.格林公式的应用格林公式具有广泛的应用,在流体力学、电磁学、热力学等领域都能够找到它的身影。
下面将以几个例子来说明格林公式的具体应用。
2.1流体力学中的应用格林公式在流体力学中常常用于计算流体的环流和散度。
例如,可以利用格林公式来推导速度势函数和流函数之间的关系,进而求解流场中的速度分布。
§11.2(2)格林公式

Q P ∫∫D( x y )dxdy = ∫L Pdx + Qdy
4
2) 若D不满足以上条件, 则可通过加辅助线将其分割 为有限个上述形式的区域 , 如图 Q P ∫∫D( x y ) dxdy
y
1 D2 D
L
= ∑∫∫
k =1 n
n
Dk
(
Q P ) dxdy x y
Dn
o
x
= ∑∫
k =1
du = xy2 dx + x2 ydy. (0,0)( Nhomakorabea, y) .
= ∫ x 0 dx + ∫
0
x
y 2 x y dy 0
(x,0)
=∫
y 2 x y dy 0
18
xd y y d x 在右半平面 ( x > 0 ) 内存在原函 例6. 验证 2 2 x +y y 数 , 并求出它. (x, y) y x , Q= 2 证: 令 P = 2 2 x +y x + y2 2 2 o (1,0) ( x,0) x P y x Q 则 = 2 = ( x > 0) 2 2 x (x + y ) y 由定理 2 可知存在原函数 定理
Q P ∫∫ x y dxdy = ∫ Pdx + Qdy ( 格林公式 ) D L
或
∫∫ P
D
x
y
Q
dxdy = ∫ Pdx + Qdy
L
2
证明: 证明 1) 若D 既是 X - 型区域 , 又是 Y - 型区域 , 且 1(x) ≤ y ≤ 2 (x) y E D: d a ≤ x ≤b
y0 x0 x0 y y0 x
格林公式及其应用 (2)45页PPT文档
D
(
Q x
P y
)dxdy
L
Pdx
Qdy
(1)
其中 L是 D的取正向的边界曲线,
公式(1)叫做格林公式.
L1
D
L2
L1
D
L2
L由 L1与 L2连成 L由 L1与 L2组成
边界曲线L的正向 当观察者沿边界行走时, 区域D总在他的左边。
y
证明 (1)
d
E y2(x)
若区域 D既是 X 型 x1(y)
L L l lD ( Q x P y)dx d l y
要求右端的二重积分及曲线l积分易于计算。l 选用直线段、折线、圆、半圆、椭圆、抛物线等。
(3)如在D上P、Q一阶偏导连续,且处处有
Q P , x y
则 L 0;
如
D
内除点
M 0(x0,y0)外均有
Q x
P y
,
则
Ll
其中 l 是包围点(x0,y0)的与 L同向的光滑的简 单闭曲线,特别地 l 是以(x0,y0)为中心的圆、椭圆 等(半径或长短半轴大小不限,只要内部没有别的
Dx
c 1(y) x
d
d
cQ (2 (y )y ) ,d y cQ (1 (y )y ) ,dy
y
Q (x ,y )d yQ (x ,y )dy
CBE
CAE
d
x1(y)
Q (x ,y )d yQ (x ,y )dy
CBE
EAC
c
LQ(x,y)dy
o
E D
C
x2(y)
x
同理可证 D P ydx dL yP(x,y)dx
由 O x 于 A d 0 ,y Bx O d 0 ,y
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
4
F rM (M 0M)dM
作为 M 0的函数,记
上页 下页 返回
R (M 0 ) 4 1 u (M ) n r M 1 0 M r M 1 0 M u (n M ) dM S
V(M 0)41F rM (M 0M)dM
因为 1 rM 0 M
是
基
本
解
,
则对M 0 ,有
u(M0)21u(M)n lnrM 10MlnrM 10Mu(n M )dM s
1
1
2lnrM0Mu dM
当u是内的调和函数时,即u 0时,若M0 ,则
有 u (M 0 ) 2 1 u (M ) n lr n M 1 0 M lr n M 1 0 M u (n M ) d M s通区域\ NhomakorabeaK 中,v
r
1
M0M
0。
K
在复连通区域 \ K中对上述函数u和
v 应用 Green 第二公式,得
\K u 1 r 1 r u d u n 1 r 1 r n u dS(2.5)
其中 1 1 。 r rM0M
上页 下页 返回
(2 .5 )式 左 u 边 1 1 u d 1 u d
若u F (M ),则当M0 时:
(2.7)
u(M0)41u(M)nrM 10MrM 10Mu(n M )dSM
1
4
F rM (M 0M)dM
(2.8)
上页 下页 返回
补:二维空间上的基本积分公式以及调和函数的 基本积分公式
设是 R2中的有界开集, ,u C 2 () C1(),
上页 下页 返回
记u
1 ()
udS ,
u n
1
()
nudS ,其中
()表
示
的面积,即
u和
u n
分别为
u和
nu在
上的
平均值,则
u n 1 r 1 r n u d S (2 )u ( ) n u
因为lim u 0
u(
格林第二公式:u ( v) v( u )d u n v v n u dS
其中n是 的单位外法向量。
上页 下页 返回
2)调和函数的积分表达式
考察函数
1
1
v(x, y,z)
rM 0 M
( x x0 )2 ( y y0 )2 (z z0 )2
容易验证,当 M ( x, y, z) M0 ( x0 , y0 , z0 ) 时,
\K r r
r \K
(2.5)式右 边 un 1 r1 r n u dS
K
un 1 r1 r n u dSun 1 r1 r n u dS
注意到在
上,
1 r
1
,n
1 r
r
1 r
1 r2
1 2
\K 1 r u d u n 1 r 1 r n u d S 1 2 u d 1 S n u dS
调和函数基本积分公式 上页 下页 返回
当u是内的调和函数,M 0 ,则由格林第二公式 有:
u (M ) n rM 1 0M rM 1 0M u (n M ) d S0
当u是内的调和函数,M0 ,类似基本积分公 式的推导,记 , \ K ,则有
u n 1 r 1 r n u d S 1 2 u d1 S n u dS
上页 下页 返回
记u
1 42
udS
,
nu
1 42
nudS
,即 u 和
nu
分别为u
和
nu在
上的平均值,则
\K 1 r u d u n 1 r 1 r n u d 4 S u 4 n u
令 0,则
1 r u d u n 1 r 1 r n u d S 4 u (M 0 )
M
0
)
,lim 0
( 4
)
2
1 ,上式两边令 2
0,
得
u n 1 r 1 r n u d S 2 u (M 0)
上页 下页 返回
综上所述,设 是以足够光滑的曲面 为边界的有界 区域,u u( x, y, z) C 2 () C1(),若u 0,则:
u n rM 1 0M rM 1 0M n u dM S 4 0 2 u u ((M M 0 0) )( ((M M M 0 0 0 )))
上页 下页 返回
从而有:
u(M0)41u(M)nrM 10MrM 10Mu(nM )dS
11
ud
4 rM0M
基本积分公式
当u是内的调和函数时,即u 0时,若M0 ,则
u (M 0) 4 1 u (M ) n rM 1 0 M rM 1 0 M u (n M ) dS
上页 下页 返回
3) 泊松方程
利用基本积分公式(2.8)很容易导得泊松方程的一个
特解表达式。
事 实 上 , 设 有 函 数 u(M ) C 2 () C1() , 满 足
u F ,其中F C 0 (),由(2.8),对M0
u(M0)41u(M)nrM 10MrM 10Mu(n M )dSM
所
以
M0
1 rM 0 M
v 0。(见P73 习题 1)称 v 1 为三维拉普拉斯 rM 0 M
方程的基本解。
设 u u( x, y, z) C 2 () C1() , M0 ( x0 , y0 , z0 ) 是 内一定点。
上页 下页 返回
为利用
Green
第二公式,取
充分小,使得以
M
为球心,
0
半径为的球 K 的球面与的边界不相交,则在复连
§2 格林公式及其应用
1. 格林(Green)公式 2. 平均值定理 3. 极值原理 4. 第一边值问题解的唯一性及稳定性
1.格林公式
1) 格林公式的推导
高斯公式: A d A d S (A n )dS
由于 uv uv u v,则由高斯公式可得
格林第一公式: u ( v)d u n v d S u v d
