北邮版17下高等数学第四章 第一节
高等数学A1教学PPT课件1:10-第10讲导数的概念

三、导数的几何意义
函数 f (x) 在点 x0 的导数 f ( x0) 就是对应的平面 曲线 y = f (x) 在点 (x0, y0) 处的切线的斜率 k :
k tan f (x0 )
此时, 切线方程为: y y0 f (x0 )(x x0 )
f (x0) = 0 y
y=c
2
22
物体由 t 到 t + t 一段的平均速度是
V (t) S(t t) S(t) 1 g(2t t t 2 )
(t t) t 2
t
gt 1 g t 2
求物体在时刻 t 的瞬时速度 vt , 就是 令 t0 的极限过程:
Vt
lim V
t 0
(t)
lim
t 0
S (t
t) t
高等院校非数学类本科数学课程
大 学 数 学(一)
—— 一元微积分学
第十讲 导数的概念
第四章 函数的导数和微分
本章学习要求: ▪ 理解导数和微分的概念。熟悉导数的几何意义以及函数的可
导、可微、连续之间的关系。 ▪ 熟悉一阶微分形式不变性。 ▪ 熟悉导数和微分的运算法则,能熟练运用求导的基本公式、
复合函数求导法、隐函数求导法、反函数求导法、参数方程 求导法、取对数求导法等方法求出函数的一、二阶导数和微 分。 ▪ 了解 n 阶导数的概念,会求常见函数的 n 阶导数。 ▪ 熟悉罗尔中值定理、拉格朗日中值定理、柯西中值定理和泰 勒中值定理,并能较好运用上述定理解决有关问题(函数方 程求解、不等式的证明等)。 ▪ 掌握罗必塔法则并能熟练运用它计算有关的不定式极限。
O
x0
x
y f (x0)不存在
f (x0) = y
北京邮电大学国际学院高等数学(下)幻灯片讲义(无穷级数)Le.

1(x 2
−
2) +
1(x 4
−
2)2
=
3−
3x 2
+
x2 4
#
8
Convergence of Power Series
Abel’s Theorem (1)
(2)
∞
∑ Consider the series an xn. n=0
If it converges at x0 , x0 ≠ 0 , then it must converge
but converges for| x − x0 |< R. The series may or may not converge at either of the endpointsx = x0 − Randx = x0 + R. 2. The series converges for every x(R = ∞) . 3. The series converges at x = x0 and diverges elsewhere (R = 0).
n=1
13
Finding the Interval of Convergence Using the Ratio Test
∑ Solution Apply the Ratio Test to the series | un | , where un
is the nth term of the series in question.
divergence points is called the divergence domain of the series.
1
2
Series of Functions
Definition (Sum function and Convergence)
北京邮电大学国际学院高等数学(下)幻灯片讲义(无穷级数)-Lecture 1

is called the partial sum of the series. The partial sum of the series form a sequence
s1 = a1 , s2 = a1 + a2 ,
, sn = ∑ ak ,
k =1 n
n approaching infinite, we say that the series converges to the sum S, and we write
1+ 1 1 1 1 + + + + 2 4 8 16
Infinite Series
∑a
n =1
∞
n
=1 +
1 1 1 1 + + + + 2 4 8 16
Partial Sum First: Second: Third:
…
Value
s1 = 1
1 s2 = 1 + 2
21
2 2 1 2 1 4
The way to do so is not to try to add all the terms at once (we cannot) but rather to add the terms one at a time from the beginning and look for a pattern in how these "partial sum" grow.
k =1 n
Convergence and Divergence
Definition (Convergence and Divergence of a series) If the sequence of partial sums of a series
北京邮电大学 数电 数字第四章辅导材料part2-2010-1-7介绍
a
&
Q
a b
b c
&
Q
(a)
c
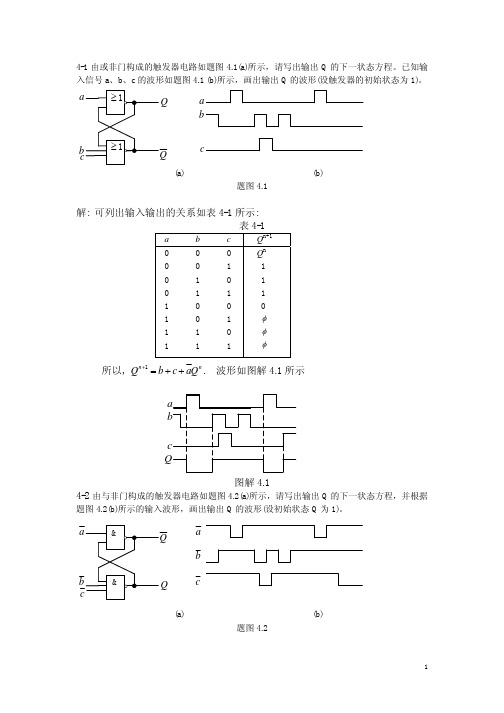
(b) 题图 4.2
1
解:下一状态方程与上题相同,即: Q n +1 = b + c + aQ n 输出波形如图解 4.2 所示:
a
b
c
图解 4.2 4-3 由与或非门构成的触发器如题图 4.3 所示,当 G=1 时,触发器处于什么状态?当 G=0
J
Qn
K
T 0 0 0 1 1 0 1 1
图解 4.9 得到 T = J Q n + KQ n 由此可得逻辑图如图解 4.10 所示:
&
≥1
&
5
图解 4.10
(2)
T→D
∵ Q n +1 = T ⊕ Q n = T Q n + TQ n
(T 触发器)
Q n +1 = D
(D 触发器)
∴ D = T ⊕ Qn ⇒ T = D ⊕ Qn
(D 触发器) (JK 触发器)
∴ 可得J = D, K = D 由此可得逻辑图如图解 4.7(a)所示:
图解 4.7(a)
(2)
JK → T
∵ Q n +1 = T ⊕ Q n = T Q n + TQ n 而Q n +1 = J Q n + KQ n
(T 触发器) (JK 触发器)
可得: ∴ 可得J = K = T 由此可得逻辑图如图解 4.7(b)所示:
4-6 列表小结 RS、D、JK 和 T 触发器的状态方程、状态表以及功能表。
高等数学第四章

1 不定积分的概念与性质
高等数学 第四章. 第一节
第 10 页
三、不定积分的几何意义
例6 已知曲线y f (x)上任意一点M (x,y)处的切线斜率为k 2x,且曲线
通过原点(0,0, ) 求该曲线的方程.
解 由导数的几何意义知:k f (x) 2x,则切线斜率为2x的全部曲线为,
3
3
x2 d x 1 x3 C. 3
例2 求不定积分 sin xd. x
解 因为( cos x) sin x,所以
sin xd x cos x C.
1 不定积分的概念与性质
高等数学 第四章. 第一节
第8 页
例3 求不定积分 ex d. x
解 因为(ex ) e, x 所以 ex d x ex C.
性质1还可以推广到有限个函数的代数和的积分,即
1 f1 (x) f2 (x) fn (x)d x f1 (x)d x f2 (x)d x fn (x)d. x 不定积分的概念与性质
高等数学 第四章. 第一节
第 13 页
性质2 被积函数中不为零的常数因子可以提到积分号前面,即
高等数学 第四章. 第一节
第4 页
一、原函数的概念 定义1 设已知函数f (x)在某区间上有定义,若存
在函数F (x, ) 对于该区间内任意一点x都有F (x) f (x) 或dF (x) f (x)d x,则称F (x)是f (x)在区间(a,b)内的一
个原函数.
1 不定积分的概念与性质
一般地,若F (x)是f (x)的一个原函数,那么在几何 上y F (x)所表示的曲线称为f (x)一条积分曲线.由于
北师大版高中数学必修一学案:第四章1

北师大版高中数学必修一学案:第四章1学习目标 1.理解二分法的原理及其适用条件.2.掌握二分法的实施步骤.3.体会二分法中蕴含的逐步逼近与程序化思想.知识点一二分法的原理思考通过上节课的学习,我们知道f(x)=ln x+2x-6的零点在区间(2,3)内,如何缩小零点所在区间(2,3)的范围?梳理二分法的概念如果在区间[a,b]上,函数f(x)的图像是______________________,且__________________,则区间[a,b]内有方程f(x)=0的解.依次取有解________________,如果取到某个区间的中点x0,恰使f(x0)=0,则x0就是所求的一个解;如果区间中点的函数值总不等于零,那么,不断地重复上述操作,就得到一系列闭区间,方程的一个解在这些区间中,区间长度____________,端点逐步逼近方程的解,可以得到一个近似解.像这样每次__________________,________________________,再经比较,按需要留下其中一个小区间的方法称为二分法.知识点二精度与精确到思考“精确到0.1”与“精度为0.1”一样吗?梳理在许多实际应用中,不需要求出方程精确的解,只要满足一定的精度就可以.设是方程f(x)=0的一个解,给定正数ε,若x0满足__________________,就称x0是满足精度ε的近似解.为了得到满足精度ε的近似解,只需找到方程的一个有解区间[a,b],________________________,那么区间(a,b)内任意一个数都是满足精度ε的近似解.事实上,任意选取两数x1,x2∈(a,b),都有|x1-x2|<ε.由于∈(a,b),所以任意选取x′∈(a,b)都有|x′-|<ε.知识点三二分法求方程近似解的步骤利用二分法求方程实数解的过程可以用下图表示出来.在这里:“初始区间”是一个两端函数值反号的区间;“M”的含义是:取新区间,一个端点是原区间的中点,另一端是原区间两端点中的一个,新区间两端点的函数值反号;“N”的含义是:方程解满足要求的精度;“P”的含义是:选取区间内的任意一个数作为方程的近似解.类型一二分法的操作例1 用二分法求函数f(x)=x3-3的一个零点.(精度为0.02)引申探究如何求的近似值?(精度为0.01)反思与感悟用二分法求函数零点的近似值关键有两点:一是初始区间的选取,符合条件(包括零点),又要使其长度尽量小;二是进行精度的判断,以决定是停止计算还是继续计算.跟踪训练 1 借助计算器或计算机用二分法求方程2x+3x=7的近似解.(精度为0.1)类型二二分法取中点的次数问题例2 若函数f(x)在(1,2)内有1个零点,要使零点的近似值满足精度为0.01,则对区间(1,2)至少二等分( )A.5次B.6次C.7次D.8次反思与感悟对于区间(a,b)二分一次区间长度为,二分二次区间长度为,…,二分n次区间长度为.令<ε,即2n>,nlg 2>lg,n>,从而估算出至少要使用多少次二分法.跟踪训练 2 在用二分法求方程的近似解时,若初始区间的长度为1,精度为0.05,则取中点的次数不小于______.1.下列函数中,只能用二分法求其零点的是( )A.y=x+7 B.y=5x-1C.y=log3x D.y=()x-x2.观察下列函数的图像,判断能用二分法求其零点的是( ) 3.方程2x-1+x=5的根所在的区间为( )A.(0,1) B.(1,2)C.(2,3) D.(3,4)4.定义在R上的函数f(x)的图像是连续不断的曲线,已知函数f(x)在区间(a,b)上有一个零点x0,且f(a)f(b)<0,用二分法求x0时,当f()=0时,则函数f(x)的零点是( )A.(a,b)外的点B.x=a+b2C.区间(a,)或(,b)内的任意一个实数D.x=a或b5.用二分法求函数y=f(x)在区间(2,4)上的唯一零点的近似值时,验证f(2)·f(4)<0,取区间(2,4)的中点x1==3,计算得f(2)·f(x1)<0,则此时零点x0所在的区间是( )A.(2,4) B.(2,3)C.(3,4) D.无法确定1.二分就是平均分成两部分.二分法就是通过不断地将所选区间一分为二,使区间的两个端点逐步逼近零点,直至找到零点附近足够小的区间,根据所要求的精度,用此区间的某个数值近似地表示真正的零点.2.二分法求方程近似解的适用范围:在包含方程解的一个区间上,函数图像是连续的,且两端点函数值反号.3.求函数零点的近似值时,所要求的精度不同,得到的结果也不相同.答案精析问题导学知识点一思考①取区间(2,3)的中点2.5.②计算f(2.5)的值,用计算器算得f(2.5)≈-0.084.因为f(2.5)·f(3)<0,所以零点在区间(2.5,3)内.梳理一条连续的曲线f(a)·f(b)<0区间的中点越来越小取区间的中点将区间一分为二知识点二思考不一样.比如得数是1.25或1.34,精确到0.1都是通过四舍五入后保留一位小数得 1.3.而“精度为0.1”指零点近似值所在区间(a,b)满足|a-b|<0.1,比如零点近似值所在区间(1.25,1.34).若精度为0.1,则近似值可以是 1.25,也可以是1.34.梳理|x0-|<ε使得区间长度b-a≤ε题型探究例1 解由于f(0)=-3<0,f(1)=-2<0,f(2)=5>0,故可取区间(1,2)作为计算的初始区间.用二分法逐次计算,列表如下:所以函数f(x)=x3-3的零点的近似值可取为1.437 5.引申探究解设x=,则x3=2,即x3-2=0,令f(x)=x3-2,则函数f(x)的零点的近似值就是的近似值,以下用二分法求其零点.由f(1)=-1<0,f(2)=6>0,故可以取区间(1,2)为计算的初始区间.用二分法逐次计算,列表如下:由于,所以1.265 625是函数的零点的近似值,即的近似值是1.265 625.跟踪训练1 解原方程即2x+3x-7=0,令f(x)=2x+3x-7,用计算器或计算机作出函数f(x)=2x+3x-7的对应值表与图像如下:有零点x0.取区间(1,2)的中点x1=1.5,用计算器算得f(1.5)≈0.33.因为f(1)·f(1.5)<0,所以x0∈(1,1.5).再取区间(1,1.5)的中点x2=1.25,用计算器算得f(1.25)≈-0.87.因为f(1.25)·f(1.5)<0,所以x0∈(1.25,1.5).同理可得,x0∈(1.375,1.5),x0∈(1.375,1.437 5).由于|1.375-1.437 5|=0.062 5<0.1,所以原方程的近似解可取为1.437 5.例2 C [设对区间(1,2)至少二等分n次,初始区间长为1.第1次二等分后区间长为;第2次二等分后区间长为;第3次二等分后区间长为;…第n次二等分后区间长为.根据题意,得<0.01,∴n>log2100.∵6<log2100<7,∴n≥7.故对区间(1,2)至少二等分7次.]跟踪训练2 5解析∵初始区间的长度为1,精度为0.05,∴≤0.05,即2n≥20.又∵n∈N*,∴n≥5,∴取中点的次数不小于5.当堂训练1.D 2.A 3.C 4.B 5.B。
(完整word版)高等数学课后习题及参考答案第四章

高等数学课后习题及参考答案(第四章)习题4-11. 求下列不定积分:(1)⎰dx x 21;解 C x C x dx x dx x +-=++-==+--⎰⎰112111222.(2)⎰dx x x ; 解 C x x C x dx x dx x x +=++==+⎰⎰212323521231.(3)⎰dx x1;解C x C x dx xdx x+=++-==+--⎰⎰21211112121. (4)⎰dx x x 32; 解 C x x C x dx x dx x x+=++==+⎰⎰3313737321031371. (5)⎰dx x x 21; 解C x x C x dx xdx xx +⋅-=++-==+--⎰⎰12312511125252. (6)dx x m n ⎰; 解C x mn mC x mn dx x dx x mn m m n m nmn++=++==++⎰⎰111.(7)⎰dx x 35;解 C x dx x dx x +==⎰⎰4334555.(8)⎰+-dx x x )23(2;解 C x x x dx dx x dx x dx x x ++-=+-=+-⎰⎰⎰⎰2233123)23(2322.(9)⎰ghdh 2(g 是常数);解C ghC h gdh hgghdh +=+⋅==⎰⎰-22212122121. (10)⎰-dx x 2)2(;解 C x x x dx dx x dx x dx x x dx x ++-=+-=+-=-⎰⎰⎰⎰⎰423144)44()2(23222.(11)⎰+dx x 22)1(;解 C x x x dx dx x dx x dx x x dx x +++=++=++=+⎰⎰⎰⎰⎰3524242232512)12()1(.(12)dx x x ⎰-+)1)(1(3;解 ⎰⎰⎰⎰⎰⎰-+-=-+-=-+dx dx x dx x dx x dx x x x dx x x 23212323)1()1)(1(C x x x x +-+-=25233523231.(13)⎰-dx x x 2)1(;解C x x x dx x x xdx xx x dx xx ++-=+-=+-=-⎰⎰⎰-2523212321212252342)2(21)1(. (14)⎰+++dx x x x 1133224; 解 C x x dx x x dx x x x ++=++=+++⎰⎰arctan )113(1133322224. (15)⎰+dx x x 221;解⎰⎰⎰+-=+-=+-+=+C x x dx xdx xx dx x x arctan )111(111122222.(16)⎰+dx xe x )32(;解 C x e dx xdx e dx x e x x x ++=+=+⎰⎰⎰||ln 32132)32(.(17)⎰--+dx xx )1213(22;解 ⎰⎰⎰+-=--+=--+C x x dx xdx x dx xx arcsin 2arctan 3112113)1213(2222.(18)dx x e e x x⎰--)1(;解 C x edx xe dx xe e xxx x+-=-=-⎰⎰--21212)()1(.(19)⎰dx e x x 3;解 C e C e e dx e dx e xx x xxx++=+==⎰⎰13ln 3)3ln()3()3(3.(20)⎰⋅-⋅dx xxx 32532;解 C x C x dx dx x xx xxx+--=+-=-=⋅-⋅⎰⎰)32(3ln 2ln 5232ln )32(52])32(52[32532. (21)⎰-dx x x x )tan (sec sec ;解 ⎰⎰+-=-=-C x x dx x x x dx x x x sec tan )tan sec (sec )tan (sec sec 2.(22)⎰dx x2cos 2;解 C x x dx x dx x dx x ++=+=+=⎰⎰⎰)sin (21)cos 1(212cos 12cos 2.(23)⎰+dx x 2cos 11;解 ⎰⎰+==+C x dx xdx x tan 21cos 212cos 112.(24)⎰-dx xx xsin cos 2cos ;解 ⎰⎰⎰+-=+=--=-C x x dx x x dx xx xx dx x x x cos sin )sin (cos sin cos sin cos sin cos 2cos 22.(25)⎰dx x x x22sin cos 2cos ; 解 ⎰⎰⎰+--=-=-=C x x dx xx dx x x x x dx x x x tan cot )cos 1sin 1(sin cos sin cos sin cos 2cos 22222222.(26)⎰-dx x x x)11(2;解 ⎰⎪⎭⎫ ⎝⎛-dx x x x 211⎰++=-=--C x x dx x x 41474543474)(.2. 一曲线通过点(e 2, 3), 且在任一点处的切线的斜率等于该点横坐标的倒数, 求该曲线的方程.解 设该曲线的方程为y =f (x ), 则由题意得xx f y 1)(='=',所以 C x dx xy +==⎰||ln 1.又因为曲线通过点(e 2, 3), 所以有=3-2=1 3=f (e 2)=ln|e 2|+C =2+C , C =3-2=1. 于是所求曲线的方程为y =ln|x |+1.3. 一物体由静止开始运动, 经t 秒后的速度是3t 2(m/s ), 问 (1)在3秒后物体离开出发点的距离是多少? (2)物体走完360m 需要多少时间?解 设位移函数为s =s (t ), 则s '=v =3 t 2, C t dt t s +==⎰323. 因为当t =0时, s =0, 所以C =0. 因此位移函数为s =t 3. (1)在3秒后物体离开出发点的距离是s =s (3)=33=27.(2)由t 3=360, 得物体走完360m 所需的时间11.73603≈=t s. 4. 证明函数x e 221, e x sh x 和e xch x 都是x x e x sh ch -的原函数.证明 x x xx x x x x x e ee e e e e e x x e 222sh ch ==--+=----. 因为x x e e 22)21(=', 所以x e 221是x x e xsh ch -的原函数.因为(e x sh x )'=e x sh x +e x ch x =e x (sh x +ch x )x x x x x x e e e e e e 2)22(=++-=--, 所以e x sh x 是xx e xsh ch -的原函数.因为(e x ch x )'=e x ch x +e x sh x =e x (ch x +sh x )x x x x x x e e e e e e 2)22(=-++=--, 所以e xch x 是xx e x sh ch -的原函数.习题4-21. 在下列各式等号右端的空白处填入适当的系数, 使等式成立(例如: )74(41+=x d dx :(1) dx = d (ax );解dx = a 1d (ax ).(2) dx = d (7x -3);解dx = 71d (7x -3).(3) xdx = d (x 2); 解xdx = 21 d (x 2).(4) x d x = d (5x 2);解x d x = 101d (5x 2).(5))1( 2x d xdx -=;解 )1( 212x d xdx --=.(6)x 3dx = d (3x 4-2);解x 3dx = 121d (3x 4-2).(7)e 2x dx = d (e 2x ); 解e 2x dx = 21 d (e 2x ).(8))1( 22x x ed dxe --+=;解 )1( 2 22x x e d dx e --+-=.(9))23(cos 23sin x d xdx =;解 )23(cos 32 23sin x d xdx -=.(10)|)|ln 5( x d xdx=; 解 |)|ln 5( 51x d x dx =. (11)|)|ln 53( x d xdx-=; 解|)|ln 53( 51x d x dx --=. (12))3(arctan 912x d x dx=+; 解 )3(arctan 31912x d x dx =+. (13))arctan 1( 12x d xdx -=-;解)arctan 1( )1( 12x d xdx --=-.(14))1( 122x d x xdx -=-.解)1( )1( 122x d x xdx --=-.2. 求下列不定积分(其中a , b , ω, ϕ均为常数): (1)⎰dt e t 5; 解 C e x d e dt e xx t +==⎰⎰55551551. (2)⎰-dx x 3)23(; 解 C x x d x dx x +--=---=-⎰⎰433)23(81)23()23(21)23(. (3)⎰-dx x 211; 解C x x d x dx x +--=---=-⎰⎰|21|ln 21)21(21121211.(4)⎰-332x dx ;解C x C x x d x xdx+--=+-⋅-=---=-⎰⎰-3232313)32(21)32(2331)32()32(3132. (5)⎰-dx e ax bx)(sin ;解C be ax ab x d e b ax d ax a dx e ax b xb xbx+--=-=-⎰⎰⎰cos 1)()(sin 1)(sin .(6)⎰dt tt sin ;解⎰⎰+-==C t t d t dt tt cos 2sin 2sin .(7)⎰⋅xdx x 210sec tan ;解 ⎰⋅xdx x 210sec tan C x x xd +==⎰1110tan 111tan tan . (8)⎰xx x dxln ln ln ;解C x x d x x d x x x x x dx +===⎰⎰⎰|ln ln |ln ln ln ln ln 1ln ln ln ln 1ln ln ln .(9)⎰+⋅+dx xx x 2211tan ;解 ⎰+⋅+dx x x x 2211tan 2222211cos 1sin 11tan x d x x x d x +++=++=⎰⎰C x x d x ++-=++-=⎰|1cos |ln 1cos 1cos 1222.(10)⎰xx dxcos sin ;解 C x x d x dx x x x x dx +===⎰⎰⎰|tan |ln tan tan 1tan sec cos sin 2.(11)⎰-+dx ee x x 1;解 ⎰-+dx e e xx 1C e de edx e e x x xx x +=+=+=⎰⎰arctan 11122.(12)⎰-dx xe x 2; 解 .21)(212222C e x d e dx xe x x x +-=--=---⎰⎰ (13)⎰⋅dx x x )cos(2;解 C x x d x dx x x +==⋅⎰⎰)sin(21)()cos(21)cos(2222. (14)⎰-dx xx 232;解C x C x x d x dx x x+--=+--=---=-⎰⎰-2212221223231)32(31)32()32(6132.(15)⎰-dx xx 4313; 解⎰⎰+--=---=-C x x d x dx x x |1|ln 43)1(11431344443.(16)⎰++dt t t ))sin((cos 2ϕωϕω; 解 C t t d t dt t t ++-=++-=++⎰⎰)(cos 31)cos()(cos 1)sin()(cos 322ϕωωϕωϕωωϕωϕω. (17)⎰dx x x3cos sin ; 解 C x C x x xd dx xx +=+=-=--⎰⎰2233sec 21cos 21cos cos cos sin . (18)⎰-+dx x x xx 3cos sin cos sin ;解 )sin cos (cos sin 1cos sin cos sin 33x x d xx dx x x x x +--=-+⎰⎰C x x x x d x x +-=--=⎰-3231)cos (sin 23)cos (sin )cos (sin .(19)⎰--dx xx 2491;解dx xx dx xdx xx ⎰⎰⎰---=--22249491491)49(49181)32()32(1121222x d x x d x --+-=⎰⎰C x x +-+=2494132arcsin 21.(20)⎰+dx x x 239;解 C x x x d xx d x x dx x x ++-=+-=+=+⎰⎰⎰)]9ln(9[21)()991(21)(9219222222223. (21)⎰-dx x 1212;解⎰⎰⎰+--=+-=-dx x x dx x x dx x )121121(21)12)(12(11212 ⎰⎰++---=)12(121221)12(121221x d x x d x C x x C x x ++-=++--=|1212|ln 221|12|ln 221|12|ln 221.(22)⎰-+dx x x )2)(1(1;解C x x C x x dx x x dx x x ++-=++--=+--=-+⎰⎰|12|ln 31|1|ln |2|(ln 31)1121(31)2)(1(1. (23)⎰xdx 3cos ;解 C x x x d x x d x xdx +-=-==⎰⎰⎰3223sin 31sin sin )sin 1(sin cos cos .(24)⎰+dt t )(cos 2ϕω; 解 C t t dt t dt t +++=++=+⎰⎰)(2sin 4121)](2cos 1[21)(cos 2ϕωωϕωϕω. (25)⎰xdx x 3cos 2sin ; 解 ⎰xdx x 3cos 2sin C x x dx x x ++-=-=⎰cos 215cos 101)sin 5(sin 21. (26)⎰dx xx 2cos cos ;解 C x x dx x x dx x x ++=+=⎰⎰21sin 23sin 31)21cos 23(cos 212cos cos .(27)⎰xdx x 7sin 5sin ; 解 C x x dx x x xdx x ++-=--=⎰⎰2sin 4112sin 241)2cos 12(cos 217sin 5sin . (28)⎰xdx x sec tan 3;解 x d x xdx x x xdx x sec tan tan sec tan sec tan 223⎰⎰⎰=⋅=C x x x d x +-=-=⎰sec sec 31sec )1(sec 32.(29)⎰-dx xx2arccos 2110;解C x d x d dx xx xxx+-=-=-=-⎰⎰⎰10ln 210)arccos 2(1021arccos 10110arccos 2arccos 2arccos 22arccos 2.(30)⎰+dx x x x )1(arctan ;解C x x d x x d x xdx x x x +==+=+⎰⎰⎰2)(arctan arctan arctan 2)1(arctan 2)1(arctan .(31)⎰-221)(arcsin xx dx;解C xx d x x x dx+-==-⎰⎰arcsin 1arcsin )(arcsin 11)(arcsin 222.(32)⎰+dx x x x 2)ln (ln 1; 解C xx x x d x x dx x x x+-==+⎰⎰ln 1)ln ()ln (1)ln (ln 122. (33)⎰dx xx xsin cos tan ln ;解⎰⎰⎰=⋅=x d x x xdx x x dx x x x tan tan tan ln sec tan tan ln sin cos tan ln 2C x x d x +==⎰2)tan (ln 21tan ln tan ln .(34)⎰-dx x a x 222(a >0);解⎰⎰⎰⎰-===-dt t a dt t a tdt a t a t a t a x dx xa x 22cos 1sin cos cos sin sin 22222222令, C x a x a x a C t a t a +--=+-=222222arcsin 22sin 421.(35)⎰-12x x dx ;解C x C t dt tdt t t t tx x x dx +=+==⋅⋅=-⎰⎰⎰1arccos tan sec tan sec 1sec 12令.或C x x d x dx xx x x dx +=--=-=-⎰⎰⎰1arccos 111111112222.(36)⎰+32)1(x dx ;解C t tdt t d t tx x dx +==+=+⎰⎰⎰sin cos tan )1(tan 1tan )1(3232令C x x ++=12.(37)⎰-dx xx 92; 解⎰⎰⎰=-=-tdt t d tt t x dx x x 222tan 3)sec 3(sec 39sec 9sec 39令 C x x C t t dt t+--=+-=-=⎰3arccos 393tan 3)1cos 1(322.(38)⎰+x dx 21; 解C x x C t t dt t tdt t tx xdx ++-=++-=+-=+=+⎰⎰⎰)21ln(2)1ln()111(11221令.(39)⎰-+211x dx ;解⎰⎰⎰⎰-=+-=+=-+dt tdt t tdt t tx x dx)2sec211()cos 111(cos cos 11sin 1122令 C xxx C t t t C t t +-+-=++-=+-=211arcsin cos 1sin 2tan .(40)⎰-+21x x dx .解⎰⎰⎰+-++=⋅+=-+dt tt tt t t tdt t t tx x x dx cos sin sin cos sin cos 21cos cos sin 1sin 12令C t t t t t d t t dt +++=+++=⎰⎰|cos sin |ln 2121)cos (sin cos sin 12121 C x x x ++-+=|1|ln 21arcsin 212.习题4-3求下列不定积分: 1. ⎰xdx x sin ; 解C x x x xdx x x x xd xdx x ++-=+-=-=⎰⎰⎰sin cos cos cos cos sin .2. ⎰xdx ln ;解 C x x x dx x x x xd x x xdx +-=-=-=⎰⎰⎰ln ln ln ln ln . 3. ⎰xdx arcsin ;解 ⎰⎰-=x xd x x xdx arcsin arcsin arcsin ⎰--=dx xx x x 21arcsinC x x x +-+=21arcsin . 4. ⎰-dx xe x ;解 ⎰⎰⎰----+-=-=dx e xe xde dx xe x x x x C x e C e xe x x x ++-=+--=---)1(. 5. ⎰xdx x ln 2; 解 ⎰⎰⎰-==x d x x x xdx xdx x ln 31ln 31ln 31ln 3332 C x x x dx x x x +-=-=⎰332391ln 3131ln 31.6. ⎰-xdx e x cos ; 解 因为⎰⎰⎰⎰------+=-==xdx e x e xde x e x d e xdx e x x x x x x sin sin sin sin sin cos ⎰⎰-----+-=-=x x x x x xde x e x e x d e x e cos cos sin cos sin⎰-----=xdx e x e x e x x x cos cos sin ,所以 C x x e C x e x e xdx e x x x x +-=+-=----⎰)cos (sin 21)cos sin (21cos .7. ⎰-dx xe x 2sin 2;解 因为⎰⎰⎰-----==x x x x de xx e x d e dx x e 22222cos 22cos 22cos 22sin⎰⎰----+=+=2sin 82cos 22cos 42cos 22222xd e x e dx x e x e x x x x⎰----+=x x x de xx e x e 2222sin 82sin 82cos 2⎰---++=dx xe x e x e x x x 2sin 162sin 82cos 2222,所以 C xx e dx x e x x ++-=--⎰)2sin 42(cos 1722sin 22.8. ⎰dx xx 2cos ;解 C xx x dx x x x x xd dx x x ++=-==⎰⎰⎰2cos 42sin 22sin 22sin 22sin 22cos .9. ⎰xdx x arctan 2; 解 ⎰⎰⎰+⋅-==dx x x x x xdx xdx x 233321131arctan 31arctan 31arctan ⎰⎰+--=+-=2232223)111(61arctan 31161arctan 31dx xx x dx x x x x C x x x x +++-=)1ln(6161arctan 31223.10. ⎰xdx x 2tan解 ⎰⎰⎰⎰⎰+-=-=-=x xd x xdx xdx x dx x x xdx x tan 21sec )1(sec tan 2222C x x x x xdx x x x +++-=-+-=⎰|cos |ln tan 21tan tan 2122.11. ⎰xdx x cos 2;解 ⎰⎰⎰⎰+=⋅-==x xd x x xdx x x x x d x xdx x cos 2sin 2sin sin sin cos 2222C x x x x x xdx x x x x +-+=-+=⎰sin 2cos 2sin cos 2cos 2sin 22. 12. ⎰-dt te t 2;解 ⎰⎰⎰----+-=-=dt e te tde dt te t t tt 2222212121 C t e C e te t t t ++-=+--=---)21(214121222.13. ⎰xdx 2ln ;解 ⎰⎰⎰-=⋅⋅-=xdx x x dx xx x x x xdx ln 2ln 1ln 2ln ln 222C x x x x x dx x x x x x x ++-=⋅+-=⎰2ln 2ln 12ln 2ln 22.14. ⎰xdx x x cos sin ; 解 ⎰⎰⎰⎰+-=-==xdx x x x xd xdx x xdx x x 2cos 412cos 412cos 412sin 21cos sin C x x x ++-=2sin 812cos 41.15. ⎰dx xx 2cos 22; 解 ⎰⎰⎰⎰-+=+=+=xdx x x x x x d x x dx x x dx x x sin sin 2161sin 2161)cos 1(212cos 2323222⎰⎰-++=++=xdx x x x x x x xd x x x cos cos sin 2161cos sin 21612323C x x x x x x +-++=sin cos sin 216123.16. ⎰-dx x x )1ln(; 解 ⎰⎰⎰-⋅--=-=-dx x x x x dx x dx x x 1121)1ln(21)1ln(21)1ln(222 ⎰-⋅++--=dx x x x x )111(21)1ln(212C x x x x x +-----=)1ln(212141)1ln(2122.17. ⎰-xdx x 2sin )1(2;解 ⎰⎰⎰⋅+--=--=-xdx x x x x d x xdx x 22cos 212cos )1(212cos )1(212sin )1(222 ⎰+--=x xd x x 2sin 212cos )1(212⎰-+--=xdx x x x x 2sin 212sin 212cos )1(212C x x x x x +++--=2cos 412sin 212cos )1(212.18. ⎰dx x x23ln ;解⎰⎰⎰⎰+-=+-=-=xdx xx x x d x x x x xd dx x x22333323ln 13ln 1ln 1ln 11ln ln⎰⎰+--=--=x d x x x x x x xd x x 22323ln 13ln 3ln 11ln 3ln 1⎰⎰---=+--=x xd x x x x dx x xx x x x 1ln 6ln 3ln 1ln 16ln 3ln 123223⎰+---=dx xx x x x x x 22316ln 6ln 3ln 1C x x x x x x x +----=6ln 6ln 3ln 123.19. ⎰dx e x3;解 ⎰⎰⎰==t t xde t dt e t t x dx e223333令⎰⎰-=-=t t t t tde e t dt te e t 636322 ⎰+-=dt e te e t t t t 6632 C e te e t t t t ++-=6632 C x x ex ++-=)22(33323.20. ⎰xdx ln cos ; 解 因为⎰⎰⋅⋅+=dx xx x x x xdx 1ln sin ln cos ln cosdx xx x x x x x xdx x x 1ln cos ln sin ln cos ln sin ln cos ⋅⋅-+=+=⎰⎰⎰-+=xdx x x x x ln cos ln sin ln cos , 所以 C x x xxdx ++=⎰)ln sin ln (cos 2ln cos .21. ⎰dx x 2)(arcsin ;解 ⎰⎰-⋅⋅-=dx xx x x x dx x 22211arcsin 2)(arcsin )(arcsin⎰-+=221arcsin 2)(arcsin x xd x x ⎰--+=dx x x x x 2arcsin 12)(arcsin 22 C x x x x x +--+=2arcsin 12)(arcsin 22. 22. ⎰xdx e x 2sin . 解 ⎰⎰⎰-=-=xdx e e dx x e xdx e xx x x 2cos 2121)2cos 1(21sin 2, 而 dx x e x e xde xdx e x x x x ⎰⎰⎰+==2sin 22cos 2cos 2cos⎰⎰-+=+=xdx e x e x e de x x e x x x x x 2cos 42sin 22cos 2sin 22cos ,C x x e xdx e x x ++=⎰)2sin 22(cos 512cos ,所以 C x x e e xdx e x x x ++-=⎰)2sin 22(cos 10121sin 2.习题4-4求下列不定积分:1. dx x x ⎰+33;解 dx x x x x dx x x dx x x ⎰⎰⎰+-+-+=+-+=+327)93)(3(327273233⎰⎰+-+-=dx x dx x x 3127)93(2C x x x x ++-+-=|3|ln 279233123.2. ⎰-++dx x x x 103322;解 C x x x x d x x dx x x x +-+=-+-+=-++⎰⎰|103|ln )103(1031103322222.3. ⎰--+dx xx x x 3458;解 ⎰⎰⎰--++++=--+dx x x x x dx x x dx x x x x 3223458)1(8⎰⎰⎰--+-+++=dx x dx x dx x x x x 13148213123C x x x x x x +--+-+++=|1|ln 3|1|ln 4||ln 8213123.4. ⎰+dx x 133;解⎰⎰⎰+-⋅++--⋅-+=+-+-++=+dx x x x x x x dx x x x x dx x )11231122111()1211(132223⎰⎰-+-++-+--+=)21()23()21(123)1(1121|1|ln 2222x d x x x d x x xC x x x x +-++-+=312arctan31|1|ln2. 5. ⎰+++)3)(2)(1(x x x xdx;解dx x x x x x x xdx )331124(21)3)(2)(1(+-+-+=+++⎰⎰C x x x ++-+-+=|)1|ln |3|ln 3|2|(ln 21.6. ⎰-++dx x x x )1()1(122;解 ⎰⎰+--⋅++⋅=-++dx x x x dx x x x ])1(111211121[)1()1(1222 C x x x +++-+-=11|1|ln 21|1|ln 21C x x +++-=11|1|ln 212.7. dx x x )1(12+⎰; 解 C x x dx x x x dx x x ++-=+-=+⎰⎰)1ln(21||ln )11()1(1222. 8. ⎰++))(1(22x x x dx;解⎰⎰+⋅-++⋅-=++dx x x x x x x x dx )112111211())(1(222⎰++-+-=dx x x x x 1121|1|ln 21||ln 2⎰⎰+-+-+-=dx x dx x x x x 11211241|1|ln 21||ln 22C x x x x +-+-+-=arctan 21)1ln(41|1|ln 21||ln 2.9. ⎰+++)1)(1(22x x x dx; 解dx x xx x x x x x dx )111()1)(1(2222⎰⎰+-+++=+++)1ln(21112111221222+-++++++=⎰⎰x dx x x x x x ⎰++++-++=dx x x x x x 1121)1ln(21|1|ln 21222C x x x x ++++-++=312arctan 33)1ln(21|1|ln 2122. 10. ⎰+dx x 114;解dx x x x x dx x ⎰⎰+-++=+)12)(12(111224⎰⎰+-+-++++=dx x x x dx x x x 12214212214222⎰⎰+----++++=dx x x x dx x x x 1222)22(21421222)22(214222 )1212(41]12)12(12)12([82222222⎰⎰⎰⎰+-+++++-+--++++=x x dxx x dx x x x x d x x x x d C x x x x x x +-++++-++=)12arctan(42)12arctan(42|1212|ln 8222. 11. ⎰++--dx x x x 222)1(2; 解 ⎰⎰⎰++-++-=++--dx x x dx x x x dx x x x 11)1(1)1(2222222 ⎰⎰⎰++-++-+++=dx x x dx x x dx x x x 11)1(123)1(122122222 ⎰⎰++-++-++⋅-=dx x x dx x x x x 11)1(12311212222, 因为)312arctan(32)312()312(11321122+=+++=++⎰⎰x x d x dx x x , 而⎰⎰++=++dx x dx x x 22222])23()21[(1)1(1由递推公式 ⎰⎰--+-++-=+])()32()([)1(21)(122122222n n n a x dxn a x x n a a x dx ,得⎰⎰++=++dx x dx x x 22222])23()21[(1)1(1312arctan 323211231)1121()23(212222+⋅++++⋅=++++++=⎰x x x x x x dx x x x , 所以 ⎰++--dx x x x 222)1(2C x x x x x x x ++-+-+++-++⋅-=312arctan 32312arctan 3211221112122C x x x x ++-+++-=312arctan34112.12. ⎰+x dx2sin 3;解⎰⎰⎰+=-=+x d x dx x x dx tan 3tan 41cos 41sin 3222C x x d x +=+=⎰3tan 2arctan321tan )23(tan 14122.13.⎰+dx x cos 31;解 ⎰⎰⎰+=+=+)2sec 1(2cos )2(2cos 121cos 31222x x x d x dx dx x ⎰+=+=C x x x d 22tanarctan 212tan 22tan 2. 或⎰⎰+⋅++=+du u u u x u dxx 221212312tancos 31令 C xC u du u +=+=+=⎰22tan arctan212arctan21)2(122. 14.⎰+dx x sin 21;解 ⎰⎰⎰+=+=+)2cot 2(csc 2sin )2(2cos 2sin 22sin 2122x x x x d x x dx dx x⎰⎰+++-=++-=222)23()212(cot )212(cot 12cot 2cot )2(cot x x d x x x dC x ++-=312cot 2arctan 32. 或⎰⎰+⋅++=+du u u u x u dxx 221212212tansin 21令 ⎰⎰++=++=du u du u u 222)23()21(111C xC u ++=++=312tan 2arctan 32312arctan 32. 15.⎰++x x dxcos sin 1;解 ⎰⎰⎰+=+=+=++C x x xd x x dx x x dx |2tan |ln 2tan1)2(tan )2tan 1(2cos 21cos sin 12. 或⎰⎰+⋅+-+++=++du u u u u ux u xx dx2222121112112tancos sin 1令C xC u du u ++=++=+=⎰|12tan |ln |1|ln 11. 16.⎰+-5cos sin 2x x dx; 解⎰⎰⎰++=+⋅++--+=+-du u u du u u u u ux u x x dx2231125111412tan5cos sin 222222令C xC u du u ++=++=++=⎰512tan 3arctan 51513arctan 51)35()31(13122. 或⎰⎰+⋅++--+=+-du uu uu u x u x x dx2222125111412tan5cos sin 2令⎰⎰++=++=du u du u u 222)35()31(1312231C xC u ++=++=512tan 3arctan 51513arctan 51. 17. ⎰++dx x 3111;解⎰⎰⎰++-=⋅+=+=++du uu du uu ux dx x )111(33111111233令 C x x x C u u u +++++-+=+++-=)11ln(313)1(23|1|ln 332333322.18.⎰++dx x x 11)(3;解C x x x dx x x dx x x ++-=+-=++⎰⎰232233221]1)[(11)(.19.⎰++-+dx x x 1111;解 ⎰⎰⎰++-=⋅+-=+++-+du u u udu u u u x dxx x )122(221111111令C u u u +++-=|)1|ln 2221(22C x x x +++++-+=)11ln(414)1(. 20.⎰+4x x dx ;解⎰⎰⋅+=+du uu u u x xx dx 324441令C u u u du uu +++-=++-=⎰|1|ln 442)111(42 C x x x +++-=)1ln(4244.21.⎰+-xdxx x 11;解 令u x x=+-11, 则2211u u x +-=, du u u dx 22)1(4+-=,⎰⎰⎰++-=+-⋅-+⋅=+-du uu du u u u u u x dx x x )1111(2)1(41111222222 C u u u +++-=arctan 2|11|ln C xxx x x x ++-+++-+--=11arctan2|1111|ln . 22.⎰-+342)1()1(x x dx.解 令u x x =-+311, 则1133-+=u u x , 232)1(6--=u u dx , 代入得C x x C u du x x dx +-+-=+-=-=-+⎰⎰334211232323)1()1(.总习题四求下列不定积分(其中a , b 为常数):1. ⎰--x x e e dx;解 C e e de e dx e e e e dxx x xx x xxx ++-=---=-⎰⎰⎰-|11|ln 2111122.2. dx x x ⎰-3)1(; 解C x x dx x dx x dx x x+-⋅+-=----=-⎰⎰⎰2323)1(12111)1(1)1(1)1(. 3. ⎰-dx xa x 662(a >0);解 C ax a x a x d x a dx x a x +-+=-=-⎰⎰||ln 61)()()(1313333332323662. 4. ⎰++dx x x xsin cos 1;解 C x x x x d x x dx x x x ++=++=++⎰⎰|sin |ln )sin (sin 1sin cos 1.5. ⎰dx xxln ln ; 解C x x x dx x x x x x x xd dx x x +-⋅=⋅⋅-⋅==⎰⎰⎰ln ln ln ln 1ln 1ln ln ln ln ln ln ln ln ln . 6. ⎰+dx x xx 4sin 1cos sin ; 解 C x x d x x d xx dx x x x +=+=+=+⎰⎰⎰222244sin arctan 21)(sin )(sin 1121sin sin 1sin sin 1cos sin . 7. ⎰xdx 4tan ; 解 xxd x x d xx xdx tan sin tan tan cos sin tan 22244⎰⎰⎰==⎰⎰++-=+=x d x x x d x x tan )1tan 11(tan tan 1tan tan 2224c x x x c x x x ++-=++-=tan tan 31tan arctan tan tan 3133.8. ⎰xdx x x 3sin 2sin sin ; 解 ⎰⎰--=xdx x x xdx x x 3sin )cos 3(cos 213sin 2sin sin ⎰⎰+-=xdx x xdx x 3sin cos 213sin 3cos 21 ⎰⎰++=dx x x x xd )2sin 4(sin 41)3(cos 3cos 61 C x x x +--=2cos 814cos 1613cos 1212. 9. ⎰+)4(6x x dx;解 C x x dx x x x x x dx++-=+-=+⎰⎰)4ln(241||ln 41)41(41)4(6656.10.)0(>-+⎰a dx xa xa ; 解⎰⎰⎰⎰-+-=-+=-+dx xa xdx x a a du x a x a dx x a x a 2222221C x a a xa +--=22arcsin .11.⎰+)1(x x dx ;解C x x C x x x d x x x dx +++=+++=+=+⎰⎰)1ln(2))(1ln(2)(112)1(22.12. ⎰xdx x 2cos ; 解 ⎰⎰⎰+=+=x xd x dx x x x xdx x 2sin 4141)2cos (21cos 22 C x x x x xdx x x x +++=-+=⎰2cos 812sin 41412sin 412sin 414122.13. ⎰bxdx e ax cos ; 解 因为dx bx e a b bx e a bxde a bxdx e ax axax ax ⎰⎰⎰+==sin cos 1cos 1cos dx bx e ab bx e a b bx e a de bx a b bx e a ax ax axax ax ⎰⎰-+=+=cos sin cos 1sin cos 12222,所以 C bx e ab bx e a b a a bxdx e axax ax+++=⎰)sin cos 1(cos 2222C bx b bx a e b a ax +++=)sin cos (122.14.⎰+xedx 1;解⎰⎰⎰⎰+--=-=-=++du u u du u u d u u e e dxx x)1111(112)1ln(11122令.c e e c u u x x +++-+=++-=1111ln |11|ln .15.⎰-122x xdx ;解C t tdt tdt t t t tx x xdx+==⋅⋅=-⎰⎰⎰sin cos tan sec tan sec 1sec 1222令C xx +-=12. 16.⎰-2/522)(x a dx;解⎰⎰⋅=-tdt a t a ta x x a dx cos )cos (1sin )(52/522令⎰⎰+==t d t adt ta tan )1(tan1cos 112444C t at a ++=tan 1tan 31434C xa x a x a x a+-+-⋅=224322341)(31.17.⎰+241x xdx;解tdt t t tx x xdx2424secsec tan 1tan 1⋅⋅=+⎰⎰令⎰⎰==t d t tdt t tsin sin cos sin cos 4243 C t tt d t t ++-=-=⎰sin 1sin 31sin )sin 1sin 1(324 C xx x x ++++-=233213)1(.18.⎰dx x x sin ;解⎰⎰⎰=⋅=tdt t tdt t t t x dx x x sin 22sin sin 2令⎰⎰⋅+-=-=tdt t t t t d t 2cos 2cos 2cos 222⎰⎰-+-=+-=tdt t t t t t td t t sin 4sin 4cos 2sin 4cos 222 C t t t t t +++-=cos 4sin 4cos 22C x x x x x +++-=cos 4sin 4cos 2. 19. ⎰+dx x )1ln(2;解 ⎰⎰+⋅-+=+dx xx x x x dx x 22212)1ln()1ln(⎰+--+=dx x x x )111(2)1ln(22C x x x x ++-+=arctan 22)1ln(2. 20.⎰dx x x32cos sin ;解 x d x xx x d x x dx x xtan )1tan tan (tan tan cos sin cos sin 2232⎰⎰⎰+-== C x x ++-=)1ln(tan 21tan 2122.21. ⎰dx x arctan ;解 x d xx x x dx x ⎰⎰+⋅-=11arctan arctan x d xx x ⎰+⋅--=)111(arctan C x x x x ++-=arctan arctan C x x x +-+=arctan )1(. 22.dx xx⎰+sin cos 1;解C x x x d x dx x x xdx x x +-===+⎰⎰⎰|2cot 2csc |ln 222csc 22cos2sin 22cos2sin cos 1. 23.⎰+dx x x 283)1(;解 C x x x dx x dx x x +++⋅=+=+⎰⎰]arctan 1[2141)1(141)1(484428283. 提示: 已知递推公式⎰⎰--+-++-=+])()32()([)1(21)(122122222n n n a x dxn a x x n a a x dx .24. ⎰++dx x x x 234811; 解 ⎰⎰⎰++=++=++dt t t t t x dx x x x dx x x x 234123412322444884811令 ⎰⎰+++-=+++-=dt t t dt t t t )11241(41)23231(412 C t t t ++++-=|1|ln 41|2|ln 41C x x x ++++=21ln 414444. 25.⎰-416x dx; 解⎰⎰⎰++-=+-=-dx xx dx x x x dx)4141(81)4)(4(11622224C xx x ++-+=)2arctan 21|22|ln 41(81C x x x ++-+=2arctan 161|22|ln 321. 26.dx x x⎰+sin 1sin ;解 ⎰⎰⎰-=--=+dx xxx dx x x x dx x x 222cos sin sin sin 1)sin 1(sin sin 1sinC x x x dx x x x++-=+-=⎰tan sec )cos 11cos sin (22.27. dx x xx ⎰++cos 1sin ;解⎰⎰⎰⎰+=+=++dx x xdx x x dx x x x dx x x x 2cossin 212cos 212cos 2sin cos 1sin 222 ⎰⎰+=dx xx xd 2tan 2tanC xx dx x dx x x x +=+-=⎰⎰2tan 2tan 2tan 2tan .28. ⎰-dx x x x x ex23sin cos sin cos ;解 ⎰⎰⎰⋅⋅-⋅⋅=-xdx x e xdx e x dx xx x x e x x xsec tan cos cos sin cos sin sin 23sin⎰⎰-=x d e x d xe x x sec sin sin sin ⎰⎰+⋅-=x x x xde e x xde sin sin sin sec sec⎰⎰⋅⋅+⋅--=xdx e x e x dx e xe x x x x cos sec sec sin sin sin sin C e x xe x x +⋅-=sin sin sec .29.⎰+dx x x x x)(33;解dt t t dt t t t t t t x dxx x x x)111(66)()(52362633+-=⋅+=+⎰⎰⎰令C x xC t t ++=++=66)1(ln 1ln6. 30.⎰+2)1(x e dx;解⎰⎰⎰---=-⋅=++dt t t t dt t tt e e dxx x )1111(1111)1(222令 C tt t ++--=1ln )1ln(C e e x xx ++++-=11)1ln(.31. ⎰+-+dx e e e e x x xx 1243;解)()(1111222243x xx x x x xx x x x x e ed e e dx e e e e dx e e e e ------+=+-+=+-+⎰⎰⎰C e e x x +-=-)arctan( C x +=)sh 2arctan(. 32.⎰+dx e xe xx 2)1(;解⎰⎰⎰+-=++=+11)1()1()1(22x x x x xe xde d e x dx e xe⎰⎰+++-=+++-=x x x x x x de e e e x dx e e x )1(11111⎰+-++-=x x xx de e e e x )111(1C e e e x x x x ++-++-=)1ln(ln 1C e e xe x x x ++-+=)1ln(1.33. ⎰++dx x x )1(ln 22;解 dx x x x x x x dx x x ])1([ln )1(ln )1(ln 222222'++⋅-++=++⎰⎰ ⎰+⋅++-++=dx xx x x x x x 22221)1ln(2)1(ln⎰+++-++=22221)1ln(2)1(ln x d x x x x x⎰'++⋅+++++-++=dx x x x x x x x x x ])1[ln(12)1ln(12)1(ln 222222 ⎰++++-++=dx x x x x x x 2)1ln(12)1(ln 2222 C x x x x x x x +++++-++=2)1ln(12)1(ln 2222.34.⎰+dx x x2/32)1(ln ; 解 因为⎰⎰⎰++=+==⋅=+C xx C t tdt tdt t tx dx x 2232/321sin cos secsec 1tan )1(1令,所以⎰⎰⎰⋅+-+=+=+dx xx xx x x x x xd dx x x111ln )1(ln )1(ln 2222/32 C x x x x x +++-+=)1ln(1ln 22.35. ⎰-xdx x arcsin 12;解⎰⎰⎰+=⋅=-dt t t t tdt t t x xdx x )2cos (21cos sin arcsin 122令 ⎰⎰-+=+=tdt t t t t t t 2sin 412sin 41412sin 414122C t t t t +++=2cos 812sin 41412122241arcsin 121)(arcsin 41C x x x x x +--+=.36.⎰-dx xx x 231arccos ;解⎰⎰⎰--=-⋅=-2222231arccos 1arccos 1arccos x xd x dx x x x x dx x x x⎰'⋅-+--=dx x x x x x x )arccos (1arccos 12222 ⎰-⋅-⋅-+--=dx xx x x x x x x )11arccos 2(1arccos 122222⎰⎰-⋅-+--=dx x xdx x x x x x 2222arccos 12arccos 1⎰-----=32322)1(arccos 3231arccos 1x xd x x x x⎰-------=dx x x x x x x x )1(32arccos )1(3231arccos 1232322。
北邮电信工程学院课程简介
电信工程学院课程简介1.课程目录2.专业基础、专业课程简介课程编号:412·01103课程名称:SDH原理与应用SDH Technology and Its Applications课程性质:选修先修课程:《数字通信》、《现代通信技术》开课学期及学分/学时:四秋(2/34)内容提要:本课程属于通信工程、电子信息工程及相关信息类专业的专业课。
SDH技术是传送网的支撑技术之一,在现代信息传输网络中占据重要地位。
它是一个将复接、线路传输及交叉连接功能融为一体的、并由统一网管系统操作的综合信息传送网络,可实现诸如网络的有效管理、开业务时的性能监视、动态网络维护、不同供应厂商设备之间的互通等多项功能。
《SDH原理与应用》主要以传输体制与相关技术为主线,讲述SDH帧结构与段开销、同步复用和映射原理、SDH网络中的基本网元、SDH自愈网原理、光传送网技术以及一些典型SDH系统的原理与应用。
使用教材:《SDH原理与技术》,肖萍萍吴键学周芳胡春琳,2002年3月,北京邮电大学出版社《光同步数字传送网》(2版,修订版),韦乐平,1998年12月,人民邮电出版社课程编号:322·01807课程名称:电子学导论Introduction to Electronics课程性质:选修先修课程:大学物理学中的近代物理,电磁场理论与微波技术,半导体物理,电子电路基础,数字系统与逻辑设计开课学期及学分/学时:三春(2/34)内容提要:大规模集成电路、通信电子电路与光电器件的迅速发展对电子学知识的掌握提出了越来越高的要求。
本课程主要内容包括:介绍半导体物理知识、半导体工艺、集成电路工艺、新的SOC(片内系统)理论;介绍电子系统的设计方法、电子电路的仿真软件及仿真方法、电路原理图与印刷版图的设计、电子电路的调试,以及最新的高速电子通信技术;介绍通信系统中常见的激光光源、光检测器、光波导器件的基本原理与应用。
使用教材:教师自选合适中英文教材及讲义课程编号:323·01101课程名称:光纤通信Optical Fiber Communications课程性质:专业选修课先修课程:通信原理Ⅰ开课学期及学分/学时:3春(3/51)内容提要:课程全面系统地介绍光纤的传输理论;半导体激光器的工作原理、性质、光源的直接调制和间接调制;光检测器的原理、性质、光接收机的组成、噪声的分析和光接收机灵敏度的计算;光纤通信系统的组成、性能指标及其分配以及系统的总体设计;光纤通信测量技术;还介绍了光纤通信新技术和新型系统,如掺铒光纤放大器、密集波分复用系统、色散补偿技术以及非线性光学效应等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
d2 y dx2
2
y
dy dx
sin
x
0
都是二阶微分方程.
12
第四章 微分方程
n 阶微分方程的一般形式是:
F (x, y, y, y , y(n) ) 0,
(10)
其中 x 为自变量, y y(x) 是未知函数.在方程(10)中 y(n) 必须出现, 而其他变
量可以不出现, 例如, n 阶方程 y(n) ex .
因此
R
R ektt0 0
即为所求.
9
第四章 微分方程
例 3 已知放射性物质镭的裂变规律是裂变速度与余存量成比例. 记在某一
时刻 t t0 , 镭的余存量为 R0 g, 试确定镭在任意时刻 t 的余存量 Rt .
注 式子 dR t kR t 即为微分方程, 它表示函数 Rt 的一个变化规律,
例 2 列车在平直线路上以 20m/ s (相当于 72km/h )的速度行驶, 当制动时列 车获得加速度 0.4m/s2 . 开始制动后多少时间列车才能停住? 列车在这段时间 里行驶了多少路程?
把条件 s |t0 0 代入(7)得 0 C2
把 C1 , C2 的值代入(6)及(7方程:
第四章 微分方程
含有未知函数及其导数(或微分)与自变量的等式称为微分方程(其 中自变量、未知函数可以在方程中不出现, 但未知函数的导数必须出现).
11
第四章 微分方程
2、微分方程的阶:
微分方程中出现的未知函数的导数(或微分)的最高阶数称为微分方程的阶.. 一阶微分方程的一般形式为
16
第四章 微分方程
4、微分方程的初值问题: 许多实际问题都要求寻找满足某些附加条件的解, 此时, 这类附加条件就可 以用来确定通解中的任意常数, 这类附加条件称为初始条件. 例如, 条件(2)和(5) 分别是微分方程(1)和(4)的初始条件. 带有初始条件的微分方程称为微分方程的初值问题.
17
第四章 微分方程
根据题意, x x(t) 还需满足条件 x(0) 0, dx 0. dt t0
O m x=x(t)
x 图4-2
20
第四章 微分方程
例 6 试指出下列方程是什么方程, 并指出微分方程的阶数.
(1) dy x2 y; dx
(3)x
2 12 C ,
由此定出 C 1. 把 C 1代入(3)式, 得所求曲线方程
y x2 1. (称为微分方程满足初始条件 y |x1 2 的特解)
5
第四章 微分方程
例 2 列车在平直线路上以 20m/ s (相当于 72km/h )的速度行驶, 当制动时列 车获得加速度 0.4m/s2 . 开始制动后多少时间列车才能停住? 列车在这段时间 里行驶了多少路程?
8
第四章 微分方程
例 3 已知放射性物质镭的裂变规律是裂变速度与余存量成比例. 记在某一
时刻 t t0 , 镭的余存量为 R0 g, 试确定镭在任意时刻 t 的余存量 Rt .
解 由于 dR t 是镭的增长速度, 因此裂变速度(减少速度)应为 dR t , 从
dt
dt
而按裂变规律, 有 dR t kR t , 其中 k 为比例系数. 要解决上述问题, 就要确
(13)
dt
其中 k (k 0) 为比例常数. 这就是物体冷却的数学模型.
根据题意, T T (t) 还需满足条件
T |t0 100 .
(14)
19
第四章 微分方程
例 5 设一质量为 m 的物体只受重力的作用由静止开
始自由垂直降落. 根据牛顿第二定律:物体所受的力 F 等
于物体的质量 m 与物体运动的加速度 a 成正比, 即
5、微分方程的积分曲线: 微分方程的解的图形是一条曲线, 称为微分方程的积分曲线. 由于通解中含 有任意常数, 所以它的图形是具有某种共同性质的积分曲线族. 例如, 例 1 中的 通解 y x2 C 是抛物线族, 这些图形的共性是每一条抛物线上任意一点
M (x, y) 处的斜率均为 2x . 而方程的特解是过点 (1, 2) 的一条抛物线, 也就是说, 特解是积分曲线中满足初始条件的某一条特定的积分曲线(见图 4-1).
v 0.4t 20,
(8)
s 0.2t2 20t ,
(9)
在(8)式中令 v 0 , 得到列车从开始制动到完全停住所需的时间
t 20 50(s) . 0.4
再把 t 50 代入(9), 得到列车在制动阶段行驶的路程
s 0.2502 2050 500m .
dt
即其减少速度 dR t 与其本身 Rt 成比例. 尽管我们是从镭的裂变这一特殊问
dt 题导出此方程, 但此方程应用远不止此, 只要某物理量的变化服从同样的规律, 就可用此方程来确定.
上面的几个例子, 尽管实际意义不同, 但是解决问题的方法都是首先建立一 个含有未知函数的导数的方程, 然后通过这个方程, 求满足所给的条件的未知函 数.
恒等式, 称这个函数为该微分方程的解. 更确切地说, 设函数 y (x) 在区间 I 上有 n 阶连续导数, 如果在区间 I 上, 有
F (x,(x),(x),(x) , (n) (x)) 0, 则称函数 y (x) 为微分方程(10)在区间 I 上的解.
15
第四章 微分方程
18
第四章 微分方程
例 4 设一物体的温度为 100℃, 将其放置在空气温度为 20℃的环境中冷却. 根据冷却定律:物体温度的变化率与物体和当时空气温度之差成正比, 设物体的 温度T 与时间 t 的函数关系为T T (t) , 则可建立起函数T (t) 满足的微分方程
dT k(T 20)
如果能从方程(10)中解出最高阶导数, 就得到微分方程
y(n) f (x, y, y, , y(n1) ).
(11)
以后我们讨论的微分方程组主要是形如(11)的微分方程, 并且假设(11)式右 端的表达式 f 在所讨论的范围内连续.
13
第四章 微分方程
如果方程(11)可表为如下形式:
y(n) a1(x) y(n1) an1(x) y an (x) y g(x)
数的方程, 例如
y ' y tan x cos x ,
dy 4x , dx y(x 3)
y '' 3y ' 2 y e3x ,
下面通过几个具体的例子来说明微分方程的基本概念.
3
例 1 一曲线通过点 (1, 2) (见图 4-1), 且在该
曲线上任一点 M (x, y) 处的切线的斜率为 2x ,
3、微分方程的解: 微分方程的解可能含有也可能不含有任意常数. 含有相互独立的任意常数, 且任意常数的个数与微分方程的阶数相等的解称为微分方程的通解(一般解). 一 般地, 微分方程的不含有任意常数的解称为微分方程的特解. 方程的通解是一类 解, 而不是指方程的“全部解”. 实际上, 我们在求解方程时得到一些解, 很难说 明这些解是否构成了方程的“全部解”, 这种工作有时会比求解方程本身还困难, 而实际工作中又告诉我们无须去做这样的工作, 因此我们将关注点放在求方程 的通解和特解上. 注 这里所说的相互独立的任意常数, 是指它们不能通过合并而使得通解 中的任意常数的个数减少.
解这种方程, 同样可以找到指定未知量之间的函数关系. 比如, 已知 y ' cos 2x ,
由不定积分的计算很容易知道 y 的表达式:
y
cos
2xdx
1 2
sin
2x
C
但是如果已知 y ' y cos 2x , 仅仅是求原函数的公式是不够的, 它需要利用
微分方程自己的一些方法和技巧才能得到 y 的表达式.
求该曲线的方程
解: 设所求曲线的方程为 y y(x) ,根据
导数的几何意义,可知未知函数 y y(x) 应满足
关系式
dy 2x (称为一阶微分方程)
(1)
dx
此外, 未知函数 y y(x) 还应满足下列条件:
第四章 微分方程
y
3
2
(1,2)
1
O
图4-1
x 1时, y 2 , 简记为 y |x1 2 (称为初始条件) (2)
简记为 s |t0 0 , s ' |t0 20 . (两个初始条件)
(5)
6
第四章 微分方程
例 2 列车在平直线路上以 20m/ s (相当于 72km/h )的速度行驶, 当制动时列
车获得加速度 0.4m/s2 . 开始制动后多少时间列车才能停住? 列车在这段时间
里行驶了多少路程?
F ma , 若取物体降落的铅垂线为 x 轴, 其正向朝下, 物
体下落的起点为原点, 并设开始下落的时间是 t 0 , 物体
下落的距离 x 与时间 t 的函数关系为 x x(t) (见图 4-2), 则
可建立起函数 x(t) 满足的微分方程
d2x dt 2
g
其中 g 为重力加速度常数. 这就是自由落体运动的数学模型.
解 设列车在开始制动后 t 时行驶的距离为 s 米 根据题意, 反映制动阶段
列车运动规律的函数 s s(t) 应满足关系式
d2s dt 2
0.4
(称为二阶微分方程)
(4)
此外, 未知函数 s s(t) 还应满足下列条件:
t 0 时, s 0 , v ds 20 dt
F(x, y, y) 0 .
例如方程 y ' y x2 0 ,
