五节MG1排队模型

合集下载

排队模型——精选推荐

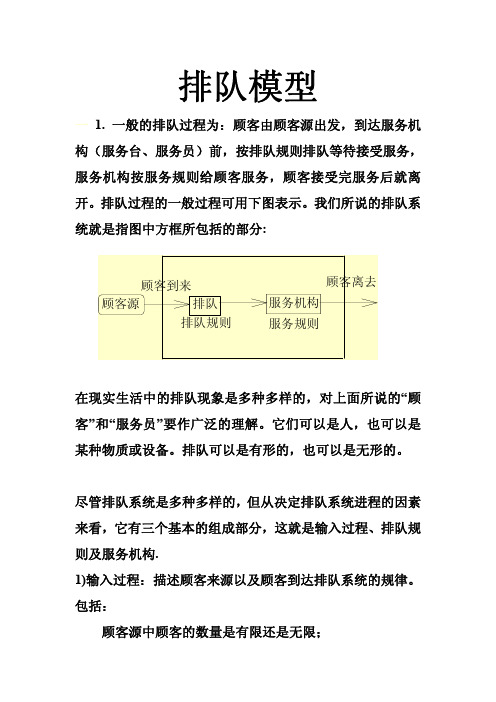
排队模型一 1. 一般的排队过程为：顾客由顾客源出发，到达服务机构（服务台、服务员）前，按排队规则排队等待接受服务，服务机构按服务规则给顾客服务，顾客接受完服务后就离开。

排队过程的一般过程可用下图表示。

我们所说的排队系统就是指图中方框所包括的部分:在现实生活中的排队现象是多种多样的，对上面所说的“顾客”和“服务员”要作广泛的理解。

它们可以是人，也可以是某种物质或设备。

排队可以是有形的，也可以是无形的。

尽管排队系统是多种多样的，但从决定排队系统进程的因素来看，它有三个基本的组成部分，这就是输入过程、排队规则及服务机构.1)输入过程：描述顾客来源以及顾客到达排队系统的规律。

包括：顾客源中顾客的数量是有限还是无限；顾客到达的方式是单个到达还是成批到达；顾客相继到达的间隔时间分布是确定型的还是随机型的，分布参数是什么，是否独立，是否平稳。

2)排队规则：描述顾客排队等待的队列和接受服务的次序。

包括：即时制还是等待制；等待制下队列的情况（是单列还是多列，顾客能不能中途退出，多列时各列间的顾客能不能相互转移）；等待制下顾客接受服务的次序（先到先服务，后到先服务，随机服务，有优先权的服务）。

3)服务机构：描述服务台(员)的机构形式和工作情况。

包括：服务台（员）的数目和排列情况；服务台（员）的服务方式；服务时间是确定型的还是随机型的，分布参数是什么，是否独立，是否平稳。

2.到达和服务过程的模型2.1 到达过程的模型用表示第i 个顾客到达的时间,.i t 称为第i 个到达时间间隔.1i i T t t +=−i 我们用的特征来刻画顾客到达过程. 最常见的情况是独立同分布. 用X 表示这样的随机变量.12,,T T 12,,T T 如果X 服从参数为λ的指数分布.这时1()()i E T E X λ==即平均每隔1λ来一个顾客.换句话说,单位时间理平均有λ个顾客到来.称λ为到达速率. 用表示到时刻t 为止到达的顾客总数,则在上面的假设下()N t ()()N t P t λ∼.除了指数分布外,常用的还有爱尔朗分布,其密度函数为1()(), 0.(1)!k RxR Rx e f x x k −−=≥− 这时2(), ()i i k k E T D T R R==. k 叫形状参数, R 叫速率参数.当取λ使得R k λ=, 则爱尔朗分布可以看成是k 个独立的服从参数为λ的指数分布随机变量的和的分布.2.2服务过程的模型一般总是认为不同顾客接受服务占用的时间长短是相互独立的. 用Y表示一个客户接受服务的时间长短, 它是一个随机变量.若Y的分布是参数为μ的指数分布, 意味着一个顾客的服务时间平均为1μ. 单位时间里可以完成的平均顾客数为μ.若Y服从形状参数为k, 速率参数为R kμ=的爱尔朗分布, 则平均服务时间为1μ, 根据爱尔朗分布的性质, 可以将Y看作是k个相继子服务的总时间, 每个子服务都服从参数为1kμ的指数分布且相互独立.在排队论中,我们常用如下字母表示特定的到达时间间隔或服务时间分布:M: i.i.d. 指数分布D: i.i.d. 的确定分布E k: i.i.d. 的形参为k的爱尔朗分布GI: 到达时间间隔是i.i.d. 的某种一般分布G: 服务时间是i.i.d. 的某种一般分布在处理实际排队系统时，需要把有关的原始资料进行统计，确定顾客到达间隔和服务时间的经验分布，然后按照统计学的方法确定符合哪种理论分布。

Min(N,V)—策略休假MG1排队系统分析的开题报告

Min(N，V)—策略休假MG1排队系统分析的开题报告1. 研究背景策略休假MG1排队系统是一种常用的队列论模型，应用广泛于诸如服务业、交通运输等领域。

队列系统是一个重要的决策问题，对于提高服务水平、优化资源配置、减少成本等方面具有重要意义。

理解和研究队列论模型对现代管理和运营具有重要价值。

2. 研究内容本文将针对策略休假MG1排队系统进行分析研究，主要研究内容包括：（1）队列系统的基本原理和相关理论。

（2）对于策略休假MG1排队系统进行建模和分析。

（3）运用MATLAB等工具进行模拟实验和数据分析。

（4）结合实际案例进行应用研究和案例分析。

3. 研究目的（1）了解队列系统的基本理论和方法，提高对于队列系统分析和研究的能力。

（2）研究策略休假MG1排队系统并建立相应的数学模型，探究其基本性质和运行机制。

（3）运用MATLAB等工具进行模拟实验和数据分析，以验证模型的合理性和可靠性。

（4）结合实际案例进行应用研究和案例分析，以求对于实际运营的队列系统分析提供帮助。

4. 研究方法（1）文献调研法：对于队列系统的基本理论和方法进行文献调研。

（2）数学建模法：针对策略休假MG1排队系统进行数学建模，并用MATLAB等工具进行模拟实验。

（3）案例分析法：结合实际案例进行应用研究和案例分析，以求对于实际运营的队列系统分析提供帮助。

5. 研究意义（1）对于队列系统的基础理论和相关方法进行了深入了解和研究，为实际应用提供了理论基础。

（2）建立策略休假MG1排队系统的数学模型并进行模拟实验和数据分析，为实际运营提供了科学依据。

（3）结合实际案例分析，为服务业等领域的队列系统管理提供了参考和借鉴。

排队模型掌握mm1,mmc,mm1k ppt课件

Ek——k阶爱尔朗分布
GI——一般相互独立的时间间隔分布
G——一般服务时间分布
四、排队模型的数量指标
1、平均队长(Ls)：指在系统中的顾客数（包括正被服务的顾客和排队等待的顾客）的期望值。 2、平均排队长(Lq)：指系统中排队等候服务的顾客数的期望值。
Ls=Lq+正被服务的顾客数 3、平均逗留时间(Ws)：指一个顾客在系统中的停留时间期望值。
4、平均等待时间(Wq)：指一个顾客在系统中排队等待的时间的期望值。 Ws=Wq+服务时间
5、忙期：指从顾客到达空闲服务机构起到服务机构再次空闲止这段时间长度，即服务机构连续繁忙的时间长度。
6、系统的状态概率[Pn( t )] ：指系统中的顾客数为n的概率。
7、稳定状态：limPn(t)→Pn
四、排队模型的数量指标
排队模型
凯里学院余英
模型要点
1、掌握排队模型的基本概念 2、了解常见的分布函数及生灭过程 3、掌握典型排队系统模型的结构及应用
排队模型的基本概念
一、引言 1、什么是排队模型（排队论）？排队论是研究拥挤现象的一门学科。
它是在研究各种排队系统概率规律性的基础上，解决有关排队系统的最优化设计（静态）和最优控制（动态）问题。
的，它们之间可以是平行排列（并列）的，也可以是前后排列（串列）的，也可以是混合的； b、服务时间可以是确定的，也可以是随机的，对于后者要知道它的概率分布； c、服务时间可以是平稳的，也可以是非平稳的，我们研究前者； d、对于等待制，服务规则又可以分为先到先服务（FCFS），后到先服务（LCFS），随机服务和有优先权的服务。
二、排队系统的特征及其组成
1、排队系统的特征即拥挤现象的共性 1）、有请求服务的人或物 2）、有为顾客服务的人或物 3）、具有随机性 4）、服务的数量超过服务机构的容量

MG1型排队系统分析与仿真

M/G/1型排队系统分析与仿真一、排队系统排队论(queuing theory), 或称随机服务系统理论, 是通过对服务对象到来及服务时间的统计研究，得出这些数量指标（等待时间、排队长度、忙期长短等）的统计规律，然后根据这些规律来改进服务系统的结构或重新组织被服务对象，使得服务系统既能满足服务对象的需要，又能使机构的费用最经济或某些指标最优。

它是数学运筹学的分支学科。

也是研究服务系统中排队现象随机规律的学科。

广泛应用于计算机网络, 生产, 运输, 库存等各项资源共享的随机服务系统。

排队论研究的内容有3个方面：统计推断，根据资料建立模型；系统的性态，即和排队有关的数量指标的概率规律性；系统的优化问题。

其目的是正确设计和有效运行各个服务系统，使之发挥最佳效益。

一般的排队过程为：顾客由顾客源出发，到达服务机构（服务台、服务员）前，按排队规则排队等待接受服务，服务机构按服务规则给顾客服务，顾客接受完服务后就离开。

排队过程的一般过程可用下图表示。

我们所说的排队系统就是指图中虚线所包括的部分。

排队系统又称服务系统。

服务系统由服务机构和服务对象（顾客）构成。

服务对象到来的时刻和对他服务的时间（即占用服务系统的时间）都是随机的。

描述一个排队系统一般需要分析其三个组成部分：输入过程、排队规则和服务机构。

输入过程输入过程考察的是顾客到达服务系统的规律。

它可以用一定时间内顾客到达数或前后两个顾客相继到达的间隔时间来描述，一般分为确定型和随机型两种。

例如，在生产线上加工的零件按规定的间隔时间依次到达加工地点，定期运行的班车、班机等都属于确定型输入。

随机型的输入是指在时间t内顾客到达数n（t）服从一定的随机分布。

如服从泊松分布,则在时间t内到达n个顾客的概率为或相继到达的顾客的间隔时间T 服从负指数分布，即式中λ为单位时间顾客期望到达数，称为平均到达率；1/λ为平均间隔时间。

在排队论中，讨论的输入过程主要是随机型的。

排队规则排队规则分为等待制、损失制和混合制三种。

无线通信网络中的M／G／1重试排队模型

用有效的功率管￣（ｐｏｗｅｒｍａｎａｇｅｍｅｎｔ）机制使节点降低能耗
０【；ｐ（ｘ）、ｂ（ｘ）、ｂ（ｘ）、ｐ及ｐ；ｇ（ｘ）、ｖ（ｘ）、及．系统只有在服务
是无线网络设计首先需要考虑的因素ＩｌＪ．另外，作为无线网络时间里才发生故障，失效率为，数据包已经服务过的时间
Ｓ＝｛０，１，２） × Ｎ× 【０，）Ｘ『０， ∞） ×［０，ｏ。）
到达的数据流．节点工作在两种状态：活动（ａｃｔｉｖｅ）状态和睡
令ａ（ｘ），ｂ（ｘ），ｖ（ｘ）分别表示在时刻ｔ重试、服务和休假的风
（２０１２ｘｋｊｑＯ０８）
设Ｃ（ｆ）＝ｉ表示节点所处的状态（ｉ＝０，１，２，分别表示在时刻
排队系统在工作中节点常因无数据传输而休假；常因为了
ｔ节点处于空闲、服务和休假期）；Ｎ（ｔ）表示在时刻ｔ在ｏｒｂｉｔ中
节省资源而具有空竭服务［３－４１；也就是笔者考虑的带有空竭
Ｖｏ１．２９Ｎｏ．６
Ｊｕｎ．２０１３
无线通信网络
（１．黄山学院
摘
数学与统计学院，安徽
黄山２４５０４１；２．江苏大学
理学院，江苏镇江２１２０１３）
试时间间隔和数据包的服务时间、处理器休假时问都服从

may排队论--将MM1类型的理论和习题自己多看看

P0
1
1 N1
1
2 3
1
2 3
6
0.356
e (1 PN ) (1 N P0 ) 4 1
2 3
5 0.356
3.808
L
(N 1)N1
2 3
(5 1)
2 3
6
2 0.577 1.423
1 1 N1
1
2 3
1
2 3
6
Lq
L e
1.423 3.808 6
顾客到达
进入队列
...
因队列满而离去
服务台
顾客接受服务后离去
...
系统的状态转移图
系统的状态概率平衡方程
对于状态0： … 对于状态k： … 对于状态N：
P0=P1 …
Pk-1+Pk+1=(+)Pk …
PN-1=PN
0<k<N
系统的状态概
率
Pk
Pk 1
k P0
k 1,2, , N
由
N
Pk 1
Sn t +t时刻
Pn(t t) Pn(t)(1t)(1 t) Pn1(t)t(1 t) Pn1(t)(1t)t o(t)
Pn
(t
t) t
Pn
(t)
Pn
(t
)(
)
Pn1(t
)
Pn1(t)
o(t) t
令t 0得：
dP0 (t)
dt dPn (t)
dt
P0 Pn
(t) P1(t) (t)( ) Pn1(t)
动态
即与特定顾客特征选择
等待的顾客数
协商
优先级

排队模型

2.2制造系统的排队网络模型
对于制造系统中的排队现象 ,同样可以通过排队理论进行描述和分析。例如 ,对于一台或一组相同功能的加工设备对相同类型零件进行加工的情况 ,可用排队系统进行描述,对于由多种类型设备组成的加工单元和车间对多种类型零件进行加工的情况,则可用排队网络进行描述。图3即为一由m台数控机床和n个夹具组成的摩托车零件数控加工系统。由于在该系统中夹具的数量是固定的 ,加工完一个零件空出一个夹具后 ,才能投入一个新的零件,因此系统中最多只有n个零件。
服务机构（从机构形式和工作状况来看可分为以下几种情况） 1服务机构可以没有服务员，也可以有一个或多个服务员。 2在有多个服务台的情形中，它们可以是平行并列的，也可以前后排列的，也可以是混合的。 a中是单队-单服务台的情形;b是多对-多服务台的情形；c是单队-多服务台的情形；d是多服务台的情形（e）是多服务台的情形
M/M/1系统的状态转移图
其中
λ 为顾客到达速率，
μ 为服务机构的服务速率
由状态转移图 ,可写出状态转移率矩阵如下式所示
é- l êm ê Q=ê 0 ê ê 0 ê ë M
l 0 0 - (m + l ) l 0 m - (m + l ) l m - (m + l ) 0 M M M
Lù Lú ú Lú Lú ú Mú û
(1-3)
矩阵Q 的建立规则是 : Q 的元素表示系统从状态 i 向状态 j 转移的速率,并且其行和为零。
根据以上给出的P和Q,可得PM/M/1系统状态方程的具体形式如下:
lpn -1 - (l + m ) pn + mpn +1 = 0,
此外 ,由概率的概念可得以下补充方程:

( 数学建模)排队论模型

导出 pn (t ) 满足的微分方程组
p0 (t t ) p0 (t )(1 t ) p1 (t ) t (1 t ) o(t ) p0 (t t ) p0 (t ) p0 (t ) t p1 (t ) t o( t )
(1)流具有平衡性对任何 a 0和 0 t1 t2 tn , x(a ti ) x(a ) (1 i n) 的分布只取决于 t1 , t2 , , tn 而与 a 无关。 (2)流具有无后效性对互不交接的时间区间序列 ai , bi (1 i n) ， x (bi ) x ( ai ) 是一组相互独立的随机变量。 (3)流具有普通性 Prx(a t ) x(a) 1
Prx(t ) k
E x (t ) t
k!
e
(k 0,1,2,)
故参数λ表示单位时间内事件发生次数的平均数。
2.Poisson流的发生时间间隔分布
当流(过程) x(t ) : t 0 构成Poisson过程时，就称为Poisson流。设流发生的时刻依次为 t1 , t2 , , tn ,…，发生的时间间隔记为 n tn tn1 (n 1,2,) ，其中t0 0 。
1.最简单流与Poisson过程
记随机过程｛x（t）：t≥0｝为时间［0，t］内流(事件)发生的次数，例如对于随机到来某电话交换台的呼叫，以x（t）表示该交换台在［0，t］这段时间内收到呼叫的次数；若是服务机构，可以用x（t）表示该机构在［0，t］时间内来到的顾客数。
最简单流应 x(t ) : t 0 具有以下特征称 5 3二、单通道等待制排队问题
（M／M／1排队系统）
对于单通道等待制排队问题主要讨论输入过程为Poisson流，服务时间服从负指数分布，单服务台的情形，即M／M／1排队系统。

排队模型(掌握mm1,mmc,mm1k)

Pn(t+Δt)= Pn(t)(1-λΔt )+Pn-1(t)λΔt+ o(Δt) [Pn(t+Δt)-Pn(t)]/Δt =-λPn(t)+λPn-1(t)+[o(Δt)]/Δt
令Δt0
d Pn(t)/dt= -λPn(t) +λPn-1(t)
Pn(0)=0
（n1）
d P0(t)/dt= -λP0(t)
T= v1+v2+...+ vk 服从k阶爱尔朗分布。
五、常见的分布函数及生灭过程
5、生灭过程定义：设{N（t），t≥0}为一随机过程，若N（t）的概
率分布具有以下性质： a、假设N（t）=n,则从时刻t起到下一个顾客到达时刻止的时间服从参数为λn的负指数分布，n=0,1,2,… b、假设假设N（t）=n,则从时刻t起到下一个顾客离去时刻止的时间服从参数为μn的负指数分布， n=0,1,2,… c、同一时刻时只有一个顾客到达或离去。则称{N（t），t≥0}为一个生灭过程。
…
…
n-1
pn =λn-1pn-1/μn+(μn-1pn-1- pn-2λn-2)/μn
=p0λn-2λn-1…λ0/(μnμn-1…μ1)
n
p3 =λnpn/μn+1+(μnpn- pn-1λn-1)/μn+1
=p0λnλn-1…λ0/(μn+1μn…μ1)
五、常见的分布函数及生灭过程
记
cn
n 1 n2...0 n n1...0
平均服务率： 41/127=0.32(人/分钟)
六、典型排队系统模型的结构及应用
M/M/C等待制排队模型研究要点： a、系统意义 b、状态转移速度图与状态转移速度矩阵 c、状态概率方程 d、系统的基本数量指标

十三章五节MG1排队模型

二.(M/D/1):( / /G)系统 (定长服务时间)
2 这时 E （），（） 0

Ls
1
2
2(1 ) 2 则 Ls 2 ( )
若设 : E ( )

Lq 2 Lq Ls , Wq 2 ( ) 2 ( ) 均为M / M /1相应指标的一半。Leabharlann 1 2(1
)
k
2
)
(k 1) 2 ， 2k (1 )
由里特公式:
Lq Ls (k 1) Lq ，Ws ，Wq 2k (1 )
可见,k=1时即(M/M/1)，k 时即(M/D/1) 注:对于到达与服务均为任意分布的情况,可采用随机模拟的方法求近似解。
可见，内部越有规律越省时间
三.(M/Ek /1 ):( / /G)系统 (k阶爱尔郎服务时间)
设 i，每个i 服从同参数的负指数分布
i 1 k
于是E ( )
1

， 2 ( )
1 k
，令 = E （）= 2
由P-K公式:
Ls
(
2
1

2

设 : 服务时间服从任意分布，E( )与 2( )存在并已知,服务强度 = E( )<1。其他条件同M / M /1。求:系统运行指标。
解:由布拉切克-钦辛(P-K)公式:
2 2 2 ( ) LS 2(1 )
由里特公式: WS LS ，Wq WS E( ),Lq Wq
第五节 M/G/1排队模型
以上讨论了M/M/1和M/M/C系统，其前提均为泊松输入和负指数服务处理，这类系统的工具是生灭工程状态转移图。在实际中，有时到达仍为泊松过程，但服务时间并不服从负指数分布，即M/G/1系统这时不能用生灭过程处理，而主要依据布拉切克-钦辛公式(P-K公式)。

排队模型(掌握mm1,mmc,mm1k)

排队模型
凯里学院余英
精选2021版课件
1
模型要点
1、掌握排队模型的基本概念 2、了解常见的分布函数及生灭过程 3、掌握典型排队系统模型的结构及应用
精选2021版课件
2
排队模型的基本概念
一、引言 1、什么是排队模型（排队论）？排队论是研究拥挤现象的一门学科。
它是在研究各种排队系统概率规律性的基础上，解决有关排队系统的最优化设计（静态）和最优控制（动态）问题。
19 72 4 8 1 29 106 1 3 1 39 135 2 4 10
20 80 3 1 0 30 109 2 5 0 40 139 4 3 8
21 81 2 2 2 31 114 1 2 0 41 142 1
9
22 83 3 3 2 32 116 8 1 0
精选2021版课件
20
到达间隔分布表
1）、输入过程(顾客到达的方式)
a、顾客的总体（顾客源）的组成可能是有限的，也可能是无限的；
b、顾客相继到达的时间间隔可以是确定的，也可以是随机的，对于随机的情形，要知道单位时间内的顾客到达数或相继到达的间隔时间的概率分布；
c 、输入过程可以是平稳的（描述相继到达的间隔时间分布和所含参数（如期望值、方差等）都是与时间无关的），否则成为非平稳的，我们研究平稳的。
到达间隔次 (分钟) 数
1
6
2
10
3
8
4
6
5
3
6
2
7
2
8
1
9
1
10以上 1
合计 40
服务时间分布表
服务时间次 (分钟) 数
1
10
2
10

实验六准备知识—MM1排队模型

n 1 n 0 n 1

Ls
——因为是均值。
其中 1。问题：为什么 L s Lq 1(而不是 1）呢？
（2）Ws与Wq
首先可证，逗留时间W 服从参数为的负指数分布，而负指数分布的均值等于其参数的倒数，故平均逗留时间 W
s

P0 1 P ( ) n (1 ), n 1 n
可解得状态概率：
记
，称为服务强度，规定 1（为什么？），则 P0 1 n P P0 n
3. 系统运行指标
（1）Ls与Lq
Ls 表示系统中的平均顾客数，由期望定义， Ls np n n n (1 ) (1 ) n n 1
(10 4) 1 1 1 4 (8) P ( W ) 1 P ( W ) 1 F ( ) e e 1.5 0.223。 4 4 4 1
2 。 5
1 人/分钟 10人/小时， 6
解：此为标准的M/M/1模型， 4人/小时，
3 (1) P0 1 ; 5 2 3 (2) P3 3 (1 ) ( ) 3 ( ) 0.0384; 5 5 2 (3) 1 P0 ; 5 4 2 (4) Ls (人/小时） ; 6 3 1 1 (5) W s Ls (小时/人） ; 6 2 2 4 (6) Lq Ls (人/小时） ; 3 5 15 1 1 1 1 (7) W q W s (小时/人） ; 6 10 15

0 1

2

...
n-1 n

排队论模型

E[N (t)] = λt ； Var[N (t)] = λt 。
当输入过程是泊松流时，那么顾客相继到达的时间间隔 T 必服从指数分布。这是
由于
P{T > t} = P{[0, t) 内呼叫次数为零} = P0 (t) = e−λt 那么，以 F (t) 表示 T 的分布函数，则有
P{T
≤
t}
=
F (t)
设 N (t) 表示在时间区间 [0, t) 内到达的顾客数（ t > 0 ），令 Pn (t1,t2 ) 表示在时间区
间 [t1,t2 )(t2 > t1 ) 内有 n(≥ 0) 个顾客到达的概率，即 Pn (t1,t2 ) = P{N (t2 ) − N (t1) = n} (t2 > t1, n ≥ 0)
=
⎧1 − e−λt , ⎨
⎩0,
t≥0 t<0
而分布密度函数为
f (t) = λe−λt , t > 0 .
-121-
对于泊松流, λ 表示单位时间平均到达的顾客数,所以 1 就表示相继顾客到达平均 λ
间隔时间，而这正和 ET 的意义相符。
对一顾客的服务时间也就是在忙期相继离开系统的两顾客的间隔时间，有时也服从
n=2
（2）
-120-
在上述条件下，我们研究顾客到达数 n 的概率分布。由条件 2o，我们总可以取时间由 0 算起，并简记 Pn (0,t) = Pn (t) 。
由条件 1o 和 2o，有
P0 (t + Δt) = P0 (t)P0 (Δt)
n
∑ Pn (t + Δt) = Pn−k (t)Pk (Δt), k =0
指数分布是单参数 λ 的非对称分布，记作 Exp(λ) ，概率密度函数为：

5-排队模型

λ=100辆/小时，µ＝240 辆/小时小时，辆小时小时
ρ= λ /µ = 100/240 = 5/12 系统空闲的概率为： P0 = 1- ρ = 1- 5/12 = 0.583 系统空闲的概率为： 1- P0 = 1- (1- ρ) = ρ = 0.417 系统忙的概率为 : 系统中有1辆车的概率为 P1 = ρ1(1- ρ) = 0.243 系统中有辆车的概率为 : 系统中有2辆车的概率为辆车的概率为：系统中有辆车的概率为： P2 = ρ2(1- ρ) = 0.101 系统中有3辆车的概率为辆车的概率为: P3 = ρ3(1- ρ) = 0.042 系统中有辆车的概率为
7
n≥1
对于状态“ 到状态到状态“ ，存在以下稳态方程：对于状态“0”到状态“n”，存在以下稳态方程：
状态 0 1 ┊ n ┊
转入 µP1 λP0 + µP2 ┊ λPn-1+ µPn+1 ┊
＝＝＝
转 λP0 λP1 + µP1 ┊ λPn+ µPn ┊
出
8
状态 0 1 ┊ n ┊
转入 µP1 λP0 + µP2 ┊ λPn-1+ µPn+1 ┊
单服务台等待制III [M/M/1]:[∞ / m/FCFS] 单服务台等待制 ∞
队列(n个队列个)
服务台
需要服务 m-n 服务完毕
现实情形：有m台机器在运转，单位时间内平均出现故障现实情形：台机器在运转，的机器数为λ 修理工修理一台设备的平均服务时间μ 的机器数为λ，修理工修理一台设备的平均服务时间μ，已修复的机器仍然可能再出现故障。已修复的机器仍然可能再出现故障。 19

《2024年带负顾客的M-M-1休假排队系统驱动的流模型》范文

《带负顾客的M-M-1休假排队系统驱动的流模型》篇一带负顾客的M-M-1休假排队系统驱动的流模型一、引言排队系统是现代服务行业中常见的模型之一，特别是在处理顾客流量和资源分配方面。

本文将探讨一个具有特殊特性的M/M/1排队系统，即带负顾客的休假模型。

负顾客在传统的排队系统中并不常见，但他们的存在对系统的性能和效率有着重要的影响。

本文将详细分析该模型，以揭示其运行机制和性能特点。

二、模型描述M/M/1排队系统是一种基本的排队模型，其中M代表指数分布的服务时间和到达时间。

在带负顾客的M/M/1休假模型中，除了常规的顾客外，还存在一类特殊的负顾客。

这些负顾客在到达系统后，不仅不会接受服务，反而会带走正在服务的顾客或使正在等待的顾客离开系统。

此外，系统还允许服务员在一定的条件下进入休假状态，进一步增加了系统的复杂性。

三、流模型分析1. 顾客到达过程：顾客的到达遵循泊松分布，即到达时间间隔服从指数分布。

负顾客和正顾客的到达率可以不同，这将影响系统的性能。

2. 服务过程：服务时间也服从指数分布，与到达时间相互独立。

服务员在服务过程中可能进入休假状态，休假时间及休假后的服务策略需详细定义。

3. 负顾客影响：负顾客的到达将导致正在接受服务的顾客立即离开系统，从而减少了系统的负载。

然而，负顾客也可能使等待的顾客离开，从而降低系统的吞吐量。

4. 休假策略：系统中的服务员在一定的条件下可以进入休假状态，以减少系统开销和能耗。

休假的时长及触发条件需根据实际情况进行设定。

四、性能指标分析对于带负顾客的M/M/1休假排队系统，我们关注的主要性能指标包括队列长度、等待时间、服务率等。

这些指标将帮助我们评估系统的性能和效率。

具体而言，我们将通过数学模型和仿真实验来分析这些指标的变化规律，以揭示负顾客和休假策略对系统性能的影响。

五、仿真实验与结果分析通过仿真实验，我们可以更直观地了解带负顾客的M/M/1休假排队系统的运行情况。

我们将设定不同的参数，如负顾客到达率、服务率、休假策略等，以观察系统性能的变化。

MG1型非空竭服务休假排队系统的随机分解的开题报告

MG1型非空竭服务休假排队系统的随机分解的开题报告一、研究目的和意义随机分解法是一种常用的优化算法，可以有效地解决多种实际问题。

非空竭排队系统是一种常见的服务系统，如银行、医院等场所，对其进行优化可以提高系统效率和顾客满意度。

本文旨在利用随机分解法对MG1型非空竭服务休假排队系统进行优化，提高系统的服务能力和效率，从而为实际应用提供可靠参考。

二、研究内容与思路1. 系统模型建立本文采用MG1型排队系统作为研究对象，建立相应的系统模型，并对系统中的各要素进行描述，如到达率、服务时间分布、休假时间、排队规则等。

2. 随机分解算法研究随机分解算法是一种常用的优化算法，包括两个部分：全局搜索和局部搜索。

在全局搜索阶段，通过对目标函数进行随机扰动，得到局部最优解；在局部搜索阶段，则对当前解进行局部优化，以得到更优解。

本文将对随机分解算法进行深入研究，并运用到MG1型非空竭服务休假排队系统优化中。

3. MG1型非空竭服务休假排队系统优化本文将通过随机分解算法对MG1型非空竭服务休假排队系统进行优化。

具体步骤为：首先建立系统模型，然后利用随机分解算法求解系统最优解，最后对优化结果进行验证和评价。

三、研究预期成果通过本文的研究，预期达到以下成果：1. 建立MG1型非空竭服务休假排队系统模型，对系统中的各要素进行描述。

2. 深入研究随机分解算法，包括全局搜索和局部搜索等关键步骤。

3. 运用随机分解算法对MG1型非空竭服务休假排队系统进行优化，提高系统的服务能力和效率。

4. 对优化结果进行验证和评价，为实际应用提供可靠参考。

综上所述，本文的研究具有一定的理论与实际意义，在服务系统优化领域具有一定的推广价值和应用前景。

排队论简要知识

例如，某排队问题为M／M／S／∞／ ∞/FCFS，则表示顾客到达间隔时间为负指数分布(泊松流)；服务时间为负指数分布；有s(s>1) 个服务台；系统等待空间容量无限(等待制)；顾客源无限，采用先到先服务规则。
某些情况下，排队问题仅用上述表达形式中的前3个符号。例如，某排队问题为M／M／S，
如不特别说明则均理解为系统等待空间容量无限；顾客源无限，先到先服务，单个服务的等待制系统。
3、服务机构――单服务台，服务时间的长短是随机的，服从相同的指数分布。
2021/10/10
33
对于M／ M／1模型有如下公式：
P0 1
L 1
W 1
Pn n(1)
Lq(2 )12L
Wq ()
W
P(Nk)k1
例1 某医院急诊室同时只能诊治一个病人，诊
治时间服从指数分布，每个病人平均需要15分钟。病人按泊松分布到达，平均每小时到达3人。试对此排队队系统进行分析。
这是指服务台从队列中选取顾客进行服务的顺序。一般可以分为损失制、等待制和混合制等3大类。
(1)损失制。这是指如果顾客到达排队系
统时，所有服务台都被先到的顾客占用，那么他们就自动离开系统永不再来。
2021/10/10
17
2．服务规则
(2)等待制这是指当顾客来到系统时，所有服务台
都不空，顾客加入排队行列等待服务。等待制中，服务台在选择顾客进行服务时常有如下四种规则： 1)先到先服务。按顾客到达的先后顺序对顾客进行服务。 2)后到先服务。 3)随机服务。即当服务台空闲时，不按照排队序列而随意指定某个顾客接受服务。 4)优先权服务。
2021/10/10
21
各符号的意义: