巧算十法
巧算和速算方法

校本课程数学计算方法目录第一讲生活中几十乘以几十巧算方法. 错误!未定义书签。
第二讲常用巧算速算中的思维与方法(1)........ - 4 - 第三讲常用巧算速算中的思维与方法(2)........ - 6 - 第四讲常用巧算速算中的思维与方法(3)........ - 8 - 第五讲常用巧算速算中的思维与方法(4)........ - 9 - 第六讲常用巧算速算中的思维与方法(5)....... - 10 - 第七讲常用巧算速算中的思维与方法(6)....... - 11 - 第八讲小数的速算与巧算...................... - 12 - 第九讲乘法速算1............................. - 13 - 第十讲乘法速算2............................. - 15 - 第十一讲乘法速算3............................. - 17 - 第十二讲乘法速算4............................. - 17 - 第十三讲乘法速算5............................. - 18 - 第十四讲乘法速算6............................. - 19 - 第十五讲乘法速算7............................. - 22 - 第十六讲乘法速算8............................. - 24 - 注:《速算技巧》.............................. - 27 - 第一讲生活中几十乘以几十巧算方法1.十几乘十几:口诀:头乘头,尾加尾,尾乘尾。
例:12×14=?解: 1 ×1 = 12+4=62×4=812×14=168注:个位相乘,不够两位数要用0占位。
速算和巧算
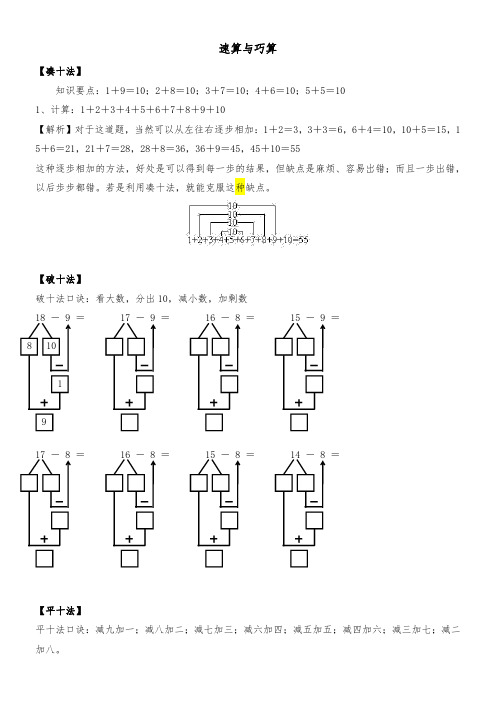
速算与巧算【凑十法】知识要点:1+9=10;2+8=10;3+7=10;4+6=10;5+5=101、计算:1+2+3+4+5+6+7+8+9+10【解析】对于这道题,当然可以从左往右逐步相加:1+2=3,3+3=6,6+4=10,10+5=15,1 5+6=21,21+7=28,28+8=36,36+9=45,45+10=55这种逐歩相加的方法,好处是可以得到每一歩的结果,但缺点是麻烦、容易岀错;而且一歩出错,以后歩步都错。
若是利用凑十法,就能克服这种缺点。
【破十法】破十法口诀:看大数,分出10,减小数,加剩数18-9=17-9=16-8=15-9=8101917-8=16-8=15-8=14-8=【平十法】平十法口诀:减九加一;减八加二;减七加三;减六加四;减五加五;减四加六;减三加七;减二加八。
18-9=17-9=16-9=15-9=8110917-8=16-8=15-8=14-8=【退十加补法】18-9=17-9=16-9=15-9=1018917-8=16-8=15-8=14-8=【凑整法】同学们还知道,有些数相加之和是整十、整百的数,如:1+19=20;11+19=30;2+18=20;12+28=40;3+17=20;13+37=504+16=20;14+46=60;5+15=20;15+55=70;6+14=20;16+64=807+13=20;17+73=90;8+12=20;18+82=100;9+11=20又如:15+85=100;14+86=100;25+75=100;24+76=10035+65=100;34+66=100;45+55=100;44+56=100等等巧用这些结果,可以使那些较大的数相加又快又准。
像10、20、30、40、50、60、70、80、90、1 00等等这些整十、整百的数就是凑整的目标。
【用已知求未知】利用己经获得较简单的知识来解决面临的更复杂的难题这是人们认识事物的一般过程,凑十法、凑整法的实质就是这个道理,可见把这种认识规律用于计算方面,可使计算更快更准。
巧算和速算方法

校本课程数学计算方法目录第一讲生活中几十乘以几十巧算方法 .............................. - 2 - 第二讲常用巧算速算中的思维与方法〔1〕 .................... - 4 - 第三讲常用巧算速算中的思维与方法〔2〕 .................... - 6 - 第四讲常用巧算速算中的思维与方法〔3〕 .................... - 9 - 第五讲常用巧算速算中的思维与方法〔4〕 ...................- 10 - 第六讲常用巧算速算中的思维与方法〔5〕 ...................- 14 - 第七讲常用巧算速算中的思维与方法〔6〕 ...................- 16 - 第八讲小数的速算与巧算.................................................- 18 - 第九讲乘法速算1..............................................................- 19 - 第十讲乘法速算2..............................................................- 21 - 第十一讲乘法速算3..............................................................- 23 - 第十二讲乘法速算4..............................................................- 23 - 第十三讲乘法速算5..............................................................- 24 - 第十四讲乘法速算6..............................................................- 25 - 第十五讲乘法速算7..............................................................- 28 - 第十六讲乘法速算8..............................................................- 30 - 注:《速算技巧》 ...............................................................- 33 -第一讲生活中几十乘以几十巧算方法1.十几乘十几:口诀:头乘头,尾加尾,尾乘尾。
破十法-演示文稿

15 - 9 =
二、探究发现
15 - 9 = 6
有15个气球, 卖了9个。 还有几个?
方法 一:
减一 个 一 个 的
15 – 9 6 =
15
方 法 破十法
二:
15 - 9=6
5 10 1
二、探究发现
有15个气球, 卖了9个。
还有几个?
15 - 9 6 ﹦
5 10 1
6
方 法 三:平十法
15 - 9=6
我有16个风车, 卖了 9 个。
还剩下多少个?
从10里面减去9, 10-9=1,1+6=7。
16-9=7
?个
17个 17-9=6(个)
?个
14个 14-9=5(个)
12-5= 7 14+4= 18 10-4= 6 13-9= 4
11+0= 11 10-6= 4 13-7= 6 11-9= 2
破十法儿歌
退位减,我会算 十几减9,是几加1, 十几减8,是几加2, 十几减7,是几加3, 十几减6,是几加4, 十几减5,是几加5,
感谢下 载
巧算“十几减9” :就是把被减 数个位上的数加1就是“十几减9”
减9去十尾加1
12-9=( 2 )+( 1 )=( ) 14-9=( 4 )+( 1 )=( ) 17-9=( )+( )=( ) 13-9=( )+( )=( ) 15-9=( )+( )=( ) 11-9=( )+( )=( ) 16-9=( )+( )=( ) 18-9=( )+( )=( )
算一算
十二朵花减去九朵还有几朵?
12-9= 3
检测练习:
十以内加减巧算技巧

十以内加减巧算技巧在学习数学的过程中,我们经常会遇到十以内的加法和减法。
正确的掌握十以内的加减法运算对我们日常生活和学习中的计算问题非常重要。
为了帮助大家更轻松、更高效地进行十以内的运算,以下是一些巧算技巧的分享。
一、加法技巧1. 定位加法:当我们遇到十以内的加法题目时,可以先确定一个数然后在数线上向右移动,再根据题目中给出的另一个数向右移动相应的步骤,最终通过数线上的位置来得到结果。
2. 拆解相加:对于一些难以计算的十以内加法题目,我们可以通过拆解相加的方式来求解。
例如,对于题目“8 + 5”,我们可以将8拆解为4+4,然后再加上5,即4+4+5=13。
3. 利用补数:当我们遇到加法题目中的一个数非常接近10时,可以利用补数的方法来简化计算。
例如,对于题目“7 + 9”,我们可以将9补充为离10更近的数1,即7+1+8=16。
4. 利用友数:在十以内的加法中,有一些数字之间存在友数的关系,即两个数相加等于10。
例如,5和5、6和4等都是友数关系。
当我们遇到这样的数字组合时,可以直接利用友数关系来计算。
例如,对于题目“5 + 5”,我们知道5和5是友数,所以结果是10。
二、减法技巧1. 利用对称性:在十以内的减法中,有一些数字的减法结果可以通过对称性来推算。
例如,对于题目“9 - 3”,我们可以找到一个与3对称的数字7,所以结果是6。
2. 利用补数:当我们遇到减法题目中的被减数和减数之间的差非常接近10时,可以利用补数的方法来简化计算。
例如,对于题目“8 - 2”,我们可以将2补充为与8之间的差6,即8 - 6 = 2。
3. 利用近似数:有时候我们并不需要得到精确的减法结果,只需要一个近似值即可。
例如,对于题目“7 - 4”,我们可以近似地认为7和4之间的差是3,所以结果是3。
4. 借位法:当我们遇到减法题目中的被减数个位比减数小,我们可以借位使得个位变大,然后再进行减法运算。
例如,对于题目“8 - 6”,我们可以从8中借出一个单位给个位的数字,即变成18 - 6 = 12。
数学常用巧算速算法

目录第一讲生活中几十乘以几十巧算方法 (2)第二讲常用巧算速算中的思维与方法(1) (4)第三讲常用巧算速算中的思维与方法(2) (7)第四讲常用巧算速算中的思维与方法(3) (10)第五讲常用巧算速算中的思维与方法(4) (12)第六讲常用巧算速算中的思维与方法(5) (17)第七讲常用巧算速算中的思维与方法(6) (19)第八讲小数的速算与巧算1——凑整 (22)第九讲乘法速算1 (23)第十讲乘法速算2 (25)第十一讲乘法速算3 (27)第十二讲乘法速算4 (28)第十三讲乘法速算5 (29)第十四讲乘法速算6 (31)第十五讲乘法速算7 (34)第十六讲乘法速算8 (37)注:《速算技巧》 (42)第一讲生活中几十乘以几十巧算方法1.十几乘十几:口诀:头乘头,尾加尾,尾乘尾。
例:12×14=?解: 1×1=12+4=62×4=812×14=168注:个位相乘,不够两位数要用0占位。
2.头相同,尾互补(尾相加等于10):口诀:一个头加1后,头乘头,尾乘尾。
例:23×27=?解:2+1=32×3=63×7=2123×27=621注:个位相乘,不够两位数要用0占位。
3.第一个乘数互补,另一个乘数数字相同:口诀:一个头加1后,头乘头,尾乘尾。
例:37×44=?解:3+1=44×4=167×4=2837×44=1628注:个位相乘,不够两位数要用0占位。
4.几十一乘几十一:口诀:头乘头,头加头,尾乘尾。
例:21×41=?解:2×4=82+4=61×1=121×41=8615.11乘任意数:口诀:首尾不动下落,中间之和下拉。
例:11×23125=?解:2+3=53+1=41+2=32+5=72和5分别在首尾11×23125=254375注:和满十要进一。
三年级巧算的方法
三年级巧算的方法嘿,咱今儿就来唠唠三年级巧算的那些事儿!你说巧算这玩意儿,就像是一把神奇的钥匙,能一下子打开数学大门,让那些复杂的算式变得简单又有趣。
咱就先说说凑整法吧。
这就好比搭积木,把合适的数字凑到一块儿,让它们变成整十、整百的数,那算起来可就轻松多啦!比如说 38+62,这不就是一对绝配嘛,加起来刚好 100 呀!就像找到了失散多年的好伙伴,一下子就亲密无间了。
还有个方法叫拆数法。
哎呀呀,就像是把一个大玩具拆成几个小零件,再重新组合。
比如 25×48,可以把 48 拆成 4×12,然后 25×4 不就等于 100 嘛,再乘上 12,答案不就手到擒来啦。
再来瞧瞧这个基准数法。
这就像给一群调皮的数字找个“带头大哥”,其他数字都围绕着它来计算。
比如说计算 98+102+99+101+100,咱就可以把 100 当作基准数,那 98 就是比基准数少 2,102 就是多 2,99少 1,101 多 1,这样一加一减,算起来多方便呀!你可别小看这些巧算方法,它们就像是武林秘籍中的绝招,能让你在数学的江湖中如鱼得水。
想象一下,其他同学还在苦哈哈地列竖式计算呢,你用巧算方法一下子就得出答案了,那得多牛呀!而且呀,巧算还能让你更喜欢数学呢,不再觉得它枯燥乏味。
就拿做练习题来说吧,本来那些长长的算式看着就头疼,可一旦你掌握了巧算方法,嘿,就像是变魔术一样,难题都迎刃而解啦。
你会觉得,哇塞,数学原来这么好玩呀!三年级的小朋友们呀,可得好好把这些巧算方法学会咯,这可是你们在数学世界里闯荡的秘密武器呀!别偷懒,多练练,以后遇到什么难题都不怕啦!加油哦,我相信你们一定能行的!这些巧算方法就是为你们打开数学宝藏的钥匙,只要紧紧握住,就能发现数学那无尽的奥秘和乐趣!所以,还等什么呢,赶紧去试试吧!。
数学十大速算技巧
数学十大速算技巧学习数学离不开计算,学生的计算能力是最基本的数学能力。
那么你知道学好数学速算的方法有哪些吗?下面店铺给你分享数学十大速算技巧,欢迎阅读。
数学十大速算技巧一、充分利用五大定律教师要扎实开展好现行教材四年级数学下册中计算的五大运算定律的教学(加法交换律、加法结合律、乘法交换律、乘法结合律、乘法分配律),引导学生弄清来龙去脉,不让一个学生掉队,训练每个学生能自觉运用简便办法,能针对不同题型灵活选择简便方法正确而快捷地进行计算。
二、巧妙运用“首同末合十”利用“首同末合十”的方法来训练。
“首同末合十”法是两个两位数,它们的十位数相同,而个位数相加的和是10。
利用“首同末合十”的两个两位数相乘,积的右边的两位数正好是个位数的乘积,积的左面的数正好是十位上的数乘以比它大1的积,合并起来就是它们的乘积。
例如,54×56=3024,81×89=7209。
三、留心“左右两数合并法”任意的两位数乘上99或任意的三位数乘上999的速算法叫做“左右两数合并法”。
1.任意两位数乘上99的巧算方法是,将这个任意的两位数减去1,作为积的左面的两位数字,再将100减去这个任意两位数的差作为积的右边两位数,合并起来就是它们的积。
例如,62×99=6138,48×99=4752。
2.任意三位数乘上999的巧算方法,就是将这个任意的三位数减去1,作为积的左面的三位数字,再将1000减去这个任意三位数的差作为积的右边的三位数字,合并起来就是它们的积。
例如,781×999=780219,396×999=395604。
四、利用分数与除法的关系来巧算在一个只有二级运算的题里,按顺序计算需要多步计算,利用乘除法的关系进行计算就会简便。
比如,24÷18×36÷12=(24÷18)×(36÷12)=24/18×36/12=4。
常用的巧算和速算方法
1.十几乘十几:口诀:头乘头,尾加尾,尾乘尾。
例:12×14=?解: 1×1=12+4=62×4=812×14=168注:个位相乘,不够两位数要用0占位。
2.头相同,尾互补(尾相加等于10):口诀:一个头加1后,头乘头,尾乘尾。
例:23×27=?解:2+1=32×3=63×7=2123×27=621注:个位相乘,不够两位数要用0占位。
3.第一个乘数互补,另一个乘数数字相同:口诀:一个头加1后,头乘头,尾乘尾。
例:37×44=?解:3+1=44×4=167×4=2837×44=1628注:个位相乘,不够两位数要用0占位。
4.几十一乘几十一:口诀:头乘头,头加头,尾乘尾。
例:21×41=?解:2×4=82+4=61×1=121×41=8615.11乘任意数:口诀:首尾不动下落,中间之和下拉。
例:11×23125=?解:2+3=53+1=41+2=32+5=72和5分别在首尾11×23125=254375注:和满十要进一。
6.十几乘任意数:口诀:第二乘数首位不动向下落,第一因数的个位乘以第二因数后面每一个数字,加下一位数,再向下落。
例:13×326=?解:13个位是33×3+2=113×2+6=123×6=1813×326=4238注:和满十要进一。
常用的巧算和速算方法【顺逆相加】用“顺逆相加”算式可求出若干个连续数的和。
例如著名的大数学家高斯(德国)小时候就做过的“百数求和”题,可以计算为1 +2 + ……+ 99 + 100所以,1+2+3+4+……+99+100=101×100÷2=5050。
“3+5+7+………+97+99=?3+5+7+……+97+99=(99+3)×49÷2= 2499。
10个神奇的速算方法
10个神奇的速算方法计算能力是所有学生学习数学的必备能力,也是学好数学的基础。
如何才能提高孩子的计算能力。
对于这一点,我觉得掌握一些高效的速算方法很有必要!对此,今天特整理了一些小学数学常见的速算方法,与各位共享学习!序|修口訟C彳啓律】j <h申制吴3^”怕竝或Fiq "冃醱**^牛口"望S ,巨TL^M-S罕为4-卫斤以.丄+ 2 + 3+ 4 +=1O1«100-2= 5050^"3+5亠7+, ........... * ^7-t-^Si= 7+丫| 29 + ->7 + 95 ■+ 亠17二 4 loi •+ 1(1-* flO- ♦- 10_-4SP~ 111+ 97 + 99=(95 + 3〉勺*2=2495.二.决Sfe巧W :用"疾他方法‘‘.常常能便计縛比较简ffi*快速.砂口;( 1 ) 99.9+11.1-(90 * 10 ) + { 9 + 1 > 4 ( 0.9+ 0.1 ) -111= 995(2 ) 9+^97 + 998 >'6壬(9 + 1 ) + ( 97 + 3 )十(998 +2 JS10 4 100 费1000^1110(3 ) 125 * 135 + 125 * 125 + 120 + 125 + I2S + 125 155 + 125 + L25 125 + ( 120 + 5 ) + 125 + 125+125-5 = 125 心5-1000-5= 995五.先48后还:"先^8后还“技X5・例如:..7 5 17 3 7 5 3 1 17 1'丿16 16 32 16 '16 16 16 16 丿3216,17 1 , 153216 32(2^>■ —•*— + * + —2 4 8 16 32 M1111111 1 (—+ — + — + — + — + — + 、——^2 4 8 16 32 64 64,64,1 6364 64做这道题•技先通分后相加的一股办法•妗必影响解速度•现在从着眼•采用■先低后还“的办法,很快就将越目解答出来了•六・由小推大:一种数学思维方法,也是一种速算.巧算技巧。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
巧算十法
数值计算充满了活力,除了遵循四则混合运算的运算顺序外,破局部考虑、立整体分析,巧妙、灵活地运用定律和方法,对处理一些貌似复杂的计算题常常有事半功倍的效果,常见的巧算方法有以下十种。
一、凑整法
运算定律是巧算的支架,是巧算的理论依据,根据式题的特征,应用定律和性质“凑整”运算数据,能使计算比较简便。
1、加法“凑整”。
利用加法交换律、结合律“凑整”,例如:
4673+27689+5327+22311
=(4673+5327)+(27689+22311)
= 10000+50000
= 60000
2、减法“凑整”。
利用减法性质“凑整”,例如:
50-13-7
= 50-(13+7)
= 30
3、乘法“凑整”。
利用乘法交换律、结合律、分配律“凑整”,例如: 125×4×8×25×78
=(125×8)×(4×25)×78
= 1000×100×78
= 7800000
4、补充数“凑整”。
末尾是一个或几个0的数,运算起来比较简便。
若数末尾不是0,而是98、51等,我们可以用(100-2)、(50+1)等来代替,使运算变得比较简便、快速。
一般地我们把100叫做98的“大约强数”,2叫做98的“补充数”;50叫做51的“大约弱数”,1叫做51的“补充数”。
把一个数先写成它的大约强(弱)数与补充数的差(和),然后再进行运算,例如:(1)387+99
=387+(100-1)
=387+100-1
=486
(2)1680-89
=1680-(100-11)
=1680-100+11
=1580+11
=1591
(3)69×101
=69×(100+1)
=6900+69
=6969
二、约分法
根据式题结构,采用约分,能使计算比较简便。
例如:
三、基数法
根据数据特征,从诸多数中选择一个做计算基础的数,通过“割”、“补”,采用“以乘代加”的方法速算。
例如:
17+18+16+17+14+19+13+14
(解题时,可以选择17为基准数,以乘代加解答如下。
)
=17×8+1-1-3+2-4-3
=17×8-8
=128
四、公式法
等差数列,是指每两个相邻的数之间差都相等的数列。
等差数列求和,可以用公式:和=(首项+尾项)×项数÷2。
例如:
13+14+15+16+17+18+19+20+21+22
=(13+22)×10÷2
=175
另外,如果加数的项数是奇数个,也可以直接用排列在正中间的数(中间项)乘以项数,去求它们的和。
例如:
3+5+7+9+11+13+15+17+19
=11(中间项)×9(项数)
=99
五、变形法
恒等变形是一种重要的思想和方法,也是一种重要的解题技巧。
它利用我们学过的知识,去进行有目的的数学变形,常常能使题目很快地获得解答。
例如:
1、计算 9999×2222+3333×3334
(此题如果直接乘,数字较大,容易出错.如果将9999变为3333×3,规律就出现了.) 9999×2222+3333×3334
=3333×3×2222+3333×3334
=3333×6666+3333×3334
=3333×(6666+3334)
=3333×10000
=33330000
2、
(将分子部分变形,可以使运算简便。
)
3
六、图形法
用长方形的长表示一个因数,用长方形的宽表示另一个因数,再用长方形的面积图进行分析,形象直观,新颖别致。
例如:
9876×9876-9875×9877
如上图,9876×9876为正方形面积,9875×9877为长方形面积,所以,9876×9876-9875×9877等于正方形面积减去长方形面积,即下边小长方形面积减去右边小长方形面积:
原式=9876×1-9875×1=1
七、分组法
一些看似很难计算的题目,采用“分组计算”的方法,往往可以使它很快地解答出来。
例如:
(观察题中给出的数据特点,应该将小括号去掉,然后适当分组,这样可使运算简便。
)
八、裂项法
裂项法是根据题目的运算符号及数字特点,把题中的某些项拆成几个数的和(差),或几个数的积(商),然后再利用运算定律和性质进行简算。
例如: 1、计算 1×2+2×3+3×4+……+10×11
将这10个等式左、右两边分别相加,可以得到
2、
九、代换法
在计算中常常把几个数的运算式子作为一个整体参与其他运算,这是一种代换的思想,例如:
1、19941994×19941993-19941995×19941992
(若要计算可是很麻烦的一件事不妨将原式分析一下,设A=19941994 B=19941993)
则原式=A×B-(A+1)×(B-1)
=A×B-AB+A-B+1
= A-B+1
=19941994-19941993+1
=2
2、计算(1+0.23+0.34)×(0.23+0.34+0.56)-(1+0.23+0.34+0.56)×(0.23+0.34)
(根据题中给出的数据,设1+0.23+0.34=a,0.23+0.34=b,)
a×(b+0.56)-(a+0.56)×b
=ab+0.56a-ab-0.56b
=0.56a-0.56b
=0.56(a-b)
=0.56×1
=0.56
十、扩缩法
在解决求整数部分的问题时,常用的方法是把它扩大或缩小,求出这个数的范围,最后确定它的整数部分。
例如:
要是先计算出正确的结果,再回答整数部分是多少,那可不是简单的计算。
观察这个式子中的除数,
假设除数中的每个分数都是20分之1,那么除数是
再假设除数中的每个分数都是39分之1,那么除数是
式子的整数部分就是1了。
