梯形的中位线
(11)梯形中位线(yony)

A
A
DEBiblioteka BF CA B
D F
C E
B
C
D
4、如图,在梯形 ABCD中,AD // BC,E、F分别为CD、AB的中点 ,EF分别交BD、AC于点G、H 求证:()FG EH 1 1 (2)GH (BC - AD) 2
A
D
F
G
H
E C
B
回顾:三角形的中位线
连接三角形两边中点的线段叫做 三角形的中位线.
A
D F
B
E
C
回顾:三角形的中位线的性质
三角形的中位线平行于第三边,并且等 于它的一半 用符号语言表示
∵DE是△ABC的中位线
A
∴ DE∥BC,
1 DE= BC. 2
E
D
C
B
取AC的中点F,假设BF与AD交于G′,
你能得出什么结论?
如图,在梯形ABCD中, AD∥BC, AE=BE, DF=CF D A
E B
F
C
连结梯形两腰中点的线段叫做梯形的 中位线 如图: 在梯形ABCD中, AD∥BC, AE=BE, DF=CF , 则EF是梯形ABCD的 中位线
A D
E B
F C
探索:梯形的中位线有什么性质? 已知:梯形ABCD中,AD∥BC, AE=BE,DF=CF 1 求证:EF∥BC,EF= (AD+BC) 2
∴ AB = 13cm
(2)如果AD=4cm , ∵ AH ⊥ BC , ∠ C= 90 ˚ (已知、已作) BC=9cm ,图中有长度 确定的线段吗?请求 ∴ AH ∥ DC (垂直于同一直线的两条直线互相平分) ∵ AD ∥ BC (已知) ∴四边形AHCD 是平行四边形 出这些线段的长.
梯形中位线的性质

梯形中位线的性质
梯形的中位线平行于两底,并且等于两底和的一半l=(a+b)÷2 s=l×h
(1)比例的基本性质如果a:b=c:d,那么ad=bc 如果ad=bc,那么a:b=c:d
(2)合比性质如果a/b=c/d,那么(a±b)/b=(c±d)/d
(3)等比性质如果a/b=c/d=…=m/n(b+d+…+n≠0),那么(a+c+…+m)/(b+d+…+n)=a/b
平行线分后线段成比例定理三条平行线封盖两条直线,税金的对应线段成比例
推论平行于三角形一边的直线截其他两边(或两边的延长线),所得的.对应线段成比例
定理如果一条直线封盖三角形的两边(或两边的延长线)税金的对应线段成比例,那么这条直线平行于三角形的第三边
平行于三角形的一边,并且和其他两边相交的直线,所截得的三角形的三边与原三角形三边对应成比例
看完梯形中位线定理,精明的同学都晓得梯形的中位线平行于两底,并且等同于两底和的一半了吧。
梯形中位线的证明

1
三角形中位线定理
A
三角形的中位线平行于第三边,
并且等于它的一半
E
D
M
F
C N
D F
C
38
A E B
D
M
F
C N
A E B
G A E B
D
M
F
C N
D F
C
39
知识巩固
1 梯形的上底长8,下底长10,则这个梯形的中位线长_9_ 2 梯形的上底长8,中位线长10,则下底长是_1_2 3 已知等腰梯形中位线长6cm,它的腰长5cm,则这个梯形 的周长为_22__cm 4 一个等腰梯形周长80,如果它的中位线与腰长相等,它的 中位线长_20_ 5 梯形的中位线长9cm,一条对角线把中位线分成1:2两部 分,则该梯形的下底长_12__cm
即EF//BC ,EF= ½BC
B
F
C
2
梯形中位线定理
梯形的中位线平行于两底,并且等于两底和的一半
已知:梯形ABCD中,
A
AD//BC,AE=EB,DF=FC
E
求证:EF//BC,EF=½ (BC+AD)
B
证明:连结AF并延长,交BC的延长线于点M
D 1F
23
C
M
∵ DF=FC,∠1=∠2,∠D=∠3,
A E B
D
M
F
C N
G A E B
D F
梯形中位线
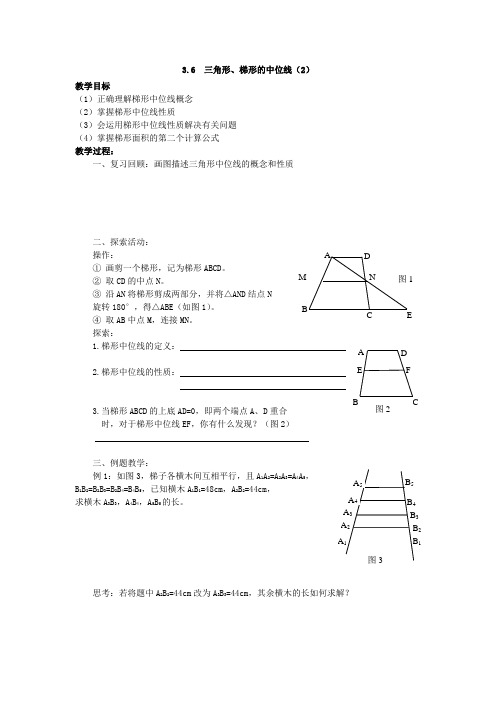
3.6 三角形、梯形的中位线(2)教学目标(1)正确理解梯形中位线概念 (2)掌握梯形中位线性质(3)会运用梯形中位线性质解决有关问题 (4)掌握梯形面积的第二个计算公式 教学过程:一、复习回顾:画图描述三角形中位线的概念和性质二、探索活动:操作: ① 画剪一个梯形,记为梯形ABCD 。
② 取CD 的中点N 。
③ 沿AN 将梯形剪成两部分,并将△AND 结点N 旋转180°,得△ABE (如图1)。
④ 取AB 中点M ,连接MN 。
探索:1.梯形中位线的定义:2.梯形中位线的性质:3.当梯形ABCD 的上底AD=0,即两个端点A 、D 重合时,对于梯形中位线EF ,你有什么发现?(图2)三、例题教学:例1:如图3,梯子各横木间互相平行,且A 1A 2=A 2A 3=A 4A 5,B 1B 2=B 2B 3=B 2B 4=B 4B 5,已知横木A 1B 1=48cm ,A 2B 2=44cm ,求横木A 3B 3,A 4B 4,A 5B 5的长。
思考:若将题中A 2B 2=44cm 改为A 3B 3=44cm ,其余横木的长如何求解?例2:如图4,梯形ABCD 中,AD∥BC,点E 是AB 中点, 连结EC 、ED 、CE ⊥DE ,CD 、AD 与BC 三条线段之间有什么 样的数量关系?请说明理由。
四、练一练(1)梯形的两底长分别为4cm 、6cm ,则中位线的长 。
(2)梯形的一底长6cm,中位线长10cm,则另一底的长 。
(3)若梯形中位线长26cm ,上、下底长度之比为1∶3,,则上底长 cm ,下底长 cm 。
(4)若梯形中位线长14cm ,高5cm ,梯形面积为 cm 2。
由(4)得:S 梯形=21(两底之和)×高 = 五、练习:⑴已知梯形中位线长是5cm ,高是4cm ,则梯形的面积是。
⑵等腰梯形的腰长是6cm ,中位线是5cm ,则梯形的周长是 。
⑶梯形上底与中位线之比是2:5,则梯形下底与中位之比是。
梯形中位线

பைடு நூலகம்
A
E·
D
B
C
探究发现: 如图,△ABC中,边BC=a, 若 D1、E1分别是 1 AB、AC的中点,则D1E1= 2 a ; 若D2、E2分别是D1B、E1C的中点, A 则D 2E 2= 1 ( 1 a a ) 3 a ;
2 2 4
D1 若D3、E3分别是D2B、E2C的中点, 则 D 3 E 3 = 1 ( 3 a a ) 7 a ; D2 D 3 2 4 8
B 若Dn、En分别是Dn-1B、En-1C的中点, 则D nE n= .
E1 E2 E C3
课堂小结
梯形的中位线定义,定理及证明
课后作业
陕西电线公司 / 陕西电线公司 xrg67yua
末考试差不多,还不留作业……”慕容凌娢趴在桌子上自顾自的碎碎念。“把背过的古文给默上了?”“不是,但是我把在学校里被过的古诗文 赏析给挪用了一大堆。其实八股文跟我们老师要求的五段式作文也没多大差别……只要写改卷人喜欢的内容,段数不错,语言好,字好,也就能 得分了。”“那真的要好好感谢你们的老师了,别看只让默写考试范围内的古诗文和赏析,但到了这个年代,比十年寒窗都有用。”茉莉还保留 着爱晒太阳的习惯,懒洋洋的坐在窗台的,看着楼下的那匹不明真相的吃草黑马。真不知道慕容凌娢为什么要叫它‘离漠’,难道是单纯的懒得 想名字吗?“你……你怎么对我们老师这么了解!”慕容凌娢猛地抬头。“难道你也会算卦?”“呵。”茉莉轻只是笑一声,“是谁当年整天一 回家就碎碎念自己语文老师从不讲课文只默写古诗词,大多数时间只检查作业却不讲题,背熟的好词好句不让用,不是五段式作文就零分,作文 课上列表格,语文课上背赏析……”“别说啦……好久之前的事了……”慕容凌娢尴尬癌都快犯了,没想到那时候的吐槽茉莉居然还记得。“你 说我们语文老师是不是从古代穿越过去的?”慕容凌娢话风一转,“不然她的教学方法在21世纪把我们班从第三带到了倒数第一再也没翻身,结 果到了这个年代,好用到爆。”“说不定。”“要是我在这里碰到她,一定好好开导她……”慕容凌娢想起了一些不好的回忆……那些年,早读 和其他时间读书背书时都是站着的。英语老师的理由是坐着不利于发音,声音小。语文老师的理由更扯,坐着读书容易缺氧……善良的化学老师 是新来的,就像童话故事里尊老爱幼的小白兔,对经验丰富的老教师言听计从,自然不敢澄清氧气比空气重的事实。结果有一次慕容凌娢站起来 的慢了点,被语文老师敲了一教鞭。校服质量好,不算疼,但是莫名的尴尬。教鞭质量也太好了吧!被它敲过的一届届学生都咀咒它赶快断掉, 可它实在太给国产货长脸了……不管怎么说,她和它送走了无数抗击打能力爆表的栋梁之才……她长的吓人,它长的吓人。而坐在第二排的慕容 凌娢只被敲过一次,就连考过年级第一的秦萌曦都因走神被敲过两次……想到这儿,慕容凌娢觉得也没什么尴尬的了……之后的殿试在皇宫中举 行,慕容凌娢属于二甲,所以是第二波被召见的。按照自古的套路,皇帝喜欢出一些实践性题。慕容凌娢觉得根据她在历史课上背过的格式,应 该没有问题。殿试结束后,下午成绩就公布出来了。慕容凌娢好不容易挤到了布告的近处,快速浏览着许多陌生的名字,认真的寻找自己的姓名。 由于是倒着往前数的,她看了一会儿才找到自己的名字。正着数了一下,第五名,安于现状的慕容凌娢十分满意。临走之前,她又
梯形中位线(中学课件201909)

则梯形的周长是
cm.
(4)若梯形的中位线长6cm,高为5cm,
你会求梯形的面积吗?
(5)一个等腰梯形的周长为80cm,如果
中位线长与腰长相等,高为12cm,求梯形
的面积.
例2.如图,在直角梯形ABCD中,点O为CD 的中点. (1)度量顶点A、B到点O的距离,你有什么 发现?
(2)你的结论正确吗?说明理由.
A
D
E · ·O
B
C
练一练: (二) 如图,梯形ABCD中,AD∥BC, E是腰AB的中 点,且DE⊥CE. 你能说明 DC=AD+CB吗? 试试看.
A
D
E·
B
C
探究发现:
如图,△ABC中,边BC=a, 若 D1、E1分别是
AB、若ADC2的、中E2点分,别则是DD11EB1、= E11 2C的a中点;,
(1)EF//AD//BC
B
(2)EF= 1 (AD+BC) 2
D F C
例1. 如图所示的梯形梯子,AA′∥EE′,
AB=BC=CD=DE,A′B′= B′C′=
C′D′= D′E′, AA′=40cm, EE′
=80cm.
求 : BB′、 CC ′、 DD′.
A
A′
B
B′
C
C′
D
D′
E
E′
试一试:
做一做: 1.画一个梯形ABCD,使AD∥BC; 2.分别取AB、CD的中点E、F,连接EF; 3.沿AF将梯形分成两部分,并画出将△AFD 绕点F旋转1800后的图形.
A
D
E
F
B
C
M
梯形中位线定理
梯形的中位线平行于两 A
上海初中数学知识点之梯形中位线定理
When your heart is tired, take a rest.勤学乐施积极进取(页眉可删)上海初中数学知识点之梯形中位线定理梯形中位线定理—上海初中数学知识点图形知识大放送:梯形的中位线平行于两底,并且等于两底和的一半。
那么下面为大家带来的是上海初中数学知识点大全之梯形中位线定理,希望大家做好笔记了。
梯形中位线定理L=(a+b)÷2 S=L×h1)比例的基本性质:如果a:b=c:d,那么ad=bc如果 ad=bc ,那么a:b=c:d2)合比性质:如果a/b=c/d,那么(a±b)/b=(c±d)/d3)等比性质:如果a/b=c/d=…=m/n(b+d+…+n≠0),那么(a+c+…+m)/(b+d+…+n)=a/b初中数学知识点大全之梯形中位线定理,相信大家肯定都已经融会贯通了吧,接下来还有更多的精彩知识尽在哦。
初中数学知识点总结:平面直角坐标系下面是对平面直角坐标系的内容学习,希望同学们很好的掌握下面的内容。
平面直角坐标系平面直角坐标系:在平面内画两条互相垂直、原点重合的数轴,组成平面直角坐标系。
水平的数轴称为x轴或横轴,竖直的数轴称为y轴或纵轴,两坐标轴的交点为平面直角坐标系的原点。
平面直角坐标系的要素:①在同一平面②两条数轴③互相垂直④原点重合三个规定:①正方向的规定横轴取向右为正方向,纵轴取向上为正方向②单位长度的规定;一般情况,横轴、纵轴单位长度相同;实际有时也可不同,但同一数轴上必须相同。
③象限的规定:右上为第一象限、左上为第二象限、左下为第三象限、右下为第四象限。
相信上面对平面直角坐标系知识的讲解学习,同学们已经能很好的掌握了吧,希望同学们都能考试成功。
初中数学知识点:平面直角坐标系的构成对于平面直角坐标系的构成内容,下面我们一起来学习哦。
平面直角坐标系的构成在同一个平面上互相垂直且有公共原点的两条数轴构成平面直角坐标系,简称为直角坐标系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
梯形的中位线
一、教学目的
使学生掌握梯形中位线定理,并能熟练地用它进行有关的论证和计算.
二、教学重点、难点
重点:梯形中位线性质及其证明.
难点:任意多边形面积的计算.
三、教学过程
复习提问
1.什么叫做三角形的中位线?它有什么性质?
2.等边三角形各边中点的连线形成什么图形?
引入新课
前边研究了三角形的中位线及其性质,同样,梯形也有中位线.现在就来研究梯形的
中位线及性质.
新课
1.梯形中位线
结合图形介绍定义:连结梯形两腰中点的线段叫做梯形的中位线.
要强调梯形中位线是连结两腰中点的线段,而不是连结两底中点的线段.
2.梯形中位线定理 梯形中位线平行于两底,并且等于两底和的一半.
该定理的证明关键是如何添加辅助线,把梯形中位线转化成三角形的中位线.可引导
学生进行如下分析:
设法把梯形中位线转化为三角形中位线.
如图4-67,欲使MN成为某一个三角形中位线,则梯形的一腰一定是三角形的一边,
而三角形的另一边一定过梯形另一腰的中点.梯形的一个底应在三角形第三边上,若连结
AN并延长交BC的延长线于E(梯形的这种辅助线也经常用到),就能得到这样的△ABE.这
时只要证明AN=EN,AD=EC问题就解决了.
E
N
M
A
D
B
C
3.梯形、多边形面积的计算
小学学过的梯形面积S=(a+b)h÷2 ,而l=(a+b)÷2,推出S=lh(l为梯形中位线长,
h为梯形高).
多边形面积的求法,任意多边形面积可以通过辅助线,把它分割成三角形、平行四边
形、梯形,就可以利用这些图形的面积公式计算任意多边形面积.
例2 有一块四边形的地ABCD,(图4-68),测得AB=26m,BC=10m,CD=5m,顶点B、C到
AD的距离分别为10m、4m,求这块地的面积.
Q
N
A
B
C
D
分析:解题的关键是通过辅助线把多边形分割成面积可以计算的常见图形(三角形、平
行四边形、梯形等),至于解答程序可不作限制.可以先列出所求面积公式,再求公式中
的未知项,最后代入公式求出结果;也可以先列出已知项,求出有关的未知项,再列出公
式,将数值代入求出结果.
小结
本节课主要讲了梯形中位线性质定理和证明,推出了梯形面积的又一计算公式.介
绍了多边形面积计算原则(分割成四边形与三角形),要求牢牢掌握。
对三角形、梯形中位线知识进行归纳:
1.三角形中位线定义、性质与判定.
2.梯形中位线的定义、性质与判定.
3.多边形面积的计算原则(分割).
作业:
四、教学注意问题
梯形中位线定理是梯形的一个重要性质,有两个结论,一是位置关系,一是数量关系,应
帮助学生分清该选用哪一个结论!
