沪教版八年级数学-三角形梯形的中位线-教师版
八年级春季班-12-梯形及中位线-教师版
初二数学春季班(教师版)梯形及中位线内容分析本章节主要讲述了两部分内容,梯形和中位线,从直角梯形和等腰梯形的性质出发,求解相关的边与角的关系,在求解的过程中,部分题目需要添加辅助线.中位线主要包括两个方面,三角形和梯形,在解题的过程中,要做到灵活应用.知识结构模块一:梯形及等腰梯形知识精讲一、梯形及梯形的有关概念(1)梯形:一组对边平行而另一组对边不平行的四边形叫做梯形.底:平行的两边叫做底,其中较长的是下底,较短的叫上底.腰:不平行的两边叫做腰.高:梯形两底之间的距离叫做高.(2)特殊梯形直角梯形:一腰垂直于底的梯形叫做直角梯形.特殊梯形等腰梯形:两腰相等的梯形叫做等腰梯形.思考讨论:若上面两个条件同时成立是否是梯形?交流:如果同时具备直角梯形和等腰梯形的特征,那么该图形是矩形. 【等腰梯形性质】等腰梯形性质定理1等腰梯形在同一底上的两个内角相等. 等腰梯形性质定理2等腰梯形的两条对角线相等. 另外:等腰梯形是轴对称图形; 【等腰梯形判定】等腰梯形判定定理1在同一底边上的两个内角相等的梯形是等腰梯形. 等腰梯形判定定理2对角线相等的梯形是等腰梯形.【例1】 (1)在周长为30cm 的梯形ABCD 中,上底CD =5cm ,DE ∥BC 交AB 于点E ,则△ADE 的周长为___________cm ;(2)如图,梯形ABCD 中,AB ∥CD ,∠ACB =90°,且AC 平分∠BAD ,∠D =120°,CD =3cm ,则梯形的周长是_________cm . 【难度】★【答案】(1)20 ; (2)15. 【解析】(1)∵DE //BC ,CD //EB ,∴四边形DCBE 是平行四边形,∴EB =CD =5,BC =DE ,∴ C △ADE = AD +DE +AE = AD +BC +AE = AD +BC +AB -EB = AD +BC +AB -CD =AD +BC +AB +CD -2CD = 30-10 = 20; (2)∵∠D =120°,∴∠DAB =60°, ∴∠DAC =∠CAB =30°,∴∠B =60°∴BC =AD =CD =3,AB =2BC =6∴C 梯形ABCD = AD +CD +CB +AB = 3+3+3+6 = 15. 【总结】本题考查利用等腰梯形的性质求梯形的周长.例题解析A BC DEDCB AEDCBA【例2】 直角梯形一腰长为12cm ,这条腰和一个底边所成的角为60°,则另一腰长为 ___________cm ,若上底为3cm ,则梯形的面积为__________. 【难度】★【答案】2cm .【解析】设直角梯形ABCD 中,AB ⊥BC ,∠C =60°,CD =12,作DE ⊥BC 于点E ,得矩形ABED ,则AD =BE =3,∵∠C =60°,∴∠CDE =30°,∴CE =12CD =6,DE =AB=,∴S =12(AD +BC )×AB=2cm . 【总结】本题考查梯形性质与面积公式的综合运用.【例3】 (1)等腰梯形的两底之差为12cm ,高为6cm ,则其锐角为________;(2)等腰梯形的对角线为17,底边分别为10和20,则梯形的面积是_________. 【难度】★【答案】(1)45°;(2)120.【解析】(1)设等腰梯形ABCD ,AD =BC ,AB //CD ,AB <CD作AE ⊥CD ,BF ⊥CD ,在矩形ABFE 中,AB =EF∵CD -AB =12,∴CD -EF =DE +CF =12.∵等腰梯形ABCD ,∴DE =CF =6. 又∵AE =BF =6,∴等腰直角△ADE 中,∠D =45°; (2)如图所示,过点A 作AE ⊥BC 于点E , 由题知,AD =10,BC =20,AC =17. 由等腰梯形性质结合全等性质,易得52BC ADBE -==, ∴CE =15,∴8AE ==,∴11()(1020)812022S AD BC AE =⨯+⨯=⨯+⨯=.【总结】本题考查梯形常见辅助线的添加及应用.【例4】 等腰梯形的高是腰长的一半,则其中的一个底角是( )A .30°B .45°C .60°D .90°【难度】★★ 【答案】A【解析】设等腰梯形ABCD 中,AB //CD ,作AE ⊥CD∵12AE AD ,∴∠D =30°,故选A .【总结】本题考查梯形性质与直角三角形性质的综合运用.【例5】 如右图,在等腰梯形ABCD 中,AD ∥BC ,AC ,BD 相交于点O ,有下列四个结论:(1)AC =BD ;(2)梯形ABCD 是轴对称图形;(3)∠ADB =∠DAC ; (4)△AOD ≌△ABO .其中正确的有( ) A .1个 B .2个C .3个D .4个【难度】★★ 【答案】C【解析】(1)正确;(2)正确;(3)正确;(4)错误,故正确的有三个,选C . 【总结】本题考查等腰梯形性质的运用.【例6】 下列图形中,两条对角线一定不相等的是() A .正方形 B .矩形 C .等腰梯形D .直角梯形【难度】★★ 【答案】D【解析】正方形,矩形,等腰梯形的对角线都相等. 【总结】本题考查几种特殊四边形对角线性质.【例7】 下列四边形既是轴对称图形又是中心对称图形的是()A .梯形B .等腰梯形C .平行四边形D .矩形【难度】★★ 【答案】D【解析】B 中等腰梯形是轴对称图形;C 中平行四边形是中心对称图形; D 中矩形既是轴对称图形又是中心对称.【总结】本题考查几何图形的对称性,要熟知每一个图形的性质.ABCDO【例8】 如右图,已知梯形ABCD 中,BC 是下底,∠ABC =60°,BD 平分∠ABC ,且BD ⊥CD ,若梯形周长是30cm ,求此梯形的面积. 【难度】★★【答案】2cm .【解析】∵BD 平分∠ABC , ∴∠ABD =∠DBC =12∠ABC =30°. ∵AD //BC ,∴∠ADB =∠DBC =30°,∴AB =AD∵BD ⊥CD ,∴∠DCB =60°,∴∠ABC =∠DCB , ∴AB =CD . 设AB = CD = AD = x ,Rt △BCD 中,∵∠DBC =30°,∴BC = 2CD = 2x , ∴30 = x +x +x +2x ,解得:x =6. 作AE ⊥BC ,Rt △ABE 中,∵∠BAE =30°, ∴BE =3,AE= ∴S =12(AD +BC )AE=2cm . 【总结】本题考查梯形面积公式及等腰梯形性质的综合运用.【例9】 如图,直角梯形ABCD 中,∠A =90°,AD ∥BC ,AD =5,∠D =45°,CD 的垂直平分线交AD 于点E ,交BA 的延长线于点F ,求BF 的长. 【难度】★★ 【答案】5 【解析】联结CE∵EG 垂直平分CD ,∴EC =ED ,∠ECD =∠D =45°,∴∠CED =90°, ∵∠A =90°,AD ∥BC , ∴四边形BAEC 是矩形, ∴BC = AE .设BC =x =AE ,∴ED =EC =AB =5-x∵∠FEA =∠GED =45°,∴△AEF 是等腰直角三角形, ∴AF =AE =x∴BF =BA +AF =5-x +x =5.【总结】本题考查中垂线的性质,等腰直角三角形,直角梯形的性质的综合运用,注意用整体思想求出线段BF 的长.ABCDOEABCEF G【例10】 如图,在梯形ABCD 中,AD ∥BC ,AB =AD =DC ,∠B =60°, (1) 求证:AB ⊥AC ;(2) 若DC =6,求梯形ABCD 的面积. 【难度】★★【答案】(1)见解析;(2).【解析】(1)∵AB =CD ,∴∠B =∠DCB =60°,∠BAD =∠D =120°∵AD =DC ,∴∠DAC =∠DCA =30° ∴∠BAC =∠BAD -∠DAC =120°- 30°=90° ∴BA ⊥AC ;(2)∵AB =AD =DC ,DC =6, ∴CD =AD =AB =6 在直角三角形ABC 中,∵∠ACB =30°, ∴BC =2AB =12 作AE ⊥BC ,则AE=∴S 梯ABCD=1()2AD BC AE +=【总结】本题主要考查含30°的直角三角形性质与梯形面积公式的综合运用.【例11】 如图,在梯形ABCD 中,AD ∥BC ,CA 平分∠BCD ,DE ∥AC ,交BC 的延长线于点E ,∠B =2∠E . 求证:AB =DC . 【难度】★★ 【答案】见解析.【解析】∵AC 平分∠BCD∴∠BCA =∠ACD =12∠DCB∵DE //AC ,∴∠E =∠ACB =12∠DCB ∵∠B =2∠E ,∴∠B =∠DCB ∵梯形ABCD 中,AD ∥BC , ∴AB =CD【总结】本题考查等腰梯形性质与角平分线的综合运用,注意对基本模型的总结运用.ABDCEABDCE【例12】 如图,在等腰三角形ABC 中,点D 、E 分别是两腰AC 、BC 上的点,联结BE 、CD相交于点O ,∠1=∠2. 求证:梯形BDEC 是等腰梯形. 【难度】★★ 【答案】见解析.【解析】∵AB AC =, ∴∠DBC =∠ECB在△BCD 与△ECB 中,∠1=∠2,BC =BC ∴△BCD ≌△ECB ,∴BD =CE∵AB =AC , ∴AD =AE ,∴∠ADE =∠AED =1(180)2A ︒-∠=∠ABC =∠ACB∴DE //BC , 又∵BD 与CE 不平行∴四边形BDEC 是梯形,且BD =CE ,∴梯形BDEC 是等腰梯形 【总结】本题考查等腰梯形判定定理的运用,注意证明梯形的方法的总结.【例13】 如图,梯形OABC 中,O 为直角坐标系的原点,A 、B 、C 的坐标分别为(14,0)、(14,3)、(4,3).点P 、Q 同时从原点出发,分别作匀速运动,点P 沿OA 以每秒1个单位向终点A 运动,点Q 沿OC 、CB 以每秒2个单位向终点B 运动.当这两点中有一点到达自己的终点时,另一点也停止运动.(1)设从出发起运动了x 秒,当x 等于多少时,四边形OPQC 为平行四边形? (2)四边形OPQC 能否成为等腰梯形?说明理由. 【难度】★★【答案】(1)x =5; (2)不能.【解析】(1)由题可知:OC =5,BC =10,OA =14.∵BC //OA∴当Q 点在BC 上,且OP =CQ 时,四边形OPQC 是平行四边形 即2x -5= x ,解得:x = 5;(2)作点C 作CE ⊥OA 于点E ,过点Q 作QF ⊥OP 与点F ∵AO //BC ,∴CE =QF当OE =PF =4时,△OCE ≌△PQF ,此时四边形OPQC 为等腰梯形, 即OP =OE +CQ +PF ,∴x =4+(2x -5)+4,解得:x =-3(舍), ∴四边形OPQC 不能成为等腰梯形.【总结】本题考查梯形的性质,平行四边形的判定与性质以及等腰梯形的判定与性质的综合运用,注意掌握辅助线的做法,以及数形结合思想与方程思想的综合运用.ABDCEO 12【例14】 如图,等腰梯形花圃ABCD 的底边AD 靠墙,另三边用长为40米的铁栏杆围成,设该花圃的腰AB 的长为x 米.(1)请求出底边BC 的长(用含x 的代数式表示);(2)若∠BAD =60°,该花圃的面积为S 米²,求S 与x 之间的函数关系式,指出自变量x 的取值范围,并求当S=时x 的值. 【难度】★★★【答案】(1)BC =40-2x ;(2)2S =+(020x <<),x =4.【解析】(1)等腰梯形ABCD 中,AB =CD =x ,∴BC =40-x -x =40-2x ;(2)作BE ⊥AD ,CF ⊥AD在Rt △ABE 中,∵∠ABE =30°, ∴AE =12x .同理FD =AE =12x , ∴BE =CF.∴EF =BC =40-2x , ∴AD =40-x∴()1(4024022BC AD BE S x x +==-+-=(020x <<),当S =x =4或683x =(舍)∴当S=时x 的值为4.【总结】本题考查等腰梯形性质与函数解析式的结合,注意面积公式中各个量的含义.【例15】 已知,一次函数144y x =-+的图像与x 轴,y 轴,分别交于A 、B 两点,梯形AOBC(O 是原点)的边AC =5,(1)求点C 的坐标;(2)如果一个一次函数y kx b =+(k 、b 为常数,且k ≠0)的图像经过A 、C 两点,求这个一次函数的解析式. 【难度】★★★【答案】(1)C (13,4)或(19,4)或(16,5); (2)46433y x =-+或46433y x =-.【解析】由题可知:A (16,0),B (0,4).当OB ∥AC 时,点C 坐标为(16,5),当BC ∥AO 时,点C 坐标为(13,4)或(19,4);(2)∵一次函数的图像经过A 、C 两点,∴C 点坐标不能为(16,5),当A (16,0),C (13,4)时,利用待定系数法可得解析式为:46433y x =-+;当A (16,0),C (19,4)时,利用待定系数法可得解析式为:46433y x =-. 【总结】本题考查直角梯形性质及一次函数的综合运用,注意分类讨论,综合性较强.EA B DF【例16】 如图,直角梯形ABCD 中,AB //CD ,∠A =90°,AB =6,AD =4,DC =3,动点P 从点A 出发,沿A →D →C →B 方向移动,动点Q 从点A 出发,在AB 边上移动.设点P 移动的路程为x ,线段AQ 的长度为y ,线段PQ 平分梯形ABCD 的周长. (1)求y 与x 的函数关系式,并求出这个函数的定义域; (2)当P 不在BC 边上时,线段PQ 能否平分梯形ABCD 的面积?若能,求出此时x 的值;若不能,请说明理由. 【难度】★★★【答案】(1)9(39)y x x =-+≤≤; (2)x =3时,PQ 平分梯形面积.【解析】(1)过点C 作CE ⊥AB 于点E ,则CD =AE =3,CE =4, 可得:BC =5,所以梯形ABCD 的周长是18.∵PQ 平分梯形ABCD 的周长, ∴x +y =9, ∵06y ≤≤, ∴39x ≤≤, ∴9(39)y x x =-+≤≤;(2)由题可知,梯形ABCD 的面积是18. 因为P 不在BC 上,所以37x ≤≤. 当3≤x <4时,P 在AD 上,此时12APQ S xy ∆=, ∵线段PQ 能平分梯形ABCD 的面积,则有192xy =可得方程组918x y xy +=⎧⎨=⎩,解得:36x y =⎧⎨=⎩或63x y =⎧⎨=⎩(舍);可得方程组92217x y x y +=⎧⎨+=⎩,方程组无解,∴当x =3时,线段PQ 能平分梯形ABCD 的面积.【总结】本题利用梯形的性质,三角形的面积公式,建立方程和方程组求解,注意针对不同情况讨论,利用数形结合的思想进行计算.QP DCBA解决梯形问题常用的方法① 作高法:使两腰在两个直角三角形中;②移腰法:使两腰在同一个三角形中,梯形两个下底角是互余的,那么一般会用到这种添辅助线的方式,构造直角三角形;③延腰法:构造具有公共角的两个等腰三角形;④等积变形法:联结梯形上底一端点和另一腰中点,并延长与下底延长线交于一点,构成三角形;⑤移对角线法:平移对角线,可以构造特殊的图形,如平行四边形,如果是对角线互相垂直 的等腰梯形,那么在平移的过程中,还可构造等腰直角三角形,结合三线合一,求梯形的高 等.【例17】 如图,已知在梯形ABCD 中,//AD BC ,13AB AD CD ===,AE BC ⊥,垂足为E ,12AE =,则BC 边的长等于( )A .20B .21C .22D .23 【难度】★★ 【答案】D【解析】∵AE BC ⊥,13AB =,12AE =, ∴BE = 5.∵梯形ABCD 中,//AD BC ,AB CD =,AE BC ⊥, ∴2132523BC AD BE =+=+⨯=, 故选D . 【总结】本题主要考查等腰梯形性质的综合运用.模块二:辅助线知识精讲例题解析 A BCDE【例18】 已知梯形ABCD 中,//AD BC ,70B ∠=,40C ∠=,2AD =,10BC =.求DC 的长. 【难度】★★ 【答案】CD = 8.【解析】作DE //AB ,则四边形ABED 是平行四边形.∴AD =BE =2,∠DEC =∠B =70°.在△DEC 中,∠C =40°,∴∠EDC =180°-40°-70°=70°,∴CD =CE =BC -BE =10-2=8. 【总结】本题考查辅助线——做一边的平行线,构造平行四边形.【例19】 如图,梯形ABCD 中,//AB CD ,90A B ∠+∠=,AB b =,CD a =,E 、F 分别为AB 、CD 的中点,则EF 的长等于( )A .2b a +B .3b a +C .2b a -D .3b a -【难度】★★ 【答案】C【解析】分别过点F 做FG //AD ,FH //BC ,分别交BA 于点G ,H可得平行四边形DFGA 与平行四边形FCBH∴AG =FD =CF =BH =1122CD a =,∴GH =b -a∵∠A +∠B =90°, ∴可得直角△FGH ,E 是GH 中点∴EF =11()22GH b a =-, 故选C .【总结】本题考查直角三角形中线性质与梯形辅助线的添加.【例20】 已知:如图,在梯形ABCD 中,AD ∥BC ,AB =AC ,∠BAC =90°,BD =BC ,BD 交AC 于O .求证:CO =CD . 【难度】★★ 【答案】见解析.【解析】作AF ⊥BC ,DE ⊥BC ,∵AD //BC ,∴AF =DE .在Rt △ABC 中,AB =AC , ∴AF =12BC .∵BC =BD , ∴DE =12BD .∴在Rt △BDE 中,∠DBC =30°,∴∠BCD =∠BDC =75°∴∠DOC =∠DBC +∠ACB =75°,∴∠CDO =∠COD =75°, ∴CD =CO .【总结】本题考查梯形的常用辅助线—做梯形的高,把梯形问题转化成三角形,矩形的问题,然后根据已知条件和三角形性质解题.ABCDEG ABCDFHOABCDEF【例21】 如图所示,在等腰梯形ABCD 中,//AD BC ,对角线AC BD ⊥,若两底长分别为a b 、,试列出这个梯形的面积S 用a b 、表示的等式.【难度】★★【答案】21()4a b +.【解析】过点D 作DE //AC 交BC 延长线于点E , 则可得平行四边形ADEC .∵等腰梯形ABCD 中,AC =BD , ∴△BDE 是等腰三角形, ∴BE =BC +CE =BC +AD =a +b .过D 作DF ⊥BC 于点F ,等腰直角△DBE 中,DF =11()22BE a b =+,∴BDE ABCD S S ∆=梯形=211()24BE DF a b ⋅=+.【总结】本题考查梯形辅助线的作法,通过平移对角线将等腰梯形转化为等腰三角形的问题.【例22】 在等腰梯形ABCD 中,AD ∥BC ,AB =DC ,对角线AC 与BD 相交于点O ,∠BOC =60°,AC =10cm ,求梯形的高DE 的长. 【难度】★★【答案】.【解析】等腰梯形ABCD 中,∵OB =OC ,∠BOC =60°,可得等边△OCB , ∴∠DBC =∠ACB =60°∵AC =BD =10,∴在直角△BDE 中,BE =152BD =,∴DE =.【总结】本题考查梯形的相关计算,注意方法的运用.ABCDEO EF【例23】 如图,在梯形ABCD 中,()0//9012AD BC BC AD D BC CD >∠===,,,045ABE ∠=,若AE =10,则CE =__________.【难度】★★★ 【答案】4或6.【解析】过点B 作DA 的垂线交DA 延长线于M ,M 为垂足,延长DM 到G ,使得MG =CE ,联结BG , 可得四边形BCDM 是正方形.∴BC =BM ,∠C =∠BMG =90°,EC =GM , ∴△BEC ≌△BMG , ∴∠MBG =∠CBE ∵∠ABE =45°,∴∠CBE +∠ABM =45°,∴∠GBM +∠ABM =45°, ∴∠ABE =∠ABG =45°,∴△ABE ≌△ABG ,AG =AE =10设CE =x ,则AM =10-x ,∴AD =12-(10-x )=2+x ,DE =12-x . 在Rt △ADE 中,由AE 2=AD 2+DE 2,解得:x =4或x =6. 故CE 的长为4或6.【总结】本题考查了直角三角形中勾股定理的运用,考查了全等三角形的判定和对应边相等的性质,注意辅助线的添加方法,将问题转化为解直角三角形的问题.三角形中位线的定义和性质:1. 定义三角形的中位线:联结三角形两边中点的线段,(强调它与三角形的中线的区别);2. 三角形中位线定理:三角形的中位线平行于第三边,并且等于它的一半. 3. 梯形中位线定理:梯形的中位线平行于底边,并且等于两底和的一半.【要点点拨】经过三角形的一边中点作另一边的平行线,也可以证明得到的平行线段为中位线.同样地,从梯形的一腰中点作底的平行线,可以证明得到的平行线段为中位线.如果把三角形看成是一个上底长度为零的特殊的梯形的话,那么三角形中位线定理就成为梯形中位线定理的特例了.模块三:中位线知识精讲A BCD E MG【例24】 (1)顺次联结四边形各边中点所组成的四边形是;(2)顺次联结平行四边形各边中点所组成的四边形是; (3)顺次联结矩形各边中点所得到的四边形是; (4)顺次联结正方形各边中点所得到的四边形是; (5)顺次联结菱形各边中点所得到的四边形是;(6)顺次联结对角线互相垂直的四边形各边中点所得到的四边形是; (7)顺次联结等腰梯形各边中点所得到的四边形是;(8)顺次联结对角线相等的四边形各边中点所得到的四边形是;(9)顺次联结对角线相等且互相垂直的四边形各边中点所得到的四边形是. 【难度】★【答案】(1)平行四边形;(2)平行四边形;(3)菱形;(4)正方形;(5)矩形; (6)矩形;(7)菱形;(8)菱形;(9)正方形. 【解析】利用三角形中位线性质可证明.【总结】本题考查中位线性质和四边形判定方法,注意对相关规律的总结.【例25】 (1)点D 、E 、F 分别是ABC 三边的中点,DEF 的周长为10cm ,则ABC 的周长为;(2)ABC 三条中位线的长为3cm 、4cm 、5cm ,则ABC 的面积为. 【难度】★【答案】(1)20cm ;(2)242cm .【解析】(1)2()20ABC C AB BC AC DE EF DF ∆=++=++=cm .(2)∵三条中位线的长为3cm 、4cm 、5cm , 且2223+45=, ∴可知△ABC 是直角三角形,∴168242S =⨯⨯=2cm .【总结】本题考查三角形中位线的性质的综合运用.例题解析【例26】 如图,ABC 中,B ∠,C ∠的平分线BE ,CF 相交于点O ,AG BE ⊥于点G ,AH CF ⊥于点H .(1)求证://GH BC ;(2)若9AB =厘米,14AC =厘米,18BC =厘米, 求GH 的长. 【难度】★★【答案】(1)见解析;(2)2.5cm .【解析】(1)分别延长AH ,AG 交BC 于M ,N 两点∵CH 是角平分线,CH ⊥AM∴可得△ACM 是等腰三角形,同理△ABN 也是等腰三角形. ∴H 、G 分别是AM 、AN 边上的中点, ∴GH //BC ;(2)由(1)得CA =CM =14cm ,BA =BN =9cm∴MN =CM +BN -BC =14+9-18=5, ∴GH =1522MN =, 即GH =2.5cm .【总结】本题考查了等腰三角形的性质,与三角形的中位线定理的综合运用,注意通过添加辅助线得到等腰三角形是本题的关键.【例27】 如图,在ABC 中,点D 是边BC 的中点,点E 在ABC 内,AE 平分BAC ∠,CE AE ⊥,点F 在边AB 上,EF //BC .(1) 求证:四边形BDEF 是平行四边形;(2) 线段BF 、AB 、AC 之间有怎么样的数量关系?并证明. 【难度】★★【答案】(1)见解析;(2)2BF +AC =AB . 【解析】(1)延长CE 交AB 于点G∵AE ⊥CG ,AE 平分∠BAC∴△AEG 与△ACE 中,∠GAE =∠CAE ,AE =AE ,∠AEG =∠AEC∴△AGE ≌△ACE ∴AG =AC ,即△AGC 是等腰三角形,∴E 是GC 的中点. ∵D 是CB 的中点,∴DE //BA , ∵EF //BD , ∴四边形BDEF 是平行四边形; (2)∵ED 是△BCG 的中位线, ∴ED =12BG .又∵平行四边形BDEF ,∴ED =BF ,∴BF =12BG ,即BG =2BF .∵AG =AC , ∴2BF +AC =BG +AG =BA .【总结】本题考查了平行四边形的判定和性质,全等三角形的判定与性质、中位线的性质等知识,解题的关键是作辅助线,构造全等三角形,用中位线的性质解题.HGOF ECBA MNABC D EFG【例28】 如图所示,在梯形ABCD 中,//AD BC ,对角线AC BD ⊥交于点O ,MN 是梯形ABCD 的中位线,30DBC ∠=,求证:AC =MN . 【难度】★★ 【答案】见解析.【解析】∵AD //BC , ∴∠ADO =∠DBC =30°.∴在Rt △AOD 和Rt △BOC 中,OA =12AD ,OC =12BC ,∴AC =OA +OC =1()2AD BC +.∵MN 是梯形ABCD 的中位线,∴MN =1()2AD BC +, ∴AC =MN .【总结】本题考查梯形中位线的性质和直角三角形中性质的综合运用.【例29】 如图所示,在正方形ABCD 中,对角线AC 、BD 交于点O ,AE 平分BAC ∠,交BC 于点E ,交OB 于点F ,求证:CE =2OF . 【难度】★★ 【答案】见解析.【解析】取AE 的中点G ,联结OG∵正方形ABCD 中,对角线AC 、BD 交于点O , ∴OG //CE ,CE =2OG∴∠AOG =∠ACB =45°,∠GOB =∠OBC =45°. ∵AE 平分∠BAC , ∴∠CAE =22.5°,∴∠EGO =∠EAC +∠AOG =22.5°+45°=67.5°, ∴△OFG 中,∠OFG =180°-67.5°-45°=67.5°, ∴∠OFG =∠EGO , ∴OG =OF , ∴CE =2OF .【总结】本题考查三角形中位线的性质的综合运用,注意利用角度得到等腰三角形.ABCD MN OABCDEF OG【例30】 如图所示,在四边形ABCD 中,CD AB >,E 、F 分别是AC 、BD 的中点.求证:1()2EF CD AB ≥-. 【难度】★★ 【答案】见解析.【解析】取AD 中点G ,联结EG ,FG∵E 、F 分别是AC 、BD 的中点,∴12EG CD =,12FG AB =.∵CD >AB ,∴EG >FG .在△EFG 中,EF >EG -FG =1()2CD AB -,当AB //CD 时,F 、E 、G 三点共线,1()2EF CD AB =-,∴1()2EF CD AB ≥-.【总结】本题考查三角形中位线定理和三角形三边关系的综合运用.【例31】 如图1所示,已知BD 、CE 分别是ABC ∆的外角平分线,过点A 作AF BD ⊥,AG ⊥CE ,垂足分别为F 、G ,连接FG ,延长AF 、AG ,与直线BC 相交,易证1()2FG AB BC AC =++.(1)若BD 、CE 分别是△ABC 的内角平分线(如图2);(2)BD 为△ABC 的内角平分线,CE 为△ABC 的外角平分线(如图3),则在图2、图3两种情况下,线段FG 与△ABC 三边又有怎样的数量关系?请写出你的猜想,并对其中的一种情况给予证明. 【难度】★★★【答案】(1)1()2FG AB AC BC =+-(2)1()2FG BC AC AB =+-.【解析】(1)图2中,分别延长AG 、AF 交BC 于H 、K ,易证△BAF 与△BKF 全等.∴AF =KF ,AB =KB ,同理可证AG =HG ,AC =HC ,∴FG =12HK又∵HK =BK -BH =AB +AC -BC ,∴1()2FG AB AC BC =+-;A BCDEFGC(2)图3中,分别延长AG 、AF 交BC 或延长线于H 、K易证△BAF 与△BKF 全等∴AF =KF ,AB =KB ,同理可证AG =HG ,AC =HC∴FG =12HK又∵HK =BH -BK =BC +AC -AB∴1()2FG BC AC AB =+-.【总结】本题考查直角三角形性质,等腰三角形性质,角平分线性质以及全等三角形的判定等知识点的综合运用.【例32】 如图,在四边形ABCD 中,M ,N 分别是AB ,CD 的中点,AN ,BN ,DM ,CM 划分四边形所成的7个区域的面积分别为1S ,2S ,3S ,4S ,5S ,6S ,7S ,那么恒成立的关系式是( ).A .2S +6S =4SB .1S +7S =4SC .2S +3S =4SD .1S +6S =4S【难度】★★★ 【答案】B【解析】过A 作AE ⊥DC 于点E ,过M 作MH ⊥DC 于H , 过点B 作BQ ⊥CD 于Q , 则AE //MH //BQ .∵M 是AB 中点,∴H 是EQ 中点,即MH 是梯形AEQB 的中位线,∴2MH =AE +BQ∵34612MDC S S S S DC MH ∆++==⨯⨯,6712BNC S S S NC BQ ∆+==⨯⨯,1312ADN S S S DN AE ∆+==⨯⨯,又DN =CN∴76131122S S S S NC BQ ND AE +++=⨯⨯+⨯⨯1()2DN AE BQ =⨯+11222DN MH DN MH CD MH =⨯=⨯=⨯∴7613346S S S S S S S +++=++, ∴174S S S +=.【总结】本题考查面积与等积变换的应用,主要考查学生的计算和推理能力.【例33】 如图,在四边形ABCD 中,AD =BC ,E 、F 分别是CD 、AB 的中点,延长AD 、BC ,分别交FE 的延长线于点H 、G ;求证:AHF BGF ∠=∠. 【难度】★★★ 【答案】见解析.【解析】联结AC ,取AC 中点M ,联结EM 、FM∵E 是CD 的中点,M 是AC 中点∴EM =12AD ,EM //AD∵M 是AC 的中点,F 是AB 的中点∴MF //BC ,MF =12BC∵AD =BC ,∴EM =MF , ∴∠MEF =∠MFE ∵EM //AH ,∴∠MEF =∠AHF , ∵FM //BG ,∴∠MFE =∠BGF . ∴∠AHF =∠BGF【总结】解题此题的关键是掌握分析题中的各种信息条件,此题考查的是三角形中位线的性质,即三角形的中位线平行第三边且等于第三边的一半.【习题1】 有两个角相等的梯形是()A .等腰梯形B .直角梯形C .一般梯形D .直角梯形或等腰梯形 【难度】★ 【答案】D【解析】如果两个相等的角是同一底上,则梯形是等腰梯形, 如果两个相等的角是同旁内角,则梯形是直角梯形. 【总结】本题考查等腰梯形判定方法和梯形性质.随堂检测M【习题2】下列命题中,真命题是()A.顺次联结等腰梯形各边的中点,所得的四边形一定是矩形B.顺次联结等腰梯形各边的中点,所得的四边形一定是菱形C.顺次联结等腰梯形各边的中点,所得的四边形一定是等腰梯形D.顺次联结等腰梯形各边的中点,所得的四边形一定是直角梯形【难度】★【答案】B【解析】等腰梯形两条对角线相等,可以用三角形中位线性质给予证明.【总结】本题考查中位线性质和菱形判定方法.【习题3】已知梯形的两个对角分别是78°和120°,则另两个角分别是( ) A.78°或120°B.102°或60°C.120°或78°D.60°或120°【难度】★【答案】B【解析】另外两个内角分别是180°-78°=102°,180°-120°=60°.【总结】本题考查平行线的性质的运用.【习题4】下列命题,错误命题的个数是( )①若一个梯形是轴对称图形,则此梯形一定是等腰梯形;②等腰梯形的两腰的延长线与经过两底中点的直线必交于一点;③一组对边相等而另一组对边不相等的四边形是梯形;④有两个内角是直角的四边形是直角梯形.A.1个B.2个C.3个D.4个【难度】★★【答案】B【解析】③、④错误.【总结】本题考查等腰梯形性质,根据四边形以及梯形的性质举例得出是本题解题关键.【习题5】 如图,在ABC 中,D 、E 分别是BC 、AC 的中点,且AD AB ⊥,4AD =,6AB =.求AC 的长.【难度】★★【答案】AC =10. 【解析】∵D 、E 分别是中点,∴DE 是△ABC 的中位线∴DE //AB ,12DE AB ==3,∠ADE =90°, ∴AE =5, ∴AC =10.【总结】本题考查中位线性质的运用.【习题6】 等腰梯形两底之差等于一腰长,求它的底角的度数. 【难度】★★【答案】60°、60°或120°、120°.【解析】设四边形ABCD 是等腰梯形,其中AB //CD ,AD =BC ,DC -AB =AD , 过点A 作AE //BC 交CD 于点E ,可得平行四边形ABCE .∴AB =CE ,AE =BC , ∴AD =BC =AE =CD -AB =DE , ∴△ADE 是等边三角形, ∴∠D =60°, ∴梯形的底角度数为60°、60°或120°、120°.【总结】本题考查等腰梯形性质与等边三角形性质的综合运用.【习题7】 如图,四边形ABCD 中,AD 不平行BC ,现给出三个条件:①CAB DBA ∠=∠,②AC BD =,③AD BC =.请从上述三个条件中选择两个条件,使得本题添上这两个条件后能够推出ABCD 是等腰梯形,并加以证明(只需证明一种情况). 【难度】★★ 【答案】①②或②③.【解析】由①②或②③均可证明△ADB ≌△BCA .过点D 作DE //BC 交AB 于点E∴∠DAB =∠CBA =∠DEA ,∴AD =DE =BC又DE //BC ,∴四边形DEBC 是平行四边形,∴CD //AB ∵AD 不平行BC ,∴四边形ABCD 是梯形 ∵AD =BC ,∴梯形ABCD 是等腰梯形【总结】本题主要考查等腰梯形的判定方法,涉及等腰梯形的判定,全等三角形的判定与性质,平行四边形的判定与性质等知识,熟练掌握等腰梯形的判定方法是解题关键.AB CD EBD CAE【习题8】 如图,在四边形ABCD 中,E 、F 、G 、H 分别是AD 、BD 、BC 、AC 上的中点,5AB =,7CD =.求四边形EFGH 的周长. 【难度】★★ 【答案】12【解析】∵E 、F 、G 、H 分别是AD 、BD 、BC 、AC 上的中点, AB =5,CD =7, ∴EF //AB ,GH //AB ,EH //CD ,FG //CD∴EF =2.5,EH =3.5,∴四边形EFGH 是平行四边形 ∴四边形EFGH 的周长=2(EF +EH )=12.【总结】本题考查了三角形的中位线定理以及平行四边形的判定和性质的综合运用.【习题9】 在梯形ABCD 中,AD //BC ,AB =4,AD =4,CD=B =60°,∠C =30°,E 为AB 上一个动点(与A 、B 不重合),EF //CD ,交BC 于点F ,联结DE 、CE . (1)求梯形ABCD 的面积;(2)设BE =x ,四边形CDEF 的面积为y ,求出y 与x 的函数解析式;(3)是否存在这样的点E ,使四边形CDEF 的面积为梯形ABCD 面积的三分之二. 【难度】★★★【答案】(1);(2)y =++;(3)BE. 【解析】(1)分别过点A 、D 作AG ⊥BC ,DH ⊥BC ,可得:BG =2,GH =4,CH =6,AG =DH=CD=∴1()2ABCD S AD BC AG =+=梯形(2)∵EF //CD , ∴∠EFB =∠DCB =30°,∵∠B =60°,∴∠BEF =90°. ∴BF =2x ,EF,BEFS ∆= △ADE 中,AE =4-x ,AD =4,作DK ⊥BA 交BA 延长线于K , ∵∠BAD =120°,∴DK=∴ADE S ∆=, ∴y =ABCD ADEBEF S S S ∆∆--==+(3)由题意,得:23+=⨯解得:x(舍负), ∴BE. 【总结】本题考查梯形的综合解题,考查知识点较多运用数形结合,分类讨论是解题关键.HFE DCBA GA BCDE F H【习题10】 已知:如图,在直角梯形COAB 中,OC AB ∥,以O 为原点建立平面直角坐标系,A B C ,,三点的坐标分别为(80)(810)(04)A B C ,,,,,,点D 为线段BC 的中点,动点P 从点O 出发,以每秒1个单位的速度,沿折线OABD 的路线移动,移动的时间为t 秒.(1)求直线BC 的解析式;(2)若动点P 在线段OA 上移动,当t 为何值时,四边形OPDC 的面积是梯形COAB 面积的27?(3)动点P 从点O 出发,沿折线OABD 的路线移动过程中,设OPD △的面积为S ,请直接写出S 与t 的函数关系式,并指出自变量t 的取值范围. 【难度】★★★ 【答案】(1)344y x =+; (2)167t =; (3)7(08)2244(818)8184(1823)55tt S t t t t ⎧<≤⎪⎪=-+<≤⎨⎪⎪-+<<⎩.【解析】(1)设BC 解析式为y =kx +b ,代入B (8,10),C (0,4),解得直线BC 的解析式为:344y x =+;(2)∵D 是线段BC 中点,∴D (4,7).∵27OPDC COAB S S =四边形梯形, ∴1121744(104)82272t ⨯+⨯⨯=+⨯⨯,解得:167t =;(3)当P 点在OA 上时,S =17722tt ⨯⨯=(08)t <≤;当P 在AB 上时,OPA BPD OCD COAB S S S S S ∆∆∆=---梯形=1111(410)8448(8)(18)4244(818)2222t t t t +⨯-⨯⨯-⨯⨯---⨯=-+<≤; 当P 在BD 上时,S =OCD OPA ABP COAB S S S S ∆∆∆---梯形=818455t -+(18<t <23); 当P 在OD 上时,S =0,(舍) ∴7(08)2244(818)8184(1823)55tt S t t t t ⎧<≤⎪⎪=-+<≤⎨⎪⎪-+<<⎩.【总结】本题综合性较强,考查中位线性质与一次函数的综合运用,注意数形结合思想与分类讨论思想的运用.【作业1】能识别四边形ABCD是等腰梯形的条件是()A.AD//BC,AB=CD B.∠A:∠B:∠C:∠D=3:2:3:2C.AD//BC,AD≠BC,AB=CDD.∠A+∠B=180°,AD=BC【难度】★【答案】C【解析】只有一组对边平行的四边形是梯形,两腰相等的梯形是等腰梯形.【总结】本题考查等腰梯形判定方法.【作业2】(1)在直角梯形ABCD中,AB⊥BC,下底BC为8cm,上底AD为6cm,∠ADB=60°,那么AC的长为__________;(2)已知梯形的中位线长为9厘米,上底长是下底长的一半,那么下底的长是__________厘米.【难度】★【答案】(1)cm;(2)12.【解析】(1)在Rt△ABD中,∠ABD=30°,∴BA=在Rt△ABC中,AC(2)设上底为x,下底为y,则有9212x yx y+=⨯⎧⎪⎨=⎪⎩,解得:y=12,∴下底为12厘米.【总结】本题考查梯形性质与中位线定理的综合运用.【作业3】若梯形中位线被它的两条对角线分成三等份,则梯形的两底之比为()A.1:2 B.1:3 C.1:4 D.1:5【难度】★【答案】A【解析】设梯形ABCD中,AB//CD,AD和BC的中点分别是E、F,AC,BD分别交EF于点H,G,易证AB=2EG,CD=2GF.∵EG=GH=HF,∴GF=2EG,∴CD=2AB.【总结】本题考查梯形中位线的性质的运用.课后作业【作业4】 如图所示,直角梯形ABCD 的中位线EF 的长为a ,垂直于底的腰AB 的长为b ,则图中阴影部分的面积等于( )A .abB .12abC .14ab D .2ab【难度】★★ 【答案】B【解析】∵EF 是梯形中位线,∴E 是AB 中点,∴AE =BE =12b∴1111122222DEC DEF EFC S S S S a b a b ab ∆∆∆==+=⋅+⋅=阴.【总结】本题考查梯形中位线定义,性质及面积公式的综合运用.【作业5A .1个B .2个C .3个D .4个 【难度】★★ 【答案】B【解析】①③正确,②④错误,故选B . 【总结】本题考查梯形中位线的运用.∵BC =BA ,∴∠BCA =∠BAC ,∴∠DCA =∠BCA 可证△ADC ≌△AEC ,∴CD =CE =4,BE =16, ∴AE =AD =12;(2)S =1()1442AD CD AB +=.【总结】本题考查全等三角形判定方法,勾股定理及梯形面积公式的综合运用.A BE A BCDEF。
初中数学-三角形中的中线的用法教师版
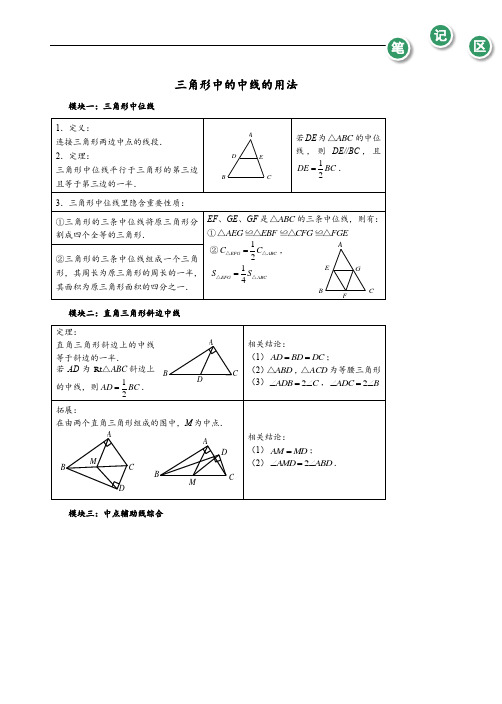
三角形中的中线的用法模块一:三角形中位线 1.定义:连接三角形两边中点的线段. 2.定理:三角形中位线平行于三角形的第三边且等于第三边的一半.若DE 为ABC △的中位线,则DE//BC ,且12DE BC =.3.三角形中位线里隐含重要性质: ①三角形的三条中位线将原三角形分割成四个全等的三角形.EF 、GE 、GF 是ABC △的三条中位线,则有:①AEG EBF CFG FGE △△△△≌≌≌②12EFG ABC C C =△△,14EFG ABC S S =△△②三角形的三条中位线组成一个三角形,其周长为原三角形的周长的一半,其面积为原三角形面积的四分之一. 模块二:直角三角形斜边中线 定理:直角三角形斜边上的中线等于斜边的一半.若AD 为Rt ABC △斜边上的中线,则12AD BC =.相关结论:(1)AD BD DC ==; (2)ABD △,ACD △为等腰三角形 (3)2ADB C ∠=∠,2ADC B ∠=∠拓展:在由两个直角三角形组成的图中,M 为中点.相关结论:(1)AM MD =;(2)2AMD ABD ∠=∠. 模块三:中点辅助线综合E DCB AMMABCDA BCDDCBAFA B CE G(1)如图1-1,在ABC△中,D,E,F分别是AB,BC,AC的中点,若ABC△的周长为20cm,则DEF△的周长为__________.(2)如图1-2,在Rt ABC△中,30A∠=︒,1BC=,点D,E分别是直角边BC,AC的中点,则DE的长为__________.图1-1 图1-2(3)如图1-3,ABC△中,6AB AC==,8BC=,AE平分BAC∠交BC于点E,点D为AB的中点,连接DE,则BDE△的周长是__________.(4)如图1-4,在四边形ABCD中,E、F分别为AB、CD的中点.求证:1()2EF AC BD<+.图1-3 图1-4【解析】(1)10cm.(2)1.(3)10.(4)证明:取AD的中点M,连结EM和FM.∵E、F是AB、CD中点,∴12EM BD=,12FM AC=.又∵EF EM FM<+,∴1()2EF AC BD<+.【教师备课提示】考察中位线产生的线段长度关系.第(4)题利用中位线构造出长为12AC,12BD的线段并将线段集中;也可以求证1()2EF AD BC<+,方法是取AC 或BD的中点.FEDCBA模块一三角形中位线例题1MAB CDEF(1)如图2-1,在四边形ABCD 中,P 是对角线BD 的中点,E ,F 分别是AB ,CD 的中点,AD BC =,18PEF ∠=︒,则PFE ∠的度数是__________度.(2)如图2-2,已知四边形ABCD 的对角线AC BD =,E 、F 分别是AD 、BC 的中点,连结EF 分别交AC 、BD 于M 、N ,求证:AMN BNM =∠∠.(3)已知,如图2-3四边形ABCD 中,AD BC =,E 、F 分别是AB 和CD 的中点,AD 、EF 、BC 的延长线分别交于M 、N 两点.求证:AME BNE ∠=∠.图2-1 图2-2 图2-3【解析】(1)18.(2)设AB 的中点为G ,连结GE 、GF ,容易证得:GE //BD ,12EG BD =,GF //AC ,12EF AC =,从而GF GE =,GEF GFE ∠=∠, ∴AMN BNM =∠∠.(构造中位线来利用对角线相等的条件,也可以取AC 或BD 的中点.) (3)连接AC ,取AC 中点H ,连接FH 、EH .∵DF CF =,AH CH =,∴FH//AD ,12FH AD =,同理,12EH BC =,EH//BC , ∵AD BC =,∴EH FH =,∴HFE HEF ∠=∠, ∵FH//AM ,EH//BC , ∴AM E HFE ∠=∠,HEF BNE ∠=∠, ∴AME BNE ∠=∠.【教师备课提示】考察中位线的性质,学会通过构造中位线去利用已知的条件.CM FEND B AA CDM FE NB例题2CM FE G NDB AA H C D MF E NB如图,在ABC △中,D 、G 分别为AB 、AC 上的点,且BD CG =,M 、N 分别是BG 、CD 的中点,过MN 的直线交AB 于点P ,交AC 于点Q ,求证:AP AQ =.【解析】连DG ,找DG 的中点E ,连ME 、NE ,∵M 、N 分别是BG 与CD 的中点.∴ME//AB ,12ME BD =,NE//AC ,12NE GC =.∴APQ EMN ∠=∠,AQP ENM ∠=∠.∵BD GC =,∴EM EN =, ∴EMN ENM ∠=∠,∴APQ AQP ∠=∠,∴AP AQ =. 【教师备课提示】还可以取BC 中点.总结:已知四边形对角线中点,则取一边中点,可出两条中位线,学会构造出中位线去利用题目中给出的等量关系.已知:在ABC △中,90ABC ∠=︒,点E 在直线AB 上,ED 与直线AC 垂直,垂足为D ,且点M 为EC 中点,连接BM 、DM .(1)如图4-1,若点E 在线段AB 上,探究线段BM 与DM 及BM D ∠与BCD ∠所满足的数量关系,并直接写出你得到的结论;(2)如图4-2,若点E 在BA 延长线上,你(1)中的结论是否发生变化?写出你的猜想并证明.图4-1 图4-2【解析】(1)BM DM =,2BMD BCD ∠=∠;(2)结论不变,由题意知MB MC MD ==,∴2BME BCM ∠=∠,2DME DCM ∠=∠,两式相减,得2BMD BCD ∠=∠.NM PQG D C BAEA BC DG Q PM N 图2图1BEM CDAMEDCBA例题3模块二直角三角形斜边中线例题4如图,90MON∠=︒,ABC△中,90BAC∠=︒,2AB=,1AC=,AB在MON∠上滑动,求OC的最大值.【解析】取AB的中点D,连结OD、DC,则1OD=,2DC=,可得12OC≤+,即OC的最大值为12+(O、D、C三点共线时).在Rt ABC△中,90BAC∠=︒,AD BC⊥,E、F、G分别是AB、AC、BC的中点,M 是DG的中点,求证:ME MF=.【解析】连结DF、EG,可证DF GE=,MDF MGE∠=∠,MD MG=,则MDF MGE△≌△,得证.例题5模块三中点辅助线综合例题6如图,在五边形ABCDE 中,90ABC AED ∠=∠=︒,BAC EAD ∠=∠,F 为CD 的中点.求证:BF EF =.【解析】方法一:如图1,取AC 中点M ,取AD 中点N ,连BM ,MF ,NF ,EN . ∵90ABC AED ∠=∠=︒,1122BM AC FN EN AD MF ====,,∴BMF FNE △≌△,∴BF EF =,方法二:如图2,延长CB 到M ,使得MB BC =, 延长DE 到N ,使得NE DE =, 连接AM ,AN ,MD ,CN . 由90ABC AED ∠=∠=°,AMC △,ADN △是等腰三角形,F 是CD 中点,则BF //MD ,12BF MD =,EF//CN ,12EF CN =,MAD CAN △≌△,MD CN =,∴BF EF =,此题的两种解法中综合了中点的三个基本用法:等腰三角形三线合一;直角三角形斜边中线;中位线,即以下三个模型:图2图1MNN MACBDEF F EDB CA例题7FEDB C A(1)如图1-1,在ABC△中,点D是BC中点,AE平分∠BAC,BE⊥AE于E,延长BE 交AC于F.若AB=10厘米,AC=16厘米,则DE的长度为__________.(2)如图1-2,已知,在四边形ABCD中,AD BC=,P是对角线BD的中点,N是DC 的中点,M是AB的中点,30DBC∠=︒,70ADB∠=︒.求MNP∠度数.图1-1 图1-2【解析】(1)3厘米;(2)∵在四边形ABCD中,P是对角线BD的中点,M、N分别是AB、CD的中点,∴NP,PM分别是CDB△与DAB△的中位线,∴12PN BC=,12PM AD=,PN//BC,PM//AD,∴30NPD DBC∠=∠=︒,70MPB ADB∠=∠=︒,∴110DPM∠=︒;∴140NPM∠=︒,∵AD BC=;∴PN PM=,故NMP△是等腰三角形.∵140NPM∠=︒,∴20PMN PNM∠=∠=︒.复习巩固模块一三角形中位线演练1(1)如图2-1,ABC △中,过点A 分别作ABC ∠、ACB ∠的外角平分线.....的垂线..AD 、AE ,垂足为D 、E .求证:①//ED BC ;②1()2ED AB AC BC =++.(2)(四川省中考题)如图2-2,已知:AD 是ABC △的中线,AE 是ABD △的中线,且AB BD =,求证:2AC AE =.图2-1 图2-2【解析】(1)①分别延长AD 、AE 与直线BC 交于点F 、G ,∵BD ⊥AD ,且BD 为ABF ∠的角平分线∴AD FD =,且AB BF =(等腰三角形的三线合一) 同理可得AE GE =,AC GC =, ∴DE 为AFG △的中位线,∴ED //BC ,且12DE FG =.②由(1)知12DE FG =,且AB BF =,AC GC =,∴111()()222ED FG=FB BC CG AB BC AC =++=++.(2)取AC 的中点F ,连结DF ,易得DF//AB ,12DF AB =,ADF BAD ∠=∠,而1122DE BD AB ==,故DF DE =.再证ADE ADF △≌△,∴AE AF =,∴2AC AE =.C ED BA演练2CF E D B A(1)如图3-1,四边形ABCD 中,90ADC ∠=︒,取AC 中点O ,BC 中点E ,连接OD 、OE 、DE ,20CAD CAB ∠=∠=︒,则DOE ∠=__________.(2)如图3-2所示,ABC △中,AH BC ⊥于H ,点E 、D 、F 分别是AB 、BC 、AC 的中点,10cm HF =,则ED 的长度是__________.图3-1 图3-2【解析】(1)60︒.(2)10cm .(1)如图4-1,在ABC △中,2B C ∠=∠,M 是BC 中点,AD BC ⊥于D .求证:12DM AB =.(2)如图4-2,已知:ABD △和ACE △都是直角三角形,且90ABD ACE ∠=∠=︒,BAD CAE ∠=∠.连接DE ,设M 为DE 的中点.求证:MB MC =.【解析】(1)法一:取AB 中点G ,连结GD 、GM ,则12GD AB =,GM AC ∥.则GMD C ∠=∠. 而GD GB B GDB GMD DGM =⇒∠=∠=∠+∠ C DGM =∠+∠,由于2B C ∠=∠,所以DGM C GMD ∠=∠=∠.∴12MD GD AB ==. OEDC B AMEDCBA模块二直角三角形斜边中线演练3模块三中点辅助线综合演练4CAB GNDMC AB D M法二:同理可以取AC的中点N,连接DN,MN.(2)如图,分别取AD、AE的中点P、Q,连接PB、PM、QC、QM,由P、M、Q分别是AD、DE、AE的中点,∴PM//AE,12PM AE=,QM//AD,12QM AD=,∵ABD△、ACE△是直角三角形,∴12PB AD=,12CQ AE=,∴PB QM=,PM QC=,∵BAD CAE∠=∠,∴ADB AEC∠=∠,∴DPB CQE∠=∠,由AD//QM,AE//PM,∴APM AQM∠=∠,∴BPM MQC∠=∠,∴BPM MQC△≌△,∴MB MC=.QPAB CDE M图3。
八年级数学下册22.6三角形梯形的中位线3教学设计沪教版五四制

八年级数学下册22.6三角形梯形的中位线3教学设计沪教版五四制一. 教材分析《三角形梯形的中位线》是沪教版八年级数学下册第22章第6节的内容,本节课主要让学生掌握三角形和梯形的中位线定理,并能够运用该定理解决相关问题。
教材通过引入中位线的概念,引导学生探究中位线的性质,进而推导出中位线的长度等于它所对的边的长度,以及中位线平行于第三边。
这一内容是学生进一步学习几何的基础,对于培养学生的空间想象能力和逻辑思维能力具有重要意义。
二. 学情分析八年级的学生已经掌握了平行线、三角形和梯形的基本知识,具备了一定的空间想象能力和逻辑思维能力。
但学生在学习过程中,可能对中位线的概念和性质理解不深,对中位线定理的应用还不够熟练。
因此,在教学过程中,教师需要通过丰富的教学手段,帮助学生理解和掌握中位线定理,提高学生的解题能力。
三. 教学目标1.让学生理解三角形和梯形的中位线定理,掌握中位线的性质。
2.培养学生运用中位线定理解决实际问题的能力。
3.提高学生的空间想象能力和逻辑思维能力。
四. 教学重难点1.重难点:三角形和梯形的中位线定理的推导和应用。
2.难点:学生对中位线定理的理解和运用。
五. 教学方法1.采用问题驱动的教学方法,引导学生主动探究中位线的性质。
2.利用几何画板和实物模型,帮助学生直观地理解中位线定理。
3.通过例题和练习题,让学生巩固中位线定理的应用。
4.分组讨论和合作交流,提高学生的团队协作能力。
六. 教学准备1.准备几何画板和实物模型,用于展示中位线的性质。
2.准备相关的PPT和教学课件,用于辅助教学。
3.准备一系列的例题和练习题,用于巩固学生的学习效果。
七. 教学过程1.导入(5分钟)通过提问方式复习三角形和梯形的基本知识,引导学生思考中位线的作用和意义。
2.呈现(10分钟)利用几何画板和实物模型,呈现三角形和梯形的中位线,引导学生观察和思考中位线的性质。
3.操练(10分钟)让学生分组讨论,每组尝试找出三角形和梯形的中位线,并测量中位线的长度,验证中位线定理。
20202-2021学年沪教版(上海)八年级第二学期数学 22.6 三角形、梯形的中位线(含答案)

22.6 三角形、梯形的中位线一、单选题1.已知等腰三角形的两条中位线的长分别为3和5,则此等腰三角形的周长为( ) A .22B .26C .22或26D .13 2.如图,在ABC 中,7AB =,6AC =,5BC =,D 、E 分别是AB 、AC 的中点,则DE 的长为( )A .3B .2.5C .4D .3.5 3.如图所示,在ABC 中,E ,D ,F 分别是AB ,BC ,CA 的中点,6AB =,4AC =,则四边形AEDF 的周长是( )A .10B .20C .30D .40 4.如图,在Rt△ABC 中,△ACB =90°,点D 、E 分别是AB 、BC 的中点,点F 是BD 的中点,若AB =5,则EF =( )A .54B .52C .32D .2 5.如图,在△ABC 中,AD 是BC 边上的高线,CE 是AB 边上的中线,DG △CE 于点G ,CD =AE .若BD =6,CD =5,则△DCG 的面积是( )A .10B .5C .103D .53 6.如图,在ABC ∆中,D 是AB 上一点,,AD AC AE CD =⊥于点E ,点F 是BC 的中点,若10BD =,则EF 的长为( )A .8B .6C .5D .4 7.如图,在梯形ABCD 中,AD △BC ,EF 是梯形ABCD 的中位线,若△BEF 的面积为4cm 2,则梯形ABCD 的面积为( )A .8cm 2B .12cm 2C .16cm 2D .20cm 2 8.如图,在梯形ABCD 中,AD△BC ,点E 、F 分别是AB 、CD 的中点且EF=6,则AD+BC 的值是( )A .9B .10.5C .12D .15 9.如图,周长为24的平行四边形ABCD 对角线AC 、BD 交于点O ,ACCD ⊥且BE CE =,若6AC =,则AOE △的周长为( ).A .6B .9C .12D .15 10.如图,等腰梯形ABCD 中,AB//CD ,点E 、F 、G 、H 分别为各边中点,对角线AC 5=,则四边形EFGH 的周长为( )A .2.5B .5C .10D .20二、填空题11.在ABCD 中,E 是AD 边上的中点,连接BE ,并延长BE 交CD 的延长线于点F .已知AB =120A ∠=︒,5BF =:则FD =__________,ABCD S =__________.12.若一个梯形的中位线长为15,一条对角线把中位线分成两条线段.这两条线段的比是3:2,则梯形的上、下底长分别________.13.如图ABC 的中线AE 、BD 交于点G ,过点D 作//DM BC 交AE 于点M ,则AMD 、DMG △和BEG 的面积之比为______.14.如图所示,DE 为△ABC 的中位线,点F 在DE 上,且△AFB =90°,若AB =4,BC =10,则EF 的长为_____.15.如图,在直角梯形ABCD 中,//,90AD BC DAB ABC∠=∠=︒,点E 在DC 上,且ABE △是以AB 为底的等腰直角三角形,若2cm,4cm AD BC ==,则AB =_______cm ,DC =______cm .三、解答题16.已知:如图,DE是ABC的中位线,AF是BC边上的中线,DE和AF交于点O.求证:DE与AF互相平分.17.如图,在梯形ABCD中,AD△BC,BC=12,AB=DC=8.△B=60°.(1)求梯形的中位线长.(2)求梯形的面积.18.已知:如图,AB△CD,E是AD中点,CF△AB于F求证:CE=EF.参考答案1.C2.B3.A4.A5.B6.C7.C8.C9.B10.C116212.12,1813.3△1△414.315.616.证明:如图所示,连接DF、EF,△DE是△ABC的中位线,△点D是AB中点、点E是AC中点,又△AF是BC边上的中线,△F是BC中点,△DF、EF是△ABC的中位线,△DF△AC,EF△AB,△四边形ADFE是平行四边形,△DE与AF互相平分.17.解:(1)过A 作AE △CD 交BC 于E , △AD △BC ,△四边形AECD 是平行四边形, △AD =EC ,AE =DC ,△AB =DC ,△AB =AE ,△△B =60°,△△ABE 是等边三角形,△BE =AB =8,△AD =EC =BC ﹣BE =12﹣8=4, △梯形ABCD 的中位线长=12(AD +BC )=12(4+12)=8; (2)作AF △BC 于F ,则△BAF =90°﹣△B =30°,△BF =12AB =4,AF =△梯形ABCD 的面积=12(AD +BC )×AF =12(4+12)18.取CF 的中点为G ,连接EG , △AB△CD ,E 是AD 的中点△EG 是梯形AFCD 的中位线, △EG△AB ,△CF△AB ,△CF△EG ,又△G 是CF 的中点,△EG是CF的垂直平分线,△CE=EF.。
22.6三角形中位线(第1课时)(教学课件)-2022-2023学年八年级数学下册同步精品课堂(沪教

∵E,F,G,H分别为各边的中点,
A E
∴EF∥AC, EF 1 AC
2
HG∥AC, HG 1 AC
2
∴ EF∥HG, EF=HG.
B
H F
D
G
C
∴四边形EFGH是平行四边形.
随堂检测
1.如左图,MN 为△ABC 的中位线,若∠ABC =61°,则
∠AMN = 61°,若MN =12 ,则BC = 24 .
第 22章 四边形
22.6三角形中位线(第1课时)
思考与归纳
一张三角形纸片,用一条平行于这个三角形一边的直
线把它分割成一个梯形和一个小三角形.如果所得的梯形
和小三角形恰好拼成一个平行四边形,那么这条用于分
割的直线与三角形另外两边的交点在什么位置?为什么?
A
D
E
D
E
B
C
B
C
(A)
观察:三角形的中位线段DE与边BC有什么样的数量关 系和位置关系?
3、如图,B、C两点被海水隔开,在B、C外选择一点A,找到 AB、AC的中点E、F,测量得EF=22米.这样就能求出B、C两点 间的距离.请说出这是为什么?
答:∵ 点E、F分别为AB、AC的中点, ∴ EF∥BC,且BC=2EF=44米
B
(三角形的中位线平行于第三边,
并且等于第三边的一半).
E
A
F
C
4.求证:顺次联结四边形四条边的中点,所得的四边形 是平行四边形 已知:如图,在四边形ABCD中, E,F,G,H分别为各边的中
点.求证:四边形EFGH是平行四边形. A
E B
H F
D
G
C
分析:将四边形ABCD分割为三角形,利用三角形的中位线可
2024春八年级数学下册22.6三角形梯形的中位线3教学设计沪教版五四制

2024春八年级数学下册22.6三角形梯形的中位线3教学设计沪教版五四制一. 教材分析《2024春八年级数学下册》第22.6节主要讲述三角形和梯形的中位线性质。
本节内容是在学生已经掌握了三角形和梯形的定义、性质的基础上进行教学的,对于学生来说,本节内容具有一定的挑战性。
教材通过详细的讲解和丰富的例题,帮助学生理解和掌握三角形和梯形的中位线性质,为后续的学习打下基础。
二. 学情分析八年级的学生已经掌握了一定的数学基础知识,对于三角形和梯形的定义、性质有一定的了解。
但是,对于三角形和梯形的中位线性质,学生可能还没有听说过,或者只是一知半解。
因此,在教学过程中,需要教师通过生动的讲解和丰富的实例,帮助学生理解和掌握中位线的性质。
三. 教学目标1.让学生了解三角形和梯形的中位线性质。
2.让学生能够运用中位线性质解决一些几何问题。
3.培养学生的逻辑思维能力和空间想象力。
四. 教学重难点1.重点:三角形和梯形的中位线性质。
2.难点:如何运用中位线性质解决几何问题。
五. 教学方法采用讲解法、实例分析法、问题解决法、小组合作法等,通过生动的语言、形象的图形、实际的问题,激发学生的学习兴趣,引导学生主动参与课堂,培养学生的动手操作能力和思维能力。
六. 教学准备1.准备相关的教学PPT或黑板报。
2.准备一些实际的例子,用于讲解和练习。
3.准备一些练习题,用于巩固所学知识。
七. 教学过程1.导入(5分钟)通过提问方式引导学生回顾三角形和梯形的定义、性质,为新课的学习做好铺垫。
2.呈现(15分钟)教师通过PPT或黑板报,呈现三角形和梯形的中位线性质,并用生动的图形进行解释,让学生初步了解中位线的性质。
3.操练(15分钟)教师给出一些实际的例子,让学生运用中位线性质进行解答,巩固所学知识。
期间,教师可引导学生进行小组讨论,分享解题心得。
4.巩固(10分钟)教师给出一些练习题,让学生独立完成,检查学生对中位线性质的掌握情况。
三角形梯形中位线定理教师版

三角形、梯形中位线定理应用练习课一、复习题组1.知识要点A 1,三角形中位线性质定理的条件是,(1) 如图结论是;DE三角形中位线判定定理的条件是,CB结论是。
1)(图AD如图2,梯形中位线性质定理的条件是,(2)结论是;EF梯形中位线判定定理的条件是,CB 2 结论是。
(图)2.基本方法三角形、梯形中位线定理不仅反映了线段的相等关系,也反映了线段间的倍半关系。
此外,证明线段相等或倍半关系还有其他方法,你能指出一些其他的常用方法吗?全等三角形对应边相等;(1)(2) 等角对等边,等腰三角形“三线合一”性质;线段垂直平分线上的点到线段两端点的距离相等;(3)角平分线上的点到角的两边距离相等;(4)(5) 直角三角形斜边上的中线等于斜边的一半;30°角所对的直角边等于斜边的一半;(6) 直角三角形中,(7) 平行四边形(包括矩形、菱形、正方形)的性质;(8) 等腰梯形的两腰相等,两条对角线相等。
二、基本题组1.顺次连结四边形各边中点所得的四边形是;.顺次连结平行四边形各边中点所得的四边形是;2 .顺次连结矩形各边中点所得的四边形是;3 4.顺次连结菱形各边中点所得的四边形是;5.顺次连结正方形各边中点所得的四边形是;.顺次连结梯形各边中点所得的四边形是。
6 7.顺次连结直角梯形各边中点所得的四边形是。
8.顺次连结等腰梯形各边中点所得的四边形是。
1 / 8.顺次连结对角线的四边形各边中点所得的四边形是菱形;9 .顺次连结对角线的四边形各边中点所得的四边形是矩形;10 11.顺次连结对角线的四边形各边中点所得的四边形是正方形。
系统小结,深刻理解的周长比为,面积比为。
各边的中点,则△DEF与△ABCD、E、F是△ABC 12.已知,AC的四等分点,BC=28的四等分点,D'、E'、F' 是13.如图3,在△ABC中,D、E、F是AB FF' = EE' =,。
《22.6三角形、梯形的中位线》作业设计方案-初中数学沪教版上海八年级第二学期

《三角形、梯形的中位线》作业设计方案(第一课时)一、作业目标1. 巩固学生对于三角形和梯形中位线的基本概念,掌握其性质及运用方法。
2. 提升学生的空间想象力和逻辑思维能力,培养学生的解题策略意识。
3. 通过练习与实际生活中的应用问题,培养学生数学学习兴趣及解题自信。
二、作业内容本课时的作业内容主要围绕三角形和梯形的中位线展开,具体包括:1. 基础概念练习:要求学生掌握中位线的定义、性质及与三角形、梯形的关系,并完成相关概念题。
2. 性质运用:通过例题和习题,让学生理解并掌握中位线在三角形、梯形中的性质及运用方法,包括角度、边长关系等。
3. 解题策略:布置具有实际意义的情境问题,要求学生通过绘制图示、理解问题情境并应用中位线的性质来解题。
4. 综合应用:选取典型问题,要求学生在解决过程中综合考虑三角形的边角关系和中位线的运用,并灵活应用相关知识解决实际问题。
三、作业要求1. 学生需在完成作业时注意题目中给定的图形与实际情况是否相符,需对题目中的信息加以核对与验证。
2. 在完成练习时,需标明解题步骤和结果,书写规范、整洁,对易错、易混淆的点进行重点标注。
3. 作业需独立完成,严禁抄袭他人答案或使用其他不正当手段。
4. 遇到问题时,应积极思考并尝试自己解决,如无法解决可查阅相关资料或向老师请教。
四、作业评价1. 评价标准:作业的完成情况、解题思路的正确性、步骤的完整性及答案的准确性等。
2. 评价方式:教师批改、学生自评和互评相结合。
教师批改时需对每道题目进行详细评阅,给出明确的对错判断及改进意见;学生自评和互评时,需根据评价标准对作业进行自我评价和相互评价,提出自己的看法和建议。
五、作业反馈1. 教师需及时批改作业,对学生的错误进行指导纠正,并提供详细的解题思路和步骤。
2. 对于学生的疑问和困惑,教师需及时解答和指导,帮助学生掌握相关知识。
3. 通过作业反馈,教师可以了解学生的学习情况及存在的问题,以便调整教学计划和教学方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
在△ABC 中①、BC AB F E 、为、 的中点 ②、∵M 、N 分别是BC 、AC 的中点∴线段EF 是 △ABC 的中位线 ∴ 线段MN 是△ABC 的中位线2)、三角形有 3 条中位线,它们构成的三角形叫中点三角形。
3)、三角形的中位线定理: 三角形的中位线平行于第三边并且等于第三边的一半。
4)、在△ABC 中,AB =3,BC =5,CA =7,顺次连结三边中点得△DEF 的周长为___7.5______.5)、在△ABC 中,D 、E 、F 分别 为AB 、BC 、CA 的中点,△DEF 的周长为10,则△ABC 的周长是 20 。
6)、三角形的三条中位线的长分别是3,4,5,则这个三角形的周长是__ 24 。
结论:中点三角形的周长等于原三角形的 一半 . 7)、一个三角形的面积是40,则它的中点三角形的面积是__10结论:中点三角形的面积是原三角形面积的_二、中点四边形1、定义:顺次连接四边形各边中点的四边形叫 中点四边形2、中点四边形的形状与原四边形的对角线数量和位置有关 1)、原四边形的对角线相等时,中点四边形是菱形; 2)、原四边形的对角线垂直时,中点四边形是矩形;3)、原四边形的对角线既相等又垂直时,中点四边形是正方形; 4)、原四边形的对角线既不相等又不垂直时,中点四边形是平行四边形。
5)、任意四边形的中点四边形是平行四边形;菱形的中点四边形是矩形;矩形、等腰梯形的中点四边形是菱形;正方形的中点四边形是正方形。
三、梯形中位线1、定义:联结梯形两腰中点的线段叫做梯形的中位线。
2、梯形中位线定理:梯形的中位线平行于两底,且等于两底和的一半 。
热身练习1.若三角形三条中位线长分别是3cm 、4cm 、5cm ,则这个三角形的面积是 24 cm 2。
2.梯形的上底长为6,下底长为10,则由中位线所分得的两个梯形的面积之比为 7:9 . 3. 梯形的两条对角线的中点的连线长为7,上底长为8,则下底长为 22 . 4. 若等腰梯形的腰长是5cm ,中位线是6cm ,则它的周长是_22__cm .415. 已知等腰梯形的上、下底长分别为 2cm 和6cm ,且它的两条对角线互相垂直,则这个梯形的面积为 16 cm 2.6. 已知三角形三边长分别为a 、b 、c ,它的三条中位线组成一个新的三角形,这个新三角形的三条中位线又组成一个小三角形,这个小三角形的三条中位线又组成一个新小三角形,则最小的三角形的周长是( C )A. (a+b+c)B. (a+b+c)C. (a+b+c)D. (a+b+c)7.若等腰梯形较长的底等于对角线,较短的底等于高,则较短的底和较长的底的长的长度之比是 ( D ) A.1:2 B. 2:3 C.4:1 D. 3:58.直角梯形中,上底和斜腰长均为a ,且斜腰和下底的夹角是60°,则梯形中位线长为( C )A. B. a C. D. 都不对9.在梯形ABCD 中,AB//CD ,DC :AB=1:2,E 、F 分别是两腰BC 、AD 的中点,则 (D ) A.1:4 B. 1:3 C. 1:2 D. 3:410. 如图,在直角梯形ABCD 中,点O 为CD 的中点,AD ∥BC,试判断OA 与OB 的关系? (OA=OB)(10题图) (11题图)11. 如图,梯形ABCD 中,AD ∥BC ,点E 是AB 中点,连结EC 、ED 、CE ⊥DE ,CD 、AD 与BC 三条线段之间有什么样的数量关系?请说明理由. (AD+BC=CD)精解名题例1.已知:如图所示,Rt △ABC 中, A C B D E 90°,、分别为AB 、BC 的中点,点F 在AC 的延长线上, F E C B。
(1)求证:CF=DE ;(2)若AC=6,AB=10,求四边形DCFE 的面积。
BD EA C F分析:由题设知DE 为△ABC 中位线,所以有DE//AC ,且DE AC 12,可证DC//EF ,四边形DCFE 为平行四边形,易求出面积。
(1)证明:∵D 、E 分别为AB 、BC 的中点DE AC DE AC ACB CD AB DB //,又°129012DCEF BCDFEC BFEC BCD B //∴四边形DCFE 是平行四边形。
∴CF=DE 。
(2)解: A C A B 610, 由勾股定理,得B C A B A C 228S D E C E A CB C D C F E平行四边形··121212 例2.四边形ABCD 中,E 、F 、G 、H 分别是AB 、BC 、CD 、DA 的中点, 求证:四边形EGFH 是平行四边形证明:联结AC,BD ,则GF ∥BD,EH ∥BD,GH ∥AC,EF ∥AC ∴GF ∥EH ,GH ∥EF ∴四边形EGFH 是平行四边形变式1.四边形ABCD 中,E 、F 、G 、H 分别是AB 、CD 、AC 、BD 的中点。
求证:四边形EGFH 是平行四边形证明:∵E 、F 、G 、H 分别是AB 、CD 、AC 、BD 的中点∴BC GE BC FH 21//,21//∴FH平行并且等于GE ∴四边形EGFH是平行四边形结论:任意四边形的中点四边形是平行四边形变式2. 四边形ABCD中,对角线AC=BD,E、F、G、H分别是AB、BC、CD、DA的中点求证:四边形EFGH是菱形。
GHEFACGHACEF//,21//,21//∴四边形EFGH是菱形。
结论:对角线相等的四边形的中点四边形是菱形变式3.已知菱形ABCD,E、F、G、H分别是AB、BC、CD、DA的中点,求证:四边形EFGH是矩形。
FGEFBDACBDFGEH,,21////结论菱形的中点四边形是矩形例3.已知四边形ABCD中,AC、BD交于O点,E、F、G、H分别是AO、BO、CO、DO的中点,四边形ABCD与四边形EFGH周长的和等于33厘米.求四边形EFGH的周长.分析:由已知得EF是ΔAOB的中位线,则EF=AB/2,同理可得FG=BC/2,GH=CD/2,HE=DA/2,由此可得四边形EFGH的周长是四边形ABCD周长的一半.故四边形EFGH的周长为11cm.例4.已知:如图,在梯形ABCD中,AB∥CD,且AB>CD,E,F分别是AC,BD的中点.求证:EF=21(AB-CD)A BCDE F例1图NMDCBA分析:遇到腰上中点的问题构造梯形中位线可证明,也可以因为腰上有中点,延长DM与CB的延长线交于E点进行证明。
例2.如图,△ABC的三边长分别为AB=14,BC=16,AC=26,P为∠A的平分线AD上一点,且BP ⊥AD,M为BC的中点,求PM的长。
例2图QPMD CBA分析:∠A的平分线与BP边上的垂线互相重合,通过作辅助线延长BP交AC于点Q,由△ABP≌△AQP知AB=AQ=14,又知M是BC的中点,所以PM是△BQC的中位线。
答案:PM=6例3.E、F为凸四边形ABCD的一组对边AD、BC的中点,若EF=)(21CDAB ,问:ABCD是什么四边形?请说明理由。
分析与结论:如图,利用三角形和梯形的中位线定理,连结AC,取AC的中点G,连EG、FG,则EG∥21CD,FG∥21AB,∴EG+FG=)(21CDAB ,即EG+FG=EF,则G点在EF上,EF∥CD,EF∥AB,故AB∥CD。
(1)若AD∥BC,则凸四边形ABCD为平行四边形;(2)若AD不平行于BC,则凸四边形ABCD为梯形。
评注:利用中位线构造出21CD、21AB,其关键是连AC,并取其中点G。
巩固练习1.一个等腰梯形的周长为100cm ,如果它的中位线与腰长相等,它的高为20cm ,那么这个梯形的面积是 500cm 2 。
2.若梯形中位线被它的两条对角线分成三等分,则梯形的两底之比为 1∶2 。
3.三角形各边分别是3cm 、5cm 、6cm ,则连结各边中点所围成的三角形的周长是 7cm . 4. 已知梯形的中位线长16cm ,梯形的一条对角线把中位线分成两条线段,这两条线段的差是4cm,则梯形上底长是 12 cm.5.如图5,△ABC 中,AD 、BE 是中线且交于G ,那么 = .图5 图66. 如图6,梯形ABCD 中,AD ∥BC ,AD =12,BC =16,中位线EF 与对角线分别相交于H 和G ,则GH 的长是 2 .自我测试1.若梯形的一底长是14cm ,中位线长是16cm ,则另一底长为_18__cm . 2.已知梯形中位线长是5cm ,高是4cm ,则梯形的面积是 20cm 2 . 3.梯形上底与中位线之比是2:5,则梯形下底与中位线之比是 8:5 .4.如图,ABC 沿DE 折叠后,点A 落在BC 边上的A 处,若点D 为AB 边的中点, 50 B ,则A BD 的度数为 80° .5.如图,梯形ABCD 中,AD ∥BC ,EF 是梯形的中位线,G 是BC 上任意一点,如果22 GEF S cm 2,那么梯形ABCD 的面积是 28 。
第5题图GFEDCBA第6题图N MFEDCBA第7题图G Q PFE DCBA6.如图,在梯形ABCD 中,AD ∥BC ,∠B =300,∠C =600,E 、F 、M 、N 分别为AB 、CD 、BC 、DA 的中点,已知BC =7,MN =3,则EF = 4 。
7.如图,D 、E 、F 分别为△ABC 三边上的中点,G 为AE 的中点,BE 与DF 、DG 分别交于P 、Q 两点,则PQ ∶BE = 1∶4 。
8. 在梯形ABCD 中,AD ∥BC ,BD 是对角线,EF 为中位线,若ABD S ∶BDC S =1∶2,则AEFD S 梯形∶EBCF S = 5:7 。
9. 等腰梯形的两条对角线互相垂直,中位线长为8cm ,则它的高为( C ) A 、4 cm B 、24cm C 、8cm D 、28cm10. 已知等腰梯形ABCD 中,BC ∥AD ,它的中位线长为28cm ,周长为104cm ,AD 比AB 少6cm ,则AD ∶AB ∶BC =( D )A 、8∶12∶5B 、2∶3∶5C 、8∶12∶20D 、9∶12∶1911.如图,已知△ABC 的周长为1,连结△ABC 三边的中点构成第二个三角形,再连结第二个三角形三边的中点构成第三个三角形,依此类推,第2004个三角形的周长为( C ) A 、20031 B 、20041 C 、200321 D 、200421(11题图) (12题图)12. 如图,E 、F 、G 、H 分别是BD 、BC 、AC 、AD 的中点,又AB =DC ,下列结论:①EFGH 为矩形;②FH 平分EG 于T ;③EG ⊥FH ;④HF 平分∠EHG 。
