材料力学第四版_编者干光瑜课后习题
《材料力学》第四篇课后习题参考答案
反思与改进
不足之处
在解题过程中，我发现自己在 某些知识点上还存在理解不够 深入的问题，需要进一步加强 学习。
改进方向
在未来的学习中，我将更加注 重理论与实践的结合，通过更 多的实际案例来加深对知识点 的理解。
学习计划调整
针对自己的不足之处，我将制 定更为详细的学习计划，加强 针对性的练习和复习，以提高 自己的学习效果。
总结词
考虑非线性效应
详细描述
本题目需要考虑非线性效应对结构性能的影响，如大变形 、塑性变形等，需要运用材料力学的基本理论，对这些非 线性效应进行分析和计算。
总结词
结合实际工程背景
详细描述
本题目需要结合实际工程背景，对结构进行详细的分析和 设计。需要考虑实际工程中的各种因素，如施工条件、环 境因素等，以确保结构的可靠性和安全性。
这种方法需要熟练掌握 材料力学的基本概念和 公式，对问题的理解要 深入，能够准确判断和 选择适用的公式。
解析方法二
01
图解法
02
图解法
03
图解法
04
图解法
解析方法三
数学解析法
数学解析法是通过建立数学模型，将实际问题转 化为数学问题，利用数学工具进行求解。
•·
这种方法需要具备较高的数学水平，能够建立准 确的数学模型，并选择适当的数学方法进行求解 。
05
总结与反思
学习总结
80%
知识掌握情况
通过完成课后习题，我深入理解 了材料力学中的基本概念和原理 ，掌握了解决实际问题的基本方 法。
100%
解题能力提升
通过不断练习和反思，我提高了 自己的解题能力和思维逻辑性， 能够更加熟练地运用所学知识解 决复杂问题。
工程力学材料力学第四版(北京科技大学与东北大学)习题答案
(北京科技大学与东 北大学)
第 一意轴向拉伸和压缩
, 1-1 lfJ截 Illi法 求 下列各轩指 定的 lii fl'J 内 )J
2
f
2
F 2k N
I
(a 1
2
f
(bl
3P
11
(d 1
2kN P
2
2
(e 1
题 1 ) [fI
解
P
({)
P rlp|p
iE
『
e-
I Iz Il
F
5,
为 20 俐 ， 许用应力 I δ]=50 Mpa . 试
根据吊钩螺纹部分的强主确定吊钩的阵 111 起重盐 1 解 P= 119kN
P
3m
B
P
E
题1-1 8 固
lIlí l - l ~ 罔
1 - 1 9 如入所示结构的 ABH 为钢轩，其帧故而积 -4.:::6 cm2 • 咛用阻力 ( σ 1=140 MPa ; BC
<.l
(bl
题 1-3 归
且ø 1 -4 因
1-4 : 桩杆起lli:机如 l 国所示，起lli:忏 AB 为钢管 ， J[外径 。=2ûrnm ， 内径 d= 1 8mrn;制绳
CB 的棋极而而积为 01cnEZe 己知l起重证
P=2脱lO N ，
试计fI起重机轩;归 钢丝绳的应 )J.
解 受力分析得
解
E = GPa . v = 0.3 17
1- 10: i主杆端部与的如1I相迹 ， 其构应如罔 ，谊作用在连杆的轴向 jJ P=l28KN ， 蝉挟处的内
径 d = 3.7cm ， 螺栓材料的冉川剧
工程力学材料力学第四版[北京科技大学及东北大学]习题答案解析
![工程力学材料力学第四版[北京科技大学及东北大学]习题答案解析](https://img.taocdn.com/s3/m/53eb761f0a4e767f5acfa1c7aa00b52acfc79ce1.png)
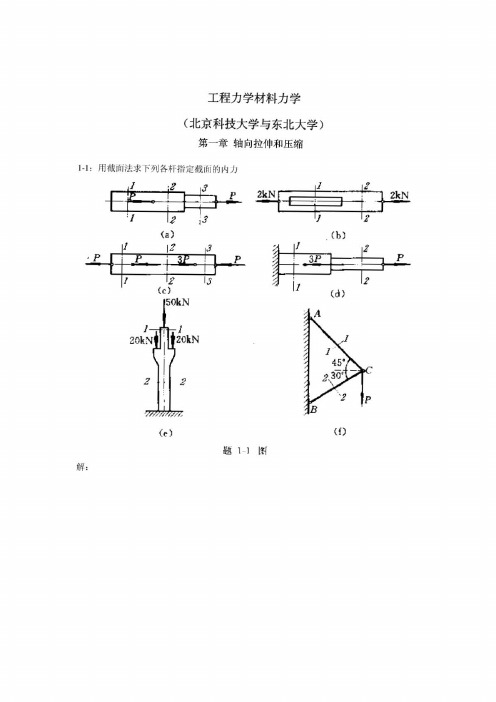
工程力学材料力学（北京科技大学与东北大学）第一章轴向拉伸和压缩1-1:用截面法求下列各杆指定截面的内力解：(a):N1=0，N2=N3=P(b）：N1=N2=2kN(c）：N1=P，N2=2P，N3= -P（d)：N1=—2P，N2=P（e）：N1= —50N，N2= -90N（f)：N1=0.896P，N2=—0。
732P注（轴向拉伸为正，压缩为负）1—2：高炉装料器中的大钟拉杆如图a所示,拉杆下端以连接楔与大钟连接，连接处拉杆的横截面如图b所示;拉杆上端螺纹的内径d=175mm.以知作用于拉杆上的静拉力P=850kN,试计算大钟拉杆的最大静应力。
解：σ1= =35。
3Mpaσ2= =30。
4MPa∴σmax=35。
3Mpa1—3:试计算图a所示钢水包吊杆的最大应力。
以知钢水包及其所盛钢水共重90kN，吊杆的尺寸如图b所示。
解：下端螺孔截面：σ1= =15。
4Mpa上端单螺孔截面：σ2==8。
72MPa上端双螺孔截面:σ3= =9.15Mpa∴σmax=15。
4Mpa1—4：一桅杆起重机如图所示,起重杆AB为一钢管，其外径D=20mm，内径d=18mm;钢绳CB 的横截面面积为0.1cm2。
已知起重量P=2000N，试计算起重机杆和钢丝绳的应力。
解：受力分析得:F1＊sin15=F2＊sin45F1*cos15=P+F2＊sin45∴σAB= =-47。
7MPaσBC==103。
5 MPa1—5：图a所示为一斗式提升机.斗与斗之间用链条连接，链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N。
钢链又两层钢板构成，如c所示。
每个链板厚t=4。
5mm，宽h=40mm,H=65mm，钉孔直径d=30mm。
试求链板的最大应力。
解：F=6PS1=h*t=40＊4。
5=180mm2S2=（H-d)＊t=（65-30）＊4。
5=157.5mm2∴σmax==38.1MPa1—6：一长为30cm的钢杆,其受力情况如图所示。
工程力学第四版张秉荣主编课后习题解析
列平衡方程∑MA（F）=0
2WQ-2.5G-5.5Gp=0
Gp=7.41kN
FAFB
2-7、如图2-7所示，重力为G的球夹在墙和均质杆
之间。AB杆的重力为GQ=4G/3，长为l，AD=2l/3。已知
G、α=30°，求绳子BC和铰链A的约束反力。
解题提示
物系平衡问题的解题步骤：
解题提示
方法一：
分别取AC杆、BC杆为研究对象，画其
受力图，列平衡方程求解。
方法二：
分别取BC杆、构架整体为研究对象，
画其受力图，列平衡方程求解。
图2-8
2-9*、图2-9所示为火箭发动机试验台。发动机固定在台上，测力计M指示绳子的拉力为FT，工作台和发动机的重力为G，火箭推力为F。已知FTG、G以及尺寸h、H、a和b，试求推力F和BD杆所受的力。
1、选取研究对象，画其分离体受力图。
2、选择直角坐标轴系，列平衡方程并求解。
以2-2图c）为例
①选AB梁为研究对象，画受力图c′）y
②选直角坐标系如图示，列平衡方程
并求解。FAxx
∑Fx=0FAx=0（1）FAyFB
∑Fy=0FAy–F+FB–q（2a）= 0（2）图c′）
∑MA（F）=0FB（2a）–F（3a）–q（2a）a+M=0（小：
FR′=√（∑Fx）2+（∑Fy）2
方向：
tanα=∣∑Fy∕ ∑Fx∣
α为主矢FR′与x轴所夹的锐角。
主矩的计算方法：MO=∑MO（F）。
图2-1
2-2、如图2-2所示，已知q、a，且F=qa、M=qa2。求图示各梁的支座反力。
图2-2
解题提示
一、平面任意力系的平衡方程
工程力学材料力学第四版 北京科技大学与东北大学 习题答案
F ，气 in 15=F2*sin45
F I*co s 15= P+ F2*s in45
F
.:..L
OAF SI= 477MPa
FZ Oasc= 5 24035MPa
1- 5 罔 a 所示为一斗式提升机斗与 1- .i:间用链条连接 ! 链盔的计fI简罔如同 b 所示，每个
料斗连 l uj 物抖的总豆 -IIH二 2 0 00 N 制链卫
d =40mm 在压盐的外 :&íl目上沿姐户l 贴有测韭JlNIJ 电阳 l 含金片若测得轧辑两 端两个压头的辄 lúJ
!也 变均为 ε =0 .9* 1 0.2 武斗占轧机 WJAA 轧
制压力压J、材料的神tl 棋盘E=2仅JGp，
解
A-E -J UN 川
N
e=
EA N = eEA = 2 . 54 叫 0' N
l'! 1 - 21 图
1-2 1 一小变形的问 m梁 AB 搁于三 个相同的弹iE t ， 在梁 r. D 扯作用 -)J p ，如同所示，
5
设 已知 弹i齿 刚性系数 C (= 1 ) ， 试求
A 、 B 、 C 处 三 个弹贺各圭 )J 多少?
解
P_ 7 FA = 同 F. =-'-- P,F" ='- P
F o mllX= 5 2 =38.1 MPa
' -6 一长为 30cm 的钢 材，其受力恬况如国所示己知什 JX 面面积 A= I Oc rn2 材料的于l'性愤主 t E=2阳Gpa ，试求
(1) AC. CD DB 各段的应力和 l 变形
(2) AB 村 的 IJ、变形
解 ( 1 ) 0 Ac=-20MPa ， σ co=û ， σm=20MPa， NL σ'AC L
工程力学（静力学材料力学）第四版习题答案
静力学部分第一章基本概念受力图工程力学（静力学与材料力学）第四版习题答案全解由新疆大学&东华大学汤2-1 解：由解析法，23co s 80R X F X P P Nθ==+=∑12sin 140R Y F YP P Nθ==+=∑故：161.2R F N==1(,)a rc c o s 2944R Y R RF F P F '∠==工程力学（静力学与材料力学）第四版习题答案全解由新疆大学&东华大学 汤2-2解：即求此力系的合力，沿OB 建立x 坐标，由解析法，有123co s 45co s 453R X F X P P P K N==++=∑13sin 45sin 450R Y F YP P ==-=∑故：3R F K N== 方向沿OB 。
2-3 解：所有杆件均为二力杆件，受力沿直杆轴线。
（a ） 由平衡方程有：X =∑sin 300A C AB F F -=Y=∑co s 300A C F W -=0.577A B F W=（拉力）1.155A C F W=（压力）（b ） 由平衡方程有：X =∑co s 700A C AB F F -=Y=∑sin 700A B F W -=1.064A B F W=（拉力）0.364A CF W=（压力）（c ） 由平衡方程有：X =∑co s 60co s 300A C AB F F -=Y=∑sin 30sin 600A B A C F F W +-=0.5A B F W= (拉力)0.866A C F W=（压力）（d ） 由平衡方程有：X =∑sin 30sin 300A B A C F F -=Y=∑co s 30co s 300A B A C F F W +-=0.577A B F W= (拉力)0.577A C F W= (拉力)工程力学（静力学与材料力学）第四版习题答案全解由新疆大学&东华大学 汤2-4 解：（a ）受力分析如图所示：由x =∑4c o s 450R A F P ⋅-=15.8R A F K N∴=由0Y =∑s in 450R A R B F F P ⋅+-=7.1R B F K N∴=(b)解：受力分析如图所示：由x =∑c o s 45c o s 450R A R B F F P ⋅--=Y=∑s in 45s in 450R A R B F F P ⋅+-=联立上二式，得：22.410R A R B F K N F K N==2-5解：几何法：系统受力如图所示三力汇交于点D ，其封闭的力三角形如图示所以：5R A F K N= （压力）5R B F K N=（与X 轴正向夹150度）2-6解：受力如图所示：已知，1R F G = ，2A C F G =由x =∑c o s 0A C r F F α-=12c o s G G α∴=由0Y =∑s in 0A C N F F W α+-=工程力学（静力学与材料力学）第四版习题答案全解由新疆大学&东华大学 汤2s in N F W G W α∴=-⋅=-2-7解：受力分析如图所示，取左半部分为研究对象由x =∑co s 45co s 450R A C B P F F --=Y=∑sin 45sin 450C B R A F F '-=联立后，解得：0.707R A F P=0.707R B F P=由二力平衡定理0.707R B C B C B F F F P'===2-8解：杆AB ，AC 均为二力杆，取A 点平衡由x =∑co s 60co s 300A C AB F F W ⋅--=Y=∑sin 30sin 600A B A C F F W +-=联立上二式，解得： 7.32A BF K N=-（受压）27.3A CF K N=（受压）2-9解：各处全为柔索约束，故反力全为拉力，以D ，B 点分别列平衡方程（1）取D 点，列平衡方程由x =∑s in c o s 0D B T W αα-=D B T W c tg α∴==（2）取B 点列平衡方程：由Y=∑s in c o s 0B D T T αα'-=230B D T T ctg W ctg K Nαα'∴===2-10解：取B 为研究对象：工程力学（静力学与材料力学）第四版习题答案全解由新疆大学&东华大学 汤宏宇 整理由Y=∑s in 0B C F P α-=sin B C P F α∴=取C 为研究对象：由x =∑c o s s in s in 0B C D C C E F F F ααα'--=由0Y =∑s in c o s c o s 0B C D C C E F F F ααα--+=联立上二式，且有B C B CF F '= 解得：2c o s 12s in c o s C E P F ααα⎛⎫=+ ⎪⎝⎭取E 为研究对象：由0Y =∑c o s 0N H C E F F α'-=C E C EF F '= 故有：22c o s 1c o s 2s in c o s 2s in N H P P F ααααα⎛⎫=+= ⎪⎝⎭2-11解：取A 点平衡：x =∑sin 75sin 750A B A D F F -=Y=∑co s 75co s 750A B A D F F P +-=联立后可得： 2c o s 75A D AB P F F ==取D 点平衡，取如图坐标系：x =∑co s 5co s 800AD N D F F '-=c o s 5c o s 80N D A DF F '=⋅由对称性及A D A DF F '=工程力学（静力学与材料力学）第四版习题答案全解由新疆大学&东华大学 汤宏宇 整理c o s 5c o s 5222166.2c o s 80c o s 802c o s 75N N D A D P F F F K N'∴===⋅=2-12解：整体受力交于O 点，列O 点平衡由x =∑co s co s 300R A D C F F P α+-=Y=∑sin sin 300R A F P α-=联立上二式得：2.92R A F K N=1.33D C F K N=（压力）列C 点平衡x =∑405D C A C F F -⋅=Y=∑305B C A C F F +⋅=联立上二式得：1.67A C F K N=（拉力）1.0B CF K N=-（压力）2-13解：（1）取DEH 部分，对H 点列平衡x =∑R D R E F F '=Y =∑R D F Q =联立方程后解得：R D F =2R E F Q'=（2）取ABCE 部分，对C 点列平衡x =∑co s 450R E R A F F -=Y=∑sin 450R B R A F F P --=工程力学（静力学与材料力学）第四版习题答案全解由新疆大学&东华大学 汤宏宇 整理且 R ER EF F '=联立上面各式得：R AF =2R B F Q P=+（3）取BCE 部分。
工程力学材料力学第四完整版本习题答案解析
工程力学材料力学（北京科技大学与东北大学）第一章轴向拉伸和压缩1-1：用截面法求下列各杆指定截面的内力解：(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注（轴向拉伸为正，压缩为负）1-2：高炉装料器中的大钟拉杆如图a所示，拉杆下端以连接楔与大钟连接，连接处拉杆的横截面如图b所示；拉杆上端螺纹的内径d=175mm。
以知作用于拉杆上的静拉力P=850kN，试计算大钟拉杆的最大静应力。
解：σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3：试计算图a所示钢水包吊杆的最大应力。
以知钢水包及其所盛钢水共重90kN，吊杆的尺寸如图b所示。
解：下端螺孔截面：σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面：σ2=2P S =8.72MPa上端双螺孔截面：σ3= 3P S =9.15Mpa∴σmax =15.4Mpa1-4：一桅杆起重机如图所示，起重杆AB为一钢管，其外径D=20mm,内径d=18mm;钢绳CB 的横截面面积为0.1cm2。
已知起重量P=2000N，试计算起重机杆和钢丝绳的应力。
解：受力分析得：F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5：图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS 1=h*t=40*4.5=180mm 2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2F S =38.1MPa1-6:一长为30cm 的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1) AC. CD DB 各段的应力和变形.(2) AB 杆的总变形.解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△l CD =CD LEA σ=0△L DB =DB LEA σ=-0.01mm(2) ∴ABl ∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知 材料的弹性模量E=200Gpa,试求各段的应力和应变. 解:31.8127AC ACCB CBPMPa S PMPa S σσ====AC AC AC LNL EA EA σε===1.59*104,CB CB CB LNL EA EA σε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa. 解:NllEAllε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9：用一板状试样进行拉伸试验，在试样表面贴上纵向和横向的电阻丝来测定试样的改变。
工程力学-材料力学第4版习题答案
第一章参考答案1-1：解：(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3=-P(d):N1=-2P,N2=P(e):N1=-50N,N2=-90N(f):N1=0.896P,N2=-0.732P注（轴向拉伸为正，压缩为负）1-2：解：σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3：解：下端螺孔截面：σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面：σ2=2PS =8.72MPa上端双螺孔截面：σ3=3PS =9.15Mpa∴σmax =15.4Mpa1-4：解：受力分析得：F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5MPa1-5：解:F=6PS1=h*t=40*4.5=180mm2S2=(H-d)*t=(65-30)*4.5=157.5mm2∴σmax=2FS =38.1MPa1-6:解:(1)σAC =-20MPa,σCD =0,σDB =-20MPa;△l AC =NL EA =AC LEA σ=-0.01mm△l CD =CD LEA σ=0△L DB =DB LEA σ=-0.01mm(2)∴AB l ∆=-0.02mm1-7:解:31.8127AC AC CB CB P MPa S P MPa S σσ====AC AC AC L NL EA EA σε===1.59*104,CB CB CB L NL EA EA σε===6.36*1041-8:解: Nll EAl l ε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9：解：208,0.317E GPa ν==1-10：解：[][]max59.5MPa σσ=<1-11：解：（1）当45o α=，[]11.2σσ=>强度不够（2）当60o α=，[]9.17σσ=<强度够1-12：解：[]360,200200200*1013.3100*150*10Y p kNS P kNS MPa A σσ-==∴=====<∑1-13：解：[]max 200213MPa MPaσ=<1-14：解： 1.78, 1.26d cm d cm==拉杆链环1-15解：BC F ==70.7kN70.70.505140F S FS σσ=∴=== 查表得：45*45*31-16解：(1)[]2401601.5s s n σσ===MPa [][]24P S P dσσπ≤∴≤24.4D mm∴=(2)2119.51602P P MPa MPaS d σπ===≤⎛⎫ ⎪⎝⎭1-17解：（1）2*250*6154402D F P A N π⎛⎫=== ⎪⎝⎭78.4AC F MPa S σ==300 3.8378.4s n σσ∴===[][]''''60*3.14*15*1542390F SF S Nσσ===='61544014.521542390F n F ===≈1-18解：P=119kN1-19解：::3:4:535()44AB BC AB BC S P S S P S P =∴==拉，[][][]112841123484AB AB S A kN S P kNP kN σ=====同理所以最大载荷84kN1-20解：P=33.3kN1-21解：71,,12123A B C P F F P F P ===1-22解：10MAX MPaσ=-1-23解：A B X R R R=∴==∑t r l l ∆=∆t AB l l tα∆=21211111223533131.3cd R AC DB CD AC CD CD AF CD MAX Rl Rl l l l l EA EA Rl Rl Rl l EA EA EA EA t EA t R l S MPa A ααασ∆=∆+∆+∆=+=+=∴====第二章习题2-1一螺栓连接如图所示，已知P=200kN ，=2cm ，螺栓材料的许用切应力[τ]=80Mpa，试求螺栓的直径。
工程力学--材料力学(北京科大、东北大学版)第4版1-3章习题答案
第一章参考答案1-1：解：(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注（轴向拉伸为正，压缩为负）1-2：解：σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa ∴σmax=35.3Mpa1-3：解：下端螺孔截面：σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面：σ2=2PS =8.72MPa上端双螺孔截面：σ3= 3PS =9.15Mpa∴σmax =15.4Mpa1-4：解：受力分析得：F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5：解:F=6PS1=h*t=40*4.5=180mm2S2=(H-d)*t=(65-30)*4.5=157.5mm2∴σmax=2FS =38.1MPa1-6:解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△ l CD =CD LEA σ=0△ L DB =DB LEA σ=-0.01mm(2) ∴AB l ∆=-0.02mm 1-7:解:31.8127AC ACCB CBPMPa S PMPa S σσ====AC AC AC LNL EA EA σε===1.59*104, CB CB CB LNL EA EA σε===6.36*1041-8:解:Nl l EA l l ε∆=∆=∴N EA ε=62.54*10N EA N ε∴==1-9：解：208,0.317E GPa ν==1-10：解：[][]max 59.5MPa σσ=<1-11：解：（1）当45oα=，[]11.2σσ=>强度不够（2）当60oα=，[]9.17σσ=< 强度够1-12：解：[]360,200200200*1013.3100*150*10Y p kNS P kNS MPa A σσ-==∴=====<∑1-13：解：[]max 200213MPa MPa σ=< 1-14：解： 1.78, 1.26d cm d cm ==拉杆链环 1-15 解：BC F ==70.7 kN70.70.505140F S FS σσ=∴===查表得： 45*45*3 1-16解：(1)[]2401601.5ssn σσ===MPa[][]24PS Pd σσπ≤∴≤24.4D mm∴=(2)2119.51602PPMPa MPaSd σπ===≤⎛⎫ ⎪⎝⎭1-17 解：（1）2*250*6154402D F P A Nπ⎛⎫=== ⎪⎝⎭78.4AC FMPa S σ==300 3.8378.4s n σσ∴===[][]''''60*3.14*15*1542390F S F S Nσσ===='61544014.521542390F n F ===≈1-18 解：P=119kN 1-19 解：::3:4:535()44AB BC AB BC S P S S P S P =∴==拉，[][][]112841123484AB AB S A kNS P kNP kNσ=====同理所以最大载荷 84kN 1-20 解： P=33.3 kN 1-21 解：71,,12123A B C P F F P F P ===1-22 解：10MAX MPa σ=-1-23 解：A B X R R R =∴==∑t r l l ∆=∆ t A B l l tα∆= 21211111223533131.3cdR AC DB CD AC CD CDAF CD MAX Rl Rl l l l l EA EA Rl Rl Rl l EA EA EA EA t EA tR l SMPa A ααασ∆=∆+∆+∆=+=+=∴====第二章习题2-1 一螺栓连接如图所示，已知P=200 kN ， =2 cm ，螺栓材料的许用切应力[τ]=80Mpa ，试求螺栓的直径。
《材料力学》Ⅱ(第四版)答案
P u \:PN1PD[ u TO 0$ FRV FRV PD[PD[u M 00]PN1 $ VLQ VLQ PD[PD[u M 00\PN1PD[PD[ u uu u \\]]$:0:0V 03D \$%PO\¸¸¹·¨¨©§ ¸¸¹·¨¨©§]\\]\],T ,T (O Z Z Z¸¸¹·¨¨©§u u ¸¸¹·¨¨©§u u u uuPuu uu uuPPhPPhPP%]]:0PD[PD[V \\:0PD[PD[VPD[\%\%%Z Z Z Z &%]&$]&$&%\&\&\%O (,O)(,O )O Z Z u uTPu u u u u K Z ,]]u u u u u u u u u u u u u \%Z P u Pu u u u uE Z ,\\\$%]%(,O )ZPu u u u u u u)PD[]0u:03D PN1PD[ uV =\U\³³1GG$$)$$VV³³GG$$$\($\(UU³³GG$$$\,$\,,(,(U³³GG$$$\($\(@>@>QQQQ[\\E(\K[\E(&&\[\[K$E[$[K EQ&&\$(\$(\$($(N1)*3DZ(UV\(]³³GG$$$\($\(UU]6]]6(6(@>@>uuuuuuuu KKKPP³³³³G G G G $$$$,(,($\($\($\$\0UUU VV¦6 6 \)\)0$,\\PPH$DVLQ U $6]$WDD D VLQ VLQ VLQ 6 6 6UW )W U $U $)W ,6)DD VLQ U H |$TD$DD D D D D FRV VLQ FRV VLQ UH\PPP\PD[uuuu uG G 0:0VVHH$VV))%VVV$)&&VVVVVVV$)$)$)&&$)%V V ¦ D)D )D )0%$FRVV X D V $)VV VFRV V V D V $)FRVV V V V)))) V V D V V V)X)PPPP'GVVVXuuuu³G7G WUWUPN1@>VVKXuuu³G'7'G WUWUXV777VVVVVVU5UUU75UU³³WWUUWUUWUW75UW75UV::EFWFVGVLQGTG M UU$\666:GGGGGU UUUUGGGGGGU UUUUUVEK EK ::03DVV PPu u \\\F W V\\\66: uPP @ > u u \P N1 V V X u u u :0VPPPP KE 03DVVD$X X0O T O )00%$XD OD O T D O )%X XD OD O T D O D O TDE(GO)(GO)G (O )($O )9LLL ¦u[G [)991DFO[T[[0dd³³O O[[0[[0(,9(,O TO TO T(,[TO[T[(,OO@>@GG>³³($O )[[0[[0(,9OO@G G >1DEHV %$[$&³³ HH HH H H V@>''''HDOO[$$&$&$&»»»¼º«««¬ªD%OO%%Y[$\$$%$%$%$%''H[$\$D D%''F$DD(,)O)9$\FG($O)(,O)9ww'O)OT)T+$')GGG(,D 0\0[[D[0D (,09D D0%%%G GHH HE9$'¿¾½¯®³³9³³w wOO[[TO[TO [[TO[TO (,)9)$'(,TO$%%³³w wO O ))$\O )\O )(,[[)(,)9GG$' )))9 w wGG$TGG%TGG @>³³w w O O $\)\(,[[T[[TO)(,)9%,$%$%D&0&³³ O O \\)\\)(,9G G^ H ³G @ >O &[[O 0)O )`G @> [)O [O 0)O &³E@GG >DD[D)D \)\(,)9(,)D&T &&T &0FG@>GG^³³³ DDD [[D )\)D [)[`G @ >G G 9 $%'³³³w w D D D [[D )\)D [)[(,)9G@ >G G ^³³ DD\\))D [)[G G ³ DD )D )>G @[[+ $%'S9$%'$$$FFTw w$%0$%$%09T³³SG VLQ FRV G FRV VLQ TT T T T T )5*,5)5(,5S*,)5$%DDTTT VLQ $%TFRV($O )($O )9$&$&$%$%$))))$&$%+$'($)D )9)$%D'%9D%E³³ O O '[[T[;[(,[[[TO ;(,G G ' (,;O O T O ;(,O TO ;(,O;)O O [);O [0 w w ³³ O O $[O )O O [);O (,[[;[O )(, G @G 'O )O O );O (,O O ;O )O (,);)$)D 0$)D 0%I))D;;;E;³TO ;O;EE;;;³D[T[(,9;;9FED N1 N1 ;N1 N1 ;PN1 D ;0%PN1TE E ;D ;0&TD TDTDTD 016$%&TGO[[;[0ddwwww[0[;wwwwdd[7;7O[;[7O[;)[[;[0ddwwww;0[;O[;7O;7O;[7ddwwww³³@GG> O O[[;)[[;[[[;(,'³O3[O O;*,G(,*, SSO;O)O;(,*,O;)O;O;³G FRV VLQ VLQ T T T T (,)5 (,)5(,)5G VLQ $0$50)5(,TT T³E>FRVFRV TT T5;)50 @G@>(,)5 @(,)5G VLQFRVFRV T T T T '55)5(,;$\³FRV FRVFRVT T T (,)5TT T T G FRV VLQVLQ$;³G FRV T T T 5)5(,;$³(,)5FFRV T w w 5)³G FRV FRV T T T(,)5(,)5G VLQ FRV TT T '55)5(,;$\³G FRV TT T 5)5(,;$(,)5GVLQVLQ dd w w T T T T 55))5)5055T³³5$\55)5(,[[)[(,G VLQ VLQ T T T (,)5(,)5(,)5G FRV VLQ T T T '55)5(,;$[³G VLQGTT T³(,)5(,)5(,)5HG VLQ VLQ T T T '55)5(,$]³³³SGFRV FRV G FRV T TT T T *,)5(,)5@`^@w w w w ;7;0\³ $$$G @ VLQ FRV > T T '555(,;$[G VLQ VLQ T T T MT 5)5(,$³PPG *3D('O )7)O [7 w w³³ O O '(,[O )O (,[[)[(,G G '³³ OO[O )O *,[[)[SGG S S*,)O (,)O *,)O O O O (,)u u u uu u u uu u u u u u u u)*['[GG G G G G '' '*&*%*$*G 'G G 'G G 'G ' '*&*%*$*GGG GG 'O($O($)9L LL %%[DEO [OO [TO [0d dEO [[[0d d³O$[(,[0[0 GT ³ G O [(,T[[(,O [TO O O G @ > ³ (,TO (,TO(,TOFD$EO [[[0d d[O O [[[0O [Od d³O&[(,[0[0 GG ³ H G O [(,[[O 0³ O O [(,[O 0[O 0 H H G(,O 0(,O 0(,O 0 H H HFO [O[[0d dGD$O [T[[0d dO[O O [TO T[[0d dEO[[[0d dO[O O[O [[[0d d³G@>OO[(,O[O[TOT[(,TOP Pd d[[[[[0($F(,D$E%$ '&F&' & ' E) ) 1³³ DD [(,[)[[(,[)[G G (,)DF%&''EFGD'&)[[0+' '@G G > ³³ DD [D [D )[[)D (, (,)DG[0[0'T ³³³ D D D[[D )[)D [)[(, @G G G >(,)D&%)D [0&&F&%[0%$[0 [7EO[7 &&³ O[O TO *,S GS*,TO (,TOFVLQFRVT T T 5G VLQFRVFRV T T T T 55)5(,!S (,)5³FRV 5G )5(,$TTF))[[05[d dVLQ T T )50(,)5³³SG VLQ FRV G FRV VLQ TT T T T T T )5*,)5(,$ S*,)5(,)5$T$$G$DK$KO [0d d TE(,)O Z Z$%EF。
工程力学材料力学第四版习题答案解析
工程力学材料力学（北京科技大学与东北大学）第一章轴向拉伸和压缩1-1：用截面法求下列各杆指定截面的内力解：(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注（轴向拉伸为正，压缩为负）1-2：高炉装料器中的大钟拉杆如图a所示，拉杆下端以连接楔与大钟连接，连接处拉杆的横截面如图b所示；拉杆上端螺纹的内径d=175mm。
以知作用于拉杆上的静拉力P=850kN，试计算大钟拉杆的最大静应力。
解：σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3：试计算图a所示钢水包吊杆的最大应力。
以知钢水包及其所盛钢水共重90kN，吊杆的尺寸如图b所示。
解：下端螺孔截面：σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面：σ2=2P S =8.72MPa 上端双螺孔截面：σ3= 3P S =9.15Mpa∴σmax =15.4Mpa1-4：一桅杆起重机如图所示，起重杆AB为一钢管，其外径D=20mm,内径d=18mm;钢绳CB 的横截面面积为0.1cm2。
已知起重量P=2000N，试计算起重机杆和钢丝绳的应力。
解：受力分析得：F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5：图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS 1=h*t=40*4.5=180mm 2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2F S =38.1MPa1-6:一长为30cm 的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1) AC. CD DB 各段的应力和变形.(2) AB 杆的总变形.解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△l CD =CD LEA σ=0△L DB =DB LEA σ=-0.01mm(2) ∴ABl∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知材料的弹性模量E=200Gpa,试求各段的应力和应变.解:31.8127ACACCBCBPMPaSPMPaSσσ====ACACACLNLEA EAσε===1.59*104,CBCBCBLNLEA EAσε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa.解:QNllEAllε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9：用一板状试样进行拉伸试验，在试样表面贴上纵向和横向的电阻丝来测定试样的改变。
工程力学--材料力学第4版第三章习题答案
题3-2图试绘下列各轴的扭矩图，并求出 。
已知ma=2o oN ・ m,mb=4OoN.m,mc=6ooN,m.<10<b)弟二早习题3-1试求图视各轴在指定横截面17、2・2和3・3上的扭矩，并在各截面上表示出钮 矩的方向。
3・2试绘岀下列各轴的钮矩图，并求c=©==®zz ©=3m 2m3znm4 税(a)3-4 一传动轴如图所示，已知 ma=i3oN..cm, mb=3OoN.cm , mc=iooN.cm,md=7oN.cm;^$段轴的直径分别为：Dab=5cm, Dbc=7・5cm, Dcd=5cm （1）画出扭矩图；<2）求1-4、2-2、3-3截面的最大切应力。
3・5图示的空心圆轴，外径D=8cm,内径d二6・巧5,承受扭矩m=ioooN.m・（1）求弘、％（2）绘出横截而上的切应力分布图；（3）求单位长度扭转角，已知G=8ooooMpa・3-6已知变截而钢轴上的外力偶矩^^SooN.m, =i2ooN.m,试求最大切应力和最大相对扭矩。
已知G=8o*l沪Pa.题3-6图3-7 一钢轴的转矩n=24o/min.传递功率丹=44」kN.m.已知L可=4ol\4pa,2」」3,G=8o*l，MPa,试按强度和刚度条件计算轴的直径解：轴的直径由强度条件确泄，3-8图示实心轴通过牙嵌离合器把功率传给空心轴。
传递的功率=7-5kw,轴的转速n=ioor/min,试选择实心轴直径和空心轴外径叫2。
己知％/空2 =0.5，[rlL J=4oMpa・3-9图示AB轴的转速 n=i2or/min,AK B 轮上输入功率丹=4okw,此功率的一半通过锥齿轮传给垂直轴V,另一半功率由水平轴H传走。
已知锥齿轮的节圆直径 a=6oomm：各轴宜径为^=ioomm, ^2=8omm, ^3=6omm, t^=2oMPa.试对各轴进行强度校核。
3-1。
船用推进器的轴，一段是实心的，直径为28omm,列一段是空心的，其内径为外径的一半。
工程力学--材料力学第4版第三章习题答案
第三章习题3-1试求图视各轴在指定横截面1-1、2-2和3-3上的扭矩，并在各截面上表示出钮矩的方向。
3-2试绘出下列各轴的钮矩图，并求。
3-3试绘下列各轴的扭矩图，并求出。
已知ma=,mb=,mc=600N,m.3-4 一传动轴如图所示，已知ma=130N..cm, mb= , mc=, md=;各段轴的直径分别为：Dab=5cm, Dbc=, Dcd=5cm(1)画出扭矩图；（2）求1-1、2-2、3-3截面的最大切应力。
3-5 图示的空心圆轴，外径D=8cm,内径d=,承受扭矩m=.(1)求、（2）绘出横截面上的切应力分布图；（3）求单位长度扭转角，已知G=80000Mpa.3-6 已知变截面钢轴上的外力偶矩=, =, 试求最大切应力和最大相对扭矩。
已知G=80*Pa.3-7一钢轴的转矩n=240/min. 传递功率=已知=40Mpa,=,G=80*MPa, 试按强度和刚度条件计算轴的直径解：轴的直径由强度条件确定，。
3-8图示实心轴通过牙嵌离合器把功率传给空心轴。
传递的功率=,轴的转速n=100r/min,试选择实心轴直径和空心轴外径。
已知/=，=40Mpa.3-9 图示AB轴的转速n=120r/min,从B轮上输入功率=40kw,此功率的一半通过锥齿轮传给垂直轴V，另一半功率由水平轴H传走。
已知锥齿轮的节圆直径=600mm；各轴直径为=100mm, =80mm, =60mm, =20MPa，试对各轴进行强度校核。
3-10 船用推进器的轴，一段是实心的，直径为280mm，另一段是空心的，其内径为外径的一半。
在两段产生相同的最大切应力的条件下，求空心部分轴的外径D.3-11 有一减速器如图所示。
已知电动机的转速n=960r/min, 功率=5kw；轴的材料为45钢，=40MPa 试按扭转强度计算减速器第一轴的直径。
3-12 一传动轴传动功率=3kw，转速n=27r/min，材料为45钢，许用切应力=40MPa。
工程力学--材料力学(北京科大、东北大学版)第4版4-6习题答案
第四章习题4-1 求下列各梁指定截面上的剪力Q和弯矩M。
各截面无限趋近于梁上A、B、C等各点。
4-2 试列出下列各梁的剪力方程和弯矩方程，作剪力图和弯矩图，并求和。
4-3 用叠加法作以下各梁的弯矩图。
并求出。
4-4 用剪力、弯矩和分布载荷集度之间的微分关系校核前面已画的剪力图和弯矩图是否正确。
4-5 不列剪力方程和弯矩方程，作以下各梁的剪力图和弯矩图，并求出和。
4-6 用合适的方法作下列各梁的剪力图和弯矩图。
4-7 试根据载荷、剪力图和弯矩图之间的关系，检查下列各梁的剪力图和弯矩图是否正确，并对错误之处加以改正。
4-8 作下列构件的内力图。
4-9 在梁上行走的小车二轮的轮压均为P ，如图所示。
问小车行至何位置时梁内的弯矩最大？最大弯矩值是多少？设小车的轮距为c，大梁的跨度为。
参考答案4-1 解：题（b）（1）求支反力（见图）由，l-P l=0 =由，（2）剪力按计算剪力的规则（3）弯矩按计算弯矩的规则其它各题的答案：（a）（c）（d）（e）（f）4-2 解：题c(1)剪力和弯矩方程以左端A为原点，任一截面距左端的距离为x（图）\剪力方程:弯矩方程:(2 )剪力图与弯矩图按上述剪力方程和弯矩方程绘剪力图和弯矩图（3）与值由及得=200N =950题（f）（1）求支反力（见图）由，600-1004040=0=由，q4020-60=0=校核：+=2667+1333=4000N=q40=10040 所以支反力计算正确（2）剪力和弯矩方程以左端为原点，任一截面距左端的距离为x，则得剪力方程：弯矩方程（2）剪力图和弯矩图按上述剪力及弯矩方程绘出图及所示的剪力图和弯矩图所示剪力图和弯矩图.图中最大弯矩的截面位置可由，即剪力的条件求得Q（x）=3333-100x=0x=33.3cm（4）及由及得=2667N ，=355其他各题的答案：（a）=ql =（b）（d）（e）（g）（h）（i）（j）4-3 解：题c分别作、q单独作用时的弯矩图（图、），然后将此二图叠加得总的弯矩图。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2-1
（ 1）
2-3
A1=400mm2,A2=300mm2,试求1-1、2-2截面 上的应力。
2-5
2-5
（1）求各杆内力。以结点 B为研究对象受力分析如图 所示： 建立直角坐标系，因受力 平衡可列平衡方程： α
F F
y 0, F FNBC cos 0 F NBC F y 0, FNBC sin FNAB 0 FNAB （受压） FNBC 125kN
3
2-6
2-7
FN 解：首先根据公式 求横截面上的应力: A 3 FN 2010 N 6 10 Pa 1MPa 6 A 100 20010 m 1 2 sin 2 (1)分别代入公式 cos 、 2 得斜截面m-m上的应力为：
2 3 (cos ) 1MPa 0.75MPa ( ) 6 4 6 1 1 3 sin(2 ) 1MPa 0.433MPa ( ) 2 6 2 2 6 1 2 (1)根据公式 cos 、 sin 2 知： 2 正应力最大，此时， 当 0时， max cos2 0 1MPa 切应力最大，此时， 当 时， 4 1 max sin( 2 ) 0.5MPa 2 4
TAB l AB TBCl BC TCD lCD GI p GI p GI p
0.4m 3 3 3 ( 10 N m 2 10 N m 2 10 N m) 10 3 4 8 10 Pa (8010 m) 32
0.124102 rad
习题 第3章
3-15
解：先由杆的强度条件确定所需的直径，直径 确定后，再按杆的刚度条件校核刚度。
Tmax Tmax 由杆的强度条件： max 3 WP d 16
得：
16Tmax d3
3 16 6 10 Nm 3 91.4mm 6 4010 Pa
（3）计算板的最大拉应力
F1 F 400103 N 第1段： 1 A t (b d) 20103 m (200 30) 103 m 117.6MPa 1 1
F2 2F / 3 266.7 103 N 2 95.3MPa 第2段： 3 3 A 2 t1 (b 2d) 2010 m (200 2 30) 10 m
满足挤压强度。
习题 第3章
3-5
Ⅰ
Ⅱ Ⅲ
解：Ⅰ对Ⅱ、Ⅲ剪切强度校核： FS F 由公式， A 4 0.2 2 t
得：
F 200103 N t 83.3mm 6 4 0.2m 2 4 0.2m 2 1.5 10 Pa
习题 第3章
习题 第3章
t
2πR0
所以开口环最大切应力：
T T 3T 开 b max t 2 3 1 It 2R 0 t 2R 0 t 3
于是两杆最大切应力之比为：
T T 2 闭 2A0 t 2 R 0 t t 1 3T 3T 开 3R 0 16.5 2 2 2R 0 t 2R 0 t
F2 FN BC 35.5kN
F Min(F1, F2 )
FAB F
FBC
2-17
2-20
FN l l EA
关键：
静力方面
l1 l2 l3
几何方面
物理方面
2-21
C
D
E
静力方面 几何方面 物理方面
习题 第2章
2-22 P225 附录A
2
A钢 3.086cm
F 60103 N 78.1MPa 160MPa 2 A 0.768m
3
3
2
A t(b d) 12103 m(80103 m 16103 m) 0.768m2
习题 第3章
解：先由杆的强度条件确定所 3-4 需的直径，直径确定后，再按 杆的刚度条件校核刚度。 因t<2t1,由铆钉的强度条件：
3-5
Ⅰ
Ⅱ Ⅲ
解：Ⅰ、Ⅱ对Ⅲ剪切强度校核： FS F 由公式， A 4 0. 3 t
得：
F 200103 N t 111.1mm 6 4 0.3m 4 0.3m 1.5 10 Pa
习题 第3章
3-7
解：首先分析铆钉 和主板的受力。因 每个主板有3个材料、 直径相同的铆钉， 故每个铆钉受力为 FS F/3，因双剪切，则 FS=F/6,受力图如 图（a）所示，主板 F/3 受力如图（b）所 FS 示。 （ a）
[FN ]AB A 160106 Pa 1 3.14 (20103 m) 2 50.2kN
[FN ]AB F1 35.5kN 2
4
FAB F FBC
2-10
(2) 让杆BC充分发挥作用， 相应最大轴力为：
[FN ]BC A 160106 Pa 1 3.14 (20103 m) 2 50.2kN 4
m
习题 第3章
3-17
Tl Me l 180 2 103 N m 0.2m 180 o 0.43 4 4 GI p GI P G (D d ) 32 E G 80.99GPa G
2(1 )
E 210 GPa 1 1 0.3 2G 2 80.99GPa
习题 第2章
2-8
解：取结点A为脱离体，受力 分析如图所示,求出两杆内力 与F关系为：
Fx 0, F2 sin 30 F1 sin 45 0
F 0 , F cos 45 F cos 30 F 0 y 1 2 F1 20.7kN 联立求解得： F2 29.3kN （受拉）
20 kN
习题 第3章
3-3
Ab dt 1610 m 1210 m 0.192m
FS 60103 N 99.5MPa 140MPa 2 AS 0.201 m Fb 20103 N bs 104.2MPa bs 300MPa 2 A b 0.192m
l钢 l木
FN l l EA
习题 第2章
2-25
（1）假设卸载后钢筋受力 FI，混凝土F2，现分析两者 关系。 因卸载后无外力，所以FI、 F2应为一对相互作用力，即： △ l1 F1 F2 而且，F2一定是压力。
（2）分析两者变形关系。
l2 l3 l1
△ l3
△ l2
max FN 2 AS 1 d 2 4
2F d2
3 2 40 10 Nm 2 20.6mm 6 6010 Pa
F
得：
习题 第3章
3-4 校核挤压强度： 将d=20.6mm代入公式
Fb F 40103 N b 97.1MPa bs 120MPa 3 3 A b td 2010 mm 20.6 10 mm
E2A2 F2 F(压力） E1A1 E 2 A 2
习题 第3章
3-2
F FS b A
解题关键是求受剪 面面积A。
习题 第3章
3-3
剪切强度
挤压强度
板抗拉强度 搭接接头。
F F F 60 kN Fs 20 kN Fb n 3 n 3 A s 1 3.14 (16103 m) 2 0.201 m2 4
F 2F/3
(b)
F
+
习题 第3章
（1）计算铆钉的切应力
3
F 2F/3
2
1 + (b)
FS F6 66.7 10 N 2 94.3MPa 3 2 AS d 4 3.14 (3010 ) / 4
F
（2）计算挤压应力
Fb F 3 133.3 103 N bs 222.2MPa 3 3 A b dt 1 3010 m 2010 m
式中，△l1-F作用下钢筋的总伸长； △l2-F1、F2作用下 钢筋及混凝土的伸长； △l3-混凝土反力对钢筋造成的伸 长量。
习题 第2章
2-25
△ l1 △ l3
l2 l3 l1
F2l F2l F l E 2 A 2 E1A1 E1A1
△ l2
F2 E2F 2 (压应力） A 2 E1A1 E 2 A 2 F1 E2F A2 1 (拉应力） A1 E1A1 E 2 A 2 A1
习题 第3章
3-14
Tl GI p
T 2kNm 1kNm
+ -
+
2kNm
习题 第3章
3-14
BC TBClBC 2 103 N m 0.4m 2 0 . 248 10 rad 10 3 4 GI p 8 10 (8010 m) 32
D AB BC CD
习题 第4章
FB FC
4-1(1) 1)求支反力
2)求n-n截面剪力 3)求n-n截面弯矩
3 M C 0 F 2 l FB l 0
x
x
FNAB 75kN（受拉）
2-5 （2）求各杆应力。 根据公式： FN 得： A
FNAB 7510 N AB 25MPa AB杆应力： （拉应力） 3 2 A 3 10 m 3 FNBC 12510 N BC 41.7MPa （压应力） BC杆应力： 3 2 A 3 10 3 m FNAC 10010 N AC 33.3MPa （拉应力） AC杆应力： 3 2 A 3 10 m 3 FNCD 7510 N 25MPa （压应力） CD杆应力：CD 3 2 A 3 10 m