概率论与数理统计-数学期望
合集下载
概率论与数理统计 4.1 数学期望

则 X 的数学期望为
a xb 其它
x ab E( X ) = x f ( x) dx = dx = a ba 2 即数学期望位于[ a , b ] 的中点 .
b
8
二、随机变量函数的数学期望: 1、定理4.1: 设 Y = g(X)是随机变量 X 的函数, (g为连续函数)
=5 (元)
13
三、数学期望的性质:
设 C 为常数, X 和 Y 是随机变量,
且 E(X) 和 E(Y) 都存在 , 则 (1) E(C) = C ; (2) E(CX) = CE(X ) ; (3) E(X +Y ) = E(X ) + E(Y ) ; (4) 若 X 与 Y 相互独立, 则有 E(XY ) = E(X ) E(Y ) .
若广义积分
x f ( x )dx 绝对收敛, 则称这个
积分为随机变量 X 的数学期望, 记为
E( X ) =
x f ( x )dx
7
例2:设 X 服从 [ a , b ] 上的均匀分布, 求 E(X) 解 X 的密度函数为
1 , f ( x) = b a 0 ,
若
g( x , y ) f ( x , y ) dxdy 绝对收敛, 则有
E( Z ) =
g( x , y ) f ( x , y ) dxdy
12
例3: 某商店出售某种小饰物, 每销售一件可赚
5元, 根据以往资料, 每天的销售量 X 是随机
变量, 取值为 0, 1, 2, 3 件的概率分别为0.4, 0.3, 0.2, 0.1 . 试求一天的平均利润 . 解 设一天的利润为 Y , 由题设有 Y = 5 X , 由定理4.1, 有 E(Y) = E(5X) =5×0×0.4+5×1×0.3+5×2×0.2+5×3×0.1
a xb 其它
x ab E( X ) = x f ( x) dx = dx = a ba 2 即数学期望位于[ a , b ] 的中点 .
b
8
二、随机变量函数的数学期望: 1、定理4.1: 设 Y = g(X)是随机变量 X 的函数, (g为连续函数)
=5 (元)
13
三、数学期望的性质:
设 C 为常数, X 和 Y 是随机变量,
且 E(X) 和 E(Y) 都存在 , 则 (1) E(C) = C ; (2) E(CX) = CE(X ) ; (3) E(X +Y ) = E(X ) + E(Y ) ; (4) 若 X 与 Y 相互独立, 则有 E(XY ) = E(X ) E(Y ) .
若广义积分
x f ( x )dx 绝对收敛, 则称这个
积分为随机变量 X 的数学期望, 记为
E( X ) =
x f ( x )dx
7
例2:设 X 服从 [ a , b ] 上的均匀分布, 求 E(X) 解 X 的密度函数为
1 , f ( x) = b a 0 ,
若
g( x , y ) f ( x , y ) dxdy 绝对收敛, 则有
E( Z ) =
g( x , y ) f ( x , y ) dxdy
12
例3: 某商店出售某种小饰物, 每销售一件可赚
5元, 根据以往资料, 每天的销售量 X 是随机
变量, 取值为 0, 1, 2, 3 件的概率分别为0.4, 0.3, 0.2, 0.1 . 试求一天的平均利润 . 解 设一天的利润为 Y , 由题设有 Y = 5 X , 由定理4.1, 有 E(Y) = E(5X) =5×0×0.4+5×1×0.3+5×2×0.2+5×3×0.1
概率论与数理统计第一节随机变量的数学期望

0.95.
2. 连续型随机变量函数的数学期望的求法:
(1)设X的概率密度为f ( x),则Y g( X )的数学期望为:
EY E[g( X )] g( x) f ( x)dx.
(2) 设( X,Y )的概率密度为f ( x,y),则Z g( X,Y )的数学期望为:
EZ E[g( X ,Y )] g( x, y) f ( x, y)dxdy.
0
1 3
.
(3)
E(X 2)
x2 f ( x)dx
1 2x3dx
0
1 2
x4
1 0
1 2
.
2. 连续型随机变量函数的数学期望的求法:
(1)设X的概率密度为f ( x),则Y g( X )的数学期望为:
EY E[g( X )] g( x) f ( x)dx.
(2) 设( X,Y )的概率密度为f ( x,y),则Z g( X,Y )的数学期望为:
0
0
(
xex
)
0
exdx
0
1
e x
0
1
.
(3) 正态分布N(, 2)的数学期望
设X服从正态分布,其概率密度为:
f (x)
1
( x )2
e
2 2
,
x ,
2
则 EX .
证明:E( X )
xf ( x)dx
+
x
( x )2
e 2 2 dx
2
令t
x
1
(t
)e
t2 2
dt
甲: 环数 8
9 10 乙: 环数 8
9 10
P 0.4 0.2 0.4
P 0.2 0.5 0.3
2. 连续型随机变量函数的数学期望的求法:
(1)设X的概率密度为f ( x),则Y g( X )的数学期望为:
EY E[g( X )] g( x) f ( x)dx.
(2) 设( X,Y )的概率密度为f ( x,y),则Z g( X,Y )的数学期望为:
EZ E[g( X ,Y )] g( x, y) f ( x, y)dxdy.
0
1 3
.
(3)
E(X 2)
x2 f ( x)dx
1 2x3dx
0
1 2
x4
1 0
1 2
.
2. 连续型随机变量函数的数学期望的求法:
(1)设X的概率密度为f ( x),则Y g( X )的数学期望为:
EY E[g( X )] g( x) f ( x)dx.
(2) 设( X,Y )的概率密度为f ( x,y),则Z g( X,Y )的数学期望为:
0
0
(
xex
)
0
exdx
0
1
e x
0
1
.
(3) 正态分布N(, 2)的数学期望
设X服从正态分布,其概率密度为:
f (x)
1
( x )2
e
2 2
,
x ,
2
则 EX .
证明:E( X )
xf ( x)dx
+
x
( x )2
e 2 2 dx
2
令t
x
1
(t
)e
t2 2
dt
甲: 环数 8
9 10 乙: 环数 8
9 10
P 0.4 0.2 0.4
P 0.2 0.5 0.3
《概率论与数理统计》数学期望

§4.3 随机变量函数的数学期望 例题
§4.3 随机变量函数的数学期望 例题
§4.3 随机变量函数的数学期望 例题
概率论与数理统计
§4.4 协方差和相关系数
协方差 相关系数 授课内容 例题
§4.4 协方差和相关系数 协方差
1. 定义
§4.4 协方差和相关系数 协方差
2. 协方差的计算公式
概率论与数理统计
§4.1 数学期望
离散型随机变量的数学期望
连续型随机变量的数学期望
授课内容
数学期望的性质
§4.1 数学期望 离散型随机变量的数学期望
1. 定义
§4.1 数学期望 离散型随机变量的数学期望
关于定义的几点说明
(2) 级数的绝对收敛性保证了级数的和不随级数各项次序的改变 而改变 , 之所以这样要求是因为数学期望是反映随机变量X 取可能值 的平均值,它不应随可能值的排列次序而改变.
§4.4 协方差和相关系数 相关系数
3. 不相关的定义
§4.4 协方差和相关系数 相关系数
4. 不相关性的判定
以下四个条件等价 (1) ρ 0; (2)Cov( X ,Y ) 0; (3) D( X Y ) DX DY;
(4)3 随机变量函数的数学期望 二维随机变量函数的数学期望
§4.3 随机变量函数的数学期望 二维随机变量函数的数学期望
一维随机变量函数的数学期望 二维随机变量函数的数学期望 授课内容 例题
§4.3 随机变量函数的数学期望 例题
§4.3 随机变量函数的数学期望 例题
§4.3 随机变量函数的数学期望 例题
5 .不相关与相互独立的关系
协方差 相关系数 授课内容 例题
§4.4 协方差和相关系数 例题
【精品】概率论与数理统计PPT课件第四章 数学期望和方差

8
9
10
P
0.1 0.3 0.6
Y
8
9
10
P
0.2 0.5 0.3
试问哪一个人的射击水平较高? 9
例1(续)
甲、乙的平均环数可写为
EX 80.1 90.3 100.6 9.5 EY 80.2 90.5 100.3 9.1
10
例2.对产品进行抽样,只要发现废品就认为这批产 品不合格,并结束抽样。若抽样到第 n件仍未发现 废品则认为这批产品合格。假设产品数量很大,抽 查到废品的概率是 p,试求平均需抽查的件数。
6
(3)泊松分布 X的所有可能取值为0,1,2,…,且
7
(4)几何分布 X的可能取值为1,2,…, 且 P(X=k)= (1-p)k-1 p, k= 1,2,….
由于
这可以由等式
两边同时对x求导数得到。
8
例1:
甲、乙两人射击,他们的射击水平由下表给出: X:甲击中的环数; Y:乙击中的环数;
X
p)nm
29
注意到二项分布B(n , p)的数学期望,就有 于是
注: 最后一步用了泊松分布数学期望的结果.
30
例8: 设X ~ U[0,], Y =sinX,求E(Y)。
解: X 的概率密度为 所以
31
例9 设二维随机变量(X ,Y)的密度函数为 求E(X), E(Y), E( X + Y ), E(XY), E(Y / X) 解:
36
37
最终, 显然,y = 3500 时,E (Y )最大,
E(Y)max =8250万元.
38
例11.假设由自动线加工的某种零件的内径 X (mm)~
N ( ,1). 已知销售每个零件的利润T (元)与销售零件
概率论与数理统计课件数学期望
二、重要概率分布的方差
1. 两点分布
已知随机变量 X 的分布律为
X1
0
p
p 1 p
则有 E( X ) 1 p 0 q p, D( X ) E( X 2 ) [E( X )]2 12 p 02 (1 p) p2 pq.
2. 二项分布
设随机变量 X 服从参数为 n, p 二项分布, 其分布律为
若Y a.
E(Q) 0 QfY ( y)d y
x[my n(a y)] 1 ey θ d y ma 1ey θ d y
0
θ
x
θ
(m n)θ (m n)θea θ nx,
令 d E(Q) (m n)ea θ n 0, dx
D( X ) D(Y ).
推广 若 X1, X2 ,, Xn 相互独立,则有
D( X1 X2 Xn ) D( X1) D( X2 ) D( Xn ).
(4) D( X ) 0 的充要条件是 X 以概率 1 取常数 C ,即
P{X C} 1.
5 k nk 3.37.
k0 n
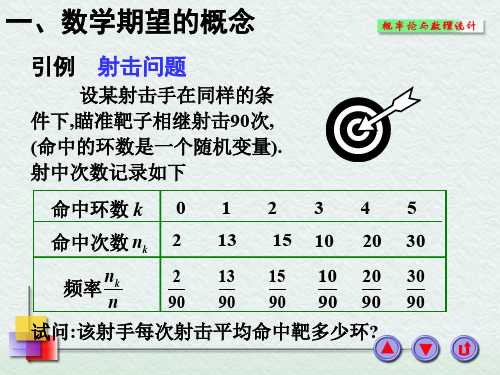
平均射中环数 5 k nk
随机波动 k0 n
频率随机波动
“平均射中环数”的稳定值 ?
5 k nk
k0 n
n
5
k pk
k0
随机波动
稳定值
“平均射中环数”等于 射中环数的可能值与其概率之积的累加
1. 离散型随机变量的数学期望
则有
E( g( X )) g( xk ) pk .
k 1
例5,P94,6
2. 连续型随机变量函数的数学期望 若 X 是连续型的,它的分布密度为 f (x) , 则
《概率论与数理统计》课件 第七章 随机变量的数字特征

i 1,2, , 如果 xi pi , 则称 i 1 E( X ) xi pi 为随机变量X的数学期望; i 1
或称为该分布的数学期望,简称期望或均值.
(2)设连续随机变量X的密度函数为p( x),
如果
+
x p( x)dx ,
则称
-
E( X ) xp( x)dx 为随机变量X的数学期望.
5
例2.求二项分布B(n, p)的数学期望.
P(X
k)
n!
k!n
k !
pk
(1
p)nk ,k
1, 2,
, n.
n
解:EX kP{ X k}
k0
n
k
k0
n!
k!n
k !
pk
(1
p)nk
n
np
k 1
k
n 1! 1!n
pk1
k!
(1
p)nk
np[ p (1 p)]n1 np.
特别地,若X服从0 1分布,则EX p.
6
例3. 求泊松分布P( )的数学期望.
注:P( X k) k e , k 1, 2, .
k!
解:EX k k e e
k1
e
k1
k0 k !
k1 k 1 !
k1 k 1 !
ee
e x 1 x 1 x2 1 xn [这里,x ]
当 a 450时,平均收益EY 最大.
28
第二节 方差与标准差
29
引例
比较随机变量X、Y 的期望
X3 4 5 Y1 4 7 P 0.1 0.8 0.1 P 0.4 0.2 0.4
01 2 3 4 5 67
概率论与数理统计-数学期望_图文

因每个球落入每个盒子是等可能的均为1/M, 所以,对第i 个盒子,一个球不落入这个盒子 内的概率为(1-1/M)。故N个球都不落入这个 盒子内的概率为(1-1/M)n ,即
最常用的数字特征是:期望和方差。
第四章 数字特征
§4.1 数学期望
4.1.1 离散型随机变量的数学期望 概念引入:
某车间对工人生产情况进行考察,车工 小张每天生产的废品数 X 是一个随机变量 。如何定义 X 的平均值?
若统计了100天小张生产产品的情况,发现 : 32天没有出废品;30天每天出一件废品; 17天每天出两件废品;21天每天出三件废品。
可以得到这n天中,每天的平均废品数为
这是以频率为 权的加权平均
由频率与概率的关系,
不难想到:求废品数X的平 均值时,用概率替代频率, 得平均值为:
这样,就得到一个确定的数
这是以概率为 权的加权平均
——随机变量X的期望(均值) 。
定义1: 设X是离散型随机变量, 概率分布为 P{X=xk}=pk , k=1,2, …。
解:设组织货源 t 吨。显然,应要求
2000≤t ≤4000。国家收益Y(单位:万元)是X
的函数Y=g(X)。表达式为
由已知条件, 知X的概率密度函为
可算得当 t = 3500 时, E(Y)=-2t2 + 14000t-8000000
达到最大值 1.55×106。 因此,应组织3500吨货源。
概率论与数理统计-数学期望_图文.ppt
前面讨论了随机变量及其分布。 如果我 们知道了随机变量 X 的概率分布,那么,关 于 X 的全部概率特征也就知道了。
然而,在实际问题中,概率分布是较难 确定的。且有时在实际应用中,我们并不需 要知道随机变量的所有性质,只要知道其一 些数字特征就够了。
概率论与数理统计-第4章-第2讲-随机变量函数的数学期望

因此只要掌握了期望的计算,所有的数字特征计算都解决了!
概率论与数理统计
学海无涯,祝你成功!主讲教 |例 设风速V是一个随机变量,它服从(0,a)上的均匀分布,而飞 机某部位受到的压力F是风速V 的函数:
F kV 2
(常数k > 0),求F 的数学期望.
01 随机变量函数的数学期望
如何计算随机变量函数的数学期望?
一种方法是: 因为g(X)也是随机变量,故应有概率分布,它 的分布可以由X的分布求出来. 一旦我们知道了g(X)的分布,就 可以按照期望的定义把E[g(X)]计算出来.
02 典型例题
例 设风速V是一个随机变量,它服从(0,a)上的均匀分布,而飞 机某部位受到的压力F 是风速V 的函数:
F kV 2
(常数k > 0),求F的数学期望.
E(Y ) g(x) f (x)dx
解
V
的概率密度为
f
(v)
1 a
,
0va
0, 其它
E(F ) E(kV 2 ) kv2 f (v)dv a kv2 1 dv 1 ka2
g(X )
3n,
n
X
,
3n,
n X,
3X (n X ), n X 4X n, n X
02 典型例题
E(Y ) g(x) fX (x)dx
1[
n
(4x n)dx
400
3ndx]
200 200
n
Y
g(X
)
3n,
n X,
4X n, n X
1 (2n2 1400n 8104 ) 200
g(xi , y j ) pij
ij
设连续 r.v. (X ,Y )的联合密度为 f (x ,y)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
近似, 该离散型r.v 的数 学期望是
阴影面积
近似为
f ( xi )xi
xi f ( xi )xi
i
这正是
x f (x)dx
的渐近和式.
小区间[Xi, Xi+1)
由此启发我们引进如下定义. 定义2 设X是连续型随机变量,其密度函数 为 f (x),如果
| x | f (x)dx
有限,定义X的数学期望为
1 101 32 0 23 0
对于一个随机变量,若它可能取的值是
X1, X2, …, 相应的概率为 p1, p2, …, 则对X作一系列观察(试验),所得X的试验值 的平均值也是随机的.
但是,如果试验次数很大,出现Xk的频率会 接近于pk,于是可期望试验值的平均值接近
xk pk
k 1
由此引入离散型r.vX的数学期望的定义如下:
k阶绝对中心矩 E(| X E( X ) |k )
其中 k 是正整数.
四、数学期望的性质
1. 设C是常数,则E(C)=C;
2. 若k是常数,则E(kX)=kE(X);
注意:由E(XY)=E(X)E(Y)
3. E(X1+X2) = E(X1)+E(X2);不一定能推出X,Y独立
n
n
推广 : E[ Xi ] E( Xi )
2 0.2
0.23
1 101 32 0 23 0
对试验次数(即天数)n,及小张的生产情况进行 统计,统计他不出废品,出一件、二件、三 件废品的天数n0,n1,n2,n3 , 并计算
M (n) 0 n0 1 n1 2 n2 3 n3 nn n n
与 0 p0 1 p1 2 p2 3 p3 进行比较.
在前面的课程中,我们讨论了随机变量 及其分布,如果知道了随机变量X的概率分 布,那么X的全部概率特征也就知道了.
P(x)
f (x)
o
x
o
x
然而,在实际问题中,概率分布一般 是较难确定的. 而在一些实际应用中,人 们并不需要知道随机变量的一切概率性质, 只要知道它的某些数字特征就够了.
某型号电视机的平均寿命 18000小时±200小时
所以权衡下来,情愿“搏一记”,去经营 西瓜,因它的期望值高.
我们介绍了随机变量的数学期望,它 反映了随机变量取值的平均水平,是随机 变量的一个重要的数字特征.
接下来我们将向大家介绍随机变量另 一个重要的数字特征:
方差
有一个箱子,里面装有10个 0 0 0 2 2 大小,形状完全相同的球, 1 1 1 3 3 号码如图.
规定从箱中任意取出一个球, 记下球上的号码,然后把球放 回箱中为一次试验.
1 101 32 0 23 0
记X为所取出的球的号码(对应废品数) . X 为随机变量,X的概率函数为
X
~
0 0.3
1 0.3
如何计算随机变量函数的数学期望? 一种方法是,因为g(X)也是随机变量,
故应有概率分布,它的分布可以由已知的X 的分布求出来. 一旦我们知道了g(X)的分布, 就可以按照期望的定义把E[g(X)]计算出来.
使用这种方法必须先求出随机变量函数 g(X)的分布,一般是比较复杂的 .
那么是否可以不先求g(X)的分布而只 根据X的分布求得E[g(X)]呢?
若设
X
i
1 0
如第i次试验成功 如第i次试验失败
i=1,2,…,n
则 X= X1+X2+…+Xn
因为 P(Xi =1)= p, P(Xi =0)= 1-p
E(Xi)= 1 p 0 (1 p)= p n
所以 E(X)= E( Xi ) = np
i 1
可见,服从参数为n和p的二项分布的随
机变量X的数学期望是np.
k 1
(n 1)!
n
1
n!
1
n
1 n
例3 设甲、乙两人玩必分胜负的赌博游戏, 假定游戏的规则不公正,以致两人获胜的概 率不等,甲为p,乙为q,p>q,p+q=1.为了补偿 乙的不利地位,另行规定两人下的赌注不相 等,甲为 a, 乙为b, a>b. 现在的问题是:a究 竟应比b大多少,才能做到公正?
E (Y
)E[g( X )]来自g( xk ) pk ,
k 1
X离散型
g(x)
f
( x)dx,
X连续型
该公式的重要性在于: 当我们求E[g(X)] 时, 不必知道g(X)的分布,而只需知道X的 分布就可以了. 这给求随机变量函数的期 望带来很大方便.
将g(X)特殊化,可得到各种数字特征: k阶原点矩 E( X k ) k阶中心矩 E([ X E( X )]k ) k阶绝对原点矩 E(| X |k )
i 1
i 1
4. 设X、Y独立,则 E(XY)=E(X)E(Y);
n
n
推广 : E[ Xi ] E( Xi() 诸Xi独立时)
i 1
i 1
五、数学期望性质的应用 例1 求二项分布的数学期望 若 X~B(n,p), 则X表示n重贝努里试验中的“成功” 次数. 现在我们来求X的数学期望 .
X~B(n,p),则X表示n重贝努里试验中的“成功” 次数.
何定义X的平均值呢?
32天没有出废品;
若统计100天,
30天每天出一件废品;
可以得到这100天中 每天的平均废品数为
17天每天出两件废品; 21天每天出三件废品;
0 32 1 30 2 17 3 21 1.27 100 100 100 100
这个数能否作为 X的平均值呢?
可以想象,若另外统计100天,车工小张不 出废品,出一件、二件、三件废品的天数与 前面的100天一般不会完全相同,这另外100 天每天的平均废品数也不一定是1.27.
例2 把数字1,2,…,n任意地排成一列,如果数 字k恰好出现在第k个位置上,则称为一个巧 合,求巧合个数的数学期望.
解: 设巧合个数为X, 引入
Xk
1, 数字k恰好出现在第k个位置上
0,
n
否则
k=1,2, …,n
则 X Xk
k1
由于 E(Xk)=P(Xk =1)
n
故 E(X ) E(Xk )
xi1 f ( x)dx xi
阴影面积
近似为
f ( xi )xi
f ( xi )( xi1 xi )
f ( xi )xi
小区间[xi, xi+1)
由于xi与xi+1很接近, 所以区间[xi, xi+1)中 的值可以用xi来近似代替.
因此X与以概率 f ( xi )xi 取值xi的离散型r.v
已知某地区成年男子身高X~ N (1.68, 2), E( X ) 1.68
这意味着,若从该地 区抽查很多个成年男子, 分别测量他们的身高,那 么,这些身高的平均值近 似是1.68.
三、随机变量函数的数学期望
1. 问题的提出:
设已知随机变量X的分布,我们需要计 算的不是X的期望,而是X的某个函数的期 望,比如说g(X)的期望. 那么应该如何计算 呢?
进行考察. 车工小张每天生产 的废品数X是一个随机变量. 如 何定义X的平均值呢?
某电话交换台每天8:00-9:00收到的呼叫数 X是一个随机变量. 如何定义X的平均值即该 交换台每天8:00-9:00收到的平均呼叫数呢?
我们来看第一个问题.
例1 某车间对工人的生产情况进行考察. 车工
小张每天生产的废品数X是一个随机变量. 如
期望与风险并存.数学家从期望值 来观察风险,分析风险,以便作出正确 的决策.
例如,有一家个体户,有资金一笔,如 经营西瓜,风险大但利润高(成功的概率为 0.7,获利2000元); 如经营工艺品,风险 小但获利少(95%会赚,但利润为1000元). 究竟该如何决策?
于是计算期望值: 若经营西瓜,期望值E1=0.7×2000=1400元. 而经营工艺品期望值E2=0.95×1000=950元.
由频率和概率的关系
这是 以频率为权的加权平均
不难想到,在求废品数X
的平均值时,用概率代替
这是
频率,得平均值为
以概率为权的加权平均
0 p0 1 p1 2 p2 3 p3 这样得到一个确定的数. 我们就用这个数作为 随机变量X的平均值 .
这样做是否合理呢?
不妨把小张生产中出废品的情形 用一个球箱模型来描述:
解: 设试开次数为X, P(X=k)= 1/n , k=1,2,…,n
于是
E(X)
n k1 k1 n
1 (1 n)n n2
n1 2
二、连续型随机变量的数学期望
设X是连续型随机变量,其密度函数为f (x),
在数轴上取很密的分点x0 <x1<x2< …,则X落
在小区间[xi, xi+1)的概率是
解:设甲赢的钱数为X,乙赢的钱数为Y, 依题意
b a
a b
X ~ p q , Y ~ q p ,
解:设甲赢的钱数为X,乙赢的钱数为Y,
依题意
X
~
b p
a q
,
a b Y ~ q p ,
E(X)=bp+(-a)q, E(Y)=aq+(-b)p
为对双方公正,应有 bp-aq=aq-bp=0, 故 a bp q
一般来说,若统计n天,
(假定小张每天至多出
三件废品)
n0天没有出废品; n1天每天出一件废品; n2天每天出两件废品; n3天每天出三件废品.
可以得到n天中每天的平均废品数为
0 n0 1 n1 2 n2 3 n3 nn n n
0 n0 1 n1 2 n2 3 n3 nn n n
下面的基本公式指出,答案是肯定的.
