2018届人教B版 简单几何体表面积和体积求法 单元测试
简单几何体的表面积与体积跟踪训练含答案

8.3简单几何体的表面积与体积跟踪训练(答案)一、选择题1、已知圆锥的底面半径为2,其侧面展开图为一个半圆,则该圆锥的母线长为( B )A.2B.2 2C.4D.4 2解:设圆锥的母线长为l,因为该圆锥的底面半径为2,侧面展开图为一个半圆,所以2π×2=πl,解得l=2 2.2、现有同底等高的圆锥和圆柱,已知圆柱的轴截面是边长为2的正方形,则圆锥的侧面积为( D )A.3πB.3π2 C.5π2 D.5π解:设底面圆的半径为R,圆柱的高为h,依题意2R=h=2,∴R=1.∴圆锥的母线l=h2+R2=22+1=5,因此S圆锥侧=πRl=1×5π=5π.3、等腰直角三角形的直角边长为1,现将该三角形绕其某一边旋转一周,则所形成的几何体的表面积为( B )A.2πB.2π或()1+2πC.22πD.22π或()2+2π解:如果绕直角边所在直线旋转,那么形成圆锥,圆锥底面半径为1,高为1,母线长就是直角三角形的斜边长2,所以所形成的几何体的表面积S=πrl+πr2=π×1×2+π×12=(2+1)π;如果绕斜边所在直线旋转,那么形成的是同底的两个圆锥,圆锥的底面半径是直角三角形斜边高为22,两个圆锥的母线长都是1,所以形成的几何体的表面积S=2×πrl=2×π×22×1=2π.综上可知,形成几何体的表面积是(2+1)π或2π.故选B.4、对24小时内降水在平地上的积水厚度(mm)进行如下定义:0~1010~2525~5050~100小雨中雨大雨暴雨小明用一个圆锥形容器接了24小时的雨水,则这一天的雨水属于哪个等级( B )A.小雨B.中雨C.大雨D.暴雨解:由相似关系可得,雨水形成的小圆锥的底面半径r =20022=50(mm),故 V 小圆锥=13×π×502×150=503·π(mm 3),从而可得积水厚度h =V 小圆锥S 大圆=503·ππ·1002=12.5(mm),属于中雨.5、埃及胡夫金字塔是古代世界建筑奇迹之一,它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则其侧面三角形底边上的高与底面正方形的边长的比值为( C )A .5-14B .5-12C .5+14D .5+12解:设正四棱锥的高为h ,底面正方形的边长为2a ,斜高为m ,依题意得h 2=12×2a ×m ,即h 2=am ①,易知h 2+a 2=m 2 ②,由①②得m =1+52a (舍负),所以m2a =1+52a 2a =1+54.故选C .6、已知圆柱的上、下底面的中心分别为O 1,O 2,过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形,则该圆柱的表面积为( B )A .122πB .12πC .82πD .10π解:设圆柱的轴截面的边长为x ,则由x 2=8,得x =22,所以S 表=2S 底+S 侧=2×π×(2)2+2π×2×22=12π.故选B .7、已知圆台的上、下底面半径和高的比为1∶4∶4,若母线长为10,则圆台的表面积为( C )A .81πB .100πC .168πD .169π解:圆台的轴截面如图,设上底面半径为r ,下底面半径为R ,高为h ,母线长为l ,则它的母线长l =h 2+(R -r )2=(4r )2+(3r )2=5r =10,所以r =2,R =8.故S 侧=π(R +r )l =π(8+2)×10=100π, S 表=S 侧+πr 2+πR 2=100π+4π+64π=168π.8、正四棱台的上、下底面的边长分别为2,4,侧棱长为2,则其体积为( D )A.20+12 3B.28 2C.563D.2823解:连接该正四棱台上、下底面的中心,如图,因为该四棱台上、下底面的边长分别为2,4,侧棱长为2,所以该棱台的高h =22-(22-2)2=2,下底面面积S 1=16,上底面面积S 2=4,所以该棱台的体积V =13h (S 1+S 2+S 1S 2)=13×2×(16+4+64)=2823.9、已知三棱锥S -ABC 中,∠SAB =∠ABC =π2,SB =4,SC =213,AB =2,BC =6,则三棱锥S -ABC 的体积是( C )A.4B.6C.4 3D.6 3解:∵∠ABC =π2,AB =2,BC =6,∴AC =AB 2+BC 2=22+62=210.∵∠SAB =π2,AB =2,SB =4,∴AS =SB 2-AB 2=42-22=2 3.由SC =213,得AC 2+AS 2=SC 2,∴AC ⊥AS .又∵SA ⊥AB ,AC ∩AB =A ,∴AS ⊥平面ABC ,∴AS 为三棱锥S -ABC 的高,∴V 三棱锥S -ABC =13×12×2×6×23=4 3. 10、如图,四面体各个面都是边长为1的正三角形,其三个顶点在一个圆柱的下底面圆周上,另一个顶点是上底面圆心,圆柱的侧面积是( C )A .23πB .324πC .223πD .22π解:如图所示,过点P 作PE ⊥平面ABC ,E 为垂足,点E 为等边三角形ABC 的中心,连接AE 并延长,交BC 于点D .AE =23AD ,AD =32, 所以AE =23×32=33, 所以PE =P A 2-AE 2=63.设圆柱底面半径为r ,则r =AE =33,所以圆柱的侧面积S =2πr ·PE =2π×33×63=22π3.11、已知三棱锥S -ABC 中,∠SAB =∠ABC =π2,SB =4,SC =213,AB =2,BC =6,则三棱锥S -ABC 的体积是( C )A .4B .6C .4 3D .6 3解:因为∠ABC =π2,AB =2,BC =6,所以AC =AB 2+BC 2=22+62=210.因为∠SAB =π2,AB =2,SB =4,所以AS =SB 2-AB 2=42-22=2 3.由SC =213,得AC 2+AS 2=SC 2,所以AC ⊥AS .又因为SA ⊥AB ,AC ∩AB =A ,所以AS ⊥平面ABC ,所以AS 为三棱锥S -ABC 的高,所以V 三棱锥S -ABC =13×12×2×6×2 3=4 3.12、(多选)已知正四棱锥的侧面与底面所成的锐二面角为θ,若θ=30°,侧棱长为21,则( AC )A.正四棱锥的底面边长为6B.正四棱锥的底面边长为3C.正四棱锥的侧面积为24 3D.正四棱锥的侧面积为12 3解: 如图,在正四棱锥S -ABCD 中,O 为正方形ABCD 的中心,SH ⊥AB ,设底面边长为2a (a >0),因为∠SHO =30°,所以OH =a ,OS =33a ,SH =233a ,在Rt △SAH 中,a 2+⎝ ⎛⎭⎪⎫233a 2=21,所以a=3,底面边长为6,侧面积为S =12×6×23×4=24 3.故选AC.二、填空题13、已知一个圆锥的底面半径为6,其体积为30π,则该圆锥的侧面积为__39π______.解:设该圆锥的高为h ,则由已知条件可得13×π×62×h =30π,解得h =52,则圆锥的母线长为h 2+62=254+36=132,故该圆锥的侧面积为π×6×132=39π.14、一个圆台上、下底面的半径分别为3 cm 和8 cm ,若两底面圆心的连线长为12 cm ,则这个圆台的母线长为____13____cm.解:如图,过点A作AC⊥OB,交OB于点C.在Rt△ABC中,AC=12 cm,BC=8-3=5(cm).所以AB=122+52=13(cm).15、已知圆锥的顶点为A,过母线AB,AC的截面面积是2 3.若AB,AC的夹角是60°,且AC与圆锥底面所成的角是30°,则该圆锥的表面积为___(6+43)π_____.解:如图所示,∵AB,AC的夹角是60°,AB=AC,∴△ABC是等边三角形,∴34×AC2=23,解得AC=2 2.∵AC与圆锥底面所成的角是30°,∴圆锥底面半径r=OC=AC cos 30°=22×32= 6.则该圆锥的表面积=π×(6)2+12×2π×6×22=(6+43)π.16、学生到工厂劳动实践,利用3D打印技术制作模型.如图,该模型为长方体ABCD-A1B1C1D1挖去四棱锥O-EFGH后所得的几何体.其中O为长方体的中心,E,F,G,H分别为所在棱的中点,AB=BC=6 cm,AA1=4 cm.3D打印所用原料密度为0.9 g/cm3,不考虑打印损耗,制作该模型所需原料的质量为__118.8____g.解:由题意得,四棱锥O-EFGH的底面积为4×6-4×12×2×3=12(cm2),其高为点O到底面EFGH的距离,为3 cm,则此四棱锥的体积为V1=13×12×3=12(cm3).又长方体ABCD-A1B1C1D1的体积为V2=4×6×6=144(cm3),所以该模型的体积V=V2-V1=144-12=132(cm3),因此模型所需原材料的质量为0.9×132=118.8(g).17、棱长为2的正方体ABCD-A1B1C1D1中,M,N分别为棱BB1,AB的中点,则三棱锥A1-D1MN的体积为____1____.解:如图,由正方体棱长为2及M,N分别为BB1,AB的中点,得S△A1MN =2×2-2×12×2×1-12×1×1=32,又易知D1A1为三棱锥D1-A1MN的高,且D1A1=2,∴V A1-D1MN =V D1-A1MN=13·S△A1MN·D1A1=13×32×2=1.18、圆台的上、下底面半径分别为10 cm,20 cm,它的侧面展开图扇环的圆心角为180°,则圆台的表面积为___1 100π_____cm2.(结果中保留π)解:如图所示,设圆台的上底面周长为c cm,因为扇环的圆心角是180°,故c=π·SA=2π×10(cm),所以SA=20 cm.同理可得SB=40 cm,所以AB=SB-SA=20 cm,所以S表=S侧+S上底+S下底=π(10+20)×20+π×102+π×202=1 100π(cm2).故圆台的表面积为1 100π cm2.19、如图,在多面体ABCDEF中,已知四边形ABCD是边长为1的正方形,且△ADE ,△BCF 均为正三角形,EF ∥AB ,EF =2,则该多面体的体积为___23_____.解:如图,分别过点A ,B 作EF 的垂线,垂足分别为G ,H ,连接DG ,CH .则原几何体分割为两个三棱锥和一个直三棱柱.依题意,三棱锥E -ADG 的高EG =12,直三棱柱AGD -BHC 的高AB =1. 则AG =AE 2-EG 2=12-⎝ ⎛⎭⎪⎫122=32.取AD 的中点M ,则MG =22, 所以S △AGD =12×1×22=24,∴V 多面体=V E -ADG +V F -BHC +V AGD -BHC =2V E -ADG +V AGD -BHC =13×24×12×2+24×1=23.20、如图,设正三棱锥S -ABC 的侧面积是底面积的2倍,正三棱锥的高SO =3,则此正三棱锥的表面积为________.解:如图,设正三棱锥的底面边长为a ,斜高为h ′,过点O 作OE ⊥AB ,与AB 交于点E ,连接SE ,则SE ⊥AB ,SE =h ′.因为S 侧=2S 底, 所以12·3a ·h ′=34a 2×2. 所以a =3h ′.因为SO ⊥OE ,所以SO 2+OE 2=SE 2.所以32+⎝ ⎛⎭⎪⎫36×3h ′2=h ′2.所以h ′=23,所以a =3h ′=6.所以S 底=34a 2=34×62=93,S 侧=2S 底=18 3. 所以S 表=S 侧+S 底=93+183=27 3.21、已知一个圆锥的底面半径为6,其体积为30π,则该圆锥的侧面积为__39π______.解;设该圆锥的高为h ,则由已知条件可得13×π×62·h =30π,解得h =52,则圆锥的母线长为h 2+62=254+36=132,故该圆锥的侧面积为π×6×132=39π.22、如图,四边形ABCD 是边长为2的正方形,ED ⊥平面ABCD ,FC ⊥平面ABCD ,ED =2FC =2,则四面体ABEF 的体积为____23____.解: ∵ED ⊥平面ABCD 且AD ⊂平面ABCD ,∴ED ⊥AD . ∵在正方形ABCD 中,AD ⊥DC , 而DC ∩ED =D , ∴AD ⊥平面CDEF .易知FC =ED2=1,V A -BEF =V ABCDEF -V F -ABCD -V A -DEF . ∵V E -ABCD =ED ×S 正方形ABCD ×13=2×2×2×13=83,V B -EFC =BC ×S △EFC ×13=2×2×1×12×13=23,∴V ABCDEF =83+23=103.又V F -ABCD =FC ×S正方形ABCD×13=1×2×2×13=43,V A-DEF=AD ×S △DEF ×13=2×2×2×12×13=43,V A -BEF =103-43-43=23.23、若E ,F 是三棱柱ABC -A 1B 1C 1侧棱BB 1和CC 1上的点,且B 1E =CF ,三棱柱的体积为m ,则四棱锥A -BEFC 的体积为____m3____.解: 如图所示,连接AB 1,AC 1.因为B 1E =CF ,所以梯形BEFC 的面积等于梯形B 1EFC 1的面积. 又四棱锥A -BEFC 的高与四棱锥A -B 1EFC 1的高相等, 所以V A -BEFC =V A -B 1EFC 1=12V A -BB 1C 1C .又V A -A 1B 1C 1=13S △A 1B 1C 1·AA 1, V ABC -A 1B 1C 1=S △A 1B 1C 1·AA 1=m , 所以V A -A 1B 1C 1=m 3,所以V A -BB 1C 1C =V ABC -A 1B 1C 1-V A -A 1B 1C 1=2m3, 所以V A -BEFC =12×2m 3=m3, 即四棱锥A -BEFC 的体积是m3.24、现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P -A 1B 1C 1D 1,下部的形状是正四棱柱ABCD -A 1B 1C 1D 1(如图所示),并要求正四棱柱的高O 1O 是正四棱锥的高PO 1的4倍,若AB =6 m ,PO 1=2 m ,则仓库的容积是多少?解:由PO 1=2 m ,知O 1O =4PO 1=8 m .因为A 1B 1=AB =6 m ,所以正四棱锥P -A 1B 1C 1D 1的体积V 锥=13·A 1B 21·PO 1=13×62×2=24(m 3);正四棱柱ABCD-A1B1C1D1的体积V柱=AB2·O1O=62×8=288(m3),所以仓库的容积V=V锥+V柱=24+288=312(m3).故仓库的容积是312 m3.25、如图所示,底面半径为1,高为1的圆柱OO1中有一内接长方体A1B1C1D1-ABCD.设矩形ABCD的面积为S,长方体A1B1C1D1-ABCD的体积为V,AB=x.(1)将S表示为x的函数;(2)求V的最大值.解:(1)连接AC(图略),因为矩形ABCD内接于⊙O,所以AC为⊙O的直径.因为AC=2,AB=x,所以BC=4-x2,所以S=AB·BC=x4-x2(0<x<2).(2)因为长方体的高AA1=1,所以V=S·AA1=x4-x2=x2(4-x2)=-(x2-2)2+4.因为0<x<2,所以0<x2<4,故当x2=2即x=2时,V取得最大值,此时V max=2.。
2018届人教B版 组合体的体积与表面积(新课标版) 检测卷

2017年高考三轮复习系列:讲练核心热点 【全国通用版】热点十五 组合体的体积与表面积【名师精讲指南篇】【高考真题再现】1.【2015全国卷2】已知,A B 是球O 的球面上两点,90AOB ∠=︒,C 为该球面上的动点,若三棱锥O ABC -体积的最大值为36,则球O 的表面积为(). A.36π B. 64π C.144π D. 256π 【答案】C2.【2015全国卷1】圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为1620+π,则r =().A .1B .2C .4D .8俯视图正视图r2rr2r【解析】由正视图和俯视图可知,该几何体是半球与半个圆柱的组合体,圆柱的半径 与球的半径都为r ,圆柱的高为2r ,其表面积为221422r r r r ⨯π+π+π⨯+22r r ⨯=25r π+241620r =+π,解得2r =.故选B . 3.【2015全国卷2】一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为(). A.81 B.71 C.61 D.51俯视图侧视图主视图【答案】D【解析】由三视图得,在正方体1111ABCD A B C D -中,截去四面体111A A B D -,如图所示,设正方体棱长为a ,则11133111326A A B D V a a -=⨯=,故剩余几何体体积为3331566a a a -=,所以截去部分体积与剩余部分体积的比值为51.故选D.4.【2016全国卷3】在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球,若AB BC ⊥,6AB =,8BC =,13AA =,则V 的最大值是( ).A.4πB.9π2C.6πD.32π35.【2016全国卷2】如图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( ).A.20πB.24πC.28πD.32π【答案】C【解析】几何体是圆锥与圆柱的组合体,设圆柱底面圆半径为,周长为,圆锥母线长为l ,圆柱高为h .由三视图得2r =,2π4πc r ==,由勾股定理得,4l ==,21π2S r ch cl =++表4π16π8π=++28π=.故选C .6.【2016全国卷1】如图所示,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是28π3,则它的表面积是( ).A. 17πB. 18πC. 20πD. 28π【答案】A7.【2016全国卷3】如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为( ).A.18+54+90 D.81【答案】B【解析】如图所示为其几何体直观图,该几何体为四棱柱1111AEFD A E F D -,所以表面积为(33363254⨯+⨯+⨯⨯=+故选B. 【热点深度剖析】从这三年高考试题来看,空间组合体的表面积、体积、球与几何体的切接等问题是高考的热点,题型既有选择题、填空题,难度为中、低档. 2014年小题中没涉及;2015年既考查了组合体的表面积,又考查了球与几何体的切接;2017年全国卷4道试题均为组合体或几何体的切割.从这三年高考试题来看, 组合体或几何体的切割及球的组合体问题是高考常考内容之一,主要考查求其表面积、体积或由几何体的表面积、体积得出某些量;主观题考查较全F 1E 1FED 1D B 1A 1C 1ABC面,考查线、面位置关系,及表面积、体积公式,试题难度在中等,有时在压轴题的位置,从整体上来看,试题难度理科比文科要大,主要考查学生的画图能力,空间想象能力,运算能力及逻辑推理能力.预测2017年高考题中,会以三视图为载体考查组合体的体积或表面积,理科也可能出现球的组合体,重点考查学生的空间想象能力、运算能力及逻辑推理能力.【重点知识整合】1. 棱柱:(1)定义:有两个面互相平行,其余各面的公共边互相平行的多面体叫做棱柱.(2)棱柱的分类:①按侧棱是否与底面垂直分类:分为斜棱柱(侧棱不垂直于底面)和直棱柱(侧棱垂直于底面),其中底面为正多边形的直棱柱叫正棱柱.②按底面边数的多少分类:底面分别为三角形,四边形,五边形…,分别称为三棱柱,四棱柱,五棱柱,…;(3)棱柱的性质:①棱柱的各个侧面都是平行四边形,所有的侧棱都相等,直棱柱的各个侧面都是矩形,正棱柱的各个侧面都是全等的矩形.②与底面平行的截面是与底面对应边互相平行的全等多边形.③过棱柱不相邻的两条侧棱的截面都是平行四边形.(4)侧面积S=直截面(与各侧棱都垂直相交的截面)周长×侧棱长,特别地,直棱柱的侧面积S=底面周长×侧棱长.全面积(也称表面积)是各个表面面积之和,故棱柱的全面积=侧面积+2×底面积.2.棱锥(1)定义:一个面是多边形,其余各面是有一个公共顶点的三角形的多面体叫做棱锥.底面是正多边形并且顶点在底面上的射影是正多边形的中心的棱锥叫做正棱锥.(2)性质:如果棱锥被平行于底面的平面所截,那么所得的截面与底面相似,截面面积与底面面积的比等于顶点至截面距离与棱锥高的平方比,截得小棱锥的体积与原来棱锥的体积比等于顶点至截面距离与棱锥高的立方比.(3))棱锥的侧面积=各侧面三角形面积的和;正棱锥的侧面积S=12×底面周长×斜高,棱锥的全面积=侧面积+底面积.3.球(1)球的概念:与定点距离等于或小于定长的点的集合,叫做球体;与定点距离等于定长的点的集合叫做球面.(2)球的截面:用一平面α去截一个球O,设OO'是平面α的垂线段,O'为垂足,且OO d'=,所得的截面是以球心在截面内的射影为圆心,以r=,截面是一个圆面.球面被经过球心的平面截得的圆叫做大圆,被不经过球心的平面截得的圆叫做小圆(3)球的表面积公式:24S R π=. 4.棱柱、棱锥与球的体积(1)棱柱:体积=底面积×高,或体积V =直截面面积×侧棱长,特别地,直棱柱的体积=底面积×侧棱长;三棱柱的体积12V Sd =(其中S 为三棱柱一个侧面的面积,d 为与此侧面平行的侧棱到此侧面的距离)(2)棱锥:体积=31×底面积×高. (3)球的体积公式:343V R π=.5.正棱台:由正棱锥截得的棱台叫做正棱台. 正棱台的性质:①各侧棱相等,侧面是全等的等腰梯形,这些等腰梯形的高叫做棱台的斜高,斜高都相等. ②两底面以及平行于底面的截面是相似多边形;③两底面中心连线、相应的边心距和斜高组成一个直角梯形; ④两底面中心连线、侧棱和两底面相应的半径也组成一个直角梯形; ⑤正棱台的上、下底面中心的连线是棱台的一条高. 6.圆柱、圆锥、圆台 (1)圆柱、圆锥、圆台的概念分别以矩形的一边、直角三角形一条直角边、直角梯形垂直于底边的腰为旋转轴,其余各边旋转而形成的曲面围成的几何体分别叫做圆柱、圆锥、圆台.(2)圆柱的结构特征①平行于底面的截面都是圆;②过轴的截面(轴截面)是全等的矩形. 除了这两条重要特征外,还应掌握下面的一些重要属性.①所有的轴截面是以两底面直径和两条母线为边的全等矩形,若该矩形为正方形,则圆柱叫等边圆柱.②用平行于轴的平面去截圆柱,所得的截面是以底面圆的弦和两条母线为边的矩形.也就是说过圆柱任意两条母线的截面一定是一个矩形,在这所有的截面矩形中,以轴截面面积最大. (3)圆锥的结构特征①平行于底面的截面都是圆;②过轴的截面(轴截面)是全等的等腰三角形;③过圆锥两条母线的截面.当轴截面的顶角不大于90°时,轴截面面积最大;当轴截面顶角大于90°时,两母线垂直时截面面积最大. (4)圆台的结构特征①平行于底面的截面都是圆;②过轴的截面是全等的等腰梯形. 7.简单几何体与球的综合问题1.正四面体与球:如图,设正四面体的棱长为a ,内切球半径为r ,外接球的半径为R ,取AB 的中点为D,连接CD,SE 为正四面体的高,在截面三角形SDC,作一个与边SD 和DC 相切,圆心在高SE 上的圆.因为正四面体本身的对称性,两个球的球心同为O .此时,,CO OS R OE r ===,,SE CE ==则有22223a R r R r CE +=-=,=, 解得:a r a R 126,46==.与正四面体各棱都相切的球的半径为相对棱的一半:r '=. 2.正方体与球(1)正方体的内切球:截面图为正方形EFGH 的内切圆,如图所示.设正方体的棱长为a ,则2a OJ r ==.(2)与正方体各棱相切的球:截面图为正方形EFGH 的外接圆.则GO R ==.(3)正方体的外接球:截面图正方形ACA 1C 1的外接圆.则1AO R '==. 3. 正棱柱(锥)与外接球以正三棱柱为例,设高为h ,底面边长为a ,如图所示.球心必落在高DD 1的中点O,因为D 和D 1分别为正三角形的中心.直角三角形AOD,R =AO, OD=2h,借助勾股定理即可求R.解决关键确定直角三角形.4. 三条侧棱互相垂直的三棱锥的外接球(1)如果三棱锥的三条侧棱互相垂直并且相等,则可以补形为一个正方体,它的外接球的球心就是三棱锥的外接球的球心.三棱锥A 1-AB 1D 1的外接球的球心和正方体ABCD-A 1B 1C 1D 1的外接球的球心重合.设1AA a =,则R =(2)如果三棱锥的三条侧棱互相垂直并且不相等,则可以补形为一个长方体,它的外接球的球心就是三棱锥的外接球的球心.222244a b c l R ++==(L 为长方体的体对角线长).5. 各面均为直角三角形三棱锥与球如右图,SA ⊥面ABC,AB ⊥BC,则可推出SB ⊥BC,即此三棱锥的四个面全是直角三角形.取SC 的中点为O,由直角三角形的性质可得:OA=OS=0B=OC,所以O 点为三棱锥的外接球的球心.2SCR =.【应试技巧点拨】 1. 求体积常见技巧当给出的几何体比较复杂,有关的计算公式无法运用,或者虽然几何体并不复杂,但条件中的已知元素彼此离散时,我们可采用“割”、“补”的技巧,化复杂几何体为简单几何体(柱、锥、台),或化离散为集中,给解题提供便利.(1)几何体的“分割”:几何体的分割即将已知的几何体按照结论的要求,分割成若干个易求体积的几何体,进而求之.(2)几何体的“补形”:与分割一样,有时为了计算方便,可将几何体补成易求体积的几何体,如长方体、正方体等.另外补台成锥是常见的解决台体侧面积与体积的方法,由台体的定义,我们在有些情况下,可以将台体补成锥体研究体积.(3)有关柱、锥、台、球的面积和体积的计算,应以公式为基础,充分利用几何体中的直角三角形、直角梯形求有关的几何元素. 2.求体积常见方法①直接法(公式法);②转移法:利用祖暅原理或等积变化,把所求的几何体转化为与它等底、等高的几何体的体积;③分割法求和法:把所求几何体分割成基本几何体的体积;④补形法:通过补形化归为基本几何体的体积;⑤四面体体积变换法;⑥利用四面体的体积性质:(ⅰ)底面积相同的两个三棱锥体积之比等于其底面积的比;(ⅱ)高相同的两个三棱锥体积之比等于其底面积的比;(ⅲ)用平行于底面的平面去截三棱锥,截得的小三棱锥与原三棱锥的体积之比等于相似比的立方.求多面体体积的常用技巧是割补法(割补成易求体积的多面体.补形:三棱锥⇒三棱柱⇒平行六面体;分割:三棱柱中三棱锥、四棱锥、三棱柱的体积关系是1:2:3和等积变换法(平行换点、换面)和比例(性质转换)法等. 3.常见的特殊几何体的性质 (1)平行六面体:①底面是平行四边形的四棱柱.②{平行六面体}⊃≠{直平行六面体}⊃≠{长方体}⊃≠{正四棱柱}⊃≠{正方体}; ③平行六面体的任何一个面都可以作为底面;④平行六面体的对角线交于一点,并且在交点处互相平分; ⑤平行六面体的四条对角线的平方和等于各棱的平方和. (2)长方体:①长方体的一条对角线的平方等于一个顶点上三条棱长的平方和;②若长方体的体对角线与过同一顶点的三条棱所成的角分别为,,αβγ,则cos 2α+cos 2β+cos 2γ=1;③若长方体的体对角线与过同一顶点的三侧面所成的角分别为,,,γβα则cos2α+cos 2β+cos 2γ=2.(3)正棱锥:如果一个棱锥的底面是正多边形,且顶点在底面的射影是底面的中心,这样的棱锥叫正棱锥.①正棱锥的各侧棱相等,各侧面都是全等的等腰三角形,各等腰三角形底边上的高(叫侧高)也相等;②正棱锥的高h 、斜高h '、斜高在底面的射影(底面的内切圆的半径r )、侧棱、侧棱在底面的射影(底面的外接圆的半径R )、底面的半边长可组成四个直角三角形; ③若正棱锥的侧面与底面所成的角为θ,则cos S S θ⋅侧底=. (4)正四面体:侧棱与底面边长相等的正三棱锥叫做正四面体.①设正四面体的棱长为a ,,为,,体积为3. ②正四面体与其截面:如图所示点E 为PA 的中点,连接EB 和EC.点F 为BC 中点,连接EF.则截面EBC ⊥PA, EBC ⊥面PAB, EBC ⊥面PAC. EF 为相对棱的公垂线,其长度为相对棱的距离; ③正四面体可补形为正方体,如图所示,四面体B-ACD 即为正四面体.各个棱为正方体的面对角线..利用这个补形为解题带来很大的方便.【考场经验分享】1.注意特殊的四棱柱的区别:直四棱柱、正四棱柱、长方体、正方体、平行六面体、直平行六面体.2.棱台的各侧棱延长线交于一点是判断棱台的主要依据,两底面平行且是相似多边形.3.注意还台为锥的解题方法的运用,将台体还原为锥体可利用锥体的性质.注意正棱锥中的四个直角三角形为:高、斜高及底面边心距组成一个直角三角形;高、侧棱与底面外接圆半径组成一个直角三角形;底面的边心距、外接圆半径及半边长组成一个直角三角形;侧棱、斜高及底边一半组成一个直角三角形.4.将几何体展开为平面图形时,要注意在何处剪开,多面体要选择一条棱剪开,旋转体要沿一条母线剪开.5.与球有关的组合体问题,一种是内切,一种是外接.解题时要认真分析图形,明确切点和接点的位置,确定有关元素间的数量关系,并作出合适的截面图,如球内切于正方体,切点为正方体各个面的中心,正方体的棱长等于球的直径;球外接于正方体,正方体的顶点均在球面上,正方体的体对角线长等于球的直径.球与旋转体的组合,通常作它们的轴截面进行解题,球与多面体的组合,通过多面体的一条侧棱和球心,或“切点”、“接点”作出截面图.6.关于组合体的考查一般放在压轴的选择题或填空题的位置,难度较大,需要有较强的画图能力,和空间想象能力,尤其是与球体相关的内切与外接问题,具有一定的规律和常用结论,故总结常用的类型,形成解题套路和模式.【名题精选练兵篇】1.【湖南省娄底市2017届二模】在体积为V的球内有一个多面体,该多面体的三视图的等腰直角三角形,则V的最小值是()A. C. 3π D. 12π 【答案】B2.【2017河北省唐山市第二次模拟】一个几何体的三视图如图所示,该几何体的表面积为( )A. 24π-B. 243π-C. 24π+D. 242π- 【答案】A【解析】由三视图可知:该几何体是以2为边长正方体从右下前方挖去18个球,该球以顶点为球心,2为半径,则该几何体的表面积为221122632422448πππ⨯⨯-⨯⨯⨯+⨯⨯⨯=-,故选A.3.【陕西省汉中市2017届4月模拟】如图中的三个直角三角形是一个体积为320cm 的几何体的三视图,则该几何体外接球的面积(单位: 2cm )等于 ( ).A. 55πB. 75πC. 77πD. 65π 【答案】C【解析】从题设中提供的三视图中的图形信息及数据信息可知该几何体是底面是边长分别为5,6的直角三角形的三棱锥,如图,设高为h ,由题设可得115652032V h h =⨯⨯⨯==,所以4h =,由题意该几何体的外接球的直径即是长方体的对角线,即2R ==,则其表面积2477S R ππ==,应选答案C.4.【湖北省六校联合体2017届高三4月联考】某几何体的三视图如下图,则该几何体的体积为( )A. 18B. 20C. 24D. 12 【答案】B【解析】由三视图可得如下图所示几何体,它为长宽高为4,3,2的长方体沿对角线去掉一半且去掉一个三棱锥的几何体,其体积11143443220232V =⨯⨯⨯-⨯⨯⨯⨯=.故本题正确答案为B.5.【山西省三区八校2017届高三第二次模拟】在矩形ABCD 中, 2AC =,现将ABC ∆沿对角线AC 折起,使点B 到达点'B 的位置,得到三棱锥'B ACD -,则三棱锥'B ACD -的外接球的表面积是( )A. πB. 2πC. 4πD. 与点'B 的位置有关 【答案】C6.【江西省南昌市十所省重点中学命制2017届高三第二次模拟】一个三棱锥的三视图如下图所示,则该几何体的体积为A. 12 【答案】C【解析】由三视图可得到如图所示几何体,该几何体是由正方体切割得到的,利用传统法或空∴该几何体的体积为2123=.7.【2017河北省五个一联盟一模】某四面体的三视图如图所示,正视图、侧视图、俯视图都是边长为1的正方形,则此四面体的外接球的体积为A.43πB. 3πD. π【答案】C8.【山西省大同市灵丘豪洋中学2017届高三下学期第三次模拟】若一个正四面体的表面积为1S ,其内切球的表面积为2S ,则12S S =( ) A.6πC.43【答案】B【解析】设四面体ABCD 的棱长为a 底面中心将高分为21:两段,所以底面中心到顶点的距离为2,3=可得正四面体的高为h ==,所以正四面体的体积213ABC V S =⨯= ,设正四面体的内切球半径为r ,则2143ABC S r r ⨯⨯⨯=⇒= ,,所以内切球表面积22246a S r ππ==,所以正四面体的表面积211246ABCS S S S =⨯=∴== ,9.【山西省大同2017届高三下学期第三次模拟】已知直三棱柱111ABC A B C -中,90BAC ∠=︒,侧面11BCC B 的面积为4,则直三棱柱111ABC A B C -外接球表面积的最小值为( )A. 4πB. 8πC. 16πD. 32π 【答案】B10.【福建省2017届高三4月单科质量检测】如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则该几何体最长的棱长为( )A.6D. 【答案】C【解析】由题可得立体图形:则4,AB AC PC BC =====6,AP BP ===所以最长棱为611.【福建省2017届高三4月单科质量检测】已知三棱锥P ABC -的三条侧棱两两互相垂直,且2AB BC AC ===,则此三棱锥的外接球的体积为( )A. 83π C. 163π D. 323π 【答案】B12.【广西桂林市、崇左市、百色市2017届高三下学期第一次联合模拟】某四棱锥的三视图如图所示,俯视图是一个等腰直角三角形,则该四棱锥的体积是( )A.4383【答案】A【解析】由已知中的某四棱锥的三视图,可得该几何体的直观图如图所示,其底面面积为2S ==,高h =,故体积1433V Sh ==,故选A.13.【安徽省合肥市2017届高三第二次教学质量检测】一个几何体的三视图及其尺寸如图所示,则该几何体的体积为( )A.283C. 28D. 22+【答案】A14.【2016河南六市高第一次联考】一个几何体的三视图如图所示,且其侧(左)视图是一个等边三角形,则这个几何体的体积为( )A C . 【答案】B.【解析】由题意得,该几何体为如下图所示的五棱锥P ABCDE -,∴体积211(212)32V =⋅⋅⋅+=故选B .15.【2016河北省衡水二调】正三角形ABC 的边长为2,将它沿高AD 翻折,使点B 与点C此时四面体ABCD 外接球表面积为( )A .7πB .19πCD 【答案】A16. 【辽宁省朝阳市三校协作体2015届高三下学期开学联考】平面四边形ABCD中,1AB AD CD ===,BD =BD CD ⊥,将其沿对角线BD 折成四面体A BCD '-,使平面A BD '⊥平面BCD ,若四面体A BCD '-的顶点在同一个球面上,则该球的体积为 ( ).A .B 3π .C .D 2π 【答案】A【解析】根据题意,如图,可知Rt A BD '∆中,1,AB AD BD ===,在Rt BCD ∆中,1,BD CD BC ===,又因为平面A BD '⊥平面BCD ,所以球心就是BC 的中点,半径为r =,所以球的体积为:343V r π==,所以答案为:A.17. 【2016届云南省弥勒市高三年级模拟测试一】三棱锥P ABC -中,PA ⊥平面ABC ,,1,AC BC AC BC PA ⊥===,则该三棱锥外接球的表面积为( )A .5πBC .20πD .4π【答案】A【名师原创测试篇】1.如图,的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将体积为43π的鸡蛋(视为球体)放入其中,蛋巢形状保持不变, 则鸡蛋最高点与蛋巢底面的距离为( )A 32+B .32C D 32+ 【答案】D2. 已知三棱锥S ABC -的所有顶点都在球O 的球面上,ABC 是边长为1的正三角形,SC 为球O 的直径,且2SC =,则此棱锥的体积为( )A B C D 【答案】A【解析】 由图可知向SC 边做垂线,垂足为E,连接BE,AE.因为SC 为直径,所以SBC SAC ≅ ,所以三棱锥S ABC -的体积为11233ABE v S SC =⨯⨯==所以答案为A.3. 三棱锥P ABC -中,PA PB PC ==,456AB BC CA ===,,,若ABC ∆的外接圆恰好是三棱锥P ABC -外接球O 的一个大圆,则三棱锥P ABC -的体积为( )A .10B .20C .30D .40【答案】A4. 已知矩形ABCD 的顶点都在半径为2的球O 的球面上,且3AB =,BC =,过点D 作DE 垂直于平面ABCD ,交球O 于E ,则棱锥E ABCD -的体积为 .【答案】.【解析】如图所示,BE 过球心O ,∴2DE ==,∴1323E ABCD V -=⨯=.5. 平面α截球O 的球面得圆M ,过圆心M 的平面β与α的夹角为6π,且平面β截球O的球面得圆N ,已知球O 的半径为5,圆M 的面积为9π,则圆N 的半径为( )【答案】B.【解析】如图,∵5OA =,3AM =,∴4OM =,又∵3NMO π∠=,∴sin 3ON OM π=⋅=又∵5OB =,∴NB ==,故选B.。
2018届人教B版(文) 几何体的表面积与体积的求解 检测卷

1.练高考1.【2016高考新课标Ⅲ文数】在封闭的直三棱柱111ABC A B C -内有一个体积为V 的球,若AB BC ⊥,6AB =,8BC =,13AA =,则V 的最大值是( )(A )4π (B )92π(C )6π (D )323π【答案】B2.【2016高考新课标3文数】如图,网格纸上小正方形的边长为1,粗实现画出的是某多面体的三视图,则该多面体的表面积为( )(A )18+(B )54+ (C )90 (D )81 【答案】B 【解析】由三视图该几何体是以侧视图为底面的斜四棱柱,所以该几何体的表面积2362332354S =⨯⨯+⨯⨯+⨯⨯=+,故选B .3.【2016高考北京文数】某四棱柱的三视图如图所示,则该四棱柱的体积为___________.【答案】3.2【解析】四棱柱高为1,底面为等腰梯形,面积为13(12)122⨯+⨯=,因此体积为3.24.【2016高考四川文科】已知某三菱锥的三视图如图所示,则该三菱锥的体积 .侧视图俯视图5.【2016高考浙江文数】某几何体的三视图如图所示(单位:cm),则该几何体的表面积是______cm2,体积是______cm3.【答案】80;40.【解析】由三视图知该组合体是一个长方体上面放置了一个小正方体,22262244242280S =⨯+⨯+⨯⨯-⨯=表,3244240V =+⨯⨯=.6.【2016高考上海文科】将边长为1的正方形AA 1O 1O (及其内部)绕OO 1旋转一周形成圆柱,如图, AC 长为56π , 11A B 长为3π,其中B 1与C 在平面AA 1O 1O 的同侧. (1)求圆柱的体积与侧面积;(2)求异面直线O 1B 1与OC 所成的角的大小.【答案】(1(2)2π.由 11A B 长为3π,可知1113π∠AOB =∠A O B =, 由 C A长为56π,可知5C 6π∠AO =,C C 2π∠OB =∠AO -∠AOB =, 所以异面直线11O B 与C O 所成的角的大小为2π.2.练模拟1.【河北省沧州市第一中学2017届高三10月月考】已知一个几何体的三视图如图所示,则这个几何体的体积是( )A .233B . 236 C.113D .103【答案】D2.【河南省开封市2017届高三上学期10月月考】某空间几何体的三视图如图所示,则该几何体的体积为A .73B .83π-C .83D .73π- 【答案】B【解析】根据三视图可以看出原几何体为一个四棱锥ABCD P -,平面⊥PCD 平面ABCD ,割去半个圆锥,圆锥底面直径为CD ,P 为顶点,其体积为38213121-222312ππ-=⨯⨯⨯⨯⨯⨯,选B.3.【2016届河北省邯郸一中高三下学期研七】一几何体的三视图如图所示,则它的体积为()A B C【答案】D4.【2016届北京市西城区高三上学期期末考试】一个几何体的三视图如图所示,那么这个几何体的表面积是()(A)16+(B)16+(C)20+(D)20+【答案】B5.【2016届江西省吉安市一中高三第二次质检】已知某几何体的三视图如图所示,则该几何体的体积为A .316 B .380 C .364 D .343 【答案】B【解析】由三视图可知,几何体表示的是三棱柱去掉三棱锥,三棱柱的体积EF S V ABE ⋅=∆13244421=⨯⨯⨯=,三棱锥的体积EF S V BFG ⨯⨯=∆3123164422131=⨯⨯⨯⨯=,因此该几何体3803163221=-=-V V ,故答案为B .3.练原创1.某几何体的三视图如下图所示,则该几何体的体积是( )【答案】D2.若某空间几何体的三视图如图所示,则该几何体的体积是( ) A .16 B .32 C .48 D .144【答案】C【解析】如图直方图是一个四棱锥,底面积为(62)6242+⨯=.高为6.所以体积为1246483⨯⨯=.故选C. 3.一个几何体的三视图如图所示,则该几何体的体积为 .【答案】114.将边长为1的正方形ABCD 沿对角线AC 折起,使ABD ∆为正三角形,则三棱锥A BCD -的体积为( )A .16B .112C D 【答案】D.【解析】取AC 的中点O ,连接BO ,DO ,由题意,,,AC BO AC DO ⊥⊥BO DO ==,因为ABD ∆为正三角形,∴1DB =,DO OB ⊥,111332A BCD D ABC ABC V V S DO --==⋅=⨯=.选D. 5.已知几何体的三视图如图,则该几何体的体积为( )A. 34 B. 4 C. 324 D. 334【答案】C。
(完整版)空间几何体的表面积与体积练习题.及答案

For personal use only in study and research; not forcommercial use空间几何体的表面积与体积专题一、选择题1.棱长为2的正四面体的表面积是( C ).A. 3 B .4 C .4 3 D .16解析 每个面的面积为:12×2×2×32= 3.∴正四面体的表面积为:4 3.2.把球的表面积扩大到原来的2倍,那么体积扩大到原来的 ( B ). A .2倍 B .22倍 C.2倍 D.32倍解析 由题意知球的半径扩大到原来的2倍,则体积V =43πR 3,知体积扩大到原来的22倍.3.如图是一个长方体截去一个角后所得多面体的三视图,则该多面体的体积为( B ). A.1423 B.2843 C.2803D.1403解析 根据三视图的知识及特点,可画出多面体 的形状,如图所示.这个多面体是由长方体截去 一个正三棱锥而得到的,所以所求多面体的体积 V =V 长方体-V 正三棱锥=4×4×6-13×⎝ ⎛⎭⎪⎫12×2×2×2=2843. 4.某几何体的三视图如下,则它的体积是( A) A .8-2π3 B .8-π3C .8-2π D.2π3解析 由三视图可知该几何体是一个边长为2的正方体内部挖去一个底面半径为1,高为2的圆锥,所以V =23-13×π×2=8-2π3.5.已知某几何体的三视图如图,其中正视图中半圆的半径为1,则该几何体的体积为( A)A .24-32π B .24-π3 C .24-π D .24-π2据三视图可得几何体为一长方体内挖去一个半圆柱,其中长方体的棱长分别为:2,3,4,半圆柱的底面半径为1,母线长为3,故其体积V =2×3×4-12×π×12×3=24-3π2.6.某品牌香水瓶的三视图如图 (单位:cm),则该几何体的表面积为( C )A.⎝ ⎛⎭⎪⎫95-π2 cm 2B.⎝ ⎛⎭⎪⎫94-π2 cm 2C.⎝ ⎛⎭⎪⎫94+π2 cm 2D.⎝⎛⎭⎪⎫95+π2 cm 2解析 这个空间几何体上面是一个四棱柱、中间部分是一个圆柱、下面是一个四棱柱.上面四棱柱的表面积为2×3×3+12×1-π4=30-π4;中间部分的表面积为2π×12×1=π,下面部分的表面积为2×4×4+16×2-π4=64-π4.故其表面积是94+π2.7.已知球的直径SC =4,A ,B 是该球球面上的两点,AB =3,∠ASC =∠BSC =30°,则棱锥S-ABC 的体积为( C).A .3 3B .2 3 C. 3 D .1解析 由题可知AB 一定在与直径SC 垂直的小圆面上,作过AB 的小圆交直径SC 于D ,设SD =x ,则DC =4-x ,此时所求棱锥即分割成两个棱锥S-ABD 和C-ABD ,在△SAD 和△SBD 中,由已知条件可得AD =BD =33x ,又因为SC 为直径,所以∠SBC =∠SAC =90°,所以∠DCB =∠DCA =60°,在△BDC 中 ,BD =3(4-x ),所以33x =3(4-x ),所以x =3,AD =BD =3,所以三角形ABD 为正三角形,所以V =13S △ABD ×4= 3.二、填空题8.三棱锥PABC 中,PA ⊥底面ABC ,PA =3,底面ABC 是边长为2的正三角形,则三棱锥PABC 的体积等于__3______.解析 依题意有,三棱锥PABC 的体积V =13S △ABC ·|PA |=13×34×22×3= 3.9.一个圆柱的轴截面是正方形,其侧面积与一个球的表面积相等,那么这个圆柱的体积与这个球的体积之比为_ 3∶2_______.解析 设圆柱的底面半径是r ,则该圆柱的母线长是2r ,圆柱的侧面积是2πr ·2r =4πr 2,设球的半径是R ,则球的表面积是4πR 2,根据已知4πR 2=4πr 2,所以R =r .所以圆柱的体积是πr 2·2r=2πr 3,球的体积是43πr 3,所以圆柱的体积和球的体积的比是2πr 343πr 3=3∶2.10.如图所示,已知一个多面体的平面展开图由一个边长为1的正方形和4个边长为1的正三角形组成,则该多面体的体积是___26_____. 解析 由题知该多面体为正四棱锥,底面边长为1,侧棱长为1,斜高为32,连接顶点和底面中心即为高,可求得高为22,所以体积V =13×1×1×22=26. 11.如图,半径为R 的球O 中有一内接圆柱.当圆柱的侧面积最大时,球的表面积与该圆柱的侧面积之差是____2πR 2____.解析 由球的半径为R ,可知球的表面积为4πR 2.设内接圆柱底面半径为r ,高为2h ,则h 2+r 2=R 2.而圆柱的侧面积为2πr ·2h =4πrh ≤4πr 2+h 22=2πR 2(当且仅当r =h 时等号成立),即内接圆柱的侧面积最大值为2πR 2,此时球的表面积与内接圆柱的侧面积之差为2πR 2.12.如图,已知正三棱柱ABCA 1B 1C 1的底面边长为2 cm ,高为5 cm ,则一质点自点A 出发,沿着三棱柱的侧面绕行两周到达点A 1的最短路线的长为___13_____cm. 解析 根据题意,利用分割法将原三棱柱分割为两个相同的三棱柱,然后将其展开为如图所示的实线部分,则可知所求最短路线的长为52+122=13 (cm). 三、解答题13.某高速公路收费站入口处的安全标识墩如图1所示,墩的上半部分是正四棱锥PEFGH ,下半部分是长方体ABCDEFGH .图2、图3分别是该标识墩的正视图和俯视图. (1)请画出该安全标识墩的侧视图; (2)求该安全标识墩的体积.解析 (1)侧视图同正视图,如图所示:(2)该安全标识墩的体积为V =V PEFGH +V ABCDEFGH =13×402×60+402×20=64 000(cm 3).14 .一个几何体的三视图如图所示.已知正视图是底边长为1的平行四边形,侧视图是一个长为3,宽为1的矩形,俯视图为两个边长为1的正方形拼成的矩形.(1)求该几何体的体积V ;(2)求该几何体的表面积S.解析 (1)由三视图可知,该几何体是一个平行六面体(如图),其底面是边长为1的正方形,高为3,所以V =1×1×3= 3.(2)由三视图可知,该平行六面体中,A1D ⊥平面ABCD ,CD ⊥平面BCC1B1, 所以AA1=2,侧面ABB1A1,CDD1C1均为矩形, S =2×(1×1+1×3+1×2)=6+2 3.15.已知某几何体的俯视图是如右图所示的矩形,正视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形.(1)求该几何体的体积V ;(2)求该几何体的侧面积S .解析 由题设可知,几何体是一个高为4的四棱锥,其底面是长、宽分别为8和6的矩形,正侧面及其相对侧面均为底边长为8,高为h 1的等腰三角形,左、 右侧面均为底边长为6,高为h 2的等腰三角形,如右图所示. (1)几何体的体积为:V =13·S 矩形·h =13×6×8×4=64.(2)正侧面及相对侧面底边上的高为:h 1=42+32=5.左、右侧面的底边上的高为:h 2=42+42=4 2.故几何体的侧面面积为:S =2×⎝ ⎛⎭⎪⎫12×8×5+12×6×42=40+24 2. 1.一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是( ). .解:设展开图的正方形边长为a ,圆柱的底面半径为r ,则2πr =a ,2ar π=,底面圆的面积是24a π,于是全面积与侧面积的比是2221222a a a πππ++=, 2.在棱长为 1 的正方体上,分别用过共顶点的三条棱中点的平面截该正方体,则截去与8个顶点相关的8个三棱锥后 ,剩下的几何体的体积是( ).2.解:正方体的体积为1,过共顶点的三条棱中点的平面截该正方体截得的三棱锥的体积是111111()3222248⨯⨯⨯⨯=,于是8个三棱锥的体积是61,剩余部分的体积是65, 3.一个直棱柱(侧棱垂直于底面的棱柱)的底面是菱形,对角线长分别是6cm 和8cm ,高是5cm ,则这个直棱柱的全面积是 。
8空间几何体的表面积和体积练习题word文档良心出品
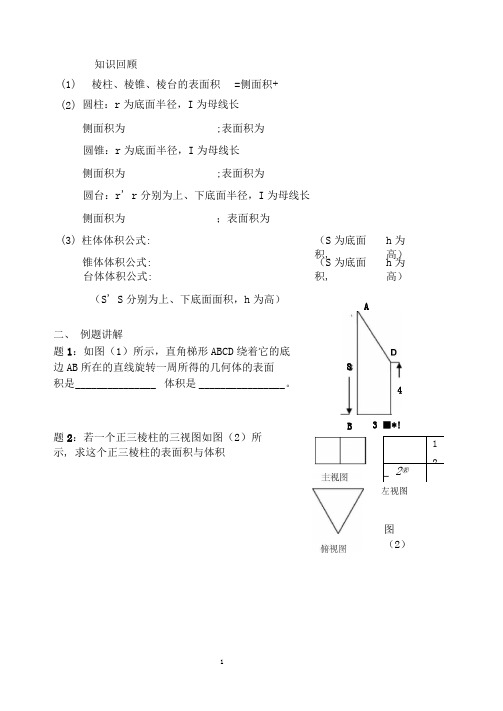
台体体积公式:(S ' S 分别为上、下底面面积,h 为高)二、 例题讲解题1:如图(1)所示,直角梯形ABCD 绕着它的底 边AB 所在的直线旋转一周所得的几何体的表面 积是 _______________ 体积是 ________________ 。
(1) 知识回顾棱柱、棱锥、棱台的表面积 =侧面积+ (2) 圆柱:r 为底面半径,I 为母线长侧面积为;表面积为圆锥:r 为底面半径,I 为母线长 侧面积为;表面积为圆台:r ' r 分别为上、下底面半径,I 为母线长 侧面积为;表面积为(3) 柱体体积公式:(S 为底面积,h 为高) 锥体体积公式:(S 为底面积,h 为高)题2:若一个正三棱柱的三视图如图(2)所示, 求这个正三棱柱的表面积与体积 图图(2)12_ 2®左视图A83 ■*!CB4题3:如图(3)所示,在多面体ABCDEF中,已知ABCD是边长为1的正方形, 且心ADE,心BCF均为正三角形,EF//AB,EF=2,则该多面体的体积为()D - 3F图(3)1若圆柱的侧面积展开图是长为6cm,宽为4cm的矩形,贝U该圆柱的体积为2、如图⑷,在正方体ABCD -A i B i C i D i中,棱长为2,E为A1B1的中点,则三棱锥E -AB j D j的体积是图3、已知某几何体的俯视图是如图(5)所示的矩形,正X]视图(或称主视图)是一个底边长为8、高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形.(1)求该几何体的体积V;(2)求该几何体的侧面积S。
图(5)(选做题)4、如图(6),一个圆锥的底面半径为2cm,咼为6cm,在其中有一个咼为xcm的内接圆柱。
(1) 试用X 表示圆柱的侧面积;(2) 当X 为何值时,圆柱的侧面积最大?一、选择题(每小题5分,共计60分。
请把选择答案填在答题卡上。
) 1•以三棱锥各面重心为顶点,得到一个新三棱锥,它的表面积是原三棱锥表面积的 A.1 - 13 B . C. D. 16 2.正六棱锥底面边长为 体积为 ,则侧棱与底面所成的角等于 兀A.— 6 3. 有棱长为6的正四面体S-ABC, A ;B ;C '分别在棱SA SB SC 上,且S A =2, S B'=3, S C '=4,则截面ABC '将此正四面体分成的两部分体积之比为1 1 1A.丄B. -C. - 9 8 4 4. 长方体的全面积是11,十二条棱长的和是A. 2(3.B. 714 5. 圆锥的全面积是侧面积的A. (0:90。
高考数学总复习 9-2 简单几何体的表面积和体积但因为测试 新人教B版

高考数学总复习 9-2 简单几何体的表面积和体积但因为测试新人教B 版1.纸制的正方体的六个面根据其实际方位分别标记为上、下、东、南、西、北,现在沿该正方体的一些棱将正方体剪开,外面朝上展平,得到如下图所示的平面图形,则标“△”的面的方位是( )A .南B .北C .西D .下[答案] A[解析] 将所给图形还原为正方体,如下图所示,最上面为上,最右面为东,则前面为△,可知“△”的实际方位为南.2.(2010·河南省南阳市调研)一个球与一个正三棱柱的三个侧面和两个底面都相切,已知这个球的体积为32π3,那么这个三棱柱的体积是( )A .963B .483C .243D .16 3[答案] B[解析] 已知正三棱柱的高为球的直径,底面正三角形的内切圆是球的大圆.设底面正三角形的边长为a ,球的半径为R ,则a =23R ,又43πR 3=32π3,∴R =2,a =43,于是V=34a 2·2R =48 3. 3.若圆锥轴截面的顶角θ满足π3<θ<π2,则其侧面展开图中心角α满足( )A.π4<α<π3 B.π3<α<π2 C.π2<α<π D .π<α<2π[答案] D[解析] ∵θ∈⎝⎛⎭⎫π3,π2 ∴θ2∈⎝⎛⎭⎫π6,π4, ∴sin θ2∈⎝⎛⎭⎫12,22,又r l =sin θ2∈⎝⎛⎭⎫12,22∴其侧面展开图中心角α=rl·2π∈(π,2π)4.(文)(2010·福建文,3)若一个底面是正三角形的三棱柱的正视图如下图所示,则其侧.面积..等于( )A.3 B .2 C .23 D .6[答案] D[解析] 原几何体是一个底面边长为2,高为1的正三棱柱,则S 侧=3×(2×1)=6.(理)(2010·陕西文,8)若某空间几何体的三视图如下图所示,则该几何体的体积是( )A .2B .1 C.23 D.13[答案] B[解析] 由几何体的三视图可知,该几何体是直三棱柱,其直观图如下图所示,其体积为V =12×2×1×2=1.5.一空间几何体的三视图如下图所示,则该几何体的体积为( )A .2π+2 3B .4π+2 3C .2π+233D .4π+233[答案] C[解析] 由几何体的三视图可知,该几何体是由一个底面直径和高都是2的圆柱和一个底面边长为2,侧棱长为2的正四棱锥叠放而成.故该几何体的体积为V =π×12×2+13×(2)2×3=2π+233,故选C.6.(文)(2011·湖南文,4)设下图是某几何体的三视图,则该几何体的体积为( )A .9π+42B .36π+18 C.92π+12 D.92π+18 [答案] D[解析] 由三视图可知,该几何体是一个球体和一个长方体的组合体.其中,V 球=43π·(32)3=9π2,V 长方体=2×3×3=18.所以V 总=92π+18. (理)(2011·山东济南一模)一个几何体的三视图如下图所示(单位长度:cm),则此几何体的表面积是( )A .(80+162)cm 2B .84cm 2C .(96+162)cm 2D .96cm 2[答案] A[解析] 其直观图如下图所示,由三视图知,棱锥底面是边长为4的正方形,高为2,棱柱与棱锥同底,高为4,因此棱锥的顶点到底边的距离是22+22=22cm ,故该几何体的表面积为S =(12×4×22)×4+(4×4)×5=80+162(cm 2).7.(2011·湖州模拟)如下图所示,已知一个多面体的平面展开图由一个边长为1的正方形和4个正三角形组成,则该多面体的体积是________.[答案]26[解析] 由展开图可知,该多面体是正四棱锥,底面正方形的边长为1,侧棱长也为1, ∴高h =322-122=22, ∴体积V =13×12×22=26.8.一个底面半径为1,高为6的圆柱被一个平面截下一部分,如图(1)所示,截下部分的母线最大长度为2,最小长度为1,则截下部分的体积是________.[答案]3π2[解析] 根据对称性把它补成如图(2)所示的圆柱,这个圆柱的高是3,体积是所求几何体体积的2倍,故所求的几何体的体积是12×π×12×3=3π2.故填3π2.9.圆柱内切球的表面积为4π,则圆柱的表面积为________. [答案] 6π[解析] 设球半径为R (R >0),则圆柱的底面半径为R ,高为2R ,由条件知,4πR 2=4π,∴R =1.∴圆柱的表面积S =2π·R 2+2πR ·2R =6πR 2=6π.10.(文)(2011·福建文,20)如下图,四棱锥P -ABCD 中,P A ⊥底面ABCD ,AB ⊥AD ,点E 在线段AD 上,且CE ∥AB .(1)求证:CE ⊥平面P AD ;(2)若P A =AB =1,AD =3,CD =2,∠CDA =45°,求四棱锥P -ABCD 的体积. [解析] (1)∵P A ⊥底面ABCD ,CE ⊂平面ABCD∴CE ⊥P A ,又∵AB ⊥AD ,CE ∥AB . ∴CE ⊥AD . 又∵P A ∩AD =A ∴CE ⊥平面P AD . (2)由(1)可知CE ⊥AD .在Rt △ECD 中,DE =CD ·cos45°=1,CE =CD ·sin45°=1. 又∵AB =CE =1,AB ∥CE ,所以四边形ABCE 为矩形. ∴S 四边形ABCD =S 矩形ABCE +S △CDE =AB ·AE +12CE ·DE=1×2+12×1×1=52.又P A ⊥底面ABCD ,P A =1所以V 四棱锥p -ABCD =13S 四边形ABCD ×P A =13×52×1=56.(理)(2010·合肥市质检)已知P 在矩形ABCD 的边DC 上,AB =2,BC =1,F 在AB 上且DF ⊥AP ,垂足为E ,将△ADP 沿AP 折起,使点D 位于D ′位置,连接D ′B 、D ′C 得四棱锥D ′-ABCP .(1)求证:D ′F ⊥AP ;(2)若PD =1,且平面D ′AP ⊥平面ABCP ,求四棱锥D ′-ABCP 的体积. [解析] (1)∵AP ⊥D ′E ,AP ⊥EF ,D ′E ∩EF =E , ∴AP ⊥平面D ′EF ,∴AP ⊥D ′F .(2)∵PD =1,∴四边形ADPF 是边长为1的正方形, ∴D ′E =DE =EF =22, ∵平面D ′AP ⊥平面ABCP ,D ′E ⊥AP ,∴D ′E ⊥平面ABCP , ∵S 梯形ABCP =12×(1+2)×1=32,∴V D ′-ABCP =13×D ′E ×S 梯形ABCP =24.11.(2010·北京文,8)如下图,正方体ABCD -A 1B 1C 1D 1的棱长为2.动点E ,F 在棱A 1B 1上,点Q 是棱CD 的中点,动点P 在棱AD 上.若EF =1,DP =x ,A 1E =y (x ,y 大于零),则三棱锥P -EFQ 的体积( )A .与x ,y 都有关B .与x ,y 都无关C .与x 有关,与y 无关D .与y 有关,与x 无关 [答案] C[解析] 设P 到平面EFQ 的距离为h ,则V P -EFQ =13×S △EFQ·h ,由于Q 为CD 的中点,∴点Q 到直线EF 的距离为定值2,又EF =1,∴S △EFQ 为定值,而P 点到平面EFQ 的距离,即P 点到平面A 1B 1CD 的距离,显然与x 有关与y 无关,故选C.12.(文)(2011·陕西文,5)某几何体的三视图如下图所示,则它的体积为( )A .8-2π3B .8-π3C .8-2π D.2π3[答案] A[解析] 由三视图知,原几何体为如下图所示一正方体挖去一个与正方体等高底面是正方形的内切圆的圆锥,则其体积为V =23-13π×12×2=8-2π3.故选A.(理)(2010·北京东城区)如图(1)所示,一只装了水的密封瓶子,其内部可以看成是由半径为1cm 和半径为3cm 的两个圆柱组成的简单几何体.当这个几何体如图(2)水平放置时,液面高度为20cm ,当这个几何体如图(3)水平放置时,液面高度为28cm ,则这个简单几何体的总高度为( )A.29cm B.30cmC.32cm D.48cm[答案] A[解析]如图(2),设下面圆柱高度为H,则上面小圆柱内液面高度20-H,又设余下部分为h,则图(3)中,下面圆柱高度为h+20-H,故上面圆柱液面高度为28-(h+20-H)=H+8-h,由两圆柱内液体体积相等得9πH+π(20-H)=π(h+20-H)+9π(H+8-h),∴h=9,几何体总高度为20+9=29cm.[点评]抓住问题的关键环节可以有效的提高解题的速度,本题中若设几何体的总高度为H,由几何体的总容积一定,内装液体的体积一定可得:π×32×(H-28)=π×12×(H-20),∴H=29(cm),解题过程就简捷多了.13.(2011·东北三校)一个几何体的三视图及部分数据如下图所示,左视图为等腰三角形,俯视图为正方形,则这个几何体的体积等于()A.13B.23C.156D.6224[答案] A[解析] 由三视图知,这是一个正四棱锥,其底面为正方形,一条侧棱垂直于底面其长度为2,底面正方形对角线长为1,∴边长为22,体积V =13×(22)2×2=13. 14.(文)一等边圆柱(轴截面是正方形的圆柱)的表面积为24π,一圆锥与此圆柱一个底面重合,顶点在另一个底面上,则此圆锥的表面积为________.[答案] 4(5+1)π[解析] 设圆柱底半径为R ,则2πR 2+2πR ·2R =24π,∴R =2, ∴圆锥的底半径为R =2,高为4, 母线长l =22+42=25,∴圆锥的表面积S =πR 2+πRl =4π+45π=4(5+1)π.(理)圆锥的高为4,侧面积为15π,其内切球的表面积为________. [答案] 9π[解析] 设圆锥底面半径为r (r >0),则母线长l =16+r 2,由πrl =15π得r ·16+r 2=15,解之得r =3,∴l =5.设内切球半径为R ,作出圆锥的轴截面如上图,则BD =BO 1=3,PD =5-3=2,PO =4-R ,∵OD ⊥PB ,∴R 2+4=(4-R )2,∴R =32,∴球的表面积S =4πR 2=9π.15.(文)(2011·安徽省淮南市高三模拟)如下图是以正方形ABCD 为底面的正四棱柱被一平面所截得的几何体,四边形EFGH 为截面,且AB =BC =2,AE =1,BF =DH =2,CG =3.(1)证明:截面四边形EFGH 是菱形; (2)求几何体C -EFGH 的体积.[解析] (1)证明:因为平面ABFE ∥平面CDHG ,且平面EFGH 分别交平面ABFE 、平面CDHG 于直线EF 、GH ,所以EF ∥GH .同理,FG ∥EH .因此,四边形EFGH 为平行四边形.因为BD ⊥AC ,而AC 为EG 在底面ABCD 上的射影, 所以EG ⊥BD .因为BF 綊DH ,所以FH ∥BD . 因此,FH ⊥EG .所以四边形EFGH 是菱形. (2)解:连接CE 、CF 、CH 、CA ,则V C -EFGH =V -V C -ABFE -V C -ADHE ,其中V 是几何体的体积,∵AE =1,BF =DH =2,CG =3且几何体是以正方形ABCD 为底面的正四棱柱的一部分,所以该几何体的体积为 V =(2)2×2=4, V C -ABFE =13×S 四边形ABFE ×BC=13×12(AE +BF )×AB ×BC =16×(1+2)×2×2=1. 同理,得V C -ADHE =1,所以,V C -EFGH =V -V C -ABFE -V C -ADHE =4-1-1=2, 即几何体C -EFGH 的体积为2.(理)(2011·江西文,18)如下图在△ABC 中,∠B =π2,AB =BC =2,P 为AB 边上一动点,PD ∥BC 交AC 于点D ,现将△PDA 沿PD 翻折至△PDA ′,使平面PDA ′⊥平面PBCD .(1)当棱锥A ′-PBCD 的体积最大时,求P A 的长;(2)若点P 为AB 的中点,E 为A ′C 的中点,求证:A ′B ⊥DE .[解析] (1)令P A =x (0<x <2),则A ′P =PD =x ,BP =2-x ,因为A ′P ⊥PD 且平面A ′PD ⊥平面PBCD ,故A ′P ⊥平面PBCD .所以V A ′-PBCD =13Sh =16(2-x )(2+x )x =16(4x -x 3).令f (x )=16(4x -x 3),由f ′(x )=16(4-3x 2)=0,得x =23 3.当x ∈(0,233)时,f ′(x )>0,f (x )单调递增;当x ∈(233,2)时,f ′(x )<0,f (x )单调递减.所以,当x =233时,f (x )取得最大值,即当V A ′-PBCD 最大时,P A =233. (2)设F 为A ′B 的中点,连接PF ,FE ,则有 EF 綊12BC ,PD 綊12BC ,∴EF 綊PD ,∴四边形EFPD 为平行四边形,∴DE ∥PF . 又A ′P =PB ,所以PF ⊥A ′B ,故DE ⊥A ′B .1.如下图,已知在多面体ABC -DEFG 中,AB 、AC 、AD 两两互相垂直,平面ABC ∥平面DEFG ,平面BEF ∥平面ADGC ,AB =AD =DG =2,AC =EF =1,则该多面体的体积为( )A .2B .4C .6D .8[答案] B[解析] 补成长方体ABMC -DEFN 并连接CF ,易知三棱锥F -BCM 与三棱锥C -FGN 的体积相等,故几何体体积等于长方体的体积4.故选B.[点评] 1.也可以用平面BCE 将此几何体分割为两部分,设平面BCE 与DG 的交点为H ,则ABC -DEH 为一个直三棱柱,由条件易证EH 綊FG 綊BC ,平面BEF ∥平面CHG ,且△BEF ≌△CHG ,∴几何体BEF -CHG 是一个斜三棱柱,这两个三棱柱的底面都是直角边长为2和1的直角三角形,高都是2,∴体积为4.2.如图(2),几何体ABC -DEFG 也可看作棱长为2的正方体中,取棱AN 、EK 的中点C 、F ,作平面BCGF 将正方体切割成两部分,易证这两部分形状相同,体积相等,∴V ABC-DEFG=12×23=4.2.(2010·安徽理,8)一个几何体的三视图如下图,该几何体的表面积为()A.280 B.292C.360 D.372[答案] C[解析]由三视图知该几何体是两个长方体的组合体,上面的长方体的表面积为(6×8)×2+(8×2)×2+6×2=140.下面的长方体的表面积为(10×8)×2+(10×2)×2+(8×2)×2-6×2=220.故表面积为140+220=360.选C.3.(2010·东营质检)用单位正方体搭几何体,使它的主视图和俯视图如下图所示,则符合条件的几何体体积的最小值与最大值分别是()A.9,13 B.7,16C .10,15D .10,16[答案] D[解析] 由俯视图知底层有七个小正方体,结合主视图知,最左边一列,最多都是三层,最少只有一行是三层,故左边一列最多9个、最少5个;中间一列最多都是二层有6个,最少只有一行二层,共4个;右边一列只一层一行,故最多9+6+1=16个,最少5+4+1=10个.4.(2010·沈阳市)如下图所示,某几何体的正(主)视图与侧(左)视图都是边长为1的正方形,且体积为12.则该几何体的俯视图可以是( )[答案] C[解析] 由正(主)视图和侧(左)视图可知,此几何体为柱体,易知高h =1,且体积V =S ×h =12(S 为底面积),得S =12,结合各选项知这个几何体的底面可以是边长为1的等腰直角三角形,故选C.5.(2011·湖南十二校)四棱锥P -ABCD 的顶点P 在底面ABCD 中的射影恰好是A ,其三视图如下图,则四棱锥P -ABCD 的表面积为________.[答案] (2+2)a 2[解析] 由三视图知,其直观图如下图.∵CD ⊥AD ,CD ⊥P A ,∴CD ⊥平面P AD ,同理CB ⊥平面P AB . ∴PD =PB =2a ,其表面积S =AB ·AD +2×(12AB ·P A )+2×(12PB ·BC )=a 2+a 2+2a 2=(2+2)a 2.6.如图(1),矩形ABCD 中,AB =2AD =2a ,E 为DC 的中点,现将△ADE 沿AE 折起,使平面ADE ⊥平面ABCE ,如(2).(1)求四棱锥D -ABCE 的体积;(2)求证:AD ⊥平面BDE .[解析] (1)取AE 的中点O ,由题意知, AB =2AD =2a ,ED =EC ,∴AD =DE ,∴DO ⊥AE , 又∵平面ADE ⊥平面ABCE , ∴DO ⊥平面ABCE . 在等腰Rt △ADE 中, AD =DE =a ,DO =22a , 又S 梯形ABCE =12(a +2a )a =32a 2,∴V D -ABCE =13S 梯形ABCE ·DO =13·32a 2·22a =24a 3.(2)连结BE ,则BE =a 2+a 2=2a ,又AE =2a ,AB =2a , ∴AB 2=AE 2+EB 2,∴AE ⊥EB ,由(1)知,DO⊥平面ABCE,∴DO⊥BE,又∵DO∩AE=O∴BE⊥平面ADE,∴BE⊥AD,又∵AD⊥DE,∴AD⊥平面BDE.。
表面积与体积练习题(含答案)

空间几何体的表面积和体积练习(录自新教材完全解读)1、一个证四棱台的两底面边长分别为)(,n m n m >,侧面积等于两个底面积之和,则这个棱台的高位( ) A.n m mn + B. n m mn - C. mn n m + D. mnnm - 2、一个圆柱的侧面展开图示一个正方形,这个圆柱的表面积与侧面积的比是( ) A.ππ221+ B. ππ441+ C. ππ21+ D. ππ241+ 3、在斜三棱柱A BC -A 1B 1C1中,∠BAC=090,0110111190,60,=∠=∠=∠==C BB C AA B AA a AC AB ,侧棱长为b ,求其侧面积。
ab )23(+4、一个三棱锥的底面是正三角形,侧面都是等腰直角三角形,底面边长为a ,求它的表面积。
2)33(41a + 5、已知圆台的上、下底面半径和高的比为1:4:4,母线长为10,求圆台的侧面积。
100π6、若正方体的棱长为2,则以该正方体各个面的中心为顶点的凸多面体的体积为( )A.62B . 32C . 33 D. 327、已知圆台两底面半径分别为)(,n m n m >,求圆台和截得它的圆锥的体积比。
333m n m - 8、直三棱柱(侧棱垂直底面的三棱柱)的高6,底面三角形的边长分别为3、4、5,将棱柱削成圆柱,求削去部分体积的最小值。
)6(6π-9、如图,三棱锥S-ABC 的三条侧棱两两垂直,且6,3,1===SC SA SB ,求该三棱锥的体积。
22 10、若两球表面积之比为4:9,则其体积之比为( )SCBAA.8:27B.16:81 C.64:729 D.2:311、如果三个球的半径之比是1:2:3,那么最大球的体积是其余两个球的体积之和的( ) A .1倍 B.2倍 C.3倍 D.4倍 12、如图所示,半径为R 的半圆内的阴影部分以直径A B所在直线为轴,旋转一周得到一几何体,求该几何体的表面积。
几何体的表面积及体积习题及答案
空间几何体的表面积与体积(时间:45分钟 满分:100分)一、选择题(每小题7分,共35分)1.正六棱柱的高为6,底面边长为4,则它的全面积为 ( )A.48(3+3)B.48(3+23)C.24(6+2)2.如图(1)所示,一只装了水的密封瓶子可以看成是由半径为1 cm 和半径为3 cm 的两个圆柱组成的几何体.当这个几何体如图(2)水平放置时,液面高度为20 cm ,当这个几何体如图(3)水平放置时,液面高度为28 cm ,则这个几何体的总高度为 ( )A.29 cmB.30 cmC.32 cmD.48 cm3.(2010·浙江)若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是 ( )A.3523 cm 3B.3203cm 3 C.2243 cm 3 D.1603cm 34.如图所示,已知三棱柱ABC —A 1B 1C 1的所有棱长均为1,且AA 1⊥底面ABC ,则三棱锥B 1—ABC 1的体积为 ( )A.312 B.34 C.612 D.645.(2010·辽宁)已知S,A,B,C是球O表面上的点,SA⊥平面ABC,AB⊥BC,SA=AB=1,BC=2,则球O的表面积等于()二、填空题(每小题6分,共24分)6.(2010·天津)一个几何体的三视图如图所示,则这个几何体的体积为.7.(2011·湖州模拟)如图所示,已知一个多面体的平面展开图由一个边长为1的正方形和4个边长为1的正三角形组成,则该多面体的体积是.8.(2010·抚顺六校第二次模拟)把边长为1的正方形ABCD沿对角线BD折起形成三棱锥C—ABD,其正视图与俯视图如图所示,则其侧视图的面积为.9.(2011·南京第一次调研)如图,已知正三棱柱ABC—A1B1C1的底面边长为2 cm,高为5 cm,则一质点自点A出发,沿着三棱柱的侧面绕行两周到达点A1的最短路线的长为cm.三、解答题(共41分)10.(13分)已知正方体AC 1的棱长为a ,E ,F 分别为棱AA 1与CC 1的中点,求四棱锥A 1—EBFD 1的体积.11.(14分)如图,已知某几何体的三视图如下(单位:cm).(1)画出这个几何体的直观图(不要求写画法);(2)求这个几何体的表面积及体积.12.(14分)(2011·广州调研)如图1,在直角梯形ABCD 中,∠ADC =90°,CD ∥AB ,AB =4,AD =CD =2,将△ADC 沿AC 折起,使平面ADC ⊥平面ABC ,得到几何体D —ABC ,如图2所示.图1 图2(1)求证:BC ⊥平面ACD ;(2)求几何体D —ABC 的体积.答案7.26 8.1410. 解 因为EB =BF =FD 1=D 1E =a 2+⎝⎛⎭⎫a 22=52a , 所以四棱锥A 1—EBFD 1的底面是菱形,连接EF ,则△EFB ≌△EFD 1,由于三棱锥A 1—EFB 与三棱锥A 1—EFD 1等底同高,所以111122A EBFD A EFB F EBA V V V ---===2·13·1EBA S ∆·a =16a 3. 11. 解 (1)这个几何体的直观图如图所示.(2)这个几何体可看成是正方体AC 1及直三棱柱B 1C 1Q —A 1D 1P 的组合体.由P A 1=PD 1=2,A 1D 1=AD =2,可得P A 1⊥PD 1.故所求几何体的表面积S =5×22+2×2×2+2×12×(2)2=22+42(cm 2),体积V =23+12×(2)2×2=10 (cm 3).12. (1)证明 在图中,可得AC =BC =22,从而AC 2+BC 2=AB 2,故AC ⊥BC ,取AC 的中点O ,连接DO ,则DO ⊥AC ,又平面ADC ⊥平面ABC ,平面ADC ∩平面ABC =AC ,DO ⊂平面ADC ,从而DO ⊥平面ABC ,∴DO ⊥BC ,又AC ⊥BC ,AC ∩DO =O ,∴BC ⊥平面ACD .(2)解 由(1)可知BC 为三棱锥B —ACD 的高,BC =22,S △ACD =2,∴V B —ACD =13S △ACD ·BC =13×2×22=423,由等体积性可知,几何体D —ABC 的体积为423.几何作图(作业)1.如图,按要求作图:(1)连接CE ;(2)延长CE 到点D ,使ED =CE ;(3)作直线AD ,作射线DB .B2.如图,已知线段AB,按要求作图:(1)分别以点A和点B为圆心、以AB的长为半径作弧,两弧相交于点C和点D;(2)作直线CD,交线段AB于点E.A3.如图,一辆汽车在公路上由A向B行驶,M、N分别为位于AB两侧的学校.(1)汽车在公路上行驶时会对学校的教学造成影响,当汽车行驶到点P的位置时对学校M的影响最大,行驶到点Q的位置时对学校N的影响最大.请在图中分别作出点P,Q的位置.(2)当汽车从A向B行驶,哪一段上对两个学校的影响越来越大?哪一段上对学校M的影响逐渐减小,而对学校N的影响逐渐增大?NMB A4.(1)如图1,在一条笔直的公路两侧,分别有A ,B 两个村庄,现在要在公路l 上建一座火力发电厂,向A ,B 两个村庄供电,为使所用电线最短,请问发电厂P 应建在何处?简要说明理由.(2)如图2,若要向4个村庄A ,B ,C ,D 供电,发电厂Q 应该建在何处使发电厂到四个村庄的距离之和最小?l A BDC B A图1 图25.下列四个生活、生产现象:①用两个钉子就可以把木条固定在墙上;②植树时,只要定出两棵树的位置,就能确定同一行所在的直线;③从A 地到B 地,架设电线,总是尽可能沿着线段AB 架设;④把弯曲的公路改直就能缩短路程.其中可用定理“两点之间,线段最短”来解释的现象有______(填序号).6.在直线l 上任取一点A ,截取AB =10cm ,再截取AC =6cm ,则线段BC 的长为__________.B A B A7.在直线l 上任取一点A ,截取AB =20cm ,再截取AC=50cm ,则AB 的中点D 与AC 的中点E 之间的距离为__________.B A B A8.已知线段AB =15cm ,C 点在直线AB 上,BC =2AB ,则AC 的长为__________.B A B A9.从O 点出发的三条射线OA ,OB ,OC ,若∠AOB =60°,∠AOC =40°,则∠BOC 的度数为__________.O B A 60° O B A60°10.已知∠AOB 为直角,∠BOC =40°,OM 平分∠AOB ,ON 平分∠BOC ,则∠MON 的度数为__________.B O A B OA【参考答案】1.(1)作图略;(2)作图略;(3)作图略;2.作图略;3.(1)作图略(提示:过点M作AB的垂线,垂足即为所求的点P,过点N作AB的垂线,垂足即为Q 点);(2)AP段,PQ段;4.(1)作图略(连接AB交直线l的交点即为P点);(2)作图略(提示:连接AD,BC,AD与BC的交点即为Q点)5.③④;6.4 cm或16 cm;7.15 cm或35 cm;8.15cm或45cm;9.20°或100°;10.20°或100°;11.25°或65°.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 【2016高考浙江理数】如图,在△ABC 中,AB =BC =2,∠ABC =120°.若平面ABC 外的点P 和线段AC 上的点D ,满足PD =DA ,PB =BA ,则四面体PBCD 的体积的最大值是.【答案】12故BD =.在PBD ∆中,PD AD x ==,2PB BA ==.由余弦定理可得222cos 2PD PB BD BPD PD PB +-∠===⋅,所以30BPD ∠=.EDCBAP过P 作直线BD 的垂线,垂足为O .设PO d =则11sin 22PBD S BD d PD PB BPD ∆=⨯=⋅∠,12sin 302d x =⋅,解得d =而BCD ∆的面积111sin )2sin 30)222S CD BC BCD x x =⋅∠=⋅=-. 设PO 与平面ABC 所成角为θ,则点P 到平面ABC 的距离sin h d θ=. 故四面体PBCD的体积11111sin )33332BcD BcD BcD V S h S d S d x θ∆∆∆=⨯=≤⋅=⨯-=.设t ==,因为0x ≤≤,所以12t ≤≤.则|x =(2x <≤||x x ==故x =+.此时,V =21414()66t t t t-=⋅=-.由(1)可知,函数()V t 在(1,2]单调递减,故141()(1)(1)612V t V <=-=. 综上,四面体PBCD 的体积的最大值为12. 考点:1、空间几何体的体积;2、用导数研究函数的最值.【思路点睛】先根据已知条件求出四面体的体积,再对x 的取值范围讨论,用导数研究函数的单调性,进而可得四面体的体积的最大值.2.【2016高考新课标1文数】(本题满分12分)如图,在已知正三棱锥P -ABC 的侧面是直角三角形,PA =6,顶点P 在平面ABC 内的正投影为点E ,连接PE 并延长交AB 于点G . (I )证明G 是AB 的中点;(II )在答题卡第(18)题图中作出点E 在平面PAC 内的正投影F (说明作法及理由),并求四面体PDEF 的体积.PABD CGE【答案】(I )见解析(II )作图见解析,体积为43【解析】所以AB ⊥平面PED ,故.AB PG ⊥又由已知可得,PA PB =,从而G 是AB 的中点.在等腰直角三角形EFP 中,可得 2.==EF PF 所以四面体PDEF 的体积114222.323=⨯⨯⨯⨯=V 考点:线面位置关系及几何体体积的计算【名师点睛】文科立体几何解答题主要考查线面位置关系的证明及几何体体积的计算,空间中线面位置关系的证明主要包括线线、线面、面面三者的平行与垂直关系,其中推理论证的关键是结合空间想象能力进行推理,要防止步骤不完整或考虑不全致推理片面,该类题目难度不大,以中档题为主.3. [2016高考新课标Ⅲ文数]如图,四棱锥P ABC -中,PA ⊥平面ABCD ,ADBC ,3AB AD AC ===,4PA BC ==,M 为线段AD 上一点,2AM MD =,N 为PC 的中点.(I )证明MN平面PAB ;(II )求四面体N BCM -的体积.【答案】(Ⅰ)见解析;【解析】(Ⅱ)因为⊥PA 平面ABCD ,N 为PC 的中点, 所以N 到平面ABCD 的距离为PA 21. 取BC 的中点E ,连结AE .由3==AC AB 得BC AE ⊥,522=-=BE AB AE .由BC AM ∥得M 到BC 的距离为5,故525421=⨯⨯=∆BCM S , 所以四面体BCM N -的体积354231=⨯⨯=∆-PA S V BCM BCM N . 考点:1、直线与平面间的平行与垂直关系;2、三棱锥的体积.【技巧点拨】(1)证明立体几何中的平行关系,常常是通过线线平行来实现,而线线平行常常利用三角形的中位线、平行四边形与梯形的平行关系来推证;(2)求三棱锥的体积关键是确定其高,而高的确定关键又推出顶点在底面上的射影位置,当然有时也采取割补法、体积转换法求解.4. 【2016高考上海理数】将边长为1的正方形11AAO O (及其内部)绕的1OO 旋转一周形成圆柱,如图,AC 长为23π,11A B 长为3π,其中1B 与C 在平面11AAO O 的同侧。
(1)求三棱锥111C O A B -的体积;(2)求异面直线1B C 与1AA 所成的角的大小。
【答案】(1(2)4π.试题解析:(1)由题意可知,圆柱的高1h =,底面半径1r =. 由11A B 的长为3π,可知1113π∠A O B =.11111111111sin 2S ∆O A B =O A ⋅O B ⋅∠A O B =111111C 1V 3S h -O A B ∆O A B =⋅=.(2)设过点1B 的母线与下底面交于点B ,则11//BB AA , 所以1C ∠B B 或其补角为直线1C B 与1AA 所成的角. 由C A 长为23π,可知2C 3π∠AO =, 又1113π∠AOB =∠A O B =,所以C 3π∠OB =,从而C ∆OB 为等边三角形,得C 1B =. 因为1B B ⊥平面C AO ,所以1C B B ⊥B . 在1C ∆B B 中,因为1C 2π∠B B =,C 1B =,11B B =,所以1C 4π∠B B =, 从而直线1C B 与1AA 所成的角的大小为4π.考点:1.几何体的体积;2.空间的角.【名师点睛】此类题目是立体几何中的常见问题.解答本题,关键在于能利用直线与直线、直线与平面、平面与平面关系的相互转化,将空间问题转化成平面问题.立体几何中的角与距离的计算问题,往往可以利用几何法、空间向量方法求解,应根据题目条件,灵活选择方法.本题能较好的考查考生的空间想象能力、逻辑推理能力\转化与化归思想及基本运算能力等.5.【2015高考山东,文9】已知等腰直角三角形的直角边的长为,将该三角形绕其斜边所在的直线旋转一周而形成的曲面所围成的几何体的体积为( )(A (B ()()【答案】B【考点定位】1.旋转体的几何特征;2.几何体的体积.【名师点睛】本题考查了旋转体的几何特征及几何体的体积计算,解答本题的关键,是理解所得旋转体的几何特征,确定得到计算体积所需要的几何量.本题属于基础题,在考查旋转体的几何特征及几何体的体积计算方法的同时,考查了考生的空间想象能力及运算能力,是“无图考图”的一道好题.6.【2015高考上海,文6】若正三棱柱的所有棱长均为a ,且其体积为316,则a .【答案】4【考点定位】等边三角形的性质,正三棱柱的性质.【名师点睛】正三棱柱的底面是正三角形,侧棱垂直于底面.柱体的体积等于底面积乘以高.边长为a 的正三角形的面积为243a . 7.【2015高考四川,文14】在三棱住ABC -A 1B 1C 1中,∠BAC =90°,其正视图和侧视图都是边长为1的正方形,俯视图是直角边长为1的等腰直角三角形,设点M ,N ,P 分别是AB ,BC ,B 1C 1的中点,则三棱锥P -A 1MN 的体积是______.【答案】124【考点定位】本题主要考查空间几何体的三视图、直观图及空间线面关系、三棱柱与三棱锥的体积等基础知识,考查空间想象能力、图形分割与转换的能力,考查基本运算能力. 【名师点睛】解决本题,首先要正确画出三棱柱的直观图,包括各个点的对应字母所在位置,结合条件,三棱锥P -A 1MN 的体积可以直接计算,但转换为三棱锥P -AMN 的体积,使得计算更为简便,基本上可以根据条件直接得出结论.属于中档偏难题.8.【2015高考新课标2,理9】已知A,B 是球O 的球面上两点,∠AOB=90,C 为该球面上的动点,若三棱锥O-ABC 体积的最大值为36,则球O 的表面积为( )A .36π B.64π C.144π D.256π【答案】C考点:外接球表面积和椎体的体积.BOAC【名师点睛】本题以球为背景考查空间几何体的体积和表面积计算,要明确球的截面性质,正确理解四面体体积最大时的情形,属于中档题. 9.【2015高考山东,理7】在梯形ABCD 中,2ABC π∠=,//,222AD BC BC AD AB === .将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体的体积为( ) (A )23π (B )43π (C )53π (D)2π 【答案】C【考点定位】1、空间几何体的结构特征;2、空间几何体的体积.【名师点睛】本题考查了空间几何体的结构特征及空间几何体的体积的计算,重点考查了圆柱、圆锥的结构特征和体积的计算,体现了对学生空间想象能力以及基本运算能力的考查,此题属中档题.【反馈练习】1. 【2016届广东汕头市普通高考高三第二次模拟数学试卷,文18】已知四棱锥P ABCD -中,PA 垂直于直角梯形ABCD 所在的平面,,,BA AD BCAD M ⊥是PC 的中点, 且2,4AB AD AP BC ====.(1)求证:DM 平面PAB ; (2)求三棱锥M PBD -的体积. 【答案】(1)证明见解析;(2)34. 【解析】(2)1184,233BCD P BCD BCD S BC CD V S PA ∆-∆====,1118422233M PBD C PBD P BCD V V V ---===⨯=. 考点:(1)直线与平面平行的判定;(2)棱柱、棱锥、棱台的体积.2. 【2016-2017学年四川成都经济技术开发区实验高二10月考数学卷,理18】如图(1)所示,在直角梯形ABCP 中,BC ∥AP ,AB ⊥BC ,CD ⊥AP ,AD =DC =PD =2,E 、F 、G 分别为线段PC 、PD 、BC 的中点,现将△PDC 折起,使平面PDC ⊥平面ABCD (图(2)).(1)求证:AP ∥平面EFG ;(2)若点Q 是线段PB 的中点,求证:PC ⊥平面ADQ ;(3)求三棱锥C -EFG 的体积.【答案】(1)详见解析(2)详见解析(3)16【解析】试题解析:(1)证明:∵E 、F 分别是PC ,PD 的中点,∴EF ∥CD ∥AB .又EF ⊄平面PAB ,AB ⊂平面PAB ,∴EF ∥平面PAB .同理,EG ∥平面PAB ,∴平面EFG ∥平面PAB .又∵AP ⊂平面PAB ,∴AP ∥平面EFG .(2)解:连接DE ,EQ ,∵E 、Q 分别是PC 、PB 的中点,∴EQ ∥BC ∥AD .∵平面PDC ⊥平面ABCD ,PD ⊥DC ,∴PD ⊥平面ABCD .∴PD ⊥AD ,又AD ⊥DC ,∴AD ⊥平面PDC ,∴AD ⊥PC .在△PDC 中,PD =CD ,E 是PC 的中点,∴DE ⊥PC ,∴PC ⊥平面ADEQ ,即PC ⊥平面ADQ .(3)V C -EFG =V G -CEF =13S △CEF ·GC =13×12×1=16.考点:直线与平面平行的判定;棱柱、棱锥、棱台的体积;直线与平面垂直的判定3. 【2016-2017学年四川成都经济技术开发区实验高二10月考数学卷,理18】如图,四边形ABCD 是平行四边形,⊥AE 平面ABCD ,AB EF //,2=AB ,1==EF BC ,6=AE ,3=DE , 60=∠BAD ,G 为BC 的中点.(1)求证://FG 平面BED ;(2)求证:平面⊥BED 平面AED ;(3)求多面体ABCD EF -的体积.【答案】(1)详见解析(2)详见解析(3【解析】试题解析:(1)证明:如图,取BD 的中点O ,连接OE ,OG ,在BCD ∆中,∵G 是BC 的中点,∴DC OG //且121==DC OG ,又∵DC AB AB EF //,//,∴OG EF //且OG EF =,即四边形OGFE 是平行四边形,∴.又⊄FG 平面BED ,⊂OE 平面BED ,∴//FG 平面BED .(3)解:连HO ,并延长交CD 于I ,连FI FH ,.∵O H ,分别为BD AB ,的中点,∴AD OH //,∴I 是CD 中点,∵AB EF //,1,2==EF AB ,∴多面体HIF ADE -为三棱柱,体积为423231621=⨯⨯⨯=⋅OD S ADE ,且四边形AEFH 为平行四边形,∴AE FH AE FH =,//,∵⊥AE 平面ABCD ,∴⊥FH 平面ABCD ,四棱锥BCIH F -的体积为22631616131=⨯⨯⨯=⋅=⋅AE S FH S ABCD BCIH , ∴多面体ABCD EF -的体积为42522423=+.考点:线面平行的判定;线面垂直的判定;多面体体积4. 【2016-2017学年河北冀州中学高二上期中考试数学卷,文18】已知长方形ABCD 中,AD =,2AB =,E 为AB 中点,将ADE ∆沿DE 折起到△PDE ,所得四棱锥P BCDE -,如图所示.(1)若点M 为PC 中点,求证://BM 平面PDE ;(2)求P BCDE -的体积;(3)求证:DE PC ⊥.【答案】(1)证明见解析;(2(3)证明见解析. 【解析】试题分析:(1)根据中位线定理可证1//2FM DC =,进而可证FEBM 是平行四边形,所以//BM EF ,再由线面平行的判定定理可得结论;(2)由平面PDE ⊥平面EBCD 可得PO ⊥平面EBCD ,算出PO 的值进而可得P BCDE -的体积;(3)先证DE AC ⊥,再根据四棱锥P EBCD -中,PN DE ⊥,然后根据线面垂直的判定定理可得DE ⊥平面POC ,进而可得结论.试题解析:(1)证明:取DP 中点F ,连接EF ,FM ,在△PDE 中,计算可得PO =,∴111(12)332P BCDE V Sh -==⨯+= (3)在矩形ABCD 中,连接AC 交DE 于N ,因为tan DEA ∠=,tan CAB ∠=,所以2DEA CAB π∠+∠=, 所以DE AC ⊥,所以在四棱锥P EBCD -中,PN DE ⊥,CN DE ⊥,又PN CN N =,所以DE ⊥平面POC ,因为PC ⊂平面POC ,所以DE PC ⊥.考点:1、线面平行的判定定理;2、线面垂直的判定定理.5. 【2017届甘肃高台县一中高三上第三次检测试卷,文18】如图,在四棱锥E ABCD -中,底面ABCD 为正方形,AE ⊥平面CDE ,已知2AE DE ==,F 为线段DE 的中点.BE平面ACF;(1)求证://-的体积.(2)求四棱锥E ABCD【答案】(1)见解析;【解析】试题解析:(1)连结BD和AC交于O,连结OF,∵ABCD为正方形,∴O为BD中点,∵F为DE中点,OF BE.∴//∵BE⊄平面ACF,OF⊂平面ACF,BE平面ACF.∴//∴四棱锥E ABCD -的体积21133ABCD V S EG =⨯=⨯= 考点:1.线面平行的判定与性质;2.线面垂直、面面垂直的判定与性质;3.多面体的体积.6. 【2017届湖南长沙长郡中学高三上第三次月考模拟试卷,文17】如图,直三棱柱111C B A ABC -中,31===AA BC AC ,BC AC ⊥,点M 在线段AB 上.(1)若M 是AB 的中点,证明://1AC 平面CM B 1;(2)当BM 长是多少时,三棱锥BCM B -1的体积是三棱柱111C B A ABC -的体积的91.【答案】(1)证明见解析;(2)2.【解析】(2)解:1311BB S V BCM BCM B ⋅=∆-,1111BB S V ABC C B A ABC ⋅=∆-, 设λ=,10<<λ,则119131BB S BB S ABC ABC ⋅=⋅∆∆λ.故31=λ,即2=BM . 故当2=BM 时,三棱锥BCM B -1的体积是三棱柱111C B A ABC -的体积的91.考点:1.线面平行的判定;2.柱锥体的体积.7. 【2017届广东省实验中学高三10月月考数学试卷,文18】如图,ABC ﹣A 1B 1C 1是底面边长为2,高为23的正三棱柱,经过AB 的截面与上底面相交于PQ ,设C 1P=λC 1A 1(0<λ<1). A 1A1B1C C B QP(Ⅰ)证明:PQ∥A 1B 1;(Ⅱ)当21=λ时,在图中作出点C 在平面ABQP 内的正投影F (说明作法及理由),并求四面体CABF 的体积.【答案】(Ⅰ)证明见解析;(Ⅱ)正投影见解析,12. 【解析】 试题分析:(I)由正三棱柱的性质可以知道,上下两个底面平行,由两个平面平行的性质定理可得PQ AB //,由此能证明11//B A PQ ;(II) 当21=λ时,Q P ,分别是1111,B A C A 的中点, 在等腰梯形ABQP 中,26=FH ,⊥∴=⋂CF H FH QP , 平面F AB ,即ABQP CF 平面⊥,所以F 点是C 在平面ABQP 内的正投影,即得.取AB 中点H ,连接,,FH CH CH =在等腰梯形ABQP 中,FH = 连接 15中,26=CF 222CH FH CF =+∴FH CF ⊥∴,⊥∴=⋂CF H FH QP , 平面ABF ,即ABQP CF 平面⊥,所以F 点是C 在平面ABQP 内的正投影。
