高中数学新教材必修第二册专题8.3 简单几何体的表面积与体积(原卷版)
高中数学人教A版(2019)必修 第二册第八章 立体几何初步8.3简单几何体的表面积与体积

必修第二册 8.3 简单几何体的表面积与体积一、单选题1.如图,位于贵州黔南的“中国天眼”是具有我国自主知识产权、世界最大单口径、最灵敏的球面射电望远镜,其反射面的形状为球冠,球冠是球面被平面所截后剩下的曲面,截得的圆为球冠的底,与截面垂直的球体直径被截得的部分为球冠的高,设球冠所在球的半径为R ,球冠底的半径为r ,球冠的高为h ,球冠底面圆的周长为C .已知球冠的表面积公式为2S Rh π=,若65000,500S C ππ==,则球冠所在球的表面积为( )A .1620000πB .1690000πC .1720000πD .1790000π 2.已知一个正四棱锥的底面边长为4,以该正四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积,则该正四棱锥的侧面积为( )A .)41B 1C .)41D .)813.已知ABC O 的球面上,若球O 的体积为32π3,则O 到平面ABC 的距离为( )AB .32C .1D 4.已知A ,B 是球O 的球面上两点,90AOB ∠=︒,C 为该球面上的动点,若三棱锥O ABC -体积的最大值为36,则球O 的表面积为( )A .36πB .64πC .128πD .144π5.如图,在棱长为a 的正方体1111ABCD A B C D -中,P 在线段1BD 上,且12BP PD =,M 为线段11B C 上的动点,则三棱锥M PBC -的体积为( )A .319aB .332aC .313aD .与点M 的位置有关6.已知正四棱锥P ABCD -的所有顶点都在球O 的球面上,且正四棱锥P ABCD -的底面面积为6,侧面积为,则球O 的表面积为( )A .323πBC .16πD .32π 7.已知圆锥的表面积为3π,它的侧面展开图是一个半圆,则此圆锥的体积为( )AB C D 8.黄金分割是指将整体一分为二,较大部分与整体的比值等于较小部分与较大部分的,约为0.618.这个比例被公认为是最能引起美感的比例,因此被称为黄金比在几何世界中有很多黄金图形,在三角形中,如果相邻两边之比等于黄金分割比,且它们的夹角的余弦值为黄金分割比值,那么这个三角形一定是直角三角形,这个三角形称为黄金分割直角三角形.在正四棱锥中,以黄金分割直角三角形的长直角边作为正四棱锥的高,以短直角边的边长作为底面正方形的边心距(正多边形的边心距是正多边形的外接圆圆心到正多边形某一边的距离),斜边作为正四棱锥的斜高,所得到的正四棱锥称为黄金分割正四棱锥.在黄金分割正四棱锥中,以四棱锥的高为边长的正方形面积与该四棱锥的侧面积之比为( )A B C .1 D .149.阿基米德(Archimedes ,公元前287年—公元前212年)是古希腊伟大的数学家、物理学家和天文学家.后人按照他生前的要求,在他的墓碑上刻着一个圆柱容器里放了一个球(如图所示),该球与圆柱的两个底面及侧面均相切,圆柱的底面直径与高都等于球的直径.若该球的体积为36π,则圆柱的体积为 ( )A .36πB .45πC .54πD .63π 10.平行四边形ABCD 中,AB BD ⊥,且2224AB BD +=,沿BD 将四边形折起成平面ABD ⊥平面BDC ,则三棱锥A BCD -外接球的表面积为( )A .2πB .2πC .4πD .16π 11.已知一个圆柱的侧面展开图是一个正方形,则这个圆柱的全面积与侧面积的比是( )A .122ππ+B .144ππ+C .12ππ+ D .142ππ+ 12.已知正四棱锥的底面边长和侧棱长均为2,则该正四棱锥的体积为( )A B .C D .二、填空题13.已知圆锥的侧面积(单位:2cm ) 为2π,且它的侧面积展开图是一个半圆,则这个圆锥的底面半径(单位:cm )是_______.14.一个正四棱锥的顶点都在同一球面上,若该棱锥的高为2,底面边长为2,则该球的表面积为______.15.已知圆柱的轴截面(经过圆柱的轴的截面)是一个边长为2的正方形,则此圆柱的体积为________.16.若球的大圆的面积为9π,则该球的体积为________17.若五棱台11111ABCDE A B C D E -的表面积是30,侧面积是25,则两底面面积的和为______.三、解答题18.圆台的母线长为2a ,母线与轴的夹角为30,一个底面的半径是另一个底面的半径的2倍,求两底面的半径及两底面面积之和.19.将棱长为2的正方体1111ABCD A B C D -截去三棱锥1D ACD -后得到如图所示几何体,O 为11A C 的中点.(1)求证://OB 平面1ACD ;(2)求几何体111ACB A D 的体积.20.如图①,有一个圆柱形状的玻璃水杯,底面圆的直径为20cm ,高为30cm ,杯内有20cm 深的溶液.如图①,现将水杯倾斜,且倾斜时点B 始终在桌面上,设直径AB 所在直线与桌面所成的角为α.(1)求图①中圆柱的母线与液面所在平面所成的角(用α表示);(2)要使倾斜后容器内的溶液不会溢出,求α的最大值.21.“圆锥的两条母线所作的一切截面中,以轴截面的面积最大”是否成立?答案第1页,共1页 参考答案:1.B2.D3.C4.D5.A6.C7.C8.D9.C10.C11.A12.A13.114.9π15.2π16.36π17.518.圆台上底面半径为a ,下底面半径为2a ,两底面面积之和为25a π. 19.(1)见解析;(2)4.20.(1)2πα-;(2)45°﹒21.答案见解析。
高中数学必修二 8 3 2 圆柱、圆锥、圆台、球的表面积和体积 练习(含答案)

8.3.2 圆柱、圆锥、圆台、球的表面积和体积一、选择题1.若圆锥的高等于底面直径,则它的底面积与侧面积之比为A.1∶2B.1C.1D2【答案】C【解析】设圆锥底面半径为r,则高h=2r,∴其母线长l=r.∴S侧=πrl=πr2,S底=πr故选C.2.(2017新课标全国Ⅲ理科)已知圆柱的高为1,它的两个底面的圆周在直径为2的同一个球的球面上,则该圆柱的体积为A.πB.3π4C.π2D.π4【答案】B 【解析】绘制圆柱的轴截面如图所示,由题意可得:11,2 AC AB==,结合勾股定理,底面半径2r==,由圆柱的体积公式,可得圆柱的体积是223ππ1π24V r h⎛⎫==⨯⨯=⎪⎪⎝⎭,故选B.3.圆柱的底面半径为1,母线长为2,则它的侧面积为()A.2πB.3πC.πD.4π【答案】D【解析】圆柱的底面半径为r=1,母线长为l=2,则它的侧面积为S侧=2πrl=2π×1×2=4π.故选:D.4.圆台的上、下底面半径和高的比为1:4:4,母线长为10,则圆台的侧面积为().A.81πB.100πC.14πD.169π【答案】B【解析】设圆台上底半径为r,则其下底半径为4r,高为4r,结合母线长10,可求出r=2.然后由圆台侧面积公式得,.5.(多选题)一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径2R相等,下列结论正确的是()A.圆柱的侧面积为22RπB.圆锥的侧面积为22RπC.圆柱的侧面积与球面面积相等D.圆柱、圆锥、球的体积之比为3:1:2【答案】CD【解析】依题意得球的半径为R,则圆柱的侧面积为2224R R Rππ⨯=,∴A错误;圆锥的侧面积为2R Rπ=,∴B错误;球面面积为24Rπ,∵圆柱的侧面积为24Rπ,∴C正确;2322V R R Rππ=⋅=圆柱,2312233V R R Rππ⋅==圆锥,343V R=π球33324:2::3:1:233:V V V R R Rπππ∴==圆柱圆锥球,∴D正确.故选:CD.6.(多选题)如图所示,ABC 的三边长分别是3AC =,4BC =,5AB =,过点C 作CD AB ⊥,垂足为D .下列说法正确的是( )A .以BC 所在直线为轴,将此三角形旋转一周,所得旋转体的侧面积为15πB .以AC 所在直线为轴,将此三角形旋转一周,所得旋转体的体积为36πC .以AC 所在直线为轴,将此三角形旋转一周,所得旋转体的侧面积为25πD .以AC 所在直线为轴,将此三角形旋转一周,所得旋转体的体积为16π【答案】AD【解析】以BC 所在直线为轴旋转时,所得旋转体为底面半径为3,母线长为5,高为4的圆锥 ∴侧面积为3515ππ⨯⨯=,体积为2134123ππ⨯⨯⨯=,∴A 正确,B 错误;以AC 所在直线为轴旋转时,所得旋转体为底面半径为4,母线长为5,高为3的圆锥侧面积为4520ππ⨯⨯=,体积为2143163ππ⨯⨯⨯=,∴C 错误,D 正确.故选:AD .二、填空题7. 已知一个正方体的所有顶点在一个球面上,若这个正方体的表面积为18,则这个球的体积为____. 【答案】92π 【解析】设正方体边长为a ,则226183a a =⇒= ,外接球直径为34427923,πππ3382R V R ====⨯=.8.如图,若球O 的半径为5,一个内接圆台的两底面半径分别为3和4(球心O 在圆台的两底面之间),则圆台的体积为______.【答案】259π3【解析】解:作经过球心的截面(如图),由题意得13O A =,24O B =,5OA OB ==,则14OO =,23OO =,127O O =,所以()22π259347π33V ⨯⨯==.9.已知圆柱的上、下底面的中心分别为12,O O ,过直线12O O 的平面截该圆柱所得的截面是面积为4的正方形,则该圆柱的表面积为_______.【答案】6π【解析】由题意,圆柱的截面是面积为4的正方形,可得其边长为2,可得圆柱的底面半径为1r =,母线2l =,所以该圆柱的表面积为221222212216S S S rl r πππππ=+=+=⨯⨯+⨯=。
人教A版高中数学(配套新教材)必修第二册-第八章 -8-3-1棱锥、棱柱、棱台的表面积与体积

高中数学 必修第二册 RJ·A
易错辨析
1.棱柱、棱锥、棱台的侧面展开图的面积就是它们的表面积.( × ) 2.棱锥的体积等于底面面积与高之积.( × ) 3.棱台的体积可转化为两个锥体的体积之差.( √ ) 4.几何体的平面展开方法可能不同,但其表面积唯一确定.( √ )
高中数学 必修第二册 RJ·A
高中数学 必修第二册 RJ·A
二 棱柱、棱锥、棱台的体积
例2 (1)已知高为3的三棱柱ABC-A1B1C1的底面是边长为1的正三角形,
如图所示,则三棱锥B1-ABC的体积为
1
1
3
3
A.4
B.2
C. 6
D. 4
D解析 设三棱锥B1-ABC的高为h,
则
V三棱锥B1-ABC =13S△ABCh=31×
43×3=
+3S△DBC+ S△A1BD = 23a2+3×12×a2+3a2= 32+9a2.
几何体 A1B1C1D1-DBC 的体积 V=V正方体ABCD-A1B1C1D1 -V三棱锥A1-ABD=a3-13×12×a×a×a=56a3.
高中数学 必修第二册 RJ·A
随堂小测
1.若长方体的长、宽、高分别为3 cm,4 cm,5 cm,则长方体的体积为
解析 V 棱台=13×(2+4+ 2×4)×3 =13×3×(6+2 2) =6+2 2.
高中数学 必修第二册 RJ·A
5.如图所示,正方体ABCD-A1B1C1D1的棱长为1,E为线段B1C上的一点, 则三棱锥A-DED1的体积为__16___.
V V 解析 = 三棱锥A-DED1 三棱锥E-DD1A
高中数学 必修第二册 RJ·A
新知学习
知识点一 棱锥、棱柱、棱台的表面积
高中数学人教A必修第二册精英同步卷:83简单几何体的表面积与体积 含答案
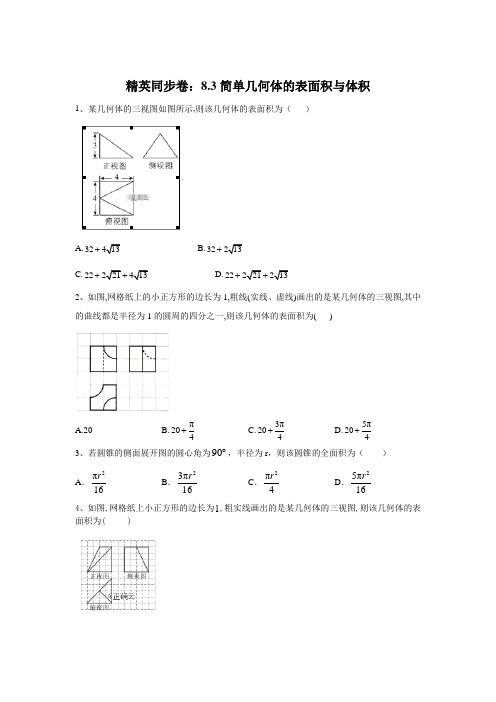
精英同步卷:8.3简单几何体的表面积与体积1、某几何体的三视图如图所示,则该几何体的表面积为()A.32413+ B.32213+C.22221413++ D.22221213++2、如图,网格纸上的小正方形的边长为1,粗线(实线、虚线)画出的是某几何体的三视图,其中的曲线都是半径为1的圆周的四分之一,则该几何体的表面积为( )A.20B.π204+ C.3π204+ D.5π204+3、若圆锥的侧面展开图的圆心角为90︒,半径为r,则该圆锥的全面积为()A.2π16rB.23π16rC.2π4rD.25π16r4、如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的表面积为( )A. 2843122++B. 3643122++C. 3642123++D. 44122+5、下图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为( )A. 20πB. 24πC. 28πD. 32π6、若某几何体的三视图(单位: cm )如图所示,其中左视图是一个边长为2的正三角形,则这个几何体的体积是( )A. 32cmB.33cmC. 333cmD. 33cm7、已知正三棱锥A BCD -的所有顶点都在球O 的球面上,3BC =.若球心O 在三棱锥的高AQ 的三等分点处,则球O 的半径为( )A .364B .2C .3D .48、已知正方体的体积是64,则其外接球的表面积是( ) A. 323π B. 192πC. 48πD.无法确定9、已知SC 是球 O 的直径, ,?A B 是球 O 球面上的两点,且1,3CA CB AB ==,若三棱锥S ABC -的体积为1,则球 O 的表面积为( ) A. 4π B. 13π C. 16π D. 52π10、某几何体的三视图如图2所示,则该几何体的表面积为( )A.16B.206π+C.142π+D.16π+11、如果一个几何体的三视图如图所示(单位长度: cm), 则此几何体的表面积是 。
8.3简单几何体的表面积与体积(学生版)-2021-2022学年人教A版(2019)高一数学必修第二

简单几何体的表面积与体积一、棱柱、棱锥、棱台的侧面积和表面积多面体的表面积就是围成多面体各个面的面积的和.棱柱、棱锥、棱台的表面积就是围成它们各个面的面积的和.求解正棱台的表面积时注意棱台的四个基本量:底面边长、高、斜高、侧棱,并注意两个直角梯形的应用(1)高、侧棱、上、下底面多边形的中心与顶点连线所成的直角梯形.(2)高、斜高、上、下底面边心距所成的直角梯形.二、棱柱、棱锥、棱台的体积棱柱:V棱柱=ShS为棱柱的底面积,h为棱柱的高棱锥:V棱锥=1 3ShS为棱锥的底面积,h为棱锥的高棱台:V棱台=13(S′+S′S+S)hS′,S分别为棱台的上、下底面面积,h为棱台的高求解正棱台的体积时,注意棱台的五个基本量(上、下底面边长、高、斜高、侧棱).常用两种解题思路:一是把基本量转化到直角梯形中解决问题;二是把正棱台还原成正棱锥.利用正棱锥的有关知识来解决问题.三、简单组合体的表面积与体积求组合体的表面积和体积,首先应弄清它的组成,其表面有哪些底面和侧面,各个面应该怎出各简单几何体的体积,然后再相加或相减.1.表面积公式:底面积:S底=2πr22.旋转体侧面积:S侧=2πrl圆柱:表面积:S=2πr(r+l);圆锥:底面积:S底=πr2;侧面积:S侧=πrl;表面积:S=πr(r+l)圆台:上底面面积:S上底=πr′2;下底面面积:S下底=πr2;侧面积:S侧=π(r′l+rl);表面积:S=π(r′2+r2+r′l+rl)圆柱、圆锥、圆台的侧面是曲面,计算侧面积时需要将这个曲面展开为平面图形计算,而表面积是侧面积与底面圆的面积之和.四、圆柱、圆锥、圆台的体积圆柱:V圆柱=Sh=πr2h圆柱底面圆的半径为r,面积为S,高为h圆锥:V圆锥=13Sh=13πr2h圆锥底面圆的半径为r,面积为S,高为h圆台:V圆台=13(S+SS′+S′)h=13π(r2+rr′+r′2)h圆台上底面圆的半径为r′,面积为S′,下底面圆的半径为r,面积为S,高为h 五、球的表面积与体积1.球的表面积公式S=4πR2(R为球的半径).2.球的体积公式V=43πR3.计算球的表面积与体积,关键是确定球心与半径.考点一 多面体表面积【例1】(2020·湖南怀化市)已知正四棱柱(即底面是正方形的直棱柱)的底面边长为3cm ,侧面的对角线长是35cm ,则这个正四棱柱的表面积为( )A .290cmB .2365cmC .272cmD .254cm【练1】(2020·全国高一课时练习)长方体的高为2,底面积等于12,过不相邻两侧棱的截面(对角面)的面积为10,则此长方体的侧面积为( )A .12B .24C .28D .32考点二 多面体台体积【例2】(2020·江苏南京市)底面边长为2,高为1的正三棱柱的体积是( )A .3B .1C .32D .13【练2】(2021·扶风县法门高中)正方体的全面积为18cm 2,则它的体积是_________ 3cm考点三 旋转体的表面积【例3】(2020·山东德州市·高一期末)若圆锥的轴截面是顶角为120的等腰三角形,且圆锥的母线长为2,则该圆锥的侧面积为( )A .3πB .2πC .23πD .43π【练3】(2021·浙江丽水市)经过圆锥的轴的截面是面积为2的等腰直角三角形,则圆锥的A.42πB.4πC.22πD.2π考点四旋转体的体积【例4】(2021·宁夏银川市·贺兰县景博中学)已知圆锥的母线长为5,底面周长为6π,则它的体积为( )A.10πB.12πC.15πD.36π【练4】(2020·山东菏泽市·高一期末)若圆锥的底面半径为3cm,侧面积为2π,则该15cm圆锥的体积为( )A.4π3cm D.36π3cmcm C.12π3cm B.9π3考点五球【例5】(2020·浙江高一期末)若一个球的直径为2,则此球的表面积为( )A.2πB.16πC.8πD.4π【练5】(2020·江苏无锡市第六高级中学高一期中)正三棱柱有一个半径为3cm的内切球,则此棱柱的体积是( ).A.393cm B.3183cm54cm C.327cm D.3考点六组合体的体积表面积【例6】(2020·全国高一课时练习)如图,一个无盖的器皿是由棱长为3的正方体木料从顶部挖掉一个直径为2的半球而成(半球的底面圆在正方体的上底面,球心为上底面的中心),则该器皿的表面积S为( )A .54B .542π+C .54π+D .543π+【练6】(2020·新疆巴音郭楞蒙古自治州·高一期末)如图,直三棱柱,高为6,底边三角形的边长分别为3、4、5,以上下底面的内切圆为底面,挖去一个圆柱,求剩余部分几何体的体积.课后练习1.(2021高一下·越秀期末)卢浮宫玻璃金字塔是著名美籍华裔建筑设计师贝聿铭的重要作品之一,主玻璃金字塔是一个底边长为35m,高为21m的正四棱锥,则该主玻璃金字塔所占空间的大小是 m3.2.(2021高一下·唐山期末)已知圆锥底面半径为1,母线长为3,该圆锥内接正方体的体积为.3.(2021·安阳模拟)如图,点C在以AB为直径的圆O上,|AC|=|BC|=5√2,若以直线AB为轴旋转一周,左半圆旋转所形成的几何体的体积为V1,△ABC旋转所形成的几何体的体积为V2,则V1+V2= .4.(2021·浙江模拟)已知圆柱的体积为15π2(单位:cm3),且它的侧面展开图是正方形,则这个圆柱的底面半径(单位:cm)是.5.(2021高三上·商丘开学考)已知某圆锥被一过该圆锥顶点的平面所截得到的几何体的正视图与侧视图如图所示,若该圆锥的顶点与底面圆周都在球O的球面上,则球O的表面积为.6.(2021高一下·河北期末)已知一圆锥的侧面展开图是半径为2√3的半圆,则该圆锥的体积是.7.(2021高二上·广州期中)已知四棱锥P−ABCD的顶点都在球O的球面上,底面ABCD,则球O 是边长为2的正方形,且PA⊥平面ABCD.若四棱锥P−ABCD的体积为163的表面积为 .8.(2020高一上·兰州期末)如果三个球的表面积之比是1:2:3,那么它们的体积之比是________.9.(2021高一下·河北期中)长方体ABCD−A1B1C1D1中,AB=1,AD=2,AA1=3,则三棱锥D1−ABC的体积为 .10.(2020高二上·嘉兴期末)一个正方体的顶点都在球面上,若该正方体的棱长为2,则球的体积是________.11(2021高一下·雅安期末)如图,在四棱锥P−ABCD中,平面PAD⊥平面ABCD,PA⊥AD,AD⊥AB,AB//CD,AD=DC=AP=2,AB=1,点E为棱PC 的中点.(1)证明:BE//平面PAD;(2)求三棱锥P−BDE的体积.12.(2021高一下·威宁县期末)如图,已知在长方体ABCD−A1B1C1D1中,E为AB上一点,且DC=2AA1=2AD=4AE=4√3.(1)求证:平面B1DE⊥平面AA1C1C;(2)求三棱锥C1−A1DE的体积.精讲答案【答案】A 【解析】由题意侧棱长为22(35)36-=.所以表面积为:224362390()S cm =⨯⨯+⨯=.故选:A.【练1】【答案】C【解析】设长方体底面矩形的长与宽分别为,a b ,则12ab =. 又由题意知22210a b +⨯=,解得4,3a b ==或3,4a b ==. 故长方体的侧面积为()243228⨯+⨯=.故选:C.【例2】【答案】A【解析】底面边长为2,高为1的正三棱柱的体积是23(2)134⨯⨯=故选:A 【练2】 【答案】33【解析】设该正方体的棱长为a cm ,由题意可得,2618a =,解得3a =, 所以该正方体的体积为333V a ==3cm . 故答案为:33【例3】【答案】C【解析】如图圆锥的轴截面是顶角为120,即60APO ∠=,2AP =,90POA ∠=, 所以3AO =,所以圆锥的侧面积为23AO PA ππ⨯⨯=.【练3】【答案】C【解析】设圆锥的底面半径为r ,母线长为l ,则2l r =, 由题可知()21222r ⨯=, ∴2,2r l ==, 侧面积为22rl ππ=,故选:C.【例4】【答案】B【解析】设圆锥的底面半径为r ,高为h ,因为底面周长为6π,所以26r ππ=,解得3r =,又因为母线长为5,所以h =4,所以圆锥的体积是21123V r h ππ==故选:B 【练4】【答案】C【解析】设圆锥母线长为l ,则侧面积为123152S l r l πππ=⋅==,故5l =. 故圆锥的高224h l r =-=,圆锥体积为21123V r h ππ==3cm .故选:C. 【例5】【答案】D【解析】因为球的直径为2,即球的半径为1,所以球的表面积为2414ππ⨯=,故选:D.【练5】【答案】B 【解析】∵正三棱柱有一个半径为3cm 的内切球,则正三棱柱的高为23cm , 底面正三角形的内切圆的半径为3cm ,设底面正三角形的边长为a cm,则31323a ⨯=,解得6a =cm , ∴正三棱柱的底面面积为13669322⨯⨯⨯=cm 2, 故此正三棱柱的体积V =932354⨯=cm 3.故选:B .【例6】【答案】C【解析】器皿的表面积是棱长为3的正方体的表面积减去半径为1的圆的面积,再加上半径为1的半球的表面积,即器皿的表面积()()221633141542542S πππππ=⨯⨯-⨯+⨯⨯=-+=+. 故选:C .【练6】【答案】366π-【解析】因为222345+=,所以底面是直角三角形, 所以上、下底面内切圆半径34512r +-==, 所以剩余部分几何体的体积21346163662V ππ=⨯⨯⨯⨯=-⨯-, 所以剩余部分几何体的体积为366π-.练习答案1.【答案】8.575【考点】棱柱、棱锥、棱台的体积【解析】【解答】V=13Sℎ=13×352×21=8575(cm3)=8.575(m3).故答案为:8.575.【分析】利用正四棱锥的几何性质以及锥体的体积公式求解即可.2.【答案】16√227【考点】棱锥的结构特征,棱柱、棱锥、棱台的体积【解析】【解答】解:作出该几何体的轴截面,如图所示,因为圆锥的底面半径为1,母线长为3,所以圆锥的高为ℎ=2√2,即OE=1,SE=3,SO=2√2,设正方体的边长为a,由轴截面的性质得ℎ−aℎ=√22aOE,即2√2−a2√2=√2a2,解得a=2√23,所以圆锥内接正方体的体积为V=a3=16√227故答案为:16√227【分析】作出圆锥过正方体AC1的对角面AA1C1 C的轴截面,利用相似三角形求出圆锥的内接正方体的棱长,即可计算正方体的体积.3.【答案】250π【考点】组合几何体的面积、体积问题,旋转体(圆柱、圆锥、圆台),球的体积和表面积【解析】左半圆旋转一周为球体,因为|AC|=|BC|=5√2,AB为直径,所以∠ACB=90°,所以AB=√AC2+BC2=10,即半径r=5,所以V1=4πr33=500π3,△ABC以直线AB为轴旋转所形成的几何体是两个接在一起的圆锥,高ℎ=OB=5,R=OC=5,所以V2=2×13πR2ℎ=2π×52×53=250π3,所以V1+V2=500π3+250π3=250π.故答案为:250π.【分析】左半圆旋转一周为球体,△ABC以直线AB为轴旋转所形成的几何体是两个接在一起的圆锥,由球体体积公式和圆锥体积公式计算可得结果。
2020年高中数学新教材同步必修第二册 第8章 8.3.2 圆柱、圆锥、圆台、球的表面积和体积

课堂小结
KE TANG XIAO JIE
1.知识清单: (1)圆柱、圆锥、圆台的表面积. (2)圆柱、圆锥、圆台的体积. (3)球的表面积和体积. 2.方法归纳:公式法. 3.常见误区:平面图形与立体图形切换不清楚.
本课结束
更多精彩内容请登录:
∵母线长为10,∴102=(4r)2+(4r-r)2,解得r=2. ∴下底面半径R=8,高h=8, ∴V 圆台=13π(r2+rR+R2)h=224π.
三、球的表面积和体积
例3 (1)已知球的表面积为64π,求它的体积; 解 设球的半径为R,则4πR2=64π,解得R=4, 所以球的体积 V=43πR3=43π·43=2356π.
V 圆锥=13Sh=_13_π_r_2h__ V 圆台=13(S+ SS′+ S′)h =_13_π_(_r2_+__r_r_′__+__r′__2_)_h_
说明 圆柱底面圆的半径为r,面积为S, 高为h 圆锥底面圆的半径为r,面积为S, 高为h
圆台上底面圆的半径为r′,面积 为S′,下底面圆的半径为r,面积 为S,高为h
第八章 8.3 简单几何体的表面积与体积
学习目标
XUE XI MU BIAO
1.了解圆柱、圆锥、圆台、球的表面积和体积的计算公式. 2.理解并掌握侧面展开图与几何体的表面积之间的关系,并能利用计算公式
求几何体的表面积与体积.
内容索引
NEI RONG SUO YIN
知识梳理 题型探究 随堂演练
1 知识梳理
√32π D. 3
解析 设球的半径为R, 则由题意可知4πR2=16π,故R=2. 所以球的半径为 2,体积 V=43πR3=332π.
3 随堂演练
PART THREE
高中数学必修二 8 简单几何体的表面积与体积(精讲)(含答案)

8.3 简单几何体的表面积与体积(精讲)考点一 旋转体的体积【例1】(2021·山东莱西·高一期末)在ABC 中,2AB =,32BC =,120ABC ∠=︒,若将ABC 绕BC 边所在的直线旋转一周,则所形成的面围成的旋转体的体积是______. 【答案】32π 【解析】依题意可知,旋转体是一个大圆锥去掉一个小圆锥,所以sin 602OA AB =︒==,1cos60212OB AB =︒=⨯=,所以旋转体的体积:()21332V OC OB ππ=⋅⋅-=故答案为:32π. 【一隅三反】1.(2021·湖南省邵东市第三中学高一期中)圆台上、下底面面积分别是π、4π积是( )A B .C D 【答案】D【解析】由题意1(4)3V ππ=+=.故选:D .2.(2021·山东任城·高一期中)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周六尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为6尺,米堆的高为5尺,问堆放的米有多少斛?”已知1斛米的体积约为1.6立方尺,圆周率约为3,估算出堆放的米约有_______斛.【答案】12.5【解析】设圆柱的底面半径为r 尺,则14⨯2πr =6,∴r ≈4,∴圆锥的体积V =21134543⨯⨯⨯⨯=20立方尺,∴堆放的米约有201.6=12.5斛. 故答案为:12.5.3.(2021·上海市七宝中学)已知圆锥的侧面展开图是半径为2的半圆,则圆锥的体积为________.【解析】由题意圆锥的母线长为2l =,设圆锥底面半径为r ,则22r ππ=,1r =,所以高为h体积为2211133V r h ππ==⨯=..考点二 旋转体的表面积【例2】(2021·吉林·延边二中高一期中)如图,圆锥的底面直径和高均是4,过PO 的中点O '作平行于底面的截面,以该截面为底面挖去一个圆柱,(1)求剩余几何体的体积 (2)求剩余几何体的表面积【答案】(1)103π;(2)8π+. 【解析】(1)由题意知,因为O '为PO 的中点,所以挖去圆柱的半径为1,高为2,剩下几何体的体积为圆锥的体积减去挖去小圆柱的体积, 所以22110241233V πππ=⋅⨯⨯-⨯⨯=.(2)因为圆锥的底面直径和高均是4,所以半径为2,母线l =所以圆锥的表面积为2122(4S πππ=⨯+⨯⨯+, 挖去的圆柱的侧面积为:22124S ππ=⨯⨯=,所以剩余几何体的表面积为12(4+4+8S S S πππ==+=+. 【一隅三反】1.(2021·广东·仲元中学高一期中)已知一个母线长为1的圆锥的侧面展开图的圆心角等于240︒,则该圆锥的侧面积为( )A B .881πCD .23π【答案】D【解析】将圆心角240︒化为弧度为:43π,设圆锥底面圆的半径为r 由圆心角、弧长和半径的公式得:4213r ππ=⨯,即23r = 由扇形面积公式得:22133S ππ=⨯⨯=所以圆锥的侧面积为23π.故选:D.2.(2021·全国·高一课时练习)已知圆台的上、下底面半径分别为10和20,它的侧面展开图的扇环的圆心角为180°,则这个圆台的侧面积为( ) A .600π B .300π C .900π D .450π【答案】A【解析】圆台的上底面圆半径10r '=,下底面圆半径20r =,设圆台的母线长为l ,扇环所在的小圆的半径为x ,依题意有:220()210l x x ππππ⨯=+⎧⎨⨯=⎩,解得2020x l =⎧⎨=⎩,所以圆台的侧面积20()()1020600+S r r l πππ'=⨯=+=. 故选:A3(2021·全国·高一课时练习)圆台的上、下底面半径和高的比为1:4:4,若母线长为10,则圆台的表面积为________. 【答案】168π【解析】圆台的轴截面如图所示,设上底面半径为r ,下底面半径为R ,高为h 则4h R r ==,则它的母线长为510l r =, 所以2r,8R =.故()(82)10100S R r l πππ=+=+⨯=侧,22100464168S S r R ππππππ=++=++=表侧.故答案为:168π考点三 多面体的体积【例3-1】(2021·全国·高一课时练习)如图所示,正方体ABCD-A 1B 1C 1D 1的棱长为1,则三棱锥D-ACD 1的体积是( )A .16B .13C .1 2D .1【答案】A【解析】三棱锥D-ACD 1的体积等于三棱锥D 1-ACD 的体积,三棱锥D 1-ACD 的底面ACD 是直角边长为1的等腰直角三角形,高D 1D=1,∴三棱锥D-ACD 1的体积为V=1132⨯×1×1×1=16.故选:A【例3-2】(2021·全国·高一课时练习)若正四棱台的斜高与上、下底面边长之比为5∶2∶8,体积为14,则棱台的高度为( ) A .8 B .4C .2D .【答案】C【解析】如图,设棱台的上、下底面边长分别为2x ,8x ,斜高h '为5x ,则棱台的高h x ,由棱台的体积公式1()3V S S h '=得:2224161)31(6444++x x x x ⋅=,解得12x =,棱台的高为h =4x =2. 故选:C 【一隅三反】1.(2021·全国·高一课时练习)设四棱锥的底面是对角线长分别为2和4的菱形,四棱锥的高为3,则该四棱锥的体积为( ) A .12 B .24 C .4 D .30【答案】C【解析】所求的体积为11324432⨯⨯⨯⨯=,故选:C.2.(2021·全国·高一课时练习)棱台的上、下底面面积分别是2,4,高为3,则棱台的体积等于( )A .6B .3+C .6+D .6【答案】C【解析】依题意,棱台的上底面面积2S '=,下底面面积4S =,高为3h =,故由公式可知,棱台的体积是()()11243633V S S h '==⨯⨯=+ 故选:C.3.(2021·全国·高一课时练习)若一个四棱锥的底面的面积为3,体积为9,则其高为( ) A .13B .1C .3D .9【答案】D【解析】设四棱锥的高为h ,则由锥体的体积公式得:13×3h =9,解得h =9,所以所求高为9. 故选:D4.(2021·广东·仲元中学高一期中)如图所示,在长方体ABCD A B C D ''''-中,用截面截下一个棱锥C A DD '''-则棱锥C A DD '''-的体积与剩余部分的体积之比为( )A .1:5B .1:4C .1:3D .1:2【答案】A【解析】由图知:13C A DD A DD V C D S'''''-''=⋅⋅,ABCD A B C D A D DA V C D S ''''''-''=⋅,而2A D DA A DD S S''''=,∴剩余部分的体积为53ABCD A B C D C A DD A DD V V C D S'''''''''--''-=⋅,∴棱锥C A DD '''-的体积与剩余部分的体积之比为1:5.故选:A考点四 多面体的表面积【例4】(2021·全国·高一课时练习)正六棱柱的底面边长为2,最长的一条对角线长为积为()A .4)B .2)C .1)D .8)【答案】B【解析】正六棱柱的底面边长为2,最长的一条对角线长为12BB =,它的表面积为)16=2622sin 6222412223S S S π=+⨯⨯⨯⨯⨯+⨯⨯==表面积底面积矩形.故选:B. 【一隅三反】1.(2021·全国·高一课时练习)若六棱柱的底面是边长为3的正六边形,侧面为矩形,侧棱长为4,则其侧面积等于( ) A .12 B .48 C .64 D .72【答案】D【解析】六棱柱的底面是边长为3的正六边形, 故底面周长6318C =⨯=, 又侧面是矩形,侧棱长为4, 故棱柱的高4h =,∴棱柱的侧面积72S Ch ==,故选:D2.(2021·全国·高一课时练习)如图,在正方体ABCD -A 1B 1C 1D 1中,三棱锥D 1AB 1C 的表面积与正方体的表面积的比为( )A .1∶1B .1C .1D .1∶2【答案】C【解析】设正方体的边长为a ,则表面积216S a =,因为三棱锥11D AB C -的各面均是正三角形,其边长为正方体侧面对角线.,三棱锥D 1AB 1C 的表面积)222142S =⨯⨯=,所以2221::6S S a ==故选:C3(2021·全国·高一课时练习)长方体同一顶点上的三条棱长分别为2,2,3,则长方体的体积与表面积分别为( ) A .12,32 B .12,24 C .22,12 D .12,11【答案】A【解析】长方体的体积为22312⨯⨯=,表面积为()222+23+2332⨯⨯⨯=, 故选:A.4.(2021·全国·高一课时练习)(多选)正三棱锥底面边长为3,侧棱长为则下列叙述正确的是( )A .正三棱锥高为3 BC D 【答案】ABD【解析】设E 为等边三角形ADC 的中心,F 为CD 的中点,连接,,PF EF PE , 则PE 为正三棱锥的高,PF 为斜高,又PF ==32EF ==,故3PE ==, 故AB 正确.而正三棱锥的体积为1393⨯=,侧面积为1332⨯⨯=故C 错误,D 正确. 故选:ABD.5(2021·全国·高一课时练习)(多选)在正方体1111ABCD A B C D -中,三棱锥11D AB C -的表面积与正方体的表面积的比不可能是( )A .1:1B .C .D .1:2【答案】ABD【解析】设正方体1111ABCD A B C D -的棱长为a ,则正方体1111ABCD A B C D -的表面积为226S a =.三棱锥11D AB C -的正四面体,其中一个面的面积为212S ==,则三棱锥11D AB C -的表面积为2214S ==所以三棱锥11D AB C -的表面积与正方体的表面积的比为22126S S a ==::故选:ABD.考点五 有关球的计算【例5-1】(2021·全国·高一课时练习)长方体的三个相邻面的面积分别是2,3,6,这个长方体的顶点都在同一个球面上,则这个球的表面积为( ) A .72π B .56π C .14π D .16π【答案】C【解析】设长方体的三条棱长分别为a ,b ,c ,由题意得236ab ac bc =⎧⎪=⎨⎪=⎩,得123a b c =⎧⎪=⎨⎪=⎩∴2414S R ππ球==. 故选:C【例5-2】(2021·广东高州·高一期末)已知正四面体ABCD的表面积为A 、B 、C ,D 四点都在球O 的球面上,则球O 的体积为( ) A. BCD .3π【答案】C【解析】正四面体各面都是全等的等边三角形,设正四面体的棱长为a ,所以该正四面体的表面积为2142S a =⨯⨯=,所以a =1, 所以正方体的外接球即为该正四面体的外接球,O 的体积为343π⨯=⎝⎭. 故选:C. 【一隅三反】1.(2021·全国·高一课时练习)表面积为16π的球的内接轴截面为正方形的圆柱的体积为( )A .B .C .16πD .8π【答案】A【解析】由题意可知,4πR 2=16π,所以R =2,即球的半径R =2.设圆柱的底面圆半径为r 2R =,即2816r =,所以r ,∴V 圆柱=πr 2·2r =2π·π.故选:A.2.(2021·全国·高一课时练习)若一个正方体内接于表面积为4π的球,则正方体的表面积等于( )A .B .8C .D .【答案】B【解析】设正方体棱长为x ,球半径为R ,则24π4πS R ==球,解得1R =,22R ==,解得x =所以该正方体的表面积为22668S x ==⨯=正.故选:B.3.(2021·全国·高一课时练习)(多选)我国古代数学名著《九章算术》中将正四棱锥称为方锥.已知半球内有一个方锥,方锥的底面内接于半球的底面,方锥的顶点在半球的球面上,若方锥的体积为18,则半球的说法正确的是( ) A .半径是3 B .体积为18π C .表面积为27π D .表面积为18π【答案】ABC【解析】如图,PAC △是正四棱锥的对角面,设球半径为r ,AC 是半圆的直径,,棱锥体积为2312)1833V r r =⨯⨯==,3r =,半球体积为332231833V r πππ==⨯=,表面积为2223327S πππ=⨯+⨯=, 故选:ABC .4.(2021·全国·高一课时练习)一个球内有相距9cm 的两个平行截面,它们的面积分别为249cm π和2400cm π2,求球的体积和表面积.【答案】球的表面积为22500cm π,球的体积为362500cm 3π. 【解析】(1)当截面在球心的同侧时,如图①所示为球的轴截面,由截面性质知12AO //BO ,1O ,2O 为两截面圆的圆心,且11OO AO ⊥,22OO BO ⊥,①设球的半径为R ,因为2249O B ππ=,所以27cm O B =,同理得120cm O A =.设1cm OO x =,则2(9)cm OO x =+, 在1Rt O OA 中,22220R x =+,① 在2Rt OO B 中,2227(9)R x =++,② 联立①②可得15x =,25R =.所以2242500cm S R ππ==球,33462500cm 33V R ππ==球.(2)当截面在球心的两侧时,如图②所示为球的轴截面,由球的截面性质知,12O A//O B ,1O ,2O 分别为两截面圆的圆心,且11OO O A ⊥,22OO O B ⊥.②设球的半径为R ,因为2249O B ππ⋅=,所以27cm O B =.因为21400O A ππ⋅=,所以120cm O A =.设1cm O O x =,则2(9)cm OO x =-. 在1Rt OO A △中,22400R x =+,在2Rt OO B 中,22(9)49R x =-+, 所以22400(9)49x x +=-+, 解得15x =-(不合题意,舍去) 综上所述,球的表面积为22500cm π. 球的体积为362500cm 3π. 考点六 综合运用【例6】(2021·全国·高一课时练习)一块边长为12cm 的正三角形薄铁片,按如图所示设计方案,裁剪下三个全等的四边形(每个四边形中有且只有一组对角为直角),然后用余下的部分加工制作成一个“无盖”的正三棱柱(底面是正三角形的直棱柱)形容器.(1)请将加工制作出来的这个“无盖”的正三棱柱形容器的容积V 表示为关于x 的函数,并标明其定义域; (2)若加工人员为了充分利用边角料,考虑在加工过程中,使用裁剪下的三个四边形材料恰好拼接成这个正三棱柱形容器的“顶盖”.请指出此时x 的值(不用说明理由),并求出这个封闭的正三棱柱形容器的侧面积S .【答案】(1)323(012)82x V x x =-+<<;(2)6cm x =,2S =侧.【解析】(1)结合平面图形数据及三棱柱直观图,求得三棱柱的高6cm 2x h ⎫=-⎪⎝⎭,其底面积22cm S =,则三棱柱容器的容积232236624282x x x x V Sh x x ⎫⎛⎫==-=-=-+⎪ ⎪⎝⎭⎝⎭, 即所求函数关系式为323(012)82x V x x =-+<<;(2)此时6cm x =,而相应棱柱的高h ,故侧面积为236S =⨯=. 【一隅三反】1.(2021·安徽镜湖·高一期中)如图所示,在边长为5的正方形ABCD 中,以A 为圆心画一个扇形,以O 为圆心画一个圆,M ,N ,K 为切点,以扇形为圆锥的侧面,以圆O 为圆锥的底面,围成一个圆锥,求该圆锥的表面积与体积.【答案】表面积10π. 【解析】设圆的半径为r ,扇形的半径为R ,由题意,得(522R r Rr ππ⎧+=⎪⎨=⎪⎩,解得r R ⎧=⎪⎨=⎪⎩所以围成的圆锥的母线长为l =r =h ∴圆锥的表面积210S rl r πππ=+=;∴圆锥的体积为213V r h π==.2.(2021·全国·高一课时练习)有一塔形几何体由3个正方体构成,构成方式如图所示,上层正方体下底面的四个顶点是下层正方体上底面各边的中点.已知最底层正方体的棱长为2,求该塔形的表面积(含最底层正方体的底面面积).【答案】36【解析】易知由下向上三个正方体的棱长依次为2,1.考虑该几何体在水平面的投影,可知其水平投影面积等于下底面最大正方体的底面面积.∴S 表=2S 下+S 侧=2×22+4×[22+2+12]=36, ∴该几何体的表面积为36.3.(2021·全国·高一课时练习)养路处建造圆锥形仓库用于贮藏食盐(供融化高速公路上的积雪之用),已建的仓库的底面直径为12 m ,高为4 m.养路处拟建一个更大的圆锥形仓库,以存放更多食盐.现有两种方案:一是新建的仓库的底面直径比原来大4 m (高不变);二是高度增加4 m (底面直径不变). (1)分别计算按这两种方案所建的仓库的体积; (2)分别计算按这两种方案所建的仓库的表面积; (3)哪个方案更经济些?【答案】(1)2563π(m 3),96π(m 3);(m 2),60π(m 2);(3)方案二比方案一更加经济. 【解析】(1)若按方案一,仓库的底面直径变成16 m ,则仓库的体积为V 1=13S ·h=13×π×2162⎛⎫⎪⎝⎭×4=2563π(m 3).若按方案二,仓库的高变成8 m ,则仓库的体积为V 2=13S ·h=13×π×2122⎛⎫⎪⎝⎭×8=96π(m 3).(2)若按方案一,仓库的底面直径变成16 m ,半径为8 m.圆锥的母线长为l 1m ),则仓库的表面积为S 1=π×8×(m 2). 若按方案二,仓库的高变成8 m.圆锥的母线长为l 210(m ), 则仓库的表面积为S 2=π×6×10=60π(m 2).(3)由(1)、(2)知,V 1<V 2,S 2<S 1,故方案二体积更大,表面积更小,所需耗材更少,即方案二比方案一更加经济.。
人教A版(2019)必修第二册《简单几何体的表面积与体积》同步练习

人教A版(2019)必修第二册《8.3 简单几何体的表面积与体积》同步练习一、单选题(本大题共15小题,共75分)1.(5分)三棱锥P−ABC的所有顶点都在球O的球面上.棱锥P−ABC的各棱长为:PA=2,PB=3,PC=4,AB=√13,BC=5,AC=2√5,则球O的表面积为()A. 28πB. 29πC. 30πD. 31π2.(5分)点A,B,C,D在同一个球的球面上,AB=BC=1,∠ABC=120°,若四面体ABCD体积的最大值为√34,则这个球的表面积为()A. 500π81B. 4π C. 25π9D. 100π93.(5分)《九章算术》是我国古代内容极为丰富的数学名著,书中《商功》有如下问题:“今有委粟平地,下周一十二丈,高一丈,问积及为粟几何?“,意思是“有粟若干,堆积在平地上,它底圆周长为12丈,高为1丈,问它的体积和粟各为多少?”如图主人意欲卖掉该堆粟已知圆周率约为3,一斛粟的体积约为2700立方寸(单位换算:1立方丈=106立方寸),一斛粟米卖270钱,一两银子1000钱,则主人卖后可得银子()A. 200两B. 240两C. 360两D. 400两4.(5分)四面体ABCD的四个顶点都在球O的表面上,AB⊥平面BCD,ΔBCD是边长为3的等边三角形.若AB=2,则球O的表面积为()A. 8πB. 12πC. 16πD. 32π5.(5分)若一个圆锥的侧面展开图是面积为4π的半圆,则该圆锥的体积为()A. 2√3π3B. 2√6π3C. 2√6πD. 4√3π6.(5分)一个三棱锥P−ABC的三条侧棱PA,PB,PC两两互相垂直,且长度分别为1,√5,2,则这个三棱锥的外接球的表面积为()A. 10πB. 15πC. 25πD. 40π7.(5分)设三棱柱ABC−A1B1C1的侧棱垂直于底面,AB=AC=2,∠BAC=120°,AA1=3√3,且三棱柱的所有顶点都在同一球面上,则该球的表面积是()A. 46πB. 35πC. 43πD. 39π8.(5分)RtΔABC中,AB=3,BC=4,AC=5,将三角形绕直角边AB旋转一周所成的几何体的侧面积为A. 10πB. 20πC. 30πD. 40π9.(5分)已知A ,B ,C 为球O 的球面上的三个点,⊙O 1为△ABC 的外接圆.若⊙O 1的面积为4π,AB =BC =AC =OO 1,则球O 的体积为()A.2563π B. 64π C. 643π D. 323π10.(5分)已知SC 是球O 的直径,A ,B 是球O 球面上的两点,且CA =CB =1,AB =√3.若三棱锥S −ABC 的体积为1,则球O 的表面积为( )A. 52πB. 16πC. 13πD. 4π11.(5分)已知体积公式V =kD 3中的常数k 称为“立圆率”.对于等边圆柱(轴截面是正方形的圆柱)、正方体也可利用公式V =kD 3求体积(在等边圆柱中,D 表示底面圆的直径;在正方体中,D 表示棱长).假设运用此体积公式求得等边圆柱(底面圆的直径为a)、正方体(棱长为a)、球(直径为a)的“立圆率”分别为k 1、k 2、k 3,那么k 1;k 2;k 3=()A. π4:1:π6 B. π4:2:π6 C. 3:2π:2D. 16:1π:1412.(5分)长方体ABCD −A 1B 1C 1D 1中,AB =2,BC =1,AA 1=2,M 为侧面CC 1D 1D 内(含边界)的动点,且满足tan ∠MAD +tan ∠MBC =2√3,则四棱锥M −ABCD 体积的最小值为( )A.2√23B.2√33C.2√39D.4√3913.(5分)有很多立体图形都体现了数学的对称美,其中半正多面体是由两种或两种以上的正多边形围成的多面体,半正多面体因其最早由阿基米德研究发现,故也被称作阿基米德体.如图所示是一个棱数为24的半正多面体,且所有顶点都在同一个正方体的表面上,它也可以看成是由一个正方体截去八个一样的四面体所得的.若被截正方体的棱长为0.5m ,则该半正多面体的表面积为( )A. 6m 2B. 3√3m 2C. (3+√3)m 2D.3+√34m 214.(5分)正四棱柱ABCD −A 1B 1C 1D 1中,AB =3,BB 1=4,长为1的线段PQ 在棱AA 1上移动,长为3的线段MN 在棱CC 1上移动,点R 在棱BB 1上移动,则四棱锥R −PQMN 的体积是( )A. 6B. 10C. 12D. 不确定15.(5分)古希腊数学家阿基米德的墓碑上刻着一个圆柱,圆柱内有一个内切球,这个球的直径恰好与圆柱的高相等,相传这个图形是阿基米德最引以为自豪的发现.现有一底面半径与高的比值为1:2的圆柱,则该圆柱的体积与其内切球的体积之比为()A. 43B. 32C. 2D. 83二、填空题(本大题共5小题,共25分)16.(5分)若正四棱锥的底面边长为2√2,体积为8,则它侧面积为______.17.(5分)已知三棱锥P−ABC内接于表面积为36π的球中,平面PAB⊥平面ABC,PA=PB=√3,PB⊥BC,∠APB=120°,则三棱锥P−ABC体积为 ______.18.(5分)如图所示,已知三棱柱ABC−A1B1C1的所有棱长均为1,且AA1⊥底面ABC,则三棱锥B1−AB C1的体积为________.19.(5分)已知ΔABC内接于球O的一个截面圆中,AB=6,AC=8,cos∠CBA=35,且球面上的点到面ABC的距离的最大值为7+2√6,则球O的表面积为______.20.(5分)已知三棱锥P−ABC的外接球的球心O在AB上,且PO⊥平面ABC,AB=2√3,AC=2,则三棱锥P−ABC的体积为______.三、多选题(本大题共5小题,共20分)21.(4分)如图,在棱长为3的正方体ABCD −A 1B 1C 1D 1中,点P 是平面A 1BC 1内一个动点,且满足PD +PB 1=2+√13,则下列结论正确的是()A. B 1D ⊥PBB. 点P 的轨迹是一个半径为√2的圆C. 直线B 1P 与平面A 1BC 1所成角为π3D. 三棱锥P −BB 1C 1体积的最大值为32+√6222.(4分)设一空心球是在一个大球(称为外球)的内部挖去一个有相同球心的小球(称为内球),已知内球面上的点与外球面上的点的最短距离为1,若某正方体的所有顶点均在外球面上、所有面均与内球相切,则A. 该正方体的棱长为2B. 该正方体的体对角线长为3+√3C. 空心球的内球半径为√3−1D. 空心球的外球表面积为(12+6√3)π23.(4分)三棱锥A −BCD 各顶点均在表面积为20π的球体表面上,AB =CB =2,∠ABC =120°,∠BCD =90°,则()A. 若CD ⊥AB ,则CD =2B. 若CD =2,则CD ⊥ABC. 线段AD 长度的最小值为√10D. 三棱锥A −BCD 体积的最大值为√324.(4分)已知正四面体ABCD 的棱长为2√2,其外接球的球心为O.点E 满足AE →=λAB →(0<λ<1),CF →=μCD →(0<μ<1),过点E 作平面α平行于AC 和BD ,平面α分别与该正四面体的棱BC ,CD ,AD 相交于点M ,G ,H ,则()A. 四边形EMGH 的周长为定值B. 当入=14时,平面α截球O 所得截面的周长为√472π C. 四棱锥A −EMGH 的体积的最大值为6481D. 当λ=μ=12时,将正四面体ABCD 绕EF 旋转90°后与原四面体的公共部分体积为4325.(4分)如图,在透明塑料制成的长方体ABCD −A 1B 1C 1D 1容器内灌进一些水,将容器底面一边BC 固定于地面上,再将容器倾斜,随着倾斜度的不同,其中正确的说法是()A. 有水的部分始终呈棱柱状B. 水面四边形EFGH的面积不改变C. 棱A1D1始终与水面EFGH平行D. 当E∈AA1时,AE+BF是定值四、解答题(本大题共6小题,共30分)26.(5分)如图,在四棱锥S−ABCD中,正ΔSBD所在平面与矩形ABCD所在平面垂直.(1)证明:S在底面ABCD的射影为线段BD的中点;(2)已知AB=4,AD=2,E为线段BD上一点,且CE⊥BD,求三棱锥E−SAD的体积.27.(5分)(1)一个正方体的顶点都在球面上,它的棱长是2cm,求球的表面积;(2)已知各面均为等边三角形的四面体S−ABC的棱长为1,求它的体积.28.(5分)三棱锥S−ABC中,侧面SBC⊥底面ABC,BC是等腰直角三角形ABC的斜边,且BC=2,SA=SB=√2.(1)求证:SA⊥BC;(2)已知平面α//平面SBC,平面α∩平面ABC=l,A∈α,D∈l,且C、D到平面SAB的距离相等,试确定直线l及点D的位置(说明作法及理由),并求三棱锥S−ABD的体积.29.(5分)如图,在底面半径为2,母线长为4的圆锥中内接一个高为√3的圆柱,求圆柱的表面积和圆锥的体积.30.(5分)正三棱锥的高为1,底面边长为2√6,内有一个球与它的四个面都相切,求:(1)棱锥的表面积;(2)内切球的半径.31.(5分)已知直三棱柱ABC−A1B1C1的底面是等腰直角三角形,AB=AC=4,且侧棱AA1=6.(Ⅰ)在给定的坐标系中,用斜二测画法画出该三棱柱的直观图(不要求写出画法,但要标上字母,并注意:先用铅笔作出草图,再用黑色字迹的签字笔或钢笔描黑,以保证扫描效果)(Ⅰ)求该三棱柱ABC−A1B1C1的外接球的表面积.答案和解析1.【答案】B;【解析】解:三棱锥P−ABC的所有顶点都在球O的球面上.棱锥P−ABC的各棱长为:PA=2,PB=3,PC=4,AB=√13,BC=5,AC=2√5,可知:PA⊥PB,PB⊥PC,PC⊥PA,所以三棱锥P−ABC是长方体的一个角,长方体的外接球与三棱锥的外接球相同,所以r=12√22+32+42=√292∴球O的表面积S=4πr2=4π×294=29π.故选:B.判断三棱锥的形状,可知三棱锥可知为长方体,利用长方体的外接球与三棱锥的外接球相同,求解外接球的半径,由此能求出球O的表面积.此题主要考查球的表面积的求法,考查推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想,是中档题.2.【答案】D;【解析】解:根据题意知,A、B、C三点均在球心O的表面上,且|AB|=|AC|=1,∠ABC=120°,∴BC=√3,∴ΔABC外接圆半径2r=2,即r=1,∴SΔABC=12×1×1×sin120°=√34,小圆的圆心为Q,若四面体ABCD的体积的最大值,由于底面积SΔABC不变,高最大时体积最大,所以,DQ与面ABC垂直时体积最大,最大值为13SΔABC×DQ=√34,∴DQ=3,设球的半径为R,则在直角ΔAQO中,OA2=AQ2+OQ2,即R2=12+(3−R)2,∴R=53,∴球的表面积为4π.259=100π9,故选:D.根据几何体的特征,小圆的圆心为Q,若四面体ABCD的体积的最大值,由于底面积SΔABC不变,高最大时体积最大,可得DQ与面ABC垂直时体积最大,从而求出球的半径,即可求出球的表面积.该题考查的知识点是球内接多面体,球的表面积,其中分析出何时四面体ABCD的体积的最大值,是解答的关键.3.【答案】D;【解析】解:∵有粟若干,堆积在平地上,它底圆周长为12丈,高为1丈,∴底面半径r=122π=2(丈),∴体积V=13×πr2×ℎ=13×3×22×1=4(立方丈)=4×106(立方寸),∴主人卖后可得银子:4×1062700×2701000=400(两).故选:D.先求出底面半径r=122π=2(丈),再求出体积V=13×πr2×ℎ=4(立方丈)=4×106(立方寸),由此能求出主人卖后可得银子数量.此题主要考查圆锥体积的求法及应用,考查圆锥的体积公式、结构特征等基础知识,考查运算求解能力,是中档题.4.【答案】C;【解析】解:取CD的中点E,连结AE,BE,∵在四面体ABCD中,AB⊥平面BCD,ΔBCD是边长为3的等边三角形.∴RtΔABC≌RtΔABD,ΔACD是等腰三角形,ΔBCD的中心为G,作OG//AB交AB的中垂线HO于O,O为外接球的中心,BE=3√32,BG=√3,R=√BG2+(12AB)2=√3+1=2.四面体ABCD外接球的表面积为:4πR2=16π.故选:C.取CD的中点E,连结AE,BE,作出外接球的球心,求出半径,即可求出表面积.该题考查球的内接体知识,考查空间想象能力,确定球的切线与半径是解答该题的关键.5.【答案】B;【解析】解:设圆锥的母线和底面圆的半径分别为l,r,根据侧面展开图是一个面积为4π的半圆,可得:12πl2=4π,2πr=12⋅2πl,解得:l=2√2,r=√2,进而可得圆锥的高ℎ=√l2−r2=√6,所以体积为:13πr2ℎ=13π×2×√6=2√6π3.故选:B.根据圆锥侧面展开图的面积以及弧长与圆锥底面以及母线长之间的关系,可求母线和底面圆半径的大小,进而根据勾股定理求高,根据体积公式即可求解.此题主要考查了圆锥体积的计算,属于基础题.6.【答案】A;【解析】解:此三棱锥的外接球即棱长分别为1,√5,2的长方体的外接球,而长方体的体对角线即为球的直径,球的直径2R=√1+5+4=√10,∴R=√102,故外接球的表面积S=4πR2=4π×104=10π,故选:A.先将三棱锥的外接球问题转化为长方体的外接球问题,再利用长方体的对角线计算公式,求得其外接球的直径,进而利用球的表面积计算公式计算即可.这道题主要考查了球与锥的接切问题,利用三条侧棱两两垂直的三棱锥的外接球即为对应长方体的外接球,可提高效率,减少运算量.7.【答案】C;【解析】解:由题意知底面△ABC外接圆的圆心为点O,设外接圆的半径为r,三棱柱ABC−A1B1C1的外接球的半径为R,AB=AC=2,∠BAC=120°,由余弦定理得BC=√AB2+AC2−2AB×ACcos∠BAC=2√3,由正弦定理得BCsin∠BAC =2√3√32=4=2r,所以r=2,过O′做垂直于底面的直线交中截面与O点,则O为外接球的球心,由题意得:R2=r2+(AA12)2=4+274=434,所以外接球的表面积S=4πR2=43π,故选:C.直棱柱的外接球的球心是过底面外接圆的圆心做垂直于底面的直线与中截面的交点,底面外接圆的半径、球的半径和直棱柱的高的一半构成直角三角形,由题意求出外接球的半径,可得答案.此题主要考查了三棱柱的外接球表面积,属于基础题.8.【答案】B;【解析】该几何体为圆锥,则侧面积即为一个扇形的面积.根据扇形面积公式可以解答.解:该几何体为圆锥,则侧面积即为一个扇形的面积.扇形面积公式:S=12lr其中l为扇形的弧长,即圆锥底面周长2π×4=8π,r为扇形母线长,即AC,所以r=5,所以S=12×8π×5=20π.故选B.9.【答案】A;【解析】解:设圆O1半径为r,球的半径为R,依题意得,πr2=4π,∴r=2,∵△ABC为等边三角形,由正弦定理可得AB=2rsin60°=2√3,∴OO1=AB=2√3,根据球的截面性质OO1⊥平面ABC,∴OO1⊥O1A,R=OA=√OO12+O1A2=√OO12+r2=4,∴球O的体积V=4π3R3=256π3,故选:A.由已知可得等边△ABC的外接圆半径,进而求出其边长,得出OO1的值,根据球的截面性质,求出球的半径,即可得出结论.此题主要考查了球的截面圆的性质以及球的体积的计算,属于基础题.10.【答案】A;【解析】此题主要考查棱锥的体积,考查球内接多面体,解答该题的关键是确定点S到面ABC的距离.根据题意作出图形,欲求球O的表面积,只须求球的半径r,利用截面圆的性质即可求出OO1,进而求出底面ABC上的高SD,从而建立关于r的方程,即可求出r,从而解决问题.解:根据题意作出图形,设球心为O ,球的半径r ,过ABC 三点的小圆的圆心为O 1,则OO 1⊥平面ABC , 延长CO 1交球于点D ,则SD ⊥平面ABC ,在三角形ABC 中,CA =CB =1,AB =√3,易知CO 1=1, ∴OO 1=√r 2−1,∴高SD =2O O 1=2√r 2−1, ∵三棱锥S −ABC 的体积为1, S ΔABC =√34, ∴V 三棱锥S −ABC =13×√34×2√r 2−1=1,∴r =√13,则球O 的表面积为52π. 故选:A.11.【答案】A;【解析】解:∵V 1=πR 2a =π(a2)2a =π4a 3,∴k 1=π4,∵V 2=a 3,∴k 2=1, ∵V 3=43πR 3=43π(a2)3=π6a 3,∴k 3=π6,∴k 1:k 2:k 3=π4:1:π6,故选:A.分别计算三个几何体的“立圆率”即可求得结果.此题主要考查立体几何中几何体体积的计算,属于基础题.12.【答案】D;【解析】解:取CD 的中点O ,以点O 为坐标原点,DA →、DC →、D →D 1的方向分别为x 、y 、z 轴的正方向建立如下图所示的空间直角坐标系,设点M(0,y,z),其中−1⩽y ⩽1,0⩽z ⩽1,则D(0,−1,0)、C(0,1,0),因为AD ⊥平面CC 1D 1D ,DM ⊂平面CC 1D 1D ,则AD ⊥DM , 所以tan ∠MAD =|DM ||AD |=|DM |,同理可得tan ∠MBC =|CM ||BC |=|CM |,所以tan ∠MAD +tan ∠MBC =|DM |+|CM |=2√3>|CD |=2, 所以点M 的轨迹是以点C 、D 为焦点,且长轴长为2√3的椭圆的一部分, 则a =√3,c =1,b =√a 2−c 2=√2, 所以点M 的轨迹方程为y 23+z 22=1(x =0,−1⩽y ⩽1,0⩽z ⩽1),点M 到平面ABCD 的距离为z ,当点M 为曲线y 23+z 22=1(x =0,−1⩽y ⩽1,0⩽z ⩽1)与棱CC 1或棱DD 1的交点时,点M 到平面ABCD 的距离取最小值, 将y =±1代入方程y 23+z 22=1(x =0,−1⩽y ⩽1,0⩽z ⩽1),得z =2√33,因此,四棱锥M −ABCD 体积的最小值为13×2×2√33=4√39. 故选:D.取CD 的中点O ,以点O 为坐标原点,DA →、DC →、D →D 1的方向分别为x 、y 、z 轴的正方向建立空间直角坐标系,分析可知点M 的轨迹是以点C 、D 为焦点的椭圆,求出椭圆的方程,可知当点M 为椭圆与棱CC 1或DD 1的交点时,点M 到平面ABCD 的距离取最小值,由此可求得四棱锥M −ABCD 体积的最小值.此题主要考查锥体体积的计算,立体几何中的最值与范围问题等知识,属于中等题.13.【答案】D;【解析】解:由图形可得,该半正多面体共有6个全等的正方形和8个全等的正三角形, 且正方形和正三角形的边长都是0.5×12×√2=√24m , 所以该半正多面体的表面积为S =6×(√24)2+8×12×(√24)2×sin 60°=3+√34m 2.故选:D.先求出半正多面体的棱长,再求解其表面积即可.此题主要考查了空间几何体的结构特征的理解与应用,空间几何体表面积的计算问题,考查了逻辑推理能力与空间想象能力,属于基础题.14.【答案】A;【解析】该题考查棱锥的体积计算,考查计算能力,属于基础题.先求出底面PQMN的面积,再求R到底面PQMN的距离,然后求四棱锥R−PQMN的体积.解:由题意可知底面PQMN的面积是1+32×3√2=6√2,R到PQMN的距离为3√22,四棱锥R−PQMN的体积是:13×6√2×3√22=6.故选:A.15.【答案】B;【解析】此题主要考查球和圆柱的体积的计算,属于基础题.设球的半径为R,则圆柱的底面半径为R,高为2R,由此利用公式即可求出结果.解:设球的半径为R,则圆柱的底面半径为R,高为2R,∴V圆柱=πR2×2R=2πR3,V球=43πR3 .∴V圆柱V球=2πR343πR3=32,故选B.16.【答案】4√22;【解析】本题目主要考查正四棱锥的侧面积,属于一般题.【解析】解:正四棱锥的底面边长为2√2,体积为8,所以高为3,斜高为√11,则侧面积为S= 4×12×2√2×√11=4√22,故答案为4√22.17.【答案】3√22;【解析】解:如图,取AB 的中点D ,连接PD ,取AC 的中点F ,连接DF , ∵PA =PB ,∴AB ⊥PD ,又平面PAB ⊥平面ABC ,平面PAB ∩平面ABC =AB , ∴PD ⊥平面ABC ,则PD ⊥BC ,又PB ⊥BC ,PD ∩PB =P ,∴BC ⊥平面PAB ,得BC ⊥AB , ∴F 为ΔABC 的外心,又ΔPAB 的外心E 在PD 的延长线上, 球心O 满足OF ⊥平面ABC ,OE ⊥平面PAB , ∵PA =PB =√3,∠APB =120°,可得PD =√32,AB =32,在ΔPAB 中,由正弦定理ABsin ∠APB =32√32=√3,则PE =√3,∵三棱锥P −ABC 内接于表面积为36π的球,∴OP =3, 求得EO =DF =√6,则BC =2√6, ∴三棱锥P −ABC 体积为V =13×12×3×√32×2√6=3√22, 故答案为:3√22. 由题意画出图形,证明BC ⊥平面PAB ,由已知球的表面积求得球的半径,然后求解三角形求得PD 与BC ,再由棱锥体积公式求三棱锥P −ABC 体积.此题主要考查球内接多面体体积的求法,考查空间想象能力与思维能力,考查运算求解能力,是中档题.18.【答案】√312; 【解析】此题主要考查棱锥的体积,属于基础题.根据图形特点三棱锥A −B 1BC 1的高为√32,底面积为12,求棱锥的体积.解:三棱锥B 1−AB C 1的体积等于三棱锥A −B 1BC 1的体积,三棱锥A −B 1BC 1的高为√32,底面积为12, 故其体积为13×12×√32=√312.故答案为:√312.19.【答案】196π;【解析】解:设截面ABC 的外接圆的圆心为O 1,连接O 1B ,OB ,做直线OO 1交球于P ,O 在线段PO 1上时,球面上的点到面ABC 的距离的最大,即PO 1=7+2√6, 设ΔABC 的外接圆的半径为r ,球的半径为R ,则r =O 1B ,R =OB ,在ΔABC 中AB =6,AC =8,cos ∠CBA =35,所以sin ∠CBA =√1−cos 2∠CBA =45, 由正弦定理可得2r =ACsin ∠CBA =845=10,所以r =5,在ΔOO 1B 中,R 2=r 2+OO 12=52+(7+2√6−R)2,解得R =7,所以求O 的表面积S =4πR 2=196π. 故答案为:196π.由∠CBA 的余弦值求出其正弦值,在三角形中由正弦定理求出三角形ABC 的外接圆的半径,当P ,O ,O 1三点共线时,球面上的点P 到面ABC 的距离的最大,在三角形中由勾股定理可得外接球的半径R ,进而求出球的表面积.该题考查正弦定理及余弦定理的应用和球的表面积公式,属于中档题.20.【答案】2√63;【解析】此题主要考查了线面垂直的性质、三棱锥的体积计算公式,考查了推理能力与计算能力,属于中档题.如图所示,由于三棱锥P −ABC 的外接球的球心O 在AB 上,且PO ⊥平面ABC ,可得PO 是三棱锥P −ABC 的高,AC ⊥BC .求出BC ,利用三棱锥的体积计算公式可得结论.解:如图所示,∵三棱锥P−ABC的外接球的球心O在AB上,且PO⊥平面ABC,∴PO是三棱锥P−ABC的高,∴∠ACB=90°,∴AC⊥BC.∵AB=2√3,AC=2,∴BC=2√2,PO=√3,∴V P−ABC=13×12×2×2√2×√3=2√63,故答案为:2√63.21.【答案】ACD;【解析】解:如图,建立空间直接坐标系,连结\(B_{1}D\),交平面\(A_{1}BC_{1}\)于点\(O\),所以\(D(0,0,0)\),\(B_{1}(3,3,3)\),\(A_{1}(3,0,3)\),\(B(3,3,0)\),\(C_{1}(0,3,3)\),\(\overrightarrow {DB_{1}}=(3,3,3),\overrightarrow {A_{1}B}=(0,3,-3),\overrightarrow {BC_{1}}=(-3,0,3)\),所以\(\overrightarrow {DB_{1}}_{}_{}⋅\overrightarrow {A_{1}B}=0,\overrightarrow {DB_{1}}_{}⋅\overrightarrow {BC_{1}}=0\),\(∴DB_{1}⊥A_{1}B\),\(DB_{1}⊥BC_{1}\),又\(A_{1}B∩BC_{1}=B\),\(∴DB_{1}⊥\)平面\(A_{1}BC_{1}\),\(∵P\in\)平面\(A_{1}BC_{1}\),\(∴PB⊥DB_{1}\),故\(A\)正确;设\(DB_{1}\)与平面\(A_{1}BC_{1}\)的交点为\(O\),并设\(O(x,y,z)\),由于\(O\)在\(DB_{1}\)上,设\(\overrightarrow {DO}=λ\overrightarrow {DB_{1}}\),得\(x=y=z=3λ,\overrightarrow {A_{1}O}=(x-3,y,z-3)\),由空间向量基本定理可知:\(\overrightarrow {A_{1}O}=m\overrightarrow{A_{1}B}+n\overrightarrow {A_{1}C_{1}}=(-3n,3m+3n,-3m)\),得方程:\(\begin{cases}3λ=-3n+3\\ 3λ=3m+3n\\ 3λ=-3m+3\end{cases}\),解得:\(m=n=\dfrac{1}{3},λ=\dfrac{2}{3}\),故\(O(2,2,2)∴DB_{1}=\sqrt{3^{2}+3^{2}+3^{2}}=3\sqrt{3}\),\(∴DO=\dfrac{2}{3}DB_{1}=2\sqrt{3}\),\(OB_{1}=\sqrt{3}\),将平面\(A_{1}BC_{1}\)的直观图分离出来如下:依题意,\(DP+PB_{1}=2+\sqrt{13}\),\(OB_{1}=\sqrt{3},OD=2\sqrt{3},DB_{1}⊥OP\),\(∴\begin{cases}{OB_{1}^{2}+OP^{2}=PB_{1}^{2}}\\{OD^{2}+OP^{2}=PD^{2}}\end{cases}\),解得\(OP=1\),\(PB_{1}=2\),\(PD=\sqrt{13}\),故\(P\)点的轨迹是以\(O\)为圆心,半径为\(1\)的圆,故\(B\)错误;\(B_{1}P\)与平面\(A_{1}BC_{1}\)的夹角就是\(∠B_{1}PO,\sin∠B_{1}PO=\dfrac{OB_{1}}{PB_{1}}=\dfrac{\sqrt{3}}{2}\),所以\(∠B_{1}PO=\dfrac{π}{3}\),故\(C\)正确;三棱锥\(P-BB_{1}C_{1}\)底面为三角形\(BB_{1}C\),其面积为\(\dfrac{1}{2}×3×3=\dfrac{9}{2}\),是定值,故当\(P\)到底面三角形\(BB_{1}C\)的距离\(h\)最大时,三棱锥的体积取得最大值,因为\(P\)在以\(O\)为圆心,半径为\(1\)的圆上,而球心\(O\)到平面\(BB_{1}C\)距离为\(\dfrac{\sqrt{6}}{3}\),故\(P\)到\(P\)到底面三角形\(BB_{1}C\)的距离\(h\)的最大值为\(1+\dfrac{\sqrt{6}}{3}\),所以三棱锥\(P-BB_{1}C_{1}\)体积的最大值为\(\dfrac{1}{3}×\dfrac{9}{2}×(1+\dfrac{\sqrt{6}}{3})=\dfrac{3}{2}+\dfrac{\sqrt{6}}{2}\),故\(D\)正确;故选:\(ACD.\)建立空间直角坐标系,结合向量法和综合法对各个选项进行逐一计算验证.此题主要考查了立体几何的综合,属于难题.22.【答案】BD; 【解析】此题主要考查了球的表面积,考查学生的计算和推理能力,属于中档题.设出内外球半径分别为r ,R ,从而结合题意即可知R 和r 的关系,进而求得R 和r ,从而求解.解:设内外球半径分别为r ,R ,则正方体的棱长为2r ,体对角线长为2R , ∴R =√3r ,又由题知R −r =1, ∴r =√3+12,R =√3+32,正方体棱长为√3+1,体对角线长为3+√3,外球表面积为π(3+√3)2=(12+6√3)π,故B 、D 正确. 故选BD .23.【答案】ACD;【解析】解:因为S =4πR 2=20π,所以R 2=5;对于A ,若CD ⊥AB ,则平面BCD ⊥平面ABC ,过BD 的中点F 作与平面BCD 垂直的直线l ,设球心为O ,则l//平面ABC ,作FH ⊥BC ,垂足为H , 则FH 即为球心O 到平面ABC 的距离d ,对于△ABC , 设其外接圆半径为r ,则AB sin120∘=2√32=2r,r =2,所以d =HF =√R 2−r 2=1,因此CD =2HF =2,故A 正确;对于B ,因为始终满足CB ⊥CD ,所以点D 的轨迹是与BC 垂直的球内某截面圆,如图所示:因为BC =2为定值,作AH ⊥D 点所在截面圆O ′,取BC 得中点M ,连接OM ,OO ′,OM=√R2−(BC2)2=2,因为OO′和BC同时满足垂直于D点所在截面圆,所以OM即为D点所在截面圆的半径,所以D点在以2为半径的圆上,C为定点,所以满足CD=2时的点D有两个点,作A点在截面圆的投影,垂足设为H,所以当H,O′,D共线时满足CD⊥AB,所以必定有另外一个符合CD=2的D点不满足,因此B选项错误;对于C,因为平面ABC(ABCH)与圆O′垂直,所以OO′与平面ABC平行,作OO1⊥AH,又因为OO1⊥BC,所以OO1⊥平面ABC,因此O1为△ABC外接圆的圆心,而△ABC外接圆半径r为2,又因为O1H=MC=1,所以AH=r+1=3,若求AD的最小值,在直角三角形ADH中,只需确定出DH的最小值即可,如图所示,点D在D′位置时,DH最小,AD也最小,即AD=√AH2+DH2=√9+DH2,由A的分析可知球心O到平面ABC的距离为1,即OO1=1,则O′H=1,而DH的最小值为D′H=O′D′−O′H=2−1=1,所以AD的最小值为√10,故C正确;对于D,△ABC的面积为定值,且D点在与△ABC垂直的截面圆上,只需当D点到平面ABC距离最大时,三棱锥A−BCD体积也最大,又因为O′H⊥平面ABC,因此当D点位于HO′与截面圆的交点处时(如图示位置)即H,O′,D共线时,高即DH最大,最大值OH′+DO′=1+2=3,故此时三棱锥A−BCD体积的最大值为13×12×2×2×sin120°×3=√3,故D正确,故选:ACD.对于A,计算出△ABC的外接圆半径,明确球心到平面ABC的距离,可求得CD=2;对于B,要明确D的轨迹是与BC垂直的球内某截面圆,由此判断满足CD=2时的点D有两个点,其中有一个不满足;对于C,借助于图示,确定点D在D′位置时,线段AD长度才可取到最小值,由此计算即可;对于D,由于△ABC的面积为定值,且D点在与△ABC垂直的截面圆上,只需当D点到平面ABC距离最大时,三棱锥A−BCD体积也最大,由此可以求先求得三棱锥的高的最大值,可求得结果.此题主要考查锥体体积导数计算,立体几何中的最值问题,空间中的垂直关系等知识,属于中等题.24.【答案】ACD;【解析】解:如图1,由AC//平面EMGH ,AC ⊂平面ABC ,平面ABC⋂平面EMGH =EM ,得AC//EM ,同理AC//HG ,所以EM//HG ,同理EH//MG ,所以EMGH 是平行四边形, AE AB =λ,则EH AD =λ,EM AC =1−λ,正四面体ABCD 的棱长为2√2,则EH =2√2λ,EM =2√2(1−λ),所以EMGH 的周长为2(EH +EM)=4√2,为定值,A 正确;如图2,把正四面体ABCD 放置在一个正方体中,正四面体的棱是正方体的面对角线, 如图,正方体的外接球就是正四面体ABCD 的外接球,由正四面体棱长为2√2得正方体的棱长为2,正方体的对角线是外接球的直径,所以外接球半径为R =2√32=√3,由于平面EMGH 与AC ,BD 平行,因此易得平面ENGH 与正方体的上下底面平行, λ=14时,AE AB =14,平面EMGH 到正方体上底面的距离为正方体棱长的14,而外接球球心O 到正方体上底面的距离为正方体棱长的12,所以O 到平面EMGH 的距离为d =(12−14)×2=12, 平面α截球O 所得截面圆半径为r =√R 2−d 2=√3−14=√112, 截面圆周长为2πr =2π×√112=√11π,B 错;如图3,取BD 中点N ,连接AN ,CN ,则AN ⊥BD ,CN ⊥BD ,又AN⋂CN =N ,AN ,CN ⊂平面ACN ,所以BD ⊥平面ACN ,而AC ⊂平面ACN ,所以BD ⊥AC ,所以EM ⊥MG ,所以S EMGH =2√2λ⋅2√2(1−λ)=8(λ−λ2),由图2知A 点到平面EMGH 的距离为2λ,所以V A−EMGH =13×8(λ−λ2)×2λ=163(λ2−λ3),设f(x)=x 2−x 3(0<x <1),则f ′(x)=2x −3x 2=−3x(x −23),0<x <23时,f ′(x)>0,f(x)递增,23<x <1时,f ′(x)<0,f(x)递减, x =23时,f(x)取得最大值f(23)=427,所以V A−EMGH 的最大值为163×427=6481,C 正确;如图4,还是如图2一样把正四面体ABCD 放置在一个正方体中,λ=μ=12时,E ,F 是正方体前后两个面的中心(对角线交点),由正方体性质,正四面体ABCD 绕EF 旋转90°后得下四面体A ′B ′C ′D ′,A ′,B ′,C ′,D ′是正方体的另外四个顶点,这两个正四面体的公共部分正好是一个正八面体,正八面体的六个顶点是正方体六个面的中心, S EMFH =√2×√2=2,正八面体的体积为V=2×13×2×1=43,D正确.故选:ACD.利用线面平行得平行四边形EMGH,由平行线性质得边长,从而可得四边形周长,判断A,把正四面体放置在一个正方体中,正四面体的棱是正方体的面对角线,由正方体的性质可求得平面α截球O所得截面圆的半径,从而得周长,判断B,证明EMGH是矩形后,由正方体的性质易得A到平面EMGH的距离,求出棱锥体积后,利用导数求得最大值判断C,在正方体中旋转正四面体,易得放置后的四面体的位置,并确定两个正四面体的公共部分,从而得体积判断D.此题主要考查正四面体的截面,考查空间几何的体积等问题,解题关键是把正四面体放置在正方体中,利用正方体的性质确定与正四面体有关的图形的性质,求解结论.对学生的空间想象能力、逻辑思维能力,运算求解能力要求较高,本题属于难题.25.【答案】ACD;【解析】解:在A中,水的部分始终呈棱柱状,从棱柱的特征平面AA1B1B平行平面CC1D1D即可判断A正确,故A正确;在B中,水面四边形EFGH的面积不改变,EF是可以变化的EH不变的,所以面积是改变的,故B不正确的;在C中,棱A1D1始终与水面EFGH平行,由直线与平面平行的判断定理,可知A1D1//EH,故C正确;在D中,当E∈AA1时,AE+BF是定值.水的体积是定值,高不变,所以底面面积不变,故D正确.故选:ACD.在A中,水的部分始终呈棱柱状;从棱柱的特征平面判断即可;在B中,水面四边形EFGH的面积不改变;可以通过EF的变化EH不变判断正误;在C中,棱A1D1始终与水面EFGH平行;利用直线与平面平行的判断定理,推出结论;在D中,当E∈AA1时,AE+BF是定值.通过水的体积判断即可.此题主要考查棱柱的结构特征,直线与平面平行的判断,棱柱的体积等基础知识,考查逻辑推理能力、运算求解能力,是中档题.26.【答案】证明:(1)取DB 的中点为O ,连接SO ,∵SB=SD ,∴SO ⊥BD∵平面SBD ⊥面ABCD .平面SBD∩面ABCD=BD .∴SO ⊥面ABCD ,∴S 在底面ABCD 的射影为线段BD 的中点.(2)∵AB=4,AD=2,CE ⊥BD ,∴BO BC =BC DB ⇒BO=2√5 ∴S △ADE =45S △ADB =45×12×2×4=165,SO=SD×sin60°=√15 三棱锥E-SAD 的体积V=V S-ADE =13.S △ADE .SO =16√1515.;【解析】(1)取DB 的中点为O ,连接SO ,只需证明SO ⊥面ABCD ,即可得S 在底面ABCD 的射影为线段BD 的中点.(2)利用三棱锥E −SAD 的体积V =V S−ADE =13.S ΔADE .SO =16√1515.即可.该题考查面面垂直的性质,考查三棱锥体积计算,考查运算求解能力,是中档题.27.【答案】解:(1)正方体的棱长为:2cm ,正方体的体对角线的长为:2√3cm ,就是球的直径,∴球的表面积为:S 2=4π(√3)2=12πc m 2.(2)解:如图,四面体S −ABC 的各棱长为1,则其四个面均为边长为1的等边三角形, 过S 作底面垂线,垂足为O ,则O 为底面三角形的中心,连接BO 并延长,交AC 于D. 显然BD =√32, 则BO =23×√32×1=√33, ∴SO =√1−(√33)2=√63,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
专题8.3 简单几何的表面积与体积运用一 体积 【例1】(1)(2019·北京高二学业考试)如图,在直三棱柱111ABC A B C -中,AB AC ⊥,如果3AB =,1AC =,12AA =,那么直三棱柱111ABC A B C -的体积为( )A.2B.3C.4D.6(2)(2019·云南省玉溪第一中学高二月考)一个四棱锥的三视图如图所示,则该四棱锥的体积为()B.D.(3)某几何体的三视图如图所示,该几何体的体积是( )A.1123 B.1363 C.48D.56【举一反三】1.(2019·北京高一期末)已知圆柱的侧面展开图是一个边长为2π的正方形,则这个圆柱的体积是( )A .22πB .2πC .22π D .23π2.(2019·河北高三月考(理))圆锥的母线长是4,侧面积是4π,则该圆锥的高为( )A B .4 C .3 D .23.设正六棱锥的底面边长为1 )A. C. D.24.已知圆台上、下底面的面积分别为π,4π,侧面积为6π,则这个圆台的体积为( ).A .14πB .143πCD .5.(2019·四川绵阳中学高一月考)圆台上底半径为2,下底半径为6,母线长为5,则圆台的体积为( )A.40πB.52πC.50πD.2123π 运用二 表面积【例2】(1)(2019·山西高二月考(文))已知圆柱的轴截面为正方形,且圆柱的体积为54π,则该圆柱的侧面积为()A.27πB.36πC.54πD.81π (2)(2019·福建高三月考(文))《九章算术》中,将底面是直角三角形的直三棱柱称为“堑堵”.某“堑堵”的三视图如图所示,则它的表面积为( )A .2B .4+C .4+D .6+(3)(2019·安徽高二期末(文))如图,长度为1的正方形网格纸中的实线图形是一个多面体的三视图,则该多面体表面积为( )A.16+B.16+C.12+D.12+【举一反三】1.(2019·湖南高一期末)已知一个圆柱的高是底面圆半径的2倍,则该圆柱的侧面积与表面积的比值为()A.14B.12C.23D.452.(2019·湖南高三期末(文))一个几何体的三视图如图所示,则该几何体的表面积为()A.B.C.D.53.若圆锥的轴截面是正三角形,则它的侧面积是底面积的()A倍B.3倍C.2倍D.5倍运用三球【例3】(1)由球O的球面上一点P作球的两两互相垂直的三条弦PA,PB,PC.已知3cmPA=,PB=,PC=,求球O的表面积和体积.(2)(2019·四川石室中学高三月考(文))已知球O 的内接圆锥体积为23π,其底面半径为1,则球O 的表面积为__________.(3)正方体的外接球与内切球的半径之比为( )ABC .2:1D .3:1【举一反三】 1.已知一个高为16的圆锥内接于一个体积为972π的球,在圆锥内又有一个内切球.求:(1)圆锥的侧面积.(2)圆锥内切球的体积.2.(2019·广东实验中学高三月考(理))三棱锥P ABC -的底面ABC 是等腰三角形,120C ∠=,侧面PAB 是等边三角形且与底面ABC 垂直,2AC =,则该三棱锥的外接球表面积为__________.3.已知棱长为a 的正方体,甲球是正方体的内切球,乙球是正方体的外接球,丙球与正方体的各棱都相切,则甲、乙、丙三球的表面积之比为( ).A .91:3:4 B .1:3:2 C.D.31:21.(2019·四川棠湖中学高二月考)一个棱长为2的正方体被一个平面截去部分后,余下部分的三视图如图所示,则截去部分与剩余部分体积的比为( )A .1:3B .1:4C .1:5D .1:62.(2019·全国高三月考(理))某几何体的三视图如图所示,则该几何体的体积是()A.23B.43C.83D.1633.(2019·天水市第一中学高三月考(理))已知一个简单几何体的三视图如图所示,则该几何体的体积为A.36π+B.66π+C.312π+D.124.(2019·安徽省泗县第一中学高二期末(文))某几何体的三视图如图所示,则该几何体的体积等于( )A .12B .15C .18D .215(2019·广东高一期末)已知圆柱的轴截面为正方形,且该圆柱的侧面积为36π,则该圆柱的体积为( )A.27πB.36πC.54πD.81π6.(2019·江西上高二中高二月考(理))圆锥的母线长为4,侧面展开图为一个半圆,则该圆锥表面积为( )A .10πB .12πC .16πD .18π7.(2019·江苏高一期末)已知圆锥的底面半径为1,母线与底面所成的角为3π,则此圆锥的侧面积为( )A. B.2π D.π 8.(2019·河北高一月考)如图,一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径相等,这时圆柱、圆锥、球的表面积之比为( )A .6:1):4+B .64C .5:1):4+D .5:49.(2018·辽宁高一期末)用一个平行于圆锥底面的平面截这个圆锥,截得圆台上下底面半径的比是1:4,且该圆台的母线长为9,则截去的圆锥的母线长为( ) A.94 B.3 C.12 D.3610.(2019·新疆乌鲁木齐市第70中高一期末(理))圆台的一个底面圆周长是另一个底面圆周长的3倍,母线长为3,圆台的侧面积为84π,则圆台较小底面圆的半径为( )A.3B.5C.6D.711.(2019·安徽高一期末)一个圆锥的侧面积为6π,底面积为4π,则该圆锥的体积为________.12.(2018·河北邢台一中高一月考(文))圆台的上下底面半径分别为1、2,母线与底面的夹角为60°,则圆台的侧面积...为________. 13.(2018·广州市培正中学高一单元测试)一个圆台的两底面的面积分别为π,16π,侧面积为25π,则这个圆台的高为_____14.(2017·浙江高二期中)若圆台的高是3,一个底面半径是另一个底面半径的2倍,母线与下底面所成的角是45,则这个圆台的侧面积是___________.15.(2017·安徽高二月考(文))一个圆台上、下底面的半径分别为3cm 和8cm ,若两底面圆心的连线长为12cm ,则这个圆台的表面积为__________2cm .16.(2019·四川双流中学高三月考(文))某简单组合体的三视图如图所示,则该组合体的体积为 .17(2019·安徽高一期末)一个几何体的三视图如图,则该几何体的体积为 .18.一个圆柱的底面直径与高都等于一个球的直径,则圆柱的全面积与球的表面积之比为.19.(2019·福建高一期末)一个圆柱的轴截面是正方形,其侧面积与一个球的表面积相等,那么这个圆柱的体积与这个球的体积之比为 .20.(2019·云南民族中学高三月考)已知直三棱柱111ABC A B C -的底面为直角三角形,且两直角边长分别为1和,则该三棱柱的外接球的体积为 .21.(2019·湖北襄阳四中高三月考(理))如图,在四棱锥P ABCD -中,顶点P 在底面的投影O 恰为正方形ABCD 的中心且AB =设点M ,N 分别为线段PD ,PO 上的动点,已知当AN MN +取得最小值时,动点M 恰为PD 的中点,则该四棱锥的外接球的表面积为____________.22(2019·陕西高一期末)在三棱锥S ABC -中,三个侧面两两互相垂直,侧面,,SAB SAC SBC ∆∆∆的面积分别为1,1,2,则此三棱锥的外接球的表面积为 .23.如图,正四棱锥P ABCD -底面的四个顶点,,,A B C D 在球O 的同一个大圆上,点P 在球面上.若163P ABCD V ,则球O 的体积是 .24.(2019·湖南衡阳市八中高三月考(文))在四面体SABC 中若三条侧棱SA ,SB ,SC 两两互相垂直,且SA =1,SB ,SC ABCD 的外接球的表面积为 .25.(2019·湖北省大冶市第六中学高二月考)如图是一个几何体的三视图,根据图中数据,可得几何体的表面积是 .26.(2019·上海市进才中学高三月考)若圆锥的侧面积为2π,底面积为π,则该圆锥的体积为____________。
27.(2019·贵州高二期末)周长为20cm 的矩形,绕一条边旋转成一个圆柱,则圆柱体积的最大值为_______3cm .28.一个几何体的三视图如图所示,则该几何体的表面积为________.29.(2019·宁夏银川一中)底面半径为1cm 的圆柱形容器里放有四个半径为12cm 的实心铁球,四个球两两相切,其中底层两球与容器底面相切. 现往容器里注水,使水面恰好浸没所有铁球,则需要注水________________.30.(2019·江苏高一期末)已知P ,A ,B ,C 是球O 的球面上的四点,PA ,PB ,PC 两两垂直,PA PB PC ==,且三棱锥P ABC -的体积为43,则球O 的表面积为______.。
