高二数学暑假作业5无答案
参考高二数学暑假作业答案

参考高二数学暑假作业答案自己整理的参考高二数学暑假作业答案相关文档,希望能对大家有所帮助,谢谢阅读![一]1?1变化率和导数1.1.1变化率1 . D2 . D3 . C4-3t-65 .x 26.3?317.(1)0?1(2)0?21(3)2?18.11m/s,10?1m/s 9.25 3t 10.128 a 64 a2 t 11 . f(x)-f(0)x=1x(x0),-1-x(x0)1?1?2导数的概念1 . D2 . C3 . C4-15 . x0,x;x06.67.a=18.a=2 9.-410.(1)2t-6(2)初速度为v0=-6,初位置为x0=1(3)运动开始3秒,在原点向左变化8m (4)x=1,v=611.水面上升速度为0?16m/min,表明 v= h75 15 h ( h) 23,那么 v t= h t 75 15 h ( h) 23,即limt0vt=limt0ht75 15h(h)23=limt0ht25,那就是v’(t)=25h’(t),那么h’(t)=1254=0?16(米/分钟)1?1?三阶导数的几何意义(一)1.C2切线的斜率。
B3。
B4。
f (x)在x0,y-f(x0)=f’(x0)(x-x0)5.36.1357.割线的斜率是3?31,正切的斜率为38.k=-1,x y 2=09.2x-y 4=010.k=14,切点坐标为12,1211.有两个交点,交点的坐标是(1,1),(-2,-8)1?1?3阶导数的几何意义(2)1.C2 a3 . B4 . y=x15。
16.37.y=4x-18.1039.1910.a=3,b=-11,c=9。
提示:首先找出a、b、c之间的关系,即c=3 2a。
B=-3a-2,然后求点(2,-1)处的斜率,得到k=a-2=1,即a=3 11.(1)y=-13x-229(2)125121?导数2的计算1?2?1几种常用函数的导数1.C2。
高二数学暑假生活答案

高二数学暑假生活(一)一、1.任何一个元素 有唯一的元素和它对应 象 原象2.定义域 值域3.图表法 图像法 解析法4.(1)R (2)不为零的实数全体构成的集合 (3)大于或等于零的实数全体构成的集合 (4)每部分式子都有 (5)使实际问题有意义5.配方法 分离常数法 换元法 数形结合法 二.1. B 2.C 3. C 4. D 5.A 6 C 7. B 解:由202xx+>-得,()f x 的定义域为22x -<<。
故22,222 2.x x⎧-<<⎪⎪⎨⎪-<<⎪⎩,解得()()4,11,4x ∈--U 。
故⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛x f x f 22的定义域为()()4,11,4Y --。
8. B 解析:图中的图象所表示的函数当0≤x ≤1时,它的解析式为32xy =,当1<x ≤2时,解析式为332y x =-+,∴解析式为|1|2323--=x y (0≤x ≤2)。
9. B 10. C 11. 【解析】1ln 2111(())(ln )222g g g e ===12. 解析:[(1)]f g =(3)1f =;当x=1时,[(1)]1,[(1)](1)3f g g f g ===,不满足条件, 当x=2时,[(2)](2)3,[(2)](3)1f g f g f g ====,满足条件, 当x=3时,[(3)](1)1,[(3)](1)3f g f g f g ====,不满足条件, ∴ 只有x=2时,符合条件。
三.13. 解:(1)由2222222221111()()1111111x x x x f x f x x x x x x++=+=+==+++++. (2)原式11117(1)((2)())((3)())((4)())323422f f f f f f f =++++++=+=点评:对规律的发现,能使我们实施巧算.正确探索出前一问的结论,是解答后一问的关键. 14. 解:函数y =ax +1(a <0且a 为常数).∵ax +1≥0,a <0,∴x ≤-1a,即函数的定义域为(-∞,-1a].∵函数在区间(-∞,1]上有意义,∴(-∞,1]⊆(-∞,-1a],∴-1a≥1,而a <0,∴-1≤a <0.即a 的取值范围是[-1,0).15. 解:(I )∵x x t -++=11,∴要使t 有意义,必须01≥+x 且01≥-x ,即11≤≤-x∵]4,2[12222∈-+=x t ,且0≥t ……① ∴t 的取值范围是]2,2[。
【推荐下载】苏教版高中高二数学暑假作业练习及答案

[键入文字]
苏教版高中高二数学暑假作业练习及答案
苏教版高中高二数学暑假作业练习及答案
【摘要】高中学生在学习中或多或少有一些困惑,的编辑为大家总结了苏教版高中高二数学暑假作业练习及答案,各位考生可以参考。
一、填空题(本大题共14小题,每小题5分,共70分)
1.命题:若a2+b2=0(a,b∈R),则a=b=0的逆否命题是____________.
解析 且的否定为或,因此逆否命题为若a≠0或b≠0,则a2+b2≠0.
答案 若a≠0或b≠0(a,b∈R),则a2+b2≠0
2.命题ax2-2ax-30不成立是真命题,则实数a的取值范围是____________.
解析 ax2-2ax-3≤0恒成立,
当a=0时,-3≤0成立;
当a≠0时,a小于0Δ=4a2+12a≤0,
解得-3≤a小于0.
1。
2021年高二下学期暑假作业数学(理)试题(5) 含答案

2021年高二下学期暑假作业数学(理)试题(5) 含答案一、选择题:1.圆上有10个点,过每三个点画一个圆内接三角形,则一共可以画的三角形个数为( )A .720B .360C .240D .1202. 的展开式中的系数是( )A .42B .35C .28D .213.从甲、乙、丙、丁、戊5个人中选1名组长1名副组长,但甲不能当副组长,不同的选法种数是( )A .6B . 10C .16D .204.从0、2中选一个数字,从1、3、5中选两个数字,组成无重复数字的三位数,其中奇数的个数为( )A .24B .18C .12D .65.分别抛掷2枚质地均匀的硬币,设是事件“第一枚为正面”, 是事件“第二枚为正面”, 是事件“2枚结果相同”.则事件与,事件与,事件与中相互独立的有( )A .0个B .1个C .2个D .3个第Ⅱ卷(共90分)二、填空题(4小题,每小题5分,满分20分,将答案填在答题纸上)6.从黄瓜、白菜、油菜、扁豆4种蔬菜品种中,共选出3种,分别种在不同土质的三块土地上,其中黄瓜必须种植,不同的种植方法共有_________(用数字作答).7. 521(2)() 1x x x -+展开式中项的系数为 . 8.有4名优秀学生全部被保送到甲、乙、丙3所学校,每所学校至少去一名,则不同的报送方案共有________(用数字作答).9. 彩票公司每天开奖一次,从1,2,3,4四个号码中随机开出一个作为中奖号码,开奖时如果开出的号码与前一天相同,就要重开,直到开出与前一天不同的号码为止.如果第一天开出的号码是4,则第五天开出的号码也同样是4的概率为 .三、解答题(本大题共6小题,共70分.)10.如图,在四棱锥P﹣ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=4,DC=3,E是PC的中点.(I)证明:PA∥平面BDE;(II)求△PAD以PA为轴旋转所围成的几何体体积.11.(本小题满分12分)已知二项式.(1)若展开式中第5项、第6项与第7项的二项式系数成等差数列,求展开式中二项式系数最大的项的系数;(2)若展开式前三项的二项式系数和等于79,求展开式中系数最大的项.12.(本小题满分12分)乒乓球单打比赛在甲、乙两名运动员间进行,比赛采用7局4胜制(即先胜4局者获胜,比赛结束),假设两人在每一局比赛中获胜的可能性相同.(1)求甲以4比1获胜的概率;(2)求乙获胜且比赛局数多于5局的概率;(3)求比赛局数的分布列.参考答案一、选择题1. D2. D3. C4. B5. D 二、 填空题6. 187.8. 369.三、解答题10.解:(I )连接AC 交BD 于O ,连接EO .∵ABCD 是正方形,∴O 为AC 中点,∵E 为PA 的中点,∴OE ∥PA .又∵OE ⊂平面BDE ,PA ⊄平面BDE ,∴PA ∥平面BDE .(II )过D 作PA 的垂线,垂足为H ,则△PAD 以以PA 为轴旋转所围成的几何体为DH 为半径,分别以PH ,AH 为高的两个圆锥的组合体∵侧棱PD ⊥底面ABCD ,AD ⊆底面ABCD∴PD ⊥AD ,∵PD=4,DA=DC=3,∴PA=5,所以,该几何体的体积为:===.11.(1),解得或,当时,展开式中二项式系数最大的项是和,()()43343344475713512,270222T C x x T C x x ⎛⎫⎛⎫==== ⎪ ⎪⎝⎭⎝⎭当时,展开式中二项式系数最大的项是,(2), 解得,设项系数最大,由于 ,,第11项最大.12.(1)由已知,甲、乙两名运动员在每一局比赛中获胜的概率都是,记“甲以4比1获胜”为事件,则;(2)记“乙获胜且比赛局数多于5局”为事件,因为,乙以4比2获胜的概率为,乙以4比3获胜的概率为,所以.(3)设比赛的局数为,则的可能值为4,5,6,7()()4343134411111142,52282224P X C P X C -⎛⎫⎛⎫⎛⎫====== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,()()35236333561115111562,722221622216P X C P X C --⎛⎫⎛⎫⎛⎫⎛⎫====== ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭, 比赛局数的分布列为:229004 714C 煌n }28026 6D7A 浺U 33107 8153 腓,.j37934 942E 鐮。
高二数学暑假作业答案-文档资料

2019年高二数学暑假作业答案亲爱的同学们,查字典数学网小编给大家整理了2019年高二数学暑假作业答案,希望能给大家到来帮助。
祝大家暑假愉快!【快乐暑假】2019年高二数学暑假作业答案一.填空题1.A.2.3.3.(1)(4)..5.212cm?4.(1)(2)..6.(2)(4).7.300..8.90°.9.①与③.10.④.11.?30.12.2:1.13.3.14.若②③④则①.二.解答题15. S=60?+4?2;V=52?-38?=3148?16.证明:作PO??,,PEABPFAC??,垂足分别为,,OEF,连结,,OEOFOA,∵,PEABPFACPAEPAFRtPAERtPAFAEAFPAPA?????????????? ???,POABPOAB??????????,又∵ABPE?,∴AB?平面PEO,∴ABOE?.同理ACOF?.在RtAOE?和RtAOF?,,AEAFOAOA??,∴RtAOE??RtAOF?,∴EAOFAO???,即点P在平面?上的射影在BAC?的平分线上.17.证明:(1)因为E,F分别是11AB,AC的中点,所以EF//BC,又EF?面ABC,BC?面ABC,所以EF∥ABC平面;(2)因为直三棱柱111ABCABC?,所以1111BBABC?面,11BBAD?,又11ADBC?,所以111ADBCC?面B,又11ADAFD?面,所以111AFDBBCC?平面平面.18.证明:(1)连结11AC,设11111ACBDO??连结1AO,?1111ABCDABCD?是正方体11AACC?是平行四边形11ACAC??且11ACAC?,又1,OO分别是11,ACAC的中点,11OCAO??且11OCAO?11AOCO?是平行四边形.111,COAOAO???面11ABD,1CO?面11ABD?1CO?面11ABD.(2)证明:////''''''ABDCDCABCDABDCDC? ?????是平行四边形'//'''''''BCADBCABD ADABD????????平面平面'//'''//'''''BC ABDCDABDBCCDC????????平面同理,平面?平面'//CDB平面''ABD.19.(本小题满分14分)(1)证明:?E.P分别为AC.A′C的中点, ?EP∥A′A,又A′A?平面AA′B, EP?平面AA′B∴即EP∥平面A′FB(2) 证明:∵BC⊥AC,EF⊥A′E,EF∥BC ∴BC⊥A′E,∴BC⊥平面A′EC BC?平面A′BC ∴平面A′BC⊥平面A′EC(3)证明:在△A′EC中,P为A′C的中点,∴EP⊥A′C,在△A′AC中,EP∥A′A,∴A′A⊥A′C由(2)知:BC⊥平面A′EC 又A′A?平面A′EC∴BC⊥AA′∴A′A⊥平面A′BC20.解:(1)证明:在DD1上取一点N使得DN=1,连接CN,EN,显然四边形CFD1N是平行四边形,所以D1F//CN,同理四边形DNEA是平行四边形,所以EN//AD,且EN=AD,又BC//AD,且AD=BC,所以EN//BC,EN=BC,所以四边形CNEB是平行四边形,所以CN//BE,所以D1F//BE,所以1,,,EBFD四点共面.(2)因为GMBF?所以BCF?∽?MBG,所以MBBGBCCF?,即2332MB?,所以MB=1,因为AE=1,所以四边形ABME是矩形,所以EM⊥BB1又平面ABB1A1⊥平面BCC1B1,且EM在平面ABB1A1内,所以EM?面11BCCB.。
2021年高二数学暑期作业(套卷)(5)含答案
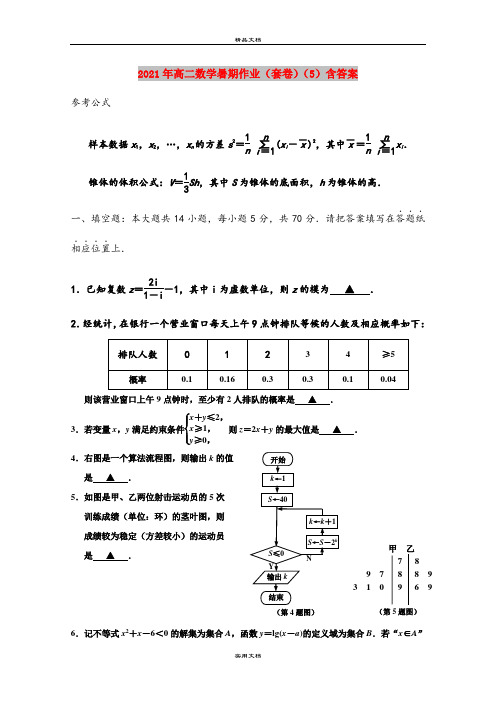
2021年高二数学暑期作业(套卷)(5)含答案参考公式样本数据x 1,x 2,…,x n 的方差s 2=1n i =1∑n (x i --x )2,其中-x =1n i =1∑nx i .锥体的体积公式:V =13Sh ,其中S 为锥体的底面积,h 为锥体的高.一、填空题:本大题共14小题,每小题5分,共70分.请把答案填写在答题纸...相应位置....上.1.已知复数z =2i1-i-1,其中i 为虚数单位,则z 的模为 ▲ . 2.经统计,在银行一个营业窗口每天上午9点钟排队等候的人数及相应概率如下:则该营业窗口上午9点钟时,至少有2人排队的概率是 ▲ .3.若变量x ,y 满足约束条件⎩⎪⎨⎪⎧x +y ≤2,x ≥1,y ≥0,则z =2x +y 的最大值是 ▲ .4.右图是一个算法流程图,则输出k 的值 是 ▲ .5.如图是甲、乙两位射击运动员的5次 训练成绩(单位:环)的茎叶图,则 成绩较为稳定(方差较小)的运动员 是 ▲ .6.记不等式x 2+x -6<0的解集为集合A ,函数y =lg(x -a )的定义域为集合B .若“x ∈A ”甲 乙8 9 7 8 93 1 0 6 97 8 9 (第5题图)(第4题图)是“x ∈B ”的充分条件,则实数a 的取值范围为 ▲ . 7.在平面直角坐标系xOy 中,过双曲线C :x 2-y 23=1的右焦点F 作x 轴的垂线l ,则l 与双曲线C 的两条渐近线所围成的三角形的面积是 ▲ .8.已知正六棱锥P -ABCDEF 的底面边长为2,侧棱长为4,则此六棱锥的体积为 ▲ . 9.在△ABC 中, ∠ABC =120︒,BA =2,BC =3,D ,E 是线段AC 的三等分点,则→BD ·→BE 的值为 ▲ .10.记等差数列{a n }的前n 项和为S n .若S k -1=8,S k =0,S k +1=-10,则正整数k = ▲ . 11.若将函数f (x )=∣sin(ωx -π6)∣(ω>0)的图象向左平移π9个单位后,所得图象对应的函数为偶函数 ,则实数ω的最小值是 ▲ .12.已知x ,y 为正实数,则4x 4x +y +yx +y的最大值为 ▲ .13.在平面直角坐标系xOy 中,圆C 的方程为(x -1)2+(y -1)2=9,直线l :y =kx +3与圆C相交于A ,B 两点,M 为弦AB 上一动点,以M 为圆心,2为半径的圆与圆C 总有公共点,则实数k 的取值范围为 ▲ .14.已知a ,t 为正实数,函数f (x )=x 2-2x +a ,且对任意的x ∈[0,t ],都有f (x )∈[-a ,a ].若对每一个正实数a ,记t 的最大值为g (a ),则函数g (a )的值域为 ▲ .二、解答题:本大题共6小题,共计90分.请在答题纸指定区域内........作答,解答时应写出文字说明、证明过程或演算步骤. 15.(本小题满分14分)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知a cos C +c cos A =2b cos A . (1)求角A 的值;(2)求sin B +sin C 的取值范围.16.(本小题满分14分)在四棱锥P -ABCD 中,BC ∥AD ,PA ⊥PD ,AD =2BC ,AB =PB , E 为PA 的中点. (1)求证:BE ∥平面PCD ; (2)求证:平面PAB ⊥平面PCD .17.(本小题满分14分)如图,摩天轮的半径OA 为50m ,它的最低点A 距地面的高度忽略不计.地面上有一长度为240m 的景观带MN ,它与摩天轮在同一竖直平面内,且AM =60m .点P 从最低点A 处按逆时针方向转动到最高点B 处,记∠AOP =θ,θ ∈(0,π).(1)当θ =2π3 时,求点P 距地面的高度PQ ;(2)试确定θ 的值,使得∠MPN 取得最大值.18.(本小题满分16分)在平面直角坐标系xOy 中,设中心在坐标原点的椭圆C 的左、右焦点分别为F 1、F 2,右准线l :x =m +1与x 轴的交点为B ,BF 2=m .(第16题图)PABCDE(第17题图)AMNBO PQθ(1)已知点(62,1)在椭圆C 上,求实数m 的值; (2)已知定点A (-2,0).①若椭圆C 上存在点T ,使得TATF 1=2,求椭圆C 的离心率的取值范围;②当m =1时,记M 为椭圆C 上的动点,直线AM ,BM 分别与椭圆C 交于另一点P ,Q ,若AM → =λAP →,BM →=μBQ →,求证:λ+μ19.(本小题满分16分)已知函数f (x )=x 2-x +t ,t ≥0,g (x )=ln x . (1)令h (x )=f (x )+g (x ),求证:h (x )是增函数;(2)直线l 与函数f (x ),g (x )的图象都相切.对于确定的正实数t ,讨论直线l 的条数,并说明理由.20.(本小题满分16分)已知数列{a n }的各项均为正数,其前n 项的和为S n ,且对任意的m ,n ∈N *, 都有(S m +n +S 1)2=4a 2m a 2n . (1)求a 2a 1的值;(2)求证:{a n }为等比数列;(第18题图)(3)已知数列{c n },{d n }满足|c n |=|d n |=a n ,p (p ≥3)是给定的正整数,数列{c n },{d n }的前p 项的和分别为T p ,R p ,且T p =R p ,求证:对任意正整数k (1≤k ≤p ),c k =d k .高二数学暑假作业(五)参考答案一、填空题:本大题共14小题,每小题5分,共70分.1. 5 2.0.74 3.4 4.6 5.甲 6.(-∞,-3] 7.4 3 8.12 9.119 10.911.32 12. 43 13.[-34,+∞) 14.(0,1)∪{2}错误!未指定书签。
北京宏志中学高二文科数学暑假作业答案

北京宏志中学高二文科数学暑假作业 参考答案暑假作业(一)A1.B 2.B 3.C 4.{-1,0} 5.C 6.D 7.D 8.D 9.010.{(0,1),(-1,2)} 11.-1<a <212.实数m 的值为8 13.(1)C (2)4m1+m 2暑假作业(一)B1.B 2.C 3.D 4.2 5.A 6.C 7.C 8.A 9.{2,4,6} 10.[0,1)∪(3,+∞) 11.23 12.A ∪B ={-7,-4,-8,4,9} 13.(1)B ={x |4<x <5} (2)a =-1暑假作业(二)1.C 2.A 3.C 4.充分不必要 5.B 6.A 7.B 8.B 9.充分不必要10.⎣⎡⎦⎤-12,43 11.m >9 12.m ≤4 13.(1)(∁U B )∩A ={x |3≤x <4}(2)⎣⎡⎭⎫-12,13∪⎝ ⎛⎦⎥⎤13,3-52 暑假作业(三)1.C 2.D 3.D 4.“所有的三角形都不是直角三角形” 5.D 6.D 7.C 8.C9.(-∞,0)∪⎝⎛⎭⎫34,+∞ 10.①②④ 11.[1,+∞) 12.-2<a ≤2 13.{a |a >2或a <-2}暑假作业(四)A1.C 2.B 3.B 4.(1,3] 5.A 6.B 7.B 8.C9.[2,+∞) 10.[-14,0)∪(34,1] 11.1201512.(1)f [g (2)]=0 g [f (2)]=2 (2)f [g (x )]=⎩⎪⎨⎪⎧x 2-2x ,x ≥0,x 2-4x +3,x <0g [f (x )]=⎩⎪⎨⎪⎧x 2-2,x ≤-1或x ≥1,3-x 2,-1<x <1 13.(1)f (x )=x 2+2x g (x )=-x 2+2x (2)(-∞,0]暑假作业(四)B1.B 2.A 3.C 4.435.C6.B7.D8.B9.[-14,+∞) 10.x3+1 11.(-∞,1]12.(1)(-3,0)∪(2,3) (2)①[-1,1] ②[1,4] (3)(-∞,0]13.(1)B (2)A暑假作业(五) 1.B 2.C 3.B 4.(-12,23) 5.A 6.A 7.D 8.D9.C 10.[3,+∞) 11.(-∞,2] 12.[2,+∞) 13.(-1,1)14.(1)b =4 (2)函数f (x )=x +cx取得最小值2 c 当c ∈[1,2)时,f (x )的最大值为2+c2当c ∈(2,4]时,f (x )的最大值为1+c 当c =2时,f (x )的最大值为315.(1)略 (2)(-∞,3]16.(1)f (1)=0 (2)略 (3)[1+10,+∞)暑假作业(六)A1.B 2.D 3.B 4.-2 5.D 6.A 7.A 8.A 9.1 10.-2 11.120712.(1)m =1 (2)f (x )是奇函数 (3)f (x )在区间(0,+∞)上单调递增13.(1)f (x )=⎩⎪⎨⎪⎧4x 3-2ax ,-1≤x <0,-4x 3+2ax ,0≤x ≤1. (2)存在a =8使得f (x )的图像的最高点在直线y =12上暑假作业(六)B1.C 2.C 3.B 4.-3 5.C 6.B 7.B 8.D 9.3210.2 11.(-2,0)∪(3,+∞) 12.(1)m =0 (2)-1<a <0 13.(1)略 (2)f (x )=x 2-6x +8(3)f (0)+f (1)+f (2)+…+f (2013)=1暑假作业(七)1.A 2.D 3.D 4.(-∞,-3] 5.B 6.C 7.C 8.A 9.C 10.-2 -4 11.y =-x 2+2x +8 12.-1或313.-3或15 14.f (x )=x 2+x15.(1)[-214,15] (2)a =-13或-116.(1)f (x )=12x 2+x (2)m =12,t =8暑假作业(八)A1.B 2.D 3.C 4.2 5.B 6.C 7.A 8.D 9.-1 10.log 23 11.3 212.(1)1 (2)-43 13.(1)略 (2)a =6,b =8,c =10暑假作业(八)B 1.C 2.B 3.D 4.a 2b 45.B6.D7.C8.A9.3 10.ab +3ab +111.①③④12.(1)略 (2)3x <4y <6z13.(1)y =at 2-3t +3 (2)a =16 x =64暑假作业(九)1.B 2.B 3.B 4.[-1,2)∪(2,3]5.B 6.D 7.C 8.B 9.B 10.3 11.0和112.(11-a,0) 13.-1和0 [-14,3]14.(-∞,0]∪[1,2]15.(1)f (12013) +f (-12013) =0 (2)(-∞,-2]∪[4,+∞)16.(1)a =1 (2)λ=43暑假作业(十)1.C 2.D 3.D 4.③ 5.C 6.A 7.D 8.C9.B 10.(-2,1) 11.-2 12.(-1,-1) 13.10<abc <1214.f (x )=⎩⎪⎨⎪⎧x +1,-1≤x ≤0,14(x -2)2-1,x >0. 15.(0,13]∪[3,+∞) 16.(1)m ≥2e (2)(-e 2+2e +1,+∞)暑假作业(十一)1.D 2.C 3.A 4.3x -y +2=0 5.D 6.C 7.A 8.B 9.B 10.1 1 11.0 12.3x +y =0 13.-cos x14.(1)13x -y -32=0 (2)切点坐标为(1,-14)或(-1,-18),切线方程为y =4x -18或y =4x -1415.(1)f (x )=x -3x(2)证明略 定值为616.(1)x 0=1 (2)a ≥ e暑假作业(十二)1.B 2.A 3.C 4.(-∞,-3)∪(6,+∞) 5.A 6.B 7.D 8.C9.C 10.9 11.(0,12) 12.-4 13.(-1,0)∪(1,+∞)14.(1)a =4,b =4 (2)极大值为4(1-e -2)15.(1)a =2 (2)①当a ≤0时,函数f (x )的单调递减区间为(0,1),单调递增区间为(1,+∞);②当0<a <2时,则函数f (x )的单调递增区间为(0,a2),(1,+∞),单调递减区间为(a2,1);③a =2时,函数f (x )的单调递增区间为(0,+∞);④a >2时,函数f (x )的单调递增区间为(0,1),(a2,+∞)单调递减区间为(1,a2)16.(1)f (x )的单调递增区间为(0,+∞),单调递减区间为(-∞,0),f (x )有极小值1(2)g (x )=sin x +1 (3)[1,+∞)暑假作业(十三)1.D 2.B 3.D 4.(0,1) 5.D 6.C 7.A 8.B9.A 10.6 cm 3 cm 4 cm 11.3-1 12.[-42,9] 13.114.(1)f (x )=x 3+2x 2-4x +5(2)f (x )在[-3,1]上的最大值为1315.(1)f (x )的单调递增区间为(-π2,0),单调递减区间为(0,π2) (2)k ≤-1216.(1)S 1的最大值为4 (2)l 的范围是[8,4 5]专题一 突破高考解答题——函数与导数1.(1)f (x )=x +1x(2)(-∞,2]2.(1)(0,1) (2)[2ln 3-5,2ln 2-4)3.(1)①当a ≤0时,函数f (x )的单调递增区间为(0,+∞)②当a >0时,函数f (x )的单调递减区间为(2a2a,+∞),单调递增区间为(0,2a2a)(2)略4.(1)(-1,13) (2)(-1,-411) (3)[-38,0]5.(1) y =x -1 (2)略 (3)f (b )-f (a )b -a>f⎝⎛⎭⎫a +b 2暑假作业(十四) 1.A 2.D 3.C 4.(-3π2,0) 5.D 6.B 7.D 8.D9.⎩⎪⎨⎪⎧2x +3y ≤60,4x +2y ≤80,y -x ≤10,x ≥0,x ∈N *,y ≥0,y ∈N*10.b a -c <ab -d11.①④12.a n +b n <c n 13.5张暑假作业(十五)1.A 2.B 3.B 4.(0,8) 5.B 6.A 7.B 8.C9.-1 10.(-7,3) 11.-21412.(1)M ={x |0<x <2} (2)[-2,2]13.(1)a1+a 2 (2)1-k 2-2k +k 2暑假作业(十六)1.C 2.D 3.C 4.6 5.A 6.B 7.A 8.B 9.B 10.2 11.22 12.2 13.20 14.略15.(1)k =50 (2)建8层时,每平方米的平均综合费用为1225元16.a 为6,b 为3时,经沉淀后流出的水中该杂质的质量分数最小暑假作业(十七)1.C 2.B 3.B 4.D 5.D 6.C 7.D 8.A 9.C10.a >c >b 11.log a (1+a )>log a ⎝⎛⎭⎫1+1a 12.a ≥0,b ≥0且a ≠b 13.3 3214.略 15.略16.(1)a n =2n -1+2,S n =n (n +2) (2)略暑假作业(十八)1.A 2.A 3.A 4.2 5.D 6.C 7.A 8.B9.A 10.3 11.-12+2i 12.2 13.3+4i14.(1)a =b =3 (2)z =1-i 时,|z |min = 2 15.(1)m =5或m =-3 (2)m ≠5且m ≠-3 (3)m =-2 (4)m <-3或m >5(5)m =-3-414或m =-3+41416.(1)|z |=1 ⎝⎛⎭⎫-12,1 (2)略 (3)1暑假作业(十九)1.已知函数f (x )=sin ⎝⎛⎭⎪⎫ωx +π3(ω>0)的最小正周期为π,则该函数的图像( )A .关于点⎝ ⎛⎭⎪⎫π3,0对称 B .关于直线x =π4对称C .关于点⎝ ⎛⎭⎪⎫π4,0对称 D .关于直线x =π3对称解析 由已知,ω=2,所以f (x )=sin ⎝⎛⎭⎪⎫2x +π3,因为f ⎝ ⎛⎭⎪⎫π3=0,所以函数图像关于点⎝ ⎛⎭⎪⎫π3,0中心对称,故选A. 答案 A2.要得到函数的图像,只要将函数的图像( )A. 向左平移1个单位B. 向右平移1个单位C. 向左平移个单位 D.向右平移 个单位 解析 因为,所以将c o s (21)y x =+c o s 2y x =12121c o s (21)c o s (2()2y xx =+=+向左平移个单位,故选C. 答案 C3. 函数f (x )=A sin(ωx +φ)A >0,ω>0,|φ|<π2的部分图象如图所示,则将y =f (x )的图象向右平移π6个单位后,得到的图象对应的函数解析式为( ). A .y =sin 2xB .y =cos 2xC .y =sin ⎝ ⎛⎭⎪⎫2x +2π3D .y =sin ⎝ ⎛⎭⎪⎫2x -π6解析 由所给图象知A =1,34T =11π12-π6=3π4,T =π,所以ω=2πT =2,由sin ⎝ ⎛⎭⎪⎫2×π6+φ=1,|φ|<π2得π3+φ=π2,解得φ=π6,所以f (x )=sin ⎝ ⎛⎭⎪⎫2x +π6,则f (x )=sin ⎝ ⎛⎭⎪⎫2x +π6的图象向右平移π6个单位后得到的图象对应的函数解析式为y =sin ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫x -π6+π6=sin ⎝ ⎛⎭⎪⎫2x -π6,故选D. 答案 D4.将函数y =sin 2x 的图象向左平移φ(φ>0)个单位,所得图象对应的函数为偶函数,则φ的最小值为( ).A.π6B.π3C.π4D.π12解析 将函数y =sin 2x 的图象向左平移φ个单位,得到函数y =sin 2(x +φ)=sin(2x +2φ)的图象,由题意得2φ=π2+k π(k ∈Z ),故φ的最小值为π4. 答案 C5. 如图,为了研究钟表与三角函数的关系,建立如图所示的坐标系,设秒针尖位置P (x ,y ).若初始位置为P 0⎝ ⎛⎭⎪⎫32,12,当秒针从P 0(注:此时t =0)正常开始走时,那么点P 的纵坐标y 与时间t 的函数关系为( ).A .y =sin ⎝ ⎛⎭⎪⎫π30t +π6B .y =sin ⎝ ⎛⎭⎪⎫-π60t -π6C .y =sin ⎝ ⎛⎭⎪⎫-π30t +π6D .y =sin ⎝ ⎛⎭⎪⎫-π30t -π3解析 由题意可得,函数的初相位是π6,排除B ,D.又函数周期是60(秒)且秒针按顺时针旋转,即T =⎪⎪⎪⎪⎪⎪2πω=60,所以|ω|=π30,即ω=-π30,故选C.答案 C6.电流强度I (安)随时间t (秒)变化的函数I =A sin(ωt +φ)(A >0,ω>0,0<φ<π2)的图像如图所示,则当t =1100秒时,电流强度是( ) A .-5安 B .5安 C .53安 D .10安解析 由函数图像知A =10,T 2=4300-1300=1100. ∴T =150=2πω,∴ω=100π. ∴I =10sin(100πt +φ). 又∵点⎝ ⎛⎭⎪⎫1300,10在图像上, ∴10=10sin ⎝ ⎛⎭⎪⎫100π×1300+φ ∴π3+φ=π2,∴φ=π6, ∴I =10sin ⎝ ⎛⎭⎪⎫100πt +π6.当t =1100时,I =10sin ⎝⎛⎭⎪⎫100π×1100+π6=-5. 答案 A 二、填空题 7.已知函数f (x )=sin(ωx+cos2y x =12φ)⎝ ⎛⎭⎪⎫ω>0,-π2≤φ≤π2的图像上的两个相邻的最高点和最低点的距离为22,则ω=________. 解析 由已知两相邻最高点和最低点的距离为22,而f (x )max -f (x )min =2,由勾股定理可得T2=22-22=2,∴T =4,∴ω=2πT =π2.答案 π28.已知函数f (x )=3sin ⎝ ⎛⎭⎪⎫ωx -π6(ω>0)和g (x )=2cos(2x+φ)+1的图象的对称轴完全相同,若x ∈⎣⎢⎡⎦⎥⎤0,π2,则f (x )的取值范围是________.解析 ∵f (x )与g (x )的图象的对称轴完全相同,∴f (x )与g (x )的最小正周期相等,∵ω>0,∴ω=2,∴f (x )=3sin ⎝ ⎛⎭⎪⎫2x -π6,∵0≤x ≤π2,∴-π6≤2x -π6≤5π6,∴-12≤sin ⎝ ⎛⎭⎪⎫2x -π6≤1,∴-32≤3sin ⎝ ⎛⎭⎪⎫2x -π6≤3,即f (x )的取值范围是⎣⎢⎡⎦⎥⎤-32,3.答案 ⎣⎢⎡⎦⎥⎤-32,39.已知函数f (x )=-2sin(2x +φ)(|φ|<π),若⎝ ⎛⎭⎪⎫π8,5π8是f (x )的一个单调递增区间,则φ的值为________.解析 令π2+2k π≤2x +φ≤3π2+2k π,k ∈Z ,k =0时,有π4-φ2≤x ≤3π4-φ2,此时函数单调递增,若⎝ ⎛⎭⎪⎫π8,5π8是f (x )的一个单调递增区间,则必有⎩⎪⎨⎪⎧π4-φ2≤π8,3π4-φ2≥5π8,解得⎩⎪⎨⎪⎧φ≥π4,φ≤π4,故φ=π4.答案 π410.在函数f (x )=A sin(ωx +φ)(A >0,ω>0)的一个周期内,当x =π9时有最大值12,当x =4π9时有最小值-12,若φ∈⎝⎛⎭⎪⎫0,π2,则函数解析式f (x )=________.解析 首先易知A =12,由于x =π9时f (x )有最大值12,当x =4π9时f (x )有最小值-12,所以T =⎝ ⎛⎭⎪⎫4π9-π9×2=2π3,ω=3.又12sin ⎝⎛⎭⎪⎫3×π9+φ=12,φ∈⎝ ⎛⎭⎪⎫0,π2,解得φ=π6,故f (x )=12sin ⎝⎛⎭⎪⎫3x +π6.答案12sin ⎝⎛⎭⎪⎫3x +π6三、解答题11.已知函数f (x )=3sin2x +2cos 2x .(1)将f (x )的图像向右平移π12个单位长度,再将周期扩大一倍,得到函数g (x )的图像,求g (x )的解析式;(2)求函数f (x )的最小正周期和单调递增区间. 解 (1)依题意f (x )=3sin2x +2·cos2x +12=3sin2x +cos2x +1 =2sin ⎝ ⎛⎭⎪⎫2x +π6+1,将f (x )的图像向右平移π12个单位长度,得到函数f 1(x )=2sin ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫x -π12+π6+1=2sin2x +1的图像,该函数的周期为π,若将其周期变为2π,则得g (x )=2sin x +1.(2)函数f (x )的最小正周期为T =π,当2k π-π2≤2x +π6≤2k π+π2(k ∈Z)时,函数单调递增, 解得k π-π3≤x ≤k π+π6(k ∈Z),∴函数的单调递增区间为⎣⎢⎡⎦⎥⎤k π-π3,k π+π6(k ∈Z).12.已知向量m =(sin x,1),n =(3A cos x ,A2cos 2x )(A >0),函数f (x )=m ·n 的最大值为6. (1)求A ;(2)将函数y =f (x )的图象向左平移π12个单位,再将所得图象上各点的横坐标缩短为原来的12倍,纵坐标不变,得到函数y =g (x )的图象,求g (x )在⎣⎢⎡⎦⎥⎤0,5π24上的值域.解 (1)f (x )=m ·n =3A sin x cos x +A2cos 2x =A ⎝ ⎛⎭⎪⎫32sin 2x +12cos 2x =A sin ⎝ ⎛⎭⎪⎫2x +π6.因为A >0,由题意知A =6. (2)由(1)知f (x )=6sin ⎝ ⎛⎭⎪⎫2x +π6.将函数y =f (x )的图象向左平移π12个单位后得到 y =6sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x +π12+π6=6sin ⎝ ⎛⎭⎪⎫2x +π3的图象; 再将得到图象上各点横坐标缩短为原来的12倍,纵坐标不变,得到y =6sin ⎝ ⎛⎭⎪⎫4x +π3的图象.因此g (x )=6sin ⎝ ⎛⎭⎪⎫4x +π3. 因为x ∈⎣⎢⎡⎦⎥⎤0,5π24,所以4x +π3∈⎣⎢⎡⎦⎥⎤π3,7π6,故g (x )在⎣⎢⎡⎦⎥⎤0,5π24上的值域为[-3,6].13.已知函数f (x )=23sin x 2+π4cos ⎝ ⎛⎭⎪⎫x 2+π4-sin(x +π).(1)求f (x )的最小正周期;(2)若将f (x )的图象向右平移π6个单位,得到函数g (x )的图象,求函数g (x )在区间[0,π]上的最大值和最小值.解 (1)因为f (x )=3sin ⎝ ⎛⎭⎪⎫x +π2+sin x=3cos x +sin x =2⎝ ⎛⎭⎪⎫32cos x +12sin x=2sin ⎝ ⎛⎭⎪⎫x +π3,所以f (x )的最小正周期为2π.(2)∵将f (x )的图象向右平移π6个单位,得到函数g (x )的图象,∴g (x )=f ⎝ ⎛⎭⎪⎫x -π6=2sin[⎝ ⎛⎭⎪⎫x -π6+π3]=2sin ⎝ ⎛⎭⎪⎫x +π6.∵x ∈[0,π],∴x +π6∈⎣⎢⎡⎦⎥⎤π6,7π6,∴当x +π6=π2,即x =π3时,sin ⎝ ⎛⎭⎪⎫x +π6=1,g (x )取得最大值2.当x +π6=7π6,即x =π时,sin ⎝ ⎛⎭⎪⎫x +π6=-12,g (x )取得最小值-1.14.设函数f (x )=22cos ⎝ ⎛⎭⎪⎫2x +π4+sin 2x .(1)求f (x )的最小正周期;(2)设函数g (x )对任意x ∈R ,有g ⎝ ⎛⎭⎪⎫x +π2=g (x ),且当x ∈⎣⎢⎡⎦⎥⎤0,π2时,g (x )=12-f (x ).求g (x )在区间[-π,0]上的解析式.解 (1)f (x )=22cos ⎝ ⎛⎭⎪⎫2x +π4+sin 2x=22⎝ ⎛⎭⎪⎫cos 2x cos π4-sin 2x sin π4+1-cos 2x 2=12-12sin 2x ,故f (x )的最小正周期为π.(2)当x ∈⎣⎢⎡⎦⎥⎤0,π2时,g (x )=12-f (x )=12sin 2x ,故 ①当x ∈⎣⎢⎡⎦⎥⎤-π2,0时,x +π2∈⎣⎢⎡⎦⎥⎤0,π2.由于对任意x ∈R ,g ⎝ ⎛⎭⎪⎫x +π2=g (x ),从而g (x )=g ⎝ ⎛⎭⎪⎫x +π2=12sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫x +π2=12sin(π+2x )=-12sin 2x .②当x ∈⎣⎢⎡⎭⎪⎫-π,-π2时,x +π∈⎣⎢⎡⎭⎪⎫0,π2.从而g (x )=g (x +π)=12sin[2(x +π)]=12sin 2x .综合①、②得g (x )在[-π,0]上的解析式为 g (x )=⎩⎪⎨⎪⎧12sin 2x ,x ∈⎣⎢⎡⎭⎪⎫-π,-π2,-12sin 2x ,x ∈⎣⎢⎡⎦⎥⎤-π2,0.15.在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c .已知cos A =23,sin B =5cos C . (1)求tan C 的值;(2)若a = 2,求△ABC 的面积. 解 (1)因为0<A <π,cos A =23, 得sin A =1-cos 2A =53.又5cos C =sin B =sin(A +C )=sin A cos C +cos A sin C=53cos C +23sin C . 所以tan C = 5.(2)由tan C =5,得sin C =56,cos C =16.于是sin B =5cos C =56.由a = 2及正弦定理a sin A =csin C ,得c = 3. 设△ABC 的面积为S ,则S =12ac sin B =52. 16. 在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,点(a ,b )在直线x (sin A -sin B )+y sin B =c sin C 上. (1)求角C 的值;(2)若a 2+b 2=6(a +b )-18,求△ABC 的面积. 解 (1)由题意得a (sin A -sin B )+b sin B =c sin C , 由正弦定理,得a (a -b )+b 2=c 2, 即a 2+b 2-c 2=ab , 由余弦定理,得cos C =a 2+b 2-c 22ab =12,结合0<C <π,得C =π3.(2)由a 2+b 2=6(a +b )-18,得(a -3)2+(b -3)2=0, 从而得a =b =3,所以△ABC 的面积S =12×32×sin π3=934. 17. 在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .已知A =π4,b sin ⎝ ⎛⎭⎪⎫π4+C -c sin ⎝ ⎛⎭⎪⎫π4+B =a .(1)求证:B -C =π2;(2)若a = 2,求△ABC 的面积.(1)证明 由b sin ⎝ ⎛⎭⎪⎫π4+C -c sin ⎝ ⎛⎭⎪⎫π4+B =a 应用正弦定理,得sin B sin ⎝ ⎛⎭⎪⎫π4+C -sin C sin ⎝ ⎛⎭⎪⎫π4+B =sin A ,sin B ⎝ ⎛⎭⎪⎫22sin C +22cos C -sin C ⎝ ⎛⎭⎪⎫22sin B +22cos B =22,整理得sin B cos C -cos B sin C =1,即sin(B -C )=1. 由于0<B ,C <34π,从而B -C =π2.(2)解 B +C =π-A =3π4,因此B =5π8,C =π8. 由a = 2,A =π4,得b =a sin B sin A =2sin 5π8,c =a sin C sin A =2sin π8, 所以△ABC 的面积S =12bc sin A = 2sin 5π8sin π8 = 2cos π8sin π8=12北京宏志中学文科暑假作业答案。
高二数学 暑假作业(5)(无答案)(新版)新人教版

—————————— 新学期 新成绩 新目标 新方向 ——————————2019年高二数学 暑假作业(5)一、选择题:1、 下列函数中,在区间()0,+∞不是增函数的是 ( )A. x y 2=B. x y lg =C. 3x y =D. 1y x= 2、函数y =(a 2-1)x 在(-∞,+∞)上是减函数,则a 的取值范围是 ( )A.|a |>1B.|a |>2C.a>2D.1<|a |<2 3、图中曲线分别表示l g a y o x =,l g b y o x =,l g c y o x =,l g d y o x =的图象,,,,a b c d 的关系是 () A 、0<a<b<1<d<cB 、0<b<a<1<c<dC 、0<d<c<1<a<bD 、0<c<d<1<a<b 二、填空题: 4、若f(x)是偶函数,其定义域为R,且在[0,+)∞上是减函数,则f(2a 2+a+1)<f(3a 2-2a+1)的a 的取值集合为________________.5、(),()x g x ϕ都是奇函数,f(x)=()()a x bg x ϕ++2在(0,+∞)上有最大值5,则f(x)在(-∞,0)上有最_______值________.三、解答题:6.设x ,y ,z ∈R +,且3x =4y =6z . (1)求证:yx z 2111=-; (2)比较3x ,4y ,6z的大小.x7、设1221)(+-=x x f (1)求f (x )的值域;(2)证明f (x )为R 上的增函数;一、选择题:1、已知b a ba 、,则2log 2log 0<<的关系是 ( )111010>>>><<<<<<b a D a b C a b B b a A 、、、、 2、函数f(x)=log 31(5-4x-x 2)的单调减区间为 ( )A.(-∞,-2)B.[-2,+∞]C.(-5,-2)D.[-2,1]3、已知)2(log ax y a-=在[0,1]上是x 的减函数,则a 的取值范围是 ( )A.(0,1)B.(1,2)C.(0,2)D.[2,+∞]二、填空题:4.函数()f x 对于任意实数x 满足条件()()12f x f x +=,若()15,f =-则()()5f f =_______.5.函数y=)124(log 221-+x x 的单调递增区间是 .三、解答题:6已知()32log ([1,9])f x x x =+∈,求函数22[()]()y f x f x =+的最大值与最小值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广东省深圳市2018年高二数学 暑假作业(5)
一、选择题:
1、下列函数中,在区间()0,+∞不是增函数的是 ()
A. x y 2=
B. x y lg =
C. 3x y =
D.
1y x = 2、函数y =(a 2-1)x 在(-∞,+∞)上是减函数,则a 的取值范围是 ( )
A.|a |>1
B.|a |>2
C.a>
D.1<|a |<
3、图中曲线分别表示l g a y o x =,l g b y o x =,l g c
y o x =,
l g d y o x =的图象,,,,a b c d 的关系是 (
) A 、0<a<b<1<d<c
B 、0<b<a<1<c<d
C 、0<d<c<1<a<b
D 、0<c<d<1<a<b 二、填空题: 4、若f(x)是偶函数,其定义域为R,且在[0,+)∞上是减函数,则f(2a 2+a+1)<f(3a 2-2a+1)的a 的取值集合为________________.
5、(),()x g x ϕ都是奇函数,f(x)=()()a x bg x ϕ++2在(0,+)上有最大值5,则f(x)在(-,0)上有最_______值________.
三、解答题:
6.设x ,y ,z ∈R +,且3x =4y =6z . (1)求证:y
x z 2111=-; (2)比较3x ,4y ,6z 的大小.
7、设1
221)(+-=x x f (1)求f (x )的值域;(2)证明f (x )为R 上的增函数;
x
一、选择题:
1、已知b a b
a 、,则2log 2log 0<<的关系是 ( )
11101
0>>>><<<<<<b a D a b C a b B b a A 、、、、 2、函数f(x)=log(5-4x-x 2)的单调减区间为 ( )
A.(-∞,-2)
B.[-2,+∞]
C.(-5,-2)
D.[-2,1]
3、已知)2(log ax y a
-=在[0,1]上是x 的减函数,则a 的取值范围是 ( )
A.(0,1)
B.(1,2)
C.(0,2)
D.[2,+∞]
二、填空题:
4.函数()f x 对于任意实数满足条件()()12f x f x +=,若()15,f =-则()()5f f =_______.
5.函数y=)
124(log 221-+x x 的单调递增区间是.
三、解答题:
6已知
()32log ([1,9])f x x x =+∈,求函数22[()]()y f x f x =+的最大值与最小值。
7.设函数)1lg()(2++=x x x f .(1)判断函数f (x )的奇偶性;(2)证明函数f (x )在其定义域上是单调增函数。
