规则刚体转动惯量的初等计算方法
刚体转动惯量计算公式

刚体转动惯量计算公式刚体转动惯量这玩意儿,在物理学里可是个挺重要的概念。
咱们先来瞧瞧啥是刚体转动惯量。
简单说,刚体转动惯量就是衡量刚体转动时惯性大小的一个物理量。
想象一下,你转一个大圆盘和转一个小圆盘,是不是感觉转大圆盘更费劲?这就是因为大圆盘的转动惯量大呀!那刚体转动惯量咋算呢?这就有个计算公式啦。
对于一个绕定轴转动的刚体,其转动惯量 I 等于各个质量元的质量乘以它到转轴距离的平方的总和。
用数学式子表示就是:I = ΣΔmiri² 。
比如说,有一个均匀的细棒,长度为 L ,质量为 M ,绕通过一端且垂直于棒的轴转动。
那这时候转动惯量 I 就等于 1/3 ML²。
我还记得有一次给学生们讲这个知识点的时候,有个小家伙一脸迷茫地问我:“老师,这转动惯量到底有啥用啊?”我笑着给他举了个例子。
我说:“你看啊,咱们骑自行车,车轮就是个刚体。
如果车轮的转动惯量大,那你起步的时候是不是就得费更大的劲儿?但是一旦转动起来,保持转动就相对容易些。
这就好比一个大胖子跑步,一开始跑起来难,但跑起来后惯性大,停下来也不容易。
”这小家伙听完,眼睛一下子亮了,好像明白了点什么。
再比如说一个圆环,质量为 M ,半径为 R ,绕通过圆心且垂直于圆环平面的轴转动,转动惯量就是 MR²。
还有那种质量分布不均匀的情况,就得把刚体分成很多小块,分别计算每一小块的转动惯量,然后再加起来。
这就有点像咱们做拼图,一块一块拼出最终的结果。
在实际生活中,转动惯量的应用可多啦。
像工厂里的大型机器轮子,设计的时候就得考虑转动惯量,不然运转起来可就麻烦喽。
总之,刚体转动惯量计算公式虽然看起来有点复杂,但只要咱们多琢磨琢磨,多结合实际例子想想,就能慢慢搞清楚啦。
就像解一道难题,一开始觉得难,多尝试几次,说不定就豁然开朗啦!希望大家都能把这个知识点掌握好,在物理学的世界里畅游无阻!。
刚体转动与转动惯量计算

刚体转动与转动惯量计算刚体转动是物理学中一个重要的概念,它描述了物体在空间中绕某个轴旋转的运动。
而转动惯量则是衡量物体对转动运动的惯性大小的物理量。
在本文中,我们将探讨刚体转动以及转动惯量的计算方法。
一、刚体转动的基本概念刚体是指其内部各点之间的相对位置保持不变的物体。
当一个刚体绕某个轴旋转时,我们可以将其看作由无数个质点组成的系统。
每个质点围绕轴线作圆周运动,但由于刚体是刚性的,各个质点的圆周运动是同步的,因此整个刚体呈现出旋转的状态。
在刚体转动中,我们常用到角度、角速度和角加速度等概念。
角度表示刚体绕轴线旋转的程度,通常用弧度制来表示。
角速度表示单位时间内刚体旋转的角度变化量,用符号ω表示。
角加速度则表示单位时间内角速度的变化量,用符号α表示。
二、转动惯量的概念转动惯量是描述物体对转动运动的惯性大小的物理量。
它与物体的质量分布和轴线的位置有关。
对于一个质量分布均匀的物体,其转动惯量可以通过以下公式计算:I = ∫r^2 dm其中,I表示转动惯量,r表示质点与轴线的距离,dm表示质点的质量元素。
对于一个质量分布不均匀的物体,我们需要将其分割成无数个质点,然后对每个质点的转动惯量进行求和,才能得到整个物体的转动惯量。
三、转动惯量的计算方法在实际计算转动惯量时,我们常用到一些常见的几何体的转动惯量公式。
以下是一些常见几何体的转动惯量计算公式:1. 球体的转动惯量计算公式:对于一个半径为r、质量为m的球体,其转动惯量可以通过以下公式计算:I = (2/5)mr^22. 圆柱体的转动惯量计算公式:对于一个半径为r、质量为m、高度为h的圆柱体,其转动惯量可以通过以下公式计算:I = (1/2)mr^2 + (1/12)mh^23. 平板的转动惯量计算公式:对于一个质量为m、边长为a的平板,其转动惯量可以通过以下公式计算:I = (1/12)ma^2除了以上几何体的转动惯量计算公式外,对于其他复杂形状的物体,我们可以利用积分的方法进行求解。
转动惯量计算公式

转动惯量计算公式
一、背景介绍
转动惯量是刻画物体抵抗转动状态变化的物理量,它在许多力学和工程问题中
都具有重要的应用。
在实际问题中,我们经常需要计算物体的转动惯量,以便更好地理解和解决与转动相关的问题。
二、转动惯量的定义
转动惯量是指物体绕某个轴旋转时,该轴相对于物体分布的质量的一种度量。
它的计算公式可以根据物体的形状和质量分布情况来确定。
三、常见的转动惯量计算公式
1. 点质量的转动惯量
对于质量为m的点质量,其绕某个轴的转动惯量计算公式为:
I = m * r^2
其中,I表示转动惯量,m表示点质量,r表示点质量相对于轴的距离。
2. 杆状物体的转动惯量
对于长度为L,质量为M的均匀杆,绕与杆垂直的轴的转动惯量计算公式为:
I = (1/3) * M * L^2
其中,I表示转动惯量,M表示杆的质量,L表示杆的长度。
3. 圆环的转动惯量
对于质量为M,半径为R的均匀圆环,绕圆环的中心轴的转动惯量计算公式为:
I = M * R^2
其中,I表示转动惯量,M表示圆环的质量,R表示圆环的半径。
4. 球体的转动惯量
对于质量为M的均匀球体,绕通过球心的轴的转动惯量计算公式为:
I = (2/5) * M * R^2
其中,I表示转动惯量,M表示球体的质量,R表示球体的半径。
四、总结
转动惯量是物体抵抗转动的一种物理量,其计算公式与物体形状和质量分布有关。
本文介绍了常见的转动惯量计算公式,包括点质量、杆状物体、圆环和球体的转动惯量计算公式。
通过理解和应用这些公式,我们可以更好地分析和解决与转动相关的问题。
转动惯量计算折算公式

转动惯量计算折算公式
转动惯量(即转动惯性矩)是描述物体对转动运动的惯性的物理量,
它可以用公式I=mr^2来计算,其中I是转动惯量,m是物体的质量,r是
物体的转动半径。
然而,在实际问题中,物体的形状往往是复杂的,不可能直接通过上
述公式来计算转动惯量。
为了解决这个问题,我们可以通过一些折算公式
来将复杂物体的转动惯量转换为一些简单形状的转动惯量之和。
以下是一些常见的折算公式:
1.对于长方体:
-绕通过质心垂直于一条边的转动轴转动:I=(1/12)*m*(a^2+b^2),
其中m是质量,a和b是长方体的两个边长。
-绕通过质心垂直于两条平行边的转动轴转动:I=(1/3)*m*(a^2+b^2),其中m是质量,a和b是长方体的两个边长。
2.对于球体:
-绕通过质心的任意轴转动:I=(2/5)*m*r^2,其中m是质量,r是球
体的半径。
3.对于圆环:
-绕通过圆环中心的垂直于其平面的转动轴转动:I=m*r^2,其中m是
质量,r是圆环的半径。
4.对于圆盘:
-绕通过圆盘中心的垂直于其平面的转动轴转动:I=(1/2)*m*r^2,其中m是质量,r是圆盘的半径。
5.对于薄杆(在转动轴与薄杆所在直线垂直的情况下):
-绕通过薄杆中心的转动轴转动:I=(1/12)*m*L^2,其中m是质量,L 是薄杆的长度。
这些折算公式可以帮助我们将复杂物体的转动惯量转换为一些简单形状的转动惯量之和,从而简化计算过程。
在实际应用中,我们可以根据物体的形状选择合适的折算公式来计算转动惯量,从而更好地描述物体的转动运动。
转动惯量的计算

转动惯量的计算转动惯量(也称为惯性矩)是描述物体对绕轴转动的惯性特性的物理量,通常用字母 "I" 表示。
它是旋转运动的类似于质量的性质,表示了物体绕轴旋转时抵抗改变转速的能力。
计算转动惯量的公式取决于物体的形状和轴线的位置。
本文将介绍几种常见物体的转动惯量计算方法。
1. 点质量的转动惯量点质量的转动惯量是最简单的情况,它表示物体质点绕某一轴旋转时的惯性。
点质量的转动惯量的计算公式如下:I = m * r^2其中,I 表示转动惯量,m 表示质量,r 表示质点到旋转轴的距离。
2. 杆状物体的转动惯量杆状物体是另一种常见情况,它是指质量均匀分布在长度为 L 的细长杆上的物体。
杆状物体绕与之垂直的一个端点旋转时的转动惯量计算公式如下:I = (1/3) * m * L^2其中,I 表示转动惯量,m 表示质量,L 表示杆的长度。
3. 薄圆环的转动惯量薄圆环是一个质量均匀分布的圆环,它绕圆心垂直于环面的轴旋转时的转动惯量计算公式如下:I = m * R^2其中,I 表示转动惯量,m 表示质量,R 表示圆环的半径。
4. 薄圆盘的转动惯量薄圆盘是一个质量均匀分布的圆盘,它绕与之垂直的轴旋转时的转动惯量计算公式如下:I = (1/2) * m * R^2其中,I 表示转动惯量,m 表示质量,R 表示圆盘的半径。
5. 球体的转动惯量球体是一个质量均匀分布的球形物体,它绕通过球心的轴旋转时的转动惯量计算公式如下:I = (2/5) * m * R^2其中,I 表示转动惯量,m 表示质量,R 表示球体的半径。
6. 转动惯量的叠加原理对于复杂形状的物体,可以将其分解为若干简单形状,并利用转动惯量的叠加原理求解总的转动惯量。
叠加原理表明,当一个物体由多个组成部分组成时,其总的转动惯量等于每个部分转动惯量的代数和。
I_total = I_1 + I_2 + I_3 + ...其中,I_total 表示总的转动惯量,I_1、I_2、I_3 等表示各个组成部分的转动惯量。
转动惯量计算公式

转动惯量计算公式转动惯量是物体对于转动的惯性特性的度量,它描述了物体绕轴旋转时所具有的抵抗外力转动的能力。
在物理学中,转动惯量用于计算物体围绕轴线旋转时所存储的动能。
1. 定义转动惯量(通常用大写字母I表示)是一个标量,定义为物体的质量分布对于给定轴线旋转的分布特性。
转动惯量可以根据物体的质量和其几何形状进行计算。
2. 计算方法2.1 离散物体的转动惯量对于任意形状的离散物体,其转动惯量可以通过以下公式计算:转动惯量公式1转动惯量公式1其中,mi为离散物体的质量,ri为离散质点到旋转轴的距离。
2.2 连续物体的转动惯量对于连续物体,其转动惯量需要进行积分计算。
其一般形式的转动惯量公式如下:转动惯量公式2转动惯量公式2其中,r为物体上不同质点到旋转轴的距离,dm为物体的质量微元。
2.3 常见几何形状的转动惯量计算具有常见几何形状的物体的转动惯量时,可以利用已知结果进行计算。
一些常见几何形状的转动惯量公式如下:•对于绕通过质心的轴旋转的刚体:–扁平圆环:转动惯量公式3,其中M为圆环的质量,R为圆环的半径。
–实心圆盘:转动惯量公式4,其中M为圆盘的质量,R为圆盘的半径。
–长棒:转动惯量公式5,其中M为棒的质量,L为棒的长度。
–球体:转动惯量公式6,其中M为球体的质量,R为球体的半径。
•对于绕平行于某个轴的球面旋转:–空心球体:转动惯量公式7,其中M为球体的质量,R为球体的外半径。
这些公式提供了一些常见几何形状的转动惯量计算方法。
对于非常规形状或复杂结构的物体,可能需要使用数值模拟或近似方法进行转动惯量的计算。
3. 转动惯量的应用转动惯量在物理学中具有广泛的应用。
下面列举了一些转动惯量的应用场景:•刚体的旋转运动:转动惯量描述了刚体绕特定轴旋转时所具有的惯性特性,可以用于求解刚体的旋转方程。
•刚体的动能计算:转动惯量可以用于计算刚体绕轴旋转时存储的动能。
•转动惯量的变化:通过分析转动惯量的变化,可以研究刚体在旋转过程中的动力学特性。
刚体转动惯量公式及计算方法
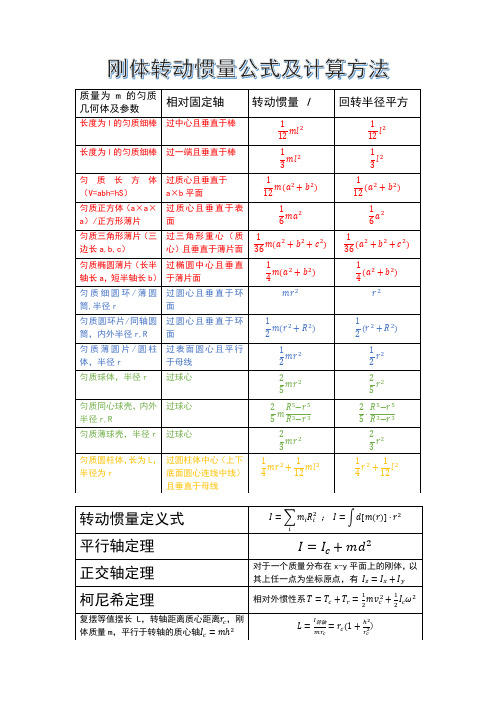
转动惯量定义式
平行轴定理
正交轴定理
对于一个质量分布在x-y平面上的刚体,以其上任一点为坐标原点,有
柯尼希定理
相对外惯性系
复摆等值摆长L,转轴距离质心距离 ,刚体质量m,平行于转轴的质心轴
)
质量为m的匀质几何体及参数
相对固定轴
转动惯量I
回转半径平方
长度为l的匀质细棒
过中心且垂直于棒
长度为匀质细棒
过一端且垂直于棒
匀质长方体(V=abh=hS)
过质心且垂直于
a×b平面
匀质正方体(a×a×a)/正方形薄片
过质心且垂直于表面
匀质三角形薄片(三边长a,b,c)
过三角形重心(质心)且垂直于薄片面
匀质椭圆薄片(长半轴长a,短半轴长b)
过椭圆中心且垂直于薄片面
匀质细圆环/薄圆筒,半径r
过圆心且垂直于环面
匀质圆环片/同轴圆筒,内外半径r,R
过圆心且垂直于环面
匀质薄圆片/圆柱体,半径r
过表面圆心且平行于母线
匀质球体,半径r
过球心
匀质同心球壳,内外半径r,R
过球心
匀质薄球壳,半径r
过球心
匀质圆柱体,长为L,半径为r
转动惯量的计算

ii
ii
即
Jz =
J
y
J
x
x
Δmi
z
m 圆盘 C
y R x
例:已知圆盘
Jz
=
1 mR2 2
求对圆盘的一条直径的Jx (或 Jy )
Jz = Jx Jy
Jx = Jy
Jx
=
Jy
=
1 4
mR2
第5章 刚体力学基础
5-3 转动惯量的计算
例 一质量为m ,长为 l 的均质细杆,转轴在O点,距
A端 l/3 。今使棒从静止开始由水平位置绕O点转动,求
第5章 刚体力学基础
5-3 转动惯量的计算
平行轴定理应用举例: 挂钟摆锤的转动惯量
J = Jl JR
Jl
=
1 3
m1l
2
JR
=
1 2
m2 R 2
m2
l
R2
o m1 l
M2 R
J
=
1 3
m1l 2
1 2
m2 R 2
m2
l
R2
第5章 刚体力学基础
5-3 转动惯量的计算
Jo = Jc md2
圆盘对P 轴的转动惯量
r r r r
= Dmi ri d ri d
d o ri'
c ri Dmi
i
=
Dmiri2
r Dmid 2 2d
r Dmiri
i
i
i
= Dmiri2 md2 i
JO = Jc md 2
刚体对任一转轴的转动惯量J 等于对通过质心的平行转轴的 转动惯量Jc 加上刚体质量m乘以两平行转轴间距离d 的平方.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
n n \ 、 n
第2 圆 :t ‘ 2 n 墨 f 1 个 环 R 兀 , l n ; r
第3 圆 : 个 环
第 个 环 圆 :
2 兀
× 1 f ;
2 一 f J 兀n n \ n R n
薄圆 转 量为 盘的 动惯
, = 1+ z ) (+ n等(3…, +3 23 ) : 等( : - 芋+ 詈
, ,… ・
,
㈩
等幂 自然 数列求 和 公式 是通 过式 ( ) 2 进行 推导得 到 的
Zi= n c + G + A + n+ h一 …+ n H
i1 =
一
( 2)
般将前几项 自然数代入 ,得到一组方程组 ,解得未知参数再进行整理即可.
2 典型例题 分析
第3 0卷
21 年 00
第2 期
3月
高 师 理 科 学 刊
J u n l f S in e o a h r Colg a d ie st o r a o ce c fTe c es le e n Unv riy
V0 . 0 No2 13 . Ma . r 20l 0
第 3 卷 O
参 考文献 :
【 1 】唐淑红 .对学生求球壳、球体转动惯量计算 中的错解分析 [.湖南人文科技学 院学报 ,20 2) 4 — 4 J ] 0 9( :16 17
文 章编号 :10 — 8 2 1 07 9 3 1( 0 0)0 — 1 2 0 2 00 —3
规则 刚体转动惯量 的初 等计算方法
尹社会 ,皮小力
( 河南 工业 职业技 术学 院 基础科 学教 学部 ,河南 南 阳 4 30 ) 70 9
摘要:根据高职学生的数学基础较差的实际情况,通过初等数 学中 数列的灵活运用计算规则刚体 转动惯量,可以回避计算中要用到的微积分知识,使 学生更容 易明白刚体转动惯量的物理意义 。 并收到 了很好的教学效果.这一尝试对提 高大学物理教学水平具有一定的积极作用. 关键 词 :转动 惯量 ;数 列 ;刚体 中图分类 号 :O 1. 3 33 文献标 识 码 :A d i 036 /i n10— 8 1 000 . 9 o:1. 9 .s. 7 93 . 1. 0 9 js 0 2 22 般情况下,刚体的转动惯量都是通过实验方法 ( 如恒力矩转动法 、三线摆法等 ) 得到.对于规则形 状的刚体 ,可 以通过数学方法计算得到 ,但是 ,计算 中往往要用到微积分运算Ⅲ .由于数学课程和物理课
21 细棒 绕轴线 的 转动惯 量 . 例 1 设细 棒 的长为 L,质量 为 m ,且 质量 分布 是均匀 的 ,设 轴线 与
棒垂直 ( 见图 1 口 ) .
将 细棒 均匀 分成 2l , 每份 质量 为 .- 且 可 以看作质 点 ,运用对 ,份 则 = m _
,
o
n
称性分析可知 ,只需计算 右边 即可.若 以 0为起点 ,第 f 份转动惯量 为
第2 期
尹社会 , : 等 规则 刚体转 动惯 量的初等计算方法
13 0
,∑ ∑‘ = i= = 2l‘ ∑ × 2 厶 筹 筹× 厶I -= - \ , “ - lL t1 I l H 由n∞所, . 于 ,以 = 事
2
L
i1 =
i1 =
6
1 × 2
所 ,= = 以 , 景 一)又 + o0故 = . , =, , , r =
第 1 圆环 : 个
r t R
பைடு நூலகம்
图 盘 轴 动 意 3圆 绕 转 示 图
解法 2 将薄圆盘分成厚度均匀的薄圆环 , 圆环对轴的转动惯量分别为 则
2 R R f 。 7一 c 1 ;
(nn ,+] + 三2 2
22 细 圆环 相对 转轴 的转 动惯 量 .
例 2 设细圆环的质量为 m , 环的半径为 R, 圆环质量均匀分 布,转轴通过圆环 中心且与环面垂直 ( 见图 2 H ) . 将圆环均匀分割成 等份 , 则每份质量为 , 且可以看作质点 , 由于对称性可以以任意位置为起点计算 ,第 i 份相对于转轴的转动
由 o所, 于 。 以= , 芋.
3 结论
在推导规则刚体转动惯量 的过程中,虽然用初等数学进行运算较为繁锁 ,但对没有积分基础的初学者 在物理概念的分析与深入理解方面更易于接受.因此 ,关于不用积分运算刚体转动惯量的研究对于提高刚 体力学的教学具有很重要的实际意义蚓 .
14 O
高 师 理 科 学 刊
图 1 细棒绕轴转动示意图
× L,以 ( j所
收稿 日期 :20 一 I2 0 9 I- 0
作者 简介 :尹社 会 (9 9 ) 17 一 ,男 ,河 南沈 丘人 ,助教 ,主要 从事 大学 物理教 学研 究 .E m i nky 2. l - a :h zn@16 Ol l C ̄
惯 量为 , :一 R2 m× ,所 以
n
图 2 圆环 绕轴 转动 示 意 图
, :
∑ 2 R n m
23 圆盘相对 转轴 的转 动惯 置 . 例 3 设 圆盘 的质 量 为 ,环 的半 径 为 R,圆环质量 均 匀分 布 , 轴 转 通 过 圆盘 中心 且与 盘 面垂直 ( 图 3)S 见 L J .
一
程的安排可能并不吻合 ,而且高职学生的数学基础较差 ,这就给学生带来理解上的困难.通过初等数学中 数列的灵活运用计算规则刚体转动惯量,可以回避计算 中要用到的微积分知识 , 使学生更容易明白刚体转 动惯量 的物 理意义 .
1 等幂 自然数列求和公式
有一类等幂 自然数列 ,其求和公式为
n
解法 1 将 圆盘分成 , l 份等厚度 的圆环( 中心是小圆盘 , 半径为Rn) / ,
则 f小 环 半 平 近 为 f喾 / +)对 于 第个 圆 的 径 方 似 亏 \厶 】 : 二 ‘,应 转
轴 的转动 惯量 为
× 。 I景 ) 兀 ) 。 磅 ) =
