2018年最新湘教版九年级数学上册《第4章锐角三角函数》单元测试题含答案
2017-2018学年度第一学期湘教版九年级数学上册_第四章_锐角三角函数_单元检测试题【有答案】

2017-2018学年度第一学期湘教版九年级数学上册_第四章_锐角三角函数_单元检测试题【有答案】1 / 82017-2018学年度第一学期湘教版九年级数学上册第四章 锐角三角函数 单元检测试题考试总分: 120 分 考试时间: 120 分钟学校:__________ 班级:__________ 姓名:__________ 考号:__________一、选择题(共 10 小题 ,每小题 3 分 ,共 30 分 )1. 的值等于( )A. B.C. D. 2.如图, 中, , ,则A. B. C. D.3.如图,某地修建高速公路,要从 地向 地修一座隧道( 、 在同一水平面上).为了测量 、 两地之间的距离,某工程师乘坐热气球从 地出发,垂直上升 到达 处,在 处观察 地的俯角为 ,则 、 两地之间的距离为( )A.B. C. D. 4.若 ,则下列结论正确的为( )A. B. C. D.5.如图,一艘海轮位于灯塔 的北偏东 方向,距离灯塔 为 海里的点 处,如果海轮沿正南方向航行到灯塔的正东方向 处,那么海轮航行的距离 的长是( )A. 海里B. 海里C. 海里D. 海里6.已知: 则A. B. C. D.7.如图,已知正方形 的边长为 ,如果将线段 绕着点 旋转后,点 落在 的延长线上的 处,那么 等于( )A. B. C. D.8.在中,是斜边上的高线,已知的正弦值是,则的值是()A. B. C. D.9.如图,是旗杆的一根拉线,测得米,,则拉线的长为()A.米B.米C.米D.米10.一人乘雪橇沿坡比的斜坡笔直滑下,滑下的距离与时间间的关系为,若滑到坡底的时间为,则此人下降的高度为()A. B. C. D.二、填空题(共 10 小题,每小题 3 分,共 30 分)11.如果为锐角,且,那么________.12.等腰一腰上的高为,这条高与底边的夹角为,则的面积是________.13.中,为锐角,,,,则的面积是________.14.在中,,,则________,________.15.如图,某海防哨所发现在它的北偏西,距离为的处有一艘船,该船向正东方向航行,经过到达哨所东北方向的处,则该船的航速为每小时________.(精确到)2017-2018学年度第一学期湘教版九年级数学上册_第四章_锐角三角函数_单元检测试题【有答案】16.已知传送带与水平面所成斜坡的坡度,如果它把物体送到离地面米高的地方,那么物体所经过的路程为________米.17.一个人从山沿的山坡登上山顶,他走了米,则这座山的高度是________.18.如图,在离地面高度处引拉线固定电线杆,拉线和地面成角,那么拉线的长约为________.(精确到)19.如图所示,太阳光线与地面成角,一棵倾斜的大树与地面成角,这时测得大树在地面上的影子约为米,则大树的高约为________米.(保留根号)20.如图,某同学用一个有角的直角三角板估测学校旗杆的高度,他将角的直角边水平放在米高的支架上,三角板的斜边与旗杆的顶点在同一直线上,他又量得、的距离为米,则旗杆的高度约为________米(精确到米,取).三、解答题(共 6 小题,每小题 10 分,共 60 分)21.观察下列等式:①,;②,;③,.根据上述规律,计算________.计算:.22.如图,一艘渔船正自西向东航行追赶鱼群,在处望见岛在船的北偏东方向,前进海里到达处,此时望见岛在船的北偏东方向,以岛为中心的海里内为军事演习的危险区.请通过计算说明:如果这艘渔船继续向东追赶鱼群是否有进入危险区的可能.(参考数据:,)3 / 823.如图,某学校的教室点东边的处有一个货物中转站,过点沿北偏西方向有一条公路,假定运货车辆产生的噪音影响范围在以内,试通过计算说明这条公路上车辆的噪音是否对学校有影响?若有影响,计划在公路边修筑一段消音墙,请你计算出消音墙的长度.24.如图,飞机于空中处探测到地面目标,此时飞行高度米,从飞机上看地平面控制点的俯角,求飞机到控制点的距离.(精确到米:参考数据,,,)25.如图,在一个坡角为的斜坡上有一棵树,树高米.当太阳光与水平线成角时,该树在斜坡上的树影恰好为线段,求树影的长.(结果保留一位小数)(参考数据:,,,,,,,)2017-2018学年度第一学期湘教版九年级数学上册_第四章_锐角三角函数_单元检测试题【有答案】26.在搜索马航的行动中,我国搜救船以海里/小时的速度由西向东进行搜寻,在处看见小岛在船的北偏东方向,分钟后,搜救船行至处,此时看见小岛在船的北偏东方向,已知以小岛为中心周围海里以内为珊瑚礁危险区,问这艘搜救船继续向东航行,是否有进入危险区的可能?(参考数据:…,…)5 / 8答案1.A2.A3.A4.B5.C6.D7.B8.D9.D10.C11.12.13.14.15.16.17.米18.19.20.21.解: ∵根据已知的式子可以得到,∴ ;.22.解:过点作,交延长线于点.由题意可知,2017-2018学年度第一学期湘教版九年级数学上册_第四章_锐角三角函数_单元检测试题【有答案】在中,,,∴ ,.在中,,∴(海里).∵,∴这艘渔船继续向东航行追赶鱼群不会进入危险区.23.解:过作于点.在中,∵ ,,∴.∵ ,∴学校会受影响.以为圆心,为半径画圆,交于点和.在中,,∴ ,即是说车辆在范围内行驶会对学校产生影响,所以消音墙要修筑在.24.解:根据题意可得:米,;则米.故飞机到控制点的距离约米.25.树影的长约为米.26.解:作轴,垂足为.设海里,∵ ,∴ 海里,又∵海里,在中,,即,∴海里海里,∴这艘搜救船继续向东航行,有进入危险区的可能.7 / 8。
【初中数学】2018秋季学期最新湘教版初中数学九年级上册精品习题:单元测试(四) 锐角三角函数

3.计算sin30°·tan45°的结果是A. B. C. D.4.如图,为了绿化荒山,某地打算从位于山脚下的机井房铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌,现测得斜坡与水平面所成角的度数是么需要准备的水管的长为5.如图,AC是电杆的一根拉线,测得AC的长为( )6.在△ABC中,∠C=90°,A. B. C. D.7.如图,某水库堤坝横断面迎水坡长度是50 m,则堤坝高A.30 mB.40 mC.50 mD.60 m8.如图,在塔AB从C点向塔底B走的高为(D)A.50米B.100二、填空题(本大题共9.在Rt△ABC中,∠C=90°,如果10.如图,△ABC12.在△ABC13.长为4 m如图所示14.如图,在高度是30°,底部米(结果可保留根号三、解答题(共15.(12分)计算下列各题:(1)tan45°(2)6sin230°+sin45°tan30°.16.(10分)如图,CD是Rt△ABC斜边上的高,AC=4,BC=3,求cos∠BCD.17.(12分)如图,在Rt△ABC中,∠C=90°,BC=8,tanB=,点D在BC上,且BD=AD.求AC的长和cos∠ADC的值.1 218.(12分)如图,放置在水平桌面上的台灯的灯臂AB长为40 cm,灯罩BC长为30 cm,底座厚度为2 cm,灯臂与底座构成的∠BAD=60°.使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?(结果精确到0.1 cm,参考数据:≈1.732)319.(12分)我市某中学在创建“特色校园”的活动中,将本校的办学理念做成宣传牌AB,放置在教学楼的顶部(如图所示).小明在操场上的点D处,用1米高的测角仪CD,从点C测得宣传牌的底部B的仰角为37°,然后向教学楼正方向走了4米到达点F处,又从点E测得宣传牌的顶部A的仰角为45°.已知教学楼高BM=17米,且点A,B,M在同一直线上,求宣传牌AB 的高度(结果精确到0.1米,参考数据:≈1.73,sin37°≈0.60,cos37°≈0.81,tan37°≈0.75).3参考答案1.A2.D3.A4.D5.D6.C7.A8.D9. 10. 11. 11.9 12. 13.2(-) 14.(7+21) 4555532315.(1)原式=1-×=1-=.32323414 (2)原式=+×=.642233561216.在Rt △ABC 中,AB ==5.222243AC BC +=+∵∠B+∠A =90°,∠B+∠BCD =90°,∴∠BCD =∠A ,∴cos ∠BCD =cos ∠A =ACAB =.4517.∵在Rt △ABC 中,BC=8,tanB=,∴AC=4.12设AD=x ,则BD=x ,CD=8-x ,由勾股定理,得 (8-x)2+42=x2.解得x=5.。
第4章 锐角三角函数数学九年级上册-单元测试卷-湘教版(含答案)

第4章锐角三角函数数学九年级上册-单元测试卷-湘教版(含答案)一、单选题(共15题,共计45分)1、下列计算结果正确的是()A. B. C. D.2、在Rt△ABC中,∠C = 90°,∠A、∠B、∠C所对的边分别为a、b、c,下列等式中不成立的是()A. B. C. D.3、如图,△ABC中AB=AC=4,∠C=72°,D是AB中点,点E在AC上,DE⊥AB,则cosA的值为()A. B. C. D.4、如图,以圆O为圆心,半径为1的弧交坐标轴于A,B两点,P是弧上一点(不与A,B重合),连接OP,设∠POB=α,则点P的坐标是( )A.(sinα,sinα)B.(cosα,cosα)C.(cosα,sinα) D.(sinα,cosα)5、在Rt△ABC中,∠C=90°,BC=4 ,AB=6,则cosA的值为()A. B.2 C. D.6、如图2所示,已知⊙O的半径为5cm,弦AB的长为8cm,P是AB延长线上一点,BP=2cm,则tan∠OPA等于()A. B. C.2 D.7、如图,有一轮船在A处测得南偏东30°方向上有一小岛F,轮船沿正南方向航行至B 处,测得小岛F在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛F在正东方向上,则A,B之间距离是( )A.10 海里B.(10 -10)海里C.10海里D.(10 -10)海里8、如图为一节楼梯的示意图,BC⊥AC,∠BAC=α,AC=6米。
现要在楼梯上铺一块地毯,楼梯宽度为1米,则地毯的面积至少需要( )平方米。
A.6tanα+6B. +6C.D.9、如图,小明从A处出发沿北偏东60°方向行走至B处,又沿北偏西20°方向行走至C 处,此时需把方向调整到与出发一致,则方向的调整应是()A.右转80°B.左转80°C.右转100°D.左转100°10、如图,AB是⊙O的直径,且经过弦CD的中点H,已知cos∠,BD=5,则OH的长为()A. B.1 C. D.11、如图,线段是的直径,为上两点,如果,那么的度数是( )A.15°B.30°C.45°D.60°12、小明在某次投篮中刚好把球打到篮板的点D处后进球,已知小明与篮框底的距离BC=5米,眼睛与地面的距离AB=1.7米,视线AD与水平线的夹角为∠α,已知tanα=,则点D到地面的距离CD是()A.2.7米B.3.0米C.3.2米D.3.4米13、如图,为了加快开凿隧道的施工进度,要在小山的两端同时施工.在上找一点,取,要使成一直线,那么开挖点离点的距离是( )A. B. C. D.14、△ABC中,∠B=90°,AC= , tan∠C=,则BC边的长为()A.2B.2C.D.415、在Rt△ABC中,∠C=90°,则是∠A的()A.正弦B.余弦C.正切D.以上都不对二、填空题(共10题,共计30分)16、在正方形网格中,△ABC的位置如图所示,则cosB的值为 ________ .17、在Rt△ABC中,∠C=90°,若AB=4,sinA= ,则斜边AB边上的高CD的长为________.18、如图,为了测量“四川大渡河峡谷”石碑的高度,佳佳在点C处测得石碑顶A点的仰角为,她朝石碑前行5米到达点D处,又测得石顶A点的仰角为,那么石碑的高度的长________米.(结果保留根号)19、用科学计算器计算:8cos31°+=________20、如图,在Rt△ABC中,∠ABC=90°,∠ACB=30°,AC=6,现将Rt△ABC绕点A顺时针旋转30°得到△AB'C’,则图中阴影部分面积为________.21、在△ABC中,∠C=90°,若tanA= ,则sinB=________.22、一直角三角形中,斜边与一直角边的比是13:12,最小角为α,则sinα=________,cosα=________,tanα=________.23、如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知折痕AE=5 cm,且tan∠EFC= ,那么矩形ABCD的周长为________cm.24、如图,已知sinO=,OA=6,点P是射线ON上一动点,当△AOP为直角三角形时,则AP=________.25、如图,△ABC为等边三角形,点D、E分别在AC、AB上,且AD=BE,连接BD、CE交于点P,在△ABC外部作∠ABF=∠ABD,过点A作AF⊥BF于点F,若∠ADB=∠ABF+90°,BF﹣AF=3,则BP=________.三、解答题(共5题,共计25分)26、计算:|﹣2|+(π﹣2017)0﹣4cos60°+ .27、如图,从热气球P上测得两建筑物A、B的底部的俯角分别为45°和30°,如果A、B 两建筑物的距离为60米,P点在地面上的正投影恰好落在线段AB上,求热气球P的高度.(结果保留根号)28、如图正方形OABC的边长等于2,且AO边与x轴正半轴的夹角为60º,O为原点坐标,求点B的坐标.29、我校举行开学仪式,为了更好的掌控时间,学校礼仪队小明同学现场进行了如下测量操作:小明同学在教学楼距地面9米高的窗口C处,测得正前方旗杆顶部A点的仰角为37°,旗杆底部B点的俯角为45°,升旗时,国旗上端悬挂在距地面2.25米处,若国旗随国歌声冉冉升起,并在国歌播放30秒结束时到达旗杆顶端,则国旗应以多少米/秒的速度上升?(参考数据:,,)30、如图,⊙O的直径AB=10,CD是⊙O的弦,AC与BD相交于点P.(1) 设∠BPC=α,如果sinα是方程5x2-13x+6=0的根,求cosα的值;(2) 在(1)的条件下,求弦CD的长.参考答案一、单选题(共15题,共计45分)1、C2、D3、C4、C5、A6、D7、D8、A9、A10、A11、B12、C13、B14、B15、B二、填空题(共10题,共计30分)17、18、19、20、21、22、23、24、25、三、解答题(共5题,共计25分)26、30、。
湘教版九年级数学上册第4章《锐角三角函数》单元复习测试题(含答案)

湘教版九年级数学上册第4章《锐角三角函数》单元复习测试题(时间:90分钟 满分100分)一、选择题(每小题3分,共30分)1.如图,在Rt△ABC 中,∠C=90°,AC=3,AB=5,则cosB 的值为( )第1题图 第2题图A. B. C. D. 2.如图,将∠AOB 放置在5×5的正方形网格中,则tan∠AOB 的值是( ) A. B. C.D.3.在直角三角形中,各边的长度都扩大3倍,则锐角A 的三角函数值 ( )A 也扩大3倍B 缩小为原来的31C 都不变D 有的扩大,有的缩小 4.△ABC 中,a 、b 、c 分别是∠A、∠B、∠C 的对边,如果a 2+b 2=c 2,那么下列结论正确的是( )A .bcosB=cB .csinA=aC .atanA=bD .5.在△ABC 中,(2cosA -2)2+|1-tanB|=0,则△ABC 一定是( ) A .直角三角形 B .等腰三角形 C .等边三角形 D .等腰直角三角形6.如图,要测量小河两岸相对的两点P ,A 的距离,可以在小河边取PA 的垂线PB 上的一点C ,测得PC=100米,∠PCA=35°,则小河宽PA 等于( )第6题图 第7题图A .100sin35°米B .100sin55°米C .100tan35°米D .100tan55°米 7.如图,A 、B 、C 是小正方形的顶点,且每个小正方形的边长为1,则tan ∠BAC 的值为( ) A .B .1C .D .8.如图,热气球的探测器显示,从热气球A 看一栋楼顶部B 的仰角为30°,看这栋楼底部C 的俯角为60°,热气球A 与楼的水平距离为120米,这栋楼的高度BC 为( )A .160米B .(60+160)C .160米D .360米第8题图第10题图 9.在△ABC 中,AB =122,AC =13,cos B =22,则BC 边长为( ) A .7 B .8 C .8或17 D .7或1710.小明利用测角仪和旗杆的拉绳测量学校旗杆的高度.如图,旗杆PA 的高度与拉绳PB 的长度相等.小明将PB 拉到PB′的位置,测得∠PB′C=α(B′C 为水平线),测角仪B′D 的高度为1米,则旗杆PA 的高度为( ) A.11-sin α B.11+sin α C.11-cos α D.11+cos α二、填空题(每小题3分,共24分) 11.﹣13+﹣12sin30°=________.12.如图,当小杰沿坡度i=1:5的坡面由B 到A 行走了26米时,小杰实际上升高度AC 为 米.(可以用根号表示)第12题图 第13题图13.如图,在△ABC 中,∠ACB=90°,CD⊥AB 于D ,若AC=4,AB=5,则cos∠BCD 的值为________. 14.如图,为了测量楼的高度,自楼的顶部A 看地面上的一点B ,俯角为30°,已知地面上的这点与楼的水平距离BC 为30m ,那么楼的高度AC 为 m (结果保留根号).第14题图第18题图15.已知α为锐角,且cos(90°-α)=12,则α= .16.在△ABC 中,∠C=90°,若tanA=,则sinB= . 17.已知△ABC 中,AB=10,AC=2,∠B=30°,则△ABC 的面积等于 .18.如图,在菱形ABCD 中,AE⊥BC,E 为垂足,若cosB=,EC=2,P 是AB 边上的一个动点,则线段PE 的长度的最小值是 . 三.简答题(共46分) 19.(9分)(1)计算:6tan230°﹣sin60°﹣2sin45°(2)22sin45°+sin60°·cos45°.20.(9分)在△ABC中,∠B、∠C 均为锐角,其对边分别为b、c,求证:=.21.(9分)如图,在△ABC中,BC=12,tanA=,∠B=30°;求AC和AB的长.22.(9分)我国海域辽阔,渔业资源丰富.如图,现有渔船B在海岛A,C附近捕鱼作业,已知海岛C位于海岛A的北偏东45°方向上.在渔船B上测得海岛A位于渔船B的北偏西30°的方向上,此时海岛C恰好位于渔船B的正北方向18(1+)海里处,则海岛A,C之间的距离为多少海里.23. (10分)甲、乙两楼相距45米,从甲楼顶部观测乙楼顶部的俯角为30°,观测乙楼的底部的俯角为45°,试求两楼的高.答案一、选择题 1 2 3 4 5 6 7 8 9 10 B B CBD C B CDA 二、填空题11 121314 15 1617 18 -51030°15或104.819.解:(1)6tan 230°﹣sin60°﹣2sin45°==﹣.300 450Ar E D BC(2)22sin45°+sin60°·cos45°. 解:原式=22×22+32×22=2+64. 20.证明:过A 作AD ⊥BC 于D ,在Rt △ABD 中,sinB=,∴AD=ABsinB ,在Rt △ADC 中,sinC=,∴AD=ACsinC ,∴ABsinB=ACsinC ,而AB=c ,AC=b ,∴csinB=bsinC ,∴=.21.解:如图作CH ⊥AB 于H .在Rt △BCH 中,∵BC=12,∠B=30°,∴CH=BC=6,BH==6,在Rt △ACH 中,tanA==,∴AH=8,∴AC==10,∴AB=AH+BH=8+6.22.解:作AD ⊥BC 于D , 设AC=x 海里,在Rt △ACD 中,AD=AC ×sin ∠ACD=x ,则CD=x ,在Rt △ABD 中,BD=x ,则x+x=18(1+),解得,x=18, 答:A ,C 之间的距离为18海里.23.解:解过D 做DE ⊥AB 于E ∵∠MAC=45° ∴∠ACB=45° BC=45在Rt ΔACB 中,BCAB tgACB =)(4545米=⋅=∴ tg BC AB在Rt ΔADE 中,∠ADE=30°DEAE tgADE =315334530=⋅=⋅=∴tg DE AE )(31545米-=-=∴AE AB CD答:甲楼高45米,乙楼高31545-米。
湘教版九年级数学上册第4章《锐角三角函数》检测试卷(含答案)
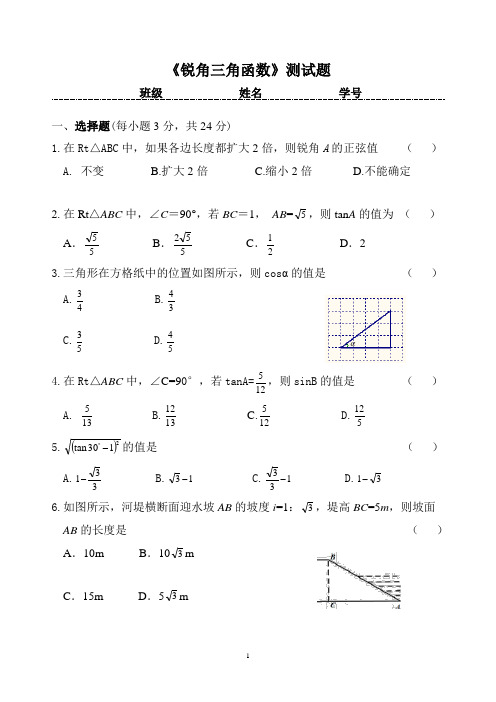
《锐角三角函数》测试题班级 姓名 学号一、选择题(每小题3分,共24分)1.在Rt △ABC 中,如果各边长度都扩大2倍,则锐角A 的正弦值 ( ) A. 不变 B.扩大2倍 C.缩小2倍 D.不能确定2.在Rt △ABC 中,∠C =90°,若BC =1, AB =5,则tan A 的值为 ( ) A .55 B .552 C .21D .2 3.三角形在方格纸中的位置如图所示,则cos α的值是 ( ) A.43 B.34C.53 D.544.在Rt △ABC 中,∠C=90°,若tanA=125,则sinB 的值是 ( ) A.135 B.1312 C.125 D.5125.()2130tan -︒的值是 ( ) A.331-B.13-C.133- D.31- 6.如图所示,河堤横断面迎水坡AB 的坡度i =1:3,堤高BC =5m ,则坡面AB 的长度是 ( ) A .10m B .103mC .15mD .53m7.如图,在Rt △ABC 中,∠ACB =90°,CD ⊥AB ,垂足为D .若AC =5,BC =2,则sin ∠ACD 的值为 ( )A .32B .552 C .25 D .358.将矩形纸片ABCD 按如图所示的方式折叠,AE 、EF 为折痕,∠BAE =30°,AB=3,折叠后,点C 落在AD 边上的C 1处,并且点B 落在EC 1边上的B 1处. 则BC 的长为 ( )A.3 B .2C .3D .32二、填空题(每小题3分,共30分)9.在Rt △ABC 中,∠C =90°,∠A ,∠B ,∠C 的对边分别为a ,b ,c ,则sinB= .10.在Rt △ABC 中,∠C =90°,∠A =60°,BC=3,则AC= . 11. 计算:︒︒︒︒+60604530tan sin tan cos = . 12. 如果α是锐角,且tan α=1,那么α= . 13. 在△ABC 中,∠A ,∠B 为锐角,sin A =21,tan B =33,则△ABC 的形状 为 .14. 如图,在菱形ABCD 中,D E ⊥AB ,垂足为E ,DE =6, sin A =53,则菱形ABCD 的周长是 .15.等腰三角形腰长为2cm ,底边长为23cm ,则顶角为 .16.边长为a 的等边三角形的高是 .17.在Rt △ABC 中,∠C =90°,BC=12,43=A tan ,则AB= . 18.如图,在平面直角坐标系中,已知点A(2,4), 连接OA ,则OA 与x 轴所成的锐角α的正弦值 为 .三、解答题(第19和20题每题8分,其余每题10分,共46分) 19. 计算:(1)186********+-+︒︒︒tan cos sin ;(2)()()2201452303-143-2-++︒︒sin tan .π20.如图,AD 是△ABC 的中线,31tan =B ,22cos =C ,2=AC .求: (1)BC 的长; (2)ADC ∠sin 的值.AB CD21.如图,某校数学兴趣小组的同学在测量建筑物AB 的高度时,在地面的C 处测得点A 的仰角为45°,向前走20米到达D 处,在D 处测得点A 的仰角为60°,求建筑物AB 的高度(得数保留根号).22.如图,在Rt △ABC 中,∠C =90°,∠A ,∠B ,∠C 的对边分别为a,b,c, (1)直接写出sinA 与cosB 的关系式; (2)求证:122=+B sin A sin ;(3)请你运用上述结论解决问题:在Rt △ABC 中,∠C =90°,135cos =B ,求B s i n 的值.45° 60°ABDCABabc23. 如图,一艘海监船位于灯塔P的东南方向,距离灯塔200海里的A处。
湘教版九年级上册数学第四章 锐角三角函数单元测试题(含答案)

第四章单元检测卷[时间:90分钟分值:150分]一、选择题(每小题4分,共40分)1.如图,在△ABC中,∠C=90°,AB=13,BC=5,则sin A的值是()A.513 B.1213 C.512 D.1352.身高相同的三个小朋友甲、乙、丙放风筝,他们放出的线长分别为300 m,250 m,200 m,线与地面所成的角度分别为30°,45°,60°(假设风筝线是拉直的),则三人所放风筝()A.甲的最高B.乙的最高C.丙的最高D.乙的最低3.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D.若AC=6,BC=2,则sin∠ACD的值为()A.155 B.255 C.52 D.62第3题图第4题图4.如图,△ABC的顶点是正方形网格的格点,则sin B的值为()A.12 B.22 C.32D.15.在Rt△ABC中,∠C=90°,已知cos A=35,那么tan A等于()A.43 B.34 C.45 D.546.如图,为测量河两岸相对的两电线杆A,B之间的距离,在距A点16 m 的C处(AC⊥AB)测得∠ACB=52°,则A,B两点间的距离为()A.16sin 52° m B.16cos 52°m C.16tan 52° m D.16tan 52°m 7.如图,在水平地面上,由点A测得旗杆BC顶点C的仰角为60°,点A 到旗杆的距离AB=12 m,则旗杆的高度为()A.6 3 m B.6 m C.12 3 m D.12 m第7题图第8题图8.如图,一艘海轮位于灯塔P的北偏东55°方向,距离灯塔2海里的点A 处,如果海轮沿正南方向航行到灯塔的正东方向,海轮航行的距离AB长是()A.2海里B.2sin 55°海里C.2cos 55°海里D.2tan 55°海里9.若α,β都是锐角,且cos α>cos β,则下列式子正确的是()A.α>βB.sin α<sin βC.tan α>tan βD.以上式子都不正确10.如图,在△ABC中,AD⊥BC,垂足为点D,若AC=62,∠C=45°,tan ∠ABC=3,则BD等于()A.2 B.3 C.3 2 D.2 3二、填空题(每小题4分,共32分)11.计算:cos2 45°+tan 30°·sin 60°=_______.12.在△ABC中,∠C=90°,AB=10,BC=6,则sin A=________,tan B=___________.13.如图所示,河堤横断面迎水坡AB的坡比(指坡面的铅直高度BC与水平宽度CA的比)是1∶3,堤高BC=5 m,则坡面AB的长度是_________m.14.如图,已知Rt△ABC中,斜边BC上的高AD=4,cos B=45,则AC=________.15.在Rt△ABC中,∠C=90°,cos B=32,a=3,那么b=______.16.如图,在Rt△ABC中,∠C=90°,边AB的垂直平分线分别交边BC,AB于点D,E.如果BC=8,tan A=43,那么BD=________.,)17.如图,一渔船由西往东航行,在A点测得海岛C位于北偏东60°的方向,前进20海里到达B点,此时,测得海岛C位于北偏东30°的方向,则海岛C到航线AB的距离CD等于_________海里.,第17题图),第18题图) 18.如图,是将一正方体货物沿坡面AB装进汽车货厢的平面示意图,已知长方体货厢的高度BC为2.6米,斜坡AB的坡比为1∶2.4,现把图中的货物继续向前平移,当货物顶点D与C重合时,仍可把货物放平装进货厢,则货物的高度BD不能超过________米.三、解答题(共7小题,满分78分)19.(10分)计算:32sin 60°-2cos 45°-33tan 30°·cos 60°.20.(10分)如图,定义:在直角三角形ABC中,锐角α的邻边与对边的比叫作角α的余切,记作cot α=角α的邻边角α的对边=ACBC.根据上述角的余切的定义,解答下列问题:(1)cot 30°=___________;(5分)(2)如图,已知tan A=34,其中∠A为锐角,试求cot A的值.21.(10分)如图,在数学实践课中,小明为了测量学校旗杆CD的高度,在地面A处放置高度为1.5 m的测角仪AB,测得旗杆顶端D的仰角为32°,AC为22 m,求旗杆CD的高度.(结果精确到0.1,参考数据:sin 32°≈0.53,cos 32°≈0.85,tan 32°≈0.62)22.(10分)如图,在△ABC中,AD是BC边上的高,∠C=45°,sin B=1 3,AD=1,求BC的长.23.(12分)某日,正在我国南海海域作业的一艘大型渔船突然发生险情,相关部门接到求救信号后,立即调遣一架直升飞机和一艘刚好在南海巡航的渔政船前往救援.当飞机到达距离海面3 000 m的高空C处时,测得A处渔政船的俯角为60°,测得B处发生险情的渔船的俯角为30°,请问此时渔政船和渔船相距多远?(结果保留根号)24.(12分)如图,AD是△ABC的中线,tan B=13,cos C=22,AC= 2.求:(1)BC的长;(2)sin∠ADC的值.25.(14分)如图所示,建筑物AB后有一座假山,其坡度为i=1∶3,山坡上E点处有一凉亭,测得假山坡脚C与建筑物水平距离BC=25米,与凉亭距离CE=20米,某人从建筑物顶端测得E点的俯角为45°,求建筑物AB的高.参考答案[时间:90分钟分值:150分]一、选择题(每小题4分,共40分)1.A2.B3.A4.B 5.A 6.C7.C 8.C9.B 10.A【解析】∵AC=62,∠C=45°,AD⊥BC,∴AD=AC·sin 45°=62×22=6.∵tan ∠ABC=3,∴ADBD=3,∴BD=AD3=2.二、填空题(每小题4分,共32分)11.1 12.354313.1014.5【解析】∵△ABC为直角三角形,AD⊥BC于点D,∴∠BAD+∠CAD=90°,∠B+∠BAD=90°,∴∠CAD=∠B,∴cos B=cos ∠CAD=ADAC=45.又∵AD=4,∴AC=5.15.1 16.25 417.10 3【解析】根据题意可知∠CAD=30°,∠CBD=60°. ∵∠CBD=∠CAD+∠ACB,∴∠CAD=∠ACB=30°,∴AB=BC=20海里.在Rt△CBD中,∠BDC=90°,∠CBD=60°,∴sin 60°=CD BC,∴CD=BC·sin 60°=20×32=103海里.18.2.4三、解答题(共7小题,满分78分)19.解:原式=32×32-2×22-33×33×12(4分)=34-1-16(8分)=-512.(10分)20(1) 3解:(2)∵tan A=BCAC=34,∴cot A=ACBC=43.(10分)21.解:在Rt△DEB中,∠DEB=90°,BE=AC=22 m,tan 32°=DE BE,(5分)∴DE=BE·tan 32°≈22×0.62=13.64(m).(8分) ∵CE=AB=1.5 m,∴CD=CE+DE≈1.5+13.64≈15.1(m).答:旗杆CD的高度约为15.1 m.(10分)22.解:在Rt△ABD中,∵AD=1,∴sin B=ADAB=13,∴AB=3,(4分)∴BD=AB2-AD2=2 2.(6分)在Rt△ADC中,∵∠C=45°,∴CD=AD=1,(8分)∴BC=BD+CD=22+1.(10分)23.解:在Rt△CDA中,∠ACD=30°,CD=3 000 m,∴AD=CD·tan∠ACD=1 000 3 m.(4分)在Rt△CDB中,∠BCD=60°,∴BD=CD·tan∠BCD=3 000 3 m,(8分)∴AB=BD-AD=2 000 3 m.答:此时渔政船和渔船相距2 000 3 m.(12分)24.答图解:(1)如答图,过点A作AE⊥BC于点E.∵cos C=22,∴∠C=45°.(1分)在Rt△ACE中,CE=AC·cos C=1,∴AE=CE=1.(3分)在Rt△ABE中,tan B=13,即AEBE=13,∴BE=3AE=3,(5分)∴BC=BE+CE=4.(6分) (2)∵AD是△ABC的中线,∴CD=12BC=2,∴DE=CD-CE=1.(8分)∵AE⊥BC,DE=AE,∴∠ADC=45°,(10分)∴sin∠ADC=22.(12分)25.答图解:如答图,过点E作EF⊥BC于点F,EN⊥AB于点N.(2分) ∵假山的坡度为i=1∶3,∴设EF=x米,则FC=3x米.(4分)∵CE=20米,∴x2+(3x)2=400,解得x=10,则FC=103米.(8分)∵BC=25米,∴BF=NE=(25+103)米.(10分)∵∠AEN=45°,∴AN=EN=(25+103)米,(12分)∴AB=AN+BN=NE+EF=25+103+10=(35+103)米.答:建筑物AB的高为(35+103)米.(14分)。
2018年秋九年级数学上册第4章锐角三角函数复习题(新版)湘教版

第4章 锐角三角函数测试题类型之一 锐角三角函数1.2017·金华在Rt△ABC 中,∠C =90°,AB =5,BC =3,则tan A 的值是( ) A.34 B.43 C.35 D.452.如图4-X -1,在△ABC 中,∠B =90°,BC =2AB ,则cos A =( ) A.52 B.12 C.2 55 D.55图4-X -1图4-X -23.如图4-X -2,AD ,BE 分别是△ABC 中BC ,AC 边上的高,BE =4,BC =6,则sin∠DAC =________.4.在Rt△ABC 中,∠C =90°,tan B =43,△ABC 的周长为36,则AC =________.5.已知a ,b ,c 分别是△ABC 中∠A ,∠B ,∠C 所对的边,a ,b ,c 满足等式(2b )2=4(c +a )(c -a ),且5a -3c =0,求sin A +sin B 的值.类型之二 特殊角的三角函数值 6.在△ABC 中,(2cos A -2)2+|1-tan B |=0,则下面对△ABC 的形状描述最确切的是( )A .直角三角形B .等腰三角形C .等边三角形D .等腰直角三角形7.已知∠A 为锐角,且tan A =23,那么下列判断正确的是( )A .0<∠A <30° B.30°<∠A <45° C .45°<∠A <60° D.60°<∠A <90°8.计算:sin 260°+cos60°-tan45°=________. 9.求满足下列条件的锐角α的度数:(1)2cos α-2=0; (2)tan(α+10°)= 3.类型之三 解直角三角形及其几何应用10.在△ABC 中,∠C =90°,AB =10,cos A =45,则BC 的长为( )A .6B .7.5C .8D .12.511.如图4-X -3,若△ABC 和△DEF 的面积分别为S 1,S 2,则( )图4-X -3A .S 1=12S 2B .S 1=72S 2C .S 1=S 2D .S 1=85S 212.如图4-X -4,在梯形ABCD 中,AD ∥BC ,∠ADC =90°,∠B =30°,CE ⊥AB ,垂足为E .若AD =0.8,AB =2 3,求CE 的长.图4-X -4类型之四解直角三角形的实际应用13.河堤横断面如图4-X-5所示,堤高BC=6 米,迎水坡AB的坡度是1∶ 3,则AB的长是( )A.12米 B.4 3米C.5 3米 D.6 3米图4-X-5图4-X-614.如图4-X-6,沿AC方向开山修建一条公路,为了加快施工进度,要在山的另一边寻找点E同时施工,从AC上的一点B取∠ABD=150°,沿BD方向前进,取∠BDE=60°,测得BD=520 m,BC=80 m,并且AC,BD和DE在同一平面内,那么公路CE段的长度为( ) A.180 m B.260 3 mC.(260 3-80)m D.(260 2-80)m15.如图4-X-7,小俊在A处利用高为1.5米的测角仪AB测得楼EF的顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.(结果精确到0.1米)16.2017·岳阳某太阳能热水器的横截面示意图如图4-X-8所示,已知真空热水管AB 与支架CD所在直线相交于点O,且OB=OD,支架CD与水平线AE垂直,∠BAC=∠CDE=30°,DE=80 cm,AC=165 cm.(1)求支架CD的长(结果保留根号);(2)求真空热水管AB的长(结果保留根号).图4-X-8类型之五数学活动17.如图4-X-9,有两条公路OM,ON相交成30°角,沿公路OM方向离O点80米处有一所学校A,当重型运输卡车P沿公路ON方向行驶时,在以点P为圆心、50米长为半径的圆形区域内都会受到卡车噪声的影响,且卡车P与学校A的距离越近噪声影响越大.若已知重型运输卡车P沿公路ON方向行驶的速度为18千米/时.(1)求对学校A的噪声影响最大时卡车P与学校A的距离;(2)求卡车P沿公路ON方向行驶一次给学校A带来噪声影响的时间.图4-X-9详解详析1.A [解析] 由勾股定理,得AC =AB 2-BC 2=4,则tan A =BC AC =34.2.D [解析] ∵∠B =90°,BC =2AB , ∴AC =AB 2+BC 2=AB 2+(2AB )2=5AB , ∴cos A =AB AC=AB 5AB =55.故选D. 3.53[解析] ∵AD ,BE 分别是△ABC 中BC ,AC 边上的高,∴∠BEC =∠ADC =90°,∴∠CBE =∠DAC .∵∠BEC =90°,BE =4,BC =6,∴CE =2 5, ∴sin∠EBC =53,∴sin∠DAC =53. 4.125.解:∵(2b )2=4(c +a )(c -a ),∴4b 2=4(c 2-a 2),∴b 2=c 2-a 2,∴a 2+b 2=c 2,∴△ABC 为直角三角形,且∠C =90°.∵5a -3c =0,∴a c =35,∴sin A =35.设a =3k ,c =5k (k >0), 则b =(5k )2-(3k )2=4k ,∴sin B =b c =4k 5k =45,∴sin A +sin B =35+45=75.6.D [解析] 由(2cos A -2)2+|1-tan B |=0,得2cos A -2=0,1-tan B =0, ∴∠A =45°,∠B =45°, 则△ABC 是等腰直角三角形. 故选D. 7.B [解析]33<23<1,由正切函数随锐角的增大而增大,得tan30°<tan A <tan45°,即30°<∠A <45°.故选B.8.14 [解析] 原式=(32)2+12-1 =34+12-1 =14. 9.解:(1)∵2cos α-2=0,∴2cos α=2, ∴cos α=22,∴α=45°. (2)∵tan(α+10°)=3,∴α+10°=60°, ∴α=50°.10.A11.C [解析] 过点A 作AG ⊥BC 于点G ,过点D 作DH ⊥EF 于点H .在Rt△ABG 中,AG =AB ·sin40°=5sin40°.在Rt△DHE 中,∠DEH =180°-140°=40°,DH =DE ·sin40°=8sin40°.因为S 1=12×8×5sin40°=20sin40°,S 2=12×5×8sin40°=20sin40°,所以S 1=S 2.故选C.12.解:过点A 作AH ⊥BC 于点H ,则AD =HC =0.8. 在Rt△ABH 中,∠B =30°,AB =2 3, cos B =BH AB,∴BH =AB cos30°=2 3×32=3, ∴BC =BH +HC =3.8. ∵CE ⊥AB ,∠B =30°, ∴CE =12BC =1.9.13.A14.C [解析] 因为∠DBE =180°-∠ABD =180°-150°=30°,∠BDE =60°,所以∠E =180°-∠DBE -∠BDE =180°-30°-60°=90°.在Rt△BDE 中,sin∠BDE =BE BD,即sin60°=BE 520,所以BE =520×sin60°=520×32=260 3(m),所以CE =BE -BC =(260 3-80)m.15.解:如图,连接BD 并延长交EF 于点G ,依题意得:EF ⊥AF ,DC ⊥AF ,BA ⊥AF ,BD ⊥EF ,则四边形GFCD ,DCAB ,GFAB 均为矩形.设楼EF 的高为x 米,可得EG =EF -GF =(x -1.5)米. 在Rt△EGD 中,DG =EG tan∠EDG=33(x -1.5)米. 在Rt△EGB 中,BG =EGtan∠EBG=3(x -1.5)米,∴CA =DB =BG -DG =2 33(x -1.5)米.∵CA =12米,∴2 33(x -1.5)=12,解得x =6 3+1.5≈11.9. 故楼EF 的高度约为11.9米.16.解:(1)在Rt△CDE 中,∠CDE =30°,DE =80 cm , ∴CD =80×cos30°=80×32=40 3(cm). (2)在Rt△OAC 中,∠BAC =30°,AC =165 cm , ∴OC =AC ×tan30°=165×33=55 3(cm), ∴OD =OC -CD =55 3-40 3=15 3(cm),∴AB =AO -OB =AO -OD =55 3×2-15 3=95 3(cm). 17.解:(1)过点A 作ON 的垂线段,交ON 于点P ′,如图①. 在Rt△AOP ′中,∠AP ′O =90°,∠P ′OA =30°,OA =80米, 所以AP ′=80×sin30°=80×12=40(米),即对学校A 的噪声影响最大时卡车P 与学校A 的距离是40米.(2)以A 为圆心、50米长为半径画弧,交ON 于点D ,E ,如图②. 在Rt△ADP ′中,∠AP ′D =90°,AP ′=40米,AD =50米, 所以DP ′=AD 2-AP ′2=502-402=30(米). 同理可得EP ′=30米,所以DE =60米. 又18千米/时=5米/秒, 所以605=12(秒),即卡车P 沿公路ON 方向行驶一次给学校A 带来噪声影响的时间为12秒.。
第4章 锐角三角函数数学九年级上册-单元测试卷-湘教版(含答案)

第4章锐角三角函数数学九年级上册-单元测试卷-湘教版(含答案)一、单选题(共15题,共计45分)1、使有意义的锐角x的取值范围是()A.x=45°B.x≠45°C.45°<x<90°D.0°<x<45°2、如图所示,菱形ABCD中,AB=2,∠A=120°,点P,Q,K分别为线段BC,CD,BD上任意一点,则PK+QK的最小值为( )A.1B.C.2D. +13、cos60°的值等于()A.1B.C.D.4、如图,OA=4,线段OA的中点为B,点P在以O为圆心,OB为半径的圆上运动,PA的中点为Q.当点Q也落在⊙O上时,cos∠OQB的值等于()A. B. C. D.5、在Rt△ABC中,∠C=90°,sinA=,则tanA的值为()A. B. C. D.6、一副三角板按图所示的位置摆放,将△DEF绕点A(F)逆时针旋转60°后,测得CG=10cm,则两个三角形重叠(阴影)部分的面积为( )A.75cm 2B.25 cm 2C.(25+)cm 2D.(25+)cm 27、如图,在菱形ABCD中,DE⊥AB,cosA=,BE=2,则tan∠DBE的值()A. B.2 C. D.8、如图,在Rt△ABC中,∠ACB=90°,CD⊥AB于点D ,如果AC=3,AB=6,那么AD的值为()A. B. C. D.9、如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,则sinB的值等于()A. B. C. D.10、如图,△ABC是锐角三角形,sinC= ,则sin A的取值范围是( )A.0<sinA<B. <SinA<1C. <sinA<D. <sinA<111、如图,巳知A点坐标为(5,0),直线y=x+b(b>0)与y轴交于点B,连接AB,∠α=75°,则b的值为()A.3B.C.4D.12、如图,延长RT△ABC斜边AB到点D,使BD=AB,连接CD,若tan∠BCD=,则tanA=()A. B.1 C. D.13、已知锐角A的tanA<,则锐角A的取值范围是()A.0<A<60°B.60°<A<90°C.0<A<30°D.30°<A<90°14、已知α为锐角,tan(90°-α)=,则α的度数为()A.30°B.45°C.60°D.75°15、如图,在某监测点B处望见一艘正在作业的渔船在南偏西15°方向的A处,若渔船沿北偏西75°方向以40海里/小时的速度航行,航行半小时后到达C处,在C处观测到B在C的北偏东60°方向上,则B、C之间的距离为()A.20海里B.10 海里C.20 海里D.30海里二、填空题(共10题,共计30分)16、如图,斜坡长为100米,坡角,现因“改小坡度”工程的需要,将斜坡改造成坡度的斜坡(、、三点在地面的同一条垂线上),那么由点到点下降了________米(结果保留根号)17、若cosA=0.6753,则锐角A=________ (用度、分、秒表示).18、如图,△ABC内接于⊙O,AB=BC,∠ABC=120°,AD为⊙O的直径,AD=6,那么BD=________19、+2sin30°-tan60°+tan45°=________.20、如图,在四边形ABCD中,∠B=∠D=90°,AB=3, BC=2,tanA=,则CD=________.21、如图,在边长为1的小正方形网格中,点A,B,C,D都在这些小正方形的顶点上,AB,CD相交于点O,则cos∠BOD=________.22、如图,,两点在以为直径的上,若,的半径为2,则的值为________.23、如图,在矩形中,,,将沿射线平移长度得到,连接,,则当是直角三角形时,a的长为________.24、如图,的顶点都是正方形网格中的格点,则________.25、如图,国庆节期间,小明一家自驾到某景区C游玩,到达A地后,导航显示车辆应沿北偏西60°方向行驶8千米至B地,再沿北偏东45°方向行驶一段距离到达景区C,小明发现景区C恰好在A地的正北方向,则B,C两地的距离为________.三、解答题(共5题,共计25分)26、计算:()﹣1+|1﹣|﹣2sin60°+(π﹣2016)0﹣.27、如图,在中,,点在边上,求的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第4章锐角三角函数
一、选择题
1.tan60°的值等于()
A. B. C. D.
2.在Rt△ABC中,∠C=90o,AC=4,AB=5,则sinB的值是 ( )
A. B. C. D.
3.如果∠α是等腰直角三角形的一个锐角,则cosα的值是()
A. B. C. 1 D.
4.如图,某水渠的横断面是等腰梯形,已知其斜坡AD的坡度为1:1.2,斜坡BC的坡度为1:0.8,现测得放水前的水面宽EF为3.8米,当水闸放水后,水渠内水面宽GH为6米.则放水后水面上升的高度是()米.
A. 1.2
B. 1.1
C. 0.8
D. 2.2
5.在△ABC中,∠C=90°,AB=15,sinA=,则BC等于()
A. 45
B. 5
C.
D.
6.王芳同学从A地沿北偏西60°方向走100m到B地,再从B地向正南方向走200m到C地,此时王芳同学离A地()
A. 50m
B. 100m
C. 150m
D. 100m
7.计算sin45°的结果是( )
A. B. 1 C. D.
8.某地下车库出口处安装了“两段式栏杆”,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图所示的位置,其中AB⊥BC,EF∥BC,∠AEF=135°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为(栏杆宽度忽略不计.参考数据:≈1.4)()
A. B. C. D.
9.如图,延长RT△ABC斜边AB到点D,使BD=AB,连接CD,若tan∠BCD=,则tanA=()
A. B. 1 C. D.
10.如图,一水库大坝的横断面为梯形ABCD,坝顶BC宽6米,坝高20米,斜坡AB的坡度i=1:2.5,斜坡CD的坡角为30度,则坝底AD的长度为()
A. 56米
B. 66米
C. (56+20)米
D. (50+20)米
二、填空题
11.若,则锐角α=________.
12.一条斜坡长4米,高度为2米,那么这条斜坡坡比i=________ .
13.如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,CD=4,cosA=,那么BC=________
14.如图,河堤横断面如图所示,迎水坡AB的坡比为1:,则坡角∠A的度数为________
15.在Rt△ABC中,∠C=90°,∠B=37°,BC=32,则AC=________.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
16.如图,从热气球C处测得地面A、B两点的俯角分别为30°、45°,如果此时热气球C处的高度为200米,点A、B、C在同一直线上,则AB两点间的距离是________米(结果保留根号).
17.在Rt 中,,,则的值为________.
18.在正方形网格中,△ABC的位置如图所示,则tanB的值为________.
19.如图是某品牌太阳能热水器的实物图和横断面示意图,已知真空集热管AB与支架CD所在直线相交于水箱横截面⊙O的圆心,支架CD与水平面AE垂直,AB=150厘米,∠BAC=30°,另一根辅助支架DE=76厘米,∠CED=60°.则垂直支架CD的长度为________厘米(结果保留根号).
三、解答题
20.如图,已知∠B=90°,AB=2cm,BC=2cm,CD=3cm,AD=5cm,求四边形ABCD的面积.
21.马航MH370 客机“失联”,我国“海巡01号”前往搜寻。
如图某天上午9时,“海巡01号” 轮船位于A处,观测到某小岛P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B 处,这时观测到小岛P位于该船的南偏西30°方向,求此时轮船所处位置B与小岛P的距离?(精确到0.1)
22.如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sinB=,AD=4.
(1)求BC的长;
(2)求tan∠DAE的值.
23.随着科技进步,无人机的应用越来越广,如图,在某一时刻,无人机上的探测器显示,从无人机A处看一栋楼顶部B点的仰角和看与顶部B在同一铅垂线上高楼的底部c的俯角.
(1)如果上述仰角与俯角分别为30。
与60。
,且该楼的高度为30米,求该时刻无人机的竖直高度CD.(2)如果上述仰角与俯角分别为α与β,且该楼的高度为m米.求用α、β、m表示该时刻无人机的竖直高度CD.
24.如图,是某广场台阶(结合轮椅专用坡道)景观设计的模型,以及该设计第一层的截面图,第一层有十级台阶,每级台阶的高为0.15米,宽为0.4米,轮椅专用坡道AB的顶端有一个宽2米的水平面BC;《城市道路与建筑物无障碍设计规范》第17条,新建轮椅专用坡道在不同坡度的情况下,坡道高度应符合以下表中的规定:
(1)选择哪个坡度建设轮椅专用坡道AB是符合要求的?说明理由;
(2)求斜坡底部点A与台阶底部点D的水平距离AD.
参考答案
一、选择题
D D B B B D B B A C
二、填空题
11.60°12.1:13.6 14.30 15.24
16.200(+1)17.18.19.38
三、解答题
20.解:连接AC,
在△ABC中,
∵∠B=90°,AB=2cm,BC=2cm,
∴AC=4cm,
在△ACD中,AC2+CD2=42+32=25,AD2=25,
∴AC2+CD2=AD2,
∴∠ACD=90°,
∴S四边形ABCD=S△ABC+S△ACD=×AB×BC+×AC×CD
=×2×2+×4×3=2+6(cm2).
21.解:过点P作PC⊥AB,垂足为C,设PC=x海里.
在Rt△APC中,∵tan∠A= ,
∴AC= .
在Rt△PCB中,∵tan∠B= ,
∴BC= .
∵AC+BC=AB=21×5,
∴,
解得.
∵,
∴(海里).∴向阳号轮船所处位置B与城市P的距离为100海里.22.(1)在△ABC中,∵AD是BC边上的高,
∴∠ADB=∠ADC=90°.
在△ADC中,∵∠ADC=90°,∠C=45°,AD=4,
∴DC=AD=4.
在△ADB中,∵∠ADB=90°,sinB=,AD=4,
∴AB=
∴BD=,
∴BC=BD+DC=
(2)∵AE是BC边上的中线,
∴CE=BC=,
∴DE=CE-CD=,
∴tan∠DAE=.
23.(1)解:过A作AD⊥CB,垂足为点D.
∵在Rt△ABD中,∠BAD=30°,
∴AB=2BD
∵在Rt△ABC中,∠CBA=60°,
∴∠ACB=30°
∴BC=2AB ,又∵BC=30米,
∴AB=15米
∴BD=7.5米
∴CD=BC-BD=30-7.5=22.5米
答:无人机的竖直高度CD为22.5米。
(2)解:设CD=x,则BD=m-x ,
在Rt△ABD中,∠BAD=α,
∴tanα==;
在Rt△ADC中,∠DCA=β ,
∴tanβ==,
∴,
tanβ·(m-x)=tanα·x
∴x=
24.(1)解:∵第一层有十级台阶,每级台阶的高为0.15米,∴最大高度为0.15×10=1.5(米),
由表知建设轮椅专用坡道AB选择符合要求的坡度是1:20;(2)解:如图,
过B作BE⊥AD于E,过C作CF⊥AD于F,
∴BE=CF=1.5,EF=BC=2,
∵= ,
∴= ,
∴AE=DF=30,
∴AD=AE+EF+DF=60+2=62,
答:斜坡底部点A与台阶底部点D的水平距离AD为62米.。
