第二章 相交线与平行线复习
相交线与平行线复习课

两条
直线
相交
相
交
两条
线
直线
被第
三条
直线
所截
邻补角、对顶角
对顶角相等
垂线及性质
点到直线的距离
同位角、内错角、同旁内角 判定
平行公理 平 行 线
平移
性质
1、一些角的概念: 对顶角、邻补角、同位角、内错
角、同旁内角
2、一些直线的概念: 平行线、垂线、垂线段
3、其他概念: 点到点的距离、点到直线的距离,
;无绳吸尘器 https:///
;
;
远远的旁观者。 ? 我赞同独行独处的个人本性。在一些生存空间里,人多有不适之感,我判断这是由于心灵膨胀而引发的疾患,言语中夹带火气,行为里散发着张扬。没有一种欲望会在得到满足后就此收敛,欲望总是比满足更为疯狂地滋长,让人估计不到最终的结局。欲望的膨胀比人口的容 集更为可怕,不是有人就论过亩产万斤粮食的可能吗?实际上就是采用了拥挤法——把许多丘田里的稻子铲来,堆在一丘;不是鼓吹钢铁超英美吗?大地上进入眼界的就是小高炉,腾腾烟雾拥挤而出。事实已经表明,拥挤的稻穗、拥挤的高炉,都是人精神疾患时的产物。很多时候,拥挤表明 了一种目的——一大群蚂蚁滚成一团,一定是搬运硕大的战利品;一大群拥挤的人喊着口号向前,观者一定产生预感——肯定又有什么事情发生了。 ? 城市,不断膨胀的根块,向山村的沃土延伸;城市的高楼,如努力攀援的藤蔓,稍不留意,卷须已经侵入空中。生长的迅速形成了拥挤。生长 又是不可抑制的,甚至眼睁睁的看着失控。“空”,意味着一切皆无。“无”现代城市最难以想像之物,因为城市什么都有,无数的有,无限的有,城市的重要标致就是无所不有。这必然越来越频繁地触及拥挤、品味拥挤——网络拥挤、信息拥挤、广告拥挤、娱乐拥挤……,我们真正进入了 一
相交线与平行线复习

相交线与平行线复习一、相交线、垂线1. 相交线的定义:在同一平面内,如果两条直线只有 点,那么这两条直线叫做 ,公共点称为两条直线的交点。
如图1所示,直线AB 与直线CD 相交于点O 。
ODCBA4321ABCDO 21OCBA图1 图2 图32. 对顶角的定义:若一个角的两条边分别是另一个角的两条边的反向延长线,那么这两个角叫做 。
如图2所示,∠1与∠3、∠2与∠4都是对顶角。
注意:两个角互为对顶角的特征是:(1)角的顶点公共;(2)角的两边互为反向延长线;(3)两条相交线形成2对对顶角。
3. 对顶角的性质:对顶角 。
4. 邻补角的定义:如果把一个角的一边反向延长,这条反向延长线与这个角的另一边构成一个角,此时就说这两个角互为 。
如图3所示,∠1与∠2互为邻补角,由平角定义可知∠1+∠2=180°。
二、垂线1. 垂线的定义:当两条直线相交所成的四个角中,有一个角是 时,就说这两条直线互相垂直,其中一条直线叫做另一条直线的垂线,它们的交点叫做垂足。
ABCD1ABC D1图4如图4所示,直线AB 与CD 互相垂直,垂足为点O ,则记作AB ⊥CD 于点O 。
其中“⊥”是“垂直”的记号;是图形中“垂直”(直角)的标记。
注意:垂线的定义有以下两层含义:(1)∵AB ⊥CD (已知) (2)∵∠1=90°(已知) ∴∠1=90°(垂线的定义) ∴AB ⊥CD (垂线的定义) 2. 垂线的性质(1)性质1:在同一平面内,经过直线外或直线上一点,有且只有一条直线与已知直线垂直,即过一点有且只有一条直线与已知直线垂直。
(2)性质2:连接直线外一点与直线上各点的所有线段中,垂线段最短。
即垂线段最短。
3. 点到直线的距离直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
mDCBAP图5 图6如图5所示,m 的垂线段PB 的长度叫做点P 到 直线m 的距离。
4. 垂线的画法(工具:三角板或量角器) 5. 画已知线段或射线的垂线 (1)垂足在线段或射线上(2)垂足在线段的延长线或射线的反向延长线上 三、三线八角两条直线被第三条线所截,可得八个角,即“三线八角”,如图6所示。
精编版平行线与相交线知识点整理总复习

精编版平行线与相交线知识点整理总复习平行线与相交线是几何学中重要的概念,它们在平面几何、解析几何以及立体几何中都有广泛的应用。
下面对平行线与相交线的相关知识点进行整理总复习。
一、平行线的定义与性质:1.定义:在平面上的两条直线,如果它们没有交点,就称为平行线。
2.平行线的判定方法:(1)同一条直线上的两条直线,如果与另一条直线平行,则它们互相平行。
(2)用直角板判定法:如果两直线上各取一点P和Q,再通过P、Q各画一条与给定直线垂直的直线,则这两条垂直线相交的点连同P、Q四点是否共线,如果共线,则给定直线与这两条垂直线平行;否则,不平行。
(3)用平行线定理判定:如果两直线上各取一点P和Q,并通过Q画一条与给定直线平行的线段,则通过P和平行线段的直线相交的点与P、Q、两直线上平行线段的两个端点是否共线,如果共线,则给定直线与平行线段平行;否则,不平行。
3.平行线性质:(1)平行线具有等斜率。
(2)平行线的判定是对称的,即如果直线l与直线m平行,那么直线m与直线l也平行。
(3)平行线的传递性。
(4)平行线的交线和倾斜度。
(5)两个平行线与同一直线的交线上的对应角相等。
(6)两个平行线分别与同一直线的两条截线上的对应角相等。
二、相交线与交角的定义与性质:1.定义:在平面上的两条直线如果有一个交点,就称为相交线。
2.存在且唯一:平面上任意两条不平行的直线都有一个且仅有一个交点。
如果两条直线有两个或多个交点,则它们必定重合。
3.交角的定义:两条相交线之间的夹角。
三、平行线与相交线的相关知识点:1.平行线的判定与构造:可以通过几何推理来判定两条直线是否平行,也可以通过构造垂直线段或平行线段等方法来构造平行线。
2.平行线于直线的夹角:直线与平行线的夹角为0度。
3.平行线与截线的夹角:一条直线与平行线的截线上的各个角的和等于180度。
4.形成平行线的条件:如果两个直线分别与一条第三条直线相交,在交点两侧所夹的内角或外角相等,则这两个直线平行。
第2章-第22课时-《相交线与平行线》单元复习(共18张PPT)

核心提要 1.对顶角___相__等_________. 2.同位角___相_等____,两直线平行. 3.内错角__相__等____,两直线平行. 4.同旁内角_互__补_____,两直线平行.
5.如果两条直线都与第三条直线平行,那么这两 条直线也互相__平__行____.
A
B
C
D
2.如图所示,点 P 到直线 l 的距离是( B )
A.线段 PA 的长度 B.线段 PB 的长度 C.线段 PC 的长度 D.线段 PD 的长度
3.下列选项中,哪个不可以得到 l1∥l2( C )
A.∠1=∠2 C.∠3=∠5
B.∠2=∠3 D.∠3+∠4=180°
4.如图,a∥b,PA⊥PB,∠1=35°,则∠2 的度 数是__5_5_°____.
5.如图,已知∠ACD=70°,∠ACB=60°,∠ ABC=50°.求证:AB∥CD.
证明:∵∠ACD=70°,∠ACB=60°, ∴∠BCD=∠ACB+∠ACD=130°. ∵∠ABC=50°, ∴∠ABC+∠BCD=180°. ∴AB∥CD.
6.如图,直线 AB,CD 相交于点 E,EF⊥AB 于
解:(1)∵∠BOE=50°,∠COE=90°, 又∵AOC+∠COE+∠BOE=180°, ∴∠AOC=180°-50°-90°=40°. (2)∵∠DOE=∠COE=90°, ∴∠BOD=90°-50°=40°. ∵OD 平分∠BOF, ∴∠BOD=∠DOF=40°, ∴∠EOF=50°+40°+40°=130°.
变式 2 已知:如图,D,E,F 和 A,B,C 分别
在一直线上,∠1=∠2,∠C=∠D.求证:∠A=∠F.
证明:∵∠1=∠2, ∠1=∠3, ∴∠2=∠3.∴BD∥CE. ∴∠ABD=∠C. ∵∠C=∠D,∴∠ABD=∠D, ∴DF∥AC.∴∠A=∠F.
第二章《相交线与平行线》综合复习完整ppt课件

1 4
a
∵a∥b
2
b
∴ ∠2=∠3 (两直线平行,内错角相等)
3、两直线平行,同旁内角互补。
∵a∥b ∴∠2 +∠4=180° (两直完整线版P平PT课行件 ,同旁内角互补)9
{ 性质
两直线平行
1.同位角相等 2.内错角相等
请注意:
判定 3.同旁内角互补
1.由_角__的__关__系__得到_两__直__线__平__行__的结论是
第二章 平行线与相交线复习
一、概念:
1、在同一平面内,两条直线的位置 关系有 相交 和 平行 。
2、若两条直线只有 一个 公共点,则
称这两条直线为相交线。 C
B
A
完整版PPT课件
O
D
2
3、具有 公共顶点 ,并且角的两边互
为反向延长线 的两个角叫做对顶角。
C B
A
O
D
4、如果两个角的和是__9_0_°_,称这两
∠EPA=∠A(两直线平行,内错角相等)
∴∠APC=∠EPC-∠EPA
=∠C-∠A(等式的性质1)
完整版PPT课件
20
(4)∠APC=∠A-∠C
A
B
理由:过P点作EF∥AB
C
D
EP F
∵EF∥AB (已作) AB∥CD(已知)
∴EF∥CD(平行于同一条直线的两条直线平行)
∴∠APE=∠A(两直线平行,内错角相等)
A
证明:∵CD ∥EF ( 已知 )
∴ ∠2= ∠3 ( 两直线平行,同位角相等 ) ∵ ∠1= ∠2 ( 已知 )
D F
1
G
∴ ∠1= ∠3 ( 等量代换 )
2 3(
教学课件:第二章相交线与平行线期末复习课件

01
02
03
角平分线
相交线在几何图形中常常 作为角平分线使用,可以 将一个角平分为两个相等 的部分。
对角线
在矩形、菱形、正方形等 图形中,相交线作为对角 线,连接对角顶点,并且 长度相等。
三角形的高
在三角形中,相交线可以 作为高,从顶点垂直于底 边。
平行线在几何图形中的应用
平行四边形
平行线是构成平行四边形 的主要元素,两组相对边 平行。
同位角相等判定法、内错角相等判定 法和同旁内角互补判定法适用于平行 线的判断,但需注意适用条件和截线 的选择。
距离判定法适用于所有情况,但需要 精确测量距离,操作较为繁琐。
在选择判定方法时,应根据具体情况 和需求进行选择,以达到准确、高效 的目的。
03 相交线与平行线的应用
相交线在几何图形中的应用
感谢您的观看
区别
平行线没有公共点,而相交线有一个公共点。平行线之间的距离相等,而相交 线形成的角有对顶角和邻补角。
02 相交线与平行线的判定方 法
相交线的判定方法
角角判定法
通过比较两条直线的夹角来判断是否相交。如果夹角为90度,则两条直线垂直相 交;如果夹角不为90度,则两条直线斜交。
距离判定法
通过测量两条直线的距离来判断是否相交。如果距离为0,则两条直线重合;如果距 离不为0,则两条直线相交。
生容易忽视这一点。
对同位角、内错角、同旁内角的理解不足
03
这些角的概念是解决相交线和平行线问题的关键,但学生往往
对这些概念的理解不够深入。
难点的解析
判断两直线是否平行
在判断两直线是否平行时,学生常常因为对平行线的判定定理理 解不透彻而出现错误。
理解平行线的传递性
第二章相交线与平行线期末复习课件
O1 R
A
探究: 下面三个图中,∠ABC的两边分别与∠DEF的两边平行, 即DE∥BA,EF∥BC。 ①在图1中,射线BA与射线ED同向,BC与EF也同向; ②在图2中,射线BA与射线ED异向,BC与EF也异向; ③在图3中,射线BA与射线ED同向,BC与EF异向。 问:(1)在上述关系中,∠B与∠E的关系怎样?
A
E
BC D
基础闯关
3、如图,在△ABF中,∠AFB=90°, A
FE⊥AB,AF=3,FB=4,AB=5,过点F作
CD∥AB,则点A到直线FB的距离 C
为__,点A到点B的距离为__,
F
点F到直线AB的距离为__,直线
CD到直线AB的距离为__ 。
E
B D
能力闯关
1:如图,已知:AC∥DE,∠1=∠2, A
过点F作EG∥AB
G
1、如图,已知AB∥CD,∠ABF=∠DCE. 试说明:∠BFE=∠FEC.
A
B
F? ?E
C
D
方法一:
A
B
O
F? ?E
C
D
方法二:
A
B
F? ?E
C
D
方法三:
A
B
F?
M
N
?E
C
D
方法四:
A
B
F? ?E
OC
D
2、⑴如图a,若AB∥CD,则∠B+∠D=∠E,你能 说明原因?
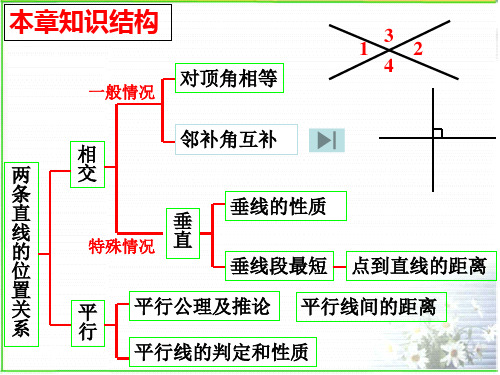
一般情况特殊情况对顶角相等邻补角互补垂线段最短点到直线的距离平行公理及推论平行线的判定和性质平行线间的距离第二章平行线不相交线复习课1平行线在同一平面内不相交的两条直线叫做平行线
本章知识结构
对顶角相等
相交线与平行线易错点复习

相交线与平行线易错点复习一、 平行线的判定与性质1、如图1所示,能判断AB ∥CD 的条件是( )A .∠3=∠4B .∠1=∠2C .∠B=∠D D .∠BAD+∠B=180°2、如图2,直线a 与直线b 互相平行,直线l 与直线a 、b 相交,则∠α的度数是( )A .40°B .60°C .140°D .160°3、已知如图3,∠A=135°,∠B= 45°,在下面的说法中,一定正确的是 ( )A .AD ∥BCB .AB ∥CDC .∠C =135°,∠D = 45° D .∠C =45°,∠D = 135°4、如图4,下列判定中正确的有( )①若∠1=∠3,AD ∥BC ,则BD 是∠ABC 的平分线;②若AD ∥BC ,则∠1=∠2 =∠3; ③若∠1=∠3,则AD ∥BC ;④若∠C + ∠3 +∠4 = 180°,则AD ∥BCA .1个B .2个C .3个D .4个5、如图5,∠1=∠2,则 ∥ ,理由是 __6、如图6,AB ∥CD ,那么∠B +∠E +∠D = °.7、解答题(1)如图,已知AB ⊥BD ,CD ⊥BD ,且∠1+∠2 =180°,求证:CD ∥EF证明: ∵ AB ⊥BD ,CD ⊥BD (已知)∴ AB ∥CD ( )又∵ ∠1+∠2 =180°(已知)∴ AB ∥EF ( )∴ CD ∥EF ( )(2)如图,已知EF ∥BC ,∠1=∠B 。
问DF 与AB 平行吗?请说明理由。
图1 图2 图3 图4 图5 图6(3)如图,已知∵AC⊥AB,BD⊥AB,且∠CAE=∠DBF,求证:AE∥BF。
如图,∵AC⊥AB,BD⊥AB(已知)∴∠CAB=90°,∠______=90°()∴∠CAB=∠______()∵∠CAE=∠DBF(已知)∴∠BAE=∠______ ()∴AE∥BF()(4)如图,已知AD∥BC,∠A=100°,BD平分∠ABC,求∠DBC的度数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 平行线与相较线复习
一、选择题。
(每题1分,共16分)
1、下面四个图形中,∠1与∠2是对顶角的图形的个数是( ) A 、0 B 、1 C 、2 D 、3
12
1
2
1
2
1
2
2、邻补角是( )
A 、 和为180°的两个角
B 、 有公共顶点且互补的两个角
C 、 有一条公共边且相等的两个角
D 、 有公共顶点且有一条公共边,另一边互为反向延长线的两个角 3、下列正确说法的个数是( )
①同位角相等 ②对顶角相等 ③等角的补角相等 ④两直线平行,同旁内角相等 A 、 1 B 、 2 C 、 3 D 、 4 4、下列图中∠1和∠2是同位角的是( )
A 、⑴、⑵、⑶
B 、⑵、⑶、⑷
C 、⑶、⑷、⑸
D 、⑴、⑵、⑸
5、如图,若m ∥n ,∠1 = 105°,则∠2 =( ) A 、 55° B 、 60° C 、 65° D 、 75°
6、如图,直线AB 、CD 相交于点O ,OE ⊥AB 于O ,若∠COE=55°,则∠BOD 的度
数为( )
A 、 40° B、 45° C、 30° D、35° 7、如图,共有内错角的对数是( ) A 、 5对
B 、 2对
C 、 3对
D 、 4对 8、如图2,可得出DE//BC 的条件是( ) A 、 ∠ACB=∠BAD B 、 ∠ABC=∠AD
E C 、 ∠ABC=180°-∠BED D 、 ∠ACB=180°-∠BAD
1 2 n
m
第5题
第7题
9、两条直线被第三条直线所截,则()
A.同位角必相等 B.内错角必相等 C.同旁内角必互补 D.同位角不一定相等10、如图,与是对顶角的为()
11、如图,直线a,b都与c相交,由下列条件能推出的是()
①②③④
A.① B.①② C.①②③ D.①②③④
(第11题)(第12题)
12、如图,下列条件中能判定的是()
A. B.C. D.
13、如图,,则下列结论中,错误的是()
(第13题)(第14题)
A. B.C. D.
14、如图,下列推理中正确的是()
A.∴
B.∴
C.∴
D.
C
B A
D
O
15、如图,由已知条件推出的结论,正确的是( ). A .由 ,可推出 B .由 ,可推出 C .由
,可推出
D .由
,可推出
16、下列角的平分线中,互相垂直的是( )
A .平行线的同旁内角的平分线
B .平行线的同位角的平分线
C .平行线的内错角的平分线
D . 对顶角的平分线 二、填空题(每题1分,共16分) 1、若
,则它的余角是_________,它的补角是________.
2、若∠α与∠β是对顶角,且∠α+∠β=1200
,则∠α= ,∠β=
3、如图, 和
相交,
和 是______角,
和 是
______角, 和
是______角,
和
是______角.
(第3题) (第4题) (第5题)
4、如图:已知: ,则
5、如图:已知: ,则
6、如图, ,则
.
(第6题) (第7题)
7、如图,已知∠AOB 、∠BOC 、∠COD 的顶点是一条直线上同一点,且∠AOB=650
15’, ∠
BOC=780
30’,则∠COD=
8、一个角的补角等于这个角的余角的4倍,这个角是________.
9、已知:如图,三直线两两相交于点P 、Q 、R ,则图中共有对顶角_____对,邻补角____对。
10、如图,直线AB 、CD 相交于点O ,已知∠AOC+∠BOD=90°,则∠BOC= 。
11、如图,直线AB 、CD 相交于点O ,OP 是角平分线,若∠BOP=30°,则∠AOD= 。
12、如图,∠1 = 82º,∠2 = 98º,∠3 = 80º,则∠4 = 度。
13、如图,直线AB ,CD ,EF 相交于点O ,AB ⊥CD ,OG 平分∠AOE , ∠FOD = 28º,则∠BOE = 度,∠AOG = 度。
14、如图,若∠ = ∠ ,可得AD ∥BC ;若∠ = ∠ ,可得 AB ∥DC ;(各写出一个正确的即可)。
三、解答题(每题6.8分,共68分) 1、如图,
,求
的度数.
A
B
C
D O
P 第11题
第13题
第12题
第14题
2、如图,已知DE∥AB,∠EAD =∠ADE,试问AD是∠BAC的平分线吗?为什么?
3、如图:已知:,求∠4的度数
4、如图:找出互相平行的直线,并说明理由.
5、如图,已知AB∥CD,∠A =1000,CB平分∠ACD.回答下列问题:(1)∠ACD等于多少度?为什么?
(2)∠ACB、∠BCD 各等于多少度?为什么?
(3)∠ABC等于多少度?为什么?
C
B A
D
E
6、如图:已知AB ∥CD ,∠α =450
,∠D=∠C .你能求出∠D 、∠C 和∠B 的度数吗?
7、如图,∠B=∠C ,AB ∥EF ,试说明:∠BGF=∠C 。
(6分) 解:∵ ∠B=∠C
∴ AB ∥CD ( ) 又∵ AB ∥EF ( )
∴ ∥ ( )
∴ ∠BGF=∠C ( )
8、如图,完成下列推理过程
已知:DE ⊥AO 于E , BO ⊥AO ,∠CFB=∠EDO.证明:CF ∥
DO 证明:∵DE ⊥AO
, BO ⊥AO (已知)
∴∠DEA=∠BOA=900 ( ) ∵DE ∥BO ( ) ∴∠EDO=∠DOF ( ) 又∵∠CFB=∠EDO ( ) ∴∠DOF=∠CFB ( ) ∴CF ∥DO ( )
9、如图,AB ∥EF ,∠B =1350
,∠C=670
,则求∠1的度数.
D
C
F
B
A
E
D O。
