巧填幻方和数阵
巧填幻方(课堂PPT)

•5
例1:把1-9这九个数填入下面的九宫 格中,不能重复,使得每一行,每一 列,每一条对角线上的三个数的和相 等。
解题过程:
1
4
2
7
5
3
8
6
9
九子斜排
9
4
2
3
5
78ຫໍສະໝຸດ 61上下对易,左右相更
4
9
2
3
5
7
8
1
6
•6
例1:把1-9这九个数填入下面的九 宫格中,不能重复,使得每一行, 每一列,每一条对角线上的三个数 的和相等。
方法二:阶梯法(下回分解)
方法三:罗伯法(徐近乔已讲)
4 92 3 57 8 16
张老师提示:对易法、阶梯法、罗伯法都只适用于奇数幻方
•7
谢谢大家
完
•8
幻和: 幻方中每行/列/对角线的数的和。
•3
492 357 816
幻和:15 总和:1+2+3+4+5+6+7+8+9=45 阶数:3
15=45÷3 幻和=总和÷阶数
•4
例1:把1-9这九个数填入下面的九宫格中, 不能重复,使得每一行,每一列,每一条对 角线上的三个数的和相等。
刚才神龟背上的九宫图,究竟是怎 么填出来的呢?
巧填幻方
主讲人:张权瑞
•1
4 92 3 57 8 16
同学们,你观察到了什么?这 些数无论横着加、竖着加还是 斜着加,结果都等于十五。
•2
幻方的基本概念
幻方: 是指横行、竖行、对角线上数的和都 相等的数的方阵,具有这一性质的3x3 的数阵称作三阶幻方,4x4的数阵称作 四阶幻方,5x5的数阵称作五阶幻方 ……….
三年级奥数简单数阵与幻方

数阵与幻方【知识点与方法】一、数阵和幻方的概念:(1)数阵:每一条直线段的数字和相等。
(2)幻方:在一个由若干个排列整齐的数组成的正方形中,任意一横行、一纵行及对角线的和都相等。
二、联系之前所学的高斯求和的知识,首先找到中心项:首项、末项、中间项。
然后对称找和相等的成对的项。
【经典例题】例1、将1、2、3、4、5这五个数分别填入下图中,使横行3个数的和与竖行3个数的和相等。
例2、将1、4、7、10、13这五个数分别填入下图中,使横行3个数的和与竖行3个数的和都等于25。
例3、将1~7这七个自然数填入左下图的七个○内,使得每条边上的三个数之和都相等。
例4、将5~11这七个自然数填入左下图的七个○内,使得每条边上的三个数之和都等于24。
例5、将1~9这九个自然数填入下图的九个方格内,使得它成为一个幻方(每行、每列、每条对角线和都相等)。
练习与思考1.将3、6、9、12、15这五个数分别填入下图中,使横行3个数的和与竖行3个数的和相等。
2. 将1、3、5、7、9这五个数分别填入下图中,使横行3个数的和与竖行3个数的和为17。
(2题图)(3题图a)(3题图b)3. 将1~9这九个数分别填入右上图的小方格里,使横行和竖列上五个数之和相等。
(至少找出两种本质上不同的填法)4.将3~9这七个数分别填入左下图的○里,使每条直线上的三个数之和等于20。
(4题图)(5题图)5.将1~11这十一个数分别填入右上图的○里,使每条直线上的三个数之和相等,并且尽可能大。
6. 将2~10这九个自然数填入下图的九个方格内,使得它成为一个幻方(每行、每列、每条对角线和都相等)。
7.将1~7这七个数分别填入下图的○里,使得每条直线上三个数之和与每个圆圈上的三个数之和都相等。
小四奥数(幻方和数阵)

1、用“罗伯法”编制一个五阶幻方。
2、在下图的空格里填上合适的数,使横、竖、斜行中三个数的和都是27.
3、在下图的七个圆圈里分别填上1-7,使每条直线上的三个数的和都相等。
4、把1-9这九个数分别填入下图“七一”图案的格子里,使每一横行、每一竖行的数的和都是13.
5、将1-8八个数分别填入下图中,是每条边上三个数的和等于12.
数阵问题的题型主要有三种:(1)辐射型;(2)封闭型;(3)综合型。幻方和数阵图的填写不能只采取试的办法,而要根据题目的要求,所给的数字的特征进行合理的分析思考,并在计算的基础上,先在计算的基础上,先填写关键位置的数,再填其他位置的数。
二、典型例题
例1将1-9九个数字填在右图内九个方格里,每格填一个数字,使每一横行、每一纵行和两条对角线上三个数之和相等。
这幅图用现在的数字表示,即为1-9这九个数字,填在九个格子里,每一纵列、每一横行以及两条对角线上的三个数字之和都是15(见上图)。我国古代数学家称它为“纵横图”或“九宫图”,国外称它为“魔方”、“幻方”或“中国方阵”。
幻方曾使不少的爱好者入迷,目前世界上最大的幻方——“1256阶泛对角幻方”就是1990年11月22日无锡以为中学教师发明,这个数字方阵方阵纵、横排成1256行,任何一条线以及对角线各数和都是990693236.
将1-7七个数字分别填入图中的七个圆圈内,使每条线上三个圆圈内的数的和相等。
想一想:从(1+2+3+、、、+7-x)除以3,商是整数而没有余数时,该怎样思考?
变式3-1把3-9这七个数填入下图中的圆圈内,使每条线段上三个圆圈内的数的和相等。
例4把1-10十个数填入下图中的小圆中,使每个大圆上六个数的和是30.
奇妙的幻方与数阵

奇妙的幻方与数阵走进来相传大禹治水时,洛水中出现了一只“神龟”,背上有美妙的图案(如图),史称“烙书”。
我国南宋时期数学家辉将它命名为“纵横图”,又名“九宫图”或“九宫和阵”。
用现在的数字翻译出来,就是三阶幻方。
幻方出现之后,曾使不少人为之入迷,古今中外有许多大数学家、大学者,如欧拉、富兰克林等对幻方都很感兴趣,并且逐步研究出了不少独特的构造幻方的方法。
一起做例1 把1,2,3,4,5,6,7,8,9这九个自然数填入右图3×3的方格中,使每行、每列及两条对角线上的三个数之和相等。
例2 认真观察例1的结果,里面蕴涵着神奇的奥妙,你发现了吗?幻方问题,可以通过计算的方法填写。
把你发现的方法写下来。
例3 在右图的空格中填入不同的自然数,使每行、每列及两条对角线上的三个数之和是18。
例4 将九个连续偶数制成一个三阶幻方,使幻和等于36.例5 在右图的每个空格填入一个自然数,使得每一行,每一列及每一条对角线上的三个数之和都相等。
我能行展现自己1、用自然数2、3、4、5、6、7、8、9、10编制成一个三阶幻方。
2、用1、3、5、7、9、11、13、15、17编制成一个三阶幻方。
3、用2、4、6、8、10、12、14、16、18编织成一个三阶幻方。
4、将9个偶数编成一个三阶幻方,使幻方和等于24。
5、将九个连续奇数制成一个三阶幻方,是幻和等于33。
6、在下面的两个图空着的方格填上合适的数,是每行、每列及两条对角线上三个数字之和都等于27。
7、在右图中的九个小方格中各有一个数字,而且每行、每列及每条对角线上的三个数字之和都相等,求x的值。
8、在右图的空格中填入七个自然数,使得每一行、每一列及每条对角线上的三个数之和都等于90。
9、在右图中的每个空格中填入一个自然数,使每行、每列及每条对角线上的三个数之和都相等。
10、在右图的空格中再填入七个自然数,使得每行、每列及每条对角线上的三个数之和都是48。
11、在右图中的每个方格里填入一个不大于12且互不相同的9个自然数(左上角已经填入8),使每行、每列、每条对角线上的三个数之和都等于21。
幻方的口诀顺口溜

幻方的口诀顺口溜
1. 幻方真奇妙,口诀要记牢,一居上行正中央,这个例子很明了,就像找到了宝藏的钥匙哟!比如3×3 的幻方,数字1 不就放在最上面一行的正中央嘛!
2. 依次斜填切莫忘,哎呀呀,可别小看它呀!就像走迷宫有了方向一样。
你看那个 4 不就斜着填下去嘛!
3. 上出框时往下填,这多有意思呀,就好比球弹到了地上又弹起来。
像 7 超出框了,不就往下填嘛!
4. 右出框时往左填,嘿,是不是很好玩呀,如同汽车拐弯换了个道儿。
数字 9 不就这样填嘛!
5. 排重便在下格填,哇塞,这感觉就像纠错一样呢!要是碰到重复的数字,不就往下一格填嘛,就像避开障碍。
6. 右上排重一个样,可不是嘛,就像遇到同样的困难有同样的解决办法。
比如右上有数字了,也得这样处理呀!
7. 幻方口诀真好用,绝对让你大不同,你想想,用了口诀解幻方多轻松呀!
8. 记住口诀不慌张,仿佛有了定海神针呀!不管遇到啥样的幻方都不怕啦!
9. 轻松玩转幻方界,哎呀呀,那感觉就像武林高手称霸江湖一样呢!
10. 幻方口诀顺口溜,大家一定要记熟,真的超级有用处哟!就像拥有了神奇的魔法棒!
我的观点结论:幻方的口诀顺口溜真的太重要啦,能让我们快速掌握幻方的技巧,大家一定要好好记住呀!。
巧填幻方

这就是传说中神秘的幻方,让我们走进今天的课堂,一起来研究一下幻方的这是传说中神秘的幻方,我们走进今天的课堂,起来研究下幻方的
阶幻方……
幻和:幻方中每行/列/对角线的数的和。
幻和:15
【幻方填法】
民谣
四海三山八仙洞,九龙五子一枝连;;二七六郎赏月半,周围十五月团圆。
周围十月团圆把1-9这九个数填入下面的九宫格中,不能重复,使得每一行,每一列,每条对角线上的三个数的和相等。
试编出一个三阶幻方,使其幻和为30,而且幻方中没有重复的数。
中间数:在奇数阶幻方中填在最中间的数。
中中中
观察下三阶幻方:
幻和=(1+2+3+…+8+9)÷3=15
中间数=15÷3=5
在下图中的A、B、C、D处填上适当的数,使下图成为一个三阶幻方。
【三阶幻方性质】
角块等于对角两棱块之和的一半
在下图空格中填入7个自然数,使每行、每列、每一对角线三数之和为90把1-16这十六个数填入下面的图中,不能重复,使得每一行,每一列,每条对角线上的四个数的和相等。
在下图的每个方格中填入一个数字,使得每行、每列以及每条对角线
上的方格中的四个数字都是1,2,3,4。
⑴幻和=总和÷3
⑵中心数=幻和÷3=总和÷9
“T型台”
⑶型台
c=(a+b)÷2
二三阶幻方填法
二、三阶幻方填法。
幻方做题技巧

幻方做题技巧幻方啊,就像一个神秘的数字魔法阵。
咱要解开它的奥秘,可得有点小窍门。
先说说三阶幻方吧。
这就好比是幻方里的小老弟,简单又有趣。
你得知道幻和这个概念,啥是幻和呢?就像是这个幻方里的一个小目标。
对于三阶幻方来说,它的幻和特别好算,你把这九个数里最大的数加上最小的数,然后乘以个1.5就成了。
比如说1到9这九个数,最大的是9,最小的是1,那幻和就是(9 + 1)×1.5 = 15。
知道了幻和,就像手里有了一把小钥匙。
咱再看这九个数怎么往幻方里填。
中间数那可是个关键的主儿,就像一个小班长,在三阶幻方里,这中间数就得填5。
为啥呢?因为它在这堆数里位置特殊呗。
你把5填在中间,就像在这个魔法阵的中心定了个桩。
然后呢,你就可以试着把和为10的数对往幻方里填,像1和9,2和8,3和7,4和6,就像给小朋友找小伙伴,一对一对的。
不过这填的时候也得有点小技巧,不能瞎填。
你可以先在角上找个位置给1,为啥是角上呢?角上的数啊,它要跟更多的数相加凑幻和呢。
你把1填在角上,那跟1凑幻和15的数就有9和5了,这样就比较容易确定其他数的位置。
再讲讲五阶幻方。
这五阶幻方可比三阶的复杂点了,就像从小学的数学题跳到了初中的难度。
这时候幻和的计算也有点不一样了。
你得把这25个数里最小的数加上最大的数,然后乘以个2.5。
这时候填数也有个小办法。
你可以先把1填在最上面一行中间的位置,就像在舞台的正中央先放了个小演员。
然后呢,你就按照斜着往上走的规则填数。
要是走到幻方的外面了,你就像这个数字坐了时光机一样,从幻方的对面钻出来接着填。
要是斜着走的位置已经被占了,那这个数字就乖乖地填在这个被占数字的下面,就像排排坐吃果果一样。
还有一种幻方是偶数阶幻方。
偶数阶幻方就像两个好朋友手拉手。
比如说四阶幻方,你可以把这个幻方分成四个小方阵。
先把1到16这16个数按顺序填进去,然后呢,你就像个调皮的小精灵,把对角线上的数进行交换。
把左上角小方阵和右下角小方阵里的对角线的数交换,右上角小方阵和左下角小方阵里的对角线的数也交换。
巧填幻方
【例6】(★★★) 已知如图是一个四阶幻方,那么标有“*”的方格中所填的数是多少? 7 12
49*
5 16 3
8 11
【超常挑战】(★★★★★)数学解题能力复试试题
麦斯将9个不同的自然数填入右图的9个空格内,使每行、每列、
每条对角线上3个数的和都相等。已知A和B的差为14,B和C的
差也为14,那么D和E的差是___________。
1
【例2】(★★★) 把2、4、6、8…50这25个偶数填入下面的九宫格中,不能重复,使得 每一行,每一列,每条对角线上的5个数的和相等。
三阶幻方的性质
492 357 816
①总和=幻和×3 ②幻和=中心数×3
abc de f gh i
①总和=幻和×3 ②幻和=中心数×3
三阶幻方的性质
b
①总和=幻和×3
幻方的填法
杨辉法 九子斜排 上下对易 左右相更 四维挺出
1 42 753 86
9
492 357 816
幻方的填法
罗伯法 首居上中央,依次右上连 上出向下看,右出往左填 顶角和填重,回来写下边 填好再检查,等差在中间
ቤተ መጻሕፍቲ ባይዱ
816 357 492
适用于等差数列 填入奇数阶幻方
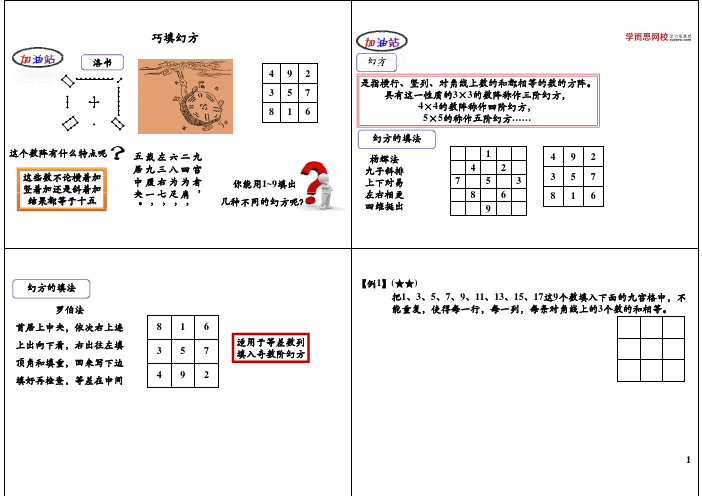
【例1】(★★) 把1、3、5、7、9、11、13、15、17这9个数填入下面的九宫格中,不 能重复,使得每一行,每一列,每条对角线上的3个数的和相等。
巧填幻方
洛书
492 357 816
这个数阵有什么特点呢 这些数不论横着加 竖着加还是斜着加 结果都等于十五
五戴左六二九 居九三八四宫 中履右为为者 央一七足肩, 。,,,,
你能用1~9填出 几种不同的幻方呢?
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
巧填幻方和数阵
在神奇的数学王国里,有一座数字谜宫,那就是幻方和谜宫,他对喜欢探究数字规律的人有着巨大的魔力,就连大数学家欧拉都对它痴迷。
有关幻方的研究在我国已经流传了两千多年,它是具有多特形式的填数字问题。
随着历史的发展,许多人对幻方作出进一步的研究,创造了许多绚丽多姿的幻方,并且探索出了一些解答方法。
我在教奥数培优班时,讲解三阶幻方和数阵时,发现书中的解答方法有点高深,不易懂。
特别是对于三年级的学生,我发现了一个简单的方法巧填三阶幻方和简单的数阵的解答方法。
(一)三阶幻方的填法
例:将1-9九个自然数填入下图的九个方格里,使每行、每列、两条对角线上的三个数的和都相等。
教材上的解法是:(一)先求出每行每列、每条对角线上之和是多少(1+2+3+4+5+6+7+8+9)/3=15 (2)将1-9这九个数中和为15的三个数的构成方式都列举出来,找出中心数为5填在中心方格中。
(3)填上四个角上的数字。
(4)把其它几个数填在合适的位置。
这些过程对于三年级的学生来说,难度太大,容易忘记。
我的解法是:(1)先填中心数,把1-9按从小到大顺序排成一排,第五个数填在中心格。
(2)将剩下的八个数排成两排,第一排为1、2、3、4、第二排为8、7、6、5即
1 2 3 4
8 7 6 5
根据两排数字填上四个角,四个角的数就是两排中第二、第四列中的四个数,这两列数字按对角填。
即如图 ( 略 )
(4)用对角线的和减去每行或每列知道的数字就完成了。
(5)例如:将20-28填入九宫格中,使每行、每列、两条对角线的和相等。
1)20、21、22、23、24、25、26、27、28第五个数是24填在中心格。
2)20、21、22、23
28、27、26、25 把第二、第四列的21、27、23、25按对角填。
3)用对角线的和72减去每行或每列知道的数字就行了。
如图:( 略 )
(二)简单数阵的填法
例如:将2-10这九个数填入下图中,使得从中心出发的每条线上的三个数之和相等。
教材上的解法是:(1)确定中心数设中心数为A,则这四条线上12个数的和为54+3*A是4的倍数,求出A的值分别为2、6、10 最后填出数阵。
这里用不定方程求A的值对于三年级的学生太难了。
我的填法是:把这九个数按顺序排成两排,第一排4或5个数从小到大排,第二排5或4个从大到小排。
只有一个数的一列的这个数就是中心数。
如图:
2、3、4、5、6 2、3、4、5、6 2、3、4、5 10、9、8、7 10、9、8、7 10、9、8、7、6 (一)(二)(三)
图一的中心数为6,图二的中心数为2,图三的中心数为10 确定中心数后,把每列的两个数填在其余的两个圆圈就完成了。
如图:( 略 )
又如:将5-15填入下图使每条线上的三个数之和相等。
(1)确定中心数
(一)5、6、7、8、9、10 (二)5、6、7、8、9
15 14 13 12 11 15 14 13 12 11 10
(2)填数阵如下图( 略 )
以上就是我对三阶幻方和简单数阵的解答方法,主要是针对学生的特点而得出的一些简单易记的方法
趣题巧解
在众多竞赛题中,有一些趣题如果按一般的思维去解答很花时间,甚至于也不一定能得到答案,对于这类题目就需要跳跃的思维来解答。
例如:我原来的号码与现在的号码都是四位数,现在的号码是原来的号码的四倍,并且是原来的号码倒着写过来。
问现在的号码是多少?
这道题按一般的方法推理出千位与个位数字很容易,但百位与十位数字有点难,如果我们换一种思考方法,把这道题变成一道数字谜来解答就非常容易了。
设原号码为ABCD,现号码则为DCBA,列式得:ABCD*4=DCBA。
从这个数字谜中可以看出A只能是1或2两种可能,又根据D*4的个位为A,那么A就只能为2。
同时也可以判断出D只能为8。
根据D为8,可以看出B只能为0、1、2这三种可能,而C*4的积加上3的个位数字一定是奇数,从而推出B只能为1,最后推出C为7,也就是现号码为8712。
又如:在0.15-0.16之间找一个分子分母尽量小的分数,这个分数是多少?
这道题..先把0.15和0.16分别化成分数就是3/20与4/25,再根据通分来解答可以求出答案,但不一定是对的。
也可以把分子变成相同的3,即3/20与3/18.75从而可以求出一个3/19。
但是这个答案还是不能满足条件。
我们也可以换一个角度思考,采用逆向思维,就是求出3/20与4/25的倒数,即20/3与25/4,我们可以找到一个13/2,最后再把13/2倒回去,即2/13就是本题的正确答案了。
因此,再一些趣题里,有时用常规方法不能求出解时,我们可以采用一些特殊方法来解答。
智力推理
题目有四对夫妇,他们的姓分别是:刘、李、赵、周、郑、王、钱及吴。
请你根据下面的几个条件指出每对夫妇分别姓什么:
1王同志结婚时,吴、钱两人同去做客,且两人穿的是同一种衣服;
2郑同志去外国考察时,其他三对夫妇各有一人去送行,且他们分别姓吴、周和赵;
3在大学读书时,李、吴、赵三人同住一室;
4李同志的爱人是郑同志的表哥。
分析与解答:我们先从性别上将这八个人分成两组。
由条件4知:李同志是女的;
由条件3知:吴、赵两人也是女同志;
由条件1知:钱也是女同志。
因此,这八个人中,女同志姓:李、吴、赵、钱;男同志姓:刘、周、郑、王。
下面就可以进一步找出各对夫妇的姓了。
由条件1知,王同志的爱人或者姓李,或者姓赵。
如果王的爱人姓李,则由条件2知王、李不能是一家。
因而王的爱人姓赵。
由2及4知,郑的爱人不可能姓吴、赵和李,因而郑的爱人姓钱。
由2知,周的爱人不可能姓吴,因而周的爱人姓李。
最后,刘、吴是一对。
归纳起来,四对夫妇是:
王与赵;郑与钱;周与李;刘与吴。
(积中)
畅游数学王国
人类进入了信息社会,动物界也跟着沾了光。
小猴家通了电话,接上了传真机,还买了电脑,足不出户就可以尽览天下大事。
一天,小猴正悠哉的在网上看电影,突然一道白光映入了小猴的眼帘,随后在白色的屏幕上出现了一些金灿灿的大字:“要想进入数学王国,就按下回车键。
”好奇心使小猴开启了数学王国
的大门。
随着一道刺眼的白光射出,原本坐在椅子上的小猴,竟凭空消失了。
原来,小猴已经来到了数学王国的大门前。
这时,一个带着一对翅膀的小机器人飞了过来,对小
猴说:“要想进入数学王国,必须要回答对两道题方能进入!”
于是小机器人出了第一道闯关题:单独完成一件工作,甲按规定时间可提前2天完成,乙则要超过规定时间3天才能完成。
如果甲、乙二人合作2天后,剩下的由乙单独做,那么刚好在规
定时间完成。
问:甲、乙二人合作需要多少天可以完成?
小猴想了一会儿说:“乙单独做要超过天3天,甲、乙合作2天后乙继续做,刚好按时完成,说明甲做2天等于乙做3天,即完成这样工作,乙需要时间是甲的3/2倍。
因为甲单独做,乙
比甲多用了3+2=5(天),所以甲需要5÷(3/2-1)=10(天),乙需要10+5=15(天);甲、乙合作需要1÷(1/10+1/15)=6(天)。
所以甲、乙二人合作需要
6天完成。
小机器人马上高兴的拍手说:“好,好!第一题答对了!”小机器人又马上转身思考了一阵,又开始了第二道题的问答:快车由A地到B地要5小时,慢车由B地到A地的时间比快车多用1/5,两车同时从两地相对开出,2小时后慢车停,快车继续行驶96千米与慢车相遇,求两地的距离是多少?
小猴被这道题给难住了,急的抓耳挠腮,冥思苦想了一阵后,才自信地做了出回答。
“
这道题用5×(1+1/5)=6(小时),1÷(1/5+1/6)=30/11(小时),再用96÷(30/11—2)×30/11=360(千米)。
随着漫天飞舞的彩带和音乐声,数学王国的大门打开了。
小猴在数学王国里玩了整整一天。
在这一天里,小猴学到了许多关于数学的知识,还做了很多的小游戏,这些都令它大开眼界,让它学到了更多知识,变得更聪明。
这次数学王国之游令它难忘。
