12.3 干涉条纹的可见度
干涉条纹的可见度

主要内容 • 干涉条纹的可见度 • 影响干涉条纹观测的因素
光源的非单色性
光源的线度
一 、干涉条纹的可见度
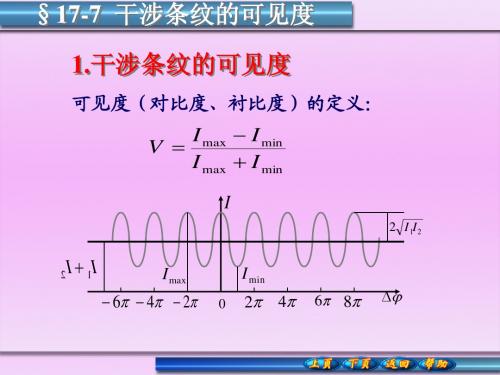
可见度(或对比度、反衬度) 定义 :
I max I min V I max I min
当I
min
0
(暗条纹全黑)时,V Vmax 1
,
条纹的反差最大,清晰可见。 当 I min I max 时, V Vmin 0 条纹核糊不清,甚至不可辨认. ,
则光强公式又可写为:
2 1
2 2
2 cos 2 I 1 V (A10+ A2 ) - (A1 - A2 ) 2A1A2 于是 : V = = 2 2 2 2 这就是双光束干涉中强度分布的另一表达式 (A1 + A2 ) + (A1 - A2 ) A1 + A2
I A A 2 A1A 2c o s
即
一定, y j
j 提高,宽度增大,可见度下降
不同级次的条纹发生重叠,这时可见度为零。 当 λ + Δλ 第j级与 λ 的第(j + 1) 级重叠时
r0 y j d
明纹宽度
j 1 j
j
可见度 为零
此时的光程差为实现相干的最大光程差:
2 1 2 2
二、光源的非单色性对干涉条纹的影响
以杨氏干涉实验为例说明光源的非单色性对 干涉条纹的影响。 设光源的波长为 λ ,其波长范围为 Δλ
由双缝干涉亮纹位置:
r0 y j d
j=0级条纹是完全重合的,其他各条纹不再重合; 同级次内,干涉级大值位置范围:
y y
第四章 光的干涉(2)

S'的条纹
缝S1和S2后在O点引起的两光振动的光程差Δ=0,O 点的光强为极大值。因为S'发出的光通过S1和S2后 在O点的干涉光强为极小,所以S'发出的光通过S1和 S2到达O点的光程差为
由 几 何R2 R,R1+R2 2R,且R2–R1='
λ Δ R2 R1 S1 R 2 S' 1 2 d h 2 2 d R1 R h S0 R2 2 2 S2 d 2 2 R R2 R h 2 2 R2 R12 ( R2 R1 )( R2 R1 ) 2hd
I I1 I 2 2 I1 I 2 cos δ
当 δ 2mπ , ( m 0,1, 2, ) 时 I max ( I1 I 2 )2 当 δ 2( m 1)π , ( m 0,1, 2, ) 时 I min ( I1 I 2 )2
2( A1 / A2 ) 2 I1 I 2 2 A1 A2 I I max min 由定义 V 2 2 2 A A 1 ( A / A ) I max I min I1 I 2 1 2 1 2
但不是最清晰。可见度越小,条纹就越不清晰。 当V很小时,条纹就模糊不清,无法辨认了。 影响干涉条纹可见度的三个主要因素: ① 两相干光的振幅不相等(I1I2)。
② 实际中不存在严格的点光源,任何光源都 有一定的宽度。 ③ 实际光源不是理想单色光,它的波列长度 有限,或说它们有一定的光谱宽度(非单色性)。 先讨论I1I2对条纹可见度的影响 对于两个理想单色点光源,两相干光束叠加 后的总光强分布为
当 A1 A2 ( I1 I 2 ) 时V 1;
而A1、A2相差越大,则V值越小。
17-7干涉条纹的可见度
I
合光强
λ + λ / 2
x1 x2 x3 x4 x5 x6 x7
x
λ λ / 2
光的非单色性对条纹可见度的影响
2.1 相干长度δm 相干长度δ
对于非单色光, λ/2 对于非单色光,当波长为 λ-λ 的第 λ 的第(k+1) λ/2 级明纹和波长为 λ+λ 的第 级明纹正好重合 λ 的第k级明纹正好重合 条纹的可见度降低,从而看不到干涉条纹, 时,条纹的可见度降低,从而看不到干涉条纹, 此时的最大光程差称为相干长度。 此时的最大光程差称为相干长度。
2π
4π
6π
8π
V << 1
2. 光的非单色性对条纹可见度的影响
普通单色光源发出的光,是有一中心波长λ 普通单色光源发出的光,是有一中心波长λ及谱线 宽度λ的准单色光,其最终干涉条纹是各种波长成分的 λ的准单色光 宽度λ的准单色光 其最终干涉条纹是各种波长成分的 干涉条纹的非相干叠加。 干涉条纹的非相干叠加。设每一波长成分干涉条纹的 可见度都为1,最终干涉条纹的强度分布可示意于下: 可见度都为 ,最终干涉条纹的强度分布可示意于下:
a1 P 2
a2
S
S1 S2
b2
光程差小于波列长 度,同一波列相干叠加
光程差大于波列 长度, 长度,同一波列不能相遇
3.光源的宽度对条纹可见度的影响 3.光源的宽度对条纹可见度的影响
双缝干涉实验的光源是面光源时, 双缝干涉实验的光源是面光源时,可把面 光源看做是许多与缝平行的线光源组成, 光源看做是许多与缝平行的线光源组成,每个 线光源的光都在屏上产生一套干涉条纹, 线光源的光都在屏上产生一套干涉条纹,总的 条纹强度是各套条纹的非相干叠加。 条纹强度是各套条纹的非相干叠加。 如图: 如图: 光源C、A、 B的中央明纹分 别位于O点、OA 点和OB点
干涉条纹的可见度 光波的时间相干性

r0 y j ( ) j d
合成光强
- (/2) + (/2)
0 0 11 2 2 3 3 4 45 56
j 1 j
j
干涉条纹的可见度V→0
x
与此干涉级 j 对应的光程差是实现相干叠加的最大光程差:
2 max j , 定义:由光的单色性所决定的能产生干涉条纹的最大光程差
z
Ap 2
Ap 2
2 sin i2 cos i1 Ap1 sin( i1 i2 ) cos(i1 i2 )
二. 半波损失的解释
1. 劳埃德镜实验中 的半波损失
As1 sin( i1 i2 ) As1 sin( i1 i2 )
2. 维纳驻波实验中的半波I A12 A2 2 A1 A2 cos
2 A1 A2 ( A1 A2 ) ,V 2 2 A1 A2
2
I1 I 2 ( I1 I 2 )V cos
令I1 I 2 I 0
I 0 (1 V cos ) ——双光束干 涉光强分布表达式
§1-4 干涉条纹的可见度 *时间相干性和空间 相干性
一、干涉条纹的可见度(对比度或反衬度)
1. 定义: 2. 讨论:
I max I min V I max I min
当Imin=0时(暗纹全黑),V=1,最清晰;
当Imax=Imin时,V=0,不可辨认;
两列光相干叠加时, I max ( A1 A2 ) , I min
As1
As1
Ap1
i1 i1
A 1 p
n1
x
n2
i2 A s2
光学干涉条纹的可见度光波导时间相干性和空间相干性

由前面的推导可知:
r2
− r1
=
d r0
y,
同理可得
r2'
− r1'
=
d r0'
b 2
因此自M点到达P点 的光程差为:
δM
=
⎛ d⎜
⎝
b 2r0'
+
y r0
⎞ ⎟ ⎠
11
δM
=
d
⎛ ⎜ ⎝
b 2r0'
+
y r0
⎞ ⎟ ⎠
由细线光源M所产生的各级明条纹的位置如下:
零级明条纹: δM = 0
y0M
=−b 2
采用点、缝光源的原因。
16
为了获得清晰的干涉条纹,光源宽度一般限制在 临界宽度的四分之一。
b ≤ bc 4
或
b ≤ r0′ λ
4d
上式称为能够产生清晰的干涉条纹的条件。
由上式可以看到,减小两缝之间的距离d,则 bc就 大,即:用更宽的光源也可以看到干涉条纹。
本节结束 17
S1
θ r1
r
dN
θ
r2
r0 r0'
第j级明条纹: δM = jλ
y jM
= r0 d
jλ
−
b 2
r0 r0'
相邻条纹间距为:
Δy
=
y j+1 −
yj
=
r0 d
λ
与光源中心S点产生的干涉条纹相比较,干涉花样规
律相同,只是整个图样向-y方向移过了y0M的距离。 12
同理可以证明,光源上每一条细线光源都在屏上 产生相同的干涉花样,这些花样在y方向上相互错 开一定的距离。
干涉条纹的可见度光场的相干性投影稿

极大条件:δ = jλ0
y = r0 jλ− r0 d' d r0 '
d⋅ d' r0 '
next
y = r0 jλ − r0 d' d r0 '
即S'处的点光源形成的
干涉条纹的下移: Δy=
r0
d'
r0 '
同理,S''处的点光源形成的
干涉条纹上移: Δy= r0 d' r0 '
光源上其它点形成 的干涉条纹怎样?
next
next
2. 光场的空间相干性 如果d'给定,上式也可以改写成:d ≤ r0 ' λ 2d'
对于给定光源,d是可 产生干涉条纹时双缝的最 大间距。
2d'≤ r0 'λ d
这种在同一时刻,空间横向两点光振动之间的 相干性,称为光场的空间相干性或 横向相干性。
d' 越 小 , d 就 越 大 , 所 以 通 常 在 光 源 与 双 缝 之
next
3. 相干长度与光的单色性的关系 单色光可表示为:E(t,z)=Acos(ωt-kz+ϕ) , 它在时间和空间上都是无限的。 实际光源发出的光的相干长度L都是有限的,理论 可以证明:有限长的波列一定是非单色的,设中心 波长为 λ,波长范围是Δλ。
L、Δλ 关系?
next
分析光源的非单色性对杨氏干涉条纹的影响 假设光源为非单色的点光源,因为
Δy= r0 d' r0 '
当移动距离达到半个条纹宽 度时,干涉条纹消失。
所以要看到干涉条纹,光源 的半径 d'应满足:
r0 d' ≤ 1(r0 λ) r0 ' 2 d
光的干涉干涉条纹的可见度和菲涅耳公式
正射两种情况下,反射光的振动方向对于入射光的振动
方向都几乎相反,即反射产生半波损失。
*但是在任何情况下,折射光在折射瞬间电矢量无位相突变,
无半波损失.
4 A1 A2 2 A12 2 A22
2 A1 / A2 1 ( A1 / A2 )2
光学 1.4 干涉条纹的可见度 时间相干性和空间相干性
V 2 A1 / A2 1 ( A1 / A2 )2
讨论:
A1 A2 ,则V 1,可见度最好 A1 0或A2 0,则V 0,可见度最差 其他情况下,V介于1和0之间
Ap1
tan(i1 i2 )
Ap1、Ap1、Ap2和 As1、As1、As2
As2 2 sin i2 cos i1
As1
sin(i1 i2 )
Ap2
2 sin i2 cos i1
Ap1 sin(i1 i2 ) cos(i1 i2 )
光学
1.5 菲涅耳公式
二、半波损失的解释 1、掠入射(洛埃镜)
d'0 则是要看见干涉条纹时扩展光源的最大线度,称为临界宽度, 超过此宽度的扩展光源则无干涉条纹。
普通光源的宽度越小,可见度越高。这也就是分波面法干涉 一类的双光束干涉装置必须采用点、缝光源的原因。
为了获得清晰的干涉条纹,光源宽度一般限制在临界宽度 的四分之一。
由上式可以看到,减小两缝之间的距离d,则 d'0就大, 即:用更宽的光源也可以看到干涉条纹。
光学 1.4 干涉条纹的可见度 时间相干性和空间相干性
五、空间相干性
公式
d '0
r'0 d
1
决定了杨氏干涉装置的参数。对给定的扩展光源(线度 d'0 ),则双孔或双缝间最大距离dmax由上式决定,为
§4 干涉条纹的可见度
§4 干涉条纹的可见度(光波的空时相干法)一、干涉条纹的可见度1、定义:10 minmax min max ≤≤+-=V I I I I V 当 1,0m i n ==V I 最大 当 0 ,m i n m a x == V I I 模糊2、单色波的V当221max )( 2A A I I j +===∆πϕ当221min )( )12(A A I j -=+=∆πϕ2221212A A A A V += 若 2122210I I A A I +=+=)c o s 1(c o s 20212221ϕϕ∆+=∆++=V I A A A A I例:有一双缝干涉装置,通过其中一缝的能量是另一缝能量的4倍。
求可见度。
解:221 ,4A I I I ==544422 22222222212121=+=+==A A A A A A A V A A 二、光源非单色性的影响1、相干长度通常的单色光源,并不是单一波长,有范围λ∆,从而影响可见度V 。
下以杨氏干涉为例λλ∆=∆=dr j y d r j y 00(1)j 大,y ∆大,可见度降低(2)如果(λλ∆+)的j 级与λ的(j +1)级重合,可见度为零时即 )()1(12λλλδ∆+=+=-=j j r rλλ∆=j 与该干涉级对应的光程差为实现相干的最大光程度,相干长度:)( )(2m a x λλλλλλδ∆>>∆=∆+=j 上式表明:光源的单色性决定产生干涉条纹的最大光程差。
2、时间相干性(1)波列长度光源向外发射的是有限长的波列,其长度由原子发光的持续时间和传播速度所确定。
杨氏装置若两路光程差太大,大于光波列的长度,则a ''刚到p 点,波到a '已过去,无法相遇,b a 与无固定位相关系,b a '''与不相干。
由此可见,波列长度至少应等于max δλλδ∆=≥2m a x L 例:白光(用眼睛观察),波列长度与波长同一数量级。
干涉条纹的可见度(1)
可见度与振幅比的关系:
●
I I1 I 2 4I1
-4 -2 2 4 可见度好 (V = 1) I1 I 2
若 A 1 A 2
I min 0
V 1
●若
I max 2 A1
条纹最清楚
0
I
A 1 A 2
Imax Imin
V 1
●若
条纹可见度差
-4 -2 0 2 4 可见度差 (V < 1)
宽度为b的整个光源在 P点的光强:
b
I
b 2
2
2 I 0 [1 cos k ( )]dx'
sin b / 2 d 2 I 0b 1 cos x b / D
b K sin b
K
扩展光源干涉条纹可见度为
K
§3
干涉条纹的可见度
3、空间相干性(Spatial Coherence ) 若通过光波场横向两点的光在空间相遇时能够 x 发生干涉,则称通过空间两点的光具有相干性。
x'
1
S θ
0’
b
θ
0
2
bc β l
1
e
ω S
2
D
bc e
相干系统不变性
光源尺寸限制了干涉孔径角就限制了一个相干空间
非 相 干 叠 加
合成光强
合成光强
b
结论 y ,条纹可见度下降 b y
§3
干涉条纹的可见度
2、光源宽度 对条纹可见度的影响
dx' S' c
r'
1
r
S
1 1
P
x
干涉条纹的可见度
(相消条件)
r 0¢ 即 d ¢= λ 2d
则干涉条纹 可见度为零
0
若杨氏实验中用的是扩展光源,它的宽度为 d
¢
S
1
ⅱ 且d0 = 2d
则扩展光源可分成许多相距
为d ¢ 的线光源对,
S ¢
d ¢ α
d
S
2
由于每对线光源在屏幕上的干涉花样的可见度为
零,故整个扩展光源在屏幕上的干涉花样的可见度
也为零,在屏幕上无法观察到干涉花样, 这个扩展光源的宽度为 d
¢0
称为临界宽度。
r0¢ ⅱ d0 = 2d = λ d
光源的线度大等于临界宽度
时,干涉条纹的可见度为零.
s
α
1
s r ¢ 2
d
s
r
2
2
p
0
r 0¢
r r d s i n d
2 1
而
dd 2 ta n r 0
S ¢
S
1
2 ⅱ d dd dd \ δ ?d α + ? ⅱ ? r 2 r r 0 0 0
d ¢ α
d
S
2
d¢ d λ 若δ = = 2 r0¢
的相干点光源发出的光来讲,主要因素是振幅比。
2 2 1 2 2
由 I A A A 2 A c A o s 1 2 2 1
可知
2 22 2 Nhomakorabea 2, j I I A A m a x 1
( 2 j1 ) ,I I A m i n 1A
j 1 j
j
可见度 为零
此时的光程差为实现相干的最大光程差:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
横向相干宽度: 横向相干宽度:对一定的光源宽度 b,光通过 Sl 和 光通过 恰好不发生干涉时所对应的这两点的距离 S2 恰好不发生干涉时所对应的这两点的距离
S1
bc l
βc d
S2
λ bC = β
⇒ d = bc d β = l
λl
2.光源非单色性对条纹可见度的影响 光源非单色性对条纹可见度的影响 S’
IM − Im 2 I1I2 K= = LLL(18) IM + Im I1 + I2
①当干涉光强的极小值 Im= 0 时,K = l,双光束 当干涉光强的极小值 光束 完全相干,图像最清晰; 完全相干,图像最清晰; ②当 IM= Im 时,K = 0,双光束完全不相干,无 当 光束完全不相干, 光束完全不相干 干涉图像; 干涉图像; ③当 IM ≠ Im≠ 0 时,0 < K < 1,双光束部分相 当 光束部分相 图像清晰度介于上面两种情况之间。 干,图像清晰度介于上面两种情况之间
S’
x R1
λ
S1
x’
β R
2
r1
θ
P
S
l
d
S2
ω
r2
D
x
0
干涉孔径角:到达干涉场某点 的两条相干光束从实 干涉孔径角:到达干涉场某点P的两条相干光束从实 d 际光源发出时的夹角 β= l
扩展光源干涉条纹可见度为
K =
K 1
λ
πbβ
sin
πbβ
λ
L ( 2 3)
0
λ 4β
λ β
2λ
β
b
随着 b 的增大,可见度 K 将通过一系列极大值和 的增大, 将通过一系列极大值和 零值后逐渐趋于零。 零值后逐渐趋于零。 光源为点光源时,V = 1; 当 b = 0、光源为点光源时 光源为点光源时 当 0< b < λ/β 时,0 < V < 1; 当 b = λ/β 时,V = 0。
c1 S c2
S1 b 1 S
2
a1 a2 P
·
b2 c1 S c2
b1 S1 b2 S2
a1 ·P a2
能干涉
a1 和 a2 经过不同的路程能再相
遇,能干涉
不能干涉
a1 和 a2 经过不同的路程不能再
相遇,不能干涉
只有同一波列 同一波列分成的两部分,经过不同的路 程再相遇 相遇时,才能发生干涉 干涉。 干涉
x R1
λ
S1
x’
β R
2
r1
θ
P
S
l
d
S2
π xd I = 4 I 0 cos λD
2
0
∆
的光源由无数个强度相同, 假设波数宽为 ∆k 的光源由无数个强度相同,宽度为 dk 的元波数光源组成。 的元波数光源组成。
I I0
0
k0-∆k/2 k0 k0+∆k/2 k
光的时间相干性 相干时间:光通过相干长度所需的时间, 相干时间:光通过相干长度所需的时间,其定义为
∆t =
∆ m ax
c
相干时间反映了同一光源在不同时刻发出光的干涉 特性,凡是在相干时间内不同时刻发出的光, 特性,凡是在相干时间内不同时刻发出的光,均可 以产生干涉,而在大于期间发出的光不能干涉. 以产生干涉,而在大于期间发出的光不能干涉.
为了获得清晰度很好的干涉图像, 为了获得清晰度很好的干涉图像,两个光源必须满足 清晰度很好的干涉图像 A、两个光波到达某一点的光程差不能大于两者最小的 波列长度(时间相干性) 波列长度(时间相干性) 光源大小必须小于临界宽度(空间相干性) B、光源大小必须小于临界宽度(空间相干性)
干涉条纹可见度: 干涉条纹可见度:表征干涉效应程度
S’
x R1
S1
λ
β
x’ R2
r1
θ
P
ω
r2
0
x
d
S2
l
S
D
S
S'
在扩展光源情况下, 在扩展光源情况下,每个点光源都将通过干涉系统在 干涉场中产生自己的一组干涉条纹, 干涉场中产生自己的一组干涉条纹,由于各个点光源 位移。 位置不同,它们所产生的干涉条纹最大值之间有位移 位置不同,它们所产生的干涉条纹最大值之间有位移。
βc
S2
S 1′′ ′′ S2
β =
λ
bC
给定时,凡是在该孔径角以外的两点( 当 b 和 λ 给定时,凡是在该孔径角以外的两点(如 S1′ 和S2′)都是不相干的;在孔径角以内的两点(如S1′′ )都是不相干的;在孔径角以内的两点( 和 S2′′)都具有一定程度的相干性;在孔径角边缘的 )都具有一定程度的相干性; 两点( 两点(S1和S2)恰好处于相干和不相干位置上
1. 相干光束振幅比的影响
K=
1+ ( A A2 ) 1
2( A A2 ) 1
2
L (20)
当A1=A2时,K = 1;当A1≠A2时,K<1。 ; 。 两光波的振幅差越大, 越小 越小。 两光波的振幅差越大,K越小。 设计干涉系统时,应尽可能使 设计干涉系统时,应尽可能使K=1。 。
2. 光源大小对条纹可见度的影响
第一个K=0 K=0时对应的扩展光源大小 光源的临界宽度;第一个K=0时对应的扩展光源大小
λ bC = β
这是求解干涉系统中光源的临近宽度的普遍公式 光源的允许宽度:实际工作中,为了获得清晰的干涉 光源的允许宽度:实际工作中, 条纹,通常使光源宽度不超过临界宽度的1/4, 条纹,通常使光源宽度不超过临界宽度的 ,此时的 可见度不小于0.9。 可见度不小于
bC λ bp = = 4 4β (24)
光源的临界宽度与干涉孔径角成反比 光源的临界宽度与干涉孔径角成反比
光的空间相干性 有光源的临界宽度可知,对于给定的光源尺寸, 有光源的临界宽度可知,对于给定的光源尺寸,其干 涉孔径角就限制了一个相干空间 涉孔径角就限制了一个相干空间
S 1′
bc l
S1
S 2′
L•
•
S1 d /2
+1L 0N 0M 0L −1N I
I 非 相 干 叠 加
b/2 M• N 光源宽 度为b 度为 I
S2 r r0 合成光强
合成光强
b↑
y y
为中心的光强均匀的扩展光源由许多无穷小的 许多无穷小的, 假设是以 S 为中心的光强均匀的扩展光源由许多无穷小的,强 度相同,宽度为dx 的元光源组成。 dx’的元光源组成 度相同,宽度为dx 的元光源组成。每一个元光源通过两个小 孔的光强度相同 λl πbd 2π I = 2bI 0 + 2bI 0 sin co s ( r2 − r1 )L ( 2 2 ) πbd λl λ
12.3 干涉条纹的可见度
当两光束满足如下相干条件时, 当两光束满足如下相干条件时,在观察区域内就可以形 成干涉图像(注意:图像不一定最清晰) 成干涉图像(注意:图像不一定最清晰) (1)两束光波的频率应当相同 ) (2)两束光波在相遇处的振动矢量具有相同方向的部分 ) (3)两束光波在相遇处应有固定不变的相位差 )
∆ sin ∆ k 2 I = 2 I0∆k + 2 I0 co s (k 0 ∆ )L 2 6) ( ∆
2
∆ sin ∆ k 2 K= ∆ ∆k 2
K 1
(2 7 )
0
λ2/∆λ
∆
干涉场总强度分布的条纹可见度随着干涉光束间光 干涉场总强度分布的条纹可见度随着干涉光束间光 程差的增大而下降,最后降为零。 程差的增大而下降,最后降为零。 光源为单色光源时,K = 1; 当∆k = 0,光源为单色光源时 光源为单色光源时 2π/∆时 0 <K<1;当 2π/∆时 K= 0。 当0< ∆k< 2π/∆时,0 <K<1 当∆k = 2π/∆时,K= 0 相干长度:当K = 0时,干涉光束间能够发生干涉的最 相干长度: 时 大光程差。 大光程差。 2 λ ∆ m ax = (∆ λ ) 光源的光谱宽度愈宽, 愈大, 愈小。 光源的光谱宽度愈宽,∆λ 愈大,相干长度 ∆max 愈小。
