宁浩数学动点压轴题专项训练七年级33题讲解
七年级下册动点问题及压轴题
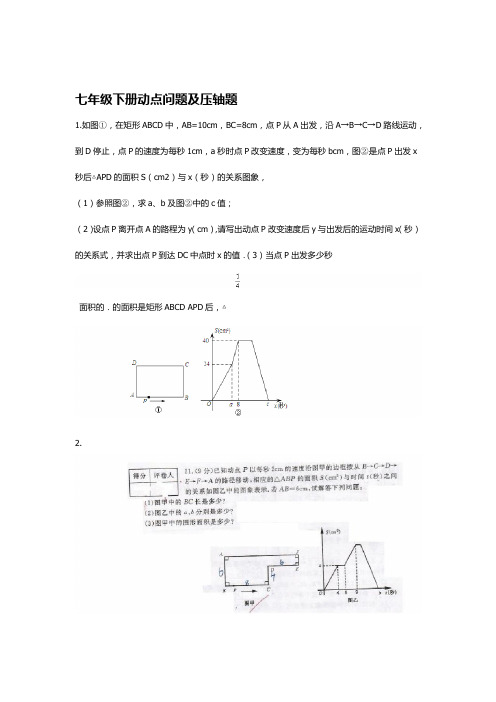
七年级下册动点问题及压轴题1.如图①,在矩形ABCD中,AB=10cm,BC=8cm,点P从A出发,沿A→B→C→D路线运动,到D停止,点P的速度为每秒1cm,a秒时点P改变速度,变为每秒bcm,图②是点P出发x 秒后△APD的面积S(cm2)与x(秒)的关系图象,(1)参照图②,求a、b及图②中的c值;(2)设点P离开点A的路程为y(cm),请写出动点P改变速度后y与出发后的运动时间x(秒)的关系式,并求出点P到达DC中点时x的值.(3)当点P出发多少秒面积的.的面积是矩形ABCD APD后,△2.1 / 63.如图,△ABC是等腰直角三角形,∠C=90°,CD∥AB,CD=AB=4cm,点P4.是边AB上一动点,从点A出发,以1cm/s的速度从点A向终点B运动,连接PD交AC于点F,过点P作PE⊥PD,交BC于点E,连接PC,设点P运动的时间为)(sx()的面积为1()若△PBC2cmy y关于的关系式;,写出x(2)在点P运动的过程中,何时图中会出现全等三角形?直接写出的值以及x相应全等三角形的对数。
2 / 6秒的速度从点2cm/,BC=6cm,动点E以△5.如图在RtABC中,∠C=90°,AC=8cm 点.AB交BC于F运动(与点向点CA,C不重合),过点E作EF∥A1)求AB的长;( EF的长为ycm.(2)设点E出发x秒后,线段上是否存ABx 的取值范围;②试问在①求y与x的函数关系式,并写出自变量为等腰直角三角形?若存在,请说出共有几个,并求出相应的EFPP,使得△在 x的值;若不存在,请简要说明理由.运A向,点D在线段AC上从C,6.在直角三角形ABC中,BC=6AC=8 .CD=x,△ABD的面积为y动.若设与1)请写出yx的关系式;(在什么位置?x为何值时,y有最大值,最大值是多少?此时点D(2)当D的面积的一半时,点在什么位置?3()当△ABD的面积是△ABC分别与的外角平分线和∠ABCAE、BD,∠<∠如图,在△7.ABC中,∠BC<∠ABAC .求∠,∠AEBD=∠BADBAC的度数.∠.若∠、的延长线交于、BCCAEDABC=米,甲乙两人分别从两对边同时向所对的另一边游去,到达对908.一游泳池长边后,再返回,这样往复数次.图中的实线和虚线分别表示甲、乙与游泳池固定一边的距离随游泳时间变化的情况,请根据图形回答:(1)甲、乙两人分别游了几个来回?3 / 6()甲、乙两人在整个游泳过程中,谁曾休息过?休息过几次?2 )甲游了多长时间?游泳的速度是多少?(3 )在整个游泳过程中,甲、乙两人相遇了几次?(4的内部,点∠BCAC的一条直线,且直线CD经过如图,9.CD是经过∠BCA顶点 CA=CB且∠BEC=∠CFA=∠α.上,已知E,F在射线CD ∠α=90°,问EF=BE-AF,成立吗?说明理由.(1)如图1,若∠BCA=90°,EF=BE(如图2),问2)将(1)中的已知条件改成∠BCA=60°,∠α=120°( -AF仍成立吗?说明理由.关系的条件,使与∠BCA<∠BCA<90°,请你添加一个关于∠α(3)若0°.(直接写出结 EF=BE-AF结论仍然成立.你添加的条件是论)AF,BE,EF3)如图,若直线CD经过∠BCA的外部,∠α=∠BCA,请提出(4 三条线段数量关系的合理猜想(不要求证明).与CEAB,△BDC为等腰直角三角形,CEAD10. .如图,梯形ABCD,∥BC,⊥).证明:(交DGCF于M1中点,连接为,,连接交于BDFAFGBC .);(CM=AB2CF=AB+AF4 / 6AP=×8×AD·1×a=24答案:解:(1)由图得知:S△APD=1.∴a=6=b==2c=8+=17(2)y=6+2(x-6)=2x-6(6≦x≦17)P到达DC中点时,y=10+8+10×=23即23=2x-6x=APD=S矩形ABCD CD中点时,S△中点和(3)当P在AB当P在AB中点时,P出发5秒;当P在CD中点时,代入(2)中y=2x-6即23=2x-6x=APD=S矩形△ABCD。
初一培优专题:数轴上动点问题(有答案)

培优专题:借助方程求解数轴上的动点问题(压轴题常考题型)数轴上的动点问题离不开数轴上两点之间的距离。
为了便于初一年级学生对这类问题的分析,不妨先明确以下几个问题:1.数轴上两点间的距离,即为这两点所对应的坐标差的绝对值,也即用右边的数减去左边的数的差。
即数轴上两点间的距离=右边点表示的数—左边点表示的数。
2.点在数轴上运动时,由于数轴向右的方向为正方向,因此向右运动的速度看作正速度,而向作运动的速度看作负速度。
这样在起点的基础上加上点的运动路程就可以直接得到运动后点的坐标。
即一个点表示的数为a,向左运动b个单位后表示的数为a—b;向右运动b个单位后所表示的数为a+b。
3.数轴是数形结合的产物,分析数轴上点的运动要结合图形进行分析,点在数轴上运动形成的路径可看作数轴上线段的和差关系。
一、相关知识准备1.数轴上表示4和1的两点之间的距离是_____________。
-,则A与B两点之间的距离用式子2.若数轴上点A表示的数为x,点B表示的数为1可以表示为_____________,若在数轴上点A在点B的右边,则式子可以化简为_____________。
3.A点在数轴上以2个单位长度/秒的速度向右运动,若运动时间为t,则A点运动的路程可以用式子表示为______________。
-,A点在数轴上以2个单位长度/秒的速度向右运动,4.若数轴上点A表示的数为1若运动时间为t,则A点运动t秒后到达的位置所表示的数可以用式子表示为______________。
答案:1、3; 2、1x+,x+1; 3、2t; 4、12t-+二、已做题再解:1、半期考卷的第25题:如图所示,在数轴上原点O表示数0,A点在原点的左侧,所表示的数是a,B点在原点的右侧,所表示的数是b,并且a、b满足-2++8=a16(b)0(1)点A表示的数为_________,点B表示的数为________。
(2)若点P从点A出发沿数轴向右运动,速度为每秒3个单位长度,点Q从点B出发沿数轴向左运动,速度为每秒1个单位长度,P、Q两点同时运动,并且在点C处相遇,试求点C所表示的数。
七年级下册数学动点问题及压轴题(带答案)

七年级下册动点问题及压轴题1.如图1,在平面直角坐标系中,A(a,0)是x轴正半轴上一点,C是第四象限一点,CB⊥y轴,交y轴负半轴于B(0,b),且(a﹣3)2+|b+4|=0,S四边形AOBC=16.(1)求C点坐标;(2)如图2,设D为线段OB上一动点,当AD⊥AC时,∠ODA的角平分线与∠CAE 的角平分线的反向延长线交于点P,求∠APD的度数.(3)如图3,当D点在线段OB上运动时,作DM⊥AD交BC于M点,∠BMD、∠DAO的平分线交于N点,则D点在运动过程中,∠N的大小是否变化?若不变,求出其值,若变化,说明理由.【解答】解:(1)∵(a﹣3)2+|b+4|=0,∴a﹣3=0,b+4=0,∴a=3,b=﹣4,∴A(3,0),B(0,﹣4),∴OA=3,OB=4,∵S四边形AOBC=16.∴(OA+BC)×OB=16,∴(3+BC)×4=16,∴BC=5,∵C是第四象限一点,CB⊥y轴,∴C(5,﹣4)(2)如图,延长CA,∵AF是∠CAE的角平分线,∴∠CAF=∠CAE,∵∠CAE=∠OAG,∴∠CAF=∠OAG,∵AD⊥AC,∴∠DAO+∠OAG=∠PAD+∠PAG=90°,∵∠AOD=90°,∴∠DAO+∠ADO=90°,∴∠ADO=∠OAG,∴∠CAF=∠ADO,∵DP是∠ODA的角平分线∴∠ADO=2∠ADP,∴∠CAF=∠ADP,∵∠CAF=∠PAG,∴∠PAG=∠ADP,∴∠APD=180°﹣(∠ADP+∠PAD)=180°﹣(∠PAG+∠PAD)=180°﹣90°=90°即:∠APD=90°(3)不变,∠ANM=45°理由:如图,∵∠AOD=90°,∴∠ADO+∠DAO=90°,∵DM⊥AD,∴∠ADO+∠BDM=90°,∴∠DAO=∠BDM,∵NA是∠OAD的平分线,∴∠DAN=∠DAO=∠BDM,∵CB⊥y轴,∴∠BDM+∠BMD=90°,∴∠DAN=(90°﹣∠BMD),∵MN是∠BMD的角平分线,∴∠DMN=∠BMD,∴∠DAN+∠DMN=(90°﹣∠BMD)+∠BMD=45°在△DAM中,∠ADM=90°,∴∠DAM+∠DMA=90°,在△AMN中,∠ANM=180°﹣(∠NAM+∠NMA)=180°﹣(∠DAN+∠DAM+∠DMN+∠DMA)=180°﹣[(∠DAN+DMN)+(∠DAM+∠DMA)]=180°﹣(45°+90°)=45°,∴D点在运动过程中,∠N的大小不变,求出其值为45°2.如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.(1)试判断直线AB与直线CD的位置关系,并说明理由;(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.【考点】JB:平行线的判定与性质.【分析】(1)利用对顶角相等、等量代换可以推知同旁内角∠AEF、∠CFE互补,所以易证AB∥CD;(2)利用(1)中平行线的性质推知°;然后根据角平分线的性质、三角形内角和定理证得∠EPF=90°,即EG⊥PF,故结合已知条件GH⊥EG,易证PF∥GH;(3)利用三角形外角定理、三角形内角和定理求得∠4=90°﹣∠3=90°﹣2∠2;然后由邻补角的定义、角平分线的定义推知∠QPK=∠EPK=45°+∠2;最后根据图形中的角与角间的和差关系求得∠HPQ的大小不变,是定值45°.【解答】解:(1)如图1,∵∠1与∠2互补,∴∠1+∠2=180°.又∵∠1=∠AEF,∠2=∠CFE,∴∠AEF+∠CFE=180°,∴AB∥CD;(2)如图2,由(1)知,AB∥CD,∴∠BEF+∠EFD=180°.又∵∠BEF与∠EFD的角平分线交于点P,∴∠FEP+∠EFP=(∠BEF+∠EFD)=90°,∴∠EPF=90°,即EG⊥PF.∵GH⊥EG,∴PF∥GH;(3)∠HPQ的大小不发生变化,理由如下:如图3,∵∠1=∠2,∴∠3=2∠2.又∵GH⊥EG,∴∠4=90°﹣∠3=90°﹣2∠2.∴∠EPK=180°﹣∠4=90°+2∠2.∵PQ平分∠EPK,∴∠QPK=∠EPK=45°+∠2.∴∠HPQ=∠QPK﹣∠2=45°,∴∠HPQ的大小不发生变化,一直是45°.3.如图①,在矩形ABCD中,AB=10cm,BC=8cm,点P从A出发,沿A→B→C→D 路线运动,到D停止,点P的速度为每秒1cm,a秒时点P改变速度,变为每秒bcm,图②是点P出发x秒后△APD的面积S(cm2)与x(秒)的关系图象,(1)参照图②,求a、b及图②中的c值;(2)设点P离开点A的路程为y(cm),请写出动点P改变速度后y与出发后的运动时间x(秒)的关系式,并求出点P到达DC中点时x的值.(3)当点P出发多少秒后,△APD的面积是矩形ABCD面积的.4.星光橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如表:进价(元/台)售价(元/台)电饭煲200250电压锅160200(1)一季度,橱具店购进这两种电器共30台,用去了5600元,并且全部售完,问橱具店在该买卖中赚了多少钱?(2)为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50台,且电饭煲的数量不少于电压锅的,问橱具店有哪几种进货方案?并说明理由;(3)在(2)的条件下,请你通过计算判断,哪种进货方案橱具店赚钱最多?【考点】一元一次不等式组的应用;二元一次方程组的应用.【分析】(1)设橱具店购进电饭煲x台,电压锅y台,根据图表中的数据列出关于x、y的方程组并解答即可,等量关系是:这两种电器共30台;共用去了5600元;(2)设购买电饭煲a台,则购买电压锅(50﹣a)台,根据“用不超过9000元的资金采购电饭煲和电压锅共50台,且电饭煲的数量不少于电压锅的”列出不等式组;(3)结合(2)中的数据进行计算.【解答】解:(1)设橱具店购进电饭煲x台,电压锅y台,依题意得,解得,所以,20×+10×=1400(元).答:橱具店在该买卖中赚了1400元;(2)设购买电饭煲a台,则购买电压锅(50﹣a)台,依题意得,解得22≤a≤25.又∵a为正整数,∴a可取23,24,25.故有三种方案:①防购买电饭煲23台,则购买电压锅27台;②购买电饭煲24台,则购买电压锅26台;③购买电饭煲25台,则购买电压锅25台.(3)设橱具店赚钱数额为W元,当a=23时,W=23×+27×=2230;当a=24时,W=24×+26×=2240;当a=25时,W=25×+25×=2250;综上所述,当a=25时,W最大,此时购进电饭煲、电压锅各25台.5.(本题12分)已知:在平面直角坐标系中,直线AB 分别与x 轴负半轴、y 轴正半轴交于点B (b ,0)、点A (0,a ),且a 、b 满足0|32|34=++++--b a b a ,点D (h ,m )是直线AB 上且不与A 、B 两点重合的动点(1) 求△AOB 的面积;(2) 如图1,点P 、点T 分别是线段OA 、x 轴正半轴上的动点,过T 作TE ∥AB ,连接TP .若∠ABO =n °,请探究∠APT 与∠PTE 之间的数量关系?(注:可用含n 的式子表达并说明理由)(3) 若32S △BOD ≥S △AOD ,求出m 的取值范围.。
初一数学期末复习数轴绝对值动点压轴题难题(附答案详解)

初一数学数轴绝对值动点压轴题(附答案详解)一、解答题(共20小题)1. 如图,数轴的原点为O,点A,B,C是数轴上的三点,点B对应的数为1,AB=6,BC=2,动点P,Q同时从A,C出发,分别以每秒2个单位长度和每秒1个单位长度的速度沿数轴正方向运动.设运动时间为t秒(t>0).(1)求点A,C分别对应的数;(2)求点P,Q分别对应的数(用含t的式子表示).(3)试问当t为何值时,OP=OQ?2. 已知点P,Q是数轴上的两个动点,且P,Q两点的速度比是1:3.(速度单位:单位长度/秒)(1)动点P从原点出发向数轴负方向运动,同时,动点Q也从原点出发向数轴正方向运动,4秒时,两点相距16个单位长度.求两个动点的速度,并在数轴上标出P,Q两点从原点出发运动4秒时的位置.(2)如果P,Q两点从(1)中4秒时的位置同时向数轴负方向运动,那么再经过几秒,点P,Q到原点的距离相等?3. 阅读下面材料:如图,点A,B在数轴上分别表示有理数a,b,则A,B两点之间的距离可以表示为∣a−b∣.根据阅读材料与你的理解回答下列问题:(1)数轴上表示3与−2的两点之间的距离是.(2)数轴上有理数x与有理数7所对应两点之间的距离用绝对值符号可以表示为.(3)代数式∣x+8∣可以表示数轴上有理数x与有理数所对应的两点之间的距离;若∣x+8∣=5,则x=.(4)求代数式∣x+1008∣+∣x+504∣+∣x−1007∣的最小值.4. 如图1,在平面直角坐标系中,A(6,a),B(b,0)且(a−6)2+√b−2=0.(1)求点A,B的坐标;(2)如图1,P点为y轴正半轴上一点,连接BP,若S△PAB=15,请求出P点的坐标;(3)如图2,已知AB=√52,若C点是x轴上一个动点,是否存在点C,使BC=AB,若存在,请直接写出所有符合条件的点C的坐标;若不存在,请说明理由.5. 如图,A,B分别为数轴上的两点,A点对应的数为−5,B点对应的数为55,现有一动点P以6个单位/秒的速度从B点出发,同时另一动点Q恰好以4个单位/秒的速度从A点出发:(1)若P向左运动,同时Q向右运动,在数轴上的C点相遇,求C点对应的数.(2)若P向左运动,同时Q向左运动,在数轴上的D点相遇,求D点对应的数.(3)若P向左运动,同时Q向右运动,当P与Q之间的距离为20个单位长度时,求此时Q点所对应的数.6. 数轴上从左到右有A,B,C三个点,点C对应的数是10,AB=BC=20.(1)点A对应的数是,点B对应的数是;(2)若数轴上有一点D,且BD=4,则点D表示的数是什么?(3)动点P从A出发,以每秒4个单位长度的速度向终点C移动,同时,动点Q从点B出发,以每秒1个单位长度的速度向终点C移动,设移动时间为t秒.当点P和点Q间的距离为8个单位长度时,求t的值.7. 如图,已知点O是原点,点A在数轴上,点A表示的数为−6,点B在原点的右侧,且OB=4OA.3(1)点B对应的数是,在数轴上标出点B.(2)已知点P、点Q是数轴上的两个动点,点P从点A出发,以1个单位/秒的速度向右运动,同时点Q从点B出发,以3个单位/秒的速度向左运动;①用含t的式子分别表示P,Q两点表示的数:P是;Q是;②若点P和点Q经过t秒后在数轴上的点D处相遇,求出t的值和点D所表示的数;③求经过几秒,点P与点Q分别到原点的距离相等?8. 如图,半径为1个单位的圆片上有一点A与数轴的原点重合,AB是圆片的直径.(1)把圆片沿数轴向左滚动1周,点A到达数轴上点C的位置,点C表示的数是数(填“无理”或“有理”),这个数是;(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是;(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,−1,−5,+4,+3,−2.当圆片结束运动时,A点运动的路程共有多少?此时点A所表示的数是多少?9. 结合数轴与绝对值的知识回答下列问题:(1)数轴上表示4和1的两点之间的距离是;表示−3和2两点之间的距离是;一般地,数轴上表示数m和数n的两点之间的距离等于∣m−n∣.如果表示数a 和−1的两点之间的距离是3,那么a=.(2)若数轴上表示数a的点位于−4与2之间,则∣a+4∣+∣a−2∣的值为;(3)利用数轴找出所有符合条件的整数点x,使得∣x+2∣+∣x−5∣=7,这些点表示的数的和是.(4)当a=时,∣a+3∣+∣a−1∣+∣a−4∣的值最小,最小值是.10. 如图,数轴上的点O和A分别表示0和10,点P是线段OA上一动点,沿O→A→O以每秒2个单位的速度往返运动1次,B是线段OA的中点,设点P运动时间为t秒(0≤t≤10).(1)线段BA的长度为;(2)当t=3时,点P所表示的数是;(3)求动点P所表示的数(用含t的代数式表示);(4)在运动过程中,当PB=2时,求运动时间t.11. A,B,C为数轴上的三点,动点A,B同时从原点出发,动点A每秒运动x个单位,动点B每秒运动y个单位,且动点A运动到的位置对应的数记为a,动点B运动到的位置对应的数记为b,定点 C 对应的数为8.(1)若2秒后,a,b满足∣a+8∣+(b−2)2=0,则x=,y=,并请在数轴上标出A,B两点的位置.(2)若动点A,B在(1)运动后的位置上保持原来的速度,且同时向正方向运动z秒后使得∣a∣=∣b∣,使得z=.(3)若动点A,B在(1)运动后的位置上都以每秒2个单位向正方向运动继续运动t秒,点A 与点C之间的距离表示为AC,点B与点C之间的距离表示为BC,点A与点B之间的距离为AB,且AC+BC=1.5AB,则t=.12. 探索研究:(1)比较下列各式的大小(用“<”或“>”或“=”连接).①∣+1∣+∣4∣∣+1+4∣;②∣−6∣+∣−3∣∣−6−3∣;③∣10∣+∣−3∣∣10−3∣;④∣8∣+∣−5∣∣8−5∣;⑤∣0∣+∣+2∣∣0+2∣;⑥∣0∣+∣−8∣∣0−8∣.(2)通过以上比较,请你分析、归纳出当a,b为有理数时,∣a∣+∣b∣∣a+b∣(用“<”或“>”或“=”或“≥”或“≤”连接).(3)根据(2)中得出的结论,当∣x∣+2017=∣x−2017∣时,则x的取值范围是;若x>0,且∣x∣+∣y∣=10,∣x+y∣=2,则y=.13. 阅读下面材料并回答问题.I阅读:数轴上表示−2和−5的两点之间的距离等于(−2)−(−5)=3;数轴上表示1和−3的两点之间的距离等于1−(−3)=4.一般地,数轴上两点之间的距离等于右边点对应的数减去左边点对应的数.II问题:如图,O为数轴原点,A,B,C是数轴上的三点,A,C两点对应的数互为相反数,且A点对应的数为−6,B点对应的数是最大负整数.(1)点B对应的数是,并请在数轴上标出点B位置;PC,求线段AP中点对应的数;(2)已知点P在线段BC上,且PB=25⋅x2−bx+2的值(a,b,c是点(3)若数轴上一动点Q表示的数为x,当QB=2时,求a+c100A,B,C在数轴上对应的数).14. 如图,已知数轴上点A表示的数为6,点B表示的数为−4,C为线段AB的中点,动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.(1)点C表示的数是;(2)当t=秒时,点P到达点A处;(3)点P表示的数是(用含字母t的代数式表示);(4)当t=秒时,线段PC的长为2个单位长度;(5)若动点Q同时从点A出发,以每秒1个单位长度的速度沿数轴向左匀速运动,那么,当t=秒时,PQ的长为1个单位长度.15. 阅读理解.小红和小明在研究绝对值的问题时,碰到了下面的问题:“当式子∣x+1∣+∣x−2∣取最小值时,相应的x的取值范围是,最小值是”.小红说:“如果去掉绝对值问题就变得简单了.”小明说:“利用数轴可以解决这个问题.”他们把数轴分为三段:x<−1,−1≤x≤2和x>2,经研究发现,当−1≤x≤2时,值最小为3.请你根据他们的解题解决下面的问题:(1)当式子∣x−2∣+∣x−4∣+∣x−6∣+∣x−8∣取最小值时,相应的x的取值范围是,最小值是.(2)已知y=∣2x+8∣−4∣x+2∣,求相应的x的取值范围及y的最大值.写出解答过程.16. 阅读思考:小聪在复习过程中,发现可以用“两数的差”来表示“数轴上两点间的距离”,探索过程如下:如图甲所示,三条线段的长度可表示为AB=4−2=2,CB=4−(−2)=6,DC=(−2)−(−4)=2,于是他归纳出这样的结论:当b>a时,AB=b−a(较大数−较小数).(1)思考:你认为小聪的结论正确吗? .(2)尝试应用:①如图乙所示,计算:EF=,FA=.②把一条数轴在数m处对折,使表示−14和2014两数的点恰好互相重合,则m=.(3)问题解决:①如图丙所示,点A表示数x,点B表示−2,点C表示数2x+8,且BC=4AB,问:点A和点C分别表示什么数?②在上述①的条件下,在如图丙所示的数轴上是否存在满足条件的点D,使DA+DC=3DB?若存在,请直接写出点D所表示的数;若不存在,请说明理由.17. 如图,数轴上有A、B、C、D四个点,分别对应的数为a、b、c、d,且满足a,b是方程∣x+9∣=1的两解(a<b),(c−16)2与∣d−20∣互为相反数.(1)求a、b、c、d的值;(2)若A、B两点以每秒6个单位的速度向右匀速运动,同时C、D两点以每秒2个单位的速度向左匀速运动,并设运动时间为t秒,问t为多少时,A、B两点都运动在线段CD上(不与C、D两个端点重合)?(3)在(2)的条件下,A、B、C、D四个点继续运动,当点B运动到点D的右侧时,问是否存在时间t,使B与C的距离是A与D的距离的4倍,若存在,求时间t;若不存在,请说明理由.18. 已知在数轴上有A,B两点,点A表示的数为8,点B在A点的左边,且AB=12.若有一动点P从数轴上点A出发,以每秒3个单位长度的速度沿数轴向左匀速运动,动点Q从点B出发,以每秒2个单位长度的速度沿着数轴向右匀速运动,设运动时间为t秒.(1)写出数轴上点B,P所表示的数(可以用含t的代数式表示);(2)若点P,Q分别从A,B两点同时出发,问点P运动多少秒与Q相距2个单位长度?(3)若M为AQ的中点,N为BP的中点.当点P在线段AB上运动过程中,探索线段MN与线段PQ的数量关系.19. 在数轴上依次有 A ,B ,C 三点,其中点 A ,C 表示的数分别为 −2,5,且 BC =6AB .(1)在数轴上表示出 A ,B ,C 三点;(2)若甲、乙、丙三个动点分别从 A ,B ,C 三点同时出发,沿数轴负方向运动,它们的速度分别是 14,12,2(单位长度/秒),当丙追上甲时,甲乙相距多少个单位长度?(3)在数轴上是否存在点 P ,使 P 到 A ,B ,C 的距离和等于 10?若存在求点 P 对应的数;若不存在,请说明理由.20. 已知数轴上三点 M ,O ,N 对应的数分别为 −3,0,1,点 P 为数轴上任意一点,其对应的数为x .(1)如果点 P 到点 M 、点 N 的距离相等,那么 x 的值是 . (2)当 x = 时,使点 P 到点 M ,点 N 的距离之和是 5;(3)如果点 P 以每秒钟 3 个单位长度的速度从点 O 向左运动时,点 M 和点 N 分别以每秒钟 1个单位长度和每秒钟 4 个单位长度的速度也向左运动,且三点同时出发,那么 秒钟时点 P 到点 M ,点 N 的距离相等.答案第一部分1. (1)∵点B对应的数为1,AB=6,BC=2,∴点A对应的数是1−6=−5,点C对应的数是1+2=3.(2)∵动点P,Q分别同时从A,C出发,分别以每秒2个单位长度和1个单位长度的速度沿数轴正方向运动,∴点P对应的数是−5+2t,点Q对应的数是3+t.(3)①当点P与点Q在原点两侧时,若OP=OQ,则5−2t=3+t,解得:t=23;②当点P与点Q在原点同侧时,若OP=OQ,则−5+2t=3+t,解得:t=8;当t为23或8时,OP=OQ.2. (1)设P的速度为x单位长度/秒,Q的速度为3x单位长度/秒.依题意,得4(x+3x)=16,∴x=1.∴P的速度为1单位长度/秒,Q的速度为3单位长度/秒.4秒时,P的位置在−4,Q的位置在12.(2)设再经过y秒时,点P,Q到原点的距离相等,①当点P,Q位于原点两侧时,12−3y=4+y,解得,y=2.②当点P,Q位于原点同侧时,3y−12=4+y,解得,y=8.所以再经过2秒或8秒时点P,Q到原点的距离相等.3. (1)5【解析】∣3−(−2)∣=5.(2)∣x−7∣(3)−8;−3或−13(4)如图,∣x+1008∣+∣x+504∣+∣x−1007∣的最小值即∣1007−(−1008)∣=2015.4. (1)∵(a−6)2+√b−2=0,又∵(a−6)2≥0,√b−2≥0,∴a=6,b=2,∴A(6,6),B(2,0).(2)设P(0,m)(m>0),∵S△PAB=S△POA+S△ABO−S△POB,∴15=12×m×6+12×2×6−12×2×m,9).∴P(0,92(3)C(2+2√13,0)或(2−2√13,0).【解析】∵AB=√52=2√13,B(2,0),∴BC=AB=2√13,∴C(2+2√13,0)或(2−2√13,0).5. (1)设相遇时间为x秒,4x+6x=55−(−5),解得:x=6,因此C点对应的数为−5+4×6=19.(2)设追及时间为y秒,6y−4y=55−(−5),解得:y=30,点D对应的数为−5−4×30=−125.(3)①相遇前PQ=20时,设相遇时间为a秒,4a+6a=55−(−5)−20,解得:a=4,因此Q点对应的数为−5+4×4=11,②相遇后PQ=20时,设相遇时间为b秒,4b+6b=55−(−5)+20,解得:b=8,因此C点对应的数为−5+4×8=27,故Q点对应的数为11或27.6. (1)−30;−10【解析】∵AB=BC=20,点C对应的数是10,点A在点B左侧,点B在点C左侧,∴点B对应的数为10−20=−10,点A对应的数为−10−20=−30.(2)由于点B对应的数为−10,BD=4,∴点D表示的数为−14或−6.(3)当运动时间为t秒时,点P对应的数是4t−30,点Q对应的数是t−10,依题意,得:∣t−10−(4t−30)∣=8,∴20−3t=8或3t−20=8,解得:t=4或t=28.3.∴t的值为4或2837. (1)8数轴表示如图所示:【解析】∵点A表示的数为−6,∴OA=6,OA,∵OB=43∵点B在原点的右侧,∴点B对应的数是8.(2)①−6+t;8−3t②∵点P和点Q经过t秒后在数轴上的点D处相遇,∴−6+t=8−3t,∴t=7,2=−2.5.∴点D所表示的数=−6+72③∵P是−6+t;Q是8−3t,∴OP=∣−6+t∣,OQ=∣8−3t∣,∵点P与点Q分别到原点的距离相等,∴∣−6+t∣=∣8−3t∣,∴−6+t=8−3t或−6+t=3t−8,或t=1,∴t=72秒或1秒,点P与点Q分别到原点的距离相等.∴经过72【解析】①∵P的路程为t,Q的路程为3t,∴P是−6+t;Q是8−3t.8. (1)无理;−2π【解析】把圆片沿数轴向左滚动1周,点A到达数轴上点C的位置,点C表示的数是无理数,这个数是−2π.(2)±4π【解析】把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是±4π.(3)2+1+5+4+3+2=17,故A点运动的路程共有34π,+2−1−5+4+3−2=1,故此时点A所表示的数是2π.9. (1)3;5;−4或2【解析】∣1−4∣=3,∣−3−2∣=5,∣a−(−1)∣=3,所以,a+1=3或a+1=−3,解得a=−4或a=2.(2)6【解析】因为表示数a的点位于−4与2之间,所以a+4>0,a−2<0,所以∣a+4∣+∣a−2∣=(a+4)+[−(a−2)]=a+4−a+2=6.(3)12【解析】使得∣x+2∣+∣x−5∣=7的整数点有−2,−1,0,1,2,3,4,5,−2−1+0+1+2+ 3+4+5=12.故这些点表示的数的和是12.(4)1;7【解析】a=1有最小值,最小值=∣1+3∣+∣1−1∣+∣1−4∣=4+0+3=7.10. (1)5【解析】∵B是线段OA的中点,∴BA=12OA=5.(2)6【解析】当t=3时,点P所表示的数是2×3=6.(3)当0≤t≤5时,动点P所表示的数是2t;当5≤t≤10时,动点P所表示的数是20−2t.(4)①当0≤t≤5时,动点P所表示的数是2t,∵PB=2,∴∣2t−5∣=2,∴2t−5=2或2t−5=−2,解得t=3.5或t=1.5;②当5≤t≤10时,动点P所表示的数是20−2t,∵PB=2,∴∣20−2t−5∣=2,∴20−2t−5=2或20−2t−5=−2,解得t=6.5或t=8.5.综上所述,所求t的值为1.5或3.5或6.5或8.5.11. (1)4;1(2)103或56(3)2.75或9.2512. (1)=;=;>;>;=;=(2)≥(3)x≤0;−6或−413. (1)−1点B位置如图:【解析】点B对应的数是−1.(2)设点P对应的数为p,∵点P在线段BC上,∴PB=p−(−1)=p+1,PC=6−p,∵PB=25PC,∴p+1=25(6−p),∴p=1.设AP中点对应的数为t,则t−(−6)=1−t,∴t=−2.5,∴AP中点对应的数为−2.5.(3)由题意:a+c=0,b=−1,当点Q在点B左侧时,−1−x=2,x=−3,∴a+c100−x2−bx+2=0=0−(−1)×(−3)+2=−1,当点Q在点B左侧时,x−(−1)=2,x=1,∴a+c100−x2−bx+2=0−(−1)×1+2=3.14. (1)1【解析】(6−4)÷2 =2÷2= 1.故点C表示的数是1.(2)5【解析】[6−(−4)]÷2 =10÷2=5(秒).答:当t=5秒时,点P到达点A处.(3)2t−4【解析】点P表示的数是2t−4.(4)1.5秒或3.5【解析】P在点C左边,[1−2−(−4)]÷2=3÷2= 1.5(秒).P在点C右边,[1+2−(−4)]÷2=7÷2= 3.5(秒).答:当t=1.5秒或3.5秒时,线段PC的长为2个单位长度.(5)3秒或113【解析】点P,Q相遇前,依题意有(2+1)t=6−(−4)−1,解得t=3;点P,Q相遇后,依题意有(2+1)t=6−(−4)+1,解得t=113.答:当t=3秒或113秒时,PQ的长为1个单位长度.15. (1)4≤x≤6;8.(2)当x≥−2时,y=∣2x+8∣−4∣x+2∣=−2x,当−4≤x≤−2时,y=∣2x+8∣−4∣x+2∣=6x+16,当x≤−4时,y=∣2x+8∣−4∣x+2∣=2x,所以x=−2时,y有最大值y=4.16. (1)正确【解析】∵当b>a时,b−a的值为线段AB的实际长度.(2)2;3;1000(3)①∵BC=2x+8−(−2)=2x+10,AB=−2−x,又∵BC=4AB,∴2x+10=4(−2−x),解得x=−3,∴点A表示数−3,点C表示数2.②存在.设点D所表示的数为y,则(a)当y<−3时,DA=−3−y,DC=2−y,DB=−2−y,若DA+DC=3DB,则−3−y+2−y=3(−2−y),解得y=−5,满足条件;(b)当−3≤y<−2时,DA=y−(−3)=y+3,DC=2−y,DB=−2−y,若DA+DC=3DB,则y+3+2−y=3(−2−y),解得y=−113<−3,不符合题意;(c)当−2≤y<2时,DA=y−(−3)=y+3,DC=2−y,DB=y−(−2)=y+2,若DA+DC=3DB,则y+3+2−y=3(y+2),解得y=−13,满足条件;(d)当y≥2时,DA=y−(−3)=y+3,DC=y−2,DB=y−(−2)=y+2,若DA+DC=3DB,则y+3+y−2=3(y+2),解得y=−5,不符合题意.综上可知,存在点D表示的数为−5或−13时满足条件.17. (1)∵a,b是方程∣x+9∣=1的两根(a<b),∴a=−10,b=−8 .∵(c−16)2与∣d−20∣互为相反数,(c−16)2≥0,∣d−20∣≥0,∴c−16=0,d−20=0.∴c=16,d=20 .(2)可知:AC=26,BD=28,AB=2,CD=4.∵A、B两点以每秒6个单位的速度向右匀速运动,C、D两点以每秒2个单位的速度向左匀速运动,∴点A、C相遇时间t=26÷(6+2)=134,点B、D的相遇时间t=28÷(6+2)=72.∵点A、C相遇之后到B、D相遇之前,A、B两点都运动在线段CD上,∴当134<t<72时,A、B两点都运动在线段CD上.(3) 存在时间,使得 BC =4AD .理由:(1) 当 t =72 时,点 B 与点 D 相遇,此时 AD =AB =2,BC =CD =4; 当 A 、 D 相遇时 t =30÷8=154; 当 72<t <154 时,点 A 在线段 CD 上,此时 BC =4+8(t −72)=8t −24,AD =2−8(t −72)=30−8t . 若 BC =4AD ,则 8t −24=4(30−8t ),解得 t =3.6;(2) 当 t =154 时,点 A 与点 D 相遇,此时 BC =CD +AB =6,AD =0; 当 t >154 时,点 A 在 CD 的延长线上,此时 BC =8t −24,AD =8t −30 .若 BC =4AD ,则 8t −24=4(8t −30),解得 t =4.综上所述,t =3.6 或 t =4 时,BC =4AD .18. (1) ∵ 点 A 表示的数为 8,B 在 A 点左边,AB =12,∴ 点 B 表示的数是 8−12=−4.∵ 动点 P 从点 A 出发,以每秒 3 个单位长度的速度沿数轴向左匀速运动,设运动时间为 t (t >0)秒, ∴ 点 P 表示的数是 8−3t .(2) 设点 P 运动 x 秒时,与 Q 相距 2 个单位长度.则 AP =3x ,BQ =2x .∵AP +BQ =AB −2,∴3x +2x =10.解得:x =2.∵AP +BQ =AB +2,∴3x +2x =14.解得:x =145.∴ 点 P 运动 2 秒或 145 秒时与点 Q 相距 2 个单位长度.(3) 如图:当 P 在 Q 的左侧时,MN =MQ +NP −PQ =12AP +12BP −PQ =12(AP +BP )−PQ =12AB −PQ =6−PQ . 即 MN +PQ =6.如图当 P 在 Q 的右侧时,MN =MQ +NP −PQ =12AP +12BP −PQ =12(AP +BP )−PQ =12AB −PQ =6−PQ . 综上,MN +PQ =6.19. (1)(2) 7÷(2−14)=4(秒),4×(12−14)−1=0.答:丙追上甲时,甲乙相距 0 个单位长度.(3) 设 P 点表示的数为 x ,由题意可得 ∣x +2∣+∣x +1∣+∣x −5∣=10.当 x <−2 时,−x −2−x −1−x +5=10.解得 x =−83. 当 −2<x <−1 时,x +2−x −1−x +5=10.解得 x =−4,不属于上述范围(舍).当 −1<x <5 时,x +2+x +1−x +5=10.解得 x =2.当 x >5 时,x +2+x +1+x −5=10.解得 x =4,不属于上述范围(舍).结合数轴,解得 x =−83,2,∴P 点表示的数为 −83 或 2.20. (1) −1(2) −3.5 或 1.5(3) 43 或 2 【解析】提示:①当点 M 和点 N 在点 P 同侧时,因为 PM =PN ,所以点 M 和点 N 重合. ②当点 M 和点 N 在点 P 两侧时,有两种情况.情况 1:如果点 M 在点 N 左侧;情况 2:如果点 M 在点 N 右侧.。
七年级数学动点压轴题专项练习

七年级数学动点压轴题专项练习1.如图,已知射线CB∥OA,∠C=∠OAB=100°,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF(1)求∠EOB的度数.(2)若平行移动AB,那么∠OBC:∠OFC的值是否随之发生变化?若变化,•找出变化规律;若不变,求出这个比值. (3)在平行移动AB的过程中,是否存在某种情况,使∠OEC=∠OBA?若存在,求出其度数;若不存在,说明理由.D C 3-1BA O x y2.如图,在平面直角坐标系中,点A ,B 的坐标分别为(-1,0),(3,0),现同时将点A ,B 分别向上平移2个单位,再向右平移1个单位,分别得到点A ,B 的对应点C ,D ,连接AC ,BD ,CD .(1)求点C ,D 的坐标及四边形ABDC 的面积ABDC S 四边形(2)在y 轴上是否存在一点P ,连接PA ,PB ,使PAB S ∆=ABDC S 四边形,若存在这样一点,求出点P 的坐标,若不存在,试说明理由.(3)点P 是线段BD 上的一个动点,连接PC ,PO ,当点P 在BD 上移动时(不与B ,D 重合)给出下列结论:①DCP BOP CPO ∠+∠∠的值不变,②DCP CPOBOP∠+∠∠的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.PD CBAOxyDC 3-1BA Oxy3.如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.(1)试判断直线AB与CD的位置关系,并说明理由;(2)如图2,∠AEF与∠EFC的角平分线交于点P,PF∥GH,求证:GH⊥EG;(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.4.在一副三角板ABC和DEF中,∠ACB=∠CDE=90°,∠BAC=60°,∠DEC=45°.(1)当AB∥DC时,如图①,求∠DCB的度数.(2)当CD与CB重合时,如图②,判断DE与AC的位置关系,并说明理由.(3)如图③,当∠DCB等于多少度时,AB∥EC?5.如图,AB∥CD,AB∥EF,EG平分∠BED,∠B=45°,∠D=30°,求∠GEF的度数.6.如图1,点E在直线BH、DC之间,点A为BH上一点,且AE⊥CE,∠DCE-∠HAE=90°.(1)求证:BH∥CD.(2)如图2:直线AF交DC于F,AM平分∠EAF,AN平分∠BAE.试探究∠MAN,∠AFG的数量关系.7.阅读材料:学习了无理数后,某数学兴趣小组开展了一次探究活动:估算的近似值。
人教版七年级下册数学期末动点问题压轴题训练(含答案)

人教版七年级下册数学期末动点问题压轴题训练1.在平面直角坐标系中,O为原点,点A(0,2),B(﹣2,0),C(4,0).(1)如图1,△ABC的面积为;(2)如图2,将点B向右平移7个单位长度,再向上平移4个单位长度,得到对应点D.△求△ACD的面积;△点P是x轴上一动点,若△P AO的面积等于3,请求出点P的坐标.2.如图,MN//OP,点A为直线MN上一定点,B为直线OP上的动点,在直线MN与OP之间且在线段AB的右方作点D,使得AD△BD.设△DAB=α(α为锐角).(1)求△NAD与△PBD的和;(2)当点B在直线OP上运动时,试说明△OBD﹣△NAD=90°;(3)当点B在直线OP上运动的过程中,若AD平分△NAB,AB也恰好平分△OBD,请求出此时α的值.3.已知在平面直角坐标系中,点A(,a b2b-=,AB△x轴于点(2)0B.(1)点A的坐标为_________ ,点B的坐标为_________ ;(2)如图1,若点M在x轴上,连接MA,使S△ABM=2,求出点M的坐标;(3)如图2,P是线段AB所在直线上一动点,连接OP,OE平分△PON,交直线AB于点E,作OF△OE,当点P在直线AB上运动过程中,请探究△OPE与△FOP的数量关系,并证明.4.如图,在直角坐标系中,A(0,a),B(4 ,b),C(0 ,c),若a、b、c满足关系式:|a-8|+(b-4)2=0.(1)求a、b、c的值;(2)若动点P从原点O出发沿x轴以每秒2个单位长度的速度向右运动,当直线PC把四边形OABC分成面积相等的两部分停止运动,求P点运动时间;(3)在(2)的条件下,在y轴上是否存在一点Q,连接PQ,使三角形CPQ的面积与四边形OABC的面积相等?若存在,求点Q的坐标;若不存在,请说明理由.5.如图所示的平面直角坐标系中,已知点A(a,0),点B(b,0),且a,b满足关系式a1,现同时将点A、B向右平移1个单位长度,再向上平移2个单位长度,得到AB的对应点C、D,连接AC、CD、BD.(1)求C、D两点的坐标;(2)若点P是线段CD(与点C、D不重合)上的动点,△连接P A、PB,△P AC与△APB、△PBD的数量关系为;△求出点P的坐标,使三角形APB的面积是三角形DPB面积的2倍.6.如图,在平面直角坐标系中,点A、B是x轴、y轴上的点,且OA=a,OB=b,其中a、b满足(a+b﹣32)2+|b﹣a+16|=0,将点B向左平移18个单位长度得到点C.(1)求点A、B、C的坐标;(2)点M、N分别为线段BC、OA上的两个动点,点M从点B以1个单位长度/秒的速度向左运动,同时点N从点A以2个单位长度/秒的速度向右运动,设运动时间为t 秒(0≤t≤12).△当BM=ON时,求t的值;△是否存在一段时间,使得S四边形NACM<1S四边形BOAC?若存在,求出t的取值范2围;若不存在,请说明理由.7.如图1,已知,点A(1,a),AH△x轴,垂足为H,将线段AO平移至线段BC,点B(b,0),其中点A与点B对应,点O与点C对应,a、b2b-=.(3)0(1)填空:△直接写出A、B、C三点的坐标A(________)、B(________)、C(________);△直接写出三角形AOH的面积________.(2)如图1,若点D(m,n)在线段OA上,证明:4m=n.(3)如图2,连OC,动点P从点B开始在x轴上以每秒2个单位的速度向左运动,同时点Q从点O开始在y轴上以每秒1个单位的速度向下运动.若经过t秒,三角形AOP与三角形COQ的面积相等,试求t的值及点P的坐标.8.如图1,在直角坐标系中,点A、C分别在x轴、y轴上,已知(,0),(,2),(0,2)A aB b bC b,其中,a b满足320-+.a b(1)求出点A、B、C的坐标;(2)如图2,动点M 从原点O 出发沿x 轴以每秒2个单位的速度向右运动,求M 运动多少秒时,MC △AB ?(3)在(2)的条件下,连接OB ,以OM 为边作△OMN =△BOM ,边MN 交y 轴于点N (如图3),连接BN ,交x 轴于点D ,求点D 的坐标.9.如图1,在平面直角坐标系中,(0,),(,0)A a B b ,且2(4)0a -=,过A ,B 两点分别做y 轴,x 轴的垂线交于C 点.(1)请直接写出A ,B ,C 三点的坐标.(2)P ,Q 为两动点,P ,Q 同时出发,其中P 从C 出发,在线段CB ,BO 上以3个单位长度每秒的速度沿着C B O →→运动,到达O 点P 停止运动;Q 从B 点出发以1个单位长度每秒速度沿着线段BO 向O 点运动,到O 点Q 停止运动,设运动时间为t ,当43t >时,t 取何值时,P ,Q ,C 三点构成的三角形面积为2? (3)如图2,连接AB ,点(,)M m n 在线段AB 上,且m ,n 满足|n |7m -=,点N 在y 轴负半轴上,连接MN 交x 轴于K 点,记M ,B ,K 三点构成的三角形面积为1S ,记N ,O ,K 三点构成的三角形面积分别记为2S ,若12S S ,求N 点的坐标.10.如图△,在平面直角坐标系中,点A 、B 的坐标分别为()1,0-,()3,0,现同时将点A 、B 向上平移2个单位长度,再向右平移1个单位长度,得到A 、B 的对应点C 、D ,连接AC 、BD 、CD . (1)直接写出点C 、D 的坐标(2)如图△,点P 是线段BD 上的一个动点,连接PC 、PO ,当点P 在线段BD 上运动时,试探究OPC ∠、PCD ∠、POB ∠的数量关系,并证明你的结论.11.如图,在平面直角坐标系中,////AB CD x 轴,////BC DE y 轴,且4cm,5cm,2cm AB CD OA DE ====,动点P 从点A 出发,以每秒1cm 的速度,沿ABC路线向点C 运动;动点Q 从点O 出发,以每秒2cm 的速度,沿OED 路线向点D 运动.若,P Q 两点同时出发,其中一点到达终点时,运动停止.(△)直接写出,,B C D 三个点的坐标;(△)设两点运动的时间为t 秒,用含t 的式子表示运动过程中三角形OPQ 的面积; (△)当三角形OPQ 的面积的范围小于16时,求运动的时间t 的范围.12.在平面直角坐标系中,点A 、B 的坐标分别为(,0)a ,(0,)b ,其中a ,b 满足21825300a b a b .将点B 向右平移26个单位长度得到点C ,如图△所示.(1)求点A ,B ,C 的坐标;(2)点M ,N 分别为线段BC ,OA 上的两个动点,点M 从点C 向左以1.5个单位长度/秒运动,同时点N 从点O 向点A 以2个单位长度/秒运动,如图△所示,设运动时间为t 秒(015t <<).△当CM AN <时,求t 的取值范围; △是否存在一段时间,使得2MNOB MNAC S S 四边形四边形?若存在,求出t 的取值范围;若不存在,说明理由.13.已知//a b ,直角ABC 的边与直线a 分别相交于O 、G 两点,与直线b 分别交于E ,F 点,且90ACB ∠=︒.(1)将直角ABC 如图1位置摆放,如果56AOG ∠=︒,则CEF ∠=________; (2)将直角ABC 如图2位置摆放,N 为AC 上一点,180NEF CEF ∠+∠=︒,请写出NEF ∠与AOG ∠之间的等量关系,并说明理由;(3)将直角ABC 如图3位置摆放,若135GOC ∠=︒,延长AC 交直线b 于点Q ,点P 是射线GF 上一动点,探究,POQ OPQ ∠∠与PQF ∠的数量关系,请直接写出结论.14.平面直角坐标系中,O 为原点,点A (0,2),B (-1,0),C (2,0)(1)如图△,三角形 ABC 的面积为 ;(2)如图△,将点B 向右平移4个单位长度,再向上平移3个单位长度,得到对应点D .△ 求三角形ACD 的面积;△ 点P (m ,2)是一动点,若三角形P AC 的面积等于三角形ACD 的面积,请直接写出点P 坐标.15.如图1, 在平面直角坐标系中,点A ,B 的坐标分别为(),0A a ,(),0B n ,且a 、n 满足20a +=,现同时将点A ,B 分别向上平移4个单位,再向右平移3个单位,分别得到点A ,B 的对应点C ,D ,连接AC ,BD ,CD .(1)直接写出A 、B 、C 、D 四点的坐标:A ( ),B ( ),C ( ),D ( ); (2)连接OC ,求四边形OBDC 的面积;(3)如图2,若点P 是线段BD 上的一个动点,连接PC ,PO ,当点P 在BD 上移动时(P 不与B 、D 重合)时,OPC ∠与DCP ∠、BOP ∠存在怎样的关系,并说明理由.16.如图,在平面直角坐标系中,四边形ABCD 为长方形,其中点A ,C 坐标分别为()()4,21,4--,,且//AD x 轴,交y 轴于点M ,AB 交x 轴于点N(1)直接写出B ,D 两点的坐标,并求出长方形ABCD 的面积.(2)一动点P 从点A 出发,以每秒12个单位长度的速度沿AB 边向B 点运动,在P 点的运动过程中,连接MP OP ,,试探究AMP MPO PON ∠∠∠,,之间的数量关系(写出探究过程以及结论).(3)在(2)的条件下,是否存在某一时刻t ,使得三角形AMP 的面积等于长方形ABCD 面积的13若存在,求t 的值以及此时点P 的坐标;若不存在,请说明理由.17.已知,在平面直角坐标系中,AB △x 轴于点B ,点A (a ,b )b ﹣3|=0,平移线段AB 使点A 与原点重合,点B 的对应点为点C . (1)a = ,b = ,点C 坐标为 ; (2)如图1,点D (m ,n )是射线CB 上一个动点.△连接OD ,利用OBC ,OBD ,OCD 的面积关系,可以得到m 、n 满足一个固定的关系式,请写出这个关系式: ;△过点A 作直线1△x 轴,在l 上取点M ,使得MA =2,若CDM 的面积为4,请直接写出点D 的坐标 .(3)如图2,以OB 为边作△BOG =△AOB ,交线段BC 于点G ,E 是线段OB 上一动点,连接CE 交OG 于点F ,当点E 在线段OB 上运动过程中,OFC FCGOEC∠+∠∠的值是否发生变化?若变化请说明理由,若不变,求出其值.18.已知:直线1l △2l ,A 为直线1l 上的一个定点,过点A 的直线交 2l 于点B ,点C 在线段BA 的延长线上.D ,E 为直线2l 上的两个动点,点D 在点E 的左侧,连接AD ,AE ,满足△AED =△DAE .点M 在2l 上,且在点B 的左侧.(1)如图1,若△BAD =25°,△AED =50°,直接写出∠ABM 的度数 ; (2)射线AF 为△CAD 的角平分线.△ 如图2,当点D 在点B 右侧时,用等式表示△EAF 与△ABD 之间的数量关系,并证明;△ 当点D 与点B 不重合,且△ABM +△EAF =150°时,直接写出△EAF 的度数 .19.综合与探究.如图1,在平面直角坐标系中,点O ,A 的坐标分别为()0,0,()0,2,将线段OA 沿x 轴方向向右平移,得到线段CB ,点O 的对应点C 的坐标为()3,0,连接AB .点P 是y 轴上一动点.(1)请你直接写出点B 的坐标____________.(2)如图1,当点P 在线段OA 上时(不与点O 、A 重合),分别连接BP ,CP .猜想BPC ∠,ABP ∠,OCP ∠之间的数量关系,并说明理由.(3)△如图2,当点P 在点A 上方时,猜想BPC ∠,ABP ∠,OCP ∠之间的数量关系,并说明理由.△如图3,当点P 在y 轴的负半轴上时,请你直接写出BPC ∠,ABP ∠,OCP ∠之间的数量关系.20.平面直角坐标系中,O 为原点,点()0,2A ,()2,0B -,()4,0C .(1)如图△,则三角形ABC 的面积为______;(2)如图△,将点B 向右平移7个单位长度,再向上平移4个单位长度,得到对应点D .△求ACD △的面积;△点(),3P m 是一动点,若三角形PAO 的面积等于三角形CAO 的面积.请直接写出点P 坐标.参考答案:1.(1)6(2)△9;△(3,0)或(−3,0)2.(1)90°(3)α=30°3.(1)(3,2),(3,0)(2)(5,0)或(1,0)(3)△OPE =2△FOP ,4.(1)8a =,4b =,4c =;(2)点P 运动时间为3秒;(3)存在点Q ,坐标为()0,12或()0,4-.5.(1)C (0,2),D (4,2);(2)△△APB =△P AC +△PBD ;△P (2,2)6.(1)点A (﹣24,0),点B (0,8),C (﹣18,8);(2)△t =8,△存在满足条件的t 值,0≤t <37.(1)△1,4;3,0;2,﹣4;△2;(2)见解析;(3)t =1.2时,P (0.6,0),t =2时,P (﹣1,0).8.(1)A (7,0),B (3,6),C (0,6);(2)M 点运动时间为2s ,MC △AB ;(3)D (127,0). 9.(1)(-8,4);(2)32或52或7;(3)(0,43-) 10.(1)点()0,2C ,点()4,2D ;(2)OPC PCD POB ∠=∠+∠;11.(△)()()()4,5,4,2,8,2B C D ;(△)当04t <<时,三角形OPQ 的面积为25cm t ;当45t ≤≤时,三角形OPQ 的面积为()2528cm t -;(△)1605t <<或952t <≤. 12.(1)A (30,0),B (0,6),C (26,6);(2)△0<t <607;△不存在; 13.(1)146°;(2)△AOG +△NEF =90°14.(1)3;(2)△ 三角形ACD 的面积为4;△点P 坐标为(4,2)或(-4,2). 15.(1)-2,0,5,0,1,4,8,4;(2)24;(3)OPC DCP BOP ∠=∠+∠, 16.(1)B (-4,-4),D (1,2),30;(3)存在,t =10,P (-4,-3)17.(1)6,3,(0,-3);(2)△m -2n =6;△(2,-2)或(4,-1);(3)不变,18.(1)125︒;(2)△2ABD EAF ∠=∠,;△30或110︒19.(1)()3,2;(2)BPC ABP OCP ∠=∠+∠,(3)(3)△BPC OCP ABP ∠=∠-∠,;△BPC ABP OCP ∠=∠-∠.20.(1)6;(2)△9ACD S =△; △()43P ,-或()4,3.。
初一七年级动点问题专题讲解(10个题目)

解咎題(共4小题)k 己知点A 在数轴上对应的数为衝点B 对应的数为怕且|2b - 6|+ (时1),0? Ax B 21闾閔距离记作AB,定义:AB=|a - b|*(I )求线段AD 的长*C2)设点P 在融轴上对应的樹小 当班-PE=2时,求耳的值*(3)M.N 分别是的中点,当P 移功时.指出当F 列结论分别成立时:氢的取值范围.并说明理由:①PMTM 的值不变'②|PM - PN|的值不变.韦黒 一元一次方程的应用:;数轴;两点间的距离.分析;(1)很揭非负数的和为仏 各项都为0:(2)应考虑到A 、B. P 三点王何的位置关系的多种可能解题七(3〕利用中点性质饕化线段之间的倍分关系得岀.斡答,解=(1) V|2b - 6|+ <a+l ) M ),Au= - b b=3,AAB=a -h|-4r 即贱段AB 的长度为也(2)当F 在点A 左側时,|R\| - |PB|= - (|?B| - |PA|) =-|AB= - A2・ 当P 在点R 右测时,|班| - PB|=|AD|=4*2,二上述两种情况的点P 不存在.当P 在仏 B 之间时r - 1<X <3TV |PA| =|x+1| =x+1, |PB|=|7t - 3|=3 - XjA|PA| -|PB|=2t Ax+1 - C3 -x) =2・Jt=2:'■3.';三百•叮谒-:;PH —丄冬.F 、l 一丄PE, 2 2a©PM FN efjfTi^变时.PM :PN-R\ :PB +②pxi - FN|菇價不空咸立+故当P 在线段AH 上时. 点评:此題主要考查了一元一次方程的应用,港透了分类讨论的思想,体现了思维的严密性,在今后解决类似的 问題时,要阴止漏解.利用中点性质转化线段之间的倍分关累是解题的关缝.在不冋的带况下灵活选用它的不闫表示方法,有利 干無題的简洁性.同时,灵活运冃銭段的和、差、倍、分轻化纯段之间的数星关至也是十分关键的一点.PM+PN -丄(PA+PB ) -1A R-2, 2 2当P 在AB 延K 线上或BA 延长线上时,2.如田1,己知数轴上两点A. B对应的敖分别为-1、3,点P为数轴上的一动点,萇对应的数为x・A B .5t1A .20t•1 o3 A Xi A OP N3 B“图1E2(1) P4= |x+ll;PB-|x・31 (用含x的式子表示)(2)在数轴上是否存在点P,使臥+PB=5?若存在,请求出x的值:若不存在,请说明理由.(3)如图2,点P以I个单位/s的谏度从点D向右运动,同时点A以5个单位/s的速度向左运动,点B以20个单位/5的速度向右运动,在运动过程中,M、N分别是AP、OB的中点,问:朋~°卩的值是否发土变化?请说明理MN由.考点:一元一次方程的应用:数馆:两点间的距离.分析:(1)根据数轴上两点之间的距离求法得岀臥,PB的长;(2)分三种情况:①当点P在A、B之间时,②当点P在B点右边时,③当点P在A点左边时,分别求出即可;<3)根据题意用t表示岀AB, OP, MN的长,进而求出答案.解答:解;(1) •・•数轴上两点A、B对应的数分别为・1、3,点P为数雜上的一动点,其对应的数为X, .•・M=|X+1| ;PB二|x・3| (用含x的式子表示);故答案为:|x+l|» |x - 3|;(2)分三种情况:①当点P在A、B之间时,PA+PB-4,故舍去.②当点P在B点右边时,BX=x+l, PB=x・3,:.(x+1) (x - 3) =5,/. x=3.5 •③当点P在A点左边时,映」x-1, PB=3-x,/. C-x-1) + (3-x) =5,:・X= - 1.5;(3)坐磐的值不发生变化.MN理由:设运动时间为〔分钟.则OIM, OA=5t+l, OB~20t+3,AB=OA+OB二2W+4, AP-OAP皆6t+l,AM=」AI>H+3t,2 2OM=OA - AM=5t+l - (l+3t) =2t+l,2 2ON=loB=10t+^,2 2・•・ MN=OM+ON= 12t+2,.AB _ 0£/5t+4 _ gMN _,・••在运动过程中,M、N分别是AP、OB的中点,齐吾的值不发生变化. 点评:此题主要考查了元一次方程的应用,根拒题意利用分类讨论得岀是解题关键.3. 如图1,直线AB±有-点P,点N 分别为线段M 、P13的中点•• • • • • • ♦ » « A M P N BA C BP AB=14・ 图1 圉2(1) 若点P 在线段AB 上,且AP=8,求线段MN 的长度;(2) 若点P 在直线AB 上运动,试说明线段MN 的长度与点P 在直线AB 上的位置无关:(3) 如图2,若点C 为线段AB 的中点,点P 在线段AB 的延长线上,下列结论:(严严的值不变:②£址巴的PCPC值不变,请选择一个正确的结论并求其值. 考点:两点间的距离.分析:(1)求岀MP, NP 的长度,即可得岀MN 的长度:(2) 分三种情况:①点P 在AB 之间;②点P 在AB 的延长线上:③点P 在BA 的延长线上,分别表示出MN 的长度即可作出判斷;(3) 设AC=BC=x, PB=y,分别表示岀①•②的值,继而可作岀判断.解答:解:<1) VAP=8,点M 是AP 中点,•••MP=2A P=4. 2ABP-AB - AP=6, 又;•点N 是PB 中点,•••PN 丄PB 3. 2AMN=MP+PN=7 ・⑵①点咗AB 之间:②点P 在AB 的延长线上:③点P 在BA 的延长线上.均有MN 寺I(3)选择②• 设 AC 二BOx, PB=y,点评|本題考査了两点何的距离.解答本題注意分类讨论思如的运用.理解线段中点的定义•难度一股.4. 如图,P 是定长线段AB±一点.C 、D 两点分别从P 、D 岀发以lcm£ 2cm ;s 的速度沿直线AB 向左运动(C 在线段AP 上,D 在线段BP 上)(1)若C\ D 运动到任一时刻时,总有PD=2AC ,请说明P 点在线段AB 上的位宜:I C P D B⑵ 在(1)的条件下,Q 是査线AB 上一点,KAQ ・EQ=PQ,求普的值.(3)在(1)的条件下,若C 、D 运动5秒后,恰好有口对肚,此时C 点停止运动,D 点继续运动(D 点在线段 PB 上),W N 分别是CD 、PD 的中点,下列结论:①PM-PN 的值不变;②螢值不变,可以说明,只有-个结论是正确的,请你找岀正确的结论并求值.考点:比较线段的长短.专赵:数形结合.分析:(1)根摇C 、D 的运动速度知BD=2PC,再由己知条件PD-2AC 求得PB=2AP,所以点P 在线段AB ±的三处;(2) 由題设画出图示,根摇AQ ・BQ=PQ 求得AQ=PQfBQ :然后求得AP=BQ,从而求得PQ 与AB 的关 系:(3) 当点C 停止运动时.有CD=^AB ,从而求得CM 与AB 的数虽关茶;然后求得以AB 表示的PM 弓PN 的PA-PB PC 型=卫(在变化片x+y x+y©PA+PB 二2x+2y PC — x+y=2 (定值).值,所以HN二PN-P胪丄;AE・解答:解:<1>根拒 6 D的运动速度知:BD-2PCVPD-2AC> •••BD+PD=2 (PC+AC),即PB=2AP, •••点P在线段AB上的丄处:3C2)如图:A P Q BVAQ - BQ=PQ, AAQ=PQ+BQ.又AQ二AP+PQ,AAP^BQt••・ PQ=^AB-•PQ 1•■—二•AB 3当点Q,在AB的延长线上时AQ • AP=PQ・所以匹二丄:AB 3②瞿的值不变.A D理由:如因,当点C停止运动时,有CD A AP*乙CM=^AP.:•WWCP 冷3 5,•・• PD=^AB・ 10,••- PN=^ (|A B-10)专AB-5, .••MN=PN-PM=^AB=当点C停止运动,D点继续运动时,MN的值不变,所以,丄理=丄乙 =丄.AB AB 12点讦:本題考査了比较线段的长短.利用中点性质转化线段之间的倍分关系是解逶的关键,在不同的情况下灵活选用它的不冋表示方法,育利于解题的简洁性.同时,灵活运用线段的和、差、倍、分转化线段之间的数丘关系也是十分关键的一点.5.如图1,己知敖轴上有三点A、B、C, AB=」AC,点C对应的数是200.2(1)若BC=300,求点A对应的数:(2)如图2,在(1)的条件下,动点P、Q分别从A、C两点同时出发向左运动,同时动点R从A点出发向右运动,点P、Q、R的速度分别为10单位长度每秒、5单位长反母秒、2鱼位长度每秒•点M为线段PR的中点,点N为线段RQ的中点,多少秒时恰好满足MR=4RN (不考虑点R与点Q相遇之后的情形〉:<3)如图3, •在(1)的条件下,若点E、D对应的数分别为・800、0.动点P、Q分别从E、D两点同时岀发向左运动•点P、Q的速度分别为10单位长度每秒、5单位长度每秒,点乂为线段PQ的中点,点Q在从是点D运动到点A的过程中,£QC・AM的值是否发生变化?若不变,求其值;若不变,请迸明理由.•4 B C -图1P R 0 20C图2考点:一元一次方程的应用;比较线段的长短.分析:(1)根据BC=300, AB二」AC,得岀A0600,利用点C灯应的数是200,即可得岀点A对应的数;2(2)假设x秒Q在R右边时,恰好满足MR-4RN,得岀等式方程求出即可:(3)假设经过的时间为y,得出PE=10y, QD=5y,进而得出叽5y・400=爭,得出年・3 (200+5y) 15岳㈣幻•工AM ------------ ----------- —y原题得证・2 2解答:解:(1) VBC=300, AB=^,2所以AC=600,C点对应200,/.A点对应的数为:200 - 600=・400;(2)设x秒时• Q在R右边时.恰好满足MR=4RN,/.MR= (10+2) 72RN=^[600・ (5+2) x]・/.MR=4RN,••• (10十2) x-?=4xl[600 - (5+2) x],2 2解得:x=60:•••60秒时怡好满足NfR=4RN;(3)设经过的时间为y,则PE=10y, QD-5y,于是PQ 点为[0 ・(・ 800) ]+10y ・ 5y=8OO+,y, 一半则是型也,2所以AM 点为:8°°+5丫+5丫- 400=芟*2 2又QC=20G+5y, 所以驱・AM*(20^y)-聖为定值.2 2 2点讦;此题考查了一元一次方程的应用,根据己知得出各线段之间的关系等童关系是解题关键,此題阅读量较大应细心分析.6.妇图1,己知点A、C、F、E、B为直线1上的点,且AB=12, CE=6, F为AE的中点.(1)如图1,若CF=2,则BE=_4_,若CF TH, BE与CF的数量关系是(2)当点E沿宜线1向左运动至图2的位宣时,(1)中BE与CF的数員关系是否仍然成立?请说明理由.(3)如图3,在(2)的条件下,在线段BE上,是否存在点D,使得DD",且DF=3DE?若存在,请求岀12匹值:若不存在,请说明理由.CA F£”B圉2BC A F J E D圉3考点:两点间的距离: ^-工口rrA f-^T 中兀-次方桂的应用•分析;(1)先根据EF=CE-CF求出EF,再根据中点的定义求出AE,然后根据BE-AB - AE代入数据进行计算即可得解;根据BE、CF的长度写出数虽关系即可;(2)根攥中点定文可得AE=2EF,再根BE=AB・AE整理即可得解;(3)设DE=x,然后表示出DF、FF、CF> BF,然后代入BE=2CF求解得到x的值,再求岀DF、CF,计算即可得解.解答:解:(1) VCE=6, CF=2,/.EF=CE ・ CF=6 ・ 2=4 ・IF为AE的中点,・・・AE 二2EF 二2x48,/. BE=AB ・ AE=12 ・ 8=4 ・若CF=m・则BE=2m,BE=2CF:(2) (1)中BE=2CF仍然成立.理由如下:TF为AE的中点,・・・AE=2EF,BE=AB - AE,=12 - 2EF,=12 ・2 (CE ・CF),=12-2 (6・ CF),=2CF;(3)存在.DF=3.理由如下:设DE=x,则DF=3x,•\EF=2x, CF=6・x, BE=x+7,由(2)知:BE=2CF,•\x+7=2 (6- x),解得,X二1,/.DF=3, CF=5..••迦=6.CF点评:本题考查了两点间的距齬,中点的定义,灌越识图,找岀图中各线段之间的关系并准确判断出BE的表示是解题的关键.7.已知:如图1, M是定长线段AB上一定点,C、D两点分别从M、B出发以lcm/s、3cm/s的速度沿貢线BA向左运动,运动方向如箭头所示(C在线段AM上,D在线段BM上)(1)若AB=10cm,当点C. D运动了2s,求AC+MD的值.(2)若点C、D运动时,总有MD=3AC,直接填空:AM二丄AB.4—(3)在(2)的条件下,N是亘线AB±一点,且AN - BN=MN,求鹉的A C M DI ______________ I _____________________________ IA AZ B值.考点;比较线段的长短.专題:分类讨论.分祈:(1)计算出CM及BD的长,进而可得出答案:(2)根据图形聞可盲接解符:(3)分两种情况讨论,①当点N在线段AB上时.②当点N在线段AB的延长线上时,然后根据数虽关系即可求解.算答:解:(1)当点C、D 运动了2s 时,CM=2cm, BD=6cme/AB=10cn), CM=2cm, BT)=6anAC+MD-AB - CM ・ BD-10 ・ 2 ・ 6=2cm(2)丄4(3)当点N在线段AB±时.如图I _______________ I ________________ I_________ IJ \f.V BT AN ・ BN=MN・又T AN ・ AM=NfN••・BN二AM=」AB, •••MN=2A B,即型=1.4 2 AB 2当点N在线段AB的延长线上时,如图.4 A/ 3 XVAN - BN=MN,又TAN ・ BWAB/.MN-AB,即翌二].综上所述翌4或1AB AB 2点讦:本題考查求线段的长短的知识,有一定难度,关德是细心阅读题目,理清題意后再解答.&己知数轴上三点M, O, N对应的数分别为・3, 0, 1,点P为数轴上汪意一点.其对应的数为X.(1)如果点P到点M,点N的距离相等,那么x的值是・1 ;(2)数轴上是否存在点P,使点P到点卜1,点N的距离之和是5?若存在,请直接写出x的值:若不存在,请说明理由.(3)如果点P以每分钟3个单位长度対速度从点O向左运动时,点M和点N分别以每分钟1个单位七:度和每分钟4个单位长度的速度也向左运动,且三点同时岀发,那么几分钟时点P到点M,点N的聲离相等?考点:一元一次方程的应用:数轴:两点间的距蔑.分析:(1〉根据三点M, O, N对应的数•得出NM的中点为:x= ( -3+1) -2进而求出即可:(2)根摇P点在N点右侧或在M点左侧分别求岀即可;(3〉分别很掳①当点M和点N在点P同侧时,②当点和点N在点P两侧时求出即可.解答:解:(1) VM, O, N对应的数分别为・3, 0, I,点P到点M,点N的距离相等,Ax的值是-1.(2〉存在符合觊意的点P,此时x= - 3.5 或1.5.(3〉设运动t分钟时,点P对应的数是・3t.点M对应的数是-3・t,点N对应的数是l・4t.①当点M和点N在点P同侧时,因为P\I=PN,所以点M和点N重合,所以・3・(=1 - 4t,解得t」,符合迦意.3②当点M和点N在点P两侧时,有两种情况.情况1:如果点M在点N左侧,PM=・3t • ( - 3・t) =3・2t. PX= (1 -4t)-(・3t) = 1・t.因为PM=PN,所以3・2t=l・t,解得t=2.此时点M对应的数是・5,点N对应的数是・7,点M在点N右侧,不符合輕意,舍去. 情况2:如果点M在点N 右侧,PM= <・3t)・(1・4t) =2t・3. PN二・3t・(l+4t) =t・1・因为PM=PN,所以2t - 3=t・1,解得t=2.此时点M对应的数是・5,点N对应的数是-7,点fd在点N右侧,符合题意.综上所述,三点冋时出发,号分钟或2分钟时点P到点M,点N的距离相寻. 故答案为:~ 1.点评:此题主要考査了数轴的应用以及一元一次方程的应用,根据M. N位置的不同进行分类讨论得出是解题关9.如图,已知数轴上点A表示的数为6, B是数紬上一点,且AB=10・动点P从点A出发,以每秒6个单位长度的速度沿数袖向左匀速运动,设运动时间为t (t>0)秒.<1)写出数轴上点B表示的数・4 ,点P表示的教6・&用含(的代数式表示九(2)动点R从点B出发,以每秒4个单位长度的速度沿数轴向左匀速运动,若点P、R同时岀发,问点P运动多少秒时追上点R?(3)若M为AP的中点,N为PB的中点•点P在运动的过程中,线段的长度是否发生变化?若变化,请说明理由;若不变,请你匝岀图形,并求岀线段MN的长;3 Q』0 6考点:数轴:一元一次方程的应用;两点间的胚离.专題:方程思想.分析:(1)B点表示的数为6 - 10=・4;点P表示的数为6・6t;(2〉点P运动X秒时,在点C处追上点R,然后建立方程6x・4x=10,解方程即可:(3)分类讨论:①当点P在点A、B两点之间运动时,②当点P运动到点B的左侧时,利用中点的定义和线段的和差易求岀MN.輕答:解:(1)答案为• 4, 6 - 6t ;(2)设点P 运动x 秒时,在点C 处追上点R (如图)二 __________ S. ____ 2 _________ 0贝!J AC=6x, BC-4x,VAC • BC -AB, .e .6x - 4x=10,解得:X =5F.••点P 运动5秒时,在点C 处追上点R.(3)线段MN 的长度不发生变化,都等于5.理由如下:gMP+NP^AP 咿吩(AP+BP 〉 _—2 --------------- 上②当点P 运动到点B 的左侧时:P N"0 MN=MP ・ NP=-^AP ・丄BP=-^ (AP - BP ) =^AB=5, 2 2 2 2・•・综上所述,线段MN 的长度不发生变化,其值为5.点讦:本题考査了数轴:数轴的三夢素(正方向、原点和单位长度).也考査了一元一次方程的应用以及数釉上两 点之间的足巨离.10・妇图,己知数轴上点A 表示的数为6, B 是数袖上一点,且AB 二10,动点P 从点A 岀发,以每秒6个单位长 度的速度沿数轴向左匀速运动,设运动时间为t (t>0)秒.<1)①写出教轴上点B 表示的数-4 ,.占P 表示的数6・6((用含(的代数式表示〉;②M 为AP 的中点,N 为PB 的中点•点P 在运动的过程中,线段MN 的长度是否发生变化?若变化,请说明理由: 若不变,请你画出图形,并求出线段MN 的长;(2)动点Q 从点A 出发,以每秒1个单位长度的速度沿数轴向左匀速运动;动点R 从点B 出发.以每秒上个单位3 长度的速度沿数釉向左匀速运动,若P 、Q 、R 三动点同时出发,当点P 遇到点R 时,立即返回向点Q 运动,遇到 点Q 后则停止运动.那么点P 从开始运动到停止运动,行驶的路程是多少个单位长度?B O A------- ・ ・»0 6考点:一元一次方程的应用;数轴;两点间的距离.专題;动点型.分析:(1)①设B,点表示的数为X,根裾数雜上两点间的距离公式建立方程求岀其鲜.再根据数轴上点的运动就 可以求出P 点的坐标;②分类讨论;当点P 在点A 、B 两点之间运动时:当点P 运动到点B 的左侧时,利用中点的定义和线段的 和差易求岀MN ;<2)先求岀P 、R 从A 、B 岀发相遇时的时间,再求岀P 、R 相遇时P 、Q 之间剩余的路程的相遇时间,就 可以求出P 一共走的时间,由P 的速度就可以求出P 点行驶的路稈.解答:解:(1)设B 点表示的数为X.白題意.得6 ・ x=10.分两种情况:①当点P 在点A 、B 两点之间运动时:x=・4AB点表示的数为:・4,点P表示的数为:6-6t;②线段MN的长度不发生变化,都等于5.理由如下: 分两种情况;当点P在点A、B两点之间运动时;MN=NfP+NP—AP+-BP=- (AP+BP) —AB=5:2 2 2 2当点P运动到点B的左侧时:MN^NIP ・ NP」AP -丄BP」(AP ・ BP)」AB=5,2 2 2 2・・・综上所述,线段MN的长度不发生变化,其值为5.(2)由題意得:A 1 C;P、R的相遇时间为:10-(6+三)亠乩W 11P、Q剰余的路程为:10・(理)J 11 11P、Q相遇的时间为:普三(6+1)二ps,•••P点走的路程为:6x (普需)丄器点评:本题考查了数轴及数轴的三要素(正方向、原点和单位长度〕.一元一次方程的应用以及数轴上两点之间的距离公式的运用,行程问題中的路程二速度%时间的运用.。
宁浩数学动点压轴题专项训练

宁浩数学动点压轴题专项训练数学是一门需要不断练习和思考的学科,而动点压轴题则是数学中的一类经典问题。
宁浩数学动点压轴题专项训练旨在帮助学生提高解决动点问题的能力,培养他们的逻辑思维和数学推理能力。
本文将介绍宁浩数学动点压轴题专项训练的内容和方法。
一、动点压轴题的基本概念动点压轴题是指在平面几何中,给定一些点和线段,要求确定一个点,使得该点到给定点的距离之和最小或最大。
这类问题常常涉及到最优解的求解,需要运用到数学中的一些基本原理和方法。
二、宁浩数学动点压轴题专项训练的内容宁浩数学动点压轴题专项训练主要包括以下几个方面的内容:1. 基础知识的巩固:通过对动点压轴题的基本概念和相关定理的学习,巩固学生的基础知识,为解决问题打下坚实的基础。
2. 典型题目的讲解:通过讲解一些典型的动点压轴题,引导学生理解问题的本质和解题的思路,培养他们的问题分析和解决能力。
3. 解题技巧的训练:针对不同类型的动点压轴题,训练学生灵活运用相关的解题技巧,提高他们的解题效率和准确性。
4. 综合应用的拓展:通过一些综合性的动点压轴题,培养学生的综合运用能力,让他们能够将所学知识应用到实际问题中,提高解决实际问题的能力。
三、宁浩数学动点压轴题专项训练的方法宁浩数学动点压轴题专项训练采用多种教学方法,旨在激发学生的学习兴趣和主动性。
以下是一些常用的训练方法:1. 理论讲解与实例演练相结合:通过对动点压轴题的理论讲解,引导学生理解问题的本质和解题的思路;同时,通过实例演练,让学生亲自动手解决问题,巩固所学知识。
2. 小组合作学习:将学生分成小组,让他们共同合作解决动点压轴题,通过合作学习,培养学生的团队合作精神和解决问题的能力。
3. 案例分析与讨论:选取一些实际问题作为案例,引导学生分析问题的关键点和解决思路,通过讨论,培养学生的问题分析和解决能力。
4. 模拟考试与评讲:定期进行模拟考试,让学生在考试环境下解决动点压轴题,通过评讲,指导学生找出解题中的问题和不足,提高他们的解题水平。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
宁浩数学动点压轴题专项训练七年级33题讲解
摘要:
一、引言
1.介绍宁浩数学动点压轴题专项训练七年级33题
2.强调动点问题在数学中的重要性
二、动点问题的基本概念和解决方法
1.动点问题的定义
2.动点问题的分类
3.解决动点问题的基本思路
三、七年级33题讲解
1.题目分析
2.解题思路
3.解题步骤
4.解题技巧
5.易错点分析
四、动点压轴题的解题策略
1.观察题目,提炼关键信息
2.建立数学模型
3.运用相关知识和技巧
4.逐步解决,确保步骤清晰
五、动点压轴题实战演练
1.例题解析
2.解题思路和方法总结
六、总结与展望
1.回顾动点压轴题的解题方法和技巧
2.强调动点问题在数学学习中的重要性
3.鼓励同学们多练习,提高解题能力
正文:
作为一名数学爱好者,你是否曾为解决动点压轴题而苦恼?不用担心,今天我们来一起学习宁浩数学动点压轴题专项训练七年级33题,掌握动点问题的解题方法和技巧。
一、引言
动点问题在数学中占有重要地位,不仅考验了同学们的基本运算能力,还考查了逻辑思维能力。
为了解决这类问题,我们要从基本的动点问题入手,逐步提高自己的解题能力。
二、动点问题的基本概念和解决方法
1.动点问题的定义
动点问题是指在平面直角坐标系中,点随着自变量的变化而运动,从而产生的数学问题。
2.动点问题的分类
动点问题可以分为直线动点、圆动点、函数动点等。
3.解决动点问题的基本思路
解决动点问题的基本思路包括观察题目、建立数学模型、运用相关知识和
技巧等。
三、七年级33题讲解
1.题目分析
七年级33题是一道典型的动点问题,主要考察了直线动点的相关知识。
2.解题思路
首先,我们要观察题目,找出关键信息,如点的位置、运动规律等。
3.解题步骤
接着,我们要根据关键信息建立数学模型,将动点问题转化为静点问题。
然后,运用相关知识和技巧,如解析几何知识,逐步解决。
4.解题技巧
在解题过程中,要注意步骤的清晰,避免遗漏。
同时,要熟练掌握各类题型的解题技巧,如消元法、代入法等。
5.易错点分析
易错点主要包括对题意的理解不清晰、计算失误等。
为了避免这些错误,我们要在解题过程中保持细心,加强运算能力的训练。
四、动点压轴题的解题策略
1.观察题目,提炼关键信息
解决动点压轴题的第一步是观察题目,提炼关键信息。
这有助于我们建立数学模型,为后续解题奠定基础。
2.建立数学模型
在动点问题中,建立数学模型是非常重要的。
我们要根据题目所给信息,将动点问题转化为静点问题,从而简化问题。
3.运用相关知识和技巧
在解题过程中,我们要善于运用相关知识和技巧,如解析几何知识、函数知识等。
这有助于提高解题效率。
4.逐步解决,确保步骤清晰
解决动点压轴题时,要逐步解决,确保步骤清晰。
这样既可以避免遗漏,又有利于提高得分。
五、动点压轴题实战演练
1.例题解析
为了让大家更好地理解动点问题的解题方法,我们挑选了几道典型例题进行解析。
2.解题思路和方法总结
通过解析,我们可以发现解决动点问题的关键在于观察题目、建立数学模型和运用相关知识和技巧。
希望大家能在实战演练中不断总结经验,提高自己的解题能力。
六、总结与展望
1.回顾动点压轴题的解题方法和技巧,我们可以发现,解决这类问题需要同学们具备扎实的基本功、敏锐的观察能力和严谨的思维。
2.强调动点问题在数学学习中的重要性,希望大家能够重视这类问题,加强训练。
3.鼓励同学们多练习,提高解题能力。
