用字母表示数综合练习题
五年级上册数学 第五单元 简易方程
4
综合运用过关
解方程(2)
c+8=48
a-4=48
4
综合运用过关
解方程(2)
8c=48
a÷4=48
4
思维能力拓展
解方程(2)
5
基础知识达标
解方程(3)
3x+38.6=53 3x
5
基础知识达标
解方程(3)
(4.8+x)×2=17.8 4.8+x
5
基础知识达标
解方程(3)
x=3.35
x=2
x=2
综合运用过关
72×1.5=108(km)
3 用字母表示数(3)
综合运用过关
ab c÷a c÷b
3 用字母表示数(3)
综合运用过关
96÷12=8(盒)
3 用字母表示数(3)
综合运用过关
c÷n at
x÷y
3 用字母表示数(3)
综合运用过关
120÷6=20(个/时)
3 用字母表示数(3)
综合运用过关
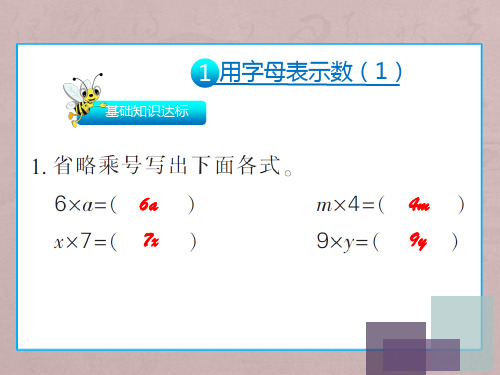
1 用字母表示数(1)
基础知识达标
6a
4m
7x
9y
1 用字母表示数(1)
基础知识达标
(x-5)
1 用字母表示数(1)
基础知识达标
3a
1 用字母表示数(1)
基础知识达标
1 用字母表示数(1)
基础知识达标
y+8
1 用字母表示数(1)
基础知识达标
(m÷4)
1 用字母表示数(1)
基础知识达标
n
2n
b
b
8
125
a
b
2 用字母表示数(2)
基础知识达标
3
9
用字母表示数综合练习题 (100)

c×x d×d b×6 t×1二、根据运算定律在__里填上适当的数或字母。
d+(6+z)=(__+__)+__a•d•4=__•(__•__)3d+9d=(__+__)•__4(c+4)=__×__+__×____+y=__+4z×__=2.3×__16×x+b×__=(__+__)×16三、用含有字母的式子表示下面的数量关系。
(1)b与8的和。
(4)n除以30的商。
(2)a减去30的差。
(5)b的3倍减去3.5的差。
四、根据条件求值。
(1)当m=4.5 ,n=7.9时,求m+n的值。
(2)当x=28 ,n=3时,求xn的值。
(3)当c=24 ,y=3时,求c÷y的值。
五、计算下面各题。
9n+8n 39z+2z 14z-z c+8cc×y b×b s×5 n×1二、根据运算定律在__里填上适当的数或字母。
d+(6+y)=(__+__)+__m•b•3=__•(__•__)3a+7a=(__+__)•__8(y+2)=__×__+__×____+y=__+5a×__=5.1×__11×x+y×__=(__+__)×11三、用含有字母的式子表示下面的数量关系。
(1)m与1的和。
(4)c除以28的商。
(2)y减去24的差。
(5)n的2倍减去2.1的差。
四、根据条件求值。
(1)当a=6.9 ,y=1.5时,求a+y的值。
(2)当a=13 ,y=9时,求ay的值。
(3)当x=6 ,n=2时,求x÷n的值。
五、计算下面各题。
5x+7x 19n-8n 16d-d z+6zd×x m×m x×13 s×1二、根据运算定律在__里填上适当的数或字母。
浙教版数学7上第四单元代数式知识梳理+习题+答案

浙教版数学七上第四单元代数式知识梳理及综合练习、检测[解析] 一.用字母表示数1.用字母表示数就是将基本的数量关系的语言文字转化为数学语言。
二、代数式1.定义:用运算符号把数或表示数的字母连结而成的式子,叫做代数式。
单独的一个数或字母也是代数式。
2.注意:(1)单个数字与字母也是代数式;(2)代数式与公式、等式的区别是代数式中不含等号,而公式和等式中都含有等号;(3)代数式可按运算关系和运算结果两种情况理解。
3.书写要求(1).代数式中出现的乘号通常用“·”表示或者省略不写;数与字母相乘时,数应写在字母前面;数与数相乘时,仍用“×”号;(2)数字与字母相乘、单项式与多项式相乘时,一般按照先写数字,再写单项式,最后写多项式的书写顺序.如式子(a+b)·2·a应写成2a(a+b);(3)带分数与字母相乘时,应先把带分数化成假分数后再与字母相乘;(4)在代数式中出现除法运算时,按分数的写法来写;(5).在一些实际问题中,有时表示数量的代数式有单位名称,如果代数式是积或商的形式,则单位直接写在式子后面;如果代数式是和或差的形式,则必须先把代数式用括号括起来,再将单位名称写在式子的后面,如2a米,(2a-b)kg。
三.代数式求值:一般地,用数值代替代数式中的字母,按照代数式中指明的运算计算的结果叫做代数式求值。
代数式求值的三种方法:1.直接代入求值;2.化简代入求值;3.整体代入求值。
注意事项:1.代数式的值有一般式到特殊数的问题,代数式字母的取值要使代数值有意义。
比如分母不为0.求代数值的步骤1.代入时的注意1.如果代数式中省略乘号,带入后必须添上称号。
2.如果字母给出的是负数或者分数,并作乘方并作乘法运算,代入时都必须添上括号。
3.带入数值时,要对号入座,谨防混乱。
4.当题目按照常规方法不能求解时,要用整体思想。
2.计算时,注意运算符号,同时考虑简便运算。
代数式一、用字母表示数(共18题)1.下列式子中,符合代数式的书写格式的是( ) A. (a -b )×7 B. 3a ÷5b C. 1 12ab D. ab 2.设n 为整数,下列式子中表示偶数的是( ) A. 2nB. 2n+1C. 2n-1D. n+23.某商品标价x 元,进价为400元,在商场开展的促销活动中,该商品按8折销售获利( )A. (8x ﹣400)元B. (400×8﹣x )元C. (0.8x ﹣400)元D. (400×0.8﹣x )元 4.一个数除以9的商为x ,余数为2,则这个数为( )A. 9x +2B. 9x -2C. -29x D. 29 x 5.“减去一个数,等于加上这个数的相反数”用字母可以表示为________. 6.用代数式表示a 、b 两数的平方和与a ,b 乘积的差________.7.全校学生总数为a , 其中女生占总数的 48% ,则男生人数是( ) A. 48a B. 0.48aC. 0.52aD. a −488.某企业今年1月份产值为x 万元,2月份的产值比1月份减少了10%,则2月份的产值是( )A. (1﹣10%)x 万元B. (1﹣10%x )万元C. (x ﹣10%)万元D. (1+10%)x 万元9.x 是一个两位数, y 是一个一位数,如果把 y 放在 x 的左边,那么所成的三位数表示为( ).A. yxB. y +xC. 100y +xD. 100y +10x10.某种牌子的书包,进价为m 元,加价n 元后作为定位出售,如果元旦期间按定价的八折销售,那么元旦期间的售价为 ( ) 元. A. m +0.8nB. 0.8nC. 0.8(m+n) D. m+n÷0.811.某商店举办促销活动,促销的方法是将原价x元的衣服以(4x−10)元出售,5则下列说法中,能正确表达该商店促销方法的是( )A. 原价减去10元后再打8折 B. 原价打8折后再减去10元C. 原价减去10元后再打2折 D. 原价打2折后再减去10元12.某种水果的售价为每千克a元,用面值为50元的人民币购买了3千克这种水果,应找回________元(用含a的代数式表示).13.一个两位数,个位数是a,十位数是b,这个两位数为________;14.为了帮助一名白血病儿童治疗疾病,某班全体师生积极捐款,捐款金额共2 800元,已知该班共有5名教师,每名教师捐款a元,则该班学生共捐款________元(用含a的代数式表示).15.代数式的书写有一些规范,比如教材上指出:“在含有字母的式子中如果出现乘号“×”,通常将乘号写作“·”或者省略不写”其实还有一些书写规范,比如,在代数式中如果出现“÷”,通常用分数线“——”来取代;数字与字母相乘时,一般数字写在前面.根据以上书写要求,将代数式(ac×4-b2)÷(4a)简写成________16.夜间温度是t ∘C,白天温度比夜间高16 ∘C,则白天的温度是________ ∘C。
四年级上册数学试题-2.用字母表示数 青岛版(五四制) 含答案

四年级上册数学单元测试-2.用字母表示数一、单选题1.一公汽上有x名乘客,某站下车a人,又上车b人,这时车上有乘客( )名.A. x+a+bB. x-a+bC. a+b-xD. x-b+a2.下面式子中等于a(b+c)的是()A. ab+cB. b+acC. ab+acD. abc3.正方形的边长是a米,周长是()A. 4aB. a×aC. 2a4. 下列多项式不能用平方差分解的是()A. B. C. D.二、判断题5.小红今年a岁,比小艺大2岁,小艺今年(a+2)岁。
6.3X可以表示3个X相加。
7.5÷b中的b可以表示我们学过的整数。
三、填空题8.根据运算定律,填上适当的字母或数.(80×b)×125=________×(________×________)9.某电脑专卖店卖出35台电脑,销售总额达b元,每台电脑卖了________元。
10.一只白兔4条腿,一只公鸡2条腿,a只白兔和b只公鸡一共有________条腿。
11.已知三角形的面积是6平方厘米,它的高是2厘米,底是________厘米.12.一本练习本的价钱是0.50元,买2本应付________元,买m本应付________元,x元可以买________本。
四、解答题13.在表中填入适当的式子.王红1小时打多少个字?五、综合题14.能简写的简写,并说明其表示的含义。
(1)a+a(2)a×a(3)2a+13(4)2a-13六、应用题15.学校买来9个足球,每个a元,又买来b个篮球,每个58元.那么9a表示什么?9a+58b表示什么?参考答案一、单选题1.【答案】B【解析】【解答】一公汽上有x名乘客,某站下车a人,又上车b人,这时车上有乘客:x-a+b(名).故答案为:B.【分析】根据题意,用原来公汽上的乘客人数-下车的人数+上车的人数=现在车上的乘客数量,据此列式解答.2.【答案】C【解析】【解答】解:根据乘法分配律可知:a(b+c)=ab+ac故答案为:【分析】可以运用乘法分配律,用a分别与b、c相乘,然后把乘积相加,这样变换式子即可.3.【答案】A【解析】【解答】解:正方形的边长是a米,周长是边长的4倍,就是4a.故答案为:A【分析】正方形周长=边长×4,由此根据正方形周长公式用字母表示周长即可.4.【答案】D【解析】【解答】解:A.把25a2﹣b2化成(5a)2﹣b2,符合平方差公式.B. = ﹣b2符合平方差公式.C.﹣a2+25b2化成(5b)2﹣a2,符合平方差公式.D.﹣4﹣b2=﹣(4+b2),不符合平方差公式.故选:D.【分析】根据平方差公式的特点,两平方项符号相反,对个选项分析后再进行选择即可.二、判断题5.【答案】错误【解析】【解答】小红今年a岁,比小艺大2岁,小艺今年(a-2)岁,原题说法错误.故答案为:错误.【分析】根据题意可知,用小红的年龄-2=小艺的年龄,据此列式解答.6.【答案】正确【解析】【解答】3x=x+x+x ,表示3个x相加。
新人教版五年级上册数学第五单元《简易方程》课时练习

第五单元简易方程1、用字母表示数用字母表示数(1)一、口算。
+=×=÷3=>+=+ 4=×=二、用含有字母的式子表示下面的数量关系。
1、a与8的和()。
2、比a的6倍少8的数()。
3、m的平方减去a的4倍()。
,4、从96里连续减去6个a()。
5、a与b的和除以它们的差()。
三、省略乘号写出下面各式。
4×a=()a×1=()×m=()b×b=()x×y=()x×9+5=()—四、连一连。
a+a×2x+x+xa²+2aa·am-(+)16²㎡(28+a)×23 xm×m16×16m--28×2+2a…五、对的打“√”,错的打“×”。
1、a·18=18a。
()2、a²表示两个a相加。
()3、b一定大于2b。
()4、8a+16a=(8+16)a。
()5、b+6可以写作6b。
()用字母表示运算定律(2)一、根据运算定律在□里填上适当的数或字母。
:1、(a+54)+46=+()2、4a+5a=()·a3)4、(a+28)×b=二、用简便方法计算下面各题,再用字母表示出来。
'(1)--(2)×+×a-b-c=(a+b)×c=[(3)××4(4)++(a×b)×c=(a+b)+c=…(5)360÷÷2 (6)1000÷(125÷)a÷b÷c=a÷(b÷c)=%2'三、开放天地:填出题中所表示的数,使等式成立。
(1)a×a=a÷aa=()(2)a÷a=a+aa=()(3)a×a=a-aa=())含有字母的算式(3)一、对的打“√”,错的打“×”。
用字母表示数综合练习题 (20)

a×z c×c c×3 d×1二、根据运算定律在__里填上适当的数或字母。
n+(5+x)=(__+__)+__a•b•7=__•(__•__)3c+6c=(__+__)•__2(b+1)=__×__+__×____+m=__+2y×__=3.5×__25×c+b×__=(__+__)×25三、用含有字母的式子表示下面的数量关系。
(1)n与7的和。
(4)n除以27的商。
(2)b减去13的差。
(5)b的9倍减去7.8的差。
四、根据条件求值。
(1)当x=0.5 ,y=3.6时,求x+y的值。
(2)当c=27 ,b=4时,求cb的值。
(3)当c=56 ,n=7时,求c÷n的值。
五、计算下面各题。
9c+5c 87c+9c 18y+y n+8nn×y n×n a×18 c×1二、根据运算定律在__里填上适当的数或字母。
m+(5+x)=(__+__)+__m•d•6=__•(__•__)5n+8n=(__+__)•__5(d+9)=__×__+__×____+y=__+8b×__=4.3×__15×m+d×__=(__+__)×15三、用含有字母的式子表示下面的数量关系。
(1)x与5的和。
(4)z除以12的商。
(2)d减去27的差。
(5)x的2倍减去1.3的差。
四、根据条件求值。
(1)当m=2 ,y=0.3时,求m+y的值。
(2)当c=12 ,y=9时,求cy的值。
(3)当a=40 ,d=8时,求a÷d的值。
五、计算下面各题。
8n+3n 63a+6a 20m-m d+9dc×x x×x m×27 c×1二、根据运算定律在__里填上适当的数或字母。
《用字母表示数》练习

《用字母表示数》练习班级:姓名:一、含有字母的式子简写规则如下:(1)数和字母相乘时,乘号可以写成“•”,也可以省略不写,省略不写时,数必须写在字母前。
如a×4和4×a可简写成4•a或4a;.(2)字母和字母之间的乘号也可以写成•,但通常省略不写。
如a×b可简写成a•b或ab。
两个相同字母相乘可以写成字母的平方,例如a×a写成a²,读作a的平方。
(3)1和任何字母相乘时,1都可以省略不写。
如a×1或1×a都可以简写成a。
二、口算题。
5×b= a×c= 1×b= n×n= 2a+7a= 3x × y= 4b-3b= 5y+y= m×n= a×3= 4m×n=a×b×c= y×1= 4a-3a= a-0.3a= 3.1x-1.7x=0.3y+3.5y-0.08y= 6.7t-t= 15t-4.7t= x-0.5x-0.04x=三、填空题。
1.一辆大客车平均每小时行85千米,x小时一共行()千米。
2.买一张电影票要35元,买y张电影票要()元。
3.哥哥今年a岁,弟弟比哥哥小b岁,弟弟今年()岁。
4.红花a朵,黄花10朵,两种花共有()朵。
5.某工地原有水泥67吨,用去x吨后,又运来9吨。
现在工地有水泥()吨。
6.果园里有18行苹果树,每行a棵。
梨树比苹果树少13棵,梨树有()棵。
7.一辆公共汽车上原来有35人,到西湖车站下车x人,又上来y人。
现在车上有()人。
8.直角三角形的一个锐角是a度,另一个锐角是()度。
9.小红买了3支毛笔和1支钢笔,毛笔每支x元,钢笔每支12元。
小红一共用了()元。
10.同学们采集标本,四年级采集是a个,五年级采集的个数是四年级的4倍。
两个年级一共采集()个。
四年级比五年级少采集()个。
数学用字母表示数试题答案及解析

数学用字母表示数试题答案及解析1.小明今年A岁,爸爸今年35岁,5年后两人相差()岁.A.35﹣AB.40﹣AC.30﹣A【答案】A【解析】两人的年龄差是永远不变的,两人原来相差35﹣A岁,5年后仍然相差35﹣A岁.解:由“小明今年A岁,爸爸今年35岁”可知:爸爸与小明年龄相差35﹣A岁,且这个数值是不变的,所以说再过5年后,他俩仍然相差35﹣A岁;故选:A.点评:抓住年龄差不变是解答此题的关键.2.下面的式子与2a相等的是()A.a•aB.a+aC.2a+2a【答案】B【解析】2a=a+a;据此选择即可.解:与2a相等的式子是a+a;故选:B.点评:解答此题的关键:应明确2a是表示两个a相加,而不是相乘.3.小晴把4x﹣2错写成4(x﹣2),结果比原来()A.多8B.少6C.多6【答案】B【解析】要求结果比原来多或少了多少,就要求出两个数,再用后来的数减去开始的数即可求解.解:4(x﹣2)=4x﹣8;4x﹣8﹣(4x﹣2),=4x﹣8﹣4x+2,=﹣6;所以结果比原来少6;故选:B.点评:此题考查了用字母表示数的基本方法,要抓住题中给出的数量关系,代入数据解答.4.长方形的周长C厘米,长是α厘米,宽是()厘米.A.C﹣2αB.(C﹣α)÷2C.C÷2﹣α【答案】C【解析】由长方形的周长公式C=(长+宽)×2,得出宽是:C÷2﹣a.据此解答即可.解:由分析得出:C=(a+宽)×2,所以宽=C÷2﹣a.故选:C.点评:此题主要考查长方形周长公式的灵活运用.5.小明今年a岁,小东今年(a﹣4)岁,再过5年,他们相差()A.4岁B.( 5+4)岁C.( 5﹣4)岁【答案】A【解析】先求出小明和小东相差的年龄,由于年龄差不随时间的变化而改变,所以再过5年,他们相差的岁数不变.解:因为小明和小东相差:a﹣(a﹣4)=a﹣a+4=4(岁),所以再过5年,他们相差的岁数仍然是4岁;故选:A.点评:年龄差不随时间的变化而改变是解答此题的关键.6.下面两个式子相等的是()A.a+a和2aB.a×2和a2C.a+a和a2【答案】A【解析】选项A,a+a表示2个a相加,写成乘法算式是2×a,一般的2和a之间的乘号不写;选项B,a×2,如果省略乘号,2必须写在字母的前面;选项C,a+a表示2个a相加,写成乘法算式,如果省略乘号,2必须写在a的前面,由此即可作出选择.解:选项A,a+a表示2个a相加,写成乘法算式是2×a,一般的2和a之间的乘号不写,所以,A是正确的;选项B,a×2,如果省略乘号,2必须写在字母的前面,所以,选项B是错误的;选项C,a+a表示2个a相加,写成乘法算式,如果省略乘号,2必须写在a的前面,所以选项C是错误的;综合以上得出A是正确的;故选:A.点评:此题主要考查了2a表示的意义(2个a相加)及字母和整数相乘时的简便写法.7.图书馆有故事书m本,比科技书的2倍多n本,科技书有多少本.正确的算式是()A.m÷2﹣n B.(m﹣n)÷2C.(m+n)÷2D.m÷2+n【答案】B【解析】先根据“故事书m本,比科技书的2倍多n本”得出:故事书数量=科技书的数量×2+n,则故事书的数量﹣n本=科技书的2倍,即科技书数量=(m﹣n)÷2,代数计算即可.解:由分析得出:科技书的数量为:(m﹣n)÷2(本).故选:B.点评:解题关键是根据已知条件,把未知的数用字母正确的表示出来,然后根据题意列式计算即可得解.8.一个奇数用m表示,它后面一个相邻奇数用式子表示是()A.m﹣2B.m+2C.2m D.m÷2【答案】B【解析】根据相邻的两个奇数相差2,进行解答即可.解:m+2;故选:B.点评:明确相邻的两个奇数相差2,是解答此题的关键.9.随着通讯市场竞争的日益激烈,某通讯公司的手机市话收费按原标准每分钟降低了a元后,再次下调了25%,现在的收费标准是每分钟b元,则原收费标准每分钟为()元.A.b﹣a B.b+a C.b+a D.b+a【答案】C【解析】设原收费标准每分钟为x元,则根据题意,以现在的收费标准为等量关系,列出等式,表示出原收费标准即可.解:设原收费标准每分钟为x元,由题意得,(x﹣a)(1﹣25%)=b,(x﹣a)×75%=b,x﹣a=b,x=b+a.故选:C.点评:解答本题的实质是实现从基本数量关系的语言表述到用字母表示一种转化,设出未知数,借助方程,列出等式,从而求出答案.10.甲数是m,比乙数的3倍多n.表示乙数的式子是()A.3m+n B.m÷3+n C.m÷3﹣n D.(m﹣n)÷3【答案】D【解析】根据“甲数是m,比乙数的3倍多n,”知道甲数=乙数×3+n,由此用甲数减n再除以3就是乙数.解:(m﹣n)÷3;故选:D.点评:此题属于典型的两步逆算的题目,解答时注意根据数量关系,列式解答.11.王大伯家养的母鸡只数是公鸡的8倍.如果养了x只公鸡,母鸡有只.【答案】8x【解析】由“母鸡只数是公鸡的8倍.”得出母鸡只数=公鸡的只数×8,而公鸡有x只,由此求出母鸡的只数.解:8×x=8x(只),答:母鸡有8x只;故答案为:8x.点评:关键是根据题意得出数量关系式:母鸡只数=公鸡的只数×8,由此解决问题.12. a与b平方和不大于它们和的平方.【答案】a2+b2≤(a+b)2【解析】根据“a与b平方和不大于它们和的平方,”得出a2+b2≤(a+b)2,利用完全平方和公式即可证明此不等式.解:因为(a+b)2=a2+b2+2ab,所以(a+b)2≥a2+b2,即a2+b2≤(a+b)2.点评:本题主要利用完全平方和公式((a+b)2=a2+b2+2ab)解决问题.13.(2011•弥渡县模拟)a2=2a..【答案】×【解析】根据平方的定义即可作出判断.解:a2=a•a,故原题错误.故答案为:×.点评:本题考查了平方的定义和用字母表示数,是基础题型.14. a2与2a一定不相等.(a≠0).(判断对错)【答案】×【解析】根据a2=a×a,2a=2×a,当a=2时,a2=22=4,2a=2×2=4,此时a2=2a;当a=1时,12=1,2×1=2,所以a2小于2a;当a>2时,a2>2a;据此解答即可.解:因为当a=2时,a2=22=4,2a=2×2=4,此时a2=2a;所以a2与2a一定不相等说法错误.故答案为:×.点评:引导学生举出反例,是判断此题最简单的方法.15.苹果有x千克,比梨的一半少8千克,梨有千克.【答案】2x+16【解析】由题意可知:梨的重量÷2﹣8=苹果的重量,进而得出:(苹果的重量+8)×2=梨的重量,代入数值,解答即可.解:(x+8)×2,=2x+16(千克);答:梨有2x+16千克.故答案为:2x+16.点评:解答此题的关键:根据已知条件,进行认真分析,找出数量间的关系,进而根据数量间的关系,进行解答得出结论.16.甲数是x,乙数比甲数多2倍,乙数是.【答案】3x【解析】根据题意可知:乙数比甲数多2倍,即乙数是甲数的(1+2)倍,根据求一个数的几倍是多少,用乘法解答即可.解:x×(1+2),=3x;故答案为:3x.点评:解答此题的关键:根据求一个数的几倍是多少,用乘法解答.17.一块长方形铁片,长l2.5cm,宽9.6cm,这块铁片的面积是多少?(先写出字母公式,再把数据代入公式求值)【答案】120平方厘米【解析】长方形的面积S=ab,据此代入数据即可求解.解:因为长方形的面积S=ab,a=12.5,b=9.6,所以S=12.5×9.6,=120(平方厘米);答:这块铁片的面积是120平方厘米.点评:此题主要考查长方形的面积的计算方法.18.x块,是面包块数的3倍,3x表示.【答案】蛋糕的块数【解析】由题意得:x表示面包的块数,则3x表示面包块数的3倍,即蛋糕的块数.据此解答即可.解:3x表示面包块数的3倍,即蛋糕的块数.故答案为:蛋糕的块数.点评:解决本题的关键是明确题中的数量关系和字母的意义.19.妈妈买5千克西红柿,每千克x元,付了20元,找回元.【答案】5(4﹣x)【解析】用总钱数减去5千克西红柿的钱数,就是应找回的钱数.解:20﹣x×5,=20﹣5x,=5(4﹣x)(元);答:应找回5(4﹣x)元.点评:本题运用“单价×数量=总价”进行解答即可.20.小明每小时行的路程是15千米,t小时行了千米.【答案】15t【解析】已知速度和时间,求路程,运用关系式:路程=速度×时间.解:15×t=15t(千米);答:t小时行了15t千米.故答案为:15t.点评:此题运用了关系式:路程=速度×时间.21.一本书有A页,3天读了B页,还剩下页,平均每天读,照这样计算,剩下的还要天才能读完.【答案】A﹣B;B÷3;(A﹣B)÷(B÷3)【解析】(1)剩下的页数=书的总页数﹣3天读的页数,即:A﹣B;(2)平均每天读的页数=3天读的总页数÷3,即:B÷3;(3)剩下页数需要的时间=剩下的页数÷每天读的页数,即(A﹣B)÷(B÷3).解:(1)还剩下的页数为:A﹣B(页).答:还剩下A﹣B页.(2)平均每天读的页数为:B÷3(页).答:平均每天读B÷3页.(3)剩下的页数为(A﹣B)页,平均每天读(B÷3)页,剩下的还需要的时间为:(A﹣B)÷(B÷3)天.答:剩下的还要(A﹣B)÷(B÷3)天才能读完.故答案为:A﹣B;B÷3;(A﹣B)÷(B÷3).点评:做这类用字母表示数的题目时,解题关键是根据已知条件,把未知的数量用字母正确的表示出来,然后根据题意列式计算即可得解.22.水果店的苹果比梨的3倍还多16千克,如果梨有X千克,那么苹果有千克.【答案】3x+16【解析】要求苹果有多少千克,由题意可得:苹果的重量=梨的重量×3+16,因为梨有X千克,然后代入即可.解:3x+16(千克);答:苹果有3x+16千克点评:解答此题应找出苹果的重量和梨的重量之间的关系,然后根据其关系解答即可.23. x比一个数的4倍多3,这个数为4x+3..【答案】错误【解析】x比一个数的4倍多3,也就是一个数的4倍比x少3,要求这个数,先求出这个数的4倍,再除以4就是这个数.解:根据分析,这个数为:(x﹣3)÷4;故判断为:错误.点评:此题属于逆思考的应用题,要求这个数关键是先求出这个数的4倍,进而问题得解.24.一支铅笔的单价是a元,买了6支,应付元.【答案】6a【解析】根据:总价=单价×数量,代数计算即可.解:a×6=6a(元);答:应付6a元;故答案为:6a.点评:此题主要考查总价、单价、数量之间的关系,要灵活运用.25. 5x表示5个x相加..(判断对错)【答案】√【解析】5x=x+x+x+x+x,表示五个x相加,由此判断.解:5x=x+x+x+x+x,表示五个x相加,故答案为:√.点评:本题主要考查了乘法的意义:表示几个几相加是多少.26. 3x+4x=7x,3a+4b=7ab.【答案】×【解析】(1)根据乘法分配律合并即可作出判断,(2)3a+4b=7ab,所含字母不同因此不能合并.解:3x+4x=7x,3a与4b不能合并.故答案为:×.点评:考查了用字母表示数,注意对运算律的灵活运用.27.x•x=2x.(判断对错)【答案】×【解析】x•x表示两个x相乘,2x表示两个x相加;据此判断即可.解:由分析可知:x•x=2x,说法错误;故答案为:×.点评:明确x•x和2x分别表示的含义,是解答此题的关键.28.运用运算定律在横线上填上合适的数或字母.(1)24×45+24×55=×(+)(2)125×25×8×4=(×)×(×)(3)a×(73+6)=×+×.【答案】24、45、55,125、8、25、4,a、73、a、6【解析】(1)24×45+24×55,符合乘法分配律的逆运算;(2)125×25×8×4,利用乘法交换律和结合律;(3)a×(73+6),利用乘法分配律即可解答.解:(1)24×45+24×55=24×(45+55);(2)125×25×8×4=(125×8)×(25×4);(3)a×(73+6)=a×73+a×6.故答案为:24、45、55,125、8、25、4,a、73、a、6.点评:此题主要考查乘法运算定律的意义.29.苹果树有a棵,梨树是苹果树的3倍,苹果树和梨树一共有棵,梨树比苹果树多棵.【答案】4a;2a【解析】(1)根据“梨树是苹果树的3倍”得:梨树的棵数=苹果树的棵数×3,即3a棵,再加上苹果树的棵数a棵即可;(2)用梨树的棵数﹣苹果树的棵数即可.解:(1)苹果树和梨树共有:a+3a=4a(棵).答:苹果树和梨树一共有4a棵.(2)3a﹣a=2a(棵).答:梨树比苹果树多2a棵.故答案为:4a;2a.点评:解答此题的关键是,根据已知条件,把未知的数用字母正确的表示出来,再结合所求的问题,即可得出答案.30.三个连续自然数中间一个是n,这三个连续自然数的和.【答案】3n【解析】因为相邻的两个自然数相差1,中间的一个是n,由此表示出三个连续自然数为:n﹣1,n,n+1.然后求和.解:因为已知三个连续自然数且中间一个为n,所以另两个为:n﹣1,n+1.则三个连续自然数的和为:n﹣1+n+n+1=3n.故答案为:3n.点评:解答此题的关键是知道相邻的两个自然数相差1,由此即可得出答案.31.当a时,a的倒数一定大于a.当a时,a的倒数一定小于a.当a时,a的倒数一定等a.【答案】<1;>1;=1【解析】当一个数小于1时,它的倒数一定大于这个数;当一个数大于1时,这个数的倒数一定小于这个数;1的倒数是它本身.据此解答即可.解:由分析得出:当a<1时,a的倒数一定大于a.当a>1时,a的倒数一定小于a.当a=1时,a的倒数一定等a.故答案为:<1;>1;=1.点评:此题考查了倒数的意义.32.张老师买篮球.每个篮球a元,买5个篮球元,买x个篮球元.【答案】5a,ax【解析】根据单价×数量=总价,用乘法列式即可用字母表示出,买5个篮球的钱数及买x个篮球的钱数.解:(1)a×5=5a(元),(2)a×x=ax(元),答:买5个篮球5a元,买x个篮球ax元;故答案为:5a,ax.点评:本题主要考查了用字母表示数及单价、数量与总价之间的关系.33.小明买了α枝钢笔和b枝圆珠笔,圆珠笔每枝2.5元,钢笔每枝8.7元,小明一共花了元.【答案】8.7a+2.5b【解析】买钢笔a枝钢笔和圆珠笔b枝,钢笔每枝8.7元,圆珠笔每枝2.5元,用每枝圆珠笔和每枝钢笔的价格和数量相乘即可求出一共用了多少钱.解:8.7a+2.5b,答:小明一共花了8.7a+2.5b元.故答案为:8.7a+2.5b.点评:此题考查了用字母表示数的方法,根据单价×数量=总价即可解答.34.如果A÷B=54,则(A×2)÷(B÷2)=.【答案】216【解析】根据商不变的性质:被除数、除数同时扩大或同时缩小相同的倍数(0除外),商不变,所以被除数扩大2倍,除数缩小2倍,那么商就会扩大(2×2)倍,列式计算即可得到答案.解:如果A÷B=54,则(A×2)÷(B÷2)=54×4=216.故答案为:216.点评:此题主要考查的是商不变性质的灵活应用.35.小明每天看书a页,小青每天看书b页,10天共看书页.【答案】10a+10b【解析】先用“a+b”求出小明和小青每天看的页数,然后根据“每天看的页数×天数=总页数”求出10天看的页数”即可.解:(a+b)×10,=10a+10b(页);答:10天共看书10a+10b页;故答案为:10a+10b.点评:此题考查了用字母表示数,先求出小明和小青每天看的页数,进而根据每天看的页数、天数和所看总页数三者之间的关系解答即可.36.加法结合律用字母表示是(a+b)+c=.【答案】a+(b+c)【解析】根据加法结合律解答即可,即:三个数相加,先把前两个数相加,再与第三个数相加,或者是先把后两个数相加,再与第一个数相加,和不变解答即可.解:(a+b)+c=a+(b+c),故答案为:a+(b+c).点评:本题理解加法的结合律是解答的关键.37.一支钢笔的单价是7.8元,老师买了n支这样的钢笔,应付元,老师带50元买笔,还剩元.【答案】7.8n;50﹣7.8n【解析】(1)用:单价×数量=总价,即可计算出应该付的钱数;(2)用付的钱数减去应付的钱数就是剩下的钱数.解:(1)应该付出:7.8n元.答:应该付7.8n元.(2)还剩:50﹣7.8n元.答:还剩50﹣7.8n元.故答案为:7.8n;50﹣7.8n.点评:解决本题的关键是灵活根据单价、数量和总价之间的关系解答.38.小明今年x岁,爸爸今年的年龄是小明的3倍,爸爸今年有岁,小明和爸爸今年一共岁.【答案】3x,4x【解析】求爸爸今年多少岁,根据求一个数的几倍是多少,用乘法解答;求小明和爸爸今年一共多少岁,把小明的年龄和爸爸的年龄相加即可.解:小明今年x岁,爸爸今年的年龄是小明的3倍,爸爸今年有3x岁,小明和爸爸今年一共:x+3x=4x(岁);故答案为:3x,4x.点评:此题考查了用字母表示数,解题关键是根据已知条件,把未知的数用字母正确的表示出来,然后根据题意列式计算即可得解.39.甲数是x,比乙数多8,乙数是x﹣8..【答案】√【解析】甲数是40,比乙数多8,即甲数=乙数+8,所以乙数等于x﹣8.解:乙数是:x﹣8,故答案为:√.点评:关键是根据题意得出数量关系式:甲数=乙数+8,由此求出乙数.40.吴婷去年重X千克,今年比去年重2.5千克,今年重千克.【答案】(X+2.5)【解析】题目中的字母X表示吴婷去年的重量,当做一个具体的数来看待即可,因为今年比去年重2.5千克,所以今年的重量就等于去年的重量加上2.5千克.解:今年的重量:X+2.5(千克),故答案为:(X+2.5).点评:本题考查了用字母表示数字,应让学生明白字母所表示的实际意义.另外,X+2.5作为一个整体来表示吴婷今年的重量,因而答案中加上括号较为规范.41.㎡=m+m=2m..【答案】×【解析】因为根据乘方的意义可得:m2=m×m;而m+m=2m,进而得出结论进行判断.解:因为m2=m×m;而m+m=2m,所以㎡=m+m=2m说法错误;故答案为:×.点评:解答此题应注意区别2m与m2的意义的不同.42.一辆公共汽车上原来有x人,到新街站下去5人.现在车上有人.【答案】x﹣5【解析】用原有人数减下车人数就是剩下的人数.解:由分析得出:现在车上有:x﹣5(人).答:现在车上有x﹣5人.故答案为:x﹣5.点评:解决本题的关键是找出数量关系,再列式解答.43.小东今年a岁,爸爸比小东大b岁,爷爷比爸爸大c岁,爷爷今年岁.【答案】a+b+c【解析】根据“小东今年a岁,爸爸比小东大b岁”求出爸爸的岁数,再根据“爷爷比爸爸大c岁”,即可求出爷爷的岁数.解:爸爸的岁数是,a+b岁,爷爷的岁数是:a+b+c岁,故答案为:a+b+c.点评:解答此题的关键是,把所给的字母看做已知数,再根据基本的数量关系解答即可.44.用字母表示乘法分配律:(a+b)×c﹦.【答案】ac+bc【解析】根据乘法分配律得:(a+b)×c﹦ac+bc,据此解答即可.解:用字母表示乘法分配律:(a+b)×c﹦ac+bc.故答案为:ac+bc.点评:此题主要考查用字母表示乘法分配律,要熟记.45.两个数的和与一个数相乘,可以先把它们与这个数相乘,再,这叫做律.用字母表示:.【答案】分别,相加,乘法分配,a×(b+c)=a×b+a×c【解析】根据乘法分配律的概念并掌握用字母表示的方法,进行解答.解:两个数的和与一个数相乘,可以先把它们与这个数(分别)相乘,再(相加),这叫做(乘法分配)律.用字母表示:a×(b+c)=a×b+a×c.故答案为:分别,相加,乘法分配,a×(b+c)=a×b+a×c.点评:此题考查了学生对乘法分配律的掌握情况.46.六年级张萌同学在教室的座位用(a,b)表示,那么张萌应坐在教室的第组,第排.【答案】a;b【解析】根据数对表示位置的方法可知:第一个数字表示列(组),第二个数字表示行(排),据此即可解答.解:张萌同学在教室的座位用(a,b)表示,那么张萌应坐在教室的第a组,第b排.故答案为:a;b.点评:此题考查了数对表示位置的方法.47. x2=x+x..【答案】错误【解析】根据x2表示的意义:表示2个x相乘;x+x表示两个x相加;据此判断.解:因为x2表示2个x相乘,所以本题x2=x+x说法错误;故答案为:错误.点评:解答此题应明确2个x相乘与2个x相加的不同,掌握算式表示的意义是解答此题的关键.48.爸爸比小明大28岁.若用x表示爸爸的年龄,小明的年龄是岁;如果小明的年龄用y表示,则爸爸的年龄是岁.【答案】x﹣28,y+28【解析】(1)求小明的年龄,根据“爸爸的年龄﹣比小明大的岁数=小明的年龄”进行解答即可;(2)求爸爸的年龄,根据“小明的年龄+比小明大的年龄=爸爸的年龄”进行解答即可.解:(1)x﹣28;(2)y+28;故答案为:x﹣28,y+28.点评:解答此题的关键:把字母看作数,根据题意,找出数量间的关系,进而解答即可.49.小青买了3个练习本,每个a元,营业员找给他b元,小青交给营业员元.【答案】3a+b【解析】先根据“单价×数量=总价”求出小青买练习本的总价,进而根据“买练习本的总价+找给小青的钱数=小青给营业元的钱数”进行解答即可.解:a×3+b=3a+b(元),故答案为:3a+b.点评:解答此题的关键是,根据已知条件,把未知的数用字母正确的表示出来,再结合所求的问题,即可得出答案.50.一枝钢笔a元,一枝铅笔b元,a÷b表示的意思是.【答案】一枝钢笔的价钱是一枝铅笔的多少倍【解析】一枝钢笔a元,a表示钢笔的单价,一枝铅笔b元,b表示铅笔的单价,a÷b表示的意思是一枝钢笔的价钱是一枝铅笔的多少倍.解:一枝钢笔a元,一枝铅笔b元,a÷b表示的意思是一枝钢笔的价钱是一枝铅笔的多少倍;故答案为:一枝钢笔的价钱是一枝铅笔的多少倍.点评:关键是根据给出的式子,找出式子中的数表示的意义,再结合式子中的运算方法,确定式子表示的意义.51. a与b的和的4倍,用字母表示可以写成4a+b..【答案】×【解析】由题意得出;先计算a与b的和,再乘4,要想先算和再算积,必须在加法算式上加上括号;据此解答即可.解:a与b的和的4倍,用字母表示可以写成:(a+b)×4;所以用字母表示可以写成4a+b说法错误.故答案为:×.点评:解决本题的关键是先根据题意明确运算顺序,再列式解答.52. m+n+m+n+m+n可以简写成或.【答案】3(m+n),3m+3n【解析】m+n+m+n+m+n表示3个m与3个n相加的和是多少,所以列式为3(m+n)或3m+3n.解:m+n+m+n+m+n=3(m+n)=3m+3n.故答案为:3(m+n),3m+3n.点评:此题考查用字母表示数,根据题中的数量关系列式解答,注意字母与数相乘时要简写,即省略乘号,把数写在字母的前面.53.苹果每千克8.5元.小明用x元可以买千克;小红买y千克要用元.【答案】x;8.5y【解析】(1)根据总价÷单价=数量,把字母与数分别代入关系式,即可得出答案;(2)根据单价×数量=总价,把字母与数分别代入关系式,即可求出小红买y千克要用的钱数.解:(1)x÷8.5=x(千克),(2)8.5×y=8.5y(元),故答案为:x;8.5y.点评:解答此题的关键是把给出的字母当做已知数,再根据单价、数量与总价三者之间的数量关系解决问题.54.因为a×100=b÷0.01,所a=b..【答案】√【解析】b÷0.01=b÷=b×100,即a×100=b×100,根据等式的性质,两边同时除以100,即可得出a=b,据此即可判断.解:因为b÷0.01=b÷=b×100,故a×100=b×100,a×100÷100=b×100÷100,所以a=b,故答案为:√.点评:解答此题的关键是把b÷0.01利用分数的除法,变形为b×100,从而得出a×100=b×100.55.元旦期间,五星电器商场销售空调χ台,销售冰箱的台数比空调台数的2倍多7台,这个电器商场销售冰箱台.【答案】2χ+7【解析】由“销售冰箱的台数比空调台数的2倍多7台”,得出这个电器商场销售冰箱的台数=空调台数×2+7,而空调χ台,由此列出含字母的式子即可.解;这个电器商场销售冰箱的台数:χ×2+7=2χ+7(台).故答案为:2χ+7.点评:解题关键是根据已知条件,得出数量关系,把未知的数用字母正确的表示出来,然后根据题意列式计算即可得解.56.甲数为x,乙数比甲数的2.5倍少7,则乙数可表示为.【答案】2.5x﹣7【解析】由“乙数比甲数的2.5倍少7,”得出乙数=甲数×2.5﹣7,由此求出乙数.解:2.5x﹣7;故答案为:2.5x﹣7.点评:关键是根据题意得出:乙数=甲数×2.5﹣7,由此列式解答即可.57. 3a=a3.【答案】×【解析】本题根据乘方的意义和乘法的意义求解.解:因为3a=a+a+a;a3=a×a×a;所以它们不相等;故答案为:×.点评:乘方表示几个相同因数积的运算,而乘法表示几个相同加数和的运算.58. a2=a×2.【答案】错误【解析】根据a2=a×a,据此判断即可.解:a2=a×a,所以a2≠a×2.故答案为:错误.点评:本题主要考查了有理数的平方的意义,即a n表示n个a相乘.59.幸福小学共有m名学生,其中男生230名,女生名.【答案】m﹣230【解析】由题意得出等量关系式:女生人数=学生总数﹣男生人数,代数即可.解:女生:m﹣230(名),答:女生有m﹣230名.故答案为:m﹣230.点评:解决本题的关键是找出数量关系式,代数计算.60.比x的8倍少2的数是8x﹣2.【答案】√【解析】先用含字母x的式子表示出x的8倍,进而表示出比它少8的数即可判断.解:x×8﹣2=8x﹣2.故判定为:√.点评:关键是把给出的字母当做已知数,再根据基本的数量关系解决问题;注意字母与数相乘时要简写,即省略乘号,把数写在字母的前面.61.小兰家养了a只黑兔,养的白兔比黑兔只数的3倍还多2只,一共养了只兔子.【答案】4a+2【解析】要想求一共养了多少只兔子,就必须知道黑、白两种兔子各多少只.已知黑兔为a只,再根据两种兔子只数的倍数关系,求出白兔的只数,列式解答即可.解:a+(3a+2),=a+3a+2,=4a+2(只);答:一共养了4a+2只兔子.故答案为:4a+2.点评:解答此题的关键:根据两种兔子只数的倍数关系,求出白兔的只数.62.水果店运来15筐橘子,每筐x千克,运来香蕉200千克.那么15x表示,200+15x表示.【答案】运来的橘子的重量;运来的橘子和香蕉的总重量【解析】(1)15x表示橘子的单价乘每筐橘子的重量计算出来是橘子的总重量;(2)200+15x表示运来的橘子和香蕉的总重量.据此解答即可.解:(1)15x表示运来的橘子的重量;(2)200+15x表示运来的橘子和香蕉的总重量.故答案为:运来的橘子的重量;运来的橘子和香蕉的总重量.点评:解决本题的关键是明确每个数字或字母表示的意义.63.大客车每小时行a千米,小汽车每小时比大客车多行15千米,a+15表示,大客车5小时行的千米数.【答案】小汽车的速度,5a【解析】(1)“a+15”表示小汽车每小时行的路程,即小汽车的速度,据此解答;(2)求大客车5小时行多少千米,根据:速度×时间=路程,解答即可.解:(1)a+15表示小汽车每小时行的路程,即小汽车的速度;(2)5a(千米),故答案为:小汽车的速度,5a.点评:此题考查了用字母表示数,根据速度、时间和路程三者之间的关系进行解答.64.小刚家去年每个季度平均用水X吨,小刚家去年共用水吨.【答案】4X【解析】一年有4个季度,用季度数乘每季度的用水量就是全年的用水量.解:1年=4季度;全年的用水量是:4×X=4X(吨);答:小刚家去年共用水4X吨.故答案为:4X.点评:用乘法表示出来要求的数,然后再根据数字与字母相乘的简写形式化简.65.若x与y都是正数,则2+x一定小于4+y..【答案】×【解析】本题可以通过取特殊值代入计算,从而作出判断.解:当x=5,y=1时,2+x=7,4+y=5,此时2+x>4+y.故若x与y都是正数,则2+x一定小于4+y的说法是错误的.故答案为:×.点评:考查了用字母表示数的比较大小,赋值法是解题的关键.66. M+1是偶数,写出后两个偶数是.【答案】M+3;M+5【解析】因为每相邻的两个偶数相差2,所以M+1.后面的偶数分别是M+1再加2、加4即可.解:M+1+2=M+3,M+1+4=M+5;故答案为:M+3;M+5.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
.
用字母表示数练习
1、甲数比乙数大5,如果乙数是m,那么甲数是( ),如果甲数是m,那么乙数是( )
2、a、b、c 三个数的平均数是( )
3、当x=15时,2x-2×4的值是( )
4、有两筐同样的梨,第一筐重a千克,第二筐重b千克,第一筐比第二筐少卖m元。
〔1〕、用式子表示出梨的价钱。
〔2〕、当a=24,b=27,m=9时,每千克梨价钱是多少元?
6、一个正方形周长是m米,这个正方形的边长是( )
7、食堂买来200千克煤,已烧了a天,还剩b千克,平均每天烧了( )千克.
8、果园里有苹果树和梨树共45棵,其中梨树有a棵,苹果树比梨树多( )棵.
9、学校有图书4000本,又买来a本,现在一共有〔〕本。
10、学校有学生a人,其中男生b人,女生有〔〕人。
11、李师傅每小时生产x个零件,10小时生产〔〕个。
12、姐姐今年a岁,比妹妹年龄的2倍少2岁,妹妹今年〔〕岁。
13、甲数是x,比乙数少y,乙数是〔〕,甲乙两数之和是〔〕,两数之差是〔〕
14、小花今年12岁,比小兰大a岁,小兰今年〔〕岁。
15、一件上衣54元,一件裤子48元,买b套这样的衣服,要用〔〕元。
16、一本故事书有a页,小明每天看x页,看了y天,看了〔〕页,还剩〔〕页没看。
17、王阿姨买了m千克香蕉和n千克苹果,香蕉每千克4.8元,苹果每千克5.4元,一共花了〔〕元。
19、学校买来a个足球,每个m元,又买来b个排球,每个n元,一共用去( )元,足球比排球多用( )元.
20、某工厂每月用水a吨,全年用水( )吨
21、2a表示( )或者( ),a2表示( ) ,
a+a+a+a+a=( ) a×a×a=( )
22、货车每小时行S千米,客车每小时行m千米,客车3小时后和货车5小时一共行驶了( )千米.
23、每个足球x元,买4个足球,付出200元,应找回( )元.
.
24、三个连续自然数,已知中间一个数是m,那么前一个数是( ),后一个数是( ),三数之和是( )
16、当x=5时,x2=( ),2x+8=( )
17、一种商品降价a元后是80元,原价是( )元.
18、长方形周长计算公式用字母表示是( )
19、李师傅每天做m个零件,比X师傅多做8个,两人一天共做( )
20、每本练习本x,买了6本,付出10元,应找回( )元.
二、根据运算定律填空。
1、a+18=□+□a×15=□×□
2、m×2.5×0.4=□×〔□×□〕
3、m-a-b=□-〔□+□〕
三、省略乘号写出下面各式。
a×12=b×b=a×b=x×y×7=
5×x=2×c×c=7x×5=2×a×b=
四、判断。
〔对的打“√〞,错的打“×〞。
〕
1、5+x=5x〔〕
2、x+x=x2〔〕
3、a×3=3a〔〕
4、y2=y×2〔〕
5、2a+3b=5ab〔〕
6、2a+3a=5a〔〕
7、5×a×b=5ab〔〕8、a×7+a=8a〔〕
五、说一说下面每个式子所表示的意义。
〔1〕、一天中午的气温是32℃,下午比中午的气温降低了x℃。
32-x表示:_____________
〔2〕、五〔2〕班有40人订阅《少年文艺》杂志,每本单价b元。
40b表示:__________
〔3〕、一个足球单价a元,一个篮球b元。
6a+4b表示:__________
〔4〕、X师傅每小时加工x个零件,朱师傅每小时加工15个零件
x-15表示:________________
5x表示:_____________
〔x-15〕×3表示:__________
六、求下列各式的值。
〔1〕、已知a=18b=25求4a+2b的值
.〔2〕、已知x=5,y=13求3y-4x的值
.。
