第2章-传递过程基本方程
合集下载
第二章2传函
n
n 1
y(t)为系统的输出,r(t)为系统输入,则零初 始条件下,对上式两边取拉氏变换,得到系 统传递函数为:
b0 s m b1s m1 bm1s bm Y ( s) G ( s) n n 1 R( s) a0 s a1s an1s an
d Cm lim ( s s1 ) F ( s ) Cm 1 lim [( s s1 ) m F ( s )] s s1 s s1 ds
m
Cm j
1 dj lim j [( s s1 ) m F ( s )] j! s s1 ds
1 d ( m 1) C1 lim ( m 1) [( s s1 ) m F ( s )] (m 1)! s s1 ds f (t ) L1[ F ( s )] Cm Cm 1 m 2 m 1 [ t t (m 1)! (m 2)! C2t C1 ]e s1t
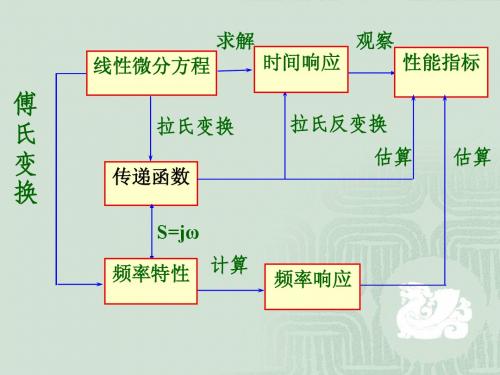
线性微分方程
性能指标
傅 氏 变 换
拉氏变换
传递函数 S=jω
频率特性
计算
频率响应
拉氏反变换
按定义求拉氏反变换很困难,一般常用部分分 式法计算:
F (s )
分解
部分分式
查表
原函数
F (s ) 的一般形式为 B ( s ) b0 s m b1s m 1 bm 1s bm F (s) n A( s ) s a1s n 1 an 1s an
Uo ( s) [例] 求如图所示电路的传递函数 U i ( s )
C i1 R1 i2 R2
[解]:解法一:列出回路电压方程和输 出节点方程
1 i1dt R1i1 R1i2 ui R2 i2 uO
第二章 传递函数-梅逊公式
第二章 自动控制系统的数学模型
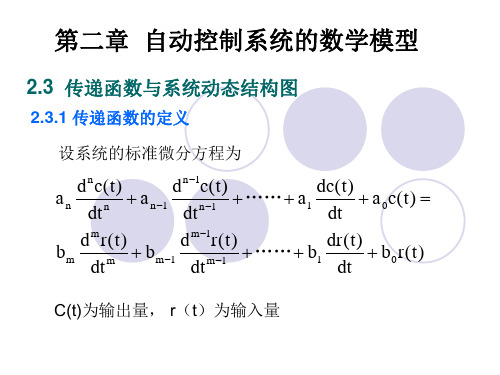
2.3 传递函数与系统动态结构图
2.3.1 传递函数的定义
设系统的标准微分方程为
an
dnc(t) dt n
a n1
dn1c(t) dt n 1
……
a1
dc(t) dt
a0c(t)
bm
dmr(t) dt m
bm1
d m 1r ( t ) dt m1
……
b1
dr(t) dt
点
上图所示的是
G(s)
(s
(s 1)(s 2) 3)(s 2 2s
2)
的零、极点分布图。
2.2 传递函数
比
比例环节(无惯性环节): c(t)=kr(t)
例
传递函数:G(S)=C(S)/R(S)=k
c(t)
环
阶跃响应:R(S)=1/S
r(t)
节
C(S)=kR(S)=k/S C(t)=k
0
方框图: R(S) k/s C(S)
3
传
递
积分调节器:
C
在A点列方程可得:
函 数
Ur(t)
R
i2
i1
A
Uc(t) i2=i1, i1=Uc(t)/R Uc(t)=1/C∫i2(t)dt=1/(RC)∫Uc(t)dt
设RC=T(积分时间常数),则有:Uc(t)=1/T∫Uc(t)dt
拉氏变换后为:Uc(S)=1/(TS)Uc(S)
5)传递函数具有正、负号(输入量和输出量的变化方向)。
6)传递函数的单位是输出量的单位与输入量的单位之比。
m
(s z j )
7)传递函数可以写成
G(s)
Kg
j1 n
2.3 传递函数与系统动态结构图
2.3.1 传递函数的定义
设系统的标准微分方程为
an
dnc(t) dt n
a n1
dn1c(t) dt n 1
……
a1
dc(t) dt
a0c(t)
bm
dmr(t) dt m
bm1
d m 1r ( t ) dt m1
……
b1
dr(t) dt
点
上图所示的是
G(s)
(s
(s 1)(s 2) 3)(s 2 2s
2)
的零、极点分布图。
2.2 传递函数
比
比例环节(无惯性环节): c(t)=kr(t)
例
传递函数:G(S)=C(S)/R(S)=k
c(t)
环
阶跃响应:R(S)=1/S
r(t)
节
C(S)=kR(S)=k/S C(t)=k
0
方框图: R(S) k/s C(S)
3
传
递
积分调节器:
C
在A点列方程可得:
函 数
Ur(t)
R
i2
i1
A
Uc(t) i2=i1, i1=Uc(t)/R Uc(t)=1/C∫i2(t)dt=1/(RC)∫Uc(t)dt
设RC=T(积分时间常数),则有:Uc(t)=1/T∫Uc(t)dt
拉氏变换后为:Uc(S)=1/(TS)Uc(S)
5)传递函数具有正、负号(输入量和输出量的变化方向)。
6)传递函数的单位是输出量的单位与输入量的单位之比。
m
(s z j )
7)传递函数可以写成
G(s)
Kg
j1 n
大连理工大学 本科 传递过程课件 第2章_

(1)质量力
质量力是指作用在整个微元体上的外力,又叫体积力,与质量大小有关,而与 周围流体的存在无关,是一种非接触力,如重力、静电力等。传递课程只考虑重 力。
x方向:Xdxdydz y方向: Ydxdydz
z方向: Zdxdydz
(2 - 3a)
X、Y、Z是作用在单位质量
(2 - 3b)
(2 - 3c)
(2 - 5a) (2 - 5b)
u x u z zx x z
(2 - 5c)
(2)法向应力表达式
法向应力表达式(推导过程可参见《讲义》p309的附录A):
Du x xx yx zx u x 2 u x u y u z X (2 - 5a) xx p 2 D x y z x 3 x y z Du y xy yy zy Y (2 - 5b) u y 2 u x u y u z D x y z yy p 2 y 3 x y z yz zz Du z Z xz (2 - 5c) D x y z u z 2 u x u y u z zz p 2 z 3 x y z ux u y yx xy y x 对于理想流体,μ=0,故: xx yy zz p u u
3.以应力表示的运动微分方程
将式(2-3)和(2-4)代入式(2-2)并简化,可得
Y dxdydz (2-3b) Z dxdydz (2-3c)
xx yx zx ( )dxdydz (2-4a) x y z ( xy yy zy )dxdydz (2-4b) x y z ( xz yz zz )dxdydz (2-4c) x y z
第2章 微分方程+传递函数

dx
(x x0 )
x x0
写成增量形式:
df f (x) f (x0 ) dx xx0 (x x0 )
y k x
9
2.2.3 微分方程的线性化
例2-15 微分方程线性化
f (h) h
A dh(t) a dt
h(t) qi (t)
其中包含非线性项 h(t) ,单独将其线性化:
df f (x) f (x0 ) dx xx0 (x x0 ) f (x) k x
b1
dr(t) dt
b0r(t)
式中nm, n是系统阶次, r(t), c(t)是系统输入量和输出量。
例2-12 RC无源网络,输入电压ei(t)和输出电压eo(t)
R
解:由基尔霍夫定律
标准式: 左出右入降阶
ei (t) i C
eo (t)
ei (t) i(t)R eo (t)
eo
(t)
1 C
16
知识巩固
传递函数和微分方程一样, 也是用于描述系统的( ); 本课程使用的三种数学模型是( ), 其中( )是最主要的; 传递函数的定义是( ); 传递函数是代数表达式吗? 传递函数的求取方法一般有二种,分别是( ); 传递函数的成立条件是( ); 系统的阶次符号为( ), 它是传递函数的( )多项式的次数; 使传递函数分子为零的点, 称为传递函数的( ); 使传递函数分母为零的点, 称为传递函数的( ), 数学上称为( ),
2
a h0
h(t)
qi (t)
线性化方程已经把系统的工作坐标
从原点移至平衡工作点(h0 , qi0 ) 10
2.2.3 微分方程的线性化
具有两个自变量x、y的非线性函数 z=f (x, y)小偏差线性化的方法:
传热学(第二章)
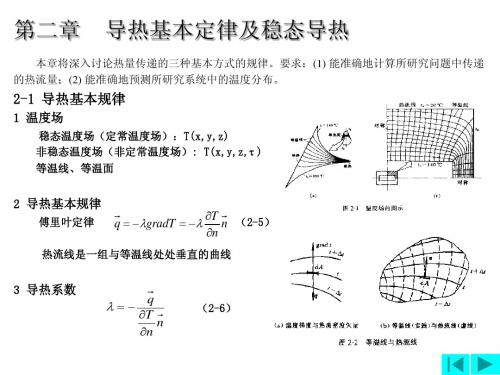
⒉ 通过圆筒壁的导热 由导热微分方程式(2—12)
边界条件:r=r1时,t=t1;r=r2时,t=t2 对(2-25)式积分两次,得其通解: t = c1 ln r + c2 将边界条件代入通解,确定积分常数
t2 − t1 t −t c2 = t1 − ln r 2 1 ln( r2 / r ) ln( r2 / r ) 1 1 t −t t = t1 + 2 1 ln( r / r ) (2-26) 1 ln( r2 / r ) 1 dt λ t1 − t2 q = −λ = (2-27) dr r ln( r2 / r ) 1 c1 =
2 1
λ1
第二章
导热基本定律及稳态导热
2-3 通过平壁、圆筒壁、球壳和其他变截面物体的导热 通过平壁、圆筒壁、
• 1∂ ∂T 1 ∂ ∂T ∂ ∂T ∂T (λr + 2 (λ ) + (λ ) + Φ = ρcp ∂τ r ∂r ∂r) r ∂ϕ ∂ϕ ∂z ∂z d dt 简化变为 dr (r dr ) = 0 (2-25)
⒉ 通过圆筒壁的导热 根据热阻的定义,通过整个圆筒壁的导热热阻为 (2-29) 29) 与分析多层平壁—样,运用串联热阻叠加的原则,可得通过图2-9所示的多层圆筒壁的 导热热流量 2πl(t1 − t4 ) Φ= (2-30) ln( d2 / d1) / λ1 + ln( d3 / d2 ) / λ2 + ln( d4 / d3) / λ3 ⒊ 通过球壳的导热 导热系数为常数,无内热源的空心球壁。内、外半径为r1、r2,其内外表面均匀 恒定温度为t1、t2,球壁内的温度仅沿半径变化,等温面是同心球面。 由傅立叶定律得: dt 各同心球面上的热流率q不相等,而热流量Φ相等。 Φ = −4πr2λ dr dr ⇒Φ 2 = −4πλdt r
机械工程控制基础-第二章-传递函数

华中科技大学材料学院
典型环节
比例环节 惯性环节 微分环节 积分环节 振荡环节 延时节例
华中科技大学材料学院
比例环节
1、传递函数函:G(s) K (放大环节)
2、特性:输入输出成正比,无惯性,不失真, 无延迟 X(s) Y(s) K 3、参数:K 4、单位阶跃响应:输出按比值复现输入, 无过渡过程。
华中科技大学材料学院
4)方框图不唯一。由于研究角度不一样,传递函数 列写出来就不一样,方框图也就不一样。 5) 研究方便。对于一个复杂的系统可以画出它的方 框图,通过方框图简化,不难求得系统的输入、输出 关系,在此基础上,无论是研究整个系统的性能,还 是评价每一个环节的作用都是很方便的。
华中科技大学材料学院
n 2
2
p1 p2 n , p1 p2 2n 2 1
n e p t e p t y (t ) 1 ( ) 2 p1 p2 2 1
1 2
华中科技大学材料学院
p1 p2 ,当 1时, p1 p2
则
n e p t y (t ) 1 2 2 1 p2
华中科技大学材料学院
延迟环节
1. 传函
W ( s) e
s
x
y
1
t
1
(t ) 2.单位阶跃响应 y(t ) L1[es 1 s ] 1 3.参数 延迟时间 4.特性:能充分复现输入,只是相差 ,该环节
t
是线性的,他对系统稳定性不利。然而过程控制中,
系统多数都存在延迟环节,常用带延迟环节的一阶
x(t )
1
y(t )
K
t
t
比例环节实例
1)分压器
第二章 (2.1,2.2)控制系统的微分方程、传递函数

拉氏变换的重要应用——解线性定常微分方程
求微分方程的拉氏变换,注意初值!!
求出 C ( s ) 的表达式 拉氏反变换,求得 c (t )
例1 已知系统的微分方程式,求系统的输出响应。
d 2c(t ) dc(t ) 2 2c(t ) r(t ) 2 dt dt d2 解: 在零初态下应用微分定理: 2 s 2
+
i (t )
R
–
u (t )
+
i (t )
u (t ) i (t ) R
du ( t ) 1 i (t ) dt C
di (t ) u (t ) L dt
电容
C
–
u (t )
+
ቤተ መጻሕፍቲ ባይዱi (t )
电感
u (t )
–
L
机械系统三要素的微分方程
设系统输入量为外力,输出量为位移
d 2 x (t) m f (t) 2 dt
d uc (t ) duc (t ) LC RC uc (t ) ur (t ) 2 dt dt
2
3.机械位移系统
输入量为外力: F (t ) 输出量为位移: y (t )
dy 2 (t ) 依据牛顿定律: F m dt 2
dy (t ) d y (t ) F (t ) ky (t ) f m 2 dt dt
d 2 y (t ) dy (t ) m f ky (t ) F (t ) 2 dt dt
微分方程结构一致 二阶线性定常微分方程
不同形式的物理环节和系统可以建立相同形式的数学模型。
系统微分方程由输出量各阶导数和输 入量各阶导数以及系统的一些参数构成。 n阶线性定常系统的微分方程可描述为:
非牛顿流体的传递过程特性-2

∞
∞
幂 律 函 数 区
直 线
∞
∞
第 二 牛 顿 区
第 一 牛 顿 区
幂 律 函 数 区
双对数坐标
(1)幂律方程:
直线区:Y=aX+b
K m K m 1 K n ,(n m 1, m n 1)
d d
对非牛顿流体:如上图:
d t 1 d
0
1 a1 假塑性:t1 a1 0
目前大多数用 μ a表示非牛顿流体的表观粘度(粘度)。 以后所讲粘度,即表观粘度。 由于计算机的发展μ t也应用广泛起来。 μ t的特点:用不同的粘度计测量结果应相同(减小系统 误差,如零点漂移)。
2)剪切速率匀速增加后再匀速减小,τ ~ 曲线不 重合,有滞后现象.
面积A1 第1次,t1,A=A1
第2次,t2,A=A2 第n次,tn,A=0
第n次--触变性消失, 变成假塑性流体。流体 的结构到达新的稳定状 态(平衡) 用滞后面积A的大小代 表流体的触变性大小, 但不好表达.
本构方程:与时间有关。 Moore方程:(无屈服应力)
a
0
1 m
1
定义 : 0 , , 为 0, 下的a
m为a ( 0 ) / 2时测出的 值.
1时: a 0,牛顿 1时: a ,假塑性 (用于PAM) 1时: a ,涨塑性
ΔY
e
y
t
y
t+ t
x
t时刻
x
t+ t时刻
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
z
uz
(y,z) y
z
ux
y
uy x
o
x
(x,y)
柱坐标系下的微元控制体
= 0
z
z u
o
r
uz
r z
ur
球坐标系下的微元控制体
= 0
= 0
u r o
ur
r
u
质量守恒与连续性方程
质量守恒定律 (Mass conservation) 若控制体内的流体包含 n 个组分,对任一组分 i 进行 质量衡算,都会有 :
uy
z
uz
V
dV
t
V
ux
x
u y
x
uz
x
dV
t
V
dV
V
ux
x
u y
x
uz
x
dV
V
ux
x
u y
x
uz
x
dV
A
undA
ρ2
u2
V
A2
ρ1
u1
A1
undA u cosdA 1u1cos1dA 2u2cos2dA A22u2 A11u1
A
A
A1
A2
t
dV
V
d dt
dV
xx, xy, xz yx, yy, yz zx, zy, zz
其中xx、yy、zz为粘性正应力
其余为粘性剪应力
下标:前一个代表作用面的法线方向 后一个代表该应力本身的方向
粘性剪应力与动量扩散通量等价 粘性正应力也具有类似性质
z
(uz)ux|z+Z
(uy)ux|y
(ux)ux|x
(ux)ux|x+x
输入控制体 - 输出控制体 + 控制体内生成 = 控制体内质量
的质量速率 的质量速率
的质量速率
的累积速率
W i,in
W i,out
ri
dmi dt
i 1,2,...,n
n
控制体内生成的质量速率和消耗的质量速率相等 ri 0 1
n
1
Wi,in Wi,out
d dt
n
(
1
mi
)
Win
Wout
V
d mV
dt
dM dt
不稳定流动系统的连续性方程
A2 2u2
A11u1
dM dt
稳定流动系统的连续性方程
A2 2u2 A11u1
不可压缩流体的连续性方程 圆管流动的连续性方程
A2u2 A1u1
u2
u1
A1 A2
u1
d1 d2
2
动量守恒与流体运动微分方程
动量守恒定律
牛顿第二定律
d
mur
r F
t
lim
x , y , z
0
(
ux
)
x
x x
(
u
x
)
x
(u y ) yy (u y ) y
y
(uz )zz (uz )z
z
连续性方程
t
x
ux
y
uy
z
uz
u
代表空间任意点处由流体质量通量 u 的空间变化率引起
该点处流体密度随时间的变化率。
(u) 代表的流体质量通量的空间变化率又被称作质量通
uzux z uzux zz xy
六个面元扩散输入控制体的x方向的动量分量
xx x xx xx yz yx y yx yy xz zx z zx zz xy
作用于控制体的所有外力在x方向的分量的总和为
p x p xx yz gxxyz
x 方向的动量分量在控制体内的累积速率为
控制体的取法 代表性:在整个流场连续可积 对称性:
控制体
正交性: 大小形状:宏观、微观 坐标系 直角坐标系、柱坐标系、球坐标系
不同坐标系下的微元控制体
常用的坐标系有直角坐标系、柱坐标系和球坐标系
直角坐标系(Cartesian coordinates):x,y,z 柱坐标系(Cylindrical coordinates):r,,z 球坐标系( Spherical coordinates):r,,
x
uy
y
uz
z
ux t
ux
ux x
uy
ux y
uz
ux z
ux
ux x
uy y
uz z
t
ux
x
uy
y
uz
z
Dux Dt
ux
u
D Dt
x方向
Dux Dt
xx
x
不同坐标系中的连续方程
直角坐标系(x,y,z)
t
x
ux
y
uy
z
uz
0
柱坐标系(r, ,z)
t
1 r
r
r
ur
1 r
u
z
uz
0
球坐标系(r,, )
t
1 r2
r
r2ur
1
r sin
u sin
1
r sin
u
0
【例2-1】 变直径管道中流体流动的连续性方程
t
x
ux
y
ux xyz
t
上四式代入动量衡算总式,以xyz通除并取其趋 于0极限,得流体在x方向运动微分方程
t
ux
x
uxux
y
u y u x
z
u
zux
xx x
yx y
zx z
p x
g
x
ux t
ux
t
ux
ux x
uy
ux y
uz
ux z
ux
ux x
uy y
uz z
uxux
dm dt
流体的速度和密度是空间与时间的连续函数
ux, y, z,t x, y, z,t
z
(uz)z+z
(uy)y
(ux)x
y
z
y x
(ux)x+x
(ux)y+y
x
(uz)z
xyz
t
yz(ux )x
(ux )xx
xz (uy )y (uy )yy xy (uz )z (uz )zz
(uy)ux|y+y (uz)ux|z
x
y
动量通量
z
τxx|x
y
τz x|z + Δz τzx|z
τyx|y τxx|x+Δx
τyx|y+Δy
x
控制体以对流和扩散方式与周围流体交换动量 六个控制面 x 方向对流输入控制体的动量分量
uxux x uxux xx yz
uyux y uyux yy xz
dt
微元控制体流体动量守恒定律
输入控制体
输出控制体
作用在控制体
控制体内动量
-
+
=
的动量流率
的动量流率
上的合力
的累积速率
▪ 控制体受力
体积力 压力 表面力
z
9
7
8
3
z
6
1
2
5 4 y
x x
y
1-xx 2-xy 3-xz 4-yx 5-yy 6-yz 7-zx 8-zy 9-zz
9个粘性应力分量
表面力 9个分量
第二章 传递过程基本方程
第二章 传递过程基本方程
▪ 衡算体系 ▪ 质量守恒与连续性方程 ▪ 动量守恒与流动微分方程 ▪ 能量守恒与传热微分方程 ▪ 质量守恒与传质微分方程
衡算体系
控制体与控制面 流动空间具有一定几何形状与大小的开放体系称为控 制体,围成控制体的空间曲面称为控制面 控制体通过控制面与环境进行质量、动量和能量交换
量的散度,其物理意义可以理解为空间某点处单位体积内 流体质量的流散速率。
连续性方程
t
ux
x
uy
y
uzuz z
D u
Dt
流体密度的随 体导数
体积通量(或速度矢量) u 的散度,物理意义为空间某点 处单位体积流体的体积形变 (扩张或收缩)速率
连续性方程是传递过程最基本的方程之一,推导过程未加 假设,因此对各种流体在各种情况下都适用。
