三角形的高中线与角平分线练习题综述
专题13.2三角形的高、中线与角平分线【十大题型】-2024-2025学年八年级数[含答案]
![专题13.2三角形的高、中线与角平分线【十大题型】-2024-2025学年八年级数[含答案]](https://img.taocdn.com/s3/m/ac74d303814d2b160b4e767f5acfa1c7aa0082e8.png)
试卷第 4 页，共 15 页
OB ，5 表示线段 OE ，从 O 点出发，按 1753 运动可得到正方形 OAHG ．从 O 点出发，按
1112445668 运动的轨迹形成的图形面积为
．
【变式 3-3】（23-24 八年级下·河南郑州·期末）
12．如图， 4 ´ 4 方格纸中小正方形的边长为 1，A，B 两点在格点上，请在图中格点上找到
【深入思考】有了这样思考问题的经历，于是小孙同学对探究四边形 ABCD 内作一条直线将
它分成面积相等的两部分给出一种思路：如图 3，小孙同学的辅助线：①连接对角线 AC ，
②作 DE ∥ AC 交 BC 的延长线于 E ；③取 BE 的中点 M ，则直线 AM 为所求直线．小孙同
学还尝试从理论上给予说明，请你帮助将说理过程补充完整：
试卷第 8 页，共 15 页
AE 的长．
【变式 5-3】（23-24 八年级上·河北廊坊·阶段练习）
20．在 V ABC 中， D 是 BC 的中点， AB = 12 ， AC = 8 ．用剪刀从点 D 入手进行裁剪，若沿
；若点 E 在 AB 上，沿 DE 剪开得到两部分周长
DA 剪成两个三角形，它们周长的差为
8
【题型 7 与角平分线有关的角度计算】
【题型 8 应用等面积法求线段长】
【题型 9 探究三角形的边、角、线】
【题型 10 三角形的稳定性】
9
10
12
13
知识点：三角形的高、中线与角平分线
（1）从三角形的一个顶点向底边作垂线，垂足与顶点之间的线段叫做三角形的高．
（2）三角形一个内角的平分线与这个内角的对边交于一点，则这个内角的顶点与所交的点
S△ DEF =
三角形中线高角平分线的30题（有答案）ok
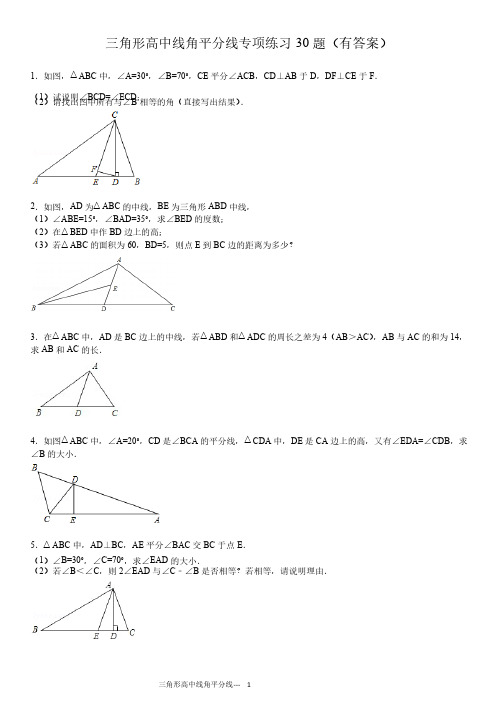
题（有答案）三角形高中线角平分线专项练习30题（有答案）1．如图，△ABC中，∠A=30°，∠B=70°，CE平分∠ACB，CD⊥AB于D，DF⊥CE于F．（1）试说明∠BCD=∠ECD；（2）请找出图中所有与∠B相等的角（直接写出结果）．2．如图，AD为△ABC的中线，BE为三角形ABD中线，中线，的度数；（1）∠ABE=15°，∠BAD=35°，求∠BED的度数；边上的高；（2）在△BED中作BD边上的高；边的距离为多少？（3）若△ABC的面积为60，BD=5，则点E到BC边的距离为多少？3．在△ABC中，AD是BC边上的中线，若△ABD和△ADC的周长之差为4（AB＞AC），AB与AC的和为14，的长．求AB和AC的长．4．如图△ABC中，∠A=20°，CD是∠BCA的平分线，△CDA中，DE是CA边上的高，又有∠EDA=∠CDB，求的大小．∠B的大小．5．△ABC中，AD⊥BC，AE平分∠BAC交BC于点E．的大小．（1）∠B=30°，∠C=70°，求∠EAD的大小．（2）若∠B＜∠C，则2∠EAD与∠C﹣∠B是否相等？若相等，请说明理由．是否相等？若相等，请说明理由．6．在△ABC中，AD是高，AE是角平分线，∠B=20°，∠C=60°，求∠CAD和∠DAE的度数．的度数．7．在△ABC中．中．（如图）（1）若∠A=60°，AB、AC边上的高CE、BD交于点O．求∠BOC的度数．（如图）（2）若∠A为钝角，AB、AC边上的高CE、BD所在直线交于点O，画出图形，并用量角器量一量∠BAC+∠BOC= _________°，再用你已学过的数学知识加以说明．，再用你已学过的数学知识加以说明．（3）由（1）（2）可以得到，无论∠A为锐角还是钝角，总有∠BAC+∠BOC=_________°．8．在△ABC中，已知∠ABC=60°，∠ACB=50°，BE是AC上的高，CF是AB上的高，H是BE和CF的交点．的交点．的度数．求∠ABE、∠ACF和∠BHC的度数．9．如图，△ACB中，∠ACB=90°，∠1=∠B．的高；（1）试说明CD是△ABC的高；（2）如果AC=8，BC=6，AB=10，求CD的长．的长．10．如图，已知△ABC的高AD，角平分线AE，∠B=26°，∠ACD=56°，求∠AED的度数．的度数．11．如图，△ABC中，∠ABC=40°，∠C=60°，AD⊥BC于D，AE是∠BAC的平分线．的平分线．（1）求∠DAE的度数；的度数；是哪几个三角形的高．（2）指出AD是哪几个三角形的高．12．如图，在△ABC中，∠ABC=66°，∠ACB=54°，BE是AC上的高，CF是AB上的高，H是BE和CF的交点，的度数．求∠ABE、∠ACF和∠BHC的度数．13．如图，在△ABC中，∠B=60°，∠C=20°，AD为△ABC的高，AE为角平分线为角平分线的度数；（1）求∠EAD的度数；的关系并说明理由．（2）寻找∠DAE与∠B、∠C的关系并说明理由．14．如图，已知：AD是△ABC的角平分线，CE是△ABC的高，∠BAC=60°，∠BCE=40°，求∠ADB的度数．的度数．15．如图，AD是△ABC的BC边上的高，AE是∠BAC的角平分线，的角平分线，的度数．（1）若∠B=47°，∠C=73°，求∠DAE的度数．的代数式表示）（2）若∠B=α°，∠C=β°（α＜β），求∠DAE的度数（用含α、β的代数式表示）16．如图，在△ABC中，AD是角平分线，∠B=60°，∠C=45°，求∠ADB和∠ADC的度数．的度数．17．已知△ABC中，∠ACB=90°，CD为AB边上的高，BE平分∠ABC，分别交CD、AC于点F、E，求证：∠CFE=∠CEF．18．如图（1），△ABC中，AD是角平分线，AE⊥BC于点E．（1）．若∠C=80°，∠B=50°，求∠DAE的度数．的度数．（2）．若∠C＞∠B，试说明∠DAE=（∠C﹣∠B）．（3）．如图（2）若将点A在AD 上移动到A´处，A´E⊥BC于点E．此时∠DAE变成∠DA´E，（2）中的结论还正确吗？为什么？确吗？为什么？19．如图，已知△ABC的周长为21cm，AB=6cm，BC边上中线AD=5cm，△ABD周长为15cm，求AC长．长．20．我们知道，任何一个三角形的三条内角平分线相交于一点，如图，若△ABC 的三条内角平分线相交于点I，过I作DE⊥AI分别交AB、AC于点D、E．）请你通过画图、度量，填写右上表（图画在草稿纸上，并尽量画准确）（1）请你通过画图、度量，填写右上表（图画在草稿纸上，并尽量画准确）之间有何数量关系，请写出来，并说明其中的道理．（2）从上表中你发现了∠BIC与∠BDI之间有何数量关系，请写出来，并说明其中的道理．40°60°90°120°∠BAC的度数的度数∠BIC的度数∠BDI的度数21．如图，△ABC中，AD是高，AE、BF是角平分线，它们相交于点O，∠CAB=50°，∠C=60°，求∠DAE和∠BOA 的度数．的度数．22．如图，在△ABC中，AE是中线，AD是角平分线，AF是高，填空：是高，填空：（1）BE=_________=_________（2）∠BAD=__________________（3）∠AFB=_________=90°（4）S△ABC=_________S△ABE．23．如图，BM是△ABC的中线，AB=5cm，BC=3cm，那么△ABM与△BCM的周长是差是多少？的周长是差是多少？24．在△ABC中，AB=AC，AD是中线，△ABC的周长为34cm，△ABD的周长为30cm，求AD的长．的长．25．如图，在三角形ABC中，AD是BC边上的中线，三角形ABD的周长比三角形ACD的周长小5，你能求出AC与AB的边长的差吗？的边长的差吗？26．如图，在△ABC中，AC=AB，AD是BC边上的中线，则AD⊥BC，请说明理由．，请说明理由．27．如图，∠BAD=∠CAD，则AD是△ABC的角平分线，对吗？说明理由．的角平分线，对吗？说明理由．28．如图，在△ABC中，AD是BC边上的中线，△ADC的周长比△ABD的周长多5cm，AB与AC的和为11cm，的长．求AC的长．29．如图所示，AD是△ABC的中线，AE是△ACD的中线，已知DE=2cm，求BD，BE，BC的长．的长．30．如图所示，AD是△ABC的中线，AB=6cm，AC=5cm，求△ABD和△ADC的周长的差．的周长的差．参考答案：1．（1）∵∠B=70°，CD ⊥AB 于D ， ∴∠BCD=90°﹣70°=20°，在△ABC 中，∵∠A=30°，∠B=70°， ∴∠ACB=180°﹣30°﹣70°=80°， ∵CE 平分∠ACB ， ∴∠BCE=∠ACB=40°，∴∠ECD=∠BCE ﹣∠BCD=40°﹣20°=20°， ∴∠BCD=∠ECD ；（2）∵CD ⊥AB 于D ，DF ⊥CE 于F ， ∴∠CED=90°﹣∠ECD=90°﹣20°=70°， ∠CDF=90°﹣∠ECD=90°﹣20°=70°，所以，与∠B 相等的角有：∠CED 和∠CDF ． 2．（1）∵∠BED 是△ABE 的一个外角，的一个外角， ∴∠BED=∠ABE+∠BAD=15°+35°=50°．（2）如图所示，EF 即是△BED 中BD 边上的高．边上的高． （3）∵AD 为△ABC 的中线，BE 为三角形ABD 中线， ∴S △BED =S △ABC =×60=15； ∵BD=5，∴EF=2S △BED ÷BD=2×15÷5=6， 即点E 到BC 边的距离为6．3．∵AD 是BC 边上的中线，边上的中线， ∴BD=CD ，∴△ABD 的周长﹣△ADC 的周长=（AB+AD+BD ）﹣（AC+AD+CD ）=AB ﹣AC=4，（2分）分） 即AB ﹣AC=4①， 又AB+AC=14②， ①+②得．2AB=18， 解得AB=9，②﹣①得，2AC=10， 解得AC=5，∴AB 和AC 的长分别为：AB=9，AC=5． 4．∵DE 是CA 边上的高，边上的高， ∴∠DEA=∠DEC=90°， ∵∠A=20°，∴∠EDA=90°﹣20°=70°， ∵∠EDA=∠CDB ，∴∠CDE=180°﹣70°×2=40°，在Rt △CDE 中，∠DCE=90°﹣40°=50°， ∵CD 是∠BCA 的平分线，的平分线，∴∠BCA=2∠DCE=2×50°=100°，在△ABC 中，∠B=180°﹣∠BCA ﹣∠A=180°﹣100°﹣20°=60°．故答案为：60 5．（1）∵∠B=30°，∠C=70° ∴∠BAC=180°﹣∠B ﹣∠C=80° ∵AE 是角平分线，是角平分线， ∴∠EAC=∠BAC=40°∵AD 是高，∠C=70° ∴∠DAC=90°﹣∠C=20°∴∠EAD=∠EAC ﹣∠DAC=40°﹣20°=20°；（2）由（1）知，∠EAD=∠EAC ﹣∠DAC=∠BAC ﹣（90°﹣∠C ）①把∠BAC=180°﹣∠B ﹣∠C 代入①，整理得，整理得 ∠EAD=∠C ﹣∠B ，∴2∠EAD=∠C ﹣∠B ．6．∵AD 是高，∠C=60°，∴∠CAD=90°﹣∠C=90°﹣60°=30°； ∵∠B=20°，∠C=60°，∴∠BAC=180°﹣∠B ﹣∠C=180°﹣20°﹣60°=100°， ∵AE 是角平分线，是角平分线， ∴∠CAE=∠BAC=×100°=50°，∴∠DAE=∠CAE ﹣∠CAD=50°﹣30°=20°． 7．（1）∵BD 、CE 分别是边AC ，AB 上的高，上的高， ∴∠ADB=∠BEC=90°， 又∵∠BAC=60°，∴∠ABD=180°﹣∠ADB ﹣∠A=180°﹣90°﹣60°=30°， ∴∠BOC=∠EBD+∠BEO=90°+30°=120°； （2）如图所示：）如图所示：∠BAC+∠BOC=180°；理由如下：∵BD 、CE 分别是边AC ，AB 上的高，上的高， ∴∠ADB=∠BEC=90°，∵∠ABD=180°﹣∠ADB ﹣∠BAD=180°﹣90°﹣∠BAD=90°﹣∠BAD ，∠O=180°﹣∠BEO ﹣∠DBA=90°﹣∠DBA=90°﹣（90°﹣∠BAD ）=∠BAD ， ∵∠BAC=180°﹣∠DAB ， ∴∠BAC=180°﹣∠O ， ∴∠BAC+∠O=180°； （3）由（1）（2）可得∠BAC+∠BOC=180°．8．∵BE是AC上的高，上的高，∴∠AEB=90°，∵∠ABC=60°，∠ACB=50°，∴∠A=180°﹣60°﹣50°=70°，∴∠ABE=180°﹣90°﹣70°=20°，∵CF是AB上的高，上的高，∴∠AFC=90°，∴∠ACF=180°﹣90°﹣70°=20°，∵∠ABE=20°，∴∠EBC=∠ABC﹣∠ABE=60°﹣20°=40°，∵∠ACF=20°，∠ACB=50°，∴∠BCH=30°，∴∠BHC=180°﹣40°﹣30°=110°．9．（1）∵∠1+∠BCD=90°，∠1=∠B ∴∠B+∠BCD=90°∴△BDC是直角三角形，即CD⊥AB，∴CD是△ABC的高；的高；（2）∵∠ACB=∠CDB=90°∴S△ABC=AC •BC=AB•CD，∵AC=8，BC=6，AB=10，∴CD===10.∵∠B=26°，∠ACD=56°∴∠BAC=30°∵AE平分∠BAC ∴∠BAE=15°∴∠AED=∠B+∠BAE=41°11．（1）∵AD⊥BC于D，∴∠ADB=∠ADC=90°，∵∠ABC=40°，∠C=60°，∴∠BAD=50°，∠CAD=30°，∴∠BAC=50°+30°=80°，∵AE是∠BAC的平分线，的平分线，∴∠BAE=40°，∴∠DAE=50°﹣40°=10°．（2）AD是△ABE、△ABD、△ABC、△AED、△AEC、△ADC的高．的高．12．∵∠ABC=66°，∠ACB=54°，∴∠A=180°﹣∠ABC﹣∠ACB=180°﹣66°﹣54°=60°．又∵BE是AC边上的高，所以∠AEB=90°，∴∠ABE=180°﹣∠BAC﹣∠AEB=180°﹣90°﹣60°=30°．同理，∠ACF=30°，∴∠BHC=∠BEC+∠ACF=90°+30°=120°．13．（1）∵在△ABC中，∠BAC=180°﹣∠C﹣∠B=180°﹣20°﹣60°=100°，又∵AE为角平分线，为角平分线，∴∠EAB=∠BAC=50°，在直角△ABD中，∠BAD=90°﹣∠B=90°﹣60°=30°，∴∠EAD=∠EAB﹣∠BAD=50°﹣30°=20°；（2）根据（1）可以得到：∠EAB=∠BAC=（180°﹣∠B﹣∠C）∠BAD=90°﹣∠B，则∠EAD=∠EAB﹣∠BAD=（180°﹣∠B﹣∠C）﹣（90°﹣∠B ）=（∠B﹣∠C）．14．∵AD是△ABC的角平分线，∠BAC=60°，∴∠DAC=∠BAD=30°，∵CE是△ABC的高，∠BCE=40°，∴∠B=50°，∴∠ADB=180°﹣∠B﹣∠BAD=180°﹣30°﹣50°=100°15．（1）∵∠B=47°，∠C=73°，∴∠BAC=180°﹣47°﹣73°=60°，∵AD是△ABC的BC边上的高，边上的高，∴∠BAD=90°﹣47°=43°，∵AE是∠BAC的角平分线，的角平分线，∴∠BAE=∠BAC=30°，∴∠DAE=∠BAD﹣∠BAE=43°﹣30°=13°；（2））∵∠B=α°，∠C=β°，∴∠BAC=180°﹣α°﹣β°，∵AD是△ABC的BC边上的高，边上的高，∴∠BAD=90°﹣α°，∵AE是∠BAC的角平分线，的角平分线，∴∠BAE=∠BAC=（180°﹣α°﹣β°），∴∠DAE=∠BAD﹣∠BAE=90°﹣α°﹣（180°﹣α°﹣β°），=90°﹣α°﹣90°+α°+β°，=（β﹣α）°16．∵∠B=60°，∠C=45°，∴∠BAC=180°﹣60°﹣45°=75°，∵AD为∠BAC的角平分线，的角平分线，∴∠BAD=∠CAD=∠BAC=37.5°，在△ABD 中，∠ADB=180°﹣∠BAD ﹣∠B=82.5°， 则∠ADC=180°﹣∠ADB=97.5°． 17．∵∠ACB=90°， ∴∠1+∠3=90°， ∵CD ⊥AB ， ∴∠2+∠4=90°，又∵BE 平分∠ABC ， ∴∠1=∠2， ∴∠3=∠4， ∵∠4=∠5， ∴∠3=∠5，即∠CFE=∠CEF．18．（1）在△ABC 中，∠BAC=180°﹣∠B ﹣∠C=180°﹣50°﹣80°=50°； ∵AD 是角平分线，是角平分线， ∴∠DAC=∠BAC=25°；在△ADC 中，∠ADC=180°﹣∠C ﹣∠DAC=75°； 在△ADE 中，∠DAE=180°﹣∠ADC ﹣AED=15°． （2）∠DAE=180°﹣∠ADC ﹣AED=180°﹣∠ADC ﹣90°=90°﹣∠ADC=90°﹣（180°﹣∠C ﹣∠DAC ）=90°﹣（180°﹣∠C ﹣∠BAC ）=90°﹣[180°﹣∠C ﹣（180°﹣∠B ﹣∠C ）]=（∠C ﹣∠B ）． （3）（2）中的结论仍正确．）中的结论仍正确．∠A ʹDE=∠B+∠BAD=∠B+∠BAC=∠B+（180°﹣∠B ﹣∠C ）=90°+∠B ﹣∠C ；在△DA ʹE 中，∠DA ʹE=180°﹣∠A ʹED ﹣∠A ʹDE=180°﹣90°﹣（90°+∠B ﹣∠C ）=（∠C ﹣∠B ）． 19．∵AB=6cm ，AD=5cm ，△ABD 周长为15cm ， ∴BD=15﹣6﹣5=4cm ， ∵AD 是BC 边上的中线，边上的中线， ∴BC=8cm ，∵△ABC 的周长为21cm ， ∴AC=21﹣6﹣8=7cm ． 故AC 长为7cm ． 20．（1）填写表格如下：）填写表格如下：∠BAC 的度数40° 60° 90°120° ∠BIC 的度数的度数 110°120°135°150°∠BDI 的度数110° 120° 135°（2）∠BIC=∠BDI ，理由如下：，理由如下：∵△ABC 的三条内角平分线相交于点I ， ∴∠BIC=180°﹣（∠IBC+∠ICB ） =180°﹣（∠ABC+∠ACB ） =180°﹣（180°﹣∠BAC ） =90+∠BAC ； ∵AI 平分∠BAC ， ∴∠DAI=∠DAE ． ∵DE ⊥AI 于I ， ∴∠AID=90°．∴∠BDI=∠AID+∠DAI=90°+∠BAC ． ∴∠BIC=∠BDI ．21．∵∠A=50°，∠C=60°∴∠ABC=180°﹣50°﹣60°=70°， 又∵AD 是高，是高， ∴∠ADC=90°，∴∠DAC=180°﹣90°﹣∠C=30°， ∵AE 、BF 是角平分线，是角平分线，∴∠CBF=∠ABF=35°，∠EAF=25°， ∴∠DAE=∠DAC ﹣∠EAF=5°，∠AFB=∠C+∠CBF=60°+35°=95°，∴∠BOA=∠EAF+∠AFB=25°+95°=120°， ∴∠DAC=30°，∠BOA=120°． 故∠DAE=5°，∠BOA=120°． 22．（1）∵AE 是中线，是中线， ∴BE=CE=BC ， （2）∵AD 是角平分线，是角平分线， ∴∠BAD=∠CAD=∠BAC ， （3）∵AF 是高，是高，∴∠AFB=∠AFC=90°，（4）S △ABC =，S △ABE =，∵BC=2BE，∴S△ABC=2S△ABE，故答案为CE，BC，∠CAD，∠BAC，∠AFC，2 23．∵BM是△ABC的中线，的中线，∴MA=MC，∴C△ABM﹣C△BCM=AB+BM+MA﹣BC﹣CM﹣BM =AB﹣BC=5﹣3=2cm．答：△ABM与△BCM的周长是差是2cm．24．方法1：由题意知：AB+AC+BC=34，AB+AD+BD=30，∵AB=AC，BD=BC，∴②×2得：2AB+2AD+BC=60③，③﹣①得：2AD=26，∴AD=13cm．方法2：∵AB=AC，D是中点，且AB+AC+BC=34，∴BD=BC，AB=（AB+AC），∴AB+BD=（AB+AC）+BC=（AB+AC+BC）=17cm （周长的一半）．∵AB+BD+AD=30cm，AD=30﹣17=13cm．25．能．．能．由题意知：△ABD的周长=AB+BD+AD，△ACD的周长=AC+CD+AD，又因为AD是BC边上的中线，边上的中线，所以BD=CD．∵△ABD的周长比△ACD的周长小5，∴AC+CD+AD﹣（AB+BD+AD）=AC﹣AB=5．即AC与AB的边长的差为5 26．∵AD是BC边上的中线，∴BD=DC，∵AC=AB，AD=AD，∴△ABD≌△ACD（SSS），∴∠ADB=∠ADC，∵∠ADB+∠ADC=180°，∴∠ADB=∠ADC=90°，∴AD⊥BC．27．错误．．错误．因为AD虽然是线段，但不符合三角形角平分线定义，这里射线AD是∠BAC的平分线．的平分线．28．∵AD是BC边上的中线，边上的中线，∴D为BC的中点，CD=BD．∵△ADC的周长﹣△ABD的周长=5cm．∴AC﹣AB=5cm．又∵AB+AC=11cm，∴AC=8cm．即AC的长度是8cm．29．∵AD是△ABC的中线，AE是△ACD的中线，的中线， ∴BD=CD=2DE=4cm，∴BE=BD+DE=6cm，∴BC=2BD=8cm．30．∵AD是△ABC中BC边上的中线，边上的中线，∴BD=DC=BC，∴△ABD和△ADC的周长的差=（AB+BC+AD）﹣（AC+BC+AD）=AB﹣AC=1．。
三角形的高、中线、角平分 线练习题
三角形的高、中线、角平分线练习题
1、三角形的三条中线、三条角平分线、三条高都是（ ）
A．直线 B．射线 C．线段 D．射线或线段
2、如果一个三角形的三条高的交点恰是三角形的一个顶点，那么这个三角形是（ ）A．锐角三角形 B．直角三角形 C．钝角三角形 D．不能确定
3、能把三角形的面积分成两个相等的三角形的线段是（ ）
A．中线B．高C．角平分线 D．以上三种情况都正确
4、如图若∠BAF=∠CAF，则____是△ABD的角平分线，____是△ABC的角平分线
5、如图AB⊥AC，则AB是△ABC的边____上的高，也是△BDC的边______上的高，也是△ABD的边____上的高.
6、如图BD、AE分别是△ABC的中线、角平分线，AC=10cm ，∠BAC=700，则AD=_____，∠BAE=____.
7、在△ABC中，AE是中线，AD是角平分线，AF是高，填空：
⑴BE＝___＝_____；
⑵∠BAD=_____=_____；⑶∠AFB=_____=90
8、在△ABC中AB=AC，AC上的中线BD把三角形的周长分为24cm和30cm的两个部分，求三角形的三边长。
9、要使四边形木架(用四根木条钉成)不变形，至少要再钉上几根木条？五边形木架和六边形木架呢？n边形木架呢？。
人教版八年级数学上11.1.2三角形的高、中线、角平分线同步练习题(解析版)
人教版八年级数学上11.1.2三角形的高、中线、角平分线同步练习题一．选择题1、下面四个图形中，线段BD是△ABC的高的是（）A. B.C. D.答案：D分析：本题考查了三角形的高线．解答：△ABC中AC边上的高是过点B且垂直于AC边（或AC边延长线）的线段，只有D 选项正确．选D．2、下列说法正确的是（）A. 三角形三条高都在三角形内B. 三角形三条中线相交于一点C. 三角形的三条角平分线可能在三角形内，也可能在三角形外D. 三角形的角平分线是射线答案：B分析：本题考查了三角形的高线、中线、角平分线．解答：∵钝角三角形的三条高有2条在三角形的外部，∴A错误；∵三角形三条中线相交于一点，∴B正确；∵三角形的三条角平分线都在在三角形内，∴C错误；∵三角形的角平分线、高、中线都是线段，∴D错误；选：B．3、如图，D、E分别是△ABC的边AC、BC的中点，那么下列说法中不正确的是（）A. DE是△BCD的中线B. BD是△ABC的中线C. AD=DC，BE=ECD. AD=EC，DC=BE答案：D分析：本题考查了三角形的中线．解答：∵D、E分别是△ABC的边AC、BC的中点，∴DE是△BCD的中线，BD是△ABC的中线，AD=DC，BE=EC．但不能得到AD=EC和DC=BE．选D．4、三角形一边上的中线把原三角形一定分成两个（）A. 形状相同的三角形B. 面积相等的三角形C. 直角三角形D. 周长相等的三角形答案：B分析：本题考查了三角形的中线．解答：三角形一边上的中线把原三角形一定分成两个面积相等的三角形．选B．5、如图所示，AD是△ABC的角平分线，AE是△ABD的角平分线．若∠BAC=80°，则∠EAD 的度数是（）A. 20°B. 30°C. 45°D. 60°答案：A分析：本题考查了三角形的角平分线．解答：∵AD△ABC的角平分线，∠BAC=80°，∴∠BAD=12∠BAC=40°．又∵AE是△ABD的角平分线，∴∠EAD=12∠BAD=20°．选A．6、在△ABC中，AD为中线，BE为角平分线，则在以下等式中：①∠BAD=∠CAD；①∠ABE=∠CBE；①BD=DC；①AE=EC. 正确的是（）A. ①②B. ③④C. ①④D. ②③答案：D分析：本题考查了三角形的中线、角平分线．解答：如下图，∵AD是△ABC的中线，BE是△ABC的角平分线，∴BD=CD，∠ABE=∠CBE，∴上述结论中正确的是①①．选D.7、三角形的高线是（）A. 直线B. 线段C. 射线D. 三种情况都可能答案：B分析：本题考查了三角形的高线．解答：由三角形高的定义：“过三角形的一个顶点向对边或对边所在的直线引垂线，顶点到垂足之间的线段叫三角形的高线”可知：三角形的高线是线段．选B．8、如图，△ABC的角平分线AD、中线BE相交于点O，则①AO是△ABE的角平分线；①BO 是△ABD的中线；①DE是△ADC的中线；①ED是△EBC的角平分线．4个结论中正确的有（）A. 1个B. 2个C. 3个D. 4个答案：B分析：本题考查了三角形的高线、中线、角平分线．解答：（1）∵AD是△ABC的角平分线，可得∠BAO=∠CAO，∴①“AO是△ABE的角平分线”这种说法是正确的；（2）由BE是△ABC的中线可得AE=CE，但不能确定AO=DO，∴①“BO是△ABD的中线”这种说法是错误的；（3）由BE是△ABC的中线可得AE=CE，∴①“DE是△ADC的中线”这种说法是正确的；（4）∵由题中条件不能得到∠ADE=∠CDE，∴①“ED是△EBC的角平分线”这种说法是错误的；即上述说法中正确的个数为：2．二、填空题9、如图，在△ABC中，∠ACB=90°，CD⊥AD，垂足为点D，有下列说法：①点A与点B的距离是线段AB的长；①点A到直线CD的距离是线段AD的长；①线段CD是△ABC边AB上的高；①线段CD是△BCD边BD上的高．上述说法中，正确的个数为______个答案：4分析：本题考查了三角形的高线、点到直线的距离．解答：（1）根据“连接两点的线段的长度叫做两点间的距离”可知：①中的说法是正确的；（2）根据“直线为一点到直线的垂线段的长度叫做这点到直线的距离”可知：①中的说法正确；（3）根据三角形高的定义：“过三角形的一个顶点向对边或对边所在的直线引垂线，顶点到垂足之间的线段叫三角形的高线”可知：①中的说法正确；（4）根据三角形高的定义：“过三角形的一个顶点向对边或对边所在的直线引垂线，顶点到垂足之间的线段叫三角形的高线”可知：①中的说法正确；即上述说法中正确的个数为4．10、如图所示，CD是△ABC的中线，AC=9cm，BC=3cm，那么△ACD和△BCD的周长差是______cm．答案：6分析：由三角形一边上的中线把三角形分成的两个新三角形的周长差等于原三角形中另外两边的差．解答：∵CD是△ABC的中线，∴AD=BD．∵C△ACD=AC+AD+CD，C△BCD=BC+BD+CD，∴C△ACD-C△BCD=（AC+AD+CD-（BC+BD+CD）=AC+AD+CD-BC-BD-CD=AC-BC=9-3=6（cm）．11、已知，AD是△ABC的一条高，如果∠BAD＝65°，∠CAD＝30°，则∠BAC＝______．答案：95°或35°．分析：本题考查了三角形的高线．解答：三角形的高可能在三角形内部，也可能在三角形的外部，要分两种情况讨论：①当AD 在三角形的内部时，∠BAC=∠BAD+∠CAD=65°+30°=95°； 当AD在三角形的外部时，∠BAC=∠BAD-∠CAD=65°-30°=35°．12、如图，在△ABC中，AC⊥BC，CD⊥AB于点D．则图中共有______个直角三角形．答案：3分析：本题考查了直角三角形的判定．解答：∵在△ABC中，AC⊥BC，CD⊥AB，∴∠ACB=∠ADC=∠BDC=90°，∴△ABC、△ADC、△BDC都是直角三角形．即图中共有3个直角三角形．13、如图，在△ABC中，BD是角平分线，BE是中线，若AC=24cm，则AE=______cm，若∠ABC=72°，则∠ABD=______度．答案：12 36分析：本题考查了三角形的角平分线、中线．解答：∵在△ABC中，BD是角平分线，BE是中线，∴AE=12AC=12（cm），∠ABD=12∠ABC=36°．14、如图所示．在△ABC中，已知点D，E，F分别为边BC，AD，CE的中点，且S△ABC=8cm2，则S阴影等于______cm2．答案：1分析：根据三角形的面积公式，知△BCE的面积是△ABC的面积的一半，进一步求得阴影部分的面积是△BEC的面积的一半．解答：解：∵点E是AD的中点，∴△BDE的面积是△ABD的面积的一半，△CDE的面积是△ACD的面积的一半．则△BCE的面积是△ABC的面积的一半，即为2cm2．∵点F是CE的中点，∴阴影部分的面积是△BCE的面积的一半，即为1cm2．三、解答题15、如图，D是△ABC中BC边上的一点，DE∥AC交AB于点E，若∠EDA=∠EAD，试说明AD是△ABC的角平分线．答案：见解答．分析：由DE∥AC交AB于点E可得∠CAD=∠EDA，结合∠EDA=∠EAD，可得∠CAD=∠EAD，即可得到结论．解答：∵DE∥AC，∴∠EDA=∠CAD．∵∠EDA=∠EAD，∴∠CAD=∠EAD．∴AD是△ABC的角平分线．16、如图，在△ABC中，AD⊥BC，BE⊥AC，BC=12，AC=8，AD=6，BE的长为多少？答案：9分析：由已知易得：S△ABC=12AC⋅BE=12BC⋅AD，代入BC=12，AC=8，AD=6即可解得BE的长．解答：∵在△ABC中，AD⊥BC，BE⊥AC，BC=12，AC=8，AD=6，∴S△ABC=12BC⋅AD=11262⨯⨯=36，又∵S△ABC=12 AC·BE，∴12×8×BE=36，解得：BE=9．17、如图，在3×2的正方形网格中，小正方形的边长为1，以图中A，B，C，D，E中的三点为顶点的三角形中，面积为1的三角形有哪些?答案：△ABC，△ADE，△BCE，△ACD．分析：根据不在同一直线上的三个点可构成一个三角形分析可知，以A、B、C、D、E中的三点为顶点的三角形共有9个，再根据题目中的已知条件计算每个三角形的面积可得答案．解答：以A、B、C、D、E中的三点为顶点的三角形有：△ABC，△ABD，△ABE，△ACD，△ACE，△ADE，△BCD，△BCE，△BDE，共9个；再根据小正方形的边长为1，计算可得其中面积为1的三角形有：△ABC，△ADE，△BCE，△ACD．18、如图，已知AD为△ABC的中线，AB＝5cm，且△ACD的周长比△ABD的周长少2cm，求AC的长．答案：3cm分析：由AD是△ABC的中线可得CD=BD，从而可得C△ABD-C△ACD=（AB+AD+BD）-（AC+AD+CD）=AB-AC=2，由AB=5，可解得AC=3（cm）．解答：∵AD为△ABC的中线，∴BD=CD．∵△ACD的周长比△ABD的周长少2cm，∴（AB+BD+AD）-（AC+AD+CD）=AB-AC=2cm，∴AC=AB-2=5-2=3（cm）．19、张大爷的四个儿子都长大成人了，也该分家了，于是张大爷准备把如图所示的一块三角形的田地平均分给四个儿子，四个儿子要求田地的形状仍然是三角形，请你帮助张大爷提出一种平分的方案．答案：见解答．分析：此题答案不唯一，（1）可根据等底、等高的三角形面积相等，把其中一边均分成4份，连接分点和对角的顶点即可；（2）根据三角形一边的中线把三角形分成面积相等的两个三角形，作一边上的中线，再作由这条中线分成的两个三角形的中线即可．解答：答案不唯一，第一种方案：如图1，四等分一条边构成的四个三角形；第二种方案：如图2，作△ABC的一条中线，再作由中线分出的两个三角形的中线就可分成四个面积相等的三角形．20、如图，AD是∠CAB的角平分线，DE∥AB，DF∥AC，EF交AD于点O.请问：DO是∠EDF的角平分线吗？如果是，请给予证明；如果不是，请说明理由．答案：是，理由见解答分析：由DE∥AB，DF∥AC，可得∠EDA=∠DAF，∠FDA=∠EAD，再结合∠EAD=∠F AD，就可得∠EDA=∠FDA，从而得到DO平分∠EDF．解答：DO是∠EDF的角平分线，理由如下：∵AD是∠CAB的角平分线，∴∠EAD=∠F AD．∵DE∥AB，DF∥AC，∴∠EDA=∠F AD，∠FDA=∠EAD．∴∠EDA=∠FDA，∴DO是∠EDF的角平分线．。
三角形的高中线与角平分线练习题
4321EDCBA1CDBA三角形的高、中线与角平分线11 如图，已知△ABC 中，AQ=PQ 、PR=PS 、PR ⊥AB 于R ，PS ⊥AC 于S ，有以下三个结论：①AS=AR ；②QP ∥AR ； ③△BRP ≌△CSP ，其中( )．(A)全部正确 (B)仅①正确 (C)仅①、②正确 (D)仅①、③正确 2、 如图，点E 在BC 的延长线上，则下列条件中，不能判定AB ∥CD 的是( )A. ∠3=∠4B.∠B=∠DCEC.∠1=∠2.D.∠D+∠DAB=180° 3．如图，ΔACB 中，∠ACB=900，∠1=∠B.（1）试说明 CD 是ΔABC 的高；（2）如果AC=8，BC=6，AB=10，求CD 的长。
4如图，直线DE 交△ABC 的边AB 、AC 于D 、E ， 交BC 延长线于F ，若∠B ＝67°，∠ACB ＝74°， ∠AED ＝48°，求∠BDF 的度数5、如图：∠1＝∠2＝∠3，完成说理过程并注明理由： 因为 ∠1＝∠2所以 ____∥____ ( ) 因为 ∠1＝∠3所以 ____∥____ ( )6．以下列各组线段为边，能组成三角形的是（ ） A ．2cm ，3cm ，5cm B ．5cm ，6cm ，10cm C ．1cm ，1cm ，3cm D ．3cm ，4cm ，9cm7．等腰三角形的一边长等于4，一边长等于9，则它的周长是（ ） A ．17 B ．22 C ．17或22 D ．138．适合条件∠A=12∠B=13∠C的△ABC是（）A．锐角三角形B．直角三角形C．钝角三角形D．等边三角形9．已知等腰三角形的一个角为75°，则其顶角为（）A．30°B．75°C．105°D．30°或75°10．一个多边形的角和比它的外角的和的2倍还大180°，这个多边形的边数是（）A．5 B．6 C．7 D．811．三角形的一个外角是锐角，则此三角形的形状是（）A．锐角三角形B．钝角三角形C．直角三角形D．无法确定12．三角形的三边长分别为5，1+2x，8，则x的取值围是________．13．如图，BD平分∠ABC，DA⊥AB，∠1=60°，∠BDC=80°，求∠C的度数．初一三角形的高、中线与角平分线21 如图，BC⊥CD，∠1=∠2=∠3，∠4=60°，∠5=∠6．（1）CO是△BCD的高吗？为什么？（2）∠5的度数是多少？（3）求四边形ABCD各角的度数．2．△ABC中，∠A=50°，∠B=60°，则∠A＋∠C=________．3 ．已知三角形的三个角的度数之比为1：2：3，则这个三角形是（）A．锐角三角形B．直角三角形C．钝角三角形D．不能确定4．△ABC中，∠A=∠B+∠C，则∠A=______度．5．如图∠1+∠2+∠3+∠4=______度．6．如图，△ABC中，AD是BC上的高，AE平分∠BAC，∠B=75°，•∠C=45°，求∠DAE与∠AEC的度数．7．以下说法错误的是（）6题A．三角形的三条高一定在三角形部交于一点B．三角形的三条中线一定在三角形部交于一点C．三角形的三条角平分线一定在三角形部交于一点D．三角形的三条高可能相交于外部一点8．如果一个三角形的三条高的交点恰好是这个三角形的一个顶点，•那么这个三角形是（）A．锐角三角形B．直角三角形C．钝角三角形D．不能确定9．如图，BD=1BC，则BC边上的中线为______，△ABD的面积=_____的面积．2(9)10．如图，△ABC中，高CD、BE、AF相交于点O，则△BOC•的三条高分别为线段________．（10）初一三角形的高、中线与角平分线31．下列图形中具有稳定性的是（）A．梯形B．菱形C．三角形D．正方形2．如图3，AD是△ABC的边BC上的中线，已知AB=5cm，AC=3cm，求△ABD•与△ACD的周长之差．3．如图，∠BAD=∠CAD，AD⊥BC，垂足为点D，且BD=CD．•可知哪些线段是哪个三角形的角平分线、中线或高？4．如图5，在等腰三角形ABC中，AB=AC，一腰上的中线BD将这个等腰三角形的周长分为15和6两部分，求该等腰三角形的腰长及底边长．5．有一块三角形优良品种试验基地，如图所示，•由于引进四个优良品种进行对比试验，需将这块土地分成面积相等的四块，请你制定出两种以上的划分方案供选择（画图说明）．6．如图，在△ABC中，D、E分别是BC、AD的中点，S△ABC=4cm2，求S△ABE．7．如图，在锐角△ABC中，CD、BE分别是AB、AC上的高，•且CD、BE交于一点P，若∠A=50°，则∠BPC的度数是（）8如图7-1-2-9，AD是△ABC的角平分线，DE∥AB，DF∥AC，EF交AD于点O．请问：DO是△DEF的角平分线吗？如果是，请给予证明；如果不是，请说明理由．初一三角形的高、中线与角平分线41．若三角形的外角中有一个是锐角，则这个三角形是________三角形．2．△ABC中，若∠C-∠B=∠A，则△ABC的外角中最小的角是______（填“锐角”、“直角”或“钝角”）．3．如图1，x=______．(1) (2) (3) 4．如图2，△ABC中，点D在BC的延长线上，点F是AB边上一点，延长CA到E，连EF，则∠1，∠2，∠3的大小关系是_________．5．如图3，在△ABC中，AE是角平分线，且∠B=52°，∠C=78°，求∠AEB的度数．7．如图所示，在△ABC中，AB=AC，AD=AE，∠BAD=60°，则∠EDC=______．8．一个零件的形状如图7-2-2-6所示，按规定∠A应等于90°，∠B、∠D应分别是30°和20°，叔叔量得∠BCD=142°，就断定这个零件不合格，你能说出道理吗？9．（1）如图（1），求出∠A+∠B+∠C+∠D+∠E+∠F的度数；（2）如图（2），求出∠A+∠B+∠C+∠D+∠E+∠F的度数．11．如图，BD、CD分别是△ABC的两个外角∠CBE、∠BCF•的平分线，试探索∠D与∠A之间的数量关系．12 如图，BD为△ABC的角平分线，CD为△ABC的外角∠ACE的平分线，它们相交于点D，试探索∠BDC与∠A之间的数量关系．7．3 多边形及其角和基础过关作业1．四边形ABCD中，如果∠A+∠C+∠D=280°，则∠B的度数是（）A．80°B．90°C．170°D．20°2．一个多边形的角和等于1080°，这个多边形的边数是（）A．9 B．8 C．7 D．63．角和等于外角和2倍的多边形是（）A．五边形B．六边形C．七边形D．八边形4．六边形的角和等于_______度．5．正十边形的每一个角的度数等于______，每一个外角的度数等于_______．6．如图，你能数出多少个不同的四边形？7．四边形的四个角可以都是锐角吗？可以都是钝角吗？可以都是直角吗？•为什么？8．求下列图形中x的值：综合创新作业9．（综合题）已知：如图，在四边形ABCD中，∠A=∠C=90°，BE平分∠ABC，•DF平分∠ADC．BE与DF有怎样的位置关系？为什么？10．（应用题）有10个城市进行篮球比赛，每个城市均派3个代表队参加比赛，规定同一城市间代表队不进行比赛，其他代表队都要比赛一场，问按此规定，•所有代表队要打多少场比赛？11．（创新题）如图，以五边形的每个顶点为圆心，以1为半径画圆，求圆与五边形重合的面积．12．（1）（2005年，）已知一个多边形的角和为540°，则这个多边形为（）A．三角形B．四边形C．五边形D．六边形（2）（2005年，）五边形的角和等于_______度．13．（易错题）一个多边形的每一个顶点处取一个外角，这些外角中最多有钝角（• ）A．1个B．2个C．3个D．4个培优作业14．（探究题）（1）四边形有几条对角线？五边形有几条对角线？六边形有几条对角线？……猜想并探索：n边形有几条对角线？（2）一个n边形的边数增加1，对角线增加多少条？15．（开放题）如果一个多边形的边数增加1，•那么这个多边形的角和增加多少度？若将n边形的边数增加1倍，则它的角和增加多少度？数学世界攻其不备壁虎在一座油罐的下底边沿A处．它发现在自己的正上方──油罐上边缘的B•处有一只害虫．壁虎决定捕捉这只害虫．为了不引起害虫的注意，它故意不走直线，而是绕着油罐，沿着一条螺旋路线，从背后对害虫进行突然袭击如图7-3-5．结果，•壁虎的偷袭得到成功，获得了一顿美餐．请问：壁虎沿着螺旋线爬行是最短的路程吗（线段AB除外）？答案:1．A 点拨：∠B=360°-（∠A+∠C+∠D）=360°-280°=80°．故选A．2．B 点拨：设这个多边形的边数为n，则（n-2）·180=1080．解得n=8．故选B．3．B 点拨：设这个多边形的边数为n，根据题意，得（n-2）·180=2×360．解得n=6．故选B．4．7205．144°；36°点拨：正十边形每一个角的度数为：(102)18010-⨯︒=144°，每一个外角的度数为：180°-144°=36°．6．有27个不同的四边形．7．解：四边形的四个角不可以都是锐角，不可以都是钝角，可以都是直角．因为四边形的角和为360°，如果四个角都是锐角或都是钝角，•则角和小于360°或大于360°，与四边形的角和为360°矛盾．•所以四个角不可以都是锐角或都是钝角．若四个角都是直角，则四个角的和等于360°，与角和定理相符，所以四个角可以都是直角．8．解：（1）90+70+150+x=360．解得x=50．（2）90+73+82+（180-x）=360．解得x=65．（3）x+（x+30）+60+x+（x-10）=（5-2）×180．解得x=115．9．解：BE∥DF．理由：∵∠A=∠C=90°，∴∠A+∠C=180°．∴∠ABC+∠ADC=360°-180°=180°．∵∠ABE=12∠ABC，∠ADF=12∠ADC，∴∠ABE+∠ADF=12（∠ABC+∠ADC）=12×180°=90°．又∵∠ABE+∠AEB=90°，∴∠AEB=∠ADF，∴BE∥DF（同位角相等，两直线平行）．10．解：12n （n-3）=12×10×（10-3）=12×10×7=35（场）．答：按此规定，所有代表队要打35场比赛．点拨：问题类似于求多边形对角线的个数．11．解：（5-2）×180°÷360°×12=1.5．点拨：不能直接求出扇形的度数，用整体法圆与五边形重合部分的角度和正好是五边形的角和．12．（1）C 点拨：设这个多边形的边数为n ，依题意，得（n-2）×180°=540°，解得n=5，故选C ．（2）540 点拨：（n-2）×180°=（5-3）×180°=540°．13．C14．解：（1）四边形有2条对角线；五边形有5条对角线；六边形有9条对角线；……n 边形有(3)2n n -条对角线． （2）当n 边形的边数增加1时，对角线增加（n-1）条．点拨：从n 边形的一个顶点出发，向其他顶点共可引（n-3）条对角线，n 个顶点共可引n （n-3）条，但这些对角线每一条都重复了一次，故n 边形的对角线条数为(3)2n n -． 15．180°，n ·180°．数学世界答案:是最短的路程．可用纸板做一个模型，沿AB 剪开便可看出结论．。
七年级7.1.2 三角形的高、中线与角平分线(专题课时练含答案)-
7.1.2 三角形的高、中线与角平分线◆知能点分类训练知能点1 三角形的高、中线与角平分线1．下列说法正确的是（）．A．直角三角形只有一条高B．如果一个三角形有两条高与这个三角形的两边重合，•那么这个三角形是直角三角形 C．三角形的三条高，可能都在三角形内部，也可能都在三角形外部D．三角形三条高中，在三角形外部的最多只有1条2．如果一个三角形的三条高的交点恰是三角形的一个顶点，那么这个三角形是（）．A．锐角三角形 B．钝角三角形 C．直角三角形 D．等边三角形3．如图所示，画△ABC的一边上的高，下列画法正确的是（）．4．三角形的角平分线是（）．A．直线 B．射线 C．线段 D．以上都不对5．如图所示，AM是△ABC的中线，那么若用S1表示△ABM的面积，用S1表示△ACM的面积，则S1与S2的大小关系是（）．A．S1>S2B．S1<S2C．S1=S2D．以上三种情况都可能6．下列说法：①三角形的角平分线、中线、高线都是线段；•②直角三角形只有一条高线；③三角形的中线可能在三角形的外部；④三角形的高线都在三角形的内部，并且相交于一点，其中说法正确的有（）．A．1个 B．2个 C．3个 D．4个7．如图所示，已知△ABC：（1）过A画出中线AD；（2）画出角平分线CE；（3）作AC边上的高．知能点2 三角形的稳定性8．下列四个图形中，具有不稳定性的图形是（）．9．照相机的支架是三条腿，这是利用了三角形的_________．•现实生活中还有利用三角形的这个特性的例子吗？如果知道，请写出来：________．10．如图所示，建筑工人在安装门窗时，先要把木头门窗固定好，这样搬运和安装起来才不会变形，请你设计一种方法固定木头门窗，这样做依据的数学道理是什么？◆规律方法应用11．如图所示，在△ABC中，AD⊥BC，BE⊥AC，BC=12，AC=8，AD=6，求BE的长．12．在△ABC中，AB=AC，AC边上的中线BD把三角形的周长分为12cm和15cm两部分，求三角形各边的长．◆开放探索创新13．将一个三角形的三边中点顺次连结可得到一个新的三角形，通常称为“中点三角形”，如图①所示，△DEF是△ABC的中点三角形．（1）画出图中另外两个三角形的中点三角形．（2）用量角器和刻度尺量△DEF和△ABC的三个内角和三条边，看看你有什么发现？并通过三个图的重复度量实验，验证你的发现．（3）你知道S△ABC和S△EDF的关系吗？怎样得出来的？（4）根据（2）中的结论，解答下列问题，如图所示，CD是△ABC的中线，DE是△ACD的中线，EF为△ADE的中线，若△AEF的面积为1cm2，求△ABC的面积．①②③④答案:1．B 2．C 3．C 4．C5．C （点拨：等底等高）6．A 7．略 8．D9．稳定性三条腿的凳子等10．可在门（窗）角上钉一根木条，或用木杆顶在门（窗）角上，•这样做根据的数学道理是三角形的稳定性．11．解：∵S△ABC =12BC·AD=12AC·BE，∴BC·AD=AC·BE，∴BE=1268BC ADAC⨯==9．12．解：设AB=x（cm），则AD=DC=12x（cm）．（1）若AB+AD=12，即x+12x=12．所以x=8．即AB=AC=8cm，则DC=4cm，故BC=15-4=11cm，此时AB+AC>BC，所以三边长分别为8cm，8cm，11cm．（2）若AB+AD=15，即x+12x=15，所以x=10，则DC=5cm，故BC=12-5=7cm，显然此时三角形存在，所以三边长分别为10cm，10cm，7cm．综上所述，此三角形的三边长分别为：8cm，8cm，11cm或10cm，10cm，7cm．13．（1）略（2）角度相同，中点三角形各边是原三角形各边长度的一半．（3）经度量知中点三角形与原三角形相比，底和高的长度分别是原三角形的底与高的12，所以面积是原三角形面积的14．（4）△ABC面积为8cm2，解略．。
三角形的高-中线-角平分线测试题
三角形的高中线角平分线测试题一、选择题1、能把一个三角形分成面积相等的两部分的是该三角形的一条（）A．中线 B．角平分线 C．高线 D．边的垂直平分线2、已知在正方形网格中，每个小方格都是边长为1的正方形，A，B两点在小方格的顶点上，位置如图所示，点C也在小方格的顶点上，且以A，B，C为顶点的三角形面积为1，则点C的个数为（）A．3个 B．4个 C．5个 D．6个3、如图，三边均不等长的△ABC，若在此三角形内找一点O，使得△OAB．△OBC．△OCA的面积均相等．判断下列作法何者正确（）A．作中线AD，再取AD的中点OB．分别作中线AD．BE，再取此两中线的交点OC．分别作AB．BC的中垂线，再取此两中垂线的交点OD．分别作∠A．∠B的角平分线，再取此两角平分线的交点O4、如图，在△ABC中E是BC上的一点，BC=2BE，点D是AC的中点，设△ABC，△ADF，△BEF的面积分别为S△ABC，S△ADF，S△BEF，且S△ABC=12，则S△ADF-S△BEF=（）A、1B、2C、3D、45、如图，G为△ABC的重心，其中∠C=90°，D在AB上，GD⊥AB．若AB=29，AC=20，BC=21，则GD的长度为（）A、7B、14C、D、则能摆出不同的三角形的个数是（）A．1 B．2 C．3 D．47、已知小明家距离学校10千米，而小蓉家距离小明家3千米．如果小蓉家到学校的距离是d千米，则d满足（）A.3＜d＜10B.3≤d≤10C.7＜d＜13D.7 ≤d≤138、△ABC中，若∠A∶∠B∶∠C＝1∶2∶3，则△ABC的形状是( )A．锐角三角形 B．直角三角形 C．钝角三角形 D．不确定9．如图，高BD与CE交于O点，若∠BAC＝72°，则∠DOE的度数( )A．72°B．18°C．108° D．162°10、已知△ABC是边长为1的等腰直角三角形，以Rt△ABC的斜边AC为直角边，画第二个等腰Rt△ACD，再以Rt△ACD的斜边AD为直角边，画第三个等腰Rt△ADE，…，依此类推，第n个等腰直角三角形的面积是（）A．2n-2 B．2n-1 C．2n D．2n+1二、填空题1、一个三角形的两边分别是2厘米和9厘米，第三边长是一个奇数，则第三边长为 .2、已知等腰三角形的一边等于5,另一边等于6,则它的周长等于3、四条线段的长分别为5cm，6cm，8cm，13cm，以其中任意三条线段为边可构成三角形个。
(完整版)三角形角平分线、中线、高线证明题
(完整版)三角形角平分线、中线、高线证明题2．证题的思路：找夹角（）性质 1、全等三角形的SAS已知两边 找直角（ HL ）对应角相等、对应边相找第三边（ SSS等。
）2、全等三角形的若边为角的对边，则找 随意角（ AAS）找已知角的另一边（ ）已知一边一角SAS 对应边上的 高对应相边为角的邻边 找已知边的对角（）AAS等。
找夹已知边的另一角（）ASA3、全等三角形的找两角的夹边（）对应角均分线相等。
已知两角ASA4、全等三角形的 找随意一边（）AAS对应中线相等。
5、全等三角形面积相等。
6、全等三角形 周长相等。
( 以上能够简称 : 全等三角形的对应元素相等 ) 7、三边对应相等的两个三角形全等。
（ SSS)8、两边和它们的夹角对应相等的两个三角形全等。
(SAS) 9、两角和它们的夹边对应相等的两个三角形全等。
(ASA)10、两个角和此中一个角的对边对应相等的两个三角形全等。
(AAS)11、斜边和一条直角边对应相等的两个直角三角形全等。
(HL)全等三角形问题中常有的协助线的作法常有协助线的作法有以下几种：1) 碰到等腰三角形，可作底边上的高，利用“三线合一”的性质解题，思想模式是全等变换中的“对折” ．2) 碰到三角形的中线，倍长中线，使延伸线段与原中线长相等，结构全等三角形，利用的思想模式是全等变换中的“旋转” ．3) 碰到角均分线，能够自角均分线上的某一点向角的两边作垂线，利用的思想模式是三角形全等变换中的“对折” ，所考知识点经常是角均分线的性质定理或逆定理． 4) 过图形上某一点作特定的均分线， 结构全等三角形， 利用的思想模式是全等变换中的“平移”或“翻转折叠”5) 截长法与补短法， 详细做法是在某条线段上截取一条线段与特定线段相等，或是将某条线段延伸，是之与特定线段相等，再利用三角形全等的相关性质加以说明． 这类作法，合适于证明线段的和、差、倍、分等类的题目．特别方法：在求相关三角形的定值一类的问题时， 常把某点到原三角形各极点的线段连结起来，利用三角形面积的知识解答．三角形协助线做法图中有角均分线，可向两边作垂线。
三角形的角平分线、中线和高的专题训练50题
三角形的角平分线、中线和高的专题训练50题本页仅作为文档页封面，使用时可以删除This document is for reference only-rar21year.March三角形的角平分线、中线和高1．已知，△ABC中，AD是BC边上的高，∠CAD=33°，则∠ACB= °．2．△ABC中，AD，CE是BC，AB边上的高，AD，CE相交于P，∠B=50°，则∠APC的度数是．3．△ABC中，∠B的外角平分线的与∠C外角平分线相交于点P，且∠BPC=80°，则∠BAP的度数为．4．在Rt△ABC中，∠ACB=90°，∠CAB=30°，∠ACB平分线与∠ABC的外角平分线交于点E，连接AE，则∠AEB= ．5．如图，AD是△ABC的中线，AB=5，AC=3，△ABD的周长和△ACD的周长相差．6．如果一个三角形的三条高的交点恰是三角形的一个顶点，那么这个三角形是（填“锐角三角形”，“直角三角形”，“钝角三角形”）7．如图，△ABC中，AD是BC边上的高，AE是∠BAC的平分线，∠B=46°，∠C=72°，则∠EAD=°．8．如图，AD、BE、CF是△ABC的三条中线，若△ABC的周长是a cm．则AE+CD+BF= cm．9．如图，△ABC中，∠A=30°，∠B=70°，CE平分∠ACB，CD⊥AB于D．则∠ECD=．10．角平分线一定垂直于底边．11．在△ABC中，已知AD是角平分线，∠B=50°，∠C=70°，∠BAD=°．12．如图，在△ABC中，BD平分∠ABC，BE是AC边上的中线，如果AC=10cm，则AE=cm，如果∠ABD=30°，则∠ABC=．13．如图六，在△ABC中，∠BAC是钝角，完成下列画图，并用适当的符号在图中表示；（1）AC边上的高；（2）BC边上的高．（在上图中直接画）14．在△ABC中，AC=3cm，AD是△ABC中线，若△ABD周长比△ADC的周长大2cm，则BA= cm．15．△ABC中，∠A等于80度，则内角∠B、∠C的平分线相交所成的锐角为°．16．如图，在△ABC中，∠ACB=90°，∠A=20°，CD与CE分别是斜边AB上的高和中线，那么∠DCE=度．17．直角三角形中，两锐角的角平分线所夹的锐角是度．18．如图，在△ABC中，BE、CF分别是∠ABC和∠ACB的角平分线，并相交于点D，EG，FG分别是∠AEB和∠AFC的角平分线，并相交于点G，如果∠A=40°，那么∠CDB=；∠G=．19．如图，△ABC中，AD是BC边上的中线，已知AB=6cm，AC=4cm，则△ABD和△ACD周长之差为．20．如图，Rt△ABC中，∠ACB=90°，∠A=40°，D为AB中点，CE⊥AB，则∠DCE=度．21．三角形中的角平分线、中线、高都是三条特殊的（填直线、射线、线段）22．如图所示，BD是△ABC的中线，AD=2，AB+BC=5，则△ABC的周长是．23．三角形一边上的中线把原三角形分成两个 相等的三角形．24．如图，AD 是△ABC 的中线，AE 是△ABD 的中线，若CE=9cm ，则BC= cm ．25．点D 是△ABC 中BC 边上的中点，若AB=3，AC=4，则△ABD 与△ACD 的周长之差为 ．26．如图，AC 、BD 相交于O ，BE 、CE 分别平分∠ABD、∠ACD，且交于E ，若∠A=60°，∠D=40°，则∠E= ．27．如图，根据图形填空： （1）AD 是△ABC 中∠BAC 的角平分线，则∠ =∠ =21∠ ． （2）（2）AE 是△ABC 中线，则 = =21 . （3）AF 是△ABC 的高，则∠ =∠ =90°．28．如图，AD⊥BC 于D ，那么图中以AD 为高的三角形有 个．29．如图所示：30．（1）在△ABC 中，BC 边上的高是 ；31．（2）在△AEC中，AE边上的高是．32．我们都晓得，三角形的高是比较活泼的，它会出现在三角形的内部，也会出现在三角形的外部，然而，当它与三角形一边相会时，你可能找不到它了，今天就请你猜一猜，如果三角形的高与一边重合了，那么这是什么三角形呢？答：三角形．31．在直角三角形、钝角三角形和锐角三角形这三种三角形中，有两条高在三角形外部的是三角形．32．如图，在△ABC中，AD、CE是边BC、AB上的高，若∠B=70°，∠CAD=30°，则∠BCE=，∠ECA=．33．如图，在△ABC中，AE是中线，AD是角平分线，AF是高，则：（1）∠BAC=2；（2）BC=2 ；（3）=90°．34．如图，∠ABD、∠ACD的平分线交于E，∠E=β1；∠EBD、∠ECD的平分线交于F，∠F=β2；如此下去，∠FBD、∠FCD的平分线的交角为β3；…若∠A=40°，∠D=32°，则β4为度．35．如图所示，在△ABC 中，BC 边上的高是，AB 边上的高是；在△BCE 中，BE 边上的高是；EC 边上的高是；在△ACD 中，AC 边上的高是； CD 边上的高是 ．36．在△ABC 中，BO 平分∠ABC，CO 平分∠ACB，当∠A=50°时，∠BOC= ．37．如图，在△ABC 中，AC⊥BC，CD⊥AB 于点D ．则图中共有 个直角三角形．38．已知：如图，在△ABC 中，∠ACD 是△ABC 的外角，∠ABC 与∠ACD 的平分线相交于点A 1，∠A 1BC 与∠A 1CD 的平分线相交于点A 2，如果∠A 2=m°， 那么∠A= °（用含m 的代数式表示）．39．如图，△ABC 的∠B 的外角的平分线与∠C 的外角的平分线交于点P ，连接AP ．若∠BPC=50°，则∠PAC= 度．40．已知△ABC 中，∠A=α．在图（1）中∠B、∠C 的角平分线交于点O 1，则可计算得∠BO 1C=90°+ 21α；在图（2）中，设∠B、∠C 的两条三等分角线分别对应交于O1、O2，则∠BO2C= ；请你猜想，当∠B、∠C同时n等分时，（n-1）条等分角线分别对应交于O1、O2，…，O n-1，如图（3），则∠BO n-1C= （用含n和α的代数式表示）．41．如图，△ABC中，∠ABC和∠ACB的平分线交于点O，若∠BOC=115°，则∠A=°．42．如图，已知△ABC中，∠BAC=80°，∠C=60°，AD、AE分别是三角形的高和角平分线，则∠CAD=°，∠DAE=°．43．如图，在△ABC中，∠A=α．∠ABC与∠ACD的平分线交于点A1，得∠A1；∠A1BC与∠A1CD的平分线相交于点A2，得∠A2；…；∠A2011BC与∠A2011CD的平分线相交于点A2012，得∠A2012，则∠A2012= ．44．如图，已知△ABC中，∠B=65°，∠C=45°，AD是∠ABC的高线，AE是∠BAC的平分线，则∠DAE=．45．如图，点O是△ABC的两条角平分线的交点，且∠A=40°，则∠BOC=．46．在△ABC中，∠A=80°，I是∠B，∠C的角平分线的交点，则∠BIC=°．47．如果三角形的三条高的交点落在一个顶点上，那么它的形状是．48．如图所示，CD是△ABC的中线，AC=9cm，BC=3cm，那么△ACD和△BCD的周长差是 cm．49．如图，∠ACB是直角，CD是中线，CD=2.5，BC=3，则AC= ．50．BM是△ABC中AC边上的中线，AB=5cm，BC=3cm，那么△ABM与△BCM的周长之差为 cm．。
三角形的高、中线、角平分线
8．如图，已知AD，AE分别是△ABC的高和中线，AB＝6 cm， AC＝8 cm，BC＝10 cm，∠CAB＝90°.试求：
(1)AD的长；
∴∠D＋∠DEG＋∠B＋∠BCH＝∠F＋∠ACH＋∠F＋∠AEG. ∴∠D＋∠B＝2∠F. ∵∠B∶∠D∶∠F＝4∶6∶x，∴x＝5.
10．如图，在△ABC中，AD⊥BC于D，AE平分 ∠BAC，∠B＝70°，∠C＝30°.
(1)求∠BAE的度数．
解：∵∠B＋∠C＋∠BAC＝180°，
∴∠BAC＝180°－∠B－∠C＝180°－70°－30°＝80°.
解：能．
∵∠B＋∠C＋∠BAC＝180°，∴∠BAC＝180°－∠B－∠C.
∵AE 平分∠BAC， ∴∠BAE＝12∠BAC＝12(180°－∠B－∠C)＝90°－12(∠B＋∠C)． ∵AD⊥BC，∴∠ADE＝90°.
∴∠B＋∠BAD＝90°. ∴∠BAD＝90°－∠B.
∴∠DAE＝∠BAE－∠BAD＝90°－12(∠B＋∠C)－(90°－∠B) ＝12(∠B－∠C)． ∵∠B－∠C＝40°，∴∠DAE＝12×40°＝20°.
9．如图，BE，CD相交于点A，CF为∠BCD的平分线，EF为 ∠BED的平分线．
(1)图中共有____6____个“8字形”；
(2)若∠B∶∠D∶∠F＝4∶6∶x，求x的值． 解：∵EF平分∠BED，CF平分∠BCD， ∴∠DEG＝∠AEG，∠ACH＝∠BCH. ∵在△DGE和△FGC中，∠DGE＝∠FGC， ∴∠D＋∠DEG＝∠F＋∠ACH. ∵在△BHC和△FHE中，∠BHC＝∠FHE， ∴∠B＋∠BCH＝∠F＋∠AEG.
三角形的角平分线、中线和高的专题训练50题
三角形的角平分线、中线和高的专题训练50题1. 在△ABC中，角A的角平分线交对边BC于点D，若BD=DC，求证：∠B=∠C。
【解答】设∠BAD=∠CAD=x，由于角A的角平分线BD、CD分别相交对边BC于点D，所以AD是△ABC的角平分线。
根据角平分线定理可知：$\frac{BD}{CD}=\frac{AB}{AC}$由于BD=CD，所以$\frac{AB}{AC}=1$，即AB=AC。
根据等边三角形的性质可知∠B=∠C。
2. 在△ABC中，角A的角平分线交对边BC于点D，若∠BAD=30°，求∠B和∠C的度数。
【解答】设∠BAD=∠CAD=x，根据题意可知角A的角平分线BD、CD分别相交对边BC于点D。
由于∠BAD=30°，所以x=30°。
根据角平分线定理可知：$\frac{BD}{CD}=\frac{AB}{AC}$由于BD=CD，所以$\frac{AB}{AC}=1$，即AB=AC。
又由等边三角形的性质可知∠B=∠C，即∠B=∠C=75°。
3. 在△ABC中，角B的角平分线交对边AC于点D，若∠BAD=80°，求∠ABC的度数。
【解答】设∠BAD=∠DAC=x，根据题意可知角B的角平分线AD相交对边AC于点D。
由于∠BAD=80°，所以x=80°。
根据角平分线定理可知：$\frac{BD}{CD}=\frac{AB}{AC}$又由于BD=CD，所以$\frac{AB}{AC}=1$，即AB=AC。
由等边三角形的性质可知∠ABC=∠ACB，设∠ABC=∠ACB=y，则∠ADB=∠ADC=180°-2x=20°。
再由三角形内角和为180°可知∠B+∠ADC=180°，即y+20°=180°，解得y=160°。
所以∠ABC=∠ACB=160°。
4. 在△ABC中，角A的角平分线交对边BC于点D，若∠B=70°,∠C=50°，求∠BAD的度数。
(完整)三角形的高、中线与角平分线练习题及答案
7.1.2 三角形的高、中线与角平分线1．以下说法错误的是（）A．三角形的三条高一定在三角形内部交于一点B．三角形的三条中线一定在三角形内部交于一点C．三角形的三条角平分线一定在三角形内部交于一点D．三角形的三条高可能相交于外部一点2．如果一个三角形的三条高的交点恰好是这个三角形的一个顶点，•那么这个三角形是（） A．锐角三角形 B．直角三角形 C．钝角三角形 D．不能确定3．如图1，BD=12BC，则BC边上的中线为______，△ABD的面积=_____的面积．(1) (2) (3)4．如图2，△ABC中，高CD、BE、AF相交于点O，则△BOC•的三条高分别为线段________．5．下列图形中具有稳定性的是（）A．梯形 B．菱形 C．三角形 D．正方形6．如图3，AD是△ABC的边BC上的中线，已知AB=5cm，AC=3cm，求△ABD•与△ACD的周长之差．7．如图，∠BAD=∠CAD，AD⊥BC，垂足为点D，且BD=CD．•可知哪些线段是哪个三角形的角平分线、中线或高？综合创新作业8．（综合题）如图5，在等腰三角形ABC中，AB=AC，一腰上的中线BD将这个等腰三角形的周长分为15和6两部分，求该等腰三角形的腰长及底边长．9．有一块三角形优良品种试验基地，如图所示，•由于引进四个优良品种进行对比试验，需将这块土地分成面积相等的四块，请你制定出两种以上的划分方案供选择（画图说明）．10．（创新题）如图，在△ABC中，D、E分别是BC、AD的中点，S△ABC=4cm2，求S△ABE．11．（2004年，陕西）如图，在锐角△ABC中，CD、BE分别是AB、AC上的高，•且CD、BE交于一点P，若∠A=50°，则∠BPC的度数是（）A．150° B．130° C．120° D．100°。
三角形的高、中线与角平分线(分层作业)(解析版)docx
11.1.2三角形的高、中线与角平分线夯实基础篇一、单选题：（每题3分，共18分）1．在△AB C中，画边BC上的高，正确的是（）A．B．C．D．【答案】A【解析】【详解】解：A．此图形中AD是BC边上的高，符合题意；B．此图形中CE不是BC边上的高，不符合题意；C．此图形中BE是AC边上的高，不符合题意；D．此图形中BG是△BCG中BC边上的高，不符合题意；故选：A．【点睛】本题考查三角形高的画法，解题关键在理解底与高的对应关系，作钝角三角形的高是易错点． 中，BC边上的高为（）2．如图，在ABCA．BD B．CF C．AE D．BF【解析】【分析】根据三角形高的定义是从一个顶点到它对边的垂线段即可判断．【详解】根据三角形的高的定义，在△AB C中，BC边上的高应是过点A垂直于BC的线段，从图中可以看出，过点A垂直于BC的线段是AE，所以AE是BC边上的高．故选：C．【点睛】本题考查了三角形高的定义，熟练掌握三角形的高概念，仔细观察图形中符合定义的线段即可．3．下列叙述中错误的一项是（）．A．三角形的中线、角平分线、高都是线段．B．三角形的三条高线中至少存在一条在三角形内部．C．只有一条高在三角形内部的三角形一定是钝角三角形．D．三角形的三条角平分线都在三角形内部．【答案】C【解析】【分析】根据三角形的角平分线、中线、高的概念和性质进行一一判断．【详解】A：三角形的中线、角平分线、高都是线段，正确；B：锐角三角形三条高在三角形内部，直角三角形一条高在三角形内部，钝角三角形一条高在三角形内部，正确；C：只有一条高在三角形内部的三角形是钝角三角形或直角三角形，错误；D：锐角三角形、钝角三角形、直角三角形的三条角平分线都在三角形内部，正确【点睛】本题考查三角形的三线，掌握高、中线、角平分线的定义是解题关键．4．已知，AE、BD是ABC的高线，AE=6cm，BD=5cm，BC=8cm，则AC的长度是（）A．8cm B．8.6cm C．9cm D．9.6cm【答案】D【解析】【分析】根据等面积法即可求解．【详解】解：∵AE、BD是ABC的高线，AE=6cm，BD=5cm，BC=8cm，∴1122AC BD AE BC，即68489.655AE BCACBDcm．故选D．【点睛】本题考查了三角形高线的相关计算，理解三角形的高线的意义是解题的关键．5．如图，在△AB C中，AB=5，AC=3，AD为BC边上的中线，则△ABD与△ACD的周长之差为（）A．2B．3C．4D．5【答案】A【解析】【分析】根据题意，AD是△ABC的边BC上的中线，可得BD=CD，进而得出△ABD的周长=AB+BD+AD，△ACD的周长=AC+CD+AD，相减即可得到周长差．【详解】解：∵AD是△ABC的中线，∴BD=CD，∴△ABD与△ACD的周长之差为：（AB+BD+AD）-（AC+CD+AD）=AB+BD+AD-AC-CD-AD=AB-AC=5-3=2；故选：A．【点睛】本题主要考查了三角形的中线、高和三角形周长的求法，熟练掌握三角形周长公式是解题的关键．的中线，角平分线，高，下列各式中错误的是（）6．如图，AD，AE，AF分别是ABCA ．2BC CDB ．12BAE BAC C ．90AFBD ．AE CE 【答案】D【解析】【分析】根据三角形的高线，角平分线和中线解答即可；【详解】解：A ．∵AD 是ABC 的中线∴2BC CD ，故选项正确，不符合题意；B ．∵AE 是ABC 的角平分线∴12BAE BAC 故选项正确，不符合题意；C ．∵AF 分别是ABC 的高，∴90AFB故选项正确，不符合题意；D ．AE CE 不一定成立，故选项错误，符合题意．故选：D ．【点睛】此题考查三角形的高线，角平分线和中线，关键是根据三角形的高线，角平分线和中线的定义进行判断即可．二、填空题：（每题3分，共15分）7．如图，90CBD E F ，则线段______是ABC 中BC 边上的高．【答案】AE【解析】【分析】根据三角形高线的定义判断即可；【详解】∵AE BC ，∴ABC 中BC 边上的高是AE ．故答案是AE ．【点睛】本题主要考查了三角形的角平分线、中线和高线，准确分析判断是解题的关键．8．如图，△AB C 中，AD 是BC 上的中线，BE 是△AB D 中AD 边的中线，若△ABC 的面积是24，AE ＝3，则点B 到直线AD 的距离为________．【答案】4【解析】【分析】由三角形的中线平分三角形面积的性质可得△ABE 的面积，再由三角形面积公式即可求得结果．【详解】∵AD 是△ABC 的BC 边上的中线，24ABC S ，∴1122ABD ABC S S ．∵BE 是△AB D 中AD 边上的中线，∴162ABE ABD S S ．设点B 到直线AD 的距离为h ，则162ABE S AE h，即1362h ，∴h =4．即点B 到直线AD 的距离为4．故答案为：4．【点睛】本题考查了三角形一边上的中线平分三角形面积的性质、三角形面积等知识，掌握三角形一9．如图，在△AB C 中，AD 、AE 分别是BC 边上的中线和高，AE ＝6，S △ABD ＝15，则CD ＝_____．【答案】5【解析】【分析】由利用三角形的面积公式可求得BD 的长，再由中线的定义可得CD =BD ，从而得解．【详解】解：∵S △ABD =15，AE 是BC 边上的高，∴12BD •AE =15，则12×6BD =15，解得：BD =5，∵AD 是BC 边上的中线，∴CD =BD =5．故答案为：5．【点睛】本题主要考查三角形的中线，三角形的高，解答的关键是由三角形的面积公式求得BD 的长．10．如图，在三角形ABC 中，AB AC ，AD BC ，垂足为D ，3AB ，4AC ，5BC ，则AD ______．【答案】2.4【解析】【分析】根据面积相等可列式1122AB AC BC AD ，代入相关数据求解即可．【详解】解：∵AB AC ，AD BC ，∴1122AB AC BC AD ∵3AB ，4AC ，5BC ，∴12 2.45AB AC AD BC 故答案諀：2.4【点睛】此题主要考查了运用等积关系求线段的长，准确识图是解答本题的关键．11．已知ABC 中，30cm AC ，中线AD 把ABC 分成两个三角形，这两个三角形的周长差是12cm ，则AB 的长是__________．【答案】42cm 或18cm【解析】【分析】先根据三角形中线的定义可得BD =CD ，再求出AD 把△ABC 周长分为的两部分的差等于|AB -AC |，然后分AB ＞AC ，AB ＜AC 两种情况分别列式计算即可得解．【详解】∵AD 是△AB C 中线，∴BD =C D ．∵AD 是两个三角形的公共边，两个三角形的周长差是12cm ，∴如果AB ＞AC ，那么AB -AC =12cm ，即AB -30=12cm∴AB =42cm ；如果AB ＜AC ，那么AC -AB =12cm ，即30-AB =12cmAB =18cm ．综上所述：AB 的长为42cm 或18cm ．故答案为：42cm 或18cm ．【点睛】考查了三角形的中线，三角形一边的中点与此边所对顶点的连线叫做三角形的中线．三、解答题：（每题8分，共40分）12．如图，BD 和CE 是△ABC 的中线，AE =3cm ，CD =2cm ，若△ABC 周长为15cm ，求BC 边的长．【答案】5cm【解析】【分析】根据中线定义可得AB ，AC ，根据△ABC 周长公式即可求解．【详解】∵BD 和CE 是△ABC 的中线，∴2236AB AE cm ，2224AC CD cm ，∵△ABC 周长为15cm ，即15AB AC BC cm ，∴1515645BC AB AC cm ．【点睛】本题考查三角形中线定义、三角形周长公式，解题的关键是根据三角形中线求出AB 和AC 的长．13．如图，△ABC 的周长是21cm ，AB ＝AC ，中线BD 分△ABC 为两个三角形，且△ABD 的周长比△BCD 的周长大6cm ，求AB ，B C ．【答案】AB＝9cm，BC＝3cm．【解析】【分析】由BD是中线，可得AD=CD，又由△ABD的周长比△BCD的周长大6cm，△ABC的周长是21cm，AB=AC，可得AB-BC=6cm，2AB+BC=21cm，继而求得答案．【详解】解：∵BD是中线，∴AD＝CD＝12AC，∵△ABD的周长比△BCD的周长大6cm，∴（AB+AD+BD）﹣（BD+CD+BC）＝AB﹣BC＝6cm①，∵△ABC的周长是21cm，AB＝AC，∴2AB+BC＝21cm②，联立①②得：AB＝9cm，BC＝3cm．【点睛】本题考查了三角形周长与三角形的中线．注意掌握数形结合思想与方程思想的应用．14．如图，△ABC的顶点都在边长为1的正方形方格纸的格点上，将△ABC向上平移4格．(1)请在图中画出平移后的三角形A′B′C′；(2)在图中画出三角形△ABC的高CD、中线BE；(3)△ABC的面积是．【答案】(1)见解析(2)见解析(3)8【解析】【分析】（1）根据图形平移的性质画出平移后的△A′B′C′即可；（2）找出线段AC的中点E，然后连接B E，再过点C向AB所在的直线作垂线，垂足为D 即可；（3）直接根据三角形的面积公式即可得出结论．(1)如图所示，三角形A′B′C′就是所要求做的图形；(2)如图所示，三角形△ABC的高CD、中线BE；(3)S △ABC ＝1144822AB CD ．故△ABC 的面积是8．【点睛】本题考查作图－平移变换，熟知图形平移不变性的性质是解答此题的关键．15．如图，已知AD ，AE 分别是ABC 的高和中线，9cm AB ，12cm AC ，15cm BC ，90BAC ．(1)求AD 的长度；(2)求ABE △的面积．【答案】(1)36cm 5(2)227cm 【解析】【分析】（1）利用等面积法，根据1122ABC S AB AC BC AD ，代值求解即可；（2）根据已知条件和（1）中求出的AD 长，利用三角形面积公式得出12ABE S BE AD ，代值求解即可．(1)解：在ABC 中，90BAC ，AD 是边BC 上的高，∵9cm AB ，12cm AC ，15cm BC ，根据1122ABC S AB AC BC AD 可得91236155cm AB AC AD BC ；(2)解：在ABC 中，BE 是边BC 上的中线，且15cm BC ，1152m 2c BE BC ，在ABE 中，AD 是边BE 上的高，且由（1）知5cm 36AD ，2111536272225cm ABE S BE AD ．【点睛】本题考查三角形面积公式，熟练掌握三角形的中线与高线是解决问题的关键．16．请补全证明过程及推理依据．已知：如图，BC //ED ，BD 平分∠ABC ，EF 平分∠AE D ．求证：BD ∥EF ．证明：∵BD平分∠ABC，EF平分∠AED，∴∠1=12∠AED，∠2=12∠ABC（______________）∵BC∥ED（________）∴∠AED=________（________________）∴12∠AED=12∠ABC∴∠1=________∴BD∥EF（________________）．【答案】角平分线的定义；已知；∠ABC；两直线平行，同位角相等；∠2；同位角相等，两直线平行【解析】【分析】根据角平分线的定义得出∠1=12∠AED，∠2=12∠ABC，根据平行线的性质定理得出∠AED=∠ABC，求出∠1=∠2，再根据平行线的判定定理推出即可．【详解】证明：∵BD平分∠ABC，EF平分∠AED，∴∠1=12∠AED，∠2=12∠ABC（角平分线的定义）∵BC∥ED（已知）∴∠AED=∠ABC（两直线平行，同位角相等）∴12∠AED=12∠ABC∴∠1=∠2∴BD∥EF（同位角相等，两直线平行）．故答案为：角平分线的定义；已知；∠ABC；两直线平行，同位角相等；∠2；同位角相等，两直线平行．【点睛】本题考查了角平分线的定义，平行线的性质定理和判定定理等知识点，能熟记平行线的性质定理和判定定理是解此题的关键．能力提升篇一、单选题：（每题3分，共9分）1．在等腰△ABC中，AB=AC，中线BD将这个三角形的周长分为15和12两个部分，则这个等腰三角形的底边长为（）A．7B．10C．7或11D．7或10【答案】C【解析】【分析】题中给出了周长关系，要求底边长，首先应先想到等腰三角形的两腰相等，寻找问题中的等量关系，列方程求解，然后结合三角形三边关系验证答案．【详解】设等腰三角形的底边长为x，腰长为y，则根据题意，得①152122yxyy＝＝或②122152yxyy＝＝解方程组①得118xy＝＝，根据三角形三边关系定理，此时能组成三角形；解方程组②得710 xy＝＝，根据三角形三边关系定理此时能组成三角形，即等腰三角形的底边长是11或7；故选：C．【点睛】本题考查等腰三角形的性质及相关计算．学生在解决本题时，有的同学会审题错误，以为15，12中包含着中线BD的长，从而无法解决问题，有的同学会忽略掉等腰三角形的分情况讨论而漏掉其中一种情况；注意：求出的结果要看看是否符合三角形的三边关系定理．2．如图，△ABC的面积为3，BD：DC＝2：1，E是AC的中点，AD与BE相交于点P，那么四边形PDCE的面积为（）A．13B．710C．35D．1320【答案】B【解析】【分析】连接CP．设△CPE的面积是x，△CDP的面积是y．根据BD：DC=2：1，E为AC的中点，得△BDP的面积是2y，△APE的面积是x，进而得到△ABP的面积是4x．再根据△ABE的面积是△BCE的面积相等，得4x+x=2y+x+y，解得y=43x，再根据△ABC的面积是3即可求得x、y的值，从而求解．【详解】连接CP，设△CPE的面积是x，△CDP的面积是y．∵BD：DC=2：1，E为AC的中点，∴△BDP的面积是2y，△APE的面积是x，∵BD：DC=2：1∴△ABD的面积是4x+2y∴△ABP的面积是4x．∴4x+x=2y+x+y，解得y=43x．又∵△ABC的面积为3∴4x+x=3 2，x=3 10．则四边形PDCE的面积为x+y=7 10．故选B．【点睛】此题能够根据三角形的面积公式求得三角形的面积之间的关系．等高的两个三角形的面积比3．如图，△ABC的面积是24，点D，E，F，G分别是BC，AD，BE，CE的中点，则△AFG 的面积是（）A．9B．10C．11D．12【答案】A【解析】【分析】首先根据点E 是AD 的中点，可知ABE BDE S S ，ACE CDE S S V ，再根据点D 是BC 的中点，可得BDE CDE S S V ，即可得164ABE BDE ACE CDE ABCS S S S S V V V V ，然后根据点F ，G 是BE ，CE 的中点，得132AEF ABE S S V V ，132AEG ACE S S V V ，可知FG 是△CBE 的中位线，可得134EFG BCE S SV V ，即可得出答案．【详解】∵点E 是AD 的中点，∴ABE BDE S S ，ACE CDE S S V ．∵点D 是BC 的中点，∴BDE CDE S S V ，∴164ABE BDE ACE CDE ABCS S S S SV V V V ．∵点F ，G 是BE ，CE 的中点，∴132AEF ABE S S V V ，13AEG ACE S S V V ，∴FG 是△CBE 的中位线，∴134EFG BCES S V V ，∴+=9AFG AEF AEG EFG S S S S V V V V ．故选：A ．【点睛】本题主要考查了三角形的面积和中线的关系，三角形中位线的定义和性质等，将一个三角形的面积转化为求三个小三角形的面积是解题的关键．二、填空题：（每题3分，共9分）4．如图，在ABC 中，2AB AC ，P 是BC 边上的任意一点，PE AB 于点E ，PF AC于点F .若2ABC S ，则PE PF ______．【答案】2【解析】【分析】根据1122ABC ABP APC S S S AB PE AC PF，结合已知条件，即可求得PE PF 的值．【详解】解：如图，连接AP ∵PE AB 于点E ，PF AC 于点F1122ABC ABP APC S S S AB PE AC PF 2AB AC ∵，2ABC S 1122AB PE AC PF 2PE PF 2【点睛】本题考查了三角形的高，掌握三角形的高的定义是解题的关键．5．如图，在 AB C 中，已知点D ，E ，F 分别为边BC ，AD ，CE 的中点，且 ABC 的面积等于24cm 2，则阴影部分图形面积等于_____cm 2【答案】6【解析】【分析】因为点F是CE的中点，所以△BEF的底是△BEC的底的一半，△BEF高等于△BEC的高；同理，D、E、分别是BC、AD的中点，可得△EBC的面积是△ABC面积的一半；利用三角形的等积变换可解答．【详解】解：如图，点F是CE的中点，∴△BEF的底是EF，△BEC的底是EC，即EF=12EC，而高相等，∴S△BEF=12S△BEC，∵E是AD的中点，∴S△BDE=12S△ABD，S△CDE=12S△ACD，∴S△EBC=12S△ABC，∴S△BEF=14S△ABC，且S△ABC=24cm2，∴S△BEF=6cm2，即阴影部分的面积为6cm2．故答案为6．【点睛】本题考查了三角形面积的等积变换：若两个三角形的高（或底）相等，面积之比等于底边（高）之比．6．在ABC 中，90B ，8AB cm ，6BC cm ，点D 是AB 的中点，点P 从A 点出发，沿线段AD 以每秒2cm 的速度运动到B ．当点P 的运动时间t ____________秒时，PCD 的面积为26cm ．【答案】1或3【解析】【分析】分为两种情况讨论：当点P 在AD 上时，当点P 在DB 上时，根据三角形的面积公式建立方程求出其解即可．【详解】∵8AB cm ，点D 是AB 的中点，∴AD =BD =4cm ，当点P 在AD 上时，AP =2t ，∴PD =4-2t∵PCD 的面积为26cm ，∴12PD ×BC =6，即 142662t 解得t =1s ，当点P 在BD 上时，AP =2t ，∴DP =2t -4，∵PCD 的面积为26cm ，∴12DP ×BC =6，即 124662t ，解得t =3s ，综上，当点P 运动时间t 1或3秒时，PCD 的面积为26cm ．故答案为：1或3．【点睛】本题考查了三角形的中线，三角形的面积公式的运用，解答时灵活运用三角形的面积公式求解是关键．三、解答题：（9分）7．如图，在ABC 中，CD 、CE 分别是ABC 的高和角平分线，,()BAC B ．(1)若70,40 ，求DCE 的度数；(2)试用 、 的代数式表示DCE 的度数_________．【答案】(1)15DCE (2)2【解析】【分析】（1）根据三角形的内角和定理求出∠ACB 的值，再由角平分线的性质以及直角三角形的性质求出∠DCE ．（2）由（1）的解题思路即可得正确结果．(1)解：∵70BAC ，40B180()180704070ACB BAC B ，∵CE 是ACB 的平分线， 1352ACE ACB ．∵CD 是高线，90ADC ，9020ACD BAC ，352015DCE ACE ACD ．(2)解：∵BAC ，B180()180ACB BAC B ，∵CE 是ACB 的平分线， 1118090222ACE ACB ．∵CD 是高线，90ADC ，9090ACD BAC ， 909022DCE ACE ACD．【点睛】思维拓展篇1.阅读下列材料：阳阳同学遇到这样一个问题：如图1，在ABC 中AB AC ，BD 是ABC 的高，P 是BC 边上一点，PM 、PN 分别与直线AB ，AC 垂直，垂足分别为点M 、N ．求证：BD PM PN ．阳阳发现，连接AP ，有ABC ABP ACP S S S ，即111222AC BD AB PM AC PN ．由AB AC ，可得BD PM PN ．他又画出了当点P 在CB 的延长线上，且上面问题中其他条件不变时的图形，如图2所示，他猜想此时BD 、PM 、PN 之间的数量关系是：BD PN PM ．请回答：（1）请补全阳阳同学证明猜想的过程；证明：连接AP ．ABC APC S S ∵________，1122AC BD AC ________12AB ________．AB AC ∵，BD PN PM ．（2）参考阳阳同学思考问题的方法，解决下列问题：在ABC 中，AB AC BC ，BD 是ABC 的高．P 是ABC 所在平面上一点，PM 、PN 、PQ 分别与直线AB 、AC 、BC 垂直，垂足分别为点M 、N 、Q ．①如图3，若点P 在ABC 的内部，猜想BD 、PM 、PN 、PQ 之间的数量关系并写出推理过程．②若点P 在如图4所示的位置，利用图4探究得此时BD 、PM 、PN 、PQ 之间的数量关系是：_______．（直接写出结论即可）【答案】（1）S △APB ；PN ；PM ；（2）①BD ＝PM ＋PN ＋PQ ，证明见解析②BD ＝PM ＋PQ −PN ．【解析】【分析】（1）根据图形，结合阅读材料填写即可；（2）①连接AP 、BP 、CP ，根据S △ABC ＝S △APC ＋S △APB ＋S △BPC 得出12AC •BD ＝12AC •PN ＋12AB •PM ＋12BC •PQ ，由AB ＝AC ＝BC ，即可得出BD ＝PM ＋PN ＋PQ ；②连接AP 、BP 、CP ，根据S △ABC ＝S △APB ＋S △BPC −S △APC ，得出12AC •BD ＝12AB •PM ＋1 2BC•PQ−12AC•PN，由于AB＝AC＝BC，即可证得BD＝PM＋PQ−PN．【详解】解：（1）证明：连接AP．∵S△ABC＝S△APC−S△APB，∴12AC•BD＝12AC•PN−12AB•PM．∵AB＝AC，∴BD＝PN−PM．故答案为：S△APB；PN；PM；（2）①BD＝PM＋PN＋PQ；如图3，连接AP、BP、CP，∵S△ABC＝S△APC＋S△APB＋S△BPC∴12AC•BD＝12AC•PN＋12AB•PM＋12BC•PQ，∵AB＝AC＝BC，∴BD＝PM＋PN＋PQ；②BD＝PM＋PQ−PN；如图4，连接AP、BP、CP，∵S△ABC＝S△APB＋S△BPC−S△AP C．∴12AC•BD＝12AB•PM＋12BC•PQ−12AC•PN，∵AB＝AC＝BC，∴BD＝PM＋PQ−PN．【点睛】本题考查了等边三角形的性质，三角形的面积等，作出辅助线构建三个三角形是解题的关键．。
三角形的高、中线与角平分线专题(含答案)
11.1.2三角形的高、中线与角平分线一、选择题1.以下说法正确的有() ①三角形的中线、角平分线都是射线; ②三角形的三条高所在直线相交于一点; ③三角形的三条角平分线在三角形内部交于一点; ④三角形的中线把三角形分成面积相等的两部分; ⑤直角三角形的三条高相交于直角顶点．A.5个B.4个C.3个D.2个2.如图所示，CD、CE、CF分别是△ABC的高、角平分线、中线，则下列各式中错误的是()A.BA=2BFB.∠ACE=12∠ACBC.AE=BED.CD⊥AB3.画△ABC中AB边上的高，下列画法中正确的是()A. B. C. D.4.如图，AC⊥BC于点C，CD⊥AB于点D，则图中可以作为三角形“高”的线段有()A.1条B.2条C.3条D.5条5.若AD是△ABC的中线，下列结论错误的是()A.AB=BCB.BD=DCC.AD平分BCD.BC=2DC6.如图，△ABC中AB边上的高线是()A.线段DAB.线段CAC.线段CDD.线段BD7.如图，AD，BE，CF依次是△ABC的高、中线和角平分线，下列各式中错误的是()A.AE=CEB.∠ADC=90∘C.∠CAD=∠CBED.∠ACB=2∠ACF8.如图，在△ABC中，D，E，F分别是BC，AD，CE的中点，S△ABC=4cm2，则S△BEF等于()A.2cm2B.1cm2C.12cm2D.14cm29.如果AD是△ABC的中线，那么下列结论： ①BD=12CB; ②AB=AC; ③S△ABD=S△ACD.其中一定成立的有()A.3个B.2个C.1个D.0个10.如图，已知P是△ABC的重心，连接AP并延长交BC于点D，若△ABC的面积为20，则△ADC的面积为()A.10B.8C.6D.511.填空：(1)如图(1)，AD，BE，CF是△ABC的三条中线，则AB=2，BD=，AE=12．(2)如图(2)，AD，BE，CF是△ABC的三条角平分线，则∠1=∠，∠3=12，∠ACB=2．12.如图，AB⊥BD于点B，AC⊥CD于点C，且AC与BD交于点E.已知AE=5，DE=2，CD=95，则AB的长为．13.若AD是△ABC的高，∠BAD=70∘，∠CAD=20∘，则∠BAC的度数为．14.如图，在△ABC中，CD平分∠ACB，DE//BC，交AC于点E.若∠AED=50°，则∠D的度数为______．15.如图，在△ABC中，AD⊥BC，垂足为点D，EC⊥BC交AB于点E，CF⊥AB，垂足为点F，BG⊥AC，垂足为点G．(1)分别写出△ABC各条边上的高；(2)CF是哪几个三角形的高？16.如图，D是△ABC中BC边上的一点，DE//AC交AB于点E，若∠EDA=∠EAD，试说明AD是△ABC的角平分线．17.如图，在△ABC中，AB=2，BC=4.△ABC的高AD与CE的比是多少？(提示：利用三角形的面积公式．)18.如图所示，已知AD，AE分别是△ABC的高和中线，AB=6cm，AC=8cm，BC=10cm，∠CAB=90∘.试求：(1)AD的长;(2)△ABE的面积;(3)△ACE与△ABE的周长的差．19.如图，AD是△ABC的角平分线．DE // AC，DE交AB于点E，DF // AB，DF交AC于点F.图中∠1与∠2有什么关系？为什么？20.在如图所示的方格纸中，每个小正方形的边长均为1，点A，点B，点C均在小正方形的顶点上．(1)画出△ABC中BC边上的高AD;(2)画出△ABC中AC边上的中线BE;(3)直接写出△ABE的面积为．11.1.2三角形的高、中线与角平分线1.【答案】B2.【答案】C3.【答案】C4.【答案】D5.【答案】A6.【答案】C7.【答案】C8.【答案】B9.【答案】B10.【答案】A11.【答案】AF或BFCDAC∠2∠ABC∠4或∠ACF12.【答案】9213.【答案】90∘或50∘14.【答案】25°15.【答案】解：(1)由题意，可得△ABC中，AB边上的高是CF，BC边上的高是AD，AC边上的高是BG；(2)∵CF⊥AB，垂足为点F，∴CF是△BCF，△BCE，△BCA，△FCE，△FCA，△ECA的高．16.【答案】解：∵DE//AC，∴∠ADE=∠CAD，∵∠EDA=∠EAD，∴∠CAD=∠EAD，∴AD是△ABC的角平分线．17.【答案】解：∵AD和CE分别是△ABC边BC和边AB上的高，∴S△ABC=12BC·AD=12AB·CE，即2AD=CE，．18.【答案】解：(1)∵∠BAC=90∘，AD是边BC上的高，∴12AB⋅AC=12BC⋅AD，∴AD=AB⋅AC BC=6×810=4.8(cm)，即AD的长为4.8cm．(2)∵△ABC是直角三角形，∠BAC=90∘，AB=6cm，AC=8cm，∴S△ABC=12AB⋅AC=12×6×8=24(cm2).又∵AE是△ABC的中线，∴BE=EC，∴12BE⋅AD=12EC⋅AD，即S△ABE=S△AEC，∴S△ABE=12S△ABC=12(cm2)，∴△ABE的面积是12cm2．(3)∵AE为BC边上的中线，∴BE=CE，∴△ACE的周长−△ABE的周长=AC+AE+CE−(AB+BE+AE)=AC−AB=8−6=2(cm)，即△ACE与△ABE的周长的差是2cm．19.【答案】解：∠1=∠2．理由如下：因为AD平分∠BAC，所以∠BAD=∠DAC.因为DE//AC，所以∠DAC=∠1.因为DF//AB，所以∠DAB=∠2．所以∠1=∠2．20.【答案】解：(1)如图所示，线段AD即为所求．(2)如图所示，线段BE即为所求．(3)4．。
三角形的高中线角平分线练习题
三角形的高中线角平分线练习题文件管理序列号：[K8UY-K9IO69-O6M243-OL889-三角形的高、中线、角平分线练习题1、分别在下列锐角三角形、直角三角形、钝角三角形中画出所有的高。
2、三角形的三条中线、三条角平分线、三条高都是（）A．直线 B．射线 C．线段 D．射线或线段3、如果一个三角形的三条高的交点恰是三角形的一个顶点，那么这个三角形是（）A．锐角三角形 B．直角三角形C．钝角三角形 D．不能确定4、能把三角形的面积分成两个相等的三角形的线段是（）A．中线B．高C．角平分线 D．以上三种情况都正确5、如图若∠BAF=∠CAF，则____是△ABD的角平分线，____是△ABC的角平分线6、如图AB⊥AC，则AB是△ABC的边____上的高，也是△BDC的边______上的高，也是△ABD的边____上的高.FB CDAB CD7、如图BD 、AE 分别是△ABC 的中线、角平分线，AC=10cm ，∠BAC=700，则AD=_____，∠BAE=____.8、在△ABC 中，AE 是中线，AD 是角平分线，AF 是高，填空： ⑴BE ＝___＝21_____；⑵∠BAD=_____=21_____；⑶∠AFB=_____=909、在△ABC 中,AB=AC,AD 是中线,△ABC 的周长为34cm,△ABD 的周长为30cm, 求AD 的长.10、在△ABC 中AB=AC ，AC 上的中线BD 把三角形的周长分为24cm 和30cm 的两个部分，求三角形的三边长。
11、要使四边形木架(用四根木条钉成)不变形，至少要再钉上几根木条？五边形木架和六边形木架呢？n 边形木架呢？BD。
八年级数学上册《三角形的高、中线与角平分线》练习题及答案
八年级数学上册《三角形的高、中线与角平分线》练习题及答案学校:___________姓名：___________班级：___________一、单选题1．如图，△ABC中BC边上的高和△AEC中AE边上的高分别是（）A．EF和CD B．BC和CD C．AB和CD D．AB和EF2．如图，ABC的面积是2，AD是ABC的中线，13AF AD=，12CE EF=，则CDE△的面积为（）A．29B．16C．23D．493．数学活动课上，小敏、小颖分别画了△ABC和△DEF，数据如图，如果把小敏画的三角形面积记作S△ABC，小颖画的三角形面积记作S△DEF，那么你认为()A．S△ABC >S△DEF B．S△ABC <S△DEFC．S△ABC =S△DEF D．不能确定4．如图，在△ABC中，已知点D、E、F分别为边BC、AD、CE的中点，且△ABC的面积是8cm2，则阴影部分面积等于（）A ．2cm 2B ．1.5cm 2C ．1cm 2D ．0.5cm 25．如图，BD 是ABC 的边AC 上的中线，AE 是ABD △的边BD 上的中线，BF 是ABE △的边AE 上的中线，若ABC 的面积是32，则阴影部分的面积是（ ）A ．9B ．12C ．18D ．206．请你量一量如图ABC 中BC 边上的高的长度，下列最接近的是( )A ．0.5cmB ．0.7cmC ．1.5cmD ．2cm7．如图，已知D 、E 分别为△ABC 的边BC 、AC 的中点，连接AD 、DE ，AF 为△ADE 的中线．若四边形ABDF 的面积为10，则△ABC 的面积为（ ）A ．12B ．16C ．18D ．208．已知A ，B 两点在数轴上的位置如图所示，原点为O ，现A 点以2m/s 的速度向左运动，B 点以1m/s 的速度向左运动，若A ，B 两点同时出发，当OA ：OB ＝1：2时，用时为（ ）A ．2sB ．14sC ．73s 或1sD ．12s 或2s二、填空题 9．填空：（1）如图（1）,,AD BE CF 是ABC 的三条中线，则2AB =______，BD =______，12AE =______． （2）如图（2）,,AD BE CF 是ABC 的三条角平分线，则1∠=______，132∠=______，2ACB ∠=______．10．已知BD 、CE 是△ABC 的高，直线BD 、CE 相交所成的角有一个角为45︒，则BAC ∠等于______． 11．如图，AC//BD ，OA ，OB 分别平分BAC ∠和ABD ∠，OE AB ⊥，垂足为E ，如果OE 5=，那么AC 与BD 的距离是________12．如图，在ABC 中，90,BAC AD ∠=︒是高，BE 是中线，CF 是角平分线，CF 交AD 于点G ，交BE 于点H ，下面说法正确的是____________．△ABE △的面积等于BCE 的面积；△AFG AGF ∠=∠；△2FAG ACF ∠=∠；△CG 是ACD △的角平分线13．如图，AD 是△ABC 的中线，BE 是△ABD 的中线，EF ⊥BC 于点F．若24ABCS=，BD = 4 ，则EF 长为___________．14．若AD是△ABC的高，△BAD=70°，△CAD=20°，则△BAC的度数为_____．15．连结三角形的一个顶点和它________________的________叫做三角形这边上的中线．如图，若BE是ABC中AC边上的中线，则AE________12EC=________．16．如图，点C、D分别是半圆AOB上的三等分点，若阴影部分的面积为32π，则半圆的半径OA的长为__________．三、解答题17．如图，△ABE 中，△E ＝90°，AC 是△BAE 的角平分线.(1)若△B ＝40°，求△BAC 的度数；(2)若D 是BC 的中点，△ADC 的面积为16，AE ＝8，求BC 的长.18．如图，在ABC 中（AB BC >），2AC BC =，BC 边上的中线AD 把ABC 的周长分成60和40两部分，求AC 和AB 的长．19．在平面内，分别用3根、5根、6根……火柴棒首尾依次相接，能搭成什么形状的三角形呢？通过尝试，列表如下．问：(1)4根火柴棒能搭成三角形吗？(2)8根、12根火柴棒分别能搭成几种不同形状的三角形？并画出它们的示意图． 20．如图，在正方形网格中有一个ABC ，按要求进行作图（只用直尺）(1)画出将ABC向右平移6格，再向上平移3格后的DEF；(2)画出ABC中AC边上的高BH；(3)请在图中直接标记出3个使BCP的面积等于3的格点1P、2P、3P．参考答案：1．C【分析】根据三角形高的定义，△ABC中BC边上的高为从BC边相对的顶点A向BC边作的垂线段，△AEC 中AE边上的高为从AE边相对的顶点C向AE边作的垂线段，观察图形，找出符合要求的线段即可．【详解】解：根据三角形高的定义可知，AB是△ABC中BC边上的高，CD是△AEC中AE边上的高，故选C．【点睛】本题考查三角形高的定义：从三角形一个端点向它的对边作一条垂线，三角形顶点和它对边垂足之间的线段称三角形这条边上的高．2．A【分析】根据中线的性质即可求出S△ACD，然后根据等高时，面积之比等于底之比，即可依此求出S△CDF，S△CDE．【详解】解：△△ABC的面积是2，AD是△ABC的中线，△S△ACD＝12S△ABC＝1，△AF＝13 AD，△DF＝23AD，△S△CDF＝23S△ACD＝23×1＝23，△CE＝12EF，△CE＝13 CF△S△CDE＝13S△CDF＝13×23＝29，故选：A．【点睛】此题考查的是三角形的面积关系，掌握中线的性质和等高时，面积之比等于底之比是解决此题的关键．3．C【分析】在两个图形中分别作BC、EF边上的高，欲比较面积，由于底边相等，所以只需比较两条高即可．【详解】解：如图，过点A、D分别作AG△BC，DH△EF，垂足分别为G、H，在△ABG和△DHE中，AB=DE=5，△B=50°，△DEH=180°-130°=50°，△△B=△DEH，△AGB=△DHE=90°，△△AGB△△DHE(AAS)，△AG=DH．△BC=4，EF=4，△S△ABC=S△DEF．故选：C．【点睛】要题考查全等三角形的判定和性质，等底等高两三角形面积相等．证明△AGB△△DHE是解题的关键．4．A【分析】先由D为BC中点，求出△ABD和△ACD面积，再由点E为AD中点求出△BCE面积，再根据F是CE中点，知阴影部分面积等于△BCE面积的一半，即可求解．【详解】解：△D是BC中点，△ABC的面积是8cm2，△1=42ABD ACD ABC S S S ==△△△cm 2， △E 是AD 中点，△1=22ABE BDE ABD S S S ==△△△cm 2，1=22ACECDEACDS SS ==cm 2，△4CBE S =△cm 2， △F 为CE 中点， △1=22CBE S S =△阴影cm 2， 故选：A ．【点睛】本题考查了三角形面积的等积变换，掌握三角形的中线将三角形分成面积相等的两部分是解题关键． 5．B【分析】利用中线等分三角形的面积进行求解即可． 【详解】△BD 是ABC 的边AC 上的中线，△11321622ABD BCD ABC S S S ===⨯=△△，△AE 是ABD △的边BD 上的中线， △1116822ABEADEABDSSS ===⨯=， 又△BF 是ABE △的边AE 上的中线，则CF 是ACE 的边AE 上的中线， △118422BEFABFABESSS ===⨯=，182CEFACFADECEDACES SSSS =====，则4812BEFCEFS SS =+=+=阴影，故选：B ．【点睛】本题考查了中线的性质，清晰明确三角形之间的等量关系，进行等量代换是解题的关键． 6．D【分析】作出三角形的高，然后利用刻度尺量取即可． 【详解】解：如图所示，过点A 作AO △BC ，用刻度尺直接量得AO 更接近2cm ，故选：D ．【点睛】题目主要考查利用刻度尺量取三角形高的长度，作出三角形的高是解题关键． 7．B【分析】根据三角形的中线平分三角形的面积即可得到结论． 【详解】设AEF S x =△， △AF 为△ADE 的中线． △,2AEFADFADESSx Sx ===△E 分别为△ABC 的边AC 的中点， △2,4ADECDECDASSx Sx ===△D 分别为△ABC 的边BC 的中点， △4,8CDABDAABCSSx Sx ===△四边形ABDF 的面积=510FDABDAS Sx +==解得2x = △816ABCSx ==故选：B【点睛】本题考查了三角形的面积，熟练三角形的中线平分三角形的面积是解题的关键． 8．C【分析】设A ，B 两点同时出发运动的时间为t s ，分类讨论△当A 点在O 点右侧时和△当A 点在O 点左侧时，分别用t 表示出OA 和OB ，再列出等式，解出t 即可． 【详解】设A ，B 两点同时出发运动的时间为t s ， 分类讨论△当A 点在O 点右侧时，即32t <时， 此时1OB t =+，32OA t =-， △OA ：OB =1：2 △(32)t -：(1)t +=1：2 解得：312t =<，符合题意； △当A 点在O 点左侧时，即32t >， 此时1OB t =+，23OA t =-，△OA ：OB =1：2 △(23)t -：(1)t +=1：2 解得：7332t =>，符合题意． 综上可知1t =或73t =时，OA ：OB =1：2 故选C ．【点睛】本题主要考查数轴上的动点问题，利用分类讨论的思想是解答本题的关键． 9． AF 或BF CD AC 2∠ ABC ∠ 4∠【分析】（1）根据三角形的中线定义：三角形一边的中点与此边所对顶点的连线叫做三角形的中线可得E 、F 、D 分别是AC 、AB 、BC 上的中点，进而得到答案．（2）根据角平分线定义，从一个角的顶点出发，把这个角分成两个相等的角的射线，叫做这个角的平分线即可解答．【详解】解：（1）△CF 是AB 边上的中线， △AB ＝2AF ＝2BF ； △AD 是BC 边上的中线， △BD ＝CD ，△BE 是AC 边上的中线， △AE ＝12AC ，（2）△AD 是BAC ∠的角平分线， △12∠=∠ ，△BE 是ABC ∠的角平分线， △132∠=ABC ∠， △CF 是ACB ∠的角平分线， △2ACB ∠=4∠．故答案为：AF 或BF ；CD ；AC ；2∠；ABC ∠；4∠【点睛】此题主要考查了三角形的中线、角平分线，解题的关键是掌握三角形的中线及角平分线的定义． 10．45°或135°【分析】分两种情况：（1）当△A 为锐角时，如图1，（2）当△A 为钝角时，如图2，根据三角形的内角和计算得出结果．【详解】解：分两种情况：（1）当△A为锐角时，如图1，△△DOC＝45°，△△EOD＝135°，△BD、CE是△ABC的高，△△AEC＝△ADB＝90°，△△EAO+△AEO+△AOE=180°=△DAO+△DOA+△ADO，△△AEO+△EAD+△ADO+△EOD=360°△△A＝360°−90°−90°−135°＝45°；（2）当△A为钝角时，如图2，△△F＝45°，△ADF＝△AEF＝90°，同理△DAE＝360°−90°−90°−45°＝135°，△△BAC＝△DAE＝135°，则△BAC的度数为45°或135°，故答案为：45°或135°．【点睛】本题考查了三角形的高和三角形的内角和，明确三角形内角和，三角形的高所构成了两个直角；本题是易错题，容易漏解，要分锐角三角形和钝角三角形两种情况进行计算．11．10【分析】过点O 作OM AC ⊥于M ，作ON BD ⊥于N ，利用平行线的性质可证得OM△BD ，进而可证得MN 为AC 和BD 的距离，根据角平分线的性质可知OE=OM=OE ，即可求得MN 的长度．【详解】解：如图，过点O 作OM AC ⊥于M ，作ON BD ⊥于N ．△OA 、OB 分别平分BAC ∠和ABD ∠，OE AB ⊥，△OM OE ON 5===，又 AC △BD ，OM AC ⊥，△OM BD ⊥，又ON BD ⊥，△M ，O ，N 三点共线，△ AC 与BD 之间的距离为MN=OM ON 10+=．故答案为：10．【点睛】本题考查求平行线间的距离、角平分线的性质、八个基本事实，熟练掌握角平分线的性质，作出AC 和BD 之间的距离是解答的关键．12．△△△△【分析】根据等底同高的三角形的面积相等即可判断△；根据直角三角形两锐角互余求出△ABC ＝△CAD ，根据三角形的外角性质即可推出△；根据直角三角形两锐角互余求出△BAD ＝△ACD ，根据角平分线定义即可判断△；根据三角形的角平分线的定义判断△即可．【详解】解：△BE 是中线，△AE ＝CE ，△△ABE 的面积＝△BCE 的面积（等底同高的三角形的面积相等），△正确；△CF 是角平分线，△△ACF ＝△BCF ，△AD 为高，△△ADC ＝90°，△△BAC ＝90°，△△ABC ＋△ACB ＝90°，△ACB ＋△CAD ＝90°，△△ABC ＝△CAD ，△△AFG ＝△ABC ＋△BCF ，△AGF ＝△CAD ＋△ACF ，△△AFG ＝△AGF ，△正确；△AD 为高，△△ADB ＝90°，△△BAC ＝90°，△△ABC ＋△ACB ＝90°，△ABC ＋△BAD ＝90°，△△ACB ＝△BAD ，△CF 是△ACB 的平分线，△△ACB ＝2△ACF ，△△BAD ＝2△ACF ，即△F AG ＝2△ACF ，△正确；△CF 是△ACB 的平分线，CF 交AD 于点G ，△CG 是△ACD 的角平分线，△正确；故答案为：△△△△．【点睛】本题考查了直角三角形两锐角互余，三角形的外角性质，三角形的角平分线、中线、高线等知识点，能综合运用定理进行推理是解此题的关键．13．3【分析】因为S △ABD =12S △ABC ，S △BDE =12S △ABD ；所以S △BDE =14S △ABC ，再根据三角形的面积公式求得即可．【详解】解：△AD 是△ABC 的中线，S △ABC =24，△S △ABD =12S △ABC =12，同理，BE 是△ABD 的中线，612BDE ABD SS ==，△S △BDE =12BD •EF ，△12BD •EF =6，即1462EF ⨯⨯= △EF =3．故答案为：3．【点睛】此题考查了三角形的面积，三角形的中线特点，理解三角形高的定义，根据三角形的面积公式求解，是解题的关键．14．90°或50°【分析】分高AD 在△ABC 内部和外部两种情况讨论求解即可．【详解】解：△如图1，当高AD 在△ABC 的内部时，△BAC =△BAD +△CAD =70°+20°=90°；△如图2，当高AD 在△ABC 的外部时，△BAC =△BAD -△CAD =70°-20°=50°，综上所述，△BAC 的度数为90°或50°．故答案为：90°或50°．【点睛】本题考查了三角形的高线，难点在于要分情况讨论．15． 所对边的中点 线段 ＝ AC【分析】根据三角形中线的定义，即可求解．【详解】解：连结三角形的一个顶点和它所对边的中点的线段叫做三角形这边上的中线．△BE 是ABC 中AC 边上的中线， △12AE EC AC == 故答案为：所对边的中点；线段；＝；AC ；【点睛】本题主要考查了三角形的中线，熟练掌握连结三角形的一个顶点和它所对边的中点的线段叫做三角形这边上的中线是解题的关键．16．3.【分析】如图，连接,,,OC OD CD 证明//,CD AB 再证明32OCD S S π=阴影扇形=，从而可以列方程求解半径． 【详解】解：如图，连接,,,OC OD CD点C 、D 分别是半圆AOB 上的三等分点，60,AOC COD DOB ∴∠=∠=∠=︒,OC OD =COD ∴为等边三角形，60,OCD ∴∠=︒,AOC DCO ∴∠=∠//,CD AB ∴,COD BCD S S ∴=32OCD S S π∴=阴影扇形=， 2603,3602OA ππ•∴= 解得：3,OA = （负根舍去），故答案为：3.【点睛】本题考查的圆的基本性质，弧，弦，圆心角之间的关系，平行线的判定与性质，扇形面积的计算，掌握以上知识是解题的关键．17．(1)25BAC ∠=︒；(2)8BC =【分析】（1）先利用互余计算出△BAE ＝50°，再利用角平分线的定义得到△BAC ＝12△BAE ＝25°；（2）先根据三角形面积公式得出DC ，利用D 是BC 的中点得到BC 即可．（1）解：△△B ＝40°，△E ＝90°，△△BAE ＝90°﹣40°＝50°，△AC 是△BAE 的角平分线，△△BAC ＝12△BAE ＝25°；（2）△S △ADC ＝12DC •AE ， △12×DC ×8＝16，△DC ＝4，△D 是BC 的中点，△BC ＝2CD ＝8.【点睛】本题考查了角平分线的定义，线段的中点，角平分线的定义的正确运用是解题的关键． 18．48AC =，28AB =【分析】由题意可得60AC CD +=，40AB BD +=，由中线的性质得244AC BC CD BD ===，故可求得48AC =，即可求得28AB =． 【详解】由题意知100AC CD BD AB +++=，60AC CD +=，40AB BD +=△2AC BC =，D 为BC 中点△244AC BC CD BD === △156044AC CD AC AC AC +=+== 即460485AC =⨯= 则BC =24，CD =BD =12则40401228AB BD =-=-=且28＞24符合题意．【点睛】本题考查了中线的性质，中线是三角形中从某边的中点连向对角的顶点的线段．19．(1)4根火柴棒不能搭成三角形(2)8根火柴棒能搭成一种三角形，12根火柴棒能搭成三种不同的三角形，画图见解析【分析】（1）把4分成3个数只能分成1，1，2三个数，故4根火柴棒不能搭成三角形；（2）利用三角形三边关系定理求解即可．（1）解：△把4分成3个数只能分成1，1，2三个数，而1+1＝2，△4根火柴棒不能搭成三角形；（2）△ 8根火柴棒能搭成一种三角形，示意图如下：△12根火柴棒能搭成三种不同的三角形，其边长分别为：(4，4，4)，(5，5，2)，(3，4，5)，示意图如下：【点睛】本题主要考查了三角形三边关系定理：任意两边之和大于第三边，任意两边之差小于第三边．20．(1)见解析(2)见解析(3)见解析【分析】（1）按要求分别画出平移A、B、C三点后的点D、E、F，并依次连接，即得到△ABC平移后的△DEF；（2）按要求画即可；（3）作三格点1P、2P、3P，使CP1=CP3=BP2=3即可．（1）平移后的△DEF如下图所示：（2）所画的高BH如下图所示：（3）由于CP1=CP3=BP2=3，则此三点1P、2P、3P满足题意．【点睛】本题考查了作图：作图形的平移，画三角形边上的高、三角形的面积，学会利用数形结合是解题的关键．。
三角形高,中线,角平分线综合应用题讲级
三角形高,中线,角平分线综合应用题讲级摘要：1.三角形高、中线、角平分线的概念及性质2.三角形高、中线、角平分线的综合应用方法3.解题步骤与实例分析正文：在几何学中，三角形的高、中线、角平分线是常见的线段类型，它们在解决三角形问题中具有重要作用。
以下将介绍这三者之间的关系及如何综合应用。
一、三角形高、中线、角平分线的概念及性质1.三角形高：从三角形一个顶点向对边作垂线，顶点和垂足之间的线段称为三角形的高。
高分为顶角平分线、底边上的高和腰上的高。
2.三角形中线：三角形两个顶点之间的中点连线，称为三角形的中线。
中线把三角形分成两个等面积的三角形。
3.三角形角平分线：从一个顶点向对边作射线，射线与对边的交点称为角平分线。
角平分线把顶点与对边的角分成两个相等的角。
二、三角形高、中线、角平分线的综合应用方法1.利用三角形高、中线、角平分线解决三角形面积问题：已知三角形的一条边和该边上的高，可以求得三角形的面积。
2.利用三角形高、中线、角平分线解决三角形角度问题：已知三角形的一个角和该角的角平分线，可以求得这个角的度数。
3.利用三角形高、中线、角平分线解决三角形形状问题：判断三角形是否为等腰三角形、直角三角形等。
三、解题步骤与实例分析1.读题，了解题意，找出已知条件和所求问题。
2.根据已知条件，找出三角形高、中线、角平分线的关系。
3.运用几何知识，建立解题方程（组）。
4.解方程（组），求解未知量。
5.检验答案，判断是否符合题意。
以下举一个实例进行分析：已知三角形ABC中，AB=AC，BC=2，AD是高，求角B的大小。
解：1.读题，了解题意，找出已知条件和所求问题。
2.根据已知条件，得出三角形ABC是等腰三角形，AD是高。
3.利用等腰三角形性质，得出∠ADB=∠ADC。
4.利用三角形面积公式，得出AB×AD=BC×AD，即AB=2AD。
5.解方程，得出AD=1，AB=2。
6.利用正弦定理，求解∠B的大小。
三角形的高、中线角平分线知识点与练习
精心整理
三角形的高，中线，角平分线知识点及练习
班级： 姓名：
知识点一：认识并会画三角形的高线，利用其解决相关问题
1、作出下列三角形三边上的高：
上的中线，则有BD = =1）三角形的三条中线相交于角形的三条中线相交于三角形的 ；（3）钝角三
条中线相交于三角形的 ；（4）直角三角形的
相交于三角形的 ；（5）交点我们叫做三角形
的重心。
练习二：如图，D 、E 是边AC 的三等分点，
图中有 个三角形，
BD 是三角形 中 边上的中线，
BE是三角形中________上的中线；
知识点三：认识并会画三角形的角平分线，利用其解决相关问题
自学课本第5页三角形的角平分线并完成下列各题：
1、作出下列三角形三角的角平分线：
形的内部，并且相交于一点，其中说法正确的有（）．
A．1个 B．2个 C．3个 D．4个
3.如图，AD是△ABC的高，AE是△ABC的角平分线，AF是△ABC的中线，写出图
中所有相等的角和相等的线段。
4．在△ABC中，AB=AC，AC边上的中线BD把三角形的周长
A
C B D
E
F
分为12cm和15cm两部分，求三角形各边的长。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
4321EDCBA1CDB三角形的高、中线与角平分线11 如图，已知△ABC 中，AQ=PQ 、PR=PS 、PR ⊥AB 于R ，PS ⊥AC 于S ，有以下三个结论：①AS=AR ；②QP ∥AR ； ③△BRP ≌△CSP ，其中( )．(A)全部正确 (B)仅①正确 (C)仅①、②正确 (D)仅①、③正确2、 如图，点E 在BC 的延长线上，则下列条件中，不能判定AB ∥CD 的是( )A. ∠3=∠4B.∠B=∠DCEC.∠1=∠2.D.∠D+∠DAB=180° 3．如图，ΔACB 中，∠ACB=900，∠1=∠B.（1）试说明 CD 是ΔABC 的高；（2）如果AC=8，BC=6，AB=10，求CD 的长。
4如图，直线DE 交△ABC 的边AB 、AC 于D 、E ， 交BC 延长线于F ，若∠B ＝67°，∠ACB ＝74°， ∠AED ＝48°，求∠BDF 的度数5、如图：∠1＝∠2＝∠3，完成说理过程并注明理由： 因为 ∠1＝∠2所以 ____∥____ ( ) 因为 ∠1＝∠3所以 ____∥____ ( )6．以下列各组线段为边，能组成三角形的是（ ） A ．2cm ，3cm ，5cm B ．5cm ，6cm ，10cm C ．1cm ，1cm ，3cm D ．3cm ，4cm ，9cmA．17 B．22 C．17或22 D．138．适合条件∠A=12∠B=13∠C的△ABC是（）A．锐角三角形 B．直角三角形 C．钝角三角形 D．等边三角形9．已知等腰三角形的一个角为75°，则其顶角为（）A．30° B．75° C．105° D．30°或75°10．一个多边形的内角和比它的外角的和的2倍还大180°，这个多边形的边数是（） A．5 B．6 C．7 D．811．三角形的一个外角是锐角，则此三角形的形状是（）A．锐角三角形 B．钝角三角形 C．直角三角形 D．无法确定12．三角形的三边长分别为5，1+2x，8，则x的取值范围是________．13．如图，BD平分∠ABC，DA⊥AB，∠1=60°，∠BDC=80°，求∠C的度数．初一三角形的高、中线与角平分线21 如图，BC⊥CD，∠1=∠2=∠3，∠4=60°，∠5=∠6．（1）CO是△BCD的高吗？为什么？（2）∠5的度数是多少？（3）求四边形ABCD各内角的度数．2．△ABC中，∠A=50°，∠B=60°，则∠A＋∠C=________．3 ．已知三角形的三个内角的度数之比为1：2：3，则这个三角形是（）A．锐角三角形 B．直角三角形 C．钝角三角形 D．不能确定4．△ABC中，∠A=∠B+∠C，则∠A=______度．5．如图∠1+∠2+∠3+∠4=______度．6．如图，△ABC中，AD是BC上的高，AE平分∠BAC，∠B=75°，•∠C=45°，求∠DAE与∠AEC的度数．7．以下说法错误的是（）6题A．三角形的三条高一定在三角形内部交于一点B．三角形的三条中线一定在三角形内部交于一点C．三角形的三条角平分线一定在三角形内部交于一点D．三角形的三条高可能相交于外部一点8．如果一个三角形的三条高的交点恰好是这个三角形的一个顶点，•那么这个三角形是（）A．锐角三角形 B．直角三角形 C．钝角三角形 D．不能确定9．如图，BD=1BC，则BC边上的中线为______，△ABD的面积=_____的面积．2(9)10．如图，△ABC中，高CD、BE、AF相交于点O，则△BOC•的三条高分别为线段________．（10）初一三角形的高、中线与角平分线31．下列图形中具有稳定性的是（）A．梯形 B．菱形 C．三角形 D．正方形2．如图3，AD是△ABC的边BC上的中线，已知AB=5cm，AC=3cm，求△ABD•与△ACD的周长之差．3．如图，∠BAD=∠CAD，AD⊥BC，垂足为点D，且BD=CD．•可知哪些线段是哪个三角形的角平分线、中线或高？4．如图5，在等腰三角形ABC中，AB=AC，一腰上的中线BD将这个等腰三角形的周长分为15和6两部分，求该等腰三角形的腰长及底边长．5．有一块三角形优良品种试验基地，如图所示，•由于引进四个优良品种进行对比试验，需将这块土地分成面积相等的四块，请你制定出两种以上的划分方案供选择（画图说明）．6．如图，在△ABC中，D、E分别是BC、AD的中点，S△ABC=4cm2，求S△ABE．7．如图，在锐角△ABC中，CD、BE分别是AB、AC上的高，•且CD、BE交于一点P，若∠A=50°，则∠BPC的度数是（）8如图7-1-2-9，AD是△ABC的角平分线，DE∥AB，DF∥AC，EF交AD于点O．请问：DO是△DEF的角平分线吗？如果是，请给予证明；如果不是，请说明理由．初一三角形的高、中线与角平分线41．若三角形的外角中有一个是锐角，则这个三角形是________三角形．2．△ABC中，若∠C-∠B=∠A，则△ABC的外角中最小的角是______（填“锐角”、3．如图1，x=______．(1) (2) (3)4．如图2，△ABC中，点D在BC的延长线上，点F是AB边上一点，延长CA到E，连EF，则∠1，∠2，∠3的大小关系是_________．5．如图3，在△ABC中，AE是角平分线，且∠B=52°，∠C=78°，求∠AEB的度数．7．如图所示，在△ABC中，AB=AC，AD=AE，∠BAD=60°，则∠EDC=______．8．一个零件的形状如图7-2-2-6所示，按规定∠A应等于90°，∠B、∠D应分别是30°和20°，李叔叔量得∠BCD=142°，就断定这个零件不合格，你能说出道理吗？9．（1）如图（1），求出∠A+∠B+∠C+∠D+∠E+∠F的度数；（2）如图（2），求出∠A+∠B+∠C+∠D+∠E+∠F的度数．11．如图，BD、CD分别是△ABC的两个外角∠CBE、∠BCF•的平分线，试探索∠D与∠A之间的数量关系．12 如图，BD为△ABC的角平分线，CD为△ABC的外角∠ACE的平分线，它们相交于点D ，试探索∠BDC与∠A之间的数量关系．7．3 多边形及其内角和1．四边形ABCD中，如果∠A+∠C+∠D=280°，则∠B的度数是（）A．80° B．90° C．170° D．20°2．一个多边形的内角和等于1080°，这个多边形的边数是（）A．9 B．8 C．7 D．63．内角和等于外角和2倍的多边形是（）A．五边形 B．六边形 C．七边形 D．八边形4．六边形的内角和等于_______度．5．正十边形的每一个内角的度数等于______，每一个外角的度数等于_______．6．如图，你能数出多少个不同的四边形？7．四边形的四个内角可以都是锐角吗？可以都是钝角吗？可以都是直角吗？•为什么？8．求下列图形中x的值：综合创新作业9．（综合题）已知：如图，在四边形ABCD中，∠A=∠C=90°，BE平分∠ABC，•DF平分∠ADC．BE与DF有怎样的位置关系？为什么？10．（应用题）有10个城市进行篮球比赛，每个城市均派3个代表队参加比赛，规定同一城市间代表队不进行比赛，其他代表队都要比赛一场，问按此规定，•所有代表队要打多少场比赛？11．（创新题）如图，以五边形的每个顶点为圆心，以1为半径画圆，求圆与五边形重合的面积．12．（1）（2005年，南通）已知一个多边形的内角和为540°，则这个多边形为（） A．三角形 B．四边形 C．五边形 D．六边形（2）（2005年，福建泉州）五边形的内角和等于_______度．13．（易错题）一个多边形的每一个顶点处取一个外角，这些外角中最多有钝角（• ） A．1个 B．2个 C．3个 D．4个培优作业14．（探究题）（1）四边形有几条对角线？五边形有几条对角线？六边形有几条对角线？……猜想并探索：n边形有几条对角线？（2）一个n边形的边数增加1，对角线增加多少条？15．（开放题）如果一个多边形的边数增加1，•那么这个多边形的内角和增加多少度？若将n边形的边数增加1倍，则它的内角和增加多少度？数学世界攻其不备壁虎在一座油罐的下底边沿A处．它发现在自己的正上方──油罐上边缘的B•处有一只害虫．壁虎决定捕捉这只害虫．为了不引起害虫的注意，它故意不走直线，而是绕着油罐，沿着一条螺旋路线，从背后对害虫进行突然袭击如图7-3-5．结果，•壁虎的偷袭得到成功，获得了一顿美餐．请问：壁虎沿着螺旋线爬行是最短的路程吗（线段AB除外）？答案:1．A 点拨：∠B=360°-（∠A+∠C+∠D）=360°-280°=80°．故选A．2．B 点拨：设这个多边形的边数为n，则（n-2）·180=1080．解得n=8．故选B．3．B 点拨：设这个多边形的边数为n，根据题意，得（n-2）·180=2×360．解得n=6．故选B．4．7205．144°；36°点拨：正十边形每一个内角的度数为：(102)18010-⨯︒=144°，每一个外角的度数为：180°-144°=36°．6．有27个不同的四边形．7．解：四边形的四个内角不可以都是锐角，不可以都是钝角，可以都是直角．因为四边形的内角和为360°，如果四个内角都是锐角或都是钝角，•则内角和小于360°或大于360°，与四边形的内角和为360°矛盾．•所以四个内角不可以都是锐角或都是钝角．若四个内角都是直角，则四个内角的和等于360°，与内角和定理相符，所以四个内角可以都是直角．8．解：（1）90+70+150+x=360．解得x=50．（2）90+73+82+（180-x）=360．解得x=65．（3）x+（x+30）+60+x+（x-10）=（5-2）×180．解得x=115．9．解：BE∥DF．理由：∵∠A=∠C=90°，∴∠A+∠C=180°．∴∠ABC+∠ADC=360°-180°=180°．∵∠ABE=12∠ABC，∠ADF=12∠ADC，∴∠ABE+∠ADF=12（∠ABC+∠ADC）=12×180°=90°．又∵∠ABE+∠AEB=90°，∴∠AEB=∠ADF，∴BE∥DF（同位角相等，两直线平行）．10．解：12n（n-3）=12×10×（10-3）=12×10×7=35（场）．答：按此规定，所有代表队要打35场比赛．点拨：问题类似于求多边形对角线的个数．11．解：（5-2）×180°÷360°×12=1.5．点拨：不能直接求出扇形的度数，用整体法圆与五边形重合部分的角度和正好是五边形的内角和．12．（1）C 点拨：设这个多边形的边数为n，依题意，得（n-2）×180°=540°，解得n=5，故选C．（2）540 点拨：（n-2）×180°=（5-3）×180°=540°．13．C14．解：（1）四边形有2条对角线；五边形有5条对角线；六边形有9条对角线；……n边形有(3)2n n-条对角线．（2）当n边形的边数增加1时，对角线增加（n-1）条．点拨：从n边形的一个顶点出发，向其他顶点共可引（n-3）条对角线，n个顶点共可引n（n-3）条，但这些对角线每一条都重复了一次，故n边形的对角线条数为(3)2n n-．15．180°，n·180°．数学世界答案:是最短的路程．可用纸板做一个模型，沿AB剪开便可看出结论．。