信号与系统特解举例
合集下载
安徽大学信号系统例题分析
现在的响应=现在的激励+以前的激励 所以该系统为因果系统。
微分方程r (t ) = e (t ) + e (t + 2)代表的系统是否是因果 系统。
t=0
r (0 ) = e (0 ) + e (+ 2 )
未来的激励 所以该系统为非因果系统。
X
第
例2-2-5
t < 0开关S处于1的位置而且已经 给定如图所示电路， 达到稳态。当t = 0时S由1转向2。建立电流i ( t )的微分 方程并求解i ( t )在t ≥ 0时的变化。
3 页
当e1 ( t ) + e2 ( t ) 同时作用于系统时，若该系统为线性系统， 应有
d [r1 (t ) + r2 (t )] + 10[r1 (t ) + r2 (t )] + 5 = e1 (t ) + e2 (t ) dt t>0 ( 5)
(3)+(4)得
d [r1 (t ) + r2 (t )] + 10[r1 (t ) + r2 (t )] + 10 = e1 (t ) + e2 (t ) dt t>0 ( 6)
f ( − t ) → f ( t ) 倒置
f ( t ) = 4δ ( t + 1)
(4) t O 1 2 3 6
X
第
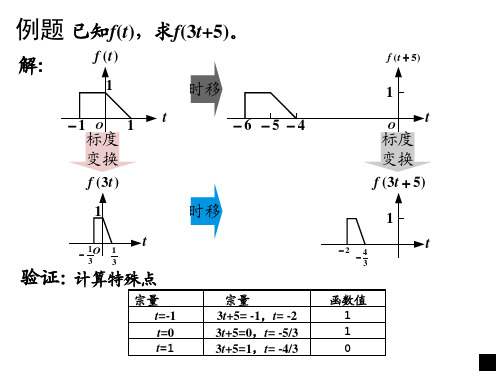
例1-5-1 求f(t)的奇分量和偶分量
f (t ) f (− t )
1 页
O
t
O
t
fe (t ) O t O
fo (t ) t
X
第
例1-6-1
d e( t ) d r (t ) d 2 r (t ) +3 + 2r ( t ) = + e( t ) 2 dt dt dt
信号与系统 典型公式
(八) 直流信号 (二)对称性
( t )e
j t
dt 1
F [1] 2 ( )
若f (t ) F ( )则F (t ) 2f ( )即F F (t ) 2 f ( )
(四)尺度变换特性
1 F [ f (at )] F( ) a a
若
t2
t1
f1 ( t ) f 2 ( t )dt 0 (p326式(6-53))
则称f1(t)与f2(t)在区间（t1,t2）上(相互)正交。 对复值函数f1(t)，f2(t)(p329)
f1 ( t ), f 2 ( t )正交 f1 ( t ) f *2 ( t )dt 0
更一般的三角函数形式傅里叶级数（FS）
f (t ) a 0 [a n cos( n 1 t ) b n sin( n 1 t )]
n 1
f (t) c0 cn cos( n1t n ) d 0 d n sin( n1t n )
n 1 n 1
f(t)的直流分量=其任意周期的直流分量
f(t)=fD(t)+fA(t)，
f(t)的功率=fD(t)的功率+fA(t)功率 三、偶分量与奇分量分解
f(t)=fe(t)+fo(t)
f(t)的功率=fe(t)功率+fo(t)功率 且
f (t ) f ( t ) f（t） e 2
f (t ) f ( t ) f（t） o 2
时域卷积定理 若
F[ f1 (t )] F1 ( )
F[ f2 (t )] F2 ()
则
F[ f1 (t )* f2 (t )] F1 () F2 ()
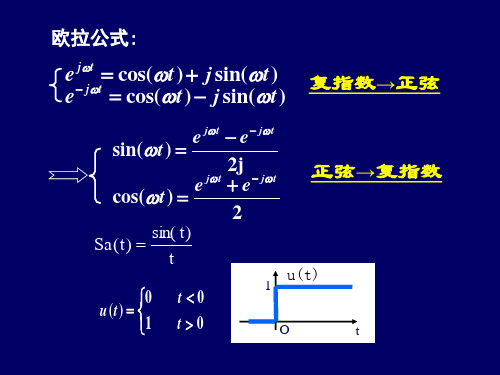
( t )e
j t
dt 1
F [1] 2 ( )
若f (t ) F ( )则F (t ) 2f ( )即F F (t ) 2 f ( )
(四)尺度变换特性
1 F [ f (at )] F( ) a a
若
t2
t1
f1 ( t ) f 2 ( t )dt 0 (p326式(6-53))
则称f1(t)与f2(t)在区间（t1,t2）上(相互)正交。 对复值函数f1(t)，f2(t)(p329)
f1 ( t ), f 2 ( t )正交 f1 ( t ) f *2 ( t )dt 0
更一般的三角函数形式傅里叶级数（FS）
f (t ) a 0 [a n cos( n 1 t ) b n sin( n 1 t )]
n 1
f (t) c0 cn cos( n1t n ) d 0 d n sin( n1t n )
n 1 n 1
f(t)的直流分量=其任意周期的直流分量
f(t)=fD(t)+fA(t)，
f(t)的功率=fD(t)的功率+fA(t)功率 三、偶分量与奇分量分解
f(t)=fe(t)+fo(t)
f(t)的功率=fe(t)功率+fo(t)功率 且
f (t ) f ( t ) f（t） e 2
f (t ) f ( t ) f（t） o 2
时域卷积定理 若
F[ f1 (t )] F1 ( )
F[ f2 (t )] F2 ()
则
F[ f1 (t )* f2 (t )] F1 () F2 ()
信号与系统_2.3-2.4
ቤተ መጻሕፍቲ ባይዱ
vR1 (t ) R1i(t )
d vL (t ) L iL (t ) dt
列节点方程：
iC (t ) iL (t ) i(t ) 0
R1i(t ) vC (t ) e(t ) 0
d L iL (t ) iL (t ) R2 vC (t ) 0 dt d C vC (t ) iL (t ) i (t ) 0 dt d iC (t ) C vC (t ) dt
a2 b 7a 12 c 7b 10a 8
r (0 ) r (0 ) a 2 d d r (0 ) r (0 ) b 2 dt dt d2 d2 r (0 ) 2 r (0 ) c 2 2 dt dt
4 14 r (0 ) 2 r (0 ) 2 5 5 d d r (0 ) 2 r (0 ) 2 dt dt
d y(t ) ak dtk 0 k 0
即系统方程为齐次方程，其解应该是齐次解。解中的待定 系数起始状态确定。 由于没有输入作用于系统，系统在t=0时刻状态不会发 生改变，此时t=0-与t=0+的状态应该是相同的。
N
k
例1、设系统方程与起始条件如下，试求系统的响应y(t)。
y(t ) 3 y(t ) 2 y(t ) 0
此微分方程的全解即系统的完全响应, 由齐次解 和特解组成
r (t ) rh (t ) rp (t )
常用激励信号对应的特解形式 激励信号 e(t )
E
p
特解 rp (t )
B
t
B1t B2t
p
p1
Bpt Bp1
e t
cos(t ) sin(t )
vR1 (t ) R1i(t )
d vL (t ) L iL (t ) dt
列节点方程：
iC (t ) iL (t ) i(t ) 0
R1i(t ) vC (t ) e(t ) 0
d L iL (t ) iL (t ) R2 vC (t ) 0 dt d C vC (t ) iL (t ) i (t ) 0 dt d iC (t ) C vC (t ) dt
a2 b 7a 12 c 7b 10a 8
r (0 ) r (0 ) a 2 d d r (0 ) r (0 ) b 2 dt dt d2 d2 r (0 ) 2 r (0 ) c 2 2 dt dt
4 14 r (0 ) 2 r (0 ) 2 5 5 d d r (0 ) 2 r (0 ) 2 dt dt
d y(t ) ak dtk 0 k 0
即系统方程为齐次方程，其解应该是齐次解。解中的待定 系数起始状态确定。 由于没有输入作用于系统，系统在t=0时刻状态不会发 生改变，此时t=0-与t=0+的状态应该是相同的。
N
k
例1、设系统方程与起始条件如下，试求系统的响应y(t)。
y(t ) 3 y(t ) 2 y(t ) 0
此微分方程的全解即系统的完全响应, 由齐次解 和特解组成
r (t ) rh (t ) rp (t )
常用激励信号对应的特解形式 激励信号 e(t )
E
p
特解 rp (t )
B
t
B1t B2t
p
p1
Bpt Bp1
e t
cos(t ) sin(t )
信号与系统第二章例题
r (0 ) 2 r (0 ) 3 r (0 ) r (0 ) 2
代入r (t ) Ae3t A2et 3e2t 1
A1 A2 3 2 得 3 A1 A2 6 3
r (t ) -4e3t 3et 3e2t
解：1）求自由响应的形式
r '' (t ) 4r ' (t ) 3r (t ) 0
特征方程为： 2 4 3 0 1 3, 2 1
rh (t ) Ae3t A2et 1
2）求强迫响应
利用筛选 特性
e(t ) e2t u(t ) e '(t ) 2e2t u(t ) e2t (t ) 2e2t u(t ) (t )
0 t 0
8
代入方程得
a 2 b 4a 1 c 4b 3a 0
a (t ) b 4a) (t ) (c 4b 3a)u (t ) （ 2 (t ) (t )
a 2 b 7 c 22
4 B 8B 3B 3
rp (t ) 4Be2t
B 3
rp (t ) 3e2t
3）求完全响应
r(t ) rh (t ) rp (t ) Ae3t A2et 3e2t 1
利用冲激函数匹配法求初始条件r (0 )和r(0 )
r '' (t ) 4r ' (t ) 3r (t ) 2 (t ) 3u(t ) r (t ) a (t ) bu (t )
1 3t 5 t (e e )u (t ) 2
注意：1、积分上下限问题； 2、积分结果的始终点问题。
信号与系统讲义-2
f (t) u 3 10
p
u pf (t) 2p 10
u(t) (Ae5t B)U(t)
2 du(t) 10u(t) df (t)
dt
dt
u(t) 5Ae5t U(t) (A B)(t)
2(A B) 1 B0
u(t) 1 e5tU(t)V 2
H
(
p)
2p2 8p 3 ( p 1)( p 3)2
求系统的响应 y(t)。
解： D(p) (p 1)(p 3)2 0 p1 1 p2 p3 3
y0 (t) K1e t K 2e3t K 3te3t
y0 (0 ) K1 K2 =2 y0 (0 ) K1 3K 2 K3=1
3、共轭复根：(欠阻尼) 即 R 2 L C
uc Aet cos(dt ) Us
R 2L
,
d
02 2 , 0
1 LC
4
三、 RLC串联电路全响应
d 2uc dt 2
R L
duc dt
1 LC
uc
1 LC Us
(二阶常系数线性非齐次微分方程)
t<0 , K在2,有 uc (0 ) U0
C
uc Aep1t Be p2t Us
2、重根：(临界阻尼) 即
R2
L C
（自然频率、固有频率）
uc (A Bt)ept Us
3、共轭复根：(欠阻尼) 即 R 2 L C
uc Aet cos(dt ) Us
R 2L
d 02 2
信号与系统-第2章例题
d2y dy 5 6 y (t ) 4 f (t ) 2 dt dt
ቤተ መጻሕፍቲ ባይዱ
t0
系统的特征方程为 系统的特征根为
s 2 5s 6 0 s1 2，s2 3
yx (t ) K1e—2t K2e—3t
y(0)=yx(0)=K1+K2=1 y' (0)= y'x(0)= 2K13K2 =3
r2 (t ) rzi (t ) 2rzs (t ) [e3t 2sin(2t )]u(t )
解得
rzi (t ) 3e3t u(t )
rzs (t ) [e3t sin(2t )]u(t )
r3 (t ) rzi (t ) rzs (t t0 )
冲激平衡法 冲激平衡法是指为保持系统对应的动态方程式的 恒等，方程式两边所具有的冲激信号函数及其各阶导 数必须相等。根据此规则即可求得系统的冲激响应h(t)。
例：
已知某线性非时变系统的动态方程式为
dy (t ) 3 y (t ) 2 f (t ) dt
试求系统的冲激响应h(t)。
(t 0)
[解] 系统的特征方程为 系统的特征根为 y(0)=yx(0)=K1=1; y'(0)= y'x(0)= 2K1+K2 =3
s 2 4s 4 0
s1 s2 2
（两相等实根）
yx (t ) K1e—2t K2te—2t
解得 K1 =1, K2=5
yx (t ) e2t 5te2t , t 0
2) 求非齐次方程y‘’(t)+6y‘(t)+8y(t) = f(t)的特解yp(t) 由输入f (t)的形式，设方程的特解为
信号与系统_2.5-2.6
−∞
y (t ) = =
∞
−∞ ∞
∫ x ( τ ) h (t − τ ) d τ =
−(t − τ)
∞
−∞
u ( τ ) e − ( t − τ ) u (t − τ ) d τ ∫
u (τ)
1
0
−∞
∫e
u ( τ )u (t − τ ) d τ
以上积分式中，积分变量是 。 以上积分式中，积分变量是τ。 式中的u(τ)u(t-τ)决定了积分的上下 式中的 决定了积分的上下 也确定了积分结果的定义区间。 限，也确定了积分结果的定义区间。
= δ(t ) − e −2t u (t )
一般的， 一般的，对于如下形式的微分方程
ak y ( k ) (t ) =∑ bk x( k ) (t ) ∑
k =0 k =0 N M
当N>M，单位冲激响应中只有自由响应；当N≤M，则还 ，单位冲激响应中只有自由响应； ， 有受迫响应分量：冲激和冲激的各阶导数。 有受迫响应分量：冲激和冲激的各阶导数。
α 2 = −2
h(t ) = A1e − t + A2 e −2t h(t ) = ( A1e −t + A2 e −2t )u (t )
确定特解，并确定t=0 时刻的初始条件。 ⑵ 确定特解，并确定 +时刻的初始条件。 比较以上方程两边可设： 比较以上方程两边可设：在t=0时刻 时刻
h′′(t ) = B1δ ′(t ) + B0δ (t ) + B∆u (t ) 于是在t=0时刻 于是在 时刻 h′(t ) = B1δ (t ) + B0 ∆u (t ) h(t ) = B1∆u (t )
rzs (t ) = ∫ e(τ )h(t −τ )dτ
y (t ) = =
∞
−∞ ∞
∫ x ( τ ) h (t − τ ) d τ =
−(t − τ)
∞
−∞
u ( τ ) e − ( t − τ ) u (t − τ ) d τ ∫
u (τ)
1
0
−∞
∫e
u ( τ )u (t − τ ) d τ
以上积分式中，积分变量是 。 以上积分式中，积分变量是τ。 式中的u(τ)u(t-τ)决定了积分的上下 式中的 决定了积分的上下 也确定了积分结果的定义区间。 限，也确定了积分结果的定义区间。
= δ(t ) − e −2t u (t )
一般的， 一般的，对于如下形式的微分方程
ak y ( k ) (t ) =∑ bk x( k ) (t ) ∑
k =0 k =0 N M
当N>M，单位冲激响应中只有自由响应；当N≤M，则还 ，单位冲激响应中只有自由响应； ， 有受迫响应分量：冲激和冲激的各阶导数。 有受迫响应分量：冲激和冲激的各阶导数。
α 2 = −2
h(t ) = A1e − t + A2 e −2t h(t ) = ( A1e −t + A2 e −2t )u (t )
确定特解，并确定t=0 时刻的初始条件。 ⑵ 确定特解，并确定 +时刻的初始条件。 比较以上方程两边可设： 比较以上方程两边可设：在t=0时刻 时刻
h′′(t ) = B1δ ′(t ) + B0δ (t ) + B∆u (t ) 于是在t=0时刻 于是在 时刻 h′(t ) = B1δ (t ) + B0 ∆u (t ) h(t ) = B1∆u (t )
rzs (t ) = ∫ e(τ )h(t −τ )dτ
[信号与系统作业解答]第二章
rzi(t) 3rzi(t) 2rzi(t) 0 rzi(0 ) rzi(0 ) 2 rzi(0 ) rzi(0 ) 1
特征方程为 2 3 2 0 ，特征根为 1
1和 2
2。
所以rzi(t) C1e t C2e 2t, t 0
将 rzi(0 ) r (0 ) 2 和rzi(0 ) r(0 ) 1代入可求得
g(t) 1 e 12t cos 3 t 2
1 e 12t sin 3 t u(t)
3
2
由于系统的冲激响应h(t) h(t) e 12t cos 3 t
2
d g(t) ，所以系统的冲激响应为 dt
1 e 12t sin 3 t u(t)
3
2
3）系统的冲激响应满足方程
d dt
h(t)
2h(t)
(t) 3 (t)
电容两端电压不会发生跳变，vc(0 ) vc(0 ) 10V ，所以i(0 ) 0 ；
因此，电阻两端无电压，电感两端电压变成 10V，所以i (0 ) 10 。
（2）换路后系统的微分方程为
i (t) i (t) i(t) e (t) e(t) 20u(t)
t 0 时间内描述系统的微分方程为
i (t) i (t) i(t) 20 (t)
e(t) (1) 0 (2)
整理得：
2vo(t) 5vo(t) 5vo(t) 3vo(t) 2e (t)
2-4 已知系统相应的齐次方程及其对应的 0+状态条件，求系统的零输入响应。
1）
d2 dt 2
r(t)
2
d dt
r(t
)
2r(t)
0 ，给定r(0 )
1 ，r (0 )
2
特征方程为 2 3 2 0 ，特征根为 1
1和 2
2。
所以rzi(t) C1e t C2e 2t, t 0
将 rzi(0 ) r (0 ) 2 和rzi(0 ) r(0 ) 1代入可求得
g(t) 1 e 12t cos 3 t 2
1 e 12t sin 3 t u(t)
3
2
由于系统的冲激响应h(t) h(t) e 12t cos 3 t
2
d g(t) ，所以系统的冲激响应为 dt
1 e 12t sin 3 t u(t)
3
2
3）系统的冲激响应满足方程
d dt
h(t)
2h(t)
(t) 3 (t)
电容两端电压不会发生跳变，vc(0 ) vc(0 ) 10V ，所以i(0 ) 0 ；
因此，电阻两端无电压，电感两端电压变成 10V，所以i (0 ) 10 。
（2）换路后系统的微分方程为
i (t) i (t) i(t) e (t) e(t) 20u(t)
t 0 时间内描述系统的微分方程为
i (t) i (t) i(t) 20 (t)
e(t) (1) 0 (2)
整理得：
2vo(t) 5vo(t) 5vo(t) 3vo(t) 2e (t)
2-4 已知系统相应的齐次方程及其对应的 0+状态条件，求系统的零输入响应。
1）
d2 dt 2
r(t)
2
d dt
r(t
)
2r(t)
0 ，给定r(0 )
1 ，r (0 )
2
信号与系统(郑君里)第二版 讲义 第二章
第二章 连续时间系统的时域分析第一讲 微分方程的建立与求解一、微分方程的建立与求解对电路系统建立微分方程，其各支路的电流、电压将为两种约束所支配： 1.来自连接方式的约束：KVL 和KIL ，与元件的性质无关。
2.来自元件伏安关系的约束：与元件的连接方式无关。
例2-1 如图2-1所示电路，激励信号为，求输出信号。
电路起始电压为零。
图2－1解以输出电压为响应变量，列回路电压方程：所以齐次解为：。
因激励信号为，若，则，将其代入微分方程：所以，从而求得完全解：由于电路起始电压为零并且输入不是冲激信号，所以电容两端电压不会发生跳变，，从而若，则特解为，将其代入微分方程，并利用起始条件求出系数，从而得到：二、起始条件的跳变——从到1.系统的状态(起始与初始状态)(1)系统的状态：系统在某一时刻的状态是一组必须知道的最少量的数据，利用这组数据和系统的模型以及该时刻接入的激励信号，就能够完全确定系统任何时刻的响应。
由于激励信号的接入，系统响应及其各阶导数可能在t=0时刻发生跳变，所以以表示激励接入之前的瞬时，而以表示激励接入以后的瞬时。
(2)起始状态：，它决定了零输入响应，在激励接入之前的瞬时t=系统的状态，它总结了计算未来响应所需要的过去的全部信息。
(3)初始状态：跳变量,它决定了零状态响应，在激励接入之后的瞬时系统的状态。
(4)初始条件：它决定了完全响应。
这三个量的关系是：。
2.初始条件的确定（换路定律）电容电压和电感电流在换路（电路接通、断开、接线突变、电路参数突变、电源突变）瞬间前后不能发生突变，即是连续的。
时不变：时变：例电路如图2-2所示，t=0以前开关位于"1"已进入稳态，t=0时刻，开关自"1"转至"2"。
(1)试从物理概念判断、和、。
(2)写出t>0时间内描述系统的微分方程式,求的完全响应。
图2－2解(1)换路前电路处于稳态电感相当于短路，电感电流，电容相当于开路= 0，= = 0。
信号与系统 微分方程式的经典解法
或写为
t 0
1 1 C1 , C2 16 16
1 5t 1 t 1 t y (t ) e e te u (t ) 16 4 16
信号与系统
完全解中的齐次解称为系统的自由响应,特解称为系统的强迫响应.特 征方程根i(i=1,2,…,n)称为系统的“固有频率”(或“自由频率”) 上例中完全解的分解如下:
d2 d t y ( t ) 6 y ( t ) 5 y ( t ) e d t2 dt
y(0) y '(0) 0
解:
齐次方程为 特征方程： 特征根：
d2 d y ( t ) 6 y (t ) 5 y (t ) 0 2 dt dt
2 6 5 0
1 5，2 1
3B1 1 4 B1 3B2 2 2 B 2 B 3 B 0 2 3 1
联解得到
1 2 10 B1 , B2 , B3 3 9 27
所以，特解为
1 2 10 rp (t ) t 2 t 3 9 27
信号与系统
(2)
e(t ) et 将其代入方程的右端，可求得自由项为 可选 rp (t ) B这里， et。 B 是待定系数。
信号与系统
例：
给定微分方程式
d 2 r (t ) d r (t ) d e(t ) 2 3 r t e(t ) 2 dt dt dt
如果已知： (1) e(t ) t 2 ; (2) e(t ) et , 分别求两种情况下此方程的特解。 （ 1）
e(t ) t 2
当
t 2e很明显，
代入方程后有：
Bet 2Bet 3Bet et et
t 0
1 1 C1 , C2 16 16
1 5t 1 t 1 t y (t ) e e te u (t ) 16 4 16
信号与系统
完全解中的齐次解称为系统的自由响应,特解称为系统的强迫响应.特 征方程根i(i=1,2,…,n)称为系统的“固有频率”(或“自由频率”) 上例中完全解的分解如下:
d2 d t y ( t ) 6 y ( t ) 5 y ( t ) e d t2 dt
y(0) y '(0) 0
解:
齐次方程为 特征方程： 特征根：
d2 d y ( t ) 6 y (t ) 5 y (t ) 0 2 dt dt
2 6 5 0
1 5，2 1
3B1 1 4 B1 3B2 2 2 B 2 B 3 B 0 2 3 1
联解得到
1 2 10 B1 , B2 , B3 3 9 27
所以，特解为
1 2 10 rp (t ) t 2 t 3 9 27
信号与系统
(2)
e(t ) et 将其代入方程的右端，可求得自由项为 可选 rp (t ) B这里， et。 B 是待定系数。
信号与系统
例：
给定微分方程式
d 2 r (t ) d r (t ) d e(t ) 2 3 r t e(t ) 2 dt dt dt
如果已知： (1) e(t ) t 2 ; (2) e(t ) et , 分别求两种情况下此方程的特解。 （ 1）
e(t ) t 2
当
t 2e很明显，
代入方程后有：
Bet 2Bet 3Bet et et