信号与系统习题解答
信号与系统习题与答案
【填空题】(为任意值)是________ (填连续信号或离散信号),若是离散信号,该信号____(填是或不是)数字信号。
【填空题】是________ (填连续信号或离散信号),若是离散信号,该信号____(填是或不是)数字信号。
【填空题】信号________ (填是或不是),若是周期信号,周期为__pi/5__。
【填空题】系统为____(填线性或非线性)系统、____(填时变或非时变)系统、____(填因果或非因果)系统。
【填空题】系统为____(填线性或非线性)系统、____(填时变或非时变)系统、____(填因果或非因果)系统。
【简答题】判断下图波形是连续时间信号还是离散时间信号,若是离散时间信号是否为数字信号。
连续时间信号【简答题】判断下图波形是连续时间信号还是离散时间信号,若是离散时间信号是否为数字信号。
离散时间信号且为数字信号【简答题】判断信号是功率信号还是能量信号,若是功率信号,平均功率是多少?若是能量信号,能量为多少?功率信号平均功率为4.5【简答题】线性时不变系统具有哪些特性?均匀性、叠加性、时不变性、微分性、因果性。
【填空题】的函数值为____。
2【填空题】的函数值为____。
【填空题】假设,的函数值为____。
1【填空题】假设,的函数值为____。
【填空题】的函数值为____。
我的答案：第一空：e^2-26【填空题】已知,将____(填左移或右移)____可得。
右移个单位7【简答题】计算的微分与积分。
8【简答题】什么是奇异信号?我的答案：奇异信号是指函数本身或其导数或高阶导数具有不连续点（跳变点）。
9【简答题】写出如下波形的函数表达式。
我的答案：f(t)=u(t)+u(t-1)+u(t-2)10【简答题】已知信号的图形如图所示,画出的波形。
我的答案：【简答题】信号微分运算具有什么特点?举一个应用实例。
特点：微分凸显了信号的变化部分。
微分方程（包括偏微分方程和积分方程）把函数和代数结合起来，级数和积分变换解决数值计算问题。
信号系统(第3版)习题解答
信号系统(第3版)习题解答《信号与系统》（第3版）习题解析高等教育出版社目录第1章习题解析 (2)第2章习题解析 (6)第3章习题解析 (16)第4章习题解析 (23)第5章习题解析 (31)第6章习题解析 (41)第7章习题解析 (49)第8章习题解析 (55)第1章习题解析1-1 题1-1图示信号中，哪些是连续信号？哪些是离散信号？哪些是周期信号？哪些是非周期信号？哪些是有始信号？(c) (d)题1-1图解 (a)、(c)、(d)为连续信号；(b)为离散信号；(d)为周期信号；其余为非周期信号；(a)、(b)、(c)为有始（因果）信号。
1-2 给定题1-2图示信号f ( t )，试画出下列信号的波形。
[提示：f ( 2t )表示将f ( t )波形压缩，f (2t )表示将f ( t )波形展宽。
] (a) 2 f ( t - 2 )(b) f ( 2t )(c) f ( 2t ) (d) f ( -t +1 )题1-2图解 以上各函数的波形如图p1-2所示。
图p1-21-3 如图1-3图示，R 、L 、C 元件可以看成以电流为输入，电压为响应的简单线性系统S R 、S L 、S C ，试写出各系统响应电压与激励电流函数关系的表达式。
题1-3图解 各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅= tt i L t u L L d )(d )(= ⎰∞-=t C C i Ct u ττd )(1)(1-4 如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成，系统属于何种联接形式？试写出该系统的微分方程。
S R S L S C题1-4图解 系统为反馈联接形式。
设加法器的输出为x ( t )，由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有 )()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5 已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|，试判定该系统是否为线性时不变系统？解 设T 为系统的运算子，则可以表示为)()]([)(t f t f T t y ==不失一般性，设f ( t ) = f 1( t ) + f 2( t )，则)()()]([111t y t f t f T ==)()()]([222t y t f t f T ==故有)()()()]([21t y t f t f t f T =+=显然)()()()(2121t f t f t f t f +≠+即不满足可加性，故为非线性时不变系统。
信号与系统课后习题参考答案
1试分别指出以下波形是属于哪种信号？题图1-11-2 试写出题1-1 图中信号的函数表达式。
1-3 已知信号x1(t)与x2(t)波形如题图1-3 中所示，试作出下列各信号的波形图，并加以标注。
题图1-3⑴x1(t2)⑵ x1(1 t)⑶ x1(2t 2)⑷ x2(t 3)⑸ x2(t 2) ⑹x2(1 2t)2⑺x1(t) x2( t)⑻x1(1 t)x2(t 1)⑼x1(2 t) x2(t 4)21- 4 已知信号x1(n)与x2 (n)波形如题图1-4中所示，试作出下列各信号的波形图，并加以标注。
题图1-4⑴x1(2n 1) ⑵ x1(4 n)⑶ x1(n)2⑷ x2 (2 n)⑸ x2(n 2) ⑹ x2(n 2) x2( n 1)⑺x1(n 2) x2(1 2n)⑻x1(1 n) x2(n 4)⑼ x1(n 1) x2(n 3)1- 5 已知信号x(5 2t )的波形如题图1-5 所示，试作出信号x(t)的波形图，并加以标注。
题图1-51- 6 试画出下列信号的波形图：1⑴ x(t) sin( t) sin(8 t)⑵ x(t) [1 sin( t )] sin(8 t)21⑶x(t) [1 sin( t)] sin(8 t)⑷ x(t) sin( 2t )1-7 试画出下列信号的波形图：⑴ x(t)1 e t u(t) ⑵ x(t) e t cos10 t[u(t 1) u(t 2)]⑶ x(t)(2 e t)u(t)⑷ x(t) e (t 1)u(t)⑸ x(t)u(t22 9) ⑹ x(t)(t2 4)1-8 试求出以下复变函数的模与幅角，并画出模与幅角的波形图1j2 ⑴ X (j ) (1 e j2)⑵ X( j1 e j4⑶ X (j ) 11 ee j ⑷ X( j )试作出下列波形的奇分量、偶分量和非零区间上的平均分量与交流分量。
题图 1-10形图。
题图 1-141-15 已知系统的信号流图如下，试写出各自系统的输入输出方程。
(完整word版)信号与系统专题练习题及答案
信号与系统专题练习题一、选择题1．设当t 〈3时，x(t)=0，则使)2()1(t x t x -+-=0的t 值为 C 。
A t>-2或t>-1 B t=1和t=2 C t>—1 D t 〉-22．设当t 〈3时，x （t)=0，则使)2()1(t x t x -⋅-=0的t 值为 D 。
A t>2或t 〉-1 B t=1和t=2 C t>—1 D t>—23．设当t<3时，x(t ）=0，则使x （t/3)=0的t 值为 C 。
A t>3 B t=0 C t<9 D t=34．信号)3/4cos(3)(π+=t t x 的周期是 C 。
A π2 B π C 2/π D π/2 5．下列各表达式中正确的是 BA. )()2(t t δδ= B 。
)(21)2(t t δδ= C. )(2)2(t t δδ= D 。
)2(21)(2t t δδ=6. 已知系统的激励e(t)与响应r(t)的关系为:)1()(t e t r -= 则该系统为 B . A 线性时不变系统 B 线性时变系统 C 非线性时不变系统 D 非线性时变系统 7。
已知 系统的激励e(t ）与响应r （t)的关系为:)()(2t e t r = 则该系统为 C .A 线性时不变系统B 线性时变系统C 非线性时不变系统D 非线性时变系统8。
⎰∞-=t d ττττδ2sin )( A 。
A 2u （t ） B )(4t δ C 4 D 4u （t) 10. dt t t )2(2cos 33+⋅⎰-δπ等于 B 。
A 0 B —1 C 2 D —211．线性时不变系统输出中的自由响应的形式由 A 决定A 系统函数极点的位置；B 激励信号的形式;C 系统起始状态；D 以上均不对。
12．若系统的起始状态为0，在x （t)的激励下，所得的响应为 D . A 强迫响应;B 稳态响应；C 暂态响应;D 零状态响应。
信号与系统课后习题答案
习 题 一 第一章习题解答基本练习题1-1 解 (a) 基频 =0f GCD （15,6）=3 Hz 。
因此，公共周期3110==f T s 。
(b) )30cos 10(cos 5.0)20cos()10cos()(t t t t t f ππππ+==基频 =0f GCD （5, 15）=5 Hz 。
因此，公共周期5110==f T s 。
(c) 由于两个分量的频率1ω=10π rad/s 、1ω=20 rad/s 的比值是无理数，因此无法找出公共周期。
所以是非周期的。
(d) 两个分量是同频率的，基频 =0f 1/π Hz 。
因此，公共周期π==01f T s 。
1-2 解 (a) 波形如图1-2(a)所示。
显然是功率信号。
t d t f TP T TT ⎰-∞→=2)(21lim16163611lim 22110=⎥⎦⎤⎢⎣⎡++=⎰⎰⎰∞→t d t d t d T T T W(b) 波形如图1.2(b)所示。
显然是能量信号。
3716112=⨯+⨯=E J (c) 能量信号 1.0101)(lim101025=-===⎰⎰∞∞---∞→T t ttT e dt edt eE J(d) 功率信号，显然有 1=P W1-3 解 周期T=7 ，一个周期的能量为 5624316=⨯+⨯=E J 信号的功率为 8756===T E P W 1-5 解 (a) )(4)2()23(2t tt δδ=+； (b) )5.2(5.0)5.2(5.0)25(5.733-=-=----t e t e t et tδδδ(c) )2(23)2()3sin()2()32sin(πδπδπππδπ+-=++-=++t t t t 题解图1-2(a) 21题解图1-2(b) 21(d) )3()3()(1)2(-=----t e t t et δδε。
1-6 解 (a) 5)3()94()3()4(2-=+-=+-⎰⎰∞∞-∞∞-dt t dt t t δδ(b) 0)4()4(632=+-⎰-dt t t δ(c) 2)]2(2)4(10[)]42(2)4()[6(63632=+++-=+++-⎰⎰--dt t t dt t t t δδδδ(d)3)3(3)(3sin )(1010=⋅=⎰⎰∞-∞-dt t Sa t dt ttt δδ。
奥本海姆《信号与系统(第二版)》习题参考答案
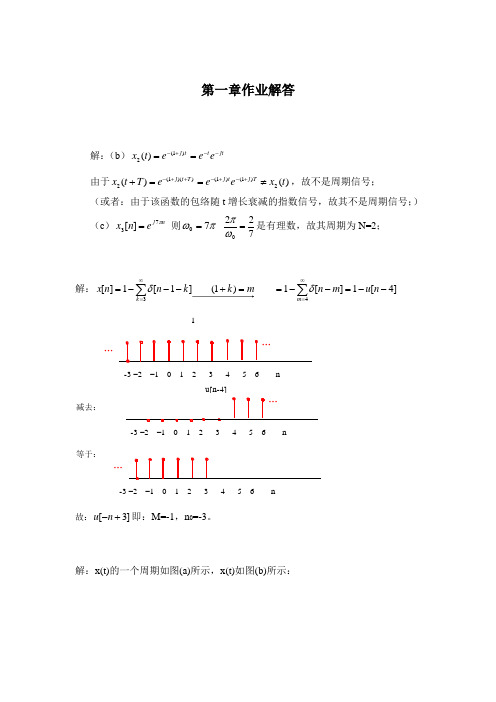
第一章作业解答解：（b ）jt t t j e e e t x --+-==)1(2)(由于)()(2)1()1())(1(2t x e e e T t x T j t j T t j ≠==++-+-++-，故不是周期信号；（或者：由于该函数的包络随t 增长衰减的指数信号，故其不是周期信号；） （c ）n j e n x π73][= 则πω70= 7220=ωπ是有理数，故其周期为N=2；解：]4[1][1)1(]1[1][43--=--==+---=∑∑∞=∞=n u m n mk k n n x m k δδ-3 –2 –1 0 1 2 3 4 5 6 n1…减去：-3 –2 –1 0 1 2 3 4 5 6 nu[n-4]等于：-3 –2 –1 0 1 2 34 5 6 n…故：]3[+-n u 即：M=-1，n 0=-3。
解：x(t)的一个周期如图(a)所示，x(t)如图(b)所示：而：g(t)如图(c)所示……dtt dx )(如图（d ）所示：……故：)1(3)(3)(--=t g t g dtt dx 则：1t ,0t 3,32121==-==；A A 1.15解：该系统如下图所示： 2[n]（1）]4[2]3[5]2[2]}4[4]3[2{21]}3[4]2[2{]3[21]2[][][1111111222-+-+-=-+-+-+-=-+-==n x n x n x n x n x n x n x n x n x n y n y即：]4[2]3[5]2[2][-+-+-=n x n x n x n y（2）若系统级联顺序改变，该系统不会改变，因为该系统是线性时不变系统。
（也可以通过改变顺序求取输入、输出关系，与前面做对比）。
解：（a ）因果性：)(sin )(t x t y =举一反例：当)0()y(,0int s x t =-=-=ππ则时输出与以后的输入有关，不是因果的；（b ）线性：按照线性的证明过程（这里略），该系统是线性的。
信号与系统复习题及答案
1．系统的激励是，响应为，若满足，则该系统为 线性、时不变、因果。
（是否线性、时不变、因果？）2．求积分的值为 5 。
3．当信号是脉冲信号时，其 低频分量 主要影响脉冲的顶部，其 高频分量 主要影响脉冲的跳变沿。
4．若信号的最高频率是2kHz ，则的乃奎斯特抽样频率为 8kHz 。
5．信号在通过线性系统不产生失真，必须在信号的全部频带内，要求系统幅频特性为 一常数相频特性为_一过原点的直线（群时延）。
6．系统阶跃响应的上升时间和系统的 截止频率 成反比。
7．若信号的，求该信号的。
8．为使LTI 连续系统是稳定的，其系统函数的极点必须在S 平面的 左半平面 。
9．已知信号的频谱函数是，则其时间信号为。
10．若信号的，则其初始值 1 。
二、判断下列说法的正误，正确请在括号里打“√”，错误请打“×”。
（每小题2分，共10分）1.单位冲激函数总是满足 （ √ ）2.满足绝对可积条件的信号一定存在傅立叶变换，不满足这一条件的信号一定不存在傅立叶变换。
（ × ）得分)t (e )t (r dt)t (de )t (r =dt )t ()t (212-+⎰∞∞-δf(t)f(t)t)f(23s F(s)=(s+4)(s+2)=)j (F ωj 3(j +4)(j +2)ωωω)s (H ））00(()j (F ωωδωωδω--+=f(t)01sin()t j ωπf(t)211)s (s )s (F +-==+)(f 0)()(t t -=δδ∞<⎰∞∞-dt t f )(3.非周期信号的脉冲宽度越小，其频带宽度越宽。
（ √ ）4.连续LTI 系统的冲激响应的形式取决于系统的特征根，于系统的零点无关。
（ √ ）5.所有周期信号的频谱都是离散谱，并且随频率的增高，幅度谱总是渐小的。
（ × ）三、计算分析题（1、3、4、5题每题10分，2题5分，6题15分，共60分）1.信号，信号，试求。
信号与系统第三版郑君里课后习题答案
信号与系统第三版郑君里课后习题答案第一章习题参考解1，判刑下列信号的类型解：()sin [()];y t A x t = 连续、模拟、周期、功率型信号 。
()()tt y t x ed τττ--∞=⎰连续、模拟、非周期、功率型信号。
()(2y n x n =） 离散、模拟、非周期、功率型信号。
()()y n n x n = 离散、模拟、非周期、功率型信号。
1－6，示意画出下列各信号的波形，并判断其类型。
(1) 0()s in ()x t A t ωθ=+ 连续、模拟、周期、功率型(2) ()t x t A e -= 连续、模拟、非周期、只是一个函数，不是物理量。
(3) ()c o s 0tx t ett -=≥ 连续、模拟、非周期、能量型 (4) ()2112,x t t t =+-≤≤ 连续、模拟、非周期、能量型(5) 4()(),0.5k x k k =≥ 离散、模拟、非周期、能量型(6) 0().j kx k eΩ= 离散、模拟、周期、功率型()s i n [()];()()()(2);()()tt y t A x t y t x ed y n x n y n n x n τττ--∞====⎰1－6题，1－4图。
t=-pi:1/200:pi;y1=1.5*sin(2*t+pi/6);subplot(4,1,1),plot(t,y1),title('1.5sin(2*t+pi/6)'),gridy2=2*exp(-t);subplot(4,1,2),plot(t,y2),title('2exp(-t)'),gridt1=0:1/200:2*pi;y3=10*exp(-t1).*cos(2*pi*t1);subplot(4,1,3),plot(t1,y3),title('10exp(-t1)cos(2*pi*t1)'),grid t2=-1:1/200:2;y4=2*t2+1;subplot(4,1,4),plot(t2,y4),title('2x+1'),grid习题1－6 5－6题n=0:pi/10:2*pi;y=(0.8).^n;subplot(4,1,1),stem(n,y,'fill'),title('(0.8)^n'),gridn1=0:pi/24:2*pi;y1=cos(2*pi*n1);y2=sin(2*pi*n1);subplot(4,1,2),stem3(y1,y2,n1,'fill'),title('exp[2*pi*n1'),gridsubplot(4,1,4),stem(n1,sin(2*pi*n1),'fill'),title('sin2pin1'),gridsubplot(4,1,3),stem(n1,cos(2*pi*n1),'fill'),title('cos2pin1)'),grid1－8，判断下列系统的类型。
信号与系统复习题(含答案)
.试题一一． 选择题（共10题，20分） 1、n j n j een x )34()32(][ππ+=，该序列是 。
A.非周期序列B.周期3=NC.周期8/3=ND. 周期24=N2、一连续时间系统y(t)= x(sint)，该系统是 。
A.因果时不变B.因果时变C.非因果时不变D.非因果时变 3、一连续时间LTI 系统的单位冲激响应)2()(4-=-t u e t h t ，该系统是 。
A.因果稳定B.因果不稳定C.非因果稳定D. 非因果不稳定4、若周期信号x[n]是实信号和奇信号，则其傅立叶级数系数a k 是 。
A.实且偶B.实且为奇C.纯虚且偶D. 纯虚且奇 5、一信号x(t)的傅立叶变换⎩⎨⎧><=2||02||1)(ωωω，，j X ，则x(t)为 。
A. t t 22sinB. tt π2sin C. t t 44sin D.t t π4sin6、一周期信号∑∞-∞=-=n n t t x )5()(δ，其傅立叶变换)(ωj X 为 。
A. ∑∞-∞=-k k )52(52πωδπ B. ∑∞-∞=-k k )52(25πωδπC. ∑∞-∞=-k k )10(10πωδπD. ∑∞-∞=-k k)10(101πωδπ7、一实信号x[n]的傅立叶变换为)(ωj e X ，则x[n]奇部的傅立叶变换为 。
A.)}(Re{ωj e X j B. )}(Re{ωj e XC. )}(Im{ωj e X j D. )}(Im{ωj e X8、一信号x(t)的最高频率为500Hz ，则利用冲激串采样得到的采样信号x(nT)能唯一表示出原信号的最大采样周期为 。
A. 500B. 1000C. 0.05D. 0.001 9、一信号x(t)的有理拉普拉斯共有两个极点s=－3和s=－5，若)()(4t x e t g t =，其傅立叶变换)(ωj G 收敛，则x(t)是 。
A. 左边B. 右边C. 双边D. 不确定10、一系统函数1}Re{1)(->+=s s e s H s，，该系统是 。
《信号与系统(第2版》【附录+习题答案】
附 录 A 常 用 数 学 公 式A.1 三角函数公式j e cos jsin t t t ωωω=+ j e e (cos jsin )t t t σωσωω+=+j j 1cos (e e )2t t t ωωω-=+j j 1sin (e e )2jt t t ωωω-=-sin()sin cos cos sin αβαβαβ±=± cos()cos cos sin sin αβαβαβ±=sin22sin cos ααα=2222cos2cos sin 12sin 2cos 1ααααα=-=-=-1sin sin [cos()cos()]2αβαβαβ=--+1cos cos [cos()cos()]2αβαβαβ=-++1sin cos [sin()sin()]2αβαβαβ=-++双曲正弦：e e sh 2x xx --=双曲余弦：e e ch 2x xx -+=A.2 微积分公式d()d Cu C u =，C 为常数（下同）d()d d u v u v ±=±，u 、v 为t 的函数（下同） d()d d uv v u u v =+ 2d d d u v u u v v v -⎛⎫= ⎪⎝⎭d d Cu t C u t =⎰⎰()d d d u v t u t v t ±=±⎰⎰⎰信号与系统288d d u v uv v u =-⎰⎰()d ()()()()d ()bb baaau t v t u t v t v t u t =-⎰⎰A.3 数列求和公式（1）等比数列123,,,,N a a a a 的通项为11n n a a q -=，q 为公比，前n 项的和为 111(1)11NN N N n n a a q a q S a q q =--===--∑（2）等差数列123,,,,N a a a a 的通项为1(1)n a a n d =+-，d 为公差，前n 项的和为111()(1)22NN N n n N a a N N dS a Na =+-===+∑附 录 B 常 用 信 号 与 系 统 公 式B.1 连续时间信号的卷积121221()()()()d ()()d x t x t x x t x x t ττττττ∞∞-∞-∞*=-=-⎰⎰B.2 离散时间信号的卷积121221()()()()()()m m x n x n x m x n m x m x n m ∞∞=-∞=-∞*=-=-∑∑B.3 连续时间三角形式的傅里叶级数0000011()[cos()sin()]cos()kk kkk k x t a ak t b k t A A k t ωωωϕ∞∞===++=++∑∑0000001()d t T t a A x t t T +==⎰000002()cos()d 1,2,t T k t a x t k t t k T ω+==⎰， 000002()sin()d 1,2,t T k t b x t k t t k T ω+==⎰，1,2,k A k = arctan 1,2,k k k b k a ϕ⎛⎫=-=⎪⎝⎭，B.4 连续时间指数形式的傅里叶级数FS000j 01()e d t T k t k t X x t t T ω+-=⎰0j 0()()ek tk x t X k ωω∞=-∞=∑信号与系统290B.5 连续时间傅里叶变换FTj (j )()e d t X x t t ωω∞--∞=⎰j 1()(j )e d 2πt x t X ωωω∞-∞=⎰B.6 双边拉普拉斯变换()()e d st X s x t t ∞--∞=⎰j j 1()()e d 2πjst x t X s s σσ+∞-∞=⎰B.7 单边拉普拉斯变换0()()e d st X s x t t ∞--=⎰j j 1()()e d 2πjst x t X s s σσ+∞-∞=⎰，0t ≥B.8 离散时间傅里叶级数DFS2πj 1()()ekn NN N n N X k x n N -=<>=∑，0,1,2,k =±±2πj()()ekn NN N k N x n X k =<>=∑，0,1,2,n =±±B.9 离散时间傅里叶变换DTFTj j (e )()enn X x n ΩΩ∞-=-∞=∑j j 2π1()(e )e d 2πn x n X ΩΩΩ=⎰B.10 离散傅里叶变换DFT1()()01N knNn X k x n Wk N -==-∑≤≤，附 录 B 常 用 信 号 与 系 统 公 式29111()()01N kn Nk x n X k Wn N N--==-∑≤≤，B.11 双边Z 变换b ()()nn X z x n z∞-=-∞=∑11()()2n cx n X z z dzj π-=⎰B.12 单边Z 变换s 0()()nn X z x n z∞-==∑11()()2n cx n X z z dzj π-=⎰习题参考答案第1章1.1（a）确定信号、连续时间信号、非周期信号、能量信号、非因果信号。
信号与系统复习题(答案全)
1、 若系统的输入f (t ）、输出y （t) 满足()3()4t y t e ft -=，则系统为 线性的 （线性的、非线性的)、 时变的 (时变的、时不变）、 稳定的 (稳定的、非稳定的).2、 非周期、连续时间信号具有 连续 、非周期频谱；周期、连续时间信号具有离散、非周期 频谱；非周期、离散时间信号具有 连续 、周期频谱；周期、离散时间信号具有离散、 周期 频谱。
3、 信号f(t)的占有频带为0-10KHz,被均匀采样后,能恢复原信号的最大采样周期为 5×10—5 s 。
4、 )100()(2t Sa t f =是 能量信号 （功率信号、能量信号、既非功率亦非能量信号）。
5、 ()2cos()f t t =+是 功率信号 (功率信号、能量信号、既非功率亦非能量信号)。
6、 连续信号f(t ）=sint 的周期T 0= 2π ,若对f （t ）以fs=1Hz 进行取样，所得离散序列f(k)=sin(k ） ，该离散序列是周期序列？ 否 。
7、 周期信号2sin(/2)()j n tn n f t e n ππ+∞=-∞=∑，此信号的周期为 1s 、直流分量为 2/π 、频率为5Hz 的谐波分量的幅值为 2/5 。
8、 f (t) 的周期为0。
1s 、傅立叶级数系数**03355532F F F F F j --=====、其余为0。
试写出此信号的时域表达式f (t ） = 5 + 6 cos （ 60 π t ) - 4 sin （100 π t ) . 9、 f (k ） 为周期N=5的实数序列，若其傅立叶级数系数()205=F ()52511,πjeF -+=()54512πjeF -+=、 则F 5 （3 )= ()54512πjeF +=- 、F 5 （4 )= ()52511πj eF +=- 、F 5 （5 ）= 2 ；f(k ） =())1.7254cos(62.052)9.3552cos(62.152525140525︒-⨯+︒-⨯+=∑=k k e n F n k jn πππ。
信号与系统课后习题答案
第一章1.8 系统的数学模型如下，试判断其线性、时不变性和因果性。
其中X （0-）为系统的初始状态。
（2）()()2f t y t e= （5）()()cos2y t f t t= （8）()()2y t f t =解：（2）()()2f t y t e=① 线性： 设()()()()1122,f t y t f t y t →→，则()()()()122212,f t f t y t ey t e==那么()()()()()()()112211222221122a f t a f t a f t a f t a f t a f t y t ee e +⎡⎤⎣⎦+→==，显然，()()()1122y t a y t a y t ≠+，所以是非线性的。
② 时不变性 设()()11,f t y t →则()()()()10122110,f t t f t y t ey t t e-=-=设()()102,f t t y t -→则()()()102210f t t y t ey t t -==-，所以是时不变的。
③ 因果性因为对任意时刻 t1，()()121f t y t e=，即输出由当前时刻的输入决定，所以系统是因果的。
（5）()()cos2y t f t t=① 线性： 设()()()()1122,f t y t f t y t →→，则()()()()1122cos2,cos2y t f t t y t f t t==那么()()()()()()()112211221122cos 2cos 2cos 2a f t a f t y t a f t a f t t a f t t a f t t+→=+=+⎡⎤⎣⎦,显然()()()1122y t a y t a y t =+，所以系统是线性的。
② 时不变性 设()()11,f t y t →则()()()()()1110100cos2,cos2y t f t t y t t f t t t t =-=--设()()102,f t t y t -→则()()()21010cos2y t f t t t y t t =-≠-，所以是时变的。
信号与系统参考习题解答
收敛域为|2z|<1，即|z|< ；极点为z= ；零点为z=0。
23．用长除法、留数定理、部分分式法求以下X(z)的z反变换：
(1) (2)
(3)
解：(1)①长除法求解
可知极点为 而收敛域为 。因而x(n)为因果序列，所以分子、分母要按降幂排列。
即
所以
②留数定理法求解
，设c为 内的逆时针方向闭合曲线。
y'(n)＝3x(n-n0)+2
因为
y(n-n0)＝2x(n-n0)+2=y'(n)
故该系统是时不变的。再讨论线性。由于
y(n)=T[ax1(n)+bx2(n)]
=3ax1(n)+3bx2(n)+2
而
T[ax1(n)]=3ax1(n)+2
T[bx2(n)]=3bx2(n)+2
所以得
T[ax1(n)+bx2(n)]≠aT[x1(n)]+bT[x2(n)]
（2）根据脉冲定理，脉冲频率fs≥2f，取=fs=2f=200Hz。脉冲时间间隔应为
T=1/f=1/200=0.005s
（3）设采样周期为T=1/f=0.005s采样信号xa(t)，则
=
=0
所以，以T=1/f=0.005s为采样周期，采样信号xa(t)，所得采样序列 无法恢复信号xa(t)。为能恢复xa(t)，应减小采样周期T(采样频率由T确定)。设新采样周期为原采样周期的一半，即T=0.0025s，则采样信号 为
(3)y(n)＝x(n-1) (4)y(n)＝x(-n)
要点提示：
利用系统线性定义和时不变定义来证明。满足可加性和比例性的系统是线性系统，即
信号系统(第3版)习题解答
《信号与系统》（第3版）习题解析高等教育目录第1章习题解析 (2)第2章习题解析 (6)第3章习题解析 (16)第4章习题解析 (23)第5章习题解析 (31)第6章习题解析 (41)第7章习题解析 (49)第8章习题解析 (55)第1章习题解析1-1 题1-1图示信号中，哪些是连续信号？哪些是离散信号？哪些是周期信号？哪些是非周期信号？哪些是有始信号？(c) (d)题1-1图解 (a)、(c)、(d)为连续信号；(b)为离散信号；(d)为周期信号；其余为非周期信号；(a)、(b)、(c)为有始（因果）信号。
1-2 给定题1-2图示信号f ( t )，试画出下列信号的波形。
[提示：f ( 2t )表示将f ( t )波形压缩，f (2t)表示将f ( t )波形展宽。
](a) 2 f ( t - 2 ) (b) f ( 2t )(c) f ( 2t)(d) f ( -t +1 )题1-2图解 以上各函数的波形如图p1-2所示。
图p1-21-3 如图1-3图示，R 、L 、C 元件可以看成以电流为输入，电压为响应的简单线性系统S R 、S L 、S C ，试写出各系统响应电压与激励电流函数关系的表达式。
题1-3图解 各系统响应与输入的关系可分别表示为)()(t i R t u R R ⋅= tt i Lt u L L d )(d )(= ⎰∞-=tC C i Ct u ττd )(1)(1-4 如题1-4图示系统由加法器、积分器和放大量为-a 的放大器三个子系统组成，系统属于何种联接形式？试写出该系统的微分方程。
S RS LS C题1-4图解 系统为反馈联接形式。
设加法器的输出为x ( t )，由于)()()()(t y a t f t x -+=且)()(,d )()(t y t x t t x t y '==⎰故有)()()(t ay t f t y -='即)()()(t f t ay t y =+'1-5 已知某系统的输入f ( t )与输出y ( t )的关系为y ( t ) = | f ( t )|，试判定该系统是否为线性时不变系统？解 设T 为系统的运算子，则可以表示为)()]([)(t f t f T t y ==不失一般性，设f ( t ) = f 1( t ) + f 2( t )，则)()()]([111t y t f t f T == )()()]([222t y t f t f T ==故有)()()()]([21t y t f t f t f T =+=显然)()()()(2121t f t f t f t f +≠+即不满足可加性，故为非线性时不变系统。
《信号与系统》课程习题与解答
《信号与系统》课程习题与解答第二章习题(教材上册第二章p81-p87)2-1,2-4～2-10,2-12～2-15,2-17～2-21,2-23,2-24第二章习题解答2-1 对下图所示电路图分别列写求电压的微分方程表示。
图(a)：微分方程：11222012()2()1()()()2()()()()2()()()c cc di t i t u t e t dtdi t i t u t dtdi t u t dt du t i t i t dt ⎧+*+=⎪⎪⎪+=⎪⇒⎨⎪=⎪⎪⎪=-⎩图（b ）：微分方程：⎪⎪⎪⎩⎪⎪⎪⎨⎧-==+++=+++⎰⎰2021'2'21'2'11)(01)(1Ri t v Ri Mi Li dt i Ct e Ri Mi Li dt i C)()(1)(2)()2()(2)()(33020022203304422t e dtd MR t v C t v dt d C R t v dt d C L R t v dt d RL t v dt d M L =+++++-⇒ 图(c)微分方程：dt i C i L t v ⎰==211'101)(⎪⎪⎪⎩⎪⎪⎪⎨⎧===⇒⎰dt t v L i t v L i dtdt v L i dt d)(1)(1)(10110'1122011∵ )(122111213t i dt d L C i i i i +=+=)(0(1]1[][101011022110331t e dt dR t v RL v dt d RR L C v dt d R C R C v dt d CC μ=+++++⇒图(d)微分方程：⎪⎩⎪⎨⎧+-=++=⎰)()()()()(1)()(11111t e t Ri t v t v dt t i C t Ri t e μRC v dt d 1)1(1+-⇒μ)(11t e V = ∵)()(10t v t v μ=)()(1)1(0'0t e R v t v R Cv v =+-⇒2-4 已知系统相应的其次方程及其对应的0+状态条件，求系统的零输入响应。
信号与系统习题及答案
10通信 信号与系统习题及答案1、无失真传输系统，其幅频特性为 ，相频特性为 。
2、某连续LTI 系统的单位冲激响应为h(t)，则该系统稳定的充要条件是 。
3、某连续LTI 系统的单位冲激响应为h(t)，则该系统因果的充要条件是 。
4、信号Sa(500t)的频谱密度函数为 ，频带宽度为 Hz(只计正频率)。
5、信号)(cos )(0t t w t f ε=的拉普拉斯变换表达式是 。
6、描述线性时不变连续系统的输入输出方程是 。
7、单边拉普拉斯变换F(s)=1+s 的原函数f(t)= 。
8、 描述线性时不变连续系统的输入输出方程是 。
已知离散信号 请问：该信号是否是周期信号 ，若是，则周期应为多少 。
9、已知,0)(≥t f )()1()(*)(t e t t f t f t ε--='，则)(jw F = ，)(t f = 。
1、下列各表达式中正确的是（ ）（A ）)()2(t t δδ= （B ）)(21)2(t t δδ=（C ）)(2)2(t t δδ= （D ）)2(21)(2t t δδ= 2、设：f(t)↔F(jω) 则f 1(t)=f(at+b)，a>0，的频谱F 1(jω)为( )(A) F 1(jω)=aF(j a ω)e -j bw (B) F 1(jω)=a 1F(j aω)e -j bw (C) F 1(jω)= a 1F(j a ω)ω-a b j e (D) F 1(jω)=aF(j aω)ω-a b j e 3、如图所示周期信号)(t f ，设其傅立叶系数为n C ，则0C = 。
A. 10B. 5C. 20D. 154、若矩形脉冲信号的脉宽加宽，则它的频带宽度（ ）(A) 不变 (B) 变窄 (C) 变宽 (D) 与脉冲宽度无关238cos()(πk k f =t f 1 (t)121-10tf 2 (t)121-10f(t)t0115、 无失真传输的条件是( )(A) 幅频特性等于常数 (B) 相位特性是通过原点的直线(C) 幅频特性等于常数，相位特性是通过原点的直线(D) 幅频特性是通过原点的直线，相位特性等于常数6、信号)()1()(2t u e t t f t --=的拉氏变换为（ ）(A) 2)2(1+s (B) 2)2(+s s (C) 22)2(+s s (D) 2)2(1++s s7、积分式⎰-+++4422)]dt -(t 2(t))[23(δδt t 的积分结果是（ ）（A) 14 （B) 24 （C ）26 （D ）288、若连续时间系统是因果稳定的，则其系统函数的极点 。
信号与系统课程习题与解答
《信号与系统》课程习题与解答第三章习题(教材上册第三章p160-p172)3-1～3-3,3-5,3-9,3-12,3-13,3-15～3-17,3-19,3-22,3-24,3-25,3-29,3-32第三章习题解答3-2 周期矩形信号如题图3-2所示。
若：求直流分量大小以及基波、二次和三次谐波的有效值。
解：直流分量⎰⎰--=⨯==2222301105)(1ττv Edt dt t f T a TTf(t)为偶函数，∴0=n b)(2cos )(222T n Sa T E tdt n t f T a n πττωττ⎰-==)(21T n Sa T E a F n n πςτ== 基波 =1a )1.0s i n (20)(2πππττ=T Sa T E有效值 39.11.0sin 22021≈=ππa二次谐波有效值 32.122≈a三次谐波有效值 21.123≈a3-3 若周期矩形信号)(1t f 和 )(2t f 波形如题图3-2所示，)(1t f 的参数为s μτ5.0=，s T μ1=，E=1V ；)(2t f 的参数为s μτ5.1=，s T μ3=，E=3V ，分别求：（1）)(1t f 的谱线间隔和带宽（第一零点位置），频率单位以kHz 表示； （2）)(2t f 的谱线间隔和带宽； （3） )(1t f 和 )(2t f 的基波幅度之比； （4） )(1t f 基波与)(2t f 三次谐波幅度之比。
解：（1）)(1t f s μτ5.0= s T μ1= E=1V 谱线间隔：khZ T 10001==∆带宽：KHzB f 20001==τ(2) )(2t f s μτ5.1= s T μ3= E=3V间隔：khZ T 310001==∆谱线带宽：KHzB f 320001==τ(3) )(1t f 基波幅度：ππτ2)2cos(4201==⎰dt t T E T a )(2t f 基波幅度：ππτ6)2cos(4201==⎰dt t T E T a幅度比：1：3（4） )(2t f 三次谐波幅度：ππτ2)23cos(4203-=⨯=⎰dt t T E T a 幅度比：1：13-5 求题图3-5所示半波余弦信号的傅立叶级数。
信号与系统课后习题答案(西安电子科技大学)
（7）
所以， cos(8kπ
/ 7)
=
cos⎢⎣⎡87π
(k
+
N )⎥⎦⎤
，即 8π 7
N
=
2πn ，则有：
N
=
7 4
n
=
7(取n
=
4)
1．5 已知连续时间信号 x(t)和 y(t)分别如题图 1．2(a)、(b)所示，试画出下列各信号 的波形图：
解：
1．6 已知离散时间信号 x(k)和 y(k)分别如题图 1．3(a)、(b)所示，试画出下列序列 的图形：
+
Cuc′
(t
)
+
1 2
u(t)
----⑴
对回路①，有：
⎧− ⎪ ⎨ ⎪⎩iL
uR (t) + LiL′ (t) + u(t) =
(t)
=
CuC′
(t)
+
1 2
u(t)
0
⇒
u
R
(t
)
=
u
′′(t
)
+
1 2
u′(t
)
+
u(t
)
----⑵
⑴、⑵式联合求解得：
is
(t)
=
1 3
u′′(t)
+
1 6
u′
(t)
1
∞
解： f (t)δT (t) = t ∑δ (t − nT ) n=−∞
∴ f1 (t) = [ f (t)δT (t)]* gτ (t) f2 (t) = f (t)[δT (t) * gτ (t)]
解： 利用卷积的微积分性质
∫ [ ] y(t) =
信号与系统经典例题答案解析
习题三——P142
∫ ∫ 3.5(b)
a0
=
2 T
T 2
−
T 2
f ( t )dt
=A, bn
=
2 T
T
2 f ( t ) sin n Ω tdt = 0
−
T 2
∫ an
=
2 T
T 2
−
T 2
f (t)cos nΩtdt
=2
A
sin(nπ nπ
/ 2)
=
ASa( nπ ) 2
∑ f (t) = 1 A + ∞ ASa( nπ )cos(nΩt)
∫ = 2 1τdτ −2
=
2
⎡ ⎢⎣
1 2
τ
2 ⎤1 ⎥⎦ −2
=
−3
P52，例2-2
1
-2
0
1
-2
2.28(2) ( p2 + 2p + 1) y(t) = ( p + 1) f (t) y(0− ) = 1, y' (0− ) = 2, f (t ) = e−2tε (t )
解： A( p) = p2 + 2p + 1 = ( p + 1)2
F1( jω) = FT[ f '(t)]= 2−e−jω −e jω
= 2(1 − cosω ) = 4sin2(ω )
2
F(
jω )
=
F1( jω ) jω
+
πF1 (0)δ
(ω )
=
4 jω
sin 2
(ω 2
)
f(t) 1
t0= 1
y f (t) = 0
-1 0 1 t
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
10、试分析系统与信号的关系。
习题
2-1
1、
解：线性验证：
4[ar1(t)+br2(t)]=
=
=
可以看出，当输入x(t)= ，r(t)=ar1(t)+br2(t)]，满足齐次性和叠加性，因此为线性系统；
时变性判断：设输入x(t-t0)，则有
第一章
思考题
1、信号有哪些类型，各类信号的特点是什么？
答：
2、信号与函数有何同异点？
3、正交函数满足什么条件？具有相似性的函数是否正交？能否正交函数集中的某个函数用其余函数表示出来？
4、信号的基函数表示法有何重要意义？
5、 函数有哪些重要性质？
6、阶跃函数有什么应用？
7、u(t)与 有何关系？
8、由信号的脉冲分解表达式解释脉冲分解的含义。
本题或者直接使用反证法求证，即i和j直接取不满足条件的值求证。
1-6 1,x,x
证明：
两函数正交的条件应满足 (i j)，而本题取i=0，j=1可得，
则该函数几何在(0,1)区间上不是正交函数集。
1-7
1、
2、
3、
4、
5、
6、
1-8
1、
2、
3、
4、
5、
6、
1-9
解：要画出g1(t)的波形，下面两种次序的解法均可：
3、如何判别系统是线性时不变系统？
4、连续系统和离散系统有何异同？
5、试解释零输入响应、零状态响应、自由响应、强迫响应、（暂态）瞬态响应、稳态响应及系统响应的物理含义。
6、零状态初始条件与零输入初始条件有什么类型？
7、单位冲激响应的意义和重要性是什么？
8、单位脉冲响应是零输入响应吗？它与零输入响应有什么关系？
x(t-t0+3)
2、
解：设 ，则
ay1(t)+by2(t)=
=
上式与当输入x(t)= 时的输出r(t)式子不符合，顾此系统为非线性系统；
（1）
（2）
要画出g2(t)的波形可以按照多种次序进行，下面介绍一种：
1-10
第3题的数学解法是先写出f(t)的表达式，再对表达式进行微分运算：
=
第四题的数学解法分段积分求取（积分使用分部积分法）：
在 上，
在 上，
1-11
第
思考题
1、试阐述系统的概念及分类，各类系统的数学模型的主要特征是什么？
2、系统分析的任务是什么？
9、信号或序列的时移、反褶、波形展缩各有什么含义？三者之间有何差异？
10、同一信号的连续函数与离散函数有什么异同点？信号采样应满足什么条件？否则会出现什么情况？
11、信号采样有哪些方法？
习题
1-1
1-2
1-3
（1）
表达式为：
（2）
表达式为：
（3）
表达式为：
1-4
证明：
1-5
证明：
上式只有i , j同时为偶数或奇数时才为0，否则不为0，故函数集在（0，π/2）内不是正交函数集。