2019年高考数学一轮课时分层训练25解三角形实际应用举例理

合集下载

专题2.5 解三角形的实际应用-2019年高考数学(理)

一、解答题1．如图，某快递小哥从地出发，沿小路以平均速度为20公里小时送快件到处，已知公里，，是等腰三角形，．（1）试问，快递小哥能否在50分钟内将快件送到处？（2）快递小哥出发15分钟后，快递公司发现快件有重大问题，由于通讯不畅，公司只能派车沿大路追赶，若汽车的平均速度为60公里小时，问，汽车能否先到达处？2．在一个特定时段内，以点E 为中心的7海里以内海域被设为警戒水域.点E 正北55海里处有一个雷达观测站A ．某时刻测得一艘匀速直线行驶的船只位于点A 北偏东45且与点A 相距海里的位置B ，经过40分钟又测得该船已行驶到点A 北偏东45+ θ (其中sin θ， 090θ<<)且与点A 相距C ．（I ）求该船的行驶速度（单位：海里/小时）;（II ）若该船不改变航行方向继续行驶.判断它是否会进入警戒水域，并说明理由.3．钓鱼岛及其附属岛屿是中国固有领土，如图:点分别表示钓鱼岛、南小岛、黄尾屿，点在点的北偏东方向，点在点的南偏西方向，点在点的南偏东方向，且两点的距离约为3海里. (1)求两点间的距离；(精确到0.01)(2)某一时刻，我国一渔船在点处因故障抛锚发出求教信号.一艘国舰艇正从点正东10海里的点处以18海里/小时的速度接近渔船，其航线为 (直线行进)，而我东海某渔政船正位于点南偏西方向20海里的点处，收到信号后赶往救助，其航线为先向正北航行8海里至点处，再折向点直线航行，航速为22海里/小时.渔政船能否先于国舰艇赶到进行救助?说明理由.4．如图，一山顶有一信号塔CD （CD 所在的直线与地平面垂直），在山脚A 处测得塔尖C 的仰角为α，沿倾斜角为θ的山坡向上前进l 米后到达B 处，测得C 的仰角为β.（1）求BC 的长；（2）若24l =， 45α=， 75β=， 30θ=，求信号塔CD 的高度.5．某渔船在航行中不幸遇险，发出呼叫信号，我海军舰艇在处获悉后，立即测出该渔船在方位角（从指北方向顺时针转到目标方向线的水平角）为，距离为15海里的处，并测得渔船正沿方位角为的方向，以15海里/小时的速度向小岛靠拢，我海军舰艇立即以海里/小时的速度前去营救，求舰艇靠近渔船所需的最少时间和舰艇的航向.6．一根长为L 的铁棒AB 欲通过如图所示的直角走廊，已知走廊的宽2AC BD == m ．（1）设BOD θ∠=，试将L 表示为θ的函数；（2）求L 的最小值，并说明此最小值的实际意义．。

2020届高考数学一轮复习：课时作业25《解三角形应用举例》(含解析)

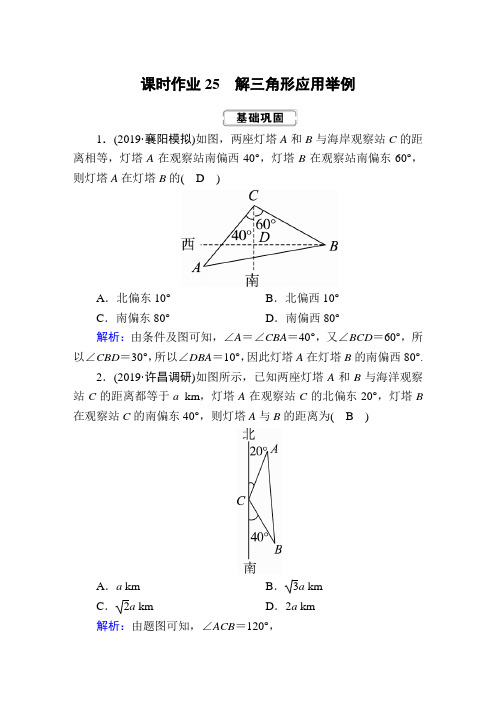
课时作业25解三角形应用举例1．(2019·襄阳模拟)如图，两座灯塔A和B与海岸观察站C的距离相等，灯塔A在观察站南偏西40°，灯塔B在观察站南偏东60°，则灯塔A在灯塔B的(D)A．北偏东10°B．北偏西10°C．南偏东80°D．南偏西80°解析：由条件及图可知，∠A＝∠CBA＝40°，又∠BCD＝60°，所以∠CBD＝30°，所以∠DBA＝10°，因此灯塔A在灯塔B的南偏西80°.2．(2019·许昌调研)如图所示，已知两座灯塔A和B与海洋观察站C的距离都等于a km，灯塔A在观察站C的北偏东20°，灯塔B 在观察站C的南偏东40°，则灯塔A与B的距离为(B)A．a km B．3a kmC．2a km D．2a km解析：由题图可知，∠ACB＝120°，由余弦定理，得AB 2＝AC 2＋BC 2－2AC ·BC ·cos ∠ACB ＝a 2＋a 2－2·a ·a ·⎝ ⎛⎭⎪⎫－12＝3a 2，解得AB ＝3a (km)． 3．如图，测量河对岸的塔高AB 时可以选与塔底B 在同一水平面内的两个测点C 与D ，测得∠BCD ＝15°，∠BDC ＝30°，CD ＝30，并在点C 测得塔顶A 的仰角为60°，则塔高AB 等于( D )A ．5 6B ．15 3C ．5 2D ．15 6解析：在△BCD 中，∠CBD ＝180°－15°－30°＝135°.由正弦定理得BC sin30°＝30sin135°，所以BC ＝15 2.在Rt △ABC 中，AB ＝BC tan ∠ACB ＝152×3＝15 6.4．如图所示，为了了解某海域海底构造，在海平面上取一条直线上的A ，B ，C 三点进行测量，已知AB ＝50 m ，BC ＝120 m ，于A 处测得水深AD ＝80 m ，于B 处测得水深BE ＝200 m ，于C 处测得水深CF ＝110 m ，则∠DEF 的余弦值为( A )A ．1665B ．1965C ．1657D ．1757解析：如图所示，作DM ∥AC 交BE 于N ，交CF 于M ，则DF ＝MF 2＋DM 2＝302＋1702＝10298(m)，DE ＝DN 2＋EN 2＝502＋1202＝130(m)，EF ＝(BE －FC )2＋BC 2＝902＋1202＝150(m)．在△DEF 中，由余弦定理，得cos ∠DEF ＝DE 2＋EF 2－DF 22DE ·EF＝1302＋1502－102×2982×130×150＝1665. 5．地面上有两座相距120 m 的塔，在矮塔塔底望高塔塔顶的仰角为α，在高塔塔底望矮塔塔顶的仰角为α2，且在两塔底连线的中点O处望两塔塔顶的仰角互为余角，则两塔的高度分别为( B )A ．50 m,100 mB ．40 m,90 mC ．40 m,50 mD ．30 m,40 m 解析：设高塔高H m ，矮塔高h m ，在O 点望高塔塔顶的仰角为β.则tan α＝H 120，tan α2＝h 120，根据三角函数的倍角公式有H 120＝2×h 1201－⎝ ⎛⎭⎪⎫h 1202.① 因为在两塔底连线的中点O 望两塔塔顶的仰角互为余角，所以在O点望矮塔塔顶的仰角为π2－β，由tan β＝H 60，tan ⎝ ⎛⎭⎪⎫π2－β＝h 60，得H 60＝60h .② 联立①②解得H ＝90，h ＝40.即两座塔的高度分别为40 m,90 m.6．如图所示，一座建筑物AB 的高为(30－103)m ，在该建筑物的正东方向有一座通信塔CD ．在它们之间的地面上的点M (B ，M ，D 三点共线)处测得楼顶A ，塔顶C 的仰角分别是15°和60°，在楼顶A 处测得塔顶C 的仰角为30°，则通信塔CD 的高为( B )A ．30 mB ．60 mC ．30 3 mD ．40 3 m解析：在Rt △ABM 中，AM ＝AB sin ∠AMB ＝30－103sin15°＝30－1036－24＝206(m).过点A 作AN ⊥CD 于点N ，如图所示．易知∠MAN ＝∠AMB ＝15°，所以∠MAC ＝30°＋15°＝45°.又∠AMC ＝180°－15°－60°＝105°，所以∠ACM＝30°.在△AMC中，由正弦定理得MCsin45°＝206sin30°，解得MC＝403(m)．在Rt△CMD中，CD＝403×sin60°＝60(m)，故通信塔CD的高为60 m.7．(2019·哈尔滨模拟)如图，某工程中要将一长为100 m，倾斜角为75°的斜坡改造成倾斜角为30°的斜坡，并保持坡高不变，则坡底需加长1002m.解析：设坡底需加长x m，由正弦定理得100sin30°＝xsin45°，解得x＝100 2.8．如图，为了测量两座山峰上P，Q两点之间的距离，选择山坡上一段长度为300 3 m且和P，Q两点在同一平面内的路段AB的两个端点作为观测点，现测得∠P AB＝90°，∠P AQ＝∠PBA＝∠PBQ＝60°，则P，Q两点间的距离为900__m.解析：由已知，得∠QAB＝∠P AB－∠P AQ＝30°.又∠PBA＝∠PBQ＝60°，∴∠AQB＝30°，∴AB＝BQ.又PB为公共边，∴△P AB≌△PQB，∴PQ＝P A．在Rt △P AB 中，AP ＝AB ·tan60°＝900，故PQ ＝900，∴P ，Q 两点间的距离为900 m.9．(2019·湖北百所重点中学模拟)我国南宋著名数学家秦九韶在他的著作《数书九章》卷五“田域类”里记载了这样一个题目：“今有沙田一段，有三斜，其小斜一十三里，中斜一十四里，大斜一十五里．里法三百步．欲知为田几何．”这道题讲的是有一块三角形的沙田，三边长分别为13里，14里，15里，假设1里按500米计算，则该沙田的面积为21__平方千米．解析：设在△ABC 中，a ＝13里，b ＝14里，c ＝15里，∴cos C ＝132＋142－1522×13×14＝132＋(14－15)×(14＋15)2×13×14＝1402×13×14＝513， ∴sin C ＝1213，故△ABC 的面积为12×13×14×1213×5002×11 0002＝21(平方千米)．10．海轮“和谐号”从A 处以每小时21海里的速度出发，海轮“奋斗号”在A 处北偏东45°的方向，且与A 相距10海里的C 处，沿北偏东105°的方向以每小时9海里的速度行驶，则海轮“和谐号”与海轮“奋斗号”相遇所需的最短时间为23 小时．解析：设海轮“和谐号”与海轮“奋斗号”相遇所需的最短时间为x 小时，如图，则由已知得△ABC 中，AC ＝10，AB ＝21x ，BC ＝9x ，∠ACB ＝120°. 由余弦定理得：(21x )2＝100＋(9x )2－2×10×9x ×cos120°，整理，得36x 2－9x －10＝0，解得x ＝23或x ＝－512(舍)．所以海轮“和谐号”与海轮“奋斗号”相遇所需的最短时间为23小时．11．(2019·武汉模拟)为了应对日益严重的气候问题，某气象仪器科研单位研究出一种新的“弹射型”气象仪器，这种仪器可以弹射到空中进行气象观测．如图所示，A ，B ，C 三地位于同一水平面上，这种仪器在C 地进行弹射实验，观测点A ，B 两地相距100米，∠BAC＝60°.在A 地听到弹射声音的时间比B 地晚217秒．在A 地测得该仪器至最高点H 处的仰角为30°.(1)求A ，C 两地的距离；(2)求这种仪器的垂直弹射高度HC ．(已知声音的传播速度为340米/秒)解：(1)由题意，设AC ＝x ，因为在A 地听到弹射声音的时间比B 地晚217秒，所以BC ＝x －217×340＝x －40，在△ABC 内，由余弦定理得BC 2＝CA 2＋BA 2－2BA ·CA ·cos ∠BAC ，即(x －40)2＝x 2＋10 000－100x ，解得x ＝420.答：A ，C 两地的距离为420米．(2)在Rt △ACH 中，AC ＝420，∠CAH ＝30°.所以CH ＝AC ·tan ∠CAH ＝1403米．答：该仪器的垂直弹射高度CH 为1403米．12．如图所示，在一条海防警戒线上的点A ，B ，C 处各有一个水声监测点，B ，C 两点到点A 的距离分别为20 km 和50 km.某时刻，B 收到发自静止目标P 的一个声波信号，8 s 后A ，C 同时接收到该声波信号，已知声波在水中的传播速度是1.5 km/s.(1)设A 到P 的距离为x km ，用x 表示B ，C 到P 的距离，并求x 的值；(2)求静止目标P 到海防警戒线AC 的距离．解：(1)依题意，有P A ＝PC ＝x ，PB ＝x －1.5×8＝x －12.在△P AB 中，AB ＝20，cos ∠P AB ＝P A 2＋AB 2－PB 22P A ·AB＝x 2＋202－(x －12)22x ·20＝3x ＋325x . 同理，在△P AC 中，AC ＝50，cos ∠P AC ＝P A 2＋AC 2－PC 22P A ·AC ＝x 2＋502－x 22x ·50＝25x .因为cos ∠P AB ＝cos ∠P AC ，所以3x ＋325x ＝25x ，解得x ＝31.(2)作PD ⊥AC 于点D ，在△ADP 中，由cos ∠P AD ＝2531，得sin ∠P AD ＝1－cos 2∠P AD ＝42131，所以PD ＝P A sin ∠P AD ＝31×42131＝421(km)．故静止目标P 到海防警戒线AC 的距离为421 km.13．如图，为了测量A ，C 两点间的距离，选取同一平面上B ，D 两点，测出四边形ABCD 各边的长度(单位：km)：AB ＝5，BC ＝8，CD ＝3，DA ＝5，且∠B 与∠D 互补，则AC 的长为( A )A ．7 kmB ．8 kmC ．9 kmD ．6 km解析：在△ACD 中，由余弦定理得：cos D ＝AD 2＋CD 2－AC 22AD ·CD＝34－AC 230. 在△ABC 中，由余弦定理得：cos B ＝AB 2＋BC 2－AC 22AB ·BC＝89－AC 280. 因为∠B ＋∠D ＝180°，所以cos B ＋cos D ＝0，即34－AC 230＋89－AC 280＝0，解得AC ＝7.14．(2019·呼和浩特调研)某人为测出所住小区的面积，进行了一些测量工作，最后将所住小区近似地画成如图所示的四边形，测得的数据如图所示，则该图所示的小区的面积是6－34km 2.解析：如图，连接AC ，由余弦定理可知AC ＝AB 2＋BC 2－2AB ·BC ·cos B ＝3，故∠ACB ＝90°，∠CAB ＝30°，∠DAC ＝∠DCA ＝15°，∠ADC ＝150°，AC sin ∠ADC ＝AD sin ∠DCA ，即AD ＝AC sin ∠DCA sin ∠ADC＝3·6－2412＝32－62，故S 四边形ABCD ＝S △ABC ＋S △ADC ＝12×1×3＋12×⎝ ⎛⎭⎪⎫32－622×12＝6－34(km 2)． 15．(2019·福州质检)如图，小明同学在山顶A 处观测到一辆汽车在一条水平的公路上沿直线匀速行驶，小明在A 处测得公路上B ，C 两点的俯角分别为30°，45°，且∠BAC ＝135°.若山高AD ＝100 m ，汽车从B 点到C 点历时14 s ，则这辆汽车的速度约为22.6__m/s(精确到0.1)．解析：因为小明在A 处测得公路上B ，C 两点的俯角分别为30°，45°，所以∠BAD ＝60°，∠CAD ＝45°.设这辆汽车的速度为v m/s ，则BC ＝14v .在Rt △ADB 中，AB ＝AD cos ∠BAD ＝AD cos60°＝200.在Rt △ADC 中，AC ＝AD cos ∠CAD ＝100cos45°＝100 2. 在△ABC 中，由余弦定理，得BC 2＝AC 2＋AB 2－2AC ·AB ·cos ∠BAC ，所以(14v )2＝(1002)2＋2002－2×1002×200×cos135°，所以v ＝50107≈22.6，所以这辆汽车的速度约为22.6 m/s.16．某港口O 要将一件重要物品用小艇送到一艘正在航行的轮船上．在小艇出发时，轮船位于港口O 北偏西30°且与该港口相距20海里的A 处，并正以30海里/小时的航行速度沿正东方向匀速行驶．假设该小艇沿直线方向以v 海里/小时的航行速度匀速行驶，经过t 小时与轮船相遇．(1)若希望相遇时小艇的航行距离最小，则小艇航行速度的大小应为多少？(2)假设小艇的最高航行速度只能达到30海里/小时，试设计航行方案(即确定航行方向和航行速度的大小)，使得小艇能以最短时间与轮船相遇，并说明理由．解：(1)设相遇时小艇航行的距离为S 海里，则S ＝900t 2＋400－2·30t ·20·cos (90°－30°)＝900t 2－600t ＋400＝900⎝ ⎛⎭⎪⎫t －132＋300. 故当t ＝13时，S min ＝103，v ＝10313＝30 3.即小艇以303海里/小时的速度航行，相遇时小艇的航行距离最小．(2)设小艇与轮船在B 处相遇．如图所示．则v 2t 2＝400＋900t 2－2·20·30t ·cos(90°－30°)，故v 2＝900－600t ＋400t 2. 因为0＜v ≤30，所以900－600t ＋400t 2≤900，即2t 2－3t ≤0，解得t ≥23.又t ＝23时，v ＝30，故v ＝30时，t 取得最小值，且最小值等于23.此时，在△OAB 中，有OA ＝OB ＝AB ＝20.故可设计航行方案如下：航行方向为北偏东30°，航行速度为30海里/小时．。

高考数学复习考点知识讲解课件25 解三角形应用举例

— 15 —
(新教材) 高三总复习•数学
— 返回 —
测量距离问题的求解策略 (1)确定所求量所在的三角形，若其他量已知则直接求解；若有未知量，则把未知量放在另外三角形中求解． (2)确定选用正弦定理还是余弦定理，如果都可用，就选择更便于计算的定理．
— 16 —
(新教材) 高三总复习•数学
— 返回 —
即 DE＝si1n0705s°itna4n51°5°＝sin17050°×sincs4oi5ns°1155°°＝sin17050°s×inss4ii5nn°1755°°＝10s0insi1n54°5°.
又 sin15°＝sin(45°－30°)＝
6－ 4
2，所以 DE＝10s0insi1n54°5°＝100(
图形表示
— 返回 —
— 5—
(新教材) 高三总复习•数学
术语名称
术语意义
图形表示例：(1)北偏东 α：
方向角
正北或正南方向线与目标方向线所成的__锐__角__，通
常表达为北(南)偏东(西)α
(2)南偏西 α：
— 返回 —
— 6—
(新教材) 高三总复习•数学
— 返回 —
术语名称
术语意义
图形表示
术语名称
术语意义
在目标视线与水平视线(两者在
同一铅垂平面内)所成的角中，仰角与俯角目标视线在水平视线__上__方__的
叫做仰角，目标视线在水平视线 _下__方__的叫做俯角
图形表示
— 返回 —
— 4—
(新教材) 高三总复习•数学
术语名称
方位角
术语意义
从某点的指北方向线起按 _顺__时__针__方向到目标方向线之间的夹角叫做方位角．方位角 θ 的范围是0_°_≤__θ_<_3_6_0_°

2019届高考数学一轮复习配餐作业25 解三角形的综合应用(含解析)理.doc

2019届高考数学一轮复习配餐作业25 解三角形的综合应用（含解析）理1．(2016·江苏高考)在△ABC 中，AC ＝6，cos B ＝45，C ＝π4。

(1)求AB 的长；(2)求cos ⎝⎛⎭⎪⎫A －π6的值。

解析 (1)因为cos B ＝45，0<B <π，所以sin B ＝1－cos 2B ＝1－⎝ ⎛⎭⎪⎫452＝35。

由正弦定理知AC sin B ＝AB sin C ，所以AB ＝AC ·sin Csin B ＝6×2235＝52。

(2)在△ABC 中，A ＋B ＋C ＝π，所以A ＝π－(B ＋C )，于是cos A ＝－cos(B ＋C )＝－cos ⎝⎛⎭⎪⎫B ＋π4＝－cos B cos π4＋sin B sin π4，又cos B ＝45，sin B ＝35，故cos A ＝－45×22＋35×22＝－210。

因为0<A <π，所以sin A ＝1－cos 2A ＝7210。

因此，cos ⎝ ⎛⎭⎪⎫A －π6＝cos A cos π6＋sin A sin π6＝－210×32＋7210×12＝72－620。

答案 (1)5 2 (2)72－6202．(2016·山东高考)在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c 。

已知2(tan A ＋tan B )＝tan A cos B ＋tan Bcos A。

(1)证明：a ＋b ＝2c ； (2)求cos C 的最小值。

解析 (1)由题意知2⎝⎛⎭⎪⎫sin A cos A ＋sin B cos B ＝sin A cos A cos B ＋sin B cos A cos B，化简得2(sin A cos B ＋sin B cos A )＝sin A ＋sin B ，即2sin(A ＋B )＝sin A ＋sin B ，因为A ＋B ＋C ＝π，所以sin(A ＋B )＝sin(π－C )＝sin C 。

数学高三复习解三角形的实际应用举例专项训练(带答案)-word文档资料

数学2019年高三复习解三角形的实际应用举例专项训练（带答案）由不在同一直线上的三条线段首尾顺次连接所组成的封闭图形叫做三角形，下面是查字典数学网整理的解三角形的实际应用举例专项训练，希望对考生复习有帮助。

一、测量中的距离问题1.有一长为10 m的斜坡,倾斜角为60,在不改变坡高和坡顶的前提下,通过加长坡面的方法将它的倾斜角改为30,则坡底要延长的长度(单位:m)是()A.5B.5C.10D.10答案:D解析:如图,在Rt△ABC中,AC=10,ACB=60.AB=5,BC=5,在Rt△ABD中,ADB=30,BD=15.CD=BD-BC=10.2.(2019福建宁德五校联考,14)一艘船以15 km/h的速度向东航行,船在A处看到灯塔B在北偏东60行驶4 h后,船到达C处,看到灯塔B在北偏东15处,这时船与灯塔的距离为km.答案:30解析:根据题意画出图形,如图所示,可得B=75-30=45,在△ABC中,根据正弦定理得,,即,BC=30 km,即此时船与灯塔的距离为30 km.3.(2019福建厦门高二期末,15)如图,某观测站C在A城的南偏西20,一条笔直公路AB,其中B在A城南偏东40,B与C相距31千米.有一人从B出发沿公路向A城走去,走了20千米后到达D处,此时C,D之间的距离为21千米,则A,C之间的距离是千米.答案:24解析:由已知得CD=21,BC=31,BD=20,在△BCD中,由余弦定理得cosBDC==-.设ADC=,则cos =,sin =.在△ACD中,由正弦定理,得AC==24.二、测量中的高度与角度问题4.如图,D,C,B三点在地面同一直线上,DC=a,从C,D两点测得A点的仰角分别是,(),则A点距离地面的高度AB等于() A. B.C. D.答案:A解析:在△ACD中,DAC=-,DC=a,ADC=,由正弦定理得AC=,在Rt△ACB中,AB=ACsin =.5.运动会开幕式上举行升旗仪式,在坡度15的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60和30,第一排和最后一排的距离为10 m(如图所示),则旗杆的高A.10 mB.30 mC.10 mD.10 m答案:B解析:如图所示,由题意知AEC=45ACE=180-60-15=105, EAC=180-45-105=30,由正弦定理知,AC==20(m),在Rt△ABC中,AB=ACsinACB=30(m).旗杆的高度为30 m.6.当甲船位于A处时获悉,在其正东方向相距20 n mile的B 处有一艘渔船遇险等待营救,甲船立即前往营救,同时把消息告知在甲船的南偏西30,相距10 n mile C处的乙船,乙船立即朝北偏东角的方向沿直线前往B处救援,则sin 的值等于()A. B. C. D.答案:D解析:根据题目条件可作图如图:在△ABC中,AB=20,AC=10,CAB=120,由余弦定理有BC2=AB2+AC2-2ABACcosCAB=202+102-22019cos 120=700, BC=10.再由正弦定理得,sinACB=无触礁的危险.8.如图,在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时刻测得一艘匀速直线行驶的船只位于点A北偏东45且与点A相距40海里的位置B,经过40分钟又测得该船已行驶到点A北偏东45+且与点A相距10海里的位置C.(1)求该船的行驶速度(单位:海里/小时);(2)若该船不改变航行方向继续行驶,判断它是否会进入警戒水域,并说明理由.解:(1)因为AB=40,AC=10,BAC=,sin =,090,所以cos =.由余弦定理得BC==10,所以该船的行驶速度为v==15(海里/小时).(2)设直线AE与BC的延长线相交于点Q.在△ABC中,由余弦定理得cosABC=所以sinABC=.在△ABQ中,由正弦定理得AQ==40.因为AE=5540=AQ,所以点Q位于点A和点E之间,且QE=AE-AQ=15.过点E作EPBC于点P,则EP为点E到直线BC的距离.在Rt△QPE中,PE=QEsinPQE=QEsinAQC=QEsin(45ABC)=15=37.故该船会进入警戒水域.(建议用时:30分钟)1.如图,已知两座灯塔A和B与海岸观察站C的距离相等,灯塔A在观察站C的北偏东40,灯塔B在观察站C的南偏东60,则灯塔A在灯塔B的()的位置.A.北偏东10B.北偏西10C.南偏东10D.南偏西10答案:B解析:由图可知,ACB=180-(40+60)=80.又AC=BC,CBA=(180-80)=50.∵CE∥BD,CBD=BCE=60,ABD=60-50=10.灯塔A在灯塔B的北偏西10的位置.2.如图所示,为测一树的高度,在地面上选取A,B两点(点A,B 与树根部在同一直线上),从A,B两点分别测得树尖的仰角为30,45,且A,B两点之间的距离为60 m,则树的高度为()A.(30+30) mB.(30+15) mC.(15+30) mD.(15+3) m答案:A解析:设树高为h,则由题意得h-h=60,h==30(+1)=(30+30)(m).3.一艘客船上午9:30在A处,测得灯塔S在它的北偏东30,之后它以32 n mile/h的速度继续沿正北方向匀速航行,上午10:00到达B处,此时测得船与灯塔S相距8 n mile,则灯塔S在B处的()A.北偏东75B.东偏南75C.北偏东75或东偏南75D.以上方位都不对答案:C解析:根据题意画出示意图,如图,由题意可知AB=32=16,BS=8,A=30.在△ABS中,由正弦定理得,sin S=,S=45或135,B=105或15,即灯塔S在B处的北偏东75或东偏南75.4.一货轮航行到M处,测得灯塔S在货轮的北偏东15方向,与灯塔S相距20 n mile,随后货轮按北偏西30的方向航行3 h后,又测得灯塔在货轮的东北方向,则货轮的速度为()A.) n mile/hB.) n mile/hC.) n mile/hD.) n mile/h答案:B解析:如图,设货轮的时速为v,则在△AMS中,AMS=45SAM=105ASM=30,SM=20,AM=3v.由正弦定理得,即v==)(n mile/h).解三角形的实际应用举例专项训练分享到这里，更多内容请关注高考数学试题栏目。

2019年高考数学一轮复习理科：解三角形实际应用举例学案

如图 383，从气球 A 上测得正前方的河流的两岸 B，C 的俯角分别为 67°，30°，此时气球的高是 46 m，则河流的宽度 BC 约等于________m． (用四舍五入法将结果精确到个位．参考数据： sin 67°≈0.92， cos 67°≈0.39，sin 37°≈0.60，cos 37°≈0.80， 3≈1.73) 【导学号：79140136】
图 382 A．50 3 m B．25 3 m C．25 2 m D．50 2 m D [因为∠ACB＝45°，∠CAB＝105°，所以∠B＝30°.由正弦定理可知
AC AB 50 ＝，即＝ sin B sin C sin 30°
AB ，解得 AB＝50 2 m．] sin 45°
5．轮船 A 和轮船 B 在中午 12 时同时离开海港 C，两船航行方向的夹角为 120°，两船的航行速度分别为 25 n
(3)方位角与方向角其实质是一样的，均是确定观察点与目标点之间的位置关系．( π 0， 2 .( (4)方位角大小的范围是[0,2π)，方向角大小的范围一般是 [答案] (1)× (2)× (3)√ (4)√ )
2．(教材改编)海面上有 A，B，C 三个灯塔，AB＝10 n mile，从 A 望 C 和 B 成 60°视角，从 B 望 C 和 A 成 75° 视角，则 BC 等于( A．10 3 n mile C．5 2 n mile D [如图，在△ABC 中， ) 10 6 B． n mile 3 D．5 6 n mile
图 383 60 [如图所示，过 A 作 AD⊥CB 且交 CB 的延长线于 D．
在 Rt△ADC 中，由 AD＝46 m，∠ACB＝30°得 AC＝92 m. 在△ABC 中，∠BAC＝67°－30°＝37°， ∠ABC＝180°－67°＝113°，AC＝92 m，由正弦定理

数学高三复习解三角形的实际应用举例专项训练(带答案)

数学高三复习解三角形的实际应用举例专项训练（带答案）由不在同不时线上的三条线段首尾依次衔接所组成的封锁图形叫做三角形，下面是查字典数学网整理的解三角形的实践运用举例专项训练，希望对考生温习有协助。

一、测量中的距离效果1.有一长为10 m的斜坡,倾斜角为60,在不改动坡高和坡顶的前提下,经过加长坡面的方法将它的倾斜角改为30,那么坡底要延伸的长度(单位:m)是()A.5B.5C.10D.10答案:D解析:如图,在Rt△ABC中,AC=10,ACB=60.AB=5,BC=5,在Rt△A BD中,ADB=30,BD=15.CD=BD-BC=10.2.(2021福建宁德五校联考,14)一艘船以15 km/h的速度向东飞行,船在A处看到灯塔B在北偏东60行驶4 h后,船抵达C处,看到灯塔B在北偏东15处,这时船与灯塔的距离为km.答案:30解析:依据题意画出图形,如下图,可得B=75-30=45,在△ABC中,依据正弦定理得,,即,BC=30 km,即此时船与灯塔的距离为30 km.3.(2021福建厦门高二期末,15)如图,某观测站C在A城的南偏西20,一条蜿蜒公路AB,其中B在A城南偏东40,B与C相距31千米.有一人从B动身沿公路向A城走去,走了20千米后抵达D处,此时C,D之间的距离为21千米,那么A,C之间的距离是千米.答案:24解析:由得CD=21,BC=31,BD=20,在△BCD中,由余弦定理得cosBDC==-.设ADC=,那么cos =,sin =.在△ACD中,由正弦定理,得AC==24.二、测量中的高度与角度效果4.如图,D,C,B三点在空中同不时线上,DC=a,从C,D两点测得A点的仰角区分是,(),那么A点距离空中的高度AB等于() A. B.C. D.答案:A解析:在△ACD中,DAC=-,DC=a,ADC=,由正弦定理得AC=,在Rt△ACB中,AB=ACsin =.5.运动会开幕式上举行升旗仪式,在坡度15的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角区分为60和30,第一排和最后一排的距离为10 m(如下图),那么旗杆的高A.10 mB.30 mC.10 mD.10 m答案:B解析:如下图,由题意知AEC=45ACE=180-60-15=105,EAC=180-45-105=30,由正弦定理知,AC==20(m),在Rt△ABC中,AB=ACsinACB=30(m).旗杆的高度为30 m.6.当甲船位于A处时得知,在其正西方向相距20 n mile的B 处有一艘渔船遇险等候营救,甲船立刻前往营救,同时把音讯告知在甲船的南偏西30,相距10 n mile C处的乙船,乙船立刻朝北偏东角的方向沿直线前往B处救援,那么sin 的值等于()A. B. C. D.答案:D解析:依据标题条件可作图如图:在△ABC中,AB=20,AC=10,CAB=120,由余弦定理有BC2=AB2+AC2-2ABACcosCAB=202+102-22021cos 120=700, BC=10.再由正弦定理得,sinACB=无触礁的风险.8.如图,在一个特定时段内,以点E为中心的7海里以内海域被设为警戒水域.点E正北55海里处有一个雷达观测站A.某时辰测得一艘匀速直线行驶的船只位于点A北偏东45且与点A相距40海里的位置B,经过40分钟又测得该船已行驶到点A北偏东45+且与点A相距10海里的位置C.(1)求该船的行驶速度(单位:海里/小时);(2)假定该船不改动飞行方向继续行驶,判别它能否会进入警戒水域,并说明理由.解:(1)由于AB=40,AC=10,BAC=,sin =,090,所以cos =.由余弦定理得BC==10,所以该船的行驶速度为v==15(海里/小时).(2)设直线AE与BC的延伸线相交于点Q.在△ABC中,由余弦定理得cosABC=所以sinABC=.在△ABQ中,由正弦定理得AQ==40.由于AE=5540=AQ,所以点Q位于点A和点E之间,且QE=AE-AQ=15.过点E作EPBC于点P,那么EP为点E到直线BC的距离.在Rt△QPE中,PE=QEsinPQE=QEsinAQC=QEsin(45ABC)=15=37.故该船会进入警戒水域.(建议用时:30分钟)1.如图,两座灯塔A和B与海岸观察站C的距离相等,灯塔A 在观察站C的北偏东40,灯塔B在观察站C的南偏东60,那么灯塔A在灯塔B的()的位置.A.北偏东10B.北偏西10C.南偏东10D.南偏西10答案:B解析:由图可知,ACB=180-(40+60)=80.又AC=BC,CBA=(180-80)=50.∵CE∥BD,CBD=BCE=60,ABD=60-50=10.灯塔A在灯塔B的北偏西10的位置.2.如下图,为测一树的高度,在空中上选取A,B两点(点A,B 与树根部在同不时线上),从A,B两点区分测得树尖的仰角为30,45,且A,B两点之间的距离为60 m,那么树的高度为()A.(30+30) mB.(30+15) mC.(15+30) mD.(15+3) m答案:A解析:设树高为h,那么由题意得h-h=60,h==30(+1)=(30+30)(m).3.一艘客船上午9:30在A处,测得灯塔S在它的北偏东30,之后它以32 n mile/h的速度继续沿正南方向匀速飞行,上午10:00抵达B处,此时测得船与灯塔S相距8 n mile,那么灯塔S在B处的()A.北偏东75B.东偏南75C.北偏东75或东偏南75D.以上方位都不对答案:C解析:依据题意画出表示图,如图,由题意可知AB=32=16,BS=8,A=30.在△ABS中,由正弦定理得,sin S=,S=45或135,B=105或15,即灯塔S在B处的北偏东75或东偏南75.4.一货轮飞行到M处,测得灯塔S在货轮的北偏东15方向,与灯塔S相距20 n mile,随后货轮按北偏西30的方向飞行3 h后,又测得灯塔在货轮的西南方向,那么货轮的速度为()A.) n mile/hB.) n mile/hC.) n mile/hD.) n mile/h答案:B解析:如图,设货轮的时速为v,那么在△AMS中,AMS=45SAM=105ASM=30,SM=20,AM=3v.由正弦定理得,即v==)(n mile/h).解三角形的实践运用举例专项训练分享到这里，更多内容请关注高考数学试题栏目。

2019届高考数学一轮复习第四章解三角形课时跟踪训练24 解三角形应用举例文

学习资料专题课时跟踪训练(二十四) 解三角形应用举例[基础巩固]一、选择题1．已知两座灯塔A、B与C的距离都是a，灯塔A在C的北偏东20°，灯塔B在C的南偏东40°，则灯塔A与灯塔B的距离为( )A．a B.3aC.2a D．2a[解析]如图所示，由余弦定理可知，AB2＝a2＋a2－2a·a·cos120°＝3a2得AB＝3a.故选B.[答案] B2．如图，设A、B两点在河的两岸，一测量者在A的同侧，在所在的河岸边选定一点C，测出AC的距离为50 m，∠ACB＝45°，∠CAB＝105°后，就可以计算出A、B两点的距离为( )A．50 2 m B．50 3 mC ．25 2 m D.2522m [解析] 由题意得∠B ＝180°－45°－105°＝30°，由正弦定理得AB sin ∠ACB ＝ACsin B，∴AB ＝AC ·sin∠ACBsin B ＝50×2212＝502(m)．[答案] A3．两座灯塔A 和B 与海岸观察站C 的距离相等，灯塔A 在观察站北偏东40°，灯塔B 在观察站南偏东60°，则灯塔A 在灯塔B 的( )A ．北偏东10°B ．北偏西10°C ．南偏东10°D ．南偏西10°[解析] 灯塔A 、B 的相对位置如图所示，由已知得∠ACB ＝80°， ∠CAB ＝∠CBA ＝50°，则α＝60°－50°＝10°，即北偏西10°. [答案] B4．在湖面上高为10 m 处测得天空中一朵云的仰角为30°，测得湖中之影的俯角为45°，则云距湖面的高度为(精确到0.1 m)( )A ．2.7 mB ．17.3 mC ．37.3 mD ．373 m[解析] 依题意画出示意图．则CM －10tan30°＝CM ＋10tan45°∴CM ＝tan45°＋tan30°tan45°－tan30°×10≈37.3. [答案] C5．张晓华同学骑电动自行车以24 km/h 的速度沿着正北方向的公路行驶，在点A 处望见电视塔S 在电动车的北偏东30°方向上，15 min 后到点B 处望见电视塔在电动车的北偏东75°方向上，则电动车在点B 时与电视塔S 的距离是( )A ．2 2 kmB ．3 2 kmC ．3 3 kmD ．2 3 km[解析] 画出示意图如图，由条件知AB ＝24×1560＝6.在△ABS 中，∠BAS ＝30°，AB ＝6，∠ABS ＝180°－75°＝105°，所以∠ASB ＝45°.由正弦定理知BS sin30°＝AB sin45°，所以BS ＝AB sin30°sin45°＝3 2.[答案] B6．在200米高的山顶上，测得山下一塔顶和塔底的俯角分别为30°，60°，则塔高为( )A.4003米 B.40033 米 C.20033米 D.2003米[解析] 作出示意图如右图，由已知，在Rt △OAC 中，OA ＝200，∠OAC ＝30°，则OC ＝OA ·tan ∠OAC ＝200tan30°＝20033.在Rt △ABD 中，AD ＝20033，∠BAD ＝30°，则BD ＝AD ·tan∠BAD ＝20033·tan30°＝2003，∴BC ＝CD －BD ＝200－2003＝4003.[答案] A 二、填空题7．一船以每小时15 km 的速度向正东航行，船在A 处看到一个灯塔M 在北偏东60°方向，行驶4 h 后，船到B 处，看到这个灯塔在北偏东15°方向，这时船与灯塔的距离为________km.[解析]如图所示，依题意有：AB ＝15×4＝60，∠MAB ＝30°，∠AMB ＝45°，在△AMB 中，由正弦定理得60sin45°＝BMsin30°，解得BM ＝302(km)． [答案] 30 28．(2017·广东广州市高三综合测试)江岸边有一炮台高30 m ，江中有两条船，船与炮台底部在同一水面上，由炮台顶部测得俯角分别为45°和60°，而且两条船与炮台底部连线成30°角，则两条船相距________m.[解析] 如图，由题意知，OA ＝30， ∠OAM ＝45°，∠OAN ＝30°， ∠MON ＝30°.在Rt △AOM 中，OM ＝OA · tan ∠OAM ＝30·tan45°＝30.在Rt △AON 中，ON ＝OA ·tan∠OAN ＝30·tan30°＝10 3. 在△MON 中，由余弦定理得MN ＝OM 2＋ON 2－2OM ·ON ·cos∠MON＝900＋300－2×30×103×32＝300＝103(m)． [答案] 10 39．(2018·山西大学附中检测)如图，从气球A 上测得正前方的河流的两岸B ，C 的俯角分别为75°，30°，此时气球的高是60 m ，则河流的宽度BC 等于________m.[解析] 如图，∠ACD ＝30°， ∠ABD ＝75°，AD ＝60 m, 在Rt △ACD 中，CD ＝AD tan ∠ACD ＝60tan30°＝603(m)，在Rt △ABD 中，BD ＝ADtan ∠ABD ＝60tan75°＝602＋3＝60(2－3)(m)，∴BC ＝CD －BD ＝603－60(2－3)＝120(3－1)(m)． [答案] 120(3－1) 三、解答题10.港口A 北偏东30°方向的C 处有一检查站，港口正东方向的B 处有一轮船，距离检查站为31海里，该轮船从B 处沿正西方向航行20海里后到达D 处观测站，已知观测站与检查站距离21海里，问此时轮船离港口A 还有多远？[解] 在△BDC 中，BC ＝31，BD ＝20，CD ＝21，由余弦定理知，cos ∠CDB ＝BD 2＋CD 2－BC 22BD ·CD＝－17，∴sin ∠CDB ＝437.∴sin ∠ACD ＝sin ⎝⎛⎭⎪⎫∠CDB －π3＝sin ∠CDB cos π3－cos ∠CDB sin π3＝5314. 在△ACD 中，由正弦定理知AD sin ∠ACD ＝CD sin A ⇒AD ＝5314×21÷32＝15.∴此时轮船距港口还有15海里．[能力提升]11．(2017·山西太原模拟)某登山队在山脚A 处测得山顶B 的仰角为45°，沿倾斜角为30°的斜坡前进1000 m 后到达D 处，又测得山顶的仰角为60 °，则山的高度BC 为( )A ．500(3＋1)mB ．500 mC ．500(2＋1)mD ．1000 m[解析]过点D 作DE ∥AC 交BC 于E ，因为∠DAC ＝30°，故∠ADE ＝150°.于是∠ADB ＝360°－150°－60°＝150°.又∠BAD ＝45°－30°＝15°，故∠ABD ＝15°，由正弦定理，得AB ＝AD sin ∠ADB sin ∠ABD ＝1000sin150°sin15°＝500(6＋2)(m)所以在Rt △ABC 中，BC ＝AB sin45°＝500(3＋1)(m)．[答案] A12．某人在C点测得某塔在南偏西80°，塔顶仰角为45°，此人沿南偏东40°方向前进10米到D，测得塔顶A的仰角为30°，则塔高为( )A．15米B．5米C．10米D．12米[解析]如图，设塔高为h，在Rt△AOC中，∠ACO＝45°，则OC＝OA＝h.在Rt△AOD中，∠ADO＝30°，则OD＝3h，在△OCD中，∠OCD＝120°，CD＝10，由余弦定理得：OD2＝OC2＋CD2－2OC·CD cos∠OCD，即(3h)2＝h2＋102－2h×10×cos120°，∴h2－5h－50＝0，解得h＝10或h＝－5(舍)．[答案] C13．甲船在A处观察乙船，乙船在它的北偏东60°的方向，两船相距a海里，乙船正向北行驶，若甲船是乙船速度的3倍，则甲船应取方向________才能追上乙船；追上时甲船行驶了________海里．[解析] 如图所示，设到C 点甲船追上乙船，乙到C 地用的时间为t ，乙船速度为v ，则BC ＝tv ，AC ＝3tv ，B ＝120°，由正弦定理知BC sin ∠CAB ＝ACsin B ，∴1sin ∠CAB ＝3sin120°，∴sin ∠CAB ＝12，∴∠CAB ＝30°，∴∠ACB ＝30°，∴BC ＝AB ＝a ，∴AC 2＝AB 2＋BC 2－2AB ·BC cos120°＝a 2＋a 2－2a 2·⎝ ⎛⎭⎪⎫－12＝3a 2，∴AC ＝3a .[答案] 北偏东30°3a14. (2017·广东省五校协作体高三一诊)如图所示，在一个坡度一定的山坡AC 的顶上有一高度为25 m 的建筑物CD ，为了测量该山坡相对于水平地面的坡角θ，在山坡的A 处测得∠DAC ＝15°，沿山坡前进50 m 到达B 处，又测得∠DBC ＝45°，根据以上数据可得cos θ＝________.[解析] 由∠DAC ＝15°，∠DBC ＝45°可得∠BDA ＝30°，∠DBA ＝135°，∠BDC ＝90°－(15°＋θ)－30°＝45°－θ，由内角和定理可得∠DCB ＝180°－(45°－θ)－45°＝90°＋θ，根据正弦定理可得50sin30°＝DBsin15°，即DB ＝100sin15°＝100×sin(45°－30°)＝252(3－1)，又25sin45°＝2523－＋θ，即25sin45°＝2523－cos θ，得到cos θ＝3－1.[答案]3－115.海岛B 上有一座高为10米的塔，塔顶有一个观测站A ，上午11时测得一游船位于岛北偏东15°方向上，且俯角为30°的C 处，一分钟后测得该游船位于岛北偏西75°方向上，且俯角为45°的D 处．(假设游船匀速行驶)(1)求该船行驶的速度(单位：米/分钟)；(2)又经过一段时间后，游船到达海岛B 的正西方向E 处，问此时游船距离海岛B 多远？ [解] (1)在Rt △ABC 中，∠BAC ＝60°，AB ＝10，则BC ＝103米；在Rt △ABD 中，∠BAD ＝45°，AB ＝10，则BD ＝10米；在△BCD 中，∠DBC ＝75°＋15°＝90°，则CD ＝ BD 2＋BC 2＝20米．所以速度v ＝CD1＝20米/分钟．(2)在Rt △BCD 中，∠BCD ＝30°，又因为∠DBE ＝15°，所以∠CBE ＝105°，所以∠CEB ＝45°. 在△BCE 中，由正弦定理可知EB sin30°＝BCsin45°，所以EB ＝BC sin30°sin45°＝56米．[延伸拓展](2017·江西宜春段考)某工厂实施煤改电工程防治雾霾，欲拆除高为AB 的烟囱，测绘人员取与烟囱底部B 在同一水平面内的两个观测点C ，D ，测得∠BCD ＝75°，∠BDC ＝60°，CD ＝40米，并在点C 处的正上方E 处观测顶部A 的仰角为30°，且CE ＝1米，则烟囱高AB＝________米．[解析] ∠CBD ＝180°－∠BCD －∠BDC ＝45°，在△CBD 中，根据正弦定理得BC ＝CD sin ∠BDCsin ∠CBD＝206，∴AB ＝1＋tan30°·CB ＝1＋202(米)． [答案] 1＋20 2。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

课时分层训练(二十五) 解三角形实际应用举例A组基础达标一、选择题1．如图388，两座灯塔A和B与海岸观察站C的距离相等，灯塔A在观察站南偏西40°，灯塔B在观察站南偏东60°，则灯塔A在灯塔B的( )图388A．北偏东10°B．北偏西10°C．南偏东80°D．南偏西80°D[由条件及题图可知，∠A＝∠B＝40°，又∠BCD＝60°，所以∠CBD＝30°，所以∠DBA＝10°，因此灯塔A在灯塔B南偏西80°.]2．如图389所示，已知两座灯塔A和B与海洋观察站C的距离都等于a km，灯塔A在观察站C的北偏东20°，灯塔B在观察站C的南偏东40°，则灯塔A与灯塔B的距离为( )图389A．a km B.3a kmC.2a km D．2a kmB[在△ABC中，AC＝BC＝a，∠ACB＝120°，∴AB2＝a2＋a2－2a2cos 120°＝3a2，AB＝3a.]3．如图3810，测量河对岸的塔高AB时可以选与塔底B在同一水平面内的两个测点C与D，测得∠BCD＝15°，∠BDC＝30°，CD＝30 m，并在点C测得塔顶A的仰角为60°，则塔高AB等于( )图3810A．5 6 m B．15 3 m C．5 2 m D．15 6 mD[在△BCD中，∠CBD＝180°－15°－30°＝135°.由正弦定理得BCsin 30°＝30sin 135°，解得BC＝152(m)．在Rt△ABC中，AB＝BC tan∠ACB＝152×3＝156(m)．]4．如图3811，一条河的两岸平行，河的宽度d＝0.6 km，一艘客船从码头A出发匀速驶往河对岸的码头B.已知AB＝1 km，水的流速为2 km/h，若客船从码头A驶到码头B所用的最短时间为6 min，则客船在静水中的速度为 ( )【导学号：79140138】图3811A．8 km/h B．6 2 km/hC．234 km/h D．10 km/hB[设AB与河岸线所成的角为θ，客船在静水中的速度为v km/h，由题意知，sin θ＝0.61＝35，从而cos θ＝45，所以由余弦定理得⎝⎛⎭⎪⎫110v2＝⎝⎛⎭⎪⎫110×22＋12－2×110×2×1×45，解得v＝6 2.]5．如图3812，在塔底D的正西方A处测得塔顶的仰角为45°，在塔底D的南偏东60°的B处测得塔顶的仰角为30°，A、B的距离是84 m，则塔高CD为( )图3812A ．24 mB ．12 5 mC ．127 mD ．36 mC [设塔高CD ＝x m ，则AD ＝x m ，DB ＝3x m.又由题意得∠ADB ＝90°＋60°＝150°，在△ABD 中，利用余弦定理，得 842＝x 2＋(3x )2－23·x 2cos 150°，解得x ＝127(负值舍去)，故塔高为127 m ．] 二、填空题6．已知A 船在灯塔C 北偏东80°处，且A 到C 的距离为2 km ，B 船在灯塔C 北偏西40°，A ，B 两船的距离为3 km ，则B 到C 的距离为________ km.6－1 [如图，由条件知，∠ACB ＝80°＋40°＝120°，设BC ＝x km ，则由余弦定理知9＝x 2＋4－4x cos 120°， ∵x ＞0，∴x ＝6－1.]7．在200 m 高的山顶上，测得山下一塔顶与塔底的俯角分别为30°，60°，则塔高是________ m.4003[如图，设塔AB 高为h ，在Rt△CDB 中，CD ＝200 m ，∠BCD ＝90°－60°＝30°， ∴BC ＝200cos 30°＝40033(m)．在△ABC 中，∠ABC ＝∠BCD ＝30°， ∠ACB ＝60°－30°＝30°， ∴∠BAC ＝120°.在△ABC中，由正弦定理得BC sin 120°＝ABsin 30°，∴AB ＝BC ·sin 30°sin 120°＝4003(m)．]8．(2018·福州质检)如图3813，小明同学在山顶A 处观测到，一辆汽车在一条水平的公路上沿直线匀速行驶，小明在A 处测得公路上B ，C 两点的俯角分别为30°，45°，且∠BAC ＝135°.若山高AD ＝100 m ，汽车从B 点到C 点历时14 s ，则这辆汽车的速度为________ m/s(精确到0.1)．参考数据：2≈1.414，5≈2.236.【导学号：79140139】图381322.6 [由题意可得AB ＝200，AC ＝1002，在△ABC 中，由余弦定理可得BC 2＝AB 2＋AC 2－2AB ·AC ·cos∠BAC ＝105，则BC ＝10010≈141.4×2.236，又历时14 s ，所以速度为BC14≈22.6 m/s.]三、解答题9．如图3814，航空测量组驾驶飞机飞行的航线和山顶在同一铅直平面内，已知飞机的飞行高度为10 000 m ，速度为50 m/s ，某一时刻飞机看山顶的俯角为15°，经过420 s 后看山顶的俯角为45°，求山顶的海拔高度．(取2≈1.4，3≈1.7)图3814[解] 如图，作CD 垂直直线AB 于点D ， ∵∠A ＝15°，∠DBC ＝45°， ∴∠ACB ＝30°，又在△ABC 中，BCsin A ＝ABsin∠ACB，AB ＝50×420＝21 000，∴BC ＝21 00012×sin 15°＝10 500(6－2)．∵CD ⊥AD ，∴CD ＝BC ·sin∠DBC ＝10 500(6－2)×22＝10 500(3－1)≈7 350. 故山顶的海拔高度为10 000－7 350＝2 650(m)．10．如图3815，渔船甲位于岛屿A 的南偏西60°方向的B 处，且与岛屿A 相距12海里，渔船乙以10海里/小时的速度从岛屿A 出发沿正北方向航行，若渔船甲同时从B 处出发沿北偏东α的方向追赶渔船乙，刚好用2小时追上．图3815(1)求渔船甲的速度； (2)求sin α的值．[解] (1)依题意知，∠BAC ＝120°，AB ＝12，AC ＝10×2＝20，∠BCA ＝α. 在△ABC 中，由余弦定理，得BC 2＝AB 2＋AC 2－2AB ·AC ·cos∠BAC＝122＋202－2×12×20×cos 120°＝784，解得BC ＝28. 所以渔船甲的速度为BC2＝14海里/小时．(2)在△ABC 中，因为AB ＝12，∠BAC ＝120°，BC ＝28，∠BCA ＝α，由正弦定理，得ABsin α＝BCsin 120°，即sin α＝AB sin 120°BC ＝12×3228＝3314. B 组能力提升11．一个大型喷水池的中央有一个强力喷水柱，为了测量喷水柱喷出的水柱的高度，某人在喷水柱正西方向的点A 测得水柱顶端的仰角为45°，沿点A 向北偏东30°前进100 m 到达点B ，在B 点测得水柱顶端的仰角为30°，则水柱的高度是 ( ) A ．50 m B ．100 m C ．120 mD ．150 mA [设水柱高度是h m ，水柱底端为C (图略)，则在△ABC 中，A ＝60°，AC ＝h ，AB ＝100，BC ＝3h ，根据余弦定理得，(3h )2＝h 2＋1002－2·h ·100·cos 60°，即h 2＋50h －5 000＝0，即(h －50)(h ＋100)＝0，即h ＝50，故水柱的高度是50 m ．]12．在不等边三角形ABC 中，角A ，B ，C 所对的边分别为a ，b ，c ，其中a 为最大边，如果sin 2(B ＋C )＜sin 2B ＋sin 2C ，则角A 的取值范围为( )A.⎝⎛⎭⎪⎫0，π2B ．⎝ ⎛⎭⎪⎫π4，π2C.⎝⎛⎭⎪⎫π6，π3D ．⎝ ⎛⎭⎪⎫π3，π2 D [由题意得sin 2A ＜sin 2B ＋sin 2C ，再由正弦定理得a 2＜b 2＋c 2，即b 2＋c 2－a 2＞0.则cos A ＝b 2＋c 2－a 22bc＞0，∵0＜A ＜π，∴0＜A ＜π2.又a 为最大边，∴A ＞π3.因此角A 的取值范围是⎝ ⎛⎭⎪⎫π3，π2.] 13．如图3816，为测量山高MN ，选择A 和另一座山的山顶C 为测量观测点．从A 点测得M 点的仰角∠MAN ＝60°，C 点的仰角∠CAB ＝45°以及∠MAC ＝75°；从C 点测得∠MCA＝60°.已知山高BC ＝100 m ，则山高MN ＝________m.图3816150 [根据题图，AC ＝100 2 m.在△MAC 中，∠CMA ＝180°－75°－60°＝45°. 由正弦定理得AC sin 45°＝AMsin 60°⇒AM ＝100 3 m.在△AMN 中，MN AM＝sin 60°， ∴MN ＝1003×32＝150(m)．] 14．“德是”号飞船返回舱顺利到达地球后，为了及时将航天员救出，地面指挥中心在返回舱预计到达的区域安排了同一条直线上的三个救援中心，如图3817(记为B ，C ，D )．当返回舱在距地面1万米的P 点时(假定以后垂直下落，并在A 点着陆)，C 救援中心测得飞船位于其南偏东60°方向，仰角为60°，B 救援中心测得飞船位于其南偏西30°方向，仰角为30°，D 救援中心测得着陆点A 位于其正东方向.【导学号：79140140】图3817(1)求B ，C 两救援中心间的距离； (2)求D 救援中心与着陆点A 间的距离．[解] (1)由题意知PA ⊥AC ，PA ⊥AB ，则△PAC ，△PAB 均为直角三角形．在Rt△PAC 中，PA ＝1，∠PCA ＝60°，解得AC ＝33，在Rt△PAB 中，PA ＝1，∠PBA ＝30°，解得AB ＝3，又∠CAB ＝90°，BC ＝AC 2＋AB 2＝303万米． (2)sin∠ACD ＝sin∠ACB ＝310，cos∠ACD ＝－110，又∠CAD ＝30°，所以sin∠ADC ＝sin(30°＋∠ACD )＝33－1210，在△ADC 中，由正弦定理，ACsin∠ADC ＝ADsin∠ACD，得AD ＝AC ·sin∠ACD sin∠ADC ＝9＋313万米．。