浙江省金华市2010届高三年级高考能力测试试卷(数学理)
2010年普通高等学校招生全国统一考试(浙江卷)数学试题 (理科)(解析版)(word版)

绝密★考试结束前2010年普通高等学校招生全国统一考试(浙江卷)数 学(理科)本试题卷分选择题和非选择题两部分。
全卷共5页,选择题部分1至2页,非选择题部分3至5页。
满分150分,考试时间120分钟。
请考生按规定用笔将所有试题的答案涂、写在答题纸上。
选择题部分(共50分)注意事项:1.答题前,考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸规定的位置上。
2.每小题选出答案后,用2B 铅笔把答题纸上对应题目的答案标号涂黑,如需改动,用像皮擦干净后,再选涂其它答案标号。
不能答在试题卷上。
参考公式:如果事件A 、B 互斥,那么 柱体的体积公式 P (A +B )=P (A )+P (B ) Sh V =如果事件A 、B 相互独立,那么 其中S 表示柱体的底面积,h 表示柱体的高P (A ·B )=P (A )·P (B ) 锥体的体积公式如果事件A 在一次试验中发生的概率是P ,那么n Sh V 31=次独立重复试验中恰好发生k 次的概率 其中S 表示锥体的底面积,h 表示锥体的高k n k kn n P P C k P --=)1()(),,2,1,0(n k = 球的表面积公式台体的体积公式 24R S π= )(312211S S S S h V ++= 球的体积公式其中S 1,S 2分别表示台体的上、下底面积 334R V π=h 表示台体的高 其中R 表示球的半径一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的. (1)设P={x ︱x <4},Q={x ︱2x <4},则( )(A )p Q ⊆ (B )Q P ⊆(C )Rp Q C ⊆(D )RQ P C ⊆解析:{}22<<x x Q -=,可知B 正确,本题主要考察了集合的基本运算,属容易题(2)某程序框图如图所示,若输出的S=57,则判断框内位( ) (A ) k >4? (B )k >5? (C ) k >6? (D )k >7?解析:选A ,本题主要考察了程序框图的结构,以及与数列有关的简 单运算,属容易题(3)设n S 为等比数列{}n a 的前n 项和,2580a a +=,则52S S =( ) (A )11 (B )5 (C )8- (D )11-解析:解析:通过2580a a +=,设公比为q ,将该式转化为08322=+q a a ,解得q =-2,带入所求式可知答案选D ,本题主要考察了本题主要考察了等比数列的通项公式与前n 项和公式,属中档题(4)设02x π<<,则“2sin 1x x <”是“sin 1x x <”的( )(A )充分而不必要条件 (B )必要而不充分条件(C )充分必要条件 (D )既不充分也不必要条件 解析:因为0<x <2π,所以sinx <1,故x sin 2x <x sinx ,结合x sin 2x 与x sinx 的取值范围相同,可知答案选B ,本题主要考察了必要条件、充分条件与充要条件的意义,以及转化思想和处理不等关系的能力,属中档题(5)对任意复数()i ,R z x y x y =+∈,i 为虚数单位,则下列结论正确的是( ) (A )2z z y -= (B )222z x y =+ (C )2z z x -≥ (D )z x y ≤+解析:可对选项逐个检查,A 项,y z z 2≥-,故A 错,B 项,xyi y x z 2222+-=,故B 错,C 项,y z z 2≥-,故C 错,D 项正确。
浙江省金华十校2010届高三上学期期末考试(数学理)

f ( x) 2 sin( x
18.已知
3
) cos( x
3
) 2 3 cos 2 ( x
3
) 3.
(1)求 f ( x) 的最大值及取得最大值时相应的 x 的值;
y f (2 x) a在区间[0, ] 4 上恰有两上零点 x1 , x 2 , 求 tan( x1 x 2 ) 的值。 (2)若函数
1 ln , x 0 x f ( x) 1 , x 0 x 6.已知 则 f ( x) 1 的解集为
A. ( ,1) (1,) C. ( 1,0) (1,) B. ( ,1) (0,1) D. ( 1,0) (0,1)
3
, t 2 4 x2
3)
由 y 2 sin t 图象性质知
t1 t 2 , 即4 x1
3
4 x2
3
…………10 分
x1 x 2
4
6
, tan( x1 x 2 ) 2 3
…………14 分
5
2 2 1 , . 19.解:(1)抽 1 次得到红球的概率为 5 ,得白球的概率为 5 得黑球的概率为 5 2 3 36 P1 C 32 ( ) 2 5 5 125 所以恰 2 次为红色球的概率为 2 2 1 24 3 P2 ( ) A3 5 5 5 125 抽全三种颜色的概率
1 ( x 1) 2 ( y ) 2 1 2 14.
13.3 16. g ( x) 3 17. 2 2 三、解答题:本大题共 5 小题,18—20 题每题 14 分,21—22 题每题 15 分,共 72 分。
浙江省2010届高三上学期高考调研考试 (数学理)
(第 20 题) 21. (本题满分 15 分) 已知抛物线 C 的顶点在原点,焦点为 F(0,1). (Ⅰ)求抛物线 C 的方程; (Ⅱ)在抛物线 C 上是否存在点 P,使得过点 P 的直线交 C 于另一点 Q,满足 PF⊥QF,且 PQ 与 C 在点 P 处的切线垂直? 若存在,求出点 P 的坐标; 若不存在,请说明理由. y Q
z B E A C M P x F y
5 , 2 13
sin∠ACP =
3 3 . 2 13
…………………(7 分)
因此 S△ACP= 3 3 .
(Ⅱ)解: BA =(1,-4 3 ,- 3 ) , MC =(0,-2 3 ,0),
BA MC 24,
1 3
如果事件 A 在一次试验中发生的概率是 p,那么 n V= Sh 次独立重复试验中事件 A 恰好发生 k 次的概率 Pn(k)=C n pk(1-p)n-k (k = 0,1,2,…,n) 棱台的体积公式
V 1 3 h ( S1 S1 S 2 S 2 )
k
其中 S 表示棱锥的底面积,h 表示棱锥的高 球的表面积公式 S = 4πR2 球的体积公式 V= πR3
A.1 B.2 C.3 D.4
(
)
非选择题部分
(共 100 分)
二、填空题:本大题共 7 小题,每小题 4 分,共 28 分。
2 x y 0, 11.若实数 x, y 满足不等式组 x y 3 0, 则 3x-y 的最小值是________. 3 x y 8 0,
F O 22. (本题满分 14 分)
3 2
P x
(第 21 题)
浙江省金华十校2010年高考模拟考试(数学理)

浙江省金华十校2010年高考模拟考试(数学理)本试卷分第Ⅰ卷和第Ⅱ卷两部分,考试时间120分钟,请考生按规定用笔将所有试题的答案涂、写在答题纸上。
参考公式:如果事件A 、B 互斥,那么柱体的体积公式P(A+B)=P(A)+P(B) V Sh =如果事件A 、B 相互独立,那么其中S 表示柱体的底面积,h 表示柱体的高P(A·B)=P(A)·P(B)锥体的体积公式如果事件A 在一次试验中发生的概率是P ,那么13V Sh=n 次独立重复试验中恰好发生k 次的概率 其中S 表示锥体的底面积,h 表示锥体的高k n kk n n P P C k P --=)1()(球的表面积公式台体的体积公式24S R π=121()3V h S S =+球的体积公式其中S1、S2分别表示台体的上、下底面积 343V π=h 表示台体的高其中R 表示球的半径第Ⅰ卷(选择题共50分)一、选择题:本大题共10小题,每小题5分,满分50分。
在每小题给出的四个选项中,只有一项是符合题目要示的。
1.设i 是虚数单位,则处长数1ii -+的虚部是( )A .2i B .12-C .12D .12-2.设全集*{|}U x N x a =∈≤,集合{1,2,3},{4,5,6},P Q ==则[)6,7a ∈是U C P Q =的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分又不必要条件3.对某种电子元件使用寿命跟踪调查,抽取容量为1000的样本,其步率分布直方图如图所示,根据此图可知这样样本中电子元件的寿命在300-500小时的数量是()A .630个B .640个C .650个D .660个4.已知公差不为0的等差数列{}n a 满足134,,a a a 成等比数列,n n S 为{a }的前n 项和,则3253S S S S --的值为( )A .2B .3C .15D .不存在5.设,a b 为两条直线,,αβ为两个平面,下列四个命题中真命题是()A .若,a b 与α所成角相等,则//a bB .若//,//,//,//a b a b αβαβ则C .若,,//,//a b a b αβαβ⊂⊂则D .若,,,a b a bαβαβ⊥⊥⊥⊥则6.已知向量(cos 2,sin ),(1,2sin 1),(,)4a b πααααπ==-∈,若2,tan(54a b πα⋅=+则的值为()A .13B .27C .17D .237.在24+的展开式中,x 的幂指数为整数的项共有( )A .3项B .4项C .5项D .6项8.函数cos sin y x x =-的图象可由函数y x =的图象()A .向左4π平移个长度单位B .向左34π平移个长度单位C .向右4π平移个长度单位D .向右34π平移个长度单位9.设F1、F2是双曲线2214x y -=的两个焦点,点P 在双曲线上,且12120,|||PF PF PF PF ⋅=⋅ 则|的值为( )A .2B.C .4D .810.已知()f x 是定义在R 上的且以2为周期的偶函数,当01x ≤≤时,2()f x x =,如果直线y x a=+与曲线()y f x =恰有两个不同的交点,则实数a 的值为( )A .2()k k Z ∈B .122()4k k k Z +∈或C .0D .122()4k k k Z -∈或第Ⅱ卷(非选择题 共100分)二、填空题:本大题7小题,每小题4分,共28分。
浙江省金华市2010届高三下学期高考能力测试(数学理)

f ( x)
(I)证明:函数
3x x3 1 (0 x ) 4 3 2 是集合 M 中的元素; 3x x3 1 1 (0 x ) [0, ) 4 3 2 具有下面的性质:对于任意 [m, n] 2 ,都存在
f ( x)
(II)证明:函数
4
x0 (m, n) ,使得等式 f (n) f (m) (n m) f ' ( x0 ) 成立。
现在投掷一
个质地均匀、每个面上标有一个数字的正方体玩具,它的六个面上分别写有两个 1、两个 2、两个 3 一共 六个数字. 质点 P 从 A 点出发,规则如下:当正方体上底面出现的数字是 1,质点 P 前进一步(如由 A
到 B) ;当正方体上底面出现的数字是 2,质点 P 前进两步(如由 A 到 C) ,当正方体上底面出现的数字是 3,质点 P 前进三步(如由 A 到 D ). 在质点 P 转一圈之前连续投掷,若超过一圈,则投掷终止. (Ⅰ)求点 P 恰好返回到 A 点的概率; (Ⅱ)在点 P 转一圈恰能返回到 A 点的所有结果中,用随机变量 表示点 P 恰能返回到 A 点的投掷次 数,求 的数学期望.
20、 (本题满分 14 分)在边长为 3 的正三角形 ABC 中,E、F、P 分别是 AB、AC、BC 边上的点,满足
3
AE CF CP 1 EB FA PB 2 ,将 AEF 沿 EF 折起到 A1 EF 的位置,使二面角 A1 EF B 成直二面角,连结
A1 B , A1 P (如图)
( C、2 D、3
)
A、0
2
B、1
2
5、已知不等式 xy ax 2 y 对于 x [1,2] , y [ 2,3] 恒成立,则实数 a 的取值范围是(
浙江省金华十校2010年高考模拟考试数学试题(理科)
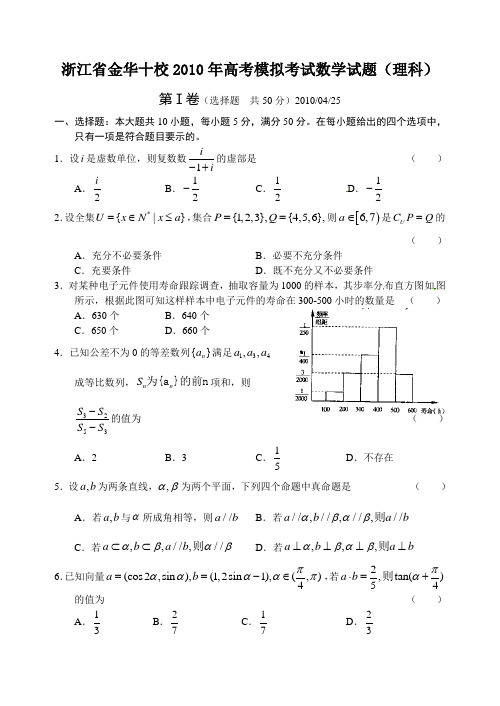
浙江省金华十校2010年高考模拟考试数学试题(理科)第Ⅰ卷(选择题 共50分)2010/04/25一、选择题:本大题共10小题,每小题5分,满分50分。
在每小题给出的四个选项中,只有一项是符合题目要示的。
1.设i 是虚数单位,则复数数1ii -+的虚部是 ( )A .2i B .12- C .12D .12-2.设全集*{|}U x N x a =∈≤,集合{1,2,3},{4,5,6},P Q ==则[)6,7a ∈是U C P Q =的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分又不必要条件3.对某种电子元件使用寿命跟踪调查,抽取容量为1000的样本,其步率分布直方图如图所示,根据此图可知这样样本中电子元件的寿命在300-500小时的数量是 ( ) A .630个 B .640个 C .650个 D .660个 4.已知公差不为0的等差数列{}n a 满足134,,a a a成等比数列,n n S 为{a }的前n 项和,则3253S S S S --的值为 ( )A .2B .3C .15D .不存在5.设,a b 为两条直线,,αβ为两个平面,下列四个命题中真命题是 ( ) A .若,a b 与α所成角相等,则//a b B .若//,//,//,//a b a b αβαβ则C .若,,//,//a b a b αβαβ⊂⊂则D .若,,,a b a b αβαβ⊥⊥⊥⊥则6.已知向量(cos 2,sin ),(1,2sin 1),(,)4a b πααααπ==-∈,若2,t a n ()54a b πα⋅=+则的值为 ( )A .13 B .27 C .17 D .237.在24的展开式中,x 的幂指数为整数的项共有 ( )A .3项B .4项C .5项D .6项8.函数cos sin y x x =-的图象可由函数y x =的图象 ( )A .向左4π平移个长度单位 B .向左34π平移个长度单位C .向右4π平移个长度单位D .向右34π平移个长度单位9.设F 1、F 2是双曲线2214x y -=的两个焦点,点P 在双曲线上,且12120,|||PF PF PF PF ⋅=⋅则|的值为( )A .2B.C .4D .810.已知()f x 是定义在R 上的且以2为周期的偶函数,当01x ≤≤时,2()f x x =,如果直线y x a =+与曲线()y f x =恰有两个不同的交点,则实数a 的值为 ( ) A .2()k k Z ∈ B .122()4k k k Z +∈或 C .0 D .122()4k k k Z -∈或 第Ⅱ卷(非选择题 共100分)二、填空题:本大题7小题,每小题4分,共28分。
全国高考理科数学试题及答案-浙江

2010年普通高等学校招生全国统一考试(浙江卷)数 学(理科)本试题卷分选择题和非选择题两部分。
全卷共5页,选择题部分1至2页,非选择题部分3至5页。
满分150分,考试时间120分钟。
参考公式:如果事件A ,B 互斥,那么 P (A +B )=P (A )+P (B ) 如果事件A ,B 相互独立,那么 P (A ·B )=P (A )·P (B )如果事件A 在一次试验中发生的概率是P ,那么n 次独立重复试验中恰好发生k 次的概率k n kk n n P P C k P --=)1()(),,2,1,0(n k =台体的体积公式)(312211S S S S h V ++=,其中1S ,2S 分别表示台体的上、下底面积,h 表示台体的高柱体的体积公式 Sh V =,其中S 表示柱体的底面积,h 表示柱体的高 锥体的体积公式Sh V 31=,其中S 表示锥体的底面积,h 表示锥体的高 球的表面积公式24R S π= 球的体积公式334R V π=,其中R 表示球的半径 第I 卷选择题部分(共50分)一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设}4|{},4|{2<=<=x x Q x x P ,则( )A.Q P ⊆B.P Q ⊆C.⊆P Q RD.⊆Q P R2.某程序框图如图所示,若输出的S=57,则判断框内为 ( ) A.?4>k B.?5>kC.?6>kD.?7>k3.设n S 为等比数列}{n a 的前n 项和,0852=+a a ,则=25S S ( ) A.11 B.5C.-8D.-114.设20π<<x ,则“1sin 2<x x ”是“1sin <x x ”的 ( )A.充分而不必不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件5.对任意复数i R y x yi x z ),,(∈+=为虚数单位,则下列结论正确的是( )A.y z z 2||=-B.222y x z +=C.x z z 2||≥-D.||||||y x z +≤6.设m l ,是两条不同的直线,α是一个平面,则下列命题正确的是 ( ) A.若αα⊥⊂⊥l m m l 则,, B.若αα⊥⊥m m l l 则,//,C.若m l m l //,,//则αα⊂D.若m l m l //,//,//则αα7.若实数y x ,满足不等式组⎪⎩⎪⎨⎧≥+-≤--≥-+,01,032,033m y x y x y x 且y x +的最大值为9,则实数=m ( )A.-2B.-1C.1D.28.设F 1,F 2分别为双曲线)0,0(12222>>=-b a by a x 的左、右焦点.若在双曲线右支上存在点P ,满足||||212F F PF =,且F 2到直线PF 1的距离等于双曲线的实轴长,则该双曲的渐近线方程为( )A.043=±y xB.053=±y xC.034=±y xD.045=±y x9.设函数x x x f -+=)12sin(4)(,则在下列区间中函数)(x f 不.存在零点的是( )A.[-4,-2]B.[-2,0]C.[0,2]D.[2,4]10.设函数的集合}1,0,1;1,21,0,31|)(log )({2-=-=++==b a b a x x f P ,平面上点的集合}1,0,1;1,21,0,21|),{(-=-==y x y x Q ,则在同一直角坐标系中,P 中函数)(x f 的图象恰好..经过Q 中两个点的函数的个数是( )A.4B.6C.8D.10第Ⅱ卷(非选择题 共90分)二、填空题:本大题共7小题,每小题4分,共28分。
2010年全国高考理科数学试题及答案-浙江

绝密★考试结束前2010年普通高等学校招生全国统一考试数 学(理科)本试题卷分选择题和非选择题两部分。
全卷共5页,选择题部分1至2页,非选择题部分3至5页。
满分150分,考试时间120分钟。
请考生按规定用笔将所有试题的答案涂、写在答题纸上。
选择题部分(共50分)注意事项:1.答题前,考生务必将自己的姓名、准考证号用黑色字迹的签字笔或钢笔填写在答题纸规定的位置上。
2.每小题选出答案后,用2B 铅笔把答题纸上对应题目的答案标号涂黑,如需改动,用像皮擦干净后,再选涂其它答案标号。
不能答在试题卷上。
参考公式:如果事件A 、B 互斥,那么 柱体的体积公式 P (A +B )=P (A )+P (B ) Sh V =如果事件A 、B 相互独立,那么 其中S 表示柱体的底面积,h 表示柱体的高 P (A ·B )=P (A )·P (B ) 锥体的体积公式 如果事件A 在一次试验中发生的概率是P ,那么n Sh V 31=次独立重复试验中恰好发生k 次的概率 其中S 表示锥体的底面积,h 表示锥体的高 k n kk n n P P C k P --=)1()(),,2,1,0(n k = 球的表面积公式台体的体积公式 24R S π= )(312211S S S S h V ++= 球的体积公式其中S 1,S 2分别表示台体的上、下底面积 334R V π=h 表示台体的高 其中R 表示球的半径一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)设}4|{},4|{2<=<=x x Q x x P (A )Q P ⊆ (B )P Q ⊆(C )QC P R ⊆(D )P C Q R ⊆(2)某程序框图如图所示,若输出的S=57,则判断框内为 (A )?4>k (B )?5>k(C )?6>k(D )?7>k(3)设n S 为等比数列}{n a 的前n 项和,0852=+a a ,则=25S S (A )11 (B )5(C )-8(D )-11(4)设20π<<x ,则“1sin 2<x x ”是“1sin <x x ”的 (A )充分而不必不必要条件 (B )必要而不充分条件 (C )充分必要条件(D )既不充分也不必要条件(5)对任意复数i R y x yi x z ),,(∈+=为虚数单位,则下列结论正确的是(A )y z z 2||=- (B )222y x z += (C )x z z 2||≥- (D )||||||y x z +≤(6)设m l ,是两条不同的直线,α是一个平面,则下列命题正确的是 (A )若αα⊥⊂⊥l m m l 则,, (B )若αα⊥⊥m m l l 则,//,(C )若m l m l //,,//则αα⊂(D )若m l m l //,//,//则αα(7)若实数y x ,满足不等式组⎪⎩⎪⎨⎧≥+-≤--≥-+,01,032,033m y x y x y x 且y x +的最大值为9,则实数=m(A )-2(B )-1(C )1(D )2(8)设F 1,F 2分别为双曲线)0,0(12222>>=-b a by a x 的左、右焦点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
金华市 高三年级高考能力测试试卷数学(理科) 2010.03注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在试卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
答在试卷上无效。
3.填空题和解答题用0、5毫米的黑色墨水签字笔答在答题卡上每题对应的答题区域内。
答在试题卷上无效。
4.考试结束,请将本试题卷和答题卡一并上交。
选择题部分(共50分)一、选择题:本大题共10个小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的,把所选项前的字母填在题后括号内. 1、设1a >,集合103x A xx -⎧⎫=>⎨⎬-⎩⎭,(){}210B x x a x a =-++<。
若A B ⊆,则a 的取值范围是( )A .13a <≤B .3a ≥C .3a >D .13a <<2、若5)1(ax -的展开式中3x 的系数是270,则实数a 的值是( )A .-3 B. 33 C. 3 D. 31-3、已知,m n 是两条不同直线,,,αβγ是三个不同平面,下列命题中正确的是( ).A .,,m n m n αα若则‖‖‖B .,,αγβγαβ⊥⊥若则‖C .,,m n αβαβ若则‖‖‖D .,,m n m n αα⊥⊥若则‖4、设1232,2()((2))log (1) 2.x e x f x f f x x -⎧⎪=⎨-≥⎪⎩<,则的值为, ( ) A 、0 B 、1 C 、2 D 、35、已知不等式222y ax xy +≤对于]2,1[∈x ,]3,2[∈y 恒成立,则实数a 的取值范围是( ) (A )]2,1[-(B )]1,(-∞(C )]2,0((D )),1[+∞-6、某五所大学进行自主招生,同时向一所重点中学的五位学习成绩优秀,并在某些方面有特长的学生发出提前录取通知单.若这五名学生都乐意进这五所大学中的任意一所就读,则仅有两名学生录取到同一所大学(其余三人在其他学校各选一所不同大学)的概率是( ) A 、15 B 、24125C 、96125D 、481252010学年第一学期7、阅读右图的程序框图(框图中的赋值符号“=”也可以写成“←”或“:=”), 若输出的S 的值等于16,那么在程序框图中的判断框内应填写的条件是 A 、i>5 B 、i> 6 C 、i> 7 D 、i> 8 8、已知平面向量→OA 与→OB 的夹角]120,60[︒︒∈θ,且3||||→→==OB OA 若→→→+=OB OA OP 3231,则→||OP 的取值范围是( )A . ]22,3[B . ]5,3[ C. ]7,5[ D . ]7,3[ 9、已知函数f(x)= x2+2x +1,F(x)=⎩⎨⎧<-≥)0()()0()(x x f x x f ,若x R ∈时,g(x )=F(x ) -k x 是增函数,则实数k 的取值范围是( )A . 22≤≤-kB . 2≥kC . 2-≤kD . φ 10是离心率相同的椭圆,外层椭圆顶点向内层椭圆引切线AC 、BD .设内层椭圆方程为22221xy ab+=(0)a b >>,则外层椭圆方程可设为22221()()xyma mb +=(0,1)a b m >>>.若AC 积为916-,则椭圆的离心率为( )A 、4B 、2C 、64D 、34非选择题部分(共100分)二、填空题:本大题共7小题,每小题4分,共28分.请将答案填在答题卡对应题号的位置上, 11、已知a R ∈,若(1)(32)ai i -+为纯虚数,则a 的值为________________。
12、若()3211nn x x ax bx +=+++++ ,且3a b =,则n =_________。
13、如图是一个简单的组合体的直观图与三视图.下面是一个棱长为4的正方体,正上面放一个球,且球的一部分嵌入正方体中,则球的半径是________________。
14、已知对于任意实数x ,函数)(x f 满足(1)(1)f x f x -=+,若方程0)(=x f有且仅有2009个实数解,则这2009个实数解之和为 。
15、双曲线22221xya b-=的左右焦点为12,F F ,线段12F F 被抛物线22y bx =的焦点分成2:1两段,则双曲线的离心率为________________。
16、在某次中外海上联合搜救演习中,参加演习的中方有4艘船、3架飞机;外方有5艘船、2架飞机,若从中、外两组中各选出2个单位(1架飞机或1艘船都作为一个单位,所有的船只飞机两两不同),且选出的四个单位中恰有一架飞机的不同选法共有___________种17、ABC ∆中,c b a ,,分别是角C B A ,,的对边,已知060=A ,7=a ,现有以下判断:① c b +不.可能..等于15;② 若12=⋅AC AB ,则36=∆ABC S ;③若3=b ,则B 有两解。
请将所有正确..的判断序号填在横线上____________。
俯视图正视图侧视图(1cos ,sin )αα+的值;)b ⋅ 的取值范围.、的正三角形ABC中,AEF沿EF折起到∆(Ⅱ)求点B到面所成角的余弦22、(本题满分15分)设M 是由满足下列条件的函数)(x f 构成的集合:“①方程0)(=-x x f 有实数根;②函数)(x f 的导数)('x f 满足.1)('0<<x f ” (I )证明:函数331()(0)432x xf x x =+≤<是集合M 中的元素;(II )证明:函数331()(0)432x xf x x =+≤<具有下面的性质:对于任意[,]m n 1[0,)2⊆,都存在),(0n m x ∈,使得等式)(')()()(0x f m n m f n f -=-成立。
(III )若集合M 中的元素)(x f 具有下面的性质:若)(x f 的定义域为D ,则对于任意[m ,n]D ⊆,都存在),(0n m x ∈,使得等式)(')()()(0x f m n m f n f -=-成立。
试用这一性质证明:对集合M 中的任一元素)(x f ,方程0)(=-x x f 只有一个实数根。
参考答案(1-5)BDDCD (6-10)DADCA 11、32-12、11 13、1 14、2009 15、55316、180 17、①② 18、解:(1)因(12cos ,12sin ),a b a b αα+=+++==3sin cos 4αα∴+=-, 两边平方得912sin cos 16αα+=,7sin 216α∴=-(2)因(0,1sin 2)a c α+=-+ ,()2211sin sin (sin ),24a c b ααα∴+⋅=-=--又[]sin 1,1α∈-,()a c b∴+⋅的取值范围为1,24⎡⎤-⎢⎥⎣⎦. 19、解:(Ⅰ)投掷一次正方体玩具,上底面每个数字的出现都是等可能的,其概率为 12163P ==因为只投掷一次不可能返回到A 点;若投掷两次点P 就恰能返回到A 点,则上底面出现的两个数字应依次为: (1,3)、(3,1)、(2,2)三种结果,其概率为2211()333P =⋅=若投掷三次点P 恰能返回到A 点,则上底面出现的三个数字应依次为: (1,1,2)、(1,2,1)、(2,1,1)三种结果,其概率为3311()339P =⋅=若投掷四次点P 恰能返回到A 点,则上底面出现的四个数字应依次为:(1,1,1,1) 其概率为4411()381P ==所以,点P 恰好返回到A 点的概率为23411137398181P P P P =++=++=┅┅┅┅┅┅┅┅7分(Ⅱ)在点P 转一圈恰能返回到A 点的所有结果共有以上问题中的7种, 因为,3(2)7P ξ==,3(3)7P ξ==,1(4)7P ξ==所以,331192347777E ξ=⋅+⋅+⋅= ┅┅┅┅┅┅┅┅12分20、证明:(I )在图1中,取BE 的中点D ,连DF ∵12A E C F C P E BF AP B===,∵2,60,AF AD A ==∠=︒又∴A D F ∆为正三角形又∵AE=ED=1∴AD ⊥EF ∴在图2中有1A E EF ⊥,B E E F =∴1A EB ∠为二面角1A EF B --的平面角 ∵二面角1A EF B --为直二面角 ∴1A E BE ⊥又∵BE EF E =∴1A E BEF ⊥面即1A E BEP ⊥面 ………………5分 (Ⅱ)∵BE//PF ∴BE//面1A PF ∵B 到面1A PF 的距离即为E 到面1A PF 的距离, ∵1BE A EF ⊥面,又BE//PF , ∴1PF A EF ⊥面 ∴11A EF PF ⊥面面A∵E 到面1P F A 的距离即为1A EF ∆中E 到1A F 的距离d=A 1E×sin 602︒=∴点B 到面1A PF的距离为2………………10分(Ⅲ)∵DF//BP ∴1D FA ∠即为所求角1A D F ∆中112,2A D DF A F === ,22211113cos 24D F A F A DD FA D F A F++∠==∴异面直线BP 与1A F 所成角的余弦值为34………………14分21、解:(Ⅰ)20PM F M +=∴点M 是线段2P F 的中点 ∴OM 是12P F F ∆的中位线又 12OM F F ⊥ 112P F F F ∴⊥ 2222211112c a b a b c=⎧⎪⎪∴+=⎨⎪⎪=+⎩ 解得2222,1,1a b c === ∴椭圆的标准方程为2212xy += ┅┅┅┅┅┅┅5分(Ⅱ) 圆O 与直线l 相切∴1= 即:221m k =+2212x y y kx m ⎧+=⎪⎨⎪=+⎩消去y :222(12)4220k x km x m +++-= 设1122(,),(,)A x y B x y2121222422,1212km m x x x x kk-+=-⋅=++121222121222()()()112y y kx m kx m k x x km x x m kk⋅=++=⋅+++-=+ 2121222221122133124112kO A O B x x y y kkkk λ+⋅=⋅+⋅==++∴≤≤+∴≤≤22、(I )证明:因为2313'(),0'()[,1)0'()1424f x x x f x f x =+≤<∈<<且,所以满足条件,又因为当x=0时,(0)00f -=,所以方程0)(=-x x f 有实数根0。
