2016_2017学年高中数学第三章指数函数和对数函数3.3.2指数函数的图像与性质高效测评
常用函数图像
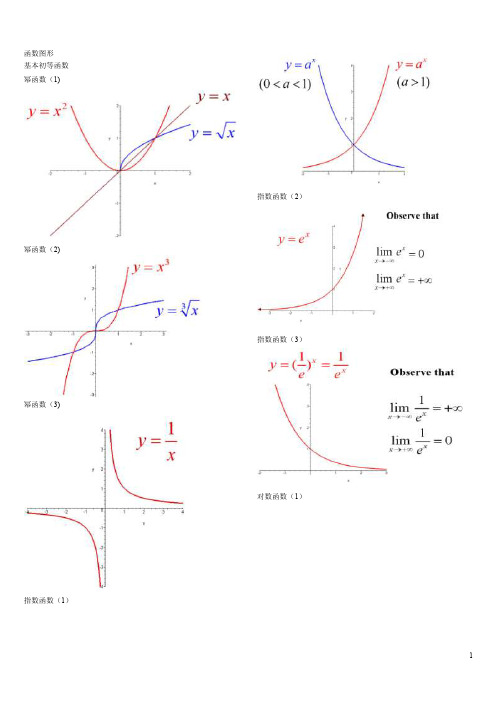
函数图形基本初等函数幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)对数函数(2)三角函数(1)三角函数(2)三角函数(3)三角函数(4)三角函数(5)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(4)反双曲函数(5)反双曲函数(6)y=sin(1/x) (1)y=sin(1/x) (2)y=sin(1/x) (3)y=sin(1/x) (4)y = [1/x](1)y = [1/x](2)y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x)y=e1/xy=sinx (x->∞)绝对值函数y = |x| 符号函数y = sgnx 取整函数y= [x]极限的几何解释(1) 极限的几何解释(2)极限的几何解释(3)极限的性质(1) (局部保号性)极限的性质(2) (局部保号性) 极限的性质(3) (不等式性质) 极限的性质(4) (局部有界性) 极限的性质(5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1)lim(1+1/x)^x 的一般形式(2)lim(1+1/x)^x 的一般形式(3)e的值(1)等价无穷小(x->0)sinx等价于xarcsinx等价于x tanx等价于x arctanx等价于x1-cosx等价于x^2/2sinx等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞) 夹逼定理(1)夹逼定理(2)数列的夹逼性(1) 数列的夹逼性(2) pi 是派的意思(如果你没有切换到公式版本)^是次方的意思,$是公式的标记符,切换到公式版(安装mathplayer)就看不到$了文案编辑词条B 添加义项?文案,原指放书的桌子,后来指在桌子上写字的人。
指数函数与对数函数思维导图

指数函数与对数函数思维导图
指数函数与对数函数
│
└─── 概念
│
├─── 指数函数
│ │
│ └─── 定义
│ 指数函数是一种形式为 y=an的函数。
其中,a>0,a≠1 且 n 为任意实数。
│ └─── 特点
│ 指数函数的图像上沿一条直线呈现出指数分布,其曲线会通过原点 (0,1),函数值以指数增长,存在无限点,此曲线由起点而有趋势向上攀升。
│
├─── 对数函数
│ │
│ └─── 定义
│ 对数函数是一种形式为 y = loga x 的函数,其中,a>0,a≠1 且 x 为正实数。
│ └─── 特点
│ 对数函数是反比例函数,函数值呈现直线函数的形式在y轴上呈对称,此函数没有凹凸把抛物线的形状,其通过的点具有可能的无穷项,抛物线上的点除去极值之外全部重合,抛物线有一条经过原
点的轴线。
│
└─── 比较
指数函数是一种可增长的快速函数,它的函数值会呈指数分布;
而对数函数是一种反比例函数,其曲线会有一对对称的轴,比较特别。
另外,两者有不同的变换性质,指数函数与其反函数是同一个函数,
而对数函数的反函数是指数函数。
北师大版高中数学必修1《三章 指数函数和对数函数 3.2 指数函数y=2^x和y=(1%2)^x的图像和性质》示范课件_32

复习回顾
指数函数的定义:
形如 y=ax (a0,且a 1)的函数叫做指数函数,
其中x是自变量,a 是常量,函数的定义域是R.
指数函数与幂函数的区别:
• 系数为1
y ax
•
底数为常数 (a0,且a 1)
• 指数为自变量X
y xa
• 系数为1 • 底数为自变量X
• 指数为常数
1:指出下列函数那些是指数函数,幂函数?
(1) y 4x ;
(4) y (4)x;
(7) y xx;
(2) yቤተ መጻሕፍቲ ባይዱ x4 ;
(3) y 4 x ;
(5) y x;
(6) y 1 x
y
y 1 x 2
y 1 x 3
y 3x y 2x
1
0
1
x
y
y
y 1 x
y2 a x
(a 1)
y 1 x 3
y
y 3x y 2x
y ax
(0 a 1)
1 1
0
x
0
1
1
0x
x
y
y ax
y 2x, y (1)x, y 3x, y (1)x
2
3
x … -3 -2 -1 0
y 2x …
1
1
8
4
y (1)x …
2
18
4
1
y 3x … 27
9
y (1)x … 27 9
3
11
2
21
指数函数、对数函数、幂函数的图像与性质

指数函数、对数函数、幂函数的图像与性质(一)指数与指数函数1.根式(1)根式的概念(2).两个重要公式①⎪⎩⎪⎨⎧⎩⎨⎧<-≥==)0()0(||a a a a a aa nn ;②a a n n =)((注意a 必须使n a 有意义)。
2.有理数指数幂 (1)幂的有关概念 ①正数的正分数指数幂:0,,1)m na a m n N n *=>∈>、且; ②正数的负分数指数幂: 10,,1)mnm naa m n N n a-*==>∈>、且③0的正分数指数幂等于0,0的负分数指数幂没有意义.注:分数指数幂与根式可以互化,通常利用分数指数幂进行根式的运算。
(2)有理数指数幂的性质 ①a r a s =a r+s (a>0,r 、s ∈Q ); ②(a r )s =a rs (a>0,r 、s ∈Q ); ③(ab)r =a r b s (a>0,b>0,r ∈Q );. 3.指数函数的图象与性质n 为奇数 n 为偶数注:如图所示,是指数函数(1)y=a x ,(2)y=b x,(3),y=c x (4),y=d x 的图象,如何确定底数a,b,c,d 与1之间的大小关系?提示:在图中作直线x=1,与它们图象交点的纵坐标即为它们各自底数的值,即c 1>d 1>1>a 1>b 1,∴c>d>1>a>b 。
即无论在轴的左侧还是右侧,底数按逆时针方向变大。
(二)对数与对数函数 1、对数的概念 (1)对数的定义如果(01)x a N a a =>≠且,那么数x 叫做以a 为底,N 的对数,记作log N a x =,其中a 叫做对数的底数,N 叫做真数。
(2)几种常见对数2、对数的性质与运算法则(1)对数的性质(0,1a a >≠且):①1log 0a =,②lo g 1aa =,③lo g Na a N =,④lo g N a aN =。
第3章 §3 第1课时指数函数的图像和性质

D [由0<a<1,知y=ax是减函数,y=(a-1)x2的图像开口向下.故选 D.]
课 时 分 层 作 业
返 首 页
指数函数的性质
自 主 预 习 • 探 新 知
[探究问题]
1 1 x 1.函数y=2 与y= 的定义域有什么关系?单调性有什么关系?
x
提示:定义域相同,单调性相同.
11 1 x 2.函数y= 2 与y=x 的定义域有什么关系?单调性有什么关系?
-1
课 时 分 层 作 业
返 首 页
自 主 预 习 • 探 新 知
指数函数的图像
(1)函数y=3 x的图像是(
-
)
当 堂 达 标 • 固 双 基
合 作 探 究 • 攻 重 难
课 时 分 层 作 业
返 首 页
(2)如图331是指数函数①y=ax,②y=bx,③y=cx,④y=dx的图像,
自 主 预 习 • 探 新 知
返 首 页
自 主 预 习 • 探 新 知
2.指数函数y=f(x)的图像过点(2,4).则f(-2)=________. 【导学号:60712233】
1 x 2 [ 设 f ( x ) = a ,由 f (2) = 4 ,得 a =4,又a>0,且a≠1,则a=2, 4 1 ∴f(x)=2 ,∴f(-2)=2 =4.]
大于0 且 不等于1 的常量,函数的定义域是实数集R.
当 堂 达 标 • 固 双 基
合 作 探 究 • 攻 重 难
课 时 分 层 作 业
返 首 页
自 主 预 习 • 探 新 知
思考1:指数函数定义中,为什么规定a>0且a≠1?
[提示] (1)若a=0,则x>0时,ax=0;当x≤0时,ax无意义. (2)若a<0,则其定义域不是R.
北师大版高中数学必修1《三章 指数函数和对数函数 3.2 指数数y=2^x和y=(1%函2)^x的图像和性质》示范课件_0

问题1 一尺之棰,日取其半,万世不竭
用x表示y的关系式是:
…
设木棒原长为1个单位
截取次数x 1 2 3 4 …
剩余长度y
…
情景设计 问题2 细胞分裂问题
用x表示y的关系式是:
………… ………… ………… …………
分裂次数x 1 2 3 4 …
细胞个数y
…
分析:
这两个解析式的形式有什么共同特征? 1.等号左右两端:左端是因变量 y,
谢 谢 , 再 见!
用图形计算器展示下列四个函数图象
(1) y 2x , (2) y 3x
(3)
y
1 2
x
,
(4)
y
1 3
x
y
y 1 x 2
y 1 x 3
y 3x y 2x
1
0
1
x
y
y
y 1 x
y2 a x
x
-3 0.125
的图象.-2 0.25
8
-1 0.5
01 1 0.5 2 0.25
y
1 2
x
6 4 2
3 0-.110 25
-5
y 2x
5
01 12 24
x
3 10 8
-2
探究2:在同一直角坐标系内作出若干个
底数不同的指数函数 y ax a 0且a 1
的图象.观察图象,你能发现它们有哪些共 同特征?
1、画出函数图象
列表 描点
连线 2、研究函数性质
图形计算 器绘图
①定义域 ②值域 ③单调性 ④奇偶性 ⑤其它
2016_2017学年高中数学第三章指数函数和对数函数3.5.1对数函数的概念5.2y=log2x的图像和性质课件

[思路探究] 可先作出y=log2x的图像,利用图像考察单调性解决问题.
[规范解答]
函数 y=log2x 的图像如图,
(1)因为 y=log2x 是增函数,若 f(a)>f(2),即 log2a>log22,则 a>2.所以 a 的取 值范围为(2,+∞). (2)∵2≤x≤14, ∴3≤2x-1≤27, ∴log23≤log2(2x-1)≤log227. ∴函数 y=log2(2x-1)在 x∈[2,14]上的最小值为 log23,最大值为 log227.
(1)要使函数有意义,
x+1>0, x>-1, 需 即 x<1. 1-x>0,
∴-1<x<1, ∴函数的定义域为(-1,1). (2)要使函数有意义,需 5-x>0, x<5, x-2>0, ∴x>2, x-2≠1, x≠3. ∴定义域为(2,3)∪(3,5).
解析:
(1)由于 y=ax 与 y=logax 互为反函数,图像关于 y=x 对称,知 A,
B 正确;当 a>1 时,它们均为增函数,当 0<a<1 时,它们均为减函数. (2)函数 f(x)的反函数为 y=logax, 由题意得,loga3=1. ∴a=3.
答y=log2x的图像与性质 根据函数 f(x)=log2x 的图像和性质解决以下问题. (1)若 f(a)>f(2),求 a 的取值范围; (2)求 y=log2(2x-1)在 x∈[2,14]上的最值.
(0,+∞) ,函数的值域为___ R . 义域是____________
[强化拓展] 根据对数函数的定义,只有形如 y=logax(a>0,且 a≠1)的函数才是对数函 数,例如,y=log3x(x>0)、y=log1 x(x>0)都是对数函数, 而 y=-log2x、y=log3(x 2 1 +1)、y= 1 等函数都不是对数函数,而是和对数函数有关的函数. log2x
北师大版高中数学必修1《三章 指数函数和对数函数 3.2 指数函数y=2^x和y=(1%2)^x的图像和性质》示范课件_4

底互为倒数的 两个函数图像 关于y轴对称
1
y 1 x
2
0 y 1 x
x
3
(三)典例精讲
类型一 两个数比较大小 (1)30.8,30.7 (2) 0 .75-0.1,0.750.1(3)1.70.3,0.93.1
解:(1)利用指数函数单调性,考虑函数y=3x ∵3>1
∴1.70.3 > 0.93.1
小结:比较两个幂的形式的数大小的方法:
(1)同底数指数幂比大小,构造指数函数,利 用单调性来判断. (2)不同底数指数幂比大小,利用指数函数图 像与底的关系来判断. (3)底数、指数都不同的两个幂比大小,则应 通过中间值来判断.常用1和0.
知识检测1: 课本第73页 练习1 1.
5
在解指数函数不等式时,将其转化为一 次不等式或通过性质求解
知识检测2 解下列不等式:
3 4 2 (1) x1 1 (2) x x1 3 0 81
四、小结归纳,拓展深化
通过本节课的学习,你学到了那些知识? 你有掌握了哪些学习数学方法?
五、布置作业.
必做题 P77:A组3,4,5 选做题 P77:B组2.
定义域: R
性
值 域: ( 0,+ ∞ )
恒 过 点: ( 0 , 1 ) ,即 x = 0 时, y = 1 .
质 在 R 上是 增函数
在 R 上是 减函数
你还能发
现指数函数图 像的关系吗?
y
y 1 x 2
y 1 x 3
在第一象限 沿箭头方向
底增大
y 3x y 2x
.
(一)复习回顾
1、指数函数的定义:一般地,形如 y =ax (a>0,a≠1)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2016-2017学年高中数学 第三章 指数函数和对数函数 3.3.2 指数
函数的图像与性质高效测评 北师大版必修1
一、选择题(每小题5分,共20分)
1.函数y =3x
与y =3-x
的图像关于下列哪条直线对称( ) A .x 轴 B .y 轴 C .直线y =x
D .直线y =-x
解析: y =3-x
=⎝ ⎛⎭
⎪⎫13x
, 由y =3x
与y =⎝ ⎛⎭
⎪⎫13x
关于y 轴对称, 所以y =3x 与y =3-x
关于y 轴对称. 答案: B
2.在同一平面直角坐标系中,函数f (x )=ax 与g (x )=a x
的图像可能是( )
解析: 需要对a 讨论:
①当a >1时,f (x )=ax 过原点且斜率大于1,g (x )=a x
是递增的.②当0<a <1时,f (x )=ax 过原点且斜率小于1,g (x )=a x
是减函数.显然B 正确.
答案: B
3.定义运算a ⊕b =⎩
⎪⎨⎪⎧a (a ≤b ),b (a >b ),则f (x )=2x ⊕2-x
的图像是( )
解析: x ≥0时,2x
≥1≥2-x
>0;
x <0时,0<2x <1<2-x .
故f (x )=2x ⊕2-x
=⎩
⎪⎨⎪⎧2-x
,x ≥0,2x ,x <0.
答案: C
4.已知a =0.80.7
,b =0.80.9
,c =1.20.8
,则a ,b ,c 的大小关系是( ) A .a >b >c B .b >a >c C .c >b >a
D .c >a >b
解析: a =0.80.7
>0.80.9
=b ,
a =0.80.7<0.80=1,∴
b <a <1.
而c =1.20.8
>1.20
=1, ∴c >a >b . 答案: D
二、填空题(每小题5分,共10分)
5.函数y =⎝ ⎛⎭
⎪⎫15x
-3x
在区间[-1,1]上的最大值等于
________________________________________________________________________.
解析: 由y =⎝ ⎛⎭⎪⎫15x 是减函数,y =3x 是增函数,可知y =⎝ ⎛⎭
⎪⎫15x
-3x
是减函数,故当x =
-1时函数有最大值14
3
.
答案:
143
6.若直线y =2a 与函数y =|a x
-1|(a >0,且a ≠1)的图像有两个公共点,则a 的取值范围是________.
解析: 当0<a <1时,如图(1)所示, 要使得y =2a 与y =|a x
-1|有两个交点, 需0<2a <1,故0<a <1
2
.
当a >1时,如图(2)所示,
由于y =2a >2,所以y =2a 与y =|a x
-1|不存在两个交点,故a 的取值范围为0<a <12.
答案: 0<a <1
2
三、解答题(每小题10分,共20分)
7.已知a >0且a ≠1,讨论f (x )=a -x 2
+3x +2的单调性.
解析: 设u =-x 2
+3x +2=-⎝ ⎛⎭
⎪⎫x -322
+17
4,则当x ≥32时,u 是减函数,当x ≤32时,
u 是增函数.
又当a >1时,y =a u
是增函数,当0<a <1时,y =a u
是减函数,
所以当a >1时,原函数f (x )=a -x 2
+3x +2在⎣⎢⎡⎭⎪⎫32,+∞上是减函数,在⎝ ⎛⎦⎥⎤-∞,32上是
增函数.
当0<a <1时,原函数f (x )=a -x 2
+3x +2在⎣⎢⎡⎭⎪⎫32,+∞上是增函数,在⎝ ⎛⎦⎥⎤-∞,32上是减
函数.
8.设a >0,f (x )=e x a +a
e x (e>1)是R 上的偶函数.
(1)求a 的值;
(2)证明:f (x )在(0,+∞)上是增函数. 解析: (1)依题意,对一切x ∈R ,都有
f (x )=f (-x ), ∴e
x
a +a e x =1a e
x +a e x
. ∴⎝ ⎛⎭⎪⎫a -1a ⎝
⎛⎭⎪⎫e x -1e x =0.
∴a -1a
=0,即a 2
=1.
又a >0,∴a =1; (2)证明:设0<x 1<x 2,
f (x 1)-f (x 2)=e x 1-e x 2+
1e x 1-1e x 2
=(e x 2-e x 1)⎝
⎛⎭
⎪
⎫1e x 1+x 2-1
=e x 1(e x 2-x 1-1)·1-e x 1+x 2
e x 1+x 2,
∵x 2>x 1>0,
∴x 2-x 1>0,x 1+x 2>0,
又由e>1知y =e x
在R 上为增函数, ∴e x 2-x 1-1>0,1-e x 1+x 2<0. ∴f (x 1)-f (x 2)<0,即f (x 1)<f (x 2).
∴f (x )在(0,+∞)上是增函数. 尖子生题库 ☆☆☆
9.(10分)已知函数f (x )=a x
在x ∈[-2,2]上恒有f (x )<2,求a 的取值范围. 解析: 当a >1时,
函数f (x )=a x
在[-2,2]上单调递增, 此时f (x )≤f (2)=a 2
, 由题意可知a 2
<2,即a <2, 所以1<a < 2. 当0<a <1时,
函数f (x )=a x
在[-2,2]上单调递减, 此时f (x )≤f (-2)=a -2
, 由题意可知a -2
<2,即a >22
, 所以
2
2
<a <1. 综上所述,所求a 的取值范围是⎝
⎛⎭
⎪⎫
22,1∪(1,2).。
