河北省唐山市迁安市2015-2016学年七年级下学期期中数学试卷及参考答案
2015-2016第二学期期中七年级数学参考答案

2015—2016学年度第二学期期中质量评估试题七年级数学参考答案及评分标准11. 9; 12. 80°; 13.(5,0); 14. 4; 15. 100°;16. 一 三、解答题(一)17. 解:34)2(3-----=3+2-2-3 ……………4分 =0 ……………6分 18. 解:∵a ∥b∴∠2=∠3 ……………2分 ∵∠1+∠3=180°∴∠1+∠2=180° ……………4分 ∴∠2=180°-∠1 ∵∠1=118°∴∠2=180°-118°=62° ……………6分 19.(1)图(略) 图……………4分(2)A 1(0,6);B 1(-1,2) ……………6分 四、解答题(二) 20. 解: )223(328)2(32---+-+-=2232322+--+- ……………4分 =2 ……………7分 21. 解:∵∠1=∠2∴AB ∥CD ……………2分 ∴∠3+∠4=180° ……………4分 ∴∠4=180°-∠3 ……………6分 ∵∠3=108°∴∠4=180°-108°=72° ……………7分 22.(每空1分)∵AB ∥DC (已知)∴∠1=∠CFE (两直线平行,同位角相等)……………2分 ∵AE 平分∠BAD (已知)∴∠1=∠2(角平分线的定义) ……………4分 ∴∠2=∠CFE ……………5分 ∵∠CFE=∠E (已知)∴∠2=∠E …………6分 ∴AD ∥BC (内错角相等,两直线平行). …………7分五、解答题(三) 23. 解:100)1(2=-x101±=-x …………4分 110+±=x11=x …………7分或9-=x …………9分24. 证明:∵DE ‖BC (已知)∴∠ADE =∠ABC (两直线平行,同位角相等) …………2分 ∵DF 、BE 分别平分∠ADE 、∠ABC ∴∠ADF =12∠ADE∠ABE =12∠ABC (角平分线的定义) …………4分∴∠ADF =∠ABE …………5分∴ DF ‖BE (同位角相等,两直线平行) …………7分 ∴∠FDE =∠DEB. (两直线平行,内错角相等) …………9分 25. 解:(1)C (0,2),D (4,2),…………2分(2)依题意,得S 四边形ABDC =AB ×OC=4×2=8; …………3分 (3)存在. …………4分。
2015-2016学年七年级下学期期中联考数学试题(含答案)

2015-2016学年七年级下数学期中测试题数 学 试 题(含答案)一、填空题(每题2分共24分)1. 在同一平面内,两条直线有 种位置关系,它们是 ;2.若直线a//b ,b//c ,则 ,其理由是 ;3.如图1直线AB ,CD ,EF 相交与点O ,图中AOE ∠的对顶角是 ,COF ∠的邻补角是 。
4.如图2,要把池中的水引到D 处,可过D 点引CD ⊥AB 于C ,然后沿CD 开渠,可使所开渠道最短,试说明设计的依据: ;5.点P (-2,3)关于X 轴对称点的坐标是 。
关于原点对称点的坐标是 。
6.把“对顶角相等”写成“如果……那么……”的形式为 。
7.如图4,170=∠,270=∠,388=∠,则4=∠_____________. 8 . 若点M (a+5,a-3)在y 轴上,则点M 的坐标为 。
9.若P (X ,Y )的坐标满足XY >0,且X+Y<0,则点P 在第 象限 。
0. 如图5,AB CD ∥,BC DE ∥,则∠B 与∠D 的关系是_____________.ABCD 图2A FC EB D图1OAB DC12 图3 图43142图4c ba5 4 32 1 图6 图511.若│x2-25│+3y -=0,则x=_______,y=_______.12.如图3,四边形ABCD 中,12∠∠与满足 关系时AB//CD ,当 时AD//BC(只要写出一个你认为成立的条件)。
二、 选择题 (下列各小题的四个选项中,有且只有一个是符合题意的,把你认为符合题意的答案代号填入答题表中,每小题2分,共12分) 题 号 1 2 3 4 56 答 案1.下列各图中,∠1与∠2是对顶角的是:( )2.一个三角形的三个内角中( )A. 至少有一个等于90°B. 至少有一个大于90°C. 不可能有两个大于89°D. 不可能都小于60°3.如图7,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐 的角∠A 是120°,第二次拐的角 ∠B 是150°,第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C 是( ) A、150°B、140°C、130° D、120°4.在直角坐标系中,点P (-2,3)向右平移3个单位长度后的坐标为( ) A .(3,6) B.(1,3) C.(1,6) D.(3,3) 5. 如图6 下列条件中,不能判断直线a//b 的是( )A 、∠1=∠3B 、∠2=∠3C 、∠4=∠5D 、∠2+∠4=180° 6.在实数范围内,下列判断正确的是 ( ) (A) .若m=n,则n m = (B) .若22b a >, 则b a >(C) .若2a =2)(b ,则b a = (D) .若3a =3b ,则b a =7.16的平方根是( )(A )2 (B )4 (C )- 2或2 (D )- 4或48. 若a 是(-3)2的平方根,则3a 等于( ) (A )-3 (B )33 (C )33或-33 (D )3或-3三.作图题。
冀教版七年级下册数学期中测试(含答案)

第二学期七年级期中考试数学试题(冀教版)考试范围6—8章说明:本试卷共4页,满分120分请将所有答都填在答题卡上,答在试卷上无效。
一、选择题(本大题共16个小题,1-10题,每小题3分11-16小题,每小题2分,共42分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列方程是二元一次方程的是( )A.z y x =+32B.54=+y xC. 0212=+y xD.)8(21+=x y 2.用两块相同的三角板按如图所示的方式作平行线AB 和CD ,能解释其中的道理的依据是( )A.内错角相等,两直线平行B.同位角相等,两直线平行C.同旁内角互补,两直线平行D.两直线平行,内错角相等3.下列命题中是假命题的是( )A.同旁内角互补,两直线平行B.垂线段最短C.在同一平面内,过一点有且只有一条直线与已知直线垂直D.两条直线被第三条直线所截,内错角相等4.解方程组⎩⎨⎧+==-②……73①……532y x y x ,下面解法正确的是( ) A.①+②得3x=12 B.①一②得x=-2C.②×2-①得6y=2 D.②一①得x=25.下列运算中,能用平方差公式计算的是( )A.(-a+b)(a-b)B.(a-b)(-b+a)C.(3a-b)(3b+a)D.(b+2a)(2a-b)6.点A 、B 、C 为直线l 上三点,点P 为直线l 外一点,且PA=3cm ,PB=4cm ,PC=5cm ,则点P 到直线l 的距离为( )A. 2cmB. 3cmC.小于3cmD.不大于3cm7.若关于x 、y 的方程组⎩⎨⎧=-+=+3)1(734y k kx y x 的解x ,y 相等,则k 的值为( )A.1B.0C.2D.-28.如图,下列条件①∠1=∠2;②∠3=∠4;③∠B=∠3;④∠1+∠ACE=180°,其中,能判定AD ∥BE 的条件有( )A.4B.3C.2D.19. 计算的结果是m m 525÷( )A.5B.20C.m 5D.m 2010.某种生物面胞的直径约为0.000056米,用科学记数法表示为( )A. 4-1056.0⨯B.5106.5-⨯C. 561056-⨯D.4106.5-⨯11.如图,把一张长方形纸条ABCD 沿EF 折叠,若∠1=56°,则∠FGE 应为( )A.68°B.34°C.56°D.不能确定12. 如果()25-+y x 与1023+-x y (互为相反数,那会y x 、的值为( ) A.2,3==y x B.3,2==y x C.5,0==y x D.0,5==y x13. 如图,从边长为(a+4)cm 的正方形纸片中剪去一个边长为(a+1)cm 的正方形a>0,剩余部分沿虚线又剪拼成一个矩形(不重叠无缝隙,则矩形的面积为( )A.2)156(cm a +B.2)153(cm a +C.2)96(cm a +D.22)52(cm a a +14. 14.若2))(1(2++=++mx x n x x ,则m 的值为( )A.-1B.1C.-2D.215.如图,AB ∥CD ,BC ∥DE ,则∠B+∠D 的度数为( )A. 120°B.150°C.180°D.210°16.如图,分别用火柴棍连续搭建正三角形和正六边形,公共边只用一根火柴棍。
心中学15—16学年下学期七年级期中考试数学试题(附答案)
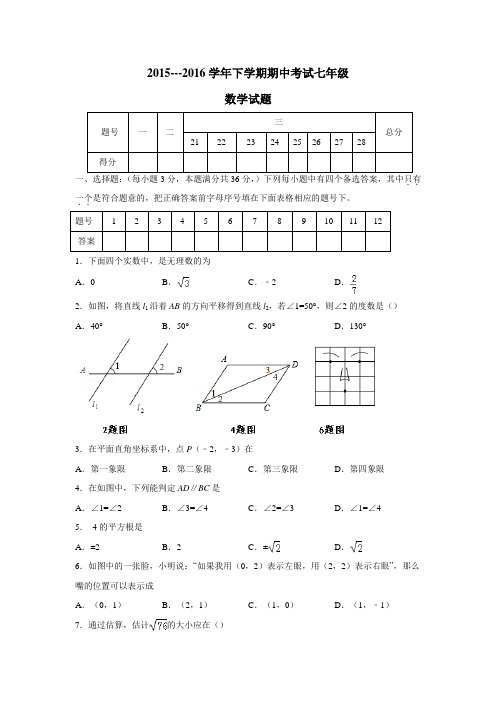
2015---2016学年下学期期中考试七年级数学试题一、选择题:(每小题3分,本题满分共36分,)下列每小题中有四个备选答案,其中只有..一个..是符合题意的,把正确答案前字母序号填在下面表格相应的题号下。
1.下面四个实数中,是无理数的为A.0B.C.﹣2 D.2.如图,将直线l1沿着AB的方向平移得到直线l2,若∠1=50°,则∠2的度数是()A.40°B.50°C.90°D.130°3.在平面直角坐标系中,点P(﹣2,﹣3)在A.第一象限B.第二象限C.第三象限D.第四象限4.在如图中,下列能判定AD∥BC是A.∠1=∠2 B.∠3=∠4 C.∠2=∠3 D.∠1=∠45.4的平方根是A.±2 B.2C.±D.6.如图中的一张脸,小明说:“如果我用(0,2)表示左眼,用(2,2)表示右眼”,那么嘴的位置可以表示成A.(0,1)B.(2,1)C.(1,0)D.(1,﹣1)7.通过估算,估计的大小应在()A.7~8之间B.8.0~8.5之间C.8.5~9.0之间D.9~10之间8.如图,直线a∥b,直角三角板的直角顶点P在直线b上,若∠1=56°,则∠2为A.24°B.34°C.44°D.54°9.如图,将△ABC沿BC方向平移1个单位得到△DEF,若△ABC的周长等于8,则四边形ABFD的周长等于A.8B.10 C.12 D.1410. 车库的电动门栏杆如图所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD的大小是A.150°B.180°C.270°D.360°11.以方程组21y xy x=-+⎧⎨=-⎩的解为坐标的点(,)x y在平面直角坐标系中的位置是A.第一象限B.第二象限C.第三象限D.第四象限12.若方程mx+ny=6的两个解是,,则m,n的值为二、填空题:本大题共8个小题,每小题4分,共32分,把答案写在题中横线上。
冀教版七年级下册数学期中考试试卷有答案

冀教版七年级下册数学期中考试试题一、单选题1.下列各式中,计算结果为7a 的是( )A .6a a +B .25a a ⋅C .()43aD .142a a ÷ 2.下列各图中,过直线l 外的点P 画直线l 的垂线,三角尺操作正确的是( ) A . B .C .D .3.若13x y =⎧⎨=⎩是二元一次方程3mx y -=的解,则m 为( )A .7B .6C .43 D .04.如图,平行线AB ,CD 被直线AE 所截.若1105∠=︒,则2∠的度数为()A .75︒B .85︒C .95︒D .105︒ 5.解方程组①3759y x x y =-⎧⎨+=-⎩,①35123156x y x y +=⎧⎨-=-⎩,比较简便的方法是( )A .都用代入法B .都用加减法C .①用代入法,①用加减法D .①用加减法,①用代入法6.下列四幅图案中,能通过平移图得到的是( )A .B .C .D . 7.下列运算正确的是( )A .()211a a a +=+B .22(2)(2)2a b a b a b +-=-C .222()a b a b -=-D .22232a a a -= 8.如图,在铁路旁有一李庄,现要建一火车站,为了使李庄人乘车最方便,请你在铁路线上选一点来建火车站,应建在( )A .点AB .点BC .点CD .点D9.如图所示,点E 在AC 的延长线上,下列条件中能判断AB //CD 的是( )A .3A ∠=∠B .12∠=∠C .D DCE ∠=∠ D .180D ACD ∠+∠=10.解方程组272a b a b +=⎧⎨-=⎩①②的下列解法中,不正确的是( ) A .代入法消去a ,由① 得2a b =+B .代入法消去b ,由① 得72b a =-C .加减法消去a ,①-①2⨯ 得23b =D .加减法消去b ,①+① 得39a =11.下列命题中是假命题的是( )A .对顶角相等B .两直线平行,同位角互补C .在同一平面内,经过一点有且只有一条直线与已知直线垂直D .平行于同一直线的两条直线平行12.在“幻方拓展课程”探索中,小明在如图的3×3方格填入了一些表示数的代数式,若图中各行、各列及对角线上的三个数之和都相等,则y ﹣x =( )A .2B .4C .﹣6D .6二、填空题 13.如图,直线//a b ,则直线a ,b 之间距离是线段__________的长度.14.写出二元一次方程411x y +=的一组整数解_____________________.15.若(x -3)(2x +m )的计算结果中不含x 一次项,则m 的值是________16.已知4311237a b a b +=⎧⎨+=⎩,则a b +=__________. 17.如图,将木条a ,b 和c 钉在一起,150,275∠=︒∠=︒,要使木条a 和b 平行,木条a 至少要旋转的度数为_______.18.对x ,y 定义一种新运算“①”,规定:x①y=mx+ny (其中m ,n 均为非零常数),若1①1=4,1①2=3.则2①1的值是____.19.某宾馆在重新装修后,准备在大厅的主楼梯上铺上红色地毯.已知这种红色地毯的售价为每平方米32元,主楼道宽2米,其侧面如图所示,则购买地毯至少需要___________元.三、解答题20.如图,将ABC 水平向右平移得到DEF ,A ,D 两点的距离为1,2CE =,70A ∠=︒.根据题意完成下列各题:(1)AC 和DF 的数量关系为__________;AC 和DF 的位置关系为___________; (2)求1∠的度数;(3)BF =__________.21.计算:(1)()32248223a a a a a -⋅+÷; (2)2(3)(3)(3)a a a +--+.22.任意给定一个非零数a ,按下列程序计算.(1)请用含a 的代数式表示计算程序,并给予化简;(2)当输入的数a =-5时,求输出结果.23.某学校教学楼前有一块长为()62a b +米,宽为()42+a b 米的长方形空地要铺地砖,如图所示,空白的甲、乙两正方形区域是草坪,不需要铺地砖.两正方形区域的边长均为()a b +米.(1)求铺设地砖的面积是多少平方米;(2)当2a =,3b =时,需要铺地砖的面积是多少?24.如图,已知//,AB CD E 是直线AB 上的一点,CE 平分ACD ∠,射线,132CF CE ⊥∠=︒,(1)求ACE ∠的度数;(2)若258∠=︒,求证://CF AG ;25.在期末一节复习课上,八年(一)班的数学老师要求同学们列二元一次方程组解下列问题:在我市“精准扶贫”工作中,甲、乙两个工程队先后接力为扶贫村庄修建3000m 的村路,甲队每天修建150m ,乙队每天修建200m ,共用18天完成.(1)粗心的张红同学,根据题意,列出的两个二元一次方程,等号后面忘记写数据,得到了个不完整的二元一次方程组,150200.p q p q +=⎧⎨+=⎩张红列出的这个不完整的方程组中未知数p表示的是______,未知数q 表示的是_________;张红所列出正确的方程组应该是__________;(2)李芳同学的思路是想设甲工程队修建了m x 村路,乙工程队修建了m y 村路.下面请你按照李芳的思路,求甲、乙两个工程队分别修建了多少天?参考答案1.B【解析】分别根据合并同类项法则,同底数幂的乘法法则,幂的乘方运算法则逐一判断即可.【详解】解:A 、a 6与a 不是同类项,所以不能合并,故本选项不合题意;B 、a 2•a 5=a 2+5=a 7,故本选项符合题意;C 、(a 3)4=a 3×4=a 12,故本选项不合题意;D 、a 14÷a 2=a 14-2=a 12,故本选项不合题意;故选:B .【点睛】本题主要考查了合并同类项,同底数幂的乘法和除法以及幂的乘方,熟记幂的运算法则是解答本题的关键.2.C【解析】根据垂线的作法,用直角三角板的一条直角边与l 重合,另一条直角边过点P 后沿直角边画直线即可;根据分析可得C的画法正确;故答案选C.【点睛】本题主要考查了垂线的作法,准确理解是解题的关键.3.B【解析】【分析】把x与y的值代入方程计算即可求出m的值.【详解】解:把13xy=⎧⎨=⎩代入方程得:33m-=,解得:6m=,故选:B.【点睛】本题考查了二元一次方程的解,方程的解即为能使方程左右两边相等的未知数的值.4.A【解析】【分析】直接利用平行线的性质得出答案.【详解】解:①AB①CD,①①1+①2=180°①1105∠=︒,①①2=75°,故选:A.【点睛】此题主要考查了平行线的性质,正确掌握平行线的性质是解题关键.5.C【解析】根据解二元一次方程组时的基本方法:代入消元法即用其中一个未知数表示另一个未知数,再代入其中一个方程,转化为一元一次方程,进而求解;加减消元法即将其中一个未知数的系数化为相同时,用加减法即可达到消元的目的,转化为一元一次方程,针对具体的方程组,要善于观察,从而选择恰当的方法.【详解】①中的第一个方程为y=x–2,用代入法比较简便;①中的x 的系数相等,用加减法比较简便;故选C .【点睛】此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.6.B【解析】【分析】根据平移的定义即可得.【详解】平移:在平面内,将一个图形沿某个方向移动一定的距离,这样的图形运动称为平移; 观察四个选项可知,只有选项B 能通过平移图得到,故选:B .【点睛】本题考查了平移的定义,掌握理解定义是解题关键.7.D【解析】【分析】根据多项式乘多项式法则、完全平方公式和平方差公式,合并同类项,逐一判断即可.【详解】解:A 、()21a a a a +=+原计算错误,不符合题意;B 、22(2)(2)4a b a b a b +-=-原计算错误,不符合题意;C 、222()2a b a ab b -=-+原计算错误,不符合题意;D、222a a a-=正确,符合题意;32故选:D.【点睛】本题考查的是整式的乘法,合并同类项,掌握多项式乘多项式法则、完全平方公式和平方差公式是解决此题的关键.8.A【解析】【分析】根据垂线段最短可得答案.【详解】解:根据垂线段最短可得:应建在A处,故选A.【点睛】此题主要考查了垂线段的性质,关键是掌握从直线外一点到这条直线所作的垂线段最短.9.B【解析】【分析】根据平行线的判定逐项判断即可.【详解】解:A、①①3=①4,①AC①BD,不能判断AB①CD,此选项不符合题意;B、①①1=①2,①AB①CD,此选项符合题意;C、①D DCE∠=∠,①AC①BD,不能判断AB①CD,此选项不符合题意;D、①180D ACD∠+∠=,①AC①BD,不能判断AB①CD,此选项不符合题意,故选:B.【点睛】本题考查平行线的判定,熟练掌握平行线的判定是解答的关键.10.C【解析】【分析】利用代入消元和加减消元法步骤判断即可.【详解】解:A、代入法消去a,由①得a=b+2,选项正确,不符合题意;B、代入法消去b,由①得b=7-2a,选项正确,不符合题意;C、加减法消去a,①-①×2得3b=3,选项错误,符合题意;D、加减法消去b,①+①得3a=9,选项正确,不符合题意;故选:C.【点睛】此题考查了解用消元法解二元一次方程组,熟练掌握运算法则是解本题的关键.11.B【解析】【分析】根据对顶角的性质、平行线的性质、平行公理判断即可.【详解】解:A、对顶角相等,是真命题;B、两直线平行,同位角相等,故原命题是假命题;C、在同一平面内,过一点有且只有一条直线与已知直线垂直,是真命题;D、平行于同一直线的两条直线互相平行,是真命题,故选:B.【点睛】本题考查的是命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.12.C【解析】【分析】根据各行、各列及对角线上的三个数之和都相等,即可得出关于x,y的二元一次方程组,解之即可得出x,y的值,再将其代入(y-x)中即可求出结论.【详解】解:依题意,得20262020x yx y y-+=-++⎧⎨-+=++⎩,解得82xy=⎧⎨=⎩,①y﹣x=﹣6.故选:C.【点睛】本题考查了二元一次方程组的应用,找准等量关系,正确列出二元一次方程组是解题的关键.13.CD【解析】【分析】从一条平行线上的任意一点到另一条直线作垂线,垂线段的长度叫两条平行线之间的距离,由此可得出答案.【详解】解:由题可得,a①b,CD①b,①直线a与直线b之间的距离是线段CD的长度,故答案为:CD.【点睛】本题考查了平行线之间的距离:从一条平行线上的任意一点到另一条直线作垂线,垂线段的长度叫两条平行线之间的距离.14.71 xy=⎧⎨=⎩【解析】【分析】把y看做已知数求出x,即可确定出整数解.【详解】解:方程整理得:x=-4y+11,当y=1时,x=7,则方程的一个整数解为71xy=⎧⎨=⎩(答案不唯一).故答案为:71xy=⎧⎨=⎩(答案不唯一).【点睛】本题考查了解二元一次方程,解题的关键是把y看做已知数求出x.15.6【解析】【分析】先利用整式的乘法运算法则化简,再根据“不含x一次项”该已知条件得到一次项系数为0进行求解.【详解】解:(x-3)(2x+m)=2x2+mx-6x-3m=2x2+(m-6)x-3m①计算结果中不含x一次项①m-6=0①m=6.故答案为:6.【点睛】本题考查的是整式的混合运算.通过不含x一次项得到一次项系数为0是本题的解题关键.16.3【解析】【分析】利用两个方程相加求解即可.【详解】解:4311 237a ba b+=⎧⎨+=⎩①②,①+①,得6a+6b=18,①6(a+b)=18,a+b=3,故答案为:3.【点睛】本题主要考查了解二元一次方程组,解二元一次方程组的基本解法有加减消元法和代入消元法.17.25°【解析】【分析】根据同位角相等两直线平行,求出旋转后①2的同位角的度数,然后用①2减去①1即可得到木条a旋转的度数.【详解】解:①①AOC=①1=50°时,AB①b,①要使木条a与b平行,木条a旋转的度数至少是75°-50°=25°.故答案是:25°.【点睛】本题考查了旋转的性质,平行线的判定,根据同位角相等两直线平行求出旋转后①2的同位角的度数是解题的关键.18.9【解析】【分析】由已知条件,根据所给定义可得到关于m、n的方程组,则可求得m、n的值,再代入计算即可.【详解】解:①1①1=4,1①2=3,①423 m nm n+=⎧⎨+=⎩解得:51 mn=⎧⎨=-⎩则x①y=5x−y①2①1=2×5−1=9,故答案为:9.【点睛】此题考查了解二元一次方程组,以及有理数的混合运算,熟练掌握运算法则是解本题的关键.19.512【解析】【分析】根据题意,结合图形,先把楼梯的横竖向上向左平移,构成一个矩形,再求得其面积,则购买地毯的钱数可求.【详解】解:利用平移线段,把楼梯的横竖向上向左平移,构成一个矩形,长宽分别为5.5米,2.5米,①地毯的长度为2.5+5.5=8米,地毯的面积为8×2=16平方米,①买地毯至少需要16×32=512元.故答案为:512.【点睛】本题考查了平移的应用,解决此题的关键是要利用平移的知识,把要求的所有线段平移到一条直线上进行计算.20.(1)AC=DF,AC①DF;(2)①1=110°;(3)4.【解析】【分析】(1)根据平移前后对应线段平行且相等直接回答即可;(2)平移前后对应角相等;(3)用EC的长加上两个平移的距离即可.【详解】解:(1)AC 和DF 的关系式为AC =DF ,AC ①DF .故答案为:AC =DF ,AC ①DF ;(2)①三角形ABC 水平向右平移得到三角形DEF ,①AB ①DE ,①①A =70°,①①1=110°;(3)BF =BE +CE +CF =1+2+1=4.故答案为:4.【点睛】本题主要考查了平移的性质,正确得出对应角是解题关键.21.(1)62a ;(2)618a +.【解析】【分析】(1)根据积的乘方、单项式乘单项式和同底数幂的除法可以解答本题;(2)根据完全平方公式、平方差公式可以解答本题.【详解】解:(1)()32248223a a a a a -⋅+÷ 66643a a a =-+62a =;(2)2(3)(3)(3)a a a +--+()22699a a a =++--22699a a a =++-+ 618a =+.【点睛】本题考查了整式的混合运算,涉及到积的乘方、同底数幂的除法、乘法公式等,解答本题的关键是明确它们各自的计算方法.22.(1)运算程序为()2435a a a -⨯-+,化简后的结果为2275a a -+;(2)当输入的数a =-5时,输出结果是90.【解析】【分析】(1)根据图中的数据,可以写出相应的运算程序,然后化简即可;(2)将a =-5代入化简后的式子即可解答本题.【详解】解:(1)由题意可得,计算程序为:()2435a a a -⨯-+,()2435a a a -⨯-+22435a a a =--+2275a a =-+,即运算程序为()2435a a a -⨯-+,化简后的结果为2275a a -+;(2)当a =-5时,输出结果为:()()222752575590a a -+=⨯--⨯-+=, 即当输入的数a =-5时,输出结果是90.【点睛】本题考查了单项式乘多项式,合并同类项,解答本题的关键是明确整式混合运算的计算方法.23.(1)铺设地砖的面积是22a 2+16ab +2b 2平方米;(2)202平方米.【解析】【分析】(1)根据长方形的面积减去空白的面积表示出铺设地砖的面积即可;(2)把a 与b 的值代入计算即可求出值.【详解】解:(1)根据题意得:铺设地砖的面积为:(6a +2b )(4a +2b )-2(a +b )2=24a 2+20ab +4b 2-2a 2-4ab -2b 2=22a 2+16ab +2b 2(平方米);(2)当a =2,b =3时,原式=88+96+18=202(平方米).【点睛】本题考查了完全平方式,以及多项式乘多项式,熟练掌握运算法则及公式是解本题的关键.24.(1)32︒;(2)见解析【解析】【分析】(1)由平行的性质得1ECD ∠=∠,再由角平分线的性质得ACE ECD ∠=∠,即可得到结果;(2)由CF CE ⊥得90ECF ∠=︒,求出ACF ∠的度数,证明2ACF ∠=∠即可得到结论.【详解】解:(1)①//AB CD ,①132ECD ∠=∠=︒,①CE 平分ACD ∠,①32ACE ECD ∠=∠=︒;(2)①CF CE ⊥,①90ECF ∠=︒,①9058ACF ACE ∠=︒-∠=︒,①258∠=︒,①2ACF ∠=∠,①//CF AG .【点睛】本题考查平行的性质和判定,角平分线的性质,解题的关键是掌握这些性质定理进行证明求解.25.(1)甲(工程)队修建的天数;乙(工程)队修建的天数;181502003000p q p q +=⎧⎨+=⎩;(2)甲队修建了12天,乙队修建了6天.【解析】【分析】(1)根据题意可直接进行求解;(2)由题意可得方程组为300018150200x y x y +=⎧⎪⎨+=⎪⎩,然后进行求解方程组即可. 【详解】(1)由题意得:未知数p 表示的是甲(工程)队修建的天数,未知数q 表示的是乙(工程)队修建的天数,181502003000p q p q +=⎧⎨+=⎩, 故答案为:甲(工程)队修建的天数,乙(工程)队修建的天数,181502003000p q p q +=⎧⎨+=⎩; (2)设甲工程队修建了m x 村路,乙工程队修建了m y 村路,根据题意,得:300018150200x y x y +=⎧⎪⎨+=⎪⎩, 解得18001200x y =⎧⎨=⎩, 所以,甲队修建的天数180012150==(天), 乙队修建的天数12006200==(天). 答:甲队修建了12天,乙队修建了6天.【点睛】本题主要考查二元一次方程组的应用,理解题意,正确建立方程组和熟练掌握二元一次方程组的解法是解题的关键.。
七年级第二学期期中数学试卷

2015— 2016学年度七年级第二学期期中试卷一.选择题(本题共30分,每小题3分)在下列各题的四个备选答案中,只有一个是正确的,请把正确结论的代号写在题后的括号内.1.25的算术平方根是( )A .5 B. C .–5 D .±5 2.和数轴上的点一一对应的是( )A .整数B .实数C .无理数D .有理数 3.下列长度的三条线段能组成三角形的是( )A .3,4,8B .5,6,11C .8,8,8D .4,4,8 4.如图,图中∠1与∠2是同位角的是( )⑴ ⑵ ⑶ ⑷ A .⑵⑶ B .⑵⑶⑷ C .⑴⑵⑷ D .⑶⑷ 5.如图一扇窗户打开后,用窗钩BC 可将其固定,这里所运用的几何原理是( )A .三角形的稳定性B .两点之间,线段最短C .两点确定一条直线D .垂线段最短6.三角形一个外角小于与它相邻的内角,这个三角形是( ) A .是直角三角形 B .是锐角三角形 C .是钝角三角形 D .属于哪一类不能确定7.如图,直线b a //,直角三角板的直角顶点P 在直线b 上,若︒=∠561,则2∠的度数为( ) A .54° B .44° C .34° D . 24°21Pba 12 1 22 11 28.在下列各数0.51525354 、0、2.0 、π3、722、101001.6、613、27 中,无理数的个数是( )A .1B .2C .3D .4 9.△ABC 中,∠B =40°,AD 为BC 边上的高,若∠DAC =30°,则∠BAC等于( )度.A .80B .60C .20或80D .40或10010.如图①,一张四边形纸片ABCD ,∠A =50︒,∠C =150︒.若将其按照图②所示方式折叠后,恰好MD′∥AB ,ND′∥BC ,则∠D 的度数为( ).A .70︒B .75︒C .80︒D .85︒二.填空题(本题共24分,其中11、18题每空2分,其余每小题2分)11. -6的相反数是_____________,21π-的绝对值是____________.12.满足不等式4040<<-x 的非正整数x 有 .13.若a b <,则132a - 132b -(用―>‖或―<‖填空).14.已知实数x ,y满足40x -=,则以x ,y 的值为两边长的等腰三角形的周长是 .15.在△ABC 中,若∠B -∠A =15°,∠C -∠B =60°,则∠C = 度. 16.互为相反数,则x +y = .17.如图,将面积为5的△ABC 沿BC 方向平移至△DEF 的位置,平移的距离是边BC 长的两倍,那么图中的四边形ACED 的面积为 .图②图①B第18题图B18.如图,线段AD 为△ABC 中BC 边上的中线, (1)作ADC ∆中AC 边上的高线DE (2)比较线段BD 与DE 的大小:BD DE (“>”“=”或“<”填空).19.是 条,这个多边形对角线有20.如图,点M 是△ABC 点N 是△ABC :3:2CMB CNB ∠∠=,则∠CAB三.计算题(本题共16分,每小题4分)21.23)21(641251625-+- 22.22)31(234-++-23.求下列各式中x 的值:(1)0491212=-x (2)512)1(3-=-x四.解答题(本题共8分)24.完成下面的证明,并在括号内填注理由.DG A EBH C F1 2 3 4 已知,如图,AB ∥CD ∥GH ,EG 平分∠BEF ,FG 平分∠EFD 求证:∠EGF =90°证明:∵HG ∥AB (已知)∴∠1=∠3( ) 又∵HG ∥CD (已知)∴∠2=∠4 ∵AB ∥CD (已知)∴∠BEF +∠___________=180°( ) 又∵EG 平分∠BEF (已知)∴∠1=21∠________( )又∵FG 平分∠EFD (已知)∴∠2=21∠_____________∴∠1+∠2=21(______________+______________)∴∠1+∠2=90°∴∠3+∠4=90°,即∠EGF =90° 五.作图题(本题共6分)25.已知∠AOB = 70,根据语句画图,并填空 (1)画∠AOB 的平分线OC(2)在OC 上任取一点P ,画垂线段PD ⊥OA 于D ,垂线段PE ⊥OB 于E (3)画直线PF ∥OB 交OA 于F(4)则DPF = 度六.解答题(本题共16分,其中26题6分,27题10分)26.已知:如图,AB ∥ED ,C 为ED 上一点,CM 平分∠BCE ,MC ⊥CN ,∠1=30°,求∠B 的大小.B27.已知:△ABC中,AD为△ABC的角平分线,M为DC上一点,ME与AD所在直线垂直,垂足为E.(1)若∠ACB=80,∠ABC=50,则∠DME= .(2)若∠ACB >∠ABC,记∠ACB -∠ABC=α,用含α的代数式表示∠DME 的值,并说明理由.(3)若点M在直线BC上运动(不与点D重合),在(2)条件下,其它条件不变,∠DME的大小是否随点M位置的变化而变化?请画出图形,并直接给出结论.附加题B1.我们规定:用[]x 表示实数x 的整数部分,如[]3.143=,2=,在此规定下解决下列问题:(1)填空:++++ = ;(2)求+++++ 的值.2.如图,D 、E 分别在△ABC 的边AC 、AB 上,BD 与CE 相交于点F . 如果2AE EB =,2AD DC =,21ABC S ∆=,求四边形AEFD 的面积.2015— 2016学年度第二学期期中试卷七年级数学参考答案及评分标准2015.4一、选择题(本题共30分,每小题3分)三、计算题(本题共16分,每小题4分)21.23)21(641251625-+-解:23)21(641251625-+-=551442-+·········································3分=12···············································4分22.(212+解:(212+=22-································2分=······································3分=·········································4分23.(1)0491212=-x解:212149x =···········································2分 117x =±··································4分 (2)512)1(3-=-x 解:18x -=-·············································2分9x =··················································4分四、解答题(本题共8分) 24.证明:∵HG ∥AB (已知)∴∠1=∠3(两直线平行,内错角相等)··················1分又∵HG ∥CD (已知)∴∠2=∠4 ∵AB ∥CD (已知)∴∠BEF +∠ EFD =180°(两直线平行,同旁内角互补)··3分 又∵EG 平分∠BEF (已知)∴∠1=21∠ BEH (角平分线定义)·············5分又∵FG 平分∠EFD (已知)∴∠2=21∠ EFD ·······················6分∴∠1+∠2=21( ∠BEH +∠EFD )··················8分∴∠1+∠2=90°∴∠3+∠4=90°,即∠EGF =90°五、作图题(本题共6分)25.解:(1)~(3)补全图形,如图;·····4分 (4)20·················6分六、解答题(本题共16分,其中26题6分,27题10分)26.解:∵MC ⊥CN ∴∠1+∠2=90° ∵∠1=30°B ∴∠2=60°···············2分∵CM 平分∠BCE∴∠BCE =2∠2=120°································4分 ∴∠BCD =60° ∵AB ∥ED∴∠B =∠BCD =60°······································6分27.解:(1)15°······································2分(2)∵ME ⊥AD∴∠DEM =90°∴∠1+∠DME =90° ∵∠1是△ABC 的外角 ∴∠1=∠BAD +∠B∵AD 为△ABC 的角平分线∴∠BAD =12∠BAC∴∠1 =12∠BAC +∠B∵在△ABC 中∴∠BAC +∠B +∠C =180°∴∠1 =12(180°-∠B -∠C )+∠B∴∠DME =90°-∠1=90°-(1802B C︒-∠-∠ +∠B )=12(∠C -∠B ) =12α·······················7分(3)①点M 在BD 上∠DME =12α····························8分 ②点M 在CB 延长线上∠DME =12α··························9分 ③点M 在BC 延长线上∠DME =12α·························10分七年级数学附加题参考答案及评分标准2015.41.解:(1)9···········································2分(2)+++++=1×3+2×5+3×7+4×9+5×11+6×13+7 =3+10+21+36+55+78+7 =210·····································5分第11页 共6页 2.解:连接AF ∵2AE EB =∴2AEF BEF S S ∆∆=,23AE AB =∴23AECABC S S ∆∆= ∵21ABC S ∆=∴14AEC S ∆=同理2CDF ADF S S ∆∆=,173ABD ABC S S ∆∆== 设BEF S x ∆=,ADF S y ∆= 则2AEF S x ∆=,2CDF S y ∆= ∴2214AEC AEF ADF CDF S S S S x y y ∆∆∆∆=++=++= 27ABD BEF AEF ADF S S S S x x y ∆∆∆∆=++=++= ∴221427x y y x x y ++=⎧⎨++=⎩ 解得14x y =⎧⎨=⎩∴26AEF AE D A F DF S S S x y ∆∆=+=+=四边形·····················5分B。
2016年河北省唐山市迁安市七年级下学期数学期中试卷与解析答案

2015-2016学年河北省唐山市迁安市七年级(下)期中数学试卷一、精心选一选,慧眼识金!(本大题共14小题,每小题3分,共42分,在每小题给出的四个选项中只有一项是正确的)1.(3分)在平面直角坐标系中,点M(﹣2,3)在()A.第一象限B.第二象限C.第三象限D.第四象限2.(3分)(﹣0.7)2的平方根是()A.﹣0.7 B.0.7 C.±0.7 D.0.493.(3分)一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是()A.第一次右拐50°,第二次左拐130°B.第一次左拐50°,第二次右拐130°C.第一次左拐50°,第二次左拐130°D.第一次右拐50°,第二次左拐50°4.(3分)如图,下列能判定AB∥CD的条件有()个.(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.A.1 B.2 C.3 D.45.(3分)下列7个实数中无理数有()3.141,﹣,,π,0,4.2,0.1010010001…A.2个 B.3个 C.4个 D.5个6.(3分)下列式子中,计算正确的是()A.﹣=﹣0.6 B.=﹣13 C.=±6 D.﹣=﹣37.(3分)在以下现象中,属于平移的是()①在挡秋千的小朋友;②打气筒打气时,活塞的运动;③钟摆的摆动;④传送带上,瓶装饮料的移动.A.①②B.①③C.②③D.②④8.(3分)把点(2,﹣3)先向右平移3个单位长度,再向下平移2个单位长度得到的点的坐标是()A.(5,﹣1)B.(﹣1,﹣5)C.(5,﹣5)D.(﹣1,﹣1)9.(3分)若点P是第二象限内的点,且点P到x轴的距离是4,到y轴的距离是3,则点P的坐标是()A.(﹣4,3)B.(4,﹣3)C.(﹣3,4)D.(3,﹣4)10.(3分)如果∠A和∠B的两边分别平行,那么∠A和∠B的关系是()A.相等B.互余或互补C.互补D.相等或互补11.(3分)下列说法不正确的是()A.坐标平面内的点与有序数对是一一对应的B.在x轴上的点纵坐标为零C.在y轴上的点横坐标为零D.平面直角坐标系把平面上的点分为四部分12.(3分)若a2=25,|b|=3,则a+b的值是()A.﹣8 B.±8 C.±2 D.±8或±213.(3分)如图,AB∥CD,那么∠A,∠P,∠C的数量关系是()A.∠A+∠P+∠C=90°B.∠A+∠P+∠C=180°C.∠A+∠P+∠C=360°D.∠P+∠C=∠A14.(3分)如图,数轴上表示1、的对应点分别为点A、点B.若点A是BC 的中点,则点C所表示的数为()A.B.1﹣C.D.2﹣二、填空题(简洁的结果,表达的是你敏锐的思维,需要的是细心!共6题,每小题3分,共18分)15.(3分)﹣=.16.(3分)把命题“垂直于同一条直线的两直线平行”,改写成“如果…,那么…”的形式:.17.(3分)线段CD是由线段AB平移得到的.点A(﹣2,5)的对应点为C(3,7),则点B(﹣3,0)的对应点D的坐标为.18.(3分)已知:A(0,4),点C在y轴上,AC=5,则点C的坐标为.19.(3分)如图,直线l1∥l2,AB⊥l1,垂足为D,BC与直线l2相交于点C,若∠1=30°,则∠2=.20.(3分)如果的平方根是±3,则=.三、解答题(耐心计算,认真推理,表露你萌动的智慧!共60分)21.(5分)计算:(1)﹣﹣(2)|﹣|﹣|3﹣|(3)求出x的值:x2﹣=0.22.(6分)阅读下列材料:∵,即,∴的整数部分为2,小数部分为.请你观察上述的规律后试解下面的问题:如果的小数部分为a,的小数部分为b,求的值.23.(9分)下面是某医院各部门的示意图,横向表示的是楼层,纵向表示的是门号,例如:院长室在4楼3门,我们用(4,3)来表示其位置,试根据上面方法,结合图形,完成下面问题:(1)儿科诊室可以表示为;(2)口腔科诊室在楼门;(3)图形中显示,与院长室同楼层的有;(4)与神经科诊室同楼层的有;(5)表示为(1,2)的诊室是;(6)表示为(3,5)的诊室是;(7)3楼7门的是.24.(10分)附加题:已知:如图∠1=∠2,∠C=∠D,试探究∠A与∠F相等吗?试说明理由.25.(10分)已知,如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD求证:∠EGF=90°(1)把下列证明过程及理由补充完整.(2 )请你用精炼准确的文字将上述结论总结出来.证明:∵HG∥AB(已知)∴∠1=∠3 ()又∵HG∥CD(已知)∴∠2=∠4(同理)∵AB∥CD(已知)∴∠BEF+ =180°()又∵EG平分∠BEF(已知)∴∠1=∠又∵FG平分∠EFD(已知)∴∠2=∠EFD (同理)∴∠1+∠2=(+ )∴∠1+∠2=90°∴∠3+∠4=90°即∠EGF=90°.26.(10分)△ABC与△A′B′C′在平面直角坐标系中的位置如图.(1)分别写出下列各点的坐标:A′;B′;C′;(2)说明△A′B′C′由△ABC经过怎样的平移得到?.(3)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为;(4)求△ABC的面积.2015-2016学年河北省唐山市迁安市七年级(下)期中数学试卷参考答案与试题解析一、精心选一选,慧眼识金!(本大题共14小题,每小题3分,共42分,在每小题给出的四个选项中只有一项是正确的)1.(3分)在平面直角坐标系中,点M(﹣2,3)在()A.第一象限B.第二象限C.第三象限D.第四象限【解答】解:∵﹣2<0,3>0,∴(﹣2,3)在第二象限,故选:B.2.(3分)(﹣0.7)2的平方根是()A.﹣0.7 B.0.7 C.±0.7 D.0.49【解答】解:(﹣0.7)2=0.49,0.49的平方根是±0.7,故选:C.3.(3分)一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是()A.第一次右拐50°,第二次左拐130°B.第一次左拐50°,第二次右拐130°C.第一次左拐50°,第二次左拐130°D.第一次右拐50°,第二次左拐50°【解答】解:如图,第一次拐的角是∠1,第二次拐的角是∠2,由于平行前进,也可以得到∠1=∠2.故选:D.4.(3分)如图,下列能判定AB∥CD的条件有()个.(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.A.1 B.2 C.3 D.4【解答】解:(1)利用同旁内角互补判定两直线平行,故(1)正确;(2)利用内错角相等判定两直线平行,∵∠1=∠2,∴AD∥BC,而不能判定AB ∥CD,故(2)错误;(3)利用内错角相等判定两直线平行,故(3)正确;(4)利用同位角相等判定两直线平行,故(4)正确.∴正确的为(1)、(3)、(4),共3个;故选:C.5.(3分)下列7个实数中无理数有()3.141,﹣,,π,0,4.2,0.1010010001…A.2个 B.3个 C.4个 D.5个【解答】解:无理数有:π,0.1010010001…共有2个.故选:A.6.(3分)下列式子中,计算正确的是()A.﹣=﹣0.6 B.=﹣13 C.=±6 D.﹣=﹣3【解答】解:A 0.62=0.36,故A错误;B ,故B错误;C =6,故C错误;D﹣=﹣3,故D正确.故选:D.7.(3分)在以下现象中,属于平移的是()①在挡秋千的小朋友;②打气筒打气时,活塞的运动;③钟摆的摆动;④传送带上,瓶装饮料的移动.A.①②B.①③C.②③D.②④【解答】解:①中是旋转运动,不是平移;②是平移;③中是旋转运动,不是平移;④是平移.故选:D.8.(3分)把点(2,﹣3)先向右平移3个单位长度,再向下平移2个单位长度得到的点的坐标是()A.(5,﹣1)B.(﹣1,﹣5)C.(5,﹣5)D.(﹣1,﹣1)【解答】解:点(2,﹣3)先向右平移3个单位长度,再向下平移2个单位长度得到的点的坐标是(2+3,﹣3﹣2),即(5,﹣5),故选:C.9.(3分)若点P是第二象限内的点,且点P到x轴的距离是4,到y轴的距离是3,则点P的坐标是()A.(﹣4,3)B.(4,﹣3)C.(﹣3,4)D.(3,﹣4)【解答】解:∵点P在第二象限,∴P点的横坐标为负,纵坐标为正,∵到x轴的距离是4,∴纵坐标为:4,∵到y轴的距离是3,∴横坐标为:﹣3,∴P(﹣3,4),故选:C.10.(3分)如果∠A和∠B的两边分别平行,那么∠A和∠B的关系是()A.相等B.互余或互补C.互补D.相等或互补【解答】解:如图知∠A和∠B的关系是相等或互补.故选:D.11.(3分)下列说法不正确的是()A.坐标平面内的点与有序数对是一一对应的B.在x轴上的点纵坐标为零C.在y轴上的点横坐标为零D.平面直角坐标系把平面上的点分为四部分【解答】解:A、由坐标平面内的点与有序数对的关系,可知坐标平面内的点与有序数对是一一对应的,原说法正确;B、由x轴上的点的坐标特征,可知在x轴上的点纵坐标为零,原说法正确;C、由y轴上的点的坐标特征,可知在y轴上的点横坐标为零,原说法正确;D、平面直角坐标系由四个象限和两个坐标轴组成,原说法错误.故选:D.12.(3分)若a2=25,|b|=3,则a+b的值是()A.﹣8 B.±8 C.±2 D.±8或±2【解答】解:∵a2=25,|b|=3∴a=±5,b=±3,则a+b的值是±8或±2.故选:D.13.(3分)如图,AB∥CD,那么∠A,∠P,∠C的数量关系是()A.∠A+∠P+∠C=90°B.∠A+∠P+∠C=180°C.∠A+∠P+∠C=360°D.∠P+∠C=∠A【解答】解:连接AC.∵AB∥CD,∴∠BAC+∠DCA=180°,∵∠P+∠PAC+∠PCA=180°,∴∠BAP+∠P+∠DCP=∠BAC+∠DCA+∠P+∠PAC+∠PCA=360°.故选:C.14.(3分)如图,数轴上表示1、的对应点分别为点A、点B.若点A是BC 的中点,则点C所表示的数为()A.B.1﹣C.D.2﹣【解答】解:设点C表示的数是x,∵数轴上表示1、的对应点分别为点A、点B,点A是BC的中点,∴=1,解得x=2﹣.故选:D.二、填空题(简洁的结果,表达的是你敏锐的思维,需要的是细心!共6题,每小题3分,共18分)15.(3分)﹣=﹣10.【解答】解:﹣=﹣10,故答案为:﹣10.16.(3分)把命题“垂直于同一条直线的两直线平行”,改写成“如果…,那么…”的形式:如果两条直线垂直于同一条直线,那么这两条直线平行.【解答】解:把命题“垂直于同一条直线的两直线平行”,改写成“如果…,那么…”的形式:如果两条直线垂直于同一条直线,那么这两条直线平行.17.(3分)线段CD是由线段AB平移得到的.点A(﹣2,5)的对应点为C(3,7),则点B(﹣3,0)的对应点D的坐标为(2,2).【解答】解:∵线段CD是由线段AB平移得到的,而点A(﹣2,5)的对应点为C(3,7),∴由A平移到C点的横坐标增加5,纵坐标增加2,则点B(﹣3,0)的对应点D的坐标为(2,2).故答案为:(2,2).18.(3分)已知:A(0,4),点C在y轴上,AC=5,则点C的坐标为(0,9)或(0,﹣1).【解答】解:∵A(0,4),点C在y轴上,AC=5,∴CO=9或CO=1,∴点C的坐标为:(0,9)或(0,﹣1).故答案为:(0,9)或(0,﹣1).19.(3分)如图,直线l1∥l2,AB⊥l1,垂足为D,BC与直线l2相交于点C,若∠1=30°,则∠2=120°.【解答】解:延长AB交直线l2于M,∵直线l1∥l2,AB⊥l1,∴AM⊥直线l2,∴∠BMC=90°,∴∠2=∠1+∠BMC=30°+90°=120°.故答案为:120°.20.(3分)如果的平方根是±3,则=4.【解答】解:∵的平方根是±3,∴=9,∴a=81,∴==4,故答案为:4.三、解答题(耐心计算,认真推理,表露你萌动的智慧!共60分)21.(5分)计算:(1)﹣﹣(2)|﹣|﹣|3﹣|(3)求出x的值:x2﹣=0.【解答】解:(1)原式=3﹣6+3=0;(2)原式=﹣﹣3+=2﹣﹣3;(3)方程整理得:x2=,开方得:x=±.22.(6分)阅读下列材料:∵,即,∴的整数部分为2,小数部分为.请你观察上述的规律后试解下面的问题:如果的小数部分为a,的小数部分为b,求的值.【解答】解:∵<,<,∴a=﹣2,b=﹣3,∴=﹣2+﹣3﹣=﹣5.23.(9分)下面是某医院各部门的示意图,横向表示的是楼层,纵向表示的是门号,例如:院长室在4楼3门,我们用(4,3)来表示其位置,试根据上面方法,结合图形,完成下面问题:(1)儿科诊室可以表示为(2,4);(2)口腔科诊室在1楼7门;(3)图形中显示,与院长室同楼层的有外科;(4)与神经科诊室同楼层的有儿科、妇科;(5)表示为(1,2)的诊室是内科;(6)表示为(3,5)的诊室是骨科;(7)3楼7门的是皮肤科.【解答】解:(1)儿科诊室可以表示为(2,4).故答案为(2,4).(2)口腔科诊室在1楼、7门.故答案为1、7.(3)图形中显示,与院长室同楼层的有外科.故答案为外科.(4)与神经科诊室同楼层的有儿科、妇科.故答案为儿科、妇科.(5)表示为(1,2)的诊室内科.故答案为内科.(6)表示为(3,5)的诊室是骨科.故答案为骨科.(7)3楼7门的是皮肤科.故答案为皮肤科.24.(10分)附加题:已知:如图∠1=∠2,∠C=∠D,试探究∠A与∠F相等吗?试说明理由.【解答】解:∠A=∠F.理由如下:∵∠1=∠2,∠1=∠DGH,∴∠2=∠DGH,∴BD∥CE,∴∠C=∠ABG,又∵∠C=∠D,∴∠ABG=∠D,∴AC∥DF,∴∠A=∠F.25.(10分)已知,如图,AB∥CD∥GH,EG平分∠BEF,FG平分∠EFD 求证:∠EGF=90°(1)把下列证明过程及理由补充完整.(2 )请你用精炼准确的文字将上述结论总结出来.证明:∵HG∥AB(已知)∴∠1=∠3 (两直线平行,内错角相等)又∵HG∥CD(已知)∴∠2=∠4(同理)∵AB∥CD(已知)∴∠BEF+ EFD=180°(两直线平行,同旁内角互补)又∵EG平分∠BEF(已知)∴∠1=∠BEF又∵FG平分∠EFD(已知)∴∠2=∠EFD (同理)∴∠1+∠2=(∠BEF+ ∠EFD)∴∠1+∠2=90°∴∠3+∠4=90°即∠EGF=90°.【解答】证明:∵HG∥AB(已知),∴∠1=∠3,又∵HG∥CD(已知),∴∠2=∠4(两直线平行,内错角相等),∵AB∥CD(已知),∴∠BEF+∠EFD=180°(两直线平行,同旁内角互补),又∵EG平分∠BEF(已知),∴∠1=∠BEF(角平分线的定义),又∵FG平分∠EFD(已知),∴∠2=∠EFD(角平分线的定义),∴∠1+∠2=(∠BEF+∠EFD),∴∠1+∠2=90°,∴∠3+∠4=90°(等量代换)即∠EGF=90°.故答案为:两直线平行,内错角相等,∠EFD,两直线平行,同旁内角互补,角平分线的定义,EFD,∠BEF.两直线平行,内错角相等;∠EFD;两直线平行,同旁内角互补;∠BEF;角平分线的定义;∠BEF;∠EFD;两条平行线被第三条直线所截,一组同旁内角的平分线互相垂直.26.(10分)△ABC与△A′B′C′在平面直角坐标系中的位置如图.(1)分别写出下列各点的坐标:A′(﹣3,1);B′(﹣2,﹣2);C′(﹣1,﹣1);(2)说明△A′B′C′由△ABC经过怎样的平移得到?先向左平移4个单位,再向下平移2个单位.(3)若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为(a﹣4,b﹣2);(4)求△ABC的面积.【解答】解:(1)A′(﹣3,1);B′(﹣2,﹣2);C′(﹣1,﹣1);(2)先向左平移4个单位,再向下平移2个单位;或:先向下平移2个单位,再向左平移4个单位;(3)P′(a﹣4,b﹣2);(4)△ABC的面积=2×3﹣×1×3﹣×1×1﹣×2×2=6﹣1.5﹣0.5﹣2=2.故答案为:(1)(﹣3,1),(﹣2,﹣2),(﹣1,﹣1);(2)先向左平移4个单位,再向下平移2个单位;(3)(a﹣4,b﹣2).赠送:初中数学几何模型举例【模型四】几何最值模型:图形特征:BAPl运用举例:1. △ABC中,AB=6,AC=8,BC=10,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为AP的中点,则MF的最小值为EM FB2.如图,在边长为6的菱形ABCD中,∠BAD=60°,E为AB的中点,F为AC上一动点,则EF+BF的最小值为_________。
2015-2016年河北省唐山市迁安市七年级下学期期中数学试卷(冀教版)和答案

2015-2016学年河北省唐山市迁安市七年级(下)期中数学试卷(冀教版)一、选择题:本大题共16个小题,1-10小题,每小题3分;11-16小题,每小题3分,共42分,在每小题给出的四个选项中,只有一项是符合要求的.1.(3分)化简a2•a3的结果是()A.a B.a5C.a6D.a82.(3分)如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是()A.两点之间线段最短B.点到直线的距离C.两点确定一条直线D.垂线段最短3.(3分)中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划,“一带一路”地区覆盖总人口约为4 400 000 000人,这个数用科学记数法表示为()A.44×108B.4.4×109C.4.4×108D.4.4×1010 4.(3分)如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=40°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转()A.15°B.20°C.25°D.30°5.(3分)下列命题中,真命题有()(1)直线外一点与直线上各点连接的所有线段中,垂线段最短;(2)两条直线被第三条直线所截,内错角相等;(3)经过两点有一条直线,并且只有一条直线;(4)如果一条直线和两条直线中的一条垂直,那么这条直线也和另一条垂直.A.1个B.2个C.3个D.4个6.(3分)若是关于x、y的二元一次方程ax﹣y=3的解,则a=()A.2B.3C.4D.57.(3分)如图,下列能判定AB∥CD的条件有()个.(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.A.1B.2C.3D.48.(3分)已知a,b满足方程组,则a+b的值为()A.﹣4B.4C.﹣2D.29.(3分)若x,y均为正整数,且2x+1•4y=128,则x+y的值为()A.3B.5C.4或5D.3或4或5 10.(3分)某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是()A.甲种方案所用铁丝最长B.乙种方案所用铁丝最长C.丙种方案所用铁丝最长D.三种方案所用铁丝一样长11.(2分)若x2+2(m﹣3)x+16是完全平方式,则m的值等于()A.3B.﹣5C.7D.7或﹣1 12.(2分)如果方程组的解为,那么被“★”“■”遮住的两个数分别是()A.10,4B.4,10C.3,10D.10,3 13.(2分)已知多项式(x+3)(x+n)=x2+mx﹣21,则m的值是()A.﹣4B.4C.﹣2D.214.(2分)根据如图给出的信息:若放入体积相同大球、体积相同小球各2个,水面将上升到()A.35cm B.36cm C.37cm D.39cm15.(2分)如图,阴影部分是边长为a的大正方形中剪去一个边长为b的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形,嘉嘉(图①)和琪琪(图②)分别给出了各自的割拼方法,其中能够验证平方差公式的是()A.嘉嘉B.琪琪C.都能D.都不能16.(2分)如图,P是直线m上一动点,A、B是直线n上的两个定点,且直线m∥n;对于下列各值:①点P到直线n的距离;②△PAB的周长;③△PAB 的面积;④∠APB的大小.其中会随点P的移动而变化的是()A.①②B.①③C.②④D.③④二、填空题:本大题共4个小题,每小题3分,共12分,把答案写在题中横线上.17.(3分)若4x2•□=8x3y,则“□”中应填入的代数式是.18.(3分)如图:AD∥BC,∠DAC=60°,∠ACF=25°,∠EFC=145°,∠B=54°,则∠BEF=°.19.(3分)定义运算“*”,规定x*y=ax2+by,其中a、b为常数,且1*2=5,2*1=6,则2*3=.20.(3分)观察下列多项式的乘法计算:(1)(x+3)(x+4)=x2+7x+12;(2)(x+3)(x﹣4)=x2﹣x﹣12;(3)(x﹣3)(x+4)=x2+x﹣12;(4)(x﹣3)(x﹣4)=x2﹣7x+12.根据你发现的规律,若(x+a)(x+b)=x2﹣8x+15,则a2+b2的值为.三、解答题:本大题共6个小题,共66分,解答应写出文字说明、证明过程或演算步骤.21.(10分)下面是老师在嘉嘉的数学作业本上截取的部分内容:问题:(1)这种解方程组的方法叫;嘉嘉的解法正确吗?如果不正确,错在哪一步?请你指出错误的原因,并求出正确的解;(2)请用不同于(1)中的方法解这个方程组.22.(10分)先化简,再求值:已知代数式(ax﹣3)(2x+4)﹣x2﹣b化简后,不含x2项和常数项.(1)求a、b的值;(2)求(2a+b)2﹣(a﹣2b)(a+2b)﹣3a(a﹣b)的值.23.(11分)已知:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.证明:∵DG⊥BC,AC⊥BC(已知)∴∠DGB=∠ACB=90°(垂直定义)∴DG∥AC()∴∠2=()∵∠1=∠2(已知)∴∠1=∠(等量代换)∴EF∥CD()∴∠AEF=∠()∵EF⊥AB(已知)∴∠AEF=90°()∴∠ADC=90°()∴CD⊥AB()24.(11分)一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元,若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:(1)甲、乙两组工作一天,商店各应付多少钱?(2)已知甲组单独完成需12天,乙组单独完成需24天,单独请哪个组,商店所需费用最少?(3)若装修完后,商店每天可盈利200元,现有三种方案:①甲组单独做;②乙组单独做;③甲、乙组同时做,你认为哪一种施工方案更有利于商店?请你帮助商店决策.(可用(1)(2)问的条件及结论)25.(11分)当我们利用两种不同的方法计算同一图形的面积时,可以得到一个等式,例如,由图1,可得等式:(a+2b)(a+b)=a2+3ab+2b2.(1)由图2,可得等式:.(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;(3)如图3,琪琪用2张A型纸片,3张B型纸片,5张C型纸片拼出一个长方形,那么该长方形较长的一条边长为.(直接写出答案)26.(13分)(1)问题发现如图①,直线AB∥CD,E是AB与AD之间的一点,连接BE,CE,可以发现∠B+∠C=∠BEC.请把下面的证明过程补充完整:证明:过点E作EF∥AB,∵AB∥DC(已知),EF∥AB(辅助线的作法),∴EF∥DC()∴∠C=∠CEF.()∵EF∥AB,∴∠B=∠BEF(同理),∴∠B+∠C=(等量代换)即∠B+∠C=∠BEC.(2)拓展探究如果点E运动到图②所示的位置,其他条件不变,求证:∠B+∠C=360°﹣∠BEC.(3)解决问题如图③,AB∥DC,∠C=120°,∠AEC=80°,则∠A=.(之间写出结论,不用写计算过程)2015-2016学年河北省唐山市迁安市七年级(下)期中数学试卷(冀教版)参考答案与试题解析一、选择题:本大题共16个小题,1-10小题,每小题3分;11-16小题,每小题3分,共42分,在每小题给出的四个选项中,只有一项是符合要求的.1.(3分)化简a2•a3的结果是()A.a B.a5C.a6D.a8【解答】解:原式=a2+3=a5,故B正确.故选:B.2.(3分)如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是()A.两点之间线段最短B.点到直线的距离C.两点确定一条直线D.垂线段最短【解答】解:要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是:垂线段最短,故选:D.3.(3分)中国倡导的“一带一路”建设将促进我国与世界各国的互利合作,根据规划,“一带一路”地区覆盖总人口约为4 400 000 000人,这个数用科学记数法表示为()A.44×108B.4.4×109C.4.4×108D.4.4×1010【解答】解:4 400 000 000=4.4×109,故选:B.4.(3分)如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=40°,若使直线b与直线c平行,则可将直线b绕点A逆时针旋转()A.15°B.20°C.25°D.30°【解答】解:∵∠1=120°,∴∠3=180°﹣120°=60°.∵∠2=40°,∴要使b∥c,则∠2=∠3,∴直线b绕点A逆时针旋转60°﹣40°=20°.故选:B.5.(3分)下列命题中,真命题有()(1)直线外一点与直线上各点连接的所有线段中,垂线段最短;(2)两条直线被第三条直线所截,内错角相等;(3)经过两点有一条直线,并且只有一条直线;(4)如果一条直线和两条直线中的一条垂直,那么这条直线也和另一条垂直.A.1个B.2个C.3个D.4个【解答】解:(1)直线外一点与直线上各点连接的所有线段中,垂线段最短,正确;(2)应为两条平行直线被第三条直线所截,内错角相等,故本选项错误;(3)经过两点有一条直线,并且只有一条直线,正确;(4)应为如果一条直线和两条平行直线中的一条垂直,那么这条直线也和另一条垂直,故本选项错误.所以(1)(3)两项是真命题.故选:B.6.(3分)若是关于x、y的二元一次方程ax﹣y=3的解,则a=()A.2B.3C.4D.5【解答】解:把代入方程得:2a﹣1=3,解得:a=2,故选:A.7.(3分)如图,下列能判定AB∥CD的条件有()个.(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.A.1B.2C.3D.4【解答】解:(1)利用同旁内角互补判定两直线平行,故(1)正确;(2)利用内错角相等判定两直线平行,∵∠1=∠2,∴AD∥BC,而不能判定AB ∥CD,故(2)错误;(3)利用内错角相等判定两直线平行,故(3)正确;(4)利用同位角相等判定两直线平行,故(4)正确.∴正确的为(1)、(3)、(4),共3个;故选:C.8.(3分)已知a,b满足方程组,则a+b的值为()A.﹣4B.4C.﹣2D.2【解答】解:,①+②×5得:16a=32,即a=2,把a=2代入①得:b=2,则a+b=4,故选:B.9.(3分)若x,y均为正整数,且2x+1•4y=128,则x+y的值为()A.3B.5C.4或5D.3或4或5【解答】解:∵2x+1•4y=2x+1+2y,27=128,∴x+1+2y=7,即x+2y=6∵x,y均为正整数,∴或∴x+y=5或4,故选:C.10.(3分)某数学兴趣小组开展动手操作活动,设计了如图所示的三种图形,现计划用铁丝按照图形制作相应的造型,则所用铁丝的长度关系是()A.甲种方案所用铁丝最长B.乙种方案所用铁丝最长C.丙种方案所用铁丝最长D.三种方案所用铁丝一样长【解答】解:由图形可得出:甲所用铁丝的长度为:2a+2b,乙所用铁丝的长度为:2a+2b,丙所用铁丝的长度为:2a+2b,故三种方案所用铁丝一样长.故选:D.11.(2分)若x2+2(m﹣3)x+16是完全平方式,则m的值等于()A.3B.﹣5C.7D.7或﹣1【解答】解:∵x2+2(m﹣3)x+16是完全平方式,∴m﹣3=±4,解得:m=7或﹣1,故选:D.12.(2分)如果方程组的解为,那么被“★”“■”遮住的两个数分别是()A.10,4B.4,10C.3,10D.10,3【解答】解:把代入2x+y=16得12+■=16,解得■=4,再把代入x+y=★得★=6+4=10,故选:A.13.(2分)已知多项式(x+3)(x+n)=x2+mx﹣21,则m的值是()A.﹣4B.4C.﹣2D.2【解答】解:(x+3)(x+n)=x2+mx﹣21,x2+nx+3x+3n=x2+mx﹣21,x2+(n+3)x+3n=x2+mx﹣21,则,解得:.故选:A.14.(2分)根据如图给出的信息:若放入体积相同大球、体积相同小球各2个,水面将上升到()A.35cm B.36cm C.37cm D.39cm【解答】解:设一个大球使水面上升xcm,一个小球使水面上升ycm,依据题意得,化简得解得,所以放入体积相同大球、体积相同小球各2个,水面将上升到26+2(3+2)=36cm,故选:B.15.(2分)如图,阴影部分是边长为a的大正方形中剪去一个边长为b的小正方形后所得到的图形,将阴影部分通过割、拼,形成新的图形,嘉嘉(图①)和琪琪(图②)分别给出了各自的割拼方法,其中能够验证平方差公式的是()A.嘉嘉B.琪琪C.都能D.都不能【解答】解:在图①中,左边的图形阴影部分的面积=a2﹣b2,右边图形中阴影部分的面积=(a+b)(a﹣b),故可得:a2﹣b2=(a+b)(a﹣b),可以验证平方差公式;在图②中,阴影部分的面积相等,左边阴影部分的面积=a2﹣b2,右边阴影部分面积=(2b+2a)•(a﹣b)=(a+b)(a﹣b),可得:a2﹣b2=(a+b)(a﹣b),可以验证平方差公式.故选:C.16.(2分)如图,P是直线m上一动点,A、B是直线n上的两个定点,且直线m∥n;对于下列各值:①点P到直线n的距离;②△PAB的周长;③△PAB 的面积;④∠APB的大小.其中会随点P的移动而变化的是()A.①②B.①③C.②④D.③④【解答】解:∵直线m∥n,∴点P到直线n的距离;故①错误;∵PA、PB的长度随点P的移动而变化,∴△PAB的周长会随点P的移动而变化,故②正确;∵点P到直线n的距离不变,AB的大小,∴△PAB的面积不变,故③错误;直线MN,AB之间的距离不随点P的移动而变化,∠APB的大小点P的移动而变化,故④正确;综上所述,会随点P的移动而变化的是②④.故选:C.二、填空题:本大题共4个小题,每小题3分,共12分,把答案写在题中横线上.17.(3分)若4x2•□=8x3y,则“□”中应填入的代数式是2xy.【解答】解:∵4x2•□=8x3y,∴“□”中应填入的代数式是:8x3y÷4x2=2xy,故答案为:2xy.18.(3分)如图:AD∥BC,∠DAC=60°,∠ACF=25°,∠EFC=145°,∠B=54°,则∠BEF=126°.【解答】解:∵AD∥BC,∴∠ACB=∠DAC=60°,∵∠ACF=25°,∴∠FCB=35°,∴∠EFC+∠FCB=145°+35°=180°,∴EF∥BC.∵∠B=54°,∴∠BEF=180°﹣54°=126°.故答案为:126.19.(3分)定义运算“*”,规定x*y=ax2+by,其中a、b为常数,且1*2=5,2*1=6,则2*3=10.【解答】解:根据题中的新定义化简已知等式得:,解得:a=1,b=2,则2*3=4a+3b=4+6=10,故答案为:10.20.(3分)观察下列多项式的乘法计算:(1)(x+3)(x+4)=x2+7x+12;(2)(x+3)(x﹣4)=x2﹣x﹣12;(3)(x﹣3)(x+4)=x2+x﹣12;(4)(x﹣3)(x﹣4)=x2﹣7x+12.根据你发现的规律,若(x+a)(x+b)=x2﹣8x+15,则a2+b2的值为34.【解答】解:根据题意,知:a+b=﹣8,ab=15,则a2+b2=(a+b)2﹣2ab=(﹣8)2﹣2×15=64﹣30=34,故答案为:34.三、解答题:本大题共6个小题,共66分,解答应写出文字说明、证明过程或演算步骤.21.(10分)下面是老师在嘉嘉的数学作业本上截取的部分内容:问题:(1)这种解方程组的方法叫代入消元法;嘉嘉的解法正确吗?如果不正确,错在哪一步?请你指出错误的原因,并求出正确的解;(2)请用不同于(1)中的方法解这个方程组.【解答】解:(1)这种解方程组的方法叫代入消元法;嘉嘉的解法不正确,错在第二步,正确解法:将方程①变形,得y=2x﹣3③,把方程③代入②,得x+2x﹣3=﹣12,解得,x=﹣3,把x=﹣3代入③,得y=﹣9,则方程组的解为:,故答案为:代入消元法;(2)①+②,得3x=﹣9,解得,x=﹣3,把x=﹣3代入①,得,y=﹣9,则方程组的解为:.22.(10分)先化简,再求值:已知代数式(ax﹣3)(2x+4)﹣x2﹣b化简后,不含x2项和常数项.(1)求a、b的值;(2)求(2a+b)2﹣(a﹣2b)(a+2b)﹣3a(a﹣b)的值.【解答】解:(1)原式=2ax2+4ax﹣6x﹣12﹣x2﹣b=(2a﹣1)x2+(4a﹣6)x+(﹣12﹣b),由结果不含x2项和常数项,得到2a﹣1=0,﹣12﹣b=0,解得:a=,b=﹣12;(2)原式=4a2+4ab+b2﹣a2+4b2﹣3a2+3ab=7ab+5b2,当a=,b=﹣12时,原式=﹣42+720=678.23.(11分)已知:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.证明:∵DG⊥BC,AC⊥BC(已知)∴∠DGB=∠ACB=90°(垂直定义)∴DG∥AC(同位角相等,两直线平行)∴∠2=∠ACD(两直线平行,内错角相等)∵∠1=∠2(已知)∴∠1=∠ACD(等量代换)∴EF∥CD(同位角相等,两直线平行)∴∠AEF=∠ADC(两直线平行,同位角相等)∵EF⊥AB(已知)∴∠AEF=90°(垂直定义)∴∠ADC=90°(等量代换)∴CD⊥AB(垂直定义)【解答】解:证明过程如下:证明:∵DG⊥BC,AC⊥BC(已知)∴∠DGB=∠ACB=90°(垂直定义)∴DG∥AC(同位角相等,两直线平行)∴∠2=∠ACD(两直线平行,内错角相等)∵∠1=∠2(已知)∴∠1=∠ACD(等量代换)∴EF∥CD(同位角相等,两直线平行)∴∠AEF=∠ADC(两直线平行,同位角相等)∵EF⊥AB(已知)∵∠AEF=90°(垂直定义)∴∠ADC=90°(等量代换)∴CD⊥AB(垂直定义).24.(11分)一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两组费用共3520元,若先请甲组单独做6天,再请乙组单独做12天可以完成,需付费用3480元,问:(1)甲、乙两组工作一天,商店各应付多少钱?(2)已知甲组单独完成需12天,乙组单独完成需24天,单独请哪个组,商店所需费用最少?(3)若装修完后,商店每天可盈利200元,现有三种方案:①甲组单独做;②乙组单独做;③甲、乙组同时做,你认为哪一种施工方案更有利于商店?请你帮助商店决策.(可用(1)(2)问的条件及结论)【解答】解:(1)设甲组单独工作一天商店应付x元,乙组单独工作一天商店应付y元.由题意可得:,解得:.答:甲组单独工作一天商店应付300元,乙组单独工作一天商店应付140元.(2)∵甲组单独完成需12天,乙组单独完成需24天,∴单独请甲组需付300×12=3600(元),单独请乙组需付140×24=3360(元),∵3600>3360,∴单独请乙组费用较少;(3)由题意,得①甲组单独做12天完成,商店需付款3600元;乙组单独做24天完成,商店需付款3360元;但甲组比乙组早12天完工,商店12天的利润为200×12=2400元,即开支为3600﹣2400=1200元<3360元,故选择甲组单独做比选择乙组单独做划算.②甲、乙合作8天可以完成,需付费用3520元,此时工期比甲单独做少4天,商店开业4天的利润为4×200=800元,开支为3520﹣800=2720元<3600元;则甲、乙合作比甲单独做12天合算.综上所述,甲、乙合作这一方案最优.25.(11分)当我们利用两种不同的方法计算同一图形的面积时,可以得到一个等式,例如,由图1,可得等式:(a+2b)(a+b)=a2+3ab+2b2.(1)由图2,可得等式:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc.(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=11,ab+bc+ac=38,求a2+b2+c2的值;(3)如图3,琪琪用2张A型纸片,3张B型纸片,5张C型纸片拼出一个长方形,那么该长方形较长的一条边长为2a+3b.(直接写出答案)【解答】解:(1)(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;(2)∵a+b+c=11,ab+bc+ac=38,∴a2+b2+c2=(a+b+c)2﹣2(ab+ac+bc)=121﹣76=45;(3)根据题意得:2a2+5ab+3b2=(2a+3b)(a+b),则较长的一边为2a+3b.故答案为:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc;2a+3b.26.(13分)(1)问题发现如图①,直线AB∥CD,E是AB与AD之间的一点,连接BE,CE,可以发现∠B+∠C=∠BEC.请把下面的证明过程补充完整:证明:过点E作EF∥AB,∵AB∥DC(已知),EF∥AB(辅助线的作法),∴EF∥DC(平行于同一直线的两直线平行)∴∠C=∠CEF.(两直线平行,内错角相等)∵EF∥AB,∴∠B=∠BEF(同理),∴∠B+∠C=∠BEF+∠CEF(等量代换)即∠B+∠C=∠BEC.(2)拓展探究如果点E运动到图②所示的位置,其他条件不变,求证:∠B+∠C=360°﹣∠BEC.(3)解决问题如图③,AB∥DC,∠C=120°,∠AEC=80°,则∠A=20°.(之间写出结论,不用写计算过程)【解答】(1)证明:如图①,过点E作EF∥AB,∵AB∥DC(已知),EF∥AB(辅助线的作法),∴EF∥DC(平行于同一直线的两直线平行),∴∠C=∠CEF.(两直线平行,内错角相等),∵EF∥AB,∴∠B=∠BEF(同理),∴∠B+∠C=∠BEF+∠CEF(等量代换)即∠B+∠C=∠BEC,故答案为:平行于同一直线的两直线平行,两直线平行,内错角相等,∠BEF+∠CEF;(2)证明:如图②,过点E作EF∥AB,∵AB∥DC(已知),EF∥AB(辅助线的作法),∴EF∥DC(平行于同一直线的两直线平行),∴∠C+∠CEF=180°,∠B+∠BEF=180°,∴∠B+∠C+∠AEC=360°,∴∠B+∠C=360°﹣∠BEC;(3)解:如图③,过点E作EF∥AB,∵AB∥DC(已知),EF∥AB(辅助线的作法),∴EF∥DC(平行于同一直线的两直线平行),∴∠C+∠CEF=180°,∠A=∠BEF,∵∠C=120°,∠AEC=80°,∴∠CEF=180°﹣120°=60°,∴∠BEF=80°﹣60°=20°,∴∠A=∠AEF=20°.故答案为:20°.第21页(共21页)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(1) 儿科诊室可以表示为; (2) 口腔科诊室在楼门; (3) 图形中显示,与院长室同楼层的有; (4) 与神经科诊室同楼层的有; (5) 表示为(1,2)的诊室是; (6) 表示为(3,5)的诊室是; (7) 3楼7门的是. 24. 附加题:已知:如图∠1=∠2,∠C=∠D,试探究∠A与∠F相等吗?试说明理由.
河北省唐山市迁安市2015-2016学年七年级下学期期中数学试卷
一、精心选一选,慧眼识金!
1. 在平面直角坐标系中,点M(﹣2,3)在( ) A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限 2. (﹣0.7)2的平方根是( )
A . ﹣0.7 B . 0.7 C . ±0.7 D . 0.49 3. 一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是( ) A . 第一次右拐50°,第二次左拐130° B . 第一次左拐50°,第二次右拐130° C . 第一次左拐50°,第二次左拐130° D . 第一次右 拐50°,第二次左拐50° 4. 如图,下列能判定AB∥CD的条件有( )个. (1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.
20. 如果 的平方根是±3,则
=________.
三、解答题
21. 计算:
(1)
﹣
﹣
(2) | ﹣ |﹣|3﹣ |
(3) 求出x的值:x2﹣
=0.
22. 阅读下列材料:
∵
,即
,
∴ 的整数部分为2,小数部分为
.
请你观察上述的规律后试解下面的问题:
如果 的小数部分为a, 的小数部分为b,求
的值.
23. 下面是某医院各部门的示意图,横向表示的是楼层,纵向表示的是门号,例如:院长室在4楼3门,我们用(4,3
25. 已知,如图,AB∥CFra bibliotek∥GH,EG平分∠BEF,FG平分∠EFD
求证:∠EGF=90°
①把下列证明过程及理由补充完整. ②请你用精炼准确的文字将上述结论总结出来.
证明:∵HG∥AB(已知) ∴∠1=∠3 (________) 又∵HG∥CD(已知) ∴∠2=∠4(同理) ∵AB∥CD(已知) ∴∠BEF+________=180° (________) 又∵EG平分∠BEF(已知) ∴∠1= ∠________
16. 把命题“垂直于同一条直线的两直线平行”,改写成“如果…,那么…”的形式:________. 17. 线段CD是由线段AB平移得到的.点A(﹣2,5)的对应点为C(3,7),则点B(﹣3,0)的对应点D的坐标为_ _______. 18. 已知:A(0,4),点C在y轴上,AC=5,则点C的坐标为________. 19. 如图,直线l1∥l2 , AB⊥l1 , 垂足为D,BC与直线l2相交于点C,若∠1=30°,则∠2=________.
A.1B.2C.3D.4
5. 下列7个实数中无理数有( )
3.141,﹣ ,
,π,0,4.2
,0.1010010001…
A . 2个 B . 3个 C . 4个 D . 5个
6. 下列式子中,计算正确的是( )
A . ﹣ =﹣0.6 B .
=﹣13 C .
7. 在以下现象中,属于平移的是( )
=±6 D . ﹣
13. 14. 15. 16. 17. 18. 19. 20. 21.
22. 23.
24.
25.
26.
A . 坐标平面内的点与有序数对是一一对应的 B . 在x轴上的点纵坐标为零 C . 在y轴上的点横坐标为零 D . 平面直角坐标系把平
面上的点分为四部分
12. 若a2=25,|b|=3,则a+b的值是( )
A . ﹣8 B . ±8 C . ±2 D . ±8或±2 13. 如图,AB∥CD,那么∠A,∠P,∠C的数量关系是( )
A . ∠A+∠P+∠C=90° B . ∠A+∠P+∠C=180° C . ∠A+∠P+∠C=360° D . ∠P+∠C=∠A 14. 如图,数轴上表示1、 的对应点分别为点A,点B.若点A是BC的中点,则点C所表示的数为( )
A.
B . 1﹣ C .
D . 2﹣
二、填空题
15. ﹣
=________.
=﹣3
①在挡秋千的小朋友;②打气筒打气时,活塞的运动;③钟摆的摆动;④传送带上,瓶装饮料的移动.
A . ①② B . ①③ C . ②③ D . ②④ 8. 把点(2,﹣3)先向右平移3个单位长度,再向下平移2个单位长度得到的点的坐标是( ) A . (5,﹣1) B . (﹣1,﹣5) C . (5,﹣5) D . (﹣1,﹣1) 9. 若点P是第二象限内的点,且点P到x轴的距离是4,到y轴的距离是3,则点P的坐标是( ) A . (﹣4,3) B . (4,﹣3) C . (﹣3,4) D . (3,﹣4) 10. 如果∠A和∠B的两边分别平行,那么∠A和∠B的关系是( ) A . 相等 B . 互余或互补 C . 互补 D . 相等或互补 11. 下列说法不正确的是( )
又∵FG平分∠EFD(已知) ∴∠2= ∠EFD (同理) ∴∠1+∠2= (________ +________) ∴∠1+∠2=90° ∴∠3+∠4=90° 即∠EGF=90°. 26. △ABC与△A′B′C′在平面直角坐标系中的位置如图.
(1) 分别写出下列各点的坐标:A′; B′;C′; (2) 说明△A′B′C′由△ABC经过怎样的平移得到?. (3) 若点P(a,b)是△ABC内部一点,则平移后△A′B′C′内的对应点P′的坐标为; (4) 求△ABC的面积. 参考答案 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12.
