matlab 实验4 解答
实验4 MATLAB绘图

实验四 MATLAB 绘图
4)在第一小题的基础上加入网格和标注。 3 绘制单位圆。 提示:使用 axis( ‘ square’ )命令保证图形的纵横坐标刻度比例相同。 4 设 R 分别为 1, 5, 10 和 20,绘制伏安特性曲线, U=RI。 5
⎧ x = t ⎪ 绘制方程 ⎨ y = sin(t ) 在 t=[0 ⎪ z = cos(t ) ⎩
三 实验内容
1 已知向量 [1, 2, 4, 0, 5, 10, 11, 21, 3, 1],请绘图表示。 2 绘制一条正弦曲线和一条余弦曲线,分别满足以下条件: 1)在同一窗口,正弦曲线用红色的点线表示,余弦曲线用蓝色的星型线表示; 2)在同一个窗口中,要求分割为一行两列的子图,子图 1 为正弦曲线,子图 2 为余弦曲线 ;(线形与上题一致 ); 3)在两个不同的窗口中绘制这两条曲线;
1
实验四 MATLAB 绘图
1) . 单 窗 口 单 曲 线 绘 图 x=[0, 0.48,0.84,1,0.91,0.6,0.14] plot (x) 2) . 单 窗 口 多 曲 线 绘 图 例: t=0:pi/100:2*pi; y=sin(t);y1=sin(t+0.25);y2=sin(t+0.5); plot(t,y,t,y1,t,y2) 3) . 单 窗 口 多 曲 线 分 图 绘 图 subplot —— 子图分割命令 调用格式: subplot(m,n,p) —— 按从左至右,从上至下排列 4) . 多 窗 口 绘 图 figure(n) —— 创建窗口函数, n 为窗口顺序号。 例 t=0:pi/100:2*pi; y=sin(t);y1=sin(t+0.25);y2=sin(t+0.5); plot(t,y) —— 自动出现第一个窗口 figure(2) plot(t,y1) —— 在第二窗口绘图 figure(3) plot(t,y2) ——在第三窗口绘图 5) .可 任 意 设 置 颜 色 与 线 型 plot(t,y,'r-',t,y1,'g:',t,y2,'b*') 6) .图 形 加 注 功 能 将标题、坐标轴标记、网格线及文字注释加注到图形上,这些函数为: title —— 给图形加标题 xlable —— 给 x 轴加标注 ylable —— 给 y 轴加标注 text —— 在图形指定位置加标注 gtext —— 将标注加到图形任意位置 grid on(off) —— 打开、关闭坐标网格线 legend —— 添加图例 axis —— 控制坐标轴的刻度 例: t=0:0.1:10 y1=sin(t);y2=cos(t);plot(t,y1,'r',t,y2,'b--'); x=[1.7*pi;1.6*pi]; y=[-0.3;0.8]; s=['sin(t)';'cos(t)']; text(x,y,s); title('正弦和余弦曲线 '); legend('正弦 ','余弦 ') xlabel('时间 t'),ylabel('正弦、余弦 ') grid
matlab实验4simulink系统仿真
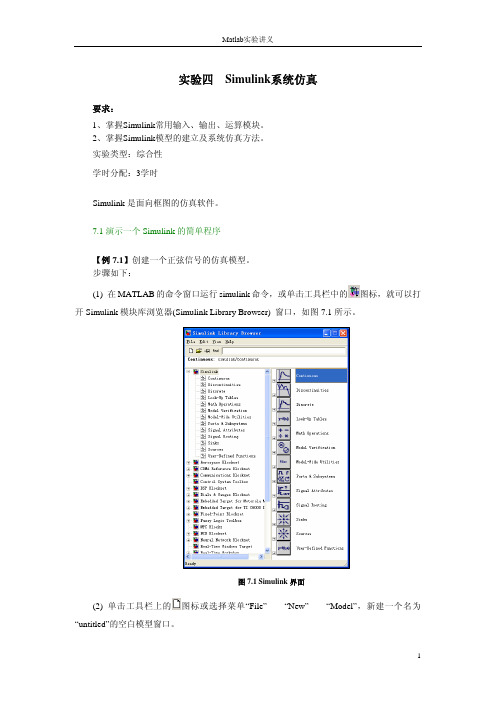
1. 模块间连线 先将光标指向一个模块的输出端,待光标变为十字符后,按下鼠标键并拖动,直到另 一模块的输入端。
6
Matlab实验讲义
2. 信号线的分支和折曲 (1) 分支的产生 将光标指向信号线的分支点上,按鼠标右键,光标变为十字符,拖动鼠标直到分支线 的终点,释放鼠标;或者按住 Ctrl 键,同时按下鼠标左键拖动鼠标到分支线的终点,如图 7.10 所示。
7.2.2 Simulink 的模型窗口
模型窗口由菜单、工具栏、模型浏览器窗口、模型框图窗口以及状态栏组成。
菜单 工具栏
模型浏览器
模型框图
状态栏
图7.5 双窗口模型窗口
1. 状态栏
3
Matlab实验讲义
2. 工具栏 模型窗口工具栏如图 7.6 所示。
创建并编译生成exe文件
展示父系统 打开调试器
开始仿真 结束仿真
(4) 用鼠标单击所需要的输入信号源模块“Sine Wave”(正弦信号),将其拖放到的空白 模型窗口“untitled”,则“Sine Wave”模块就被添加到 untitled 窗口;也可以用鼠标选中“Sine Wave”模块,单击鼠标右键,在快捷菜单中选择“add to 'untitled'”命令,就可以将“Sine Wave”模块添加到 untitled 窗口,如图 7.2 所示。
显示库链接 显示/隐藏阴影效果 设置不同的采样时间序列的颜色 粗线表示多信号构成的向量信号线 注明向量信号线的信号数 标明端口数据的类型 显示存储类型 数据浏览器 Simulink调试器 用户定义数据类型设计器 线性化分析工具
7.3 模型的创建
7.3.1 模块的操作
1. 对象的选定 (8) 选定单个对象 选定对象只要在对象上单击鼠标,被选定的对象的四角处会出现小黑块编辑框。 (9) 选定多个对象 如果选定多个对象,可以按下 Shift 键,然后再单击所需选定的模块;或者用鼠标拉出 矩形虚线框,将所有待选模块框在其中,则矩形框中所有的对象均被选中,如图 7.7 所示。
2013MATLAB原理及应用实验报告第四章

《MATLAB原理及应用》实验报告第四章MATLAB程序设计一.实验目的1、掌握脚本文件的建立2、掌握条件语句和程序语句的使用3、掌握MATLAB的程序设计方法二.实验内容1.关于M脚本文件和M函数文件M文件是在M文件编辑器窗口中编写的。
在MATLAB的桌面上单击新建按钮,就可以打开M文件编辑器窗口,也可以通过依次单击【File】/【New】/【M-File】打开文件编辑器。
【实验4-1】脚本文件在M文件编辑器窗口输入一下内容:N=3;for m=1:Nfor n=1:Nif m==nA(m,n)=1;elseA(m,n)=0;endendend单击M文件编辑器窗口中的保存按钮,以“ex1.m”为文件名保存在当前工作目录下。
在命令窗口中输入:>> ex1运行后可以在命令窗口中看到变量A的图标,继续在命令窗口输入:>> AA =1 0 00 1 00 0 1这一脚本文件创建了一个3阶单位阵【实验4-2】 M 函数在M 文件编辑器窗口输入一下内容:function [mean,stdev]=stat(x)x=input('请输入x 的值:')%[mean,stdev]=stat(x)计算输入向量的均值和平均差%输入参数x 是向量%第一个输入参数mean 是向量各元素的平均值%第二个输入参数stdev 是向量的均方差%例如,取向量x=[1,2,3,4,5];%调用[mean,stdev]=stat(x),计算可得%均值mean=3%均方差stdev=1.4142n=length(x) %计算向量长度mean=sum(x)/n %计算向量平均值stdev=sqrt(sum((x-mean).^2/n)) %计算均方差输入完毕后,单击保存按钮,把文件保存在当前工作目录下,文件名为“stat.m ”2.MATLAB 程序流程控制【实验4-3】一个简单的for 循环事例。
matlab课后习题答案第四章
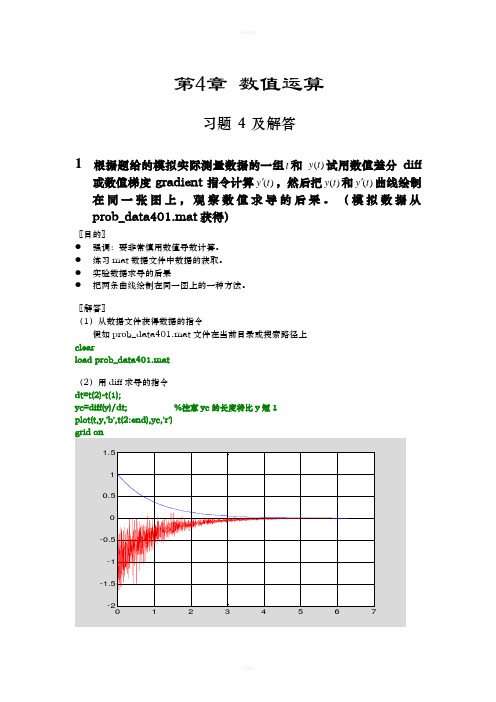
第4章数值运算习题 4 及解答1 根据题给的模拟实际测量数据的一组t和)(t y试用数值差分diff或数值梯度gradient指令计算)(t y',然后把)(t y和)(t y'曲线绘制在同一张图上,观察数值求导的后果。
(模拟数据从prob_data401.mat获得)〖目的〗●强调:要非常慎用数值导数计算。
●练习mat数据文件中数据的获取。
●实验数据求导的后果●把两条曲线绘制在同一图上的一种方法。
〖解答〗(1)从数据文件获得数据的指令假如prob_data401.mat文件在当前目录或搜索路径上clearload prob_data401.mat(2)用diff求导的指令dt=t(2)-t(1);yc=diff(y)/dt; %注意yc的长度将比y短1plot(t,y,'b',t(2:end),yc,'r')(3)用gradent 求导的指令(图形与上相似)dt=t(2)-t(1);yc=gradient(y)/dt;plot(t,y,'b',t,yc,'r')grid on〖说明〗● 不到万不得已,不要进行数值求导。
● 假若一定要计算数值导数,自变量增量dt 要取得比原有数据相对误差高1、2个量级以上。
● 求导会使数据中原有的噪声放大。
2 采用数值计算方法,画出dt tt x y x ⎰=0sin )(在]10 ,0[区间曲线,并计算)5.4(y 。
〖提示〗● 指定区间内的积分函数可用cumtrapz 指令给出。
● )5.4(y 在计算要求不太高的地方可用find 指令算得。
〖目的〗● 指定区间内的积分函数的数值计算法和cumtrapz 指令。
● find 指令的应用。
〖解答〗dt=1e-4;t=0:dt:10;t=t+(t==0)*eps;f=sin(t)./t;s=cumtrapz(f)*dt;plot(t,s,'LineWidth',3)ii=find(t==4.5);s45=s(ii)s45 =1.65413 求函数x ex f 3sin )(=的数值积分⎰=π0 )(dx x f s ,并请采用符号计算尝试复算。
2019年MATLAB)课后实验答案

实验一 MATLAB 运算基础1. 先求下列表达式的值,然后显示MATLAB 工作空间的使用情况并保存全部变量。
(1) 0122sin 851z e =+(2) 21ln(2z x =,其中2120.455i x +⎡⎤=⎢⎥-⎣⎦ (3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e az a a --+=++=--(4) 2242011122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪-+≤<⎩,其中t =0:: 解:4. 完成下列操作:(1) 求[100,999]之间能被21整除的数的个数。
(2) 建立一个字符串向量,删除其中的大写字母。
解:(1) 结果:(2). 建立一个字符串向量例如:ch='ABC123d4e56Fg9';则要求结果是:实验二 MATLAB 矩阵分析与处理1. 设有分块矩阵33322322E R A O S ⨯⨯⨯⨯⎡⎤=⎢⎥⎣⎦,其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵和对角阵,试通过数值计算验证22E R RS A O S +⎡⎤=⎢⎥⎣⎦。
解: M 文件如下;5. 下面是一个线性方程组:1231112340.951110.673450.52111456x x x ⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦(1) 求方程的解。
(2) 将方程右边向量元素b 3改为再求解,并比较b 3的变化和解的相对变化。
(3) 计算系数矩阵A 的条件数并分析结论。
解: M 文件如下:123d4e56g9实验三 选择结构程序设计1. 求分段函数的值。
2226035605231x x x x y x x x x x x x ⎧+-<≠-⎪=-+≤<≠≠⎨⎪--⎩且且及其他用if 语句实现,分别输出x=,,,,,,时的y 值。
MATLAB)课后实验答案

实验一 MATLAB 运算基础1、 先求下列表达式得值,然后显示MATLAB 工作空间得使用情况并保存全部变量。
(1) 0122sin 851z e =+(2) 21ln(2z x =+,其中2120.455i x +⎡⎤=⎢⎥-⎣⎦ (3) 0.30.330.3sin(0.3)ln , 3.0, 2.9,,2.9,3.022a a e e a z a a --+=++=--L (4) 2242011122123t t z t t t t t ⎧≤<⎪=-≤<⎨⎪-+≤<⎩,其中t =0:0、5:2、5 解:4、 完成下列操作:(1) 求[100,999]之间能被21整除得数得个数。
(2) 建立一个字符串向量,删除其中得大写字母。
解:(1) 结果:(2)、 建立一个字符串向量 例如:ch='ABC123d4e56Fg9';则要求结果就是:实验二 MATLAB 矩阵分析与处理1、 设有分块矩阵33322322E R A O S ⨯⨯⨯⨯⎡⎤=⎢⎥⎣⎦,其中E 、R 、O 、S 分别为单位矩阵、随机矩阵、零矩阵与对角阵,试通过数值计算验证22E R RS A OS +⎡⎤=⎢⎥⎣⎦。
解: M 文件如下;5、 下面就是一个线性方程组:1231112340.951110.673450.52111456x x x ⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎢⎥⎢⎥⎣⎦(1) 求方程得解。
(2) 将方程右边向量元素b 3改为0、53再求解,并比较b 3得变化与解得相对变化。
(3) 计算系数矩阵A 得条件数并分析结论。
解: M 文件如下:实验三 选择结构程序设计1、 求分段函数得值。
2226035605231x x x x y x x x x x x x ⎧+-<≠-⎪=-+≤<≠≠⎨⎪--⎩且且及其他用if 语句实现,分别输出x=-5、0,-3、0,1、0,2、0,2、5,3、0,5、0时得y 值。
matlab实验4_循环结构程序设计_参考解答

高教社刘卫国《MATLAB 程序设计与应用》(第二版)实验参考解答
实验四:循环结构程序设计
clear all; close all; clc; y=0; n=1; while y<3
y=y+1/(2*n-1); n=n+1; end n=n-1; y=y-1/(2*n-1) n=n-1
运行结果:
y= 2.9944
x1=a/(b+x0); y=abs(x1-x0); x0=x1;
MATLAB 语言
3
WangChengyou © 山东大学威海分校
高教社刘卫国《MATLAB 程序设计与应用》(第二版)实验参考解答
实验四:循环结构程序设计
n=n+1; end x1 r1=(-b+sqrt(b^2+4*a))/2 r2=(-b-sqrt(b^2+4*a))/2
clear all; close all; clc; prime=[]; for n=2:49
x=n*(n+1)-1; signx=0; for k=2:sqrt(x)
MATLAB 语言
5
WangChengyou © 山东大学威海分校
高教社刘卫国《MATLAB 程序设计与应用》(第二版)实验参考解答
根据
π2 6
=1 12
+
1 22
+1 32
+"+
1 n2
,求 π 的近似值。当
n
分别取
100、1000、10000
时,
结果是多少?
要求:分别用循环结构和向量运算(使用 sum 函数)来实现。 答:程序设计:
(1) 循环结构
matlab课后习题答案第四章
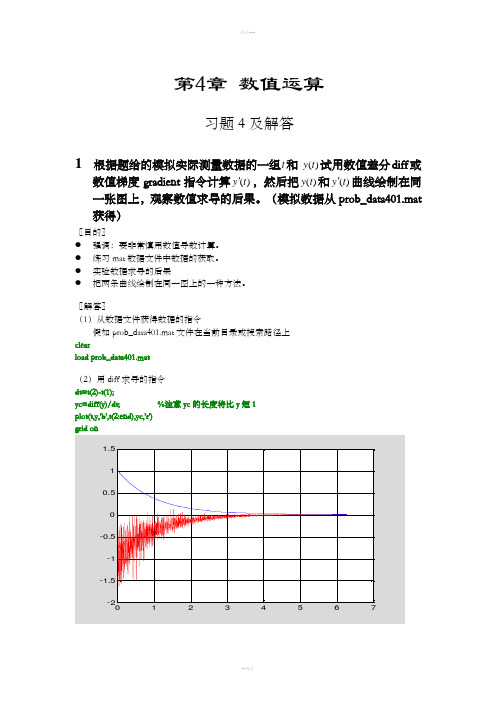
第4章数值运算习题 4 及解答1 根据题给的模拟实际测量数据的一组t和)(t y试用数值差分diff或数值梯度gradient指令计算)(t y',然后把)(t y和)(t y'曲线绘制在同一张图上,观察数值求导的后果。
(模拟数据从prob_data401.mat 获得)〖目的〗●强调:要非常慎用数值导数计算。
●练习mat数据文件中数据的获取。
●实验数据求导的后果●把两条曲线绘制在同一图上的一种方法。
〖解答〗(1)从数据文件获得数据的指令假如prob_data401.mat文件在当前目录或搜索路径上clearload prob_data401.mat(2)用diff求导的指令dt=t(2)-t(1);yc=diff(y)/dt; %注意yc的长度将比y短1plot(t,y,'b',t(2:end),yc,'r')grid on(3)用gradent 求导的指令(图形与上相似)dt=t(2)-t(1);yc=gradient(y)/dt;plot(t,y,'b',t,yc,'r')grid on〖说明〗● 不到万不得已,不要进行数值求导。
● 假若一定要计算数值导数,自变量增量dt 要取得比原有数据相对误差高1、2个量级以上。
● 求导会使数据中原有的噪声放大。
2 采用数值计算方法,画出dt tt x y x ⎰=0sin )(在]10 ,0[区间曲线,并计算)5.4(y 。
〖提示〗● 指定区间内的积分函数可用cumtrapz 指令给出。
● )5.4(y 在计算要求不太高的地方可用find 指令算得。
〖目的〗● 指定区间内的积分函数的数值计算法和cumtrapz 指令。
● find 指令的应用。
〖解答〗dt=1e-4;t=0:dt:10;t=t+(t==0)*eps;f=sin(t)./t;s=cumtrapz(f)*dt;plot(t,s,'LineWidth',3)ii=find(t==4.5);s45=s(ii)s45 =1.65413 求函数x ex f 3sin )(=的数值积分⎰=π0 )(dx x f s ,并请采用符号计算尝试复算。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验四:Matlab 的数值计算
一、实习目的
1、了解MATLAB 的数值计算功能
2、掌握常用的MATLAB 数值计算函数及其运用
二、实习要求
1.明确实习任务。
2.充分利用实习教材与教学课件,运行例题,模仿实习。
3.实习后应该认真总结,完成实习报告。
三、实习内容:
问题1:求方程组的一个特解。
A=[1 1 -3 -1;3 -1 -3 4;1 5 -9 -8]
B=[1 4 0]'
D=rank(A)
x=A\B
Warning: Rank deficient, rank = 2, tol =
8.8373e-015.
x =
-0.5333
0.6000
问题2:设A 是 一个实对称矩阵。
请给出一个算法来验证A 是否是一个正定矩阵,并举实例加以说明。
A=[2 1 3;1 4 5;3 5 6]
A =
2 1 3
1 4 5
3 5 6
⎪⎩⎪⎨⎧=--+=+--=--+0
89544331
3432143214321x x x x x x x x x x x x
B=eig(A)
B =
-0.7527
1.6797
11.0730
问题3:编写一函数,实现多项式的加减运算。
问题4:求
的商及余多项式 format rat
p1=conv([1,0,2],conv([1,4],[1,1]));
p2=[1 0 1 1];
[q,r]=deconv(p1,p2);
cq='商多项式为';cr='余多项式为';
disp([cq,poly2str(q,'s')]),disp([cr,poly2str (r,'s')])
商多项式为 s + 5
余多项式为 5 s^2 + 4 s + 3
问题5:用随机函数生成n 个数据点,对这n 个数据点做3次样条插值并绘出插值曲线。
(如n=10)
问题6:用4次多项式拟合以下数据
X=0:0.1:1; Y=[-.447,1.978,3.11,5.25,5.02,4.66,4.01,4.58,3.45,5.35,9.22];
x0=0:0.1:1;
y0=[-.447,1.978,3.11,5.25,5.02,4.66,4.01,4.58,3.45,5.35,9.22];
n=3;
p=polyfit(x0,y0,n)
xx=0:0.01:1;
yy=polyval(p,xx);
plot(xx,yy,'-b',x0,y0,'.r','markersize',20)
legend('拟合曲线','原始数据','location','southEast')
xlabel('x')
p =
5329/94 -18556/213 5721/143 -482/533
1)1)(4)(2(322-+++++s s s s s s。
