第2章 图像变换技术
《数字图像处理》习题参考答案
《数字图像处理》习题参考答案第1 章概述连续图像和数字图像如何相互转换答:数字图像将图像看成是许多大小相同、形状一致的像素组成。
这样,数字图像可以用二维矩阵表示。
将自然界的图像通过光学系统成像并由电子器件或系统转化为模拟图像(连续图像)信号,再由模拟/数字转化器(ADC)得到原始的数字图像信号。
图像的数字化包括离散和量化两个主要步骤。
在空间将连续坐标过程称为离散化,而进一步将图像的幅度值(可能是灰度或色彩)整数化的过程称为量化。
#采用数字图像处理有何优点答:数字图像处理与光学等模拟方式相比具有以下鲜明的特点:1.具有数字信号处理技术共有的特点。
(1)处理精度高。
(2)重现性能好。
(3)灵活性高。
2.数字图像处理后的图像是供人观察和评价的,也可能作为机器视觉的预处理结果。
3.数字图像处理技术适用面宽。
4.数字图像处理技术综合性强。
数字图像处理主要包括哪些研究内容答:图像处理的任务是将客观世界的景象进行获取并转化为数字图像、进行增强、变换、编码、恢复、重建、编码和压缩、分割等处理,它将一幅图像转化为另一幅具有新的意义的图像。
]讨论数字图像处理系统的组成。
列举你熟悉的图像处理系统并分析它们的组成和功能。
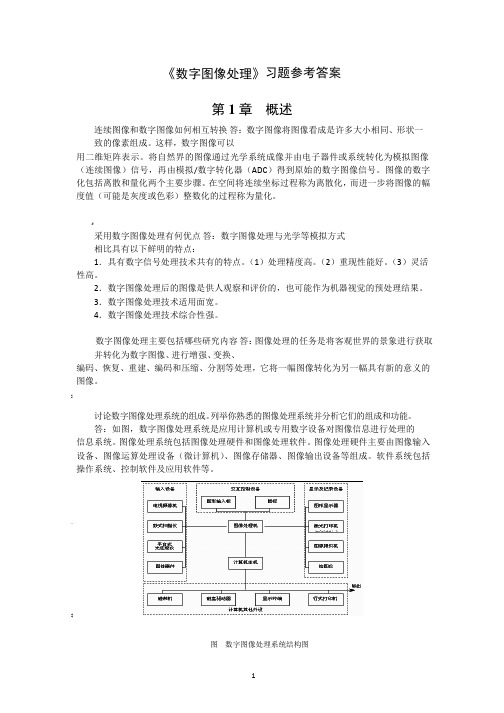
答:如图,数字图像处理系统是应用计算机或专用数字设备对图像信息进行处理的信息系统。
图像处理系统包括图像处理硬件和图像处理软件。
图像处理硬件主要由图像输入设备、图像运算处理设备(微计算机)、图像存储器、图像输出设备等组成。
软件系统包括操作系统、控制软件及应用软件等。
$图数字图像处理系统结构图1常见的数字图像处理开发工具有哪些各有什么特点答.目前图像处理系统开发的主流工具为Visual C++(面向对象可视化集成工具)和MATLAB 的图像处理工具箱(Image Processing Tool box)。
两种开发工具各有所长且有相互间的软件接口。
Microsoft 公司的VC++是一种具有高度综合性能的面向对象可视化集成工具,用它开发出来的Win 32 程序有着运行速度快、可移植能力强等优点。
高一数学第二章讲解

高一数学第二章讲解一、教学任务及对象1、教学任务本教学设计针对的是高一数学第二章的内容。
该章节涵盖了高中数学的基础知识与核心概念,包括函数的概念、性质、图像以及简单的函数变换等。
我的任务是使学生通过系统的学习,掌握函数的基本理论,形成对函数的直观认识,并能运用所学知识解决实际问题。
此外,我还需引导学生理解数学的抽象思维方式,培养他们的逻辑推理和数学思维能力。
2、教学对象本章节的教学对象是高中一年级的学生。
他们已经具备了一定的数学基础和逻辑思维能力,但面对更为抽象的函数概念,可能仍感到困惑。
因此,我需要针对学生的实际情况,采用适当的教学策略,帮助他们顺利过渡到高中数学的学习,激发他们对数学的兴趣和探索欲望。
同时,考虑到学生个体差异,教学过程中应注重因材施教,使每个学生都能在原有基础上得到提高。
二、教学目标1、知识与技能(1)理解函数的概念,掌握函数的定义及其表述方式,能够识别并区分不同类型的函数。
(2)掌握函数的性质,如单调性、奇偶性、周期性等,并能够运用这些性质解决相关问题。
(3)学会绘制函数图像,掌握基本初等函数的图像特点,能够通过图像分析函数的性质。
(4)掌握基本的函数运算,如函数的加、减、乘、除以及反函数的求法,并能够应用于实际问题的解决。
(5)学会运用函数模型解决实际问题,培养建模能力和实际应用能力。
2、过程与方法(1)通过启发式教学,引导学生积极参与课堂讨论,培养他们的逻辑思维和数学表达能力。
(2)采用问题驱动的教学方法,鼓励学生主动探究,发现问题,解决问题,提高他们的自主学习能力。
(3)运用案例分析法,让学生在实际问题中感受函数的应用价值,培养他们的数学应用意识。
(4)结合信息技术,如数学软件、图形计算器等,辅助教学,提高学生对函数图像和性质的直观认识。
(5)注重团队合作,开展小组讨论和交流,培养学生协作能力和沟通能力。
3、情感,态度与价值观(1)培养学生对数学的兴趣和热情,使他们形成积极向上的学习态度。
-第2章 图像处理基础

4.JPEG格式的图像文件
文件采用有损编码,编码后与原始图像有很大差别,但不易觉察。 文件格式: 有2种,一种是被广泛使用的JFIF格式,它包含一个常驻的JPEG数据流, 其作用是提供解码所需的数据,而不是要使用外部数据;另一种是把 JPEG图像压缩保存到TIFF格式的文件中,它在保存和读出时,很容易受 外部条件的限制和影响,目前还未得到广泛的应用。 主要特点: (l)JPEG格式图像文件的扩展名是.jpg。 (2)适用广泛,大多数图像类型都可以进行JPEG编码。 (3)对于使用计算机绘制的具有明显边界的图形,图像处理效果不佳。 (4)对于数字化照片和表达自然景观的色彩丰富的图片,具有非常好 的处理效果。 (5)使用JPEG格式的图像文件时,需要解压缩过程。
特点:
(l)TIFF格式图像文件的扩展名是.tif。 (2)支持从单色模式到32bit真彩色模式的所有图像。
(3)不针对某一个特定的操作平台,可用于多种操作平台和应用 软件。 (4)适用多种机型,可相互转换和移植。 (5)数据结构是可变的,文件具有可改写性,使用者可向文件中 写相关信息。 (6)具有多种数据压缩方式,解压缩过程复杂。
80 160 0 B 0 0 240 255 255 255
2.3 图像信号的数字化
数字图像可以由以下三种途径得到: (1)将传统的可见光图像经过数字化处理转换为数字图像,例如 将一幅照片通过扫描仪输入到计算机中,扫描的过程实质上就 是一个数字化的过程。 (2) 应用各种光电转换设备直接得到数字图像,例如卫星上搭载 的推帚式扫描仪和光机扫描仪可以直接获取地表甚至地下物体 的图像并实时存入存储器中。 (3)直接由二维离散数学函数生成数字图像。
(1)均匀量化
均匀量化最简单,最易于实现。把这个灰度动态变化范围均 匀分为k等份。每一层赋予1个固定的码字,其量化过程就是把图像 像素的样本灰度与各层灰度的判决值r0,r1相比较,凡落在相邻2 层之间的像素即赋予该层的值q.
23887《数字图像处理(第3版)》习题解答(上传)(1)

23887《数字图像处理(第3版)》习题解答(上传)(1)胡学龙编著《数字图像处理(第 3 版)》思考题与习题参考答案⽬录第1章概述 (1)第2章图像处理基本知识 (4)第3章图像的数字化与显⽰ (7)第4章图像变换与⼆维数字滤波 (10)第5章图像编码与压缩 (16)第6章图像增强 (20)第7章图像复原 (25)第8章图像分割 (27)第9章数学形态学及其应⽤ (31)第10章彩⾊图像处理 (32)第1章概述1.1连续图像和数字图像如何相互转换?答:数字图像将图像看成是许多⼤⼩相同、形状⼀致的像素组成。
这样,数字图像可以⽤⼆维矩阵表⽰。
将⾃然界的图像通过光学系统成像并由电⼦器件或系统转化为模拟图像(连续图像)信号,再由模拟/数字转化器(ADC)得到原始的数字图像信号。
图像的数字化包括离散和量化两个主要步骤。
在空间将连续坐标过程称为离散化,⽽进⼀步将图像的幅度值(可能是灰度或⾊彩)整数化的过程称为量化。
1.2采⽤数字图像处理有何优点?答:数字图像处理与光学等模拟⽅式相⽐具有以下鲜明的特点:1.具有数字信号处理技术共有的特点。
(1)处理精度⾼。
(2)重现性能好。
(3)灵活性⾼。
2.数字图像处理后的图像是供⼈观察和评价的,也可能作为机器视觉的预处理结果。
3.数字图像处理技术适⽤⾯宽。
4.数字图像处理技术综合性强。
1.3数字图像处理主要包括哪些研究内容?答:图像处理的任务是将客观世界的景象进⾏获取并转化为数字图像、进⾏增强、变换、编码、恢复、重建、编码和压缩、分割等处理,它将⼀幅图像转化为另⼀幅具有新的意义的图像。
1.4 说出图像、视频(video)、图形(drawing)及动画(animation)等视觉信息之间的联系和区别。
答:图像是⽤成像技术形成的静态画⾯;视频⽤摄像技术获取动态连续画⾯,每⼀帧可以看成是静态的图像。
图形是⼈⼯或计算机⽣成的图案,⽽动画则是通过把⼈物的表情、动作、变化等分解后画成许多动作瞬间的画幅,再⽤摄影机连续拍摄成⼀系列画⾯,给视觉造成连续变化的图画。
图像变换PPT课件

(3)量化噪声 : 为数字图像的主要噪声,产生原因是对连 续图像的量化所造成,可通过增加量化比特数,以及采用 最优量化方法来改善。 (4)“盐和胡椒“噪声:典型的如在变换域中的误差在反 变换后造成的变换噪声。
19
图像平均分为空间域和频率域平均两种方法。 1)空间域平均:对空间的每一个象素取一个邻域S,做 如下计算:(其中S可取四邻域或八邻域)
定义:
H G F
G为输入信号的频谱,F为输出信号的频谱。
从图中可以看出,滤波前 后,频谱基本不变,这点 对滤波器的设计和使用很 有意义。
30
中值滤波:一种典型的顺序统计滤波方法。还有其他几种 类似方法。
特点:基于滤波器窗口中的像素点的排序。
1)最小和最大值滤波器:
^
f
x, y
max gs,t
s,t sxy
gi x, ygr x, y
16
目的: 减少图像中的噪声。
方法: 空域方法:邻域平均等 频域方法:利用噪声主要分布在高频段的特点
进行滤波。
17
图像处理中的常见噪声: (1)加性噪声
这种噪声与图像信号的强度不相关。如传输噪声。 g=f+n
f 为理想图像,n为噪声。 (2)乘性噪声
这种噪声与图像信号的强度相关。如胶片颗粒噪声。 g=f+fn
32
作业: 5.1,5.3,5.5
选做题:就本次课的内容,自已拟定一个题目。
提出问题的能力是一个科研工作者的基本能力!它有时比解决一个问题更重要! 33
所有灰度级出现的相对频率,称P(Z)的图像为图像f的直方 图。P(Z) 经常用做图像中的灰度级概率密度的估计值。
图像与直方图之间不是一一对应的关系,同一个直方 图可与多个图像相对应。
Photoshop基本操作
Photoshop 基础教学
2.1 调整图像的尺寸及方向
调整照片大小的操作是我们经常会遇到的,例如证件照需要上传到网上的报名系统,要求尺寸 在高度500像素以内。将相机拍摄的照片作为手机壁纸,需要将横版照片裁剪为竖版照片。想要将 图片的大小限制在1M以下等等。
2.1.1调整图像尺寸
想要调整照片的尺寸,可以使用“图像大小”命令。选择需要调整尺寸的文件,执行“图像> 图像大小”命令,打开“图像大小”窗口。
Photoshop 基础教学
2.6.3 智能参考线
“智能参考线”是一种会在绘制、移动、变换等情况下自动出现的参考线,可以帮助我们对齐 特定对象。例如当我们使用“移动工具”移动某个图层时。移动过程中与其他图层对齐时就会显 示出洋红色的智能参考线,而且还会提示图层之间的间距。
Photoshop 基础教学
执行“图像>裁切”命令,在弹出的窗口中可以选择基于哪个位置的像素的颜色进行裁切,然 后设置裁切的位置。若勾选“左上角像素颜色”选项,则以将画面中与左上角颜色同样颜色的像 素裁切掉。
Photoshop 基础教学
2.1.6 旋转画布
使用相机拍摄照片时,有时会由于相机朝向使照片横着或者竖了起来,这些问题可以通过“图 像>图像旋转”下的子命令解决。
Photoshop 基础教学
2.1.3 使用裁剪工具
当我们想要裁掉画面中的部分内容时,最方便的就是使用工具箱中的“裁剪工具”直接在画面 中绘制出需要保留的区域即可。
Photoshop 基础教学
2.1.4 使用透视裁剪工具
“透视裁剪工具” 可以在对图像进行裁剪的同时调整图像的透视效果,常用于去除图像中的 透视感,或者在带有透视感的图像中提取局部,也可以为图像添加透视感。
数字图像处理教案

数字图像处理教案.(总22页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--本册教案目录常州大学教案第 1 次课 2 学时授课时间教案完成时间第 1 页常州大学教案第 2 次课 2 学时授课时间教案完成时间第 2 页常州大学教案第 3 次课 2 学时授课时间教案完成时间第 3 页常州大学教案第 4 次课 2 学时授课时间教案完成时间第 5 次课 2 学时授课时间教案完成时间第 6 次课 2 学时授课时间教案完成时间第 7 次课 2 学时授课时间教案完成时间第 8 次课 2 学时授课时间教案完成时间第 9 次课 2 学时授课时间教案完成时间第 9 页常州大学教案第 10 次课 2 学时授课时间教案完成时间第 10 页常州大学教案第 11 次课 2 学时授课时间教案完成时间第 11 页常州大学教案第 12 次课 2 学时授课时间教案完成时间第 12 页常州大学教案第 13 次课 2 学时授课时间教案完成时间第 13 页常州大学教案第 14 次课 2 学时授课时间教案完成时间第 14 页常州大学教案第 15 次课 2 学时授课时间教案完成时间第 15 页常州大学教案第 16 次课 2 学时授课时间教案完成时间第 16 页常州大学教案第 17 次课 2 学时授课时间教案完成时间第 17 页常州大学教案第 18 次课 2 学时授课时间教案完成时间第 18 页常州大学教案第 19 次课 2 学时授课时间教案完成时间第 19 页学生反馈。
数字图像处理基础2

数字图像处理基础2第二章数字图像处理基础2.1 图像数字化技术2.2 数字图像类型2.3 常用图像文件格式2.4 像素间的基本关系2.5 图像的几何变换2.1 图像数字化技术2.2 数字图像类型2.3 常用图像文件格式2.4 像素间的基本关系2.5 图像的几何变换简单的图像成像模型一幅图像可定义成一个二维函数f(x,y)。
由于幅值f 实质上反映了图像源的辐射能量,所以f(x,y)一定是非零且有限的,也即有:0<f(x,y)</f(x,y)图像是由于光照射在景物上,并经其反射或透射作用于人眼的结果。
所以,f(x,y)可由两个分量来表征:一是照射到观察景物的光的总量,二是景物反射或透射的光的总量。
设i(x,y)表示照射到观察景物表面(x,y)处的白光强度,r(x,y)表示观察景物表面(x,y)处的平均反射(或透射)系数,则有:f(x,y)=i(x,y)r(x,y)其中:0 < i(x,y) < A 1, 0 ≤r(x,y) ≤1对于消色光图像(有些文献称其为单色光图像),f(x,y)表示图像在坐标点(x,y)的灰度值l ,且:l=f(x,y)这种只有灰度属性没有彩色属性的图像称为灰度图像。
显然:L min ≤l ≤L mxa区间[L min ,L max ]称为灰度的取值范围。
在实际中,一般取L min 的值为0,L max =L-1。
这样,灰度的取值范围就可表示成[0,L-1]。
当一幅图像的x 和y 坐标及幅值f 都为连续量时,称该图像为连续图像。
为了把连续图像转换成计算机可以接受的数字形式,必须先对连续的图像进行空间和幅值的离散化处理。
图像数字化:将模拟图像经过离散化之后,得到用数字表示的图像。
图像的数字化包括采样和量化两个过程。
连续图像空间离散数字图像幅度离散采样量化采样:是将在空间上连续的图像转换成离散的采样点(即像素)集的操作。
即:空间坐标的离散化。
量化:把采样后所得的各像素的灰度值从模拟量到离散量的转换称为图像灰度的量化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Байду номын сангаас
∑ ∑ f ( x, y) exp{− j2π[(u + N ) x + vy] / N }
x =0 y =0
N −1 N −1
∑ ∑ f ( x, y) exp[− j2π(ux + vy) / N ]exp(− j2πNx / N )
P 功率谱:(u, v) = F (u, v)
2
= R 2 (u , v) + I 2 (u , v)
第2章 2.1 傅里叶变换
图像函数和傅里叶频谱的表示:
第2章 2.1 傅里叶变换
实际图像和傅里叶频谱
第2章 2.2 傅里叶变换的性质
1.分离性
1 F (u, v) = N 1 = N
N −1 N −1 x =0 y =0 N −1 x =0
第2章 2.2 傅里叶变换的性质
2.平移性质
f ( x, y ) exp[ j2π (u0 x + v0 y ) / N ] ⇔ F (u − u0 , v − v0 ) f ( x − x0 , y − y0 ) ⇔ F (u , v) exp[− j2π (ux0 + vy0 ) / N ]
证:
P (u ) = F (u )
2
= R 2 (u ) + I 2 (u )
第2章 2.1 傅里叶变换
2-D傅里叶变换:
1 F (u, v) = N
∑ ∑ f ( x, y) exp[− j2π(ux + vy) / N ]
x =0 y =0
N −1 N −1
u , v = 0, 1,
, N −1
逆变换:
令s=x-z,并交换积分次序:
F { f ( x) ∗ g ( x)} = ∫
∞ −∞
f ( z ) exp(− j 2π uz )dz ∫ g ( s ) exp(− j 2π us)ds
−∞
∞
于是: F { f ( x) ∗ g ( x)} = F (u )G (u )
第2章 2.2 傅里叶变换的性质
e e
, M − 1 y = 0,1,
, M −1
和 0≤y≤B − 1 或 B≤y≤N − 1 和 0≤y≤D − 1 或 D≤y≤N − 1
x =0 y =0
N −1 N −1
1 f ( x, y ) = 2 2-D离散函数平均值: N 比较两式可得结论。
∑ ∑ f ( x, y )
x =0 y =0
N −1 N −1
第2章 2.2 傅里叶变换的性质
8.卷积定理
卷积定义:
∞
f ( x) ∗ g ( x) =
−∞
∫
f ( z ) g ( x − z )dz
x =0 y =0
N −1 N −1
∑ ∑ f ( x, y) exp[− j2π(ux + vy) / N ]
x =0 y =0
N −1 N −1
=1
= F (u , v)
第2章 2.2 傅里叶变换的性质
证:(共轭对称性) 1 N −1 N −1 F (−u , −v) = ∑ ∑ f ( x, y ) exp[− j2π(−ux − vy ) / N ] N x =0 y =0
x =0 y =0 N −1 N −1
N −1 N −1
第2章 2.2 傅里叶变换的性质
4.旋转性质
f (r ,θ + θ 0 ) ⇔ F ( w, φ + θ 0 )
证明:借助极坐标变换
x=rcosθ y= rsinθ u=ωcosφ v=ωsinφ 将以上变换代入傅氏变换,即可得证.
第2章 2.2 傅里叶变换的性质
第2章 2.2 傅里叶变换的性质
1.分离性
⎡1 F ( x, v ) = N ⎢ ⎣N
∑
y =0
N −1
⎤ f ( x, y ) exp[− j2πvy / N ]⎥ ⎦
由2步1-D变换计算2-D变换
1 F (u , v) = N
∑ F ( x, v) exp[− j2πux / N ]
x =0
N −1
第2章 2.2 傅里叶变换的性质
7.平均值
1 f ( x, y ) = F (0, 0) N
证:将u=0,v=0代入
1 F (u, v) = N
∑ ∑ f ( x, y) exp[− j2π(ux + vy) / N ]
x =0 y =0
N −1 N −1
1 得到: F (0, 0) = N
∑ ∑ f ( x, y )
卷积定理:
f ( x) ∗ g ( x) ⇔ F (u )G (u )
f ( x) g ( x) ⇔ F (u ) ∗ G (u )
第2章 2.2 傅里叶变换的性质
∞
证:(卷积定理)
F { f ( x) ∗ g ( x)} = ∫
∞ −∞ −∞
f ( x) ∗ g ( x) =
∞
−∞
∫
f ( z ) g ( x − z )dz
运算量由O(N4) 减为O(N2)
∑ ∑ f ( x, y) exp[− j2π(ux + vy) / N ]
⎡ -j2πux ⎤ N −1 ⎡ -j2πvy ⎤ exp ⎢ ⎥ ∑ f ( x, y )exp ⎢ N ⎥ ⎣ N ⎦ y =0 ⎣ ⎦
∑
u , v = 0, 1,
, N −1
两步1-D变换:
1 = N 1 = N
∗
F (u , v) = F * (−u , −v)
∑ ∑ f ( x, y) exp[ j2π(ux + vy) / N ]
x =0 y =0
N −1 N −1
∑ ∑ f ( x, y) {cos[2π(ux + vy) / N ] + jsin[2π(ux + vy) / N ]}
5.分配率
F { f1 ( x, y ) + f 2 ( x, y )} = F { f1 ( x, y )} + F { f 2 ( x, y )} F { f1 ( x, y ) ⋅ f 2 ( x, y )} ≠ F { f1 ( x, y )} ⋅ F { f 2 ( x, y )}
乘法不满足!
x =0 y =0
N −1 N −1
1 F ( −u , − v ) = N 1 = N 1 = N
∑ ∑ f ( x, y) {cos[2π(ux + vy) / N ] − jsin[2π(ux + vy) / N ]}
x =0 y =0 x =0 y =0
N −1 N −1
∑ ∑ f ( x, y) {cos[−2π(ux + vy) / N ] + jsin[−2π(ux + vy) / N ]} ∑ ∑ f ( x, y) exp[− j2π(ux + vy) / N ] = F (u, v)
1-D函数卷积示例
f ( x) ∗ g ( x) =
∞
−∞
∫
f ( z ) g ( x − z )dz
第2章 2.2 傅里叶变换的性质
卷积的周期:
f(x)采样数为A,g(x)采样数为B 设f(x)与g(x)具有周期M,则f(x)*g(x)周期也为M。 当M< A+B-1时,卷积周期重叠; 当M= A+B-1时,卷积周期相邻接; 当M≥A+B-1时,卷积周期分离。
∫
f ( z ) g ( x − z )dz exp(− j 2π ux)dx
由于 exp(− j 2π ux) = exp(− j 2π uz ) exp[− j 2π u ( x − z )]
F { f ( x) ∗ g ( x)} = ∫
∞ −∞ −∞
∫
∞
f ( z ) exp(− j 2π uz )dzg ( x − z ) exp[− j 2π u ( x − z )]dx
1 f ( x, y ) = N
∑ ∑ F (u, v) exp[ j2π(ux + vy) / N ]
u =0 v =0
2 2 12
N −1 N −1
x, y = 0, 1,
, N −1
频谱: F (u, v) = ⎡ R (u, v) + I (u, v) ⎤ ⎣ ⎦
相位角:φ (u, v) = arctan[ I (u, v) R(u, v)]
∑ f ( x) exp[− j2πux / N ]
x =0
N −1
u = 0, 1,
, N −1
F
−1
{F (u )} =
f ( x) = ∑ F (u ) exp[ j2πux / N ]
u =0
N −1
x = 0, 1,
, N −1
第2章 2.1 傅里叶变换
1-D傅里叶变换:
1 F (u ) = N
第2章 2.2 傅里叶变换的性质
2-D离散卷积:
f(x,y)和g(x,y)分别用尺寸为A×B和C×D, 周期为M和N的离散数组表示。
1 f e ( x , y ) ∗ g e ( x, y ) = MN
x = 0,1,
M −1 N −1 m =0 n =0
∑ ∑ f (m, n) g ( x − m, y − n)
⎡1 F ( x, v ) = N ⎢ ⎣N
1 F (u , v) = N
N −1 x =0
∑
y =0
N −1
⎤ f ( x, y ) exp[− j2πvy / N ]⎥ ⎦
