函数及其表示 (2)
函数及其表示知识点

函数及其表示知识点一、函数的定义和特征在数学中,函数是一种关系,它将一个或多个输入值映射到一个唯一的输出值。
函数通常用字母表示,例如f(x)或g(y),其中x和y是输入值,f(x)和g(y)是对应的输出。
函数的定义可以用多种方式表达,比如公式、算法或图表。
函数的核心特征是单值性和一对一性。
单值性要求每个输入对应唯一的输出,而一对一性则要求每个输出值只能由一个输入产生。
二、函数的符号表示函数可以用多种符号来表示,最常见的是用函数名和自变量表示函数。
例如,f(x)表示一个以x为自变量的函数。
函数的符号表示还可以用映射符号箭头“→”表示,例如f: x→f(x)。
在离散数学中,函数也可以使用集合的形式表示。
例如,如果定义了一个函数f,将集合A中的元素映射到集合B中的元素,可以用f: A→B表示。
三、函数的图像表示函数的图像是一种常用的表示方式。
通过绘制函数的图像,我们可以直观地了解函数的特点和关系。
函数的图像通常是在笛卡尔坐标系中绘制的。
横轴表示自变量,纵轴表示函数的值。
函数的图像可以是曲线、直线、折线等不同形状。
曲线图像可以反映函数的变化趋势和特征,而直线和折线图像则更加简单明了。
四、函数的性质和分类函数有许多性质和分类。
其中一些重要的性质包括:1. 定义域和值域:函数的定义域是自变量的取值范围,值域是函数的所有可能输出值的集合。
2. 奇偶性:如果一个函数满足f(-x) = -f(x),则称其为奇函数;如果满足f(-x) = f(x),则称其为偶函数。
3. 增减性:函数的增减性描述了函数的单调性。
如果函数在定义域上是递增的,称其为增函数;如果在定义域上是递减的,称其为减函数。
根据函数的具体形式和性质,我们可以将函数进行分类,常见的函数包括:1. 线性函数:形如f(x) = kx + b的函数,其中k和b是常数。
2. 幂函数:形如f(x) = x^a的函数,其中a是常数。
3. 指数函数:形如f(x) = a^x的函数,其中a是常数。
第2章函数及其表示-2021版高三数学(新高考)一轮复习教学课件(45张ppt)

第二章 函数、导数及其应用
高考一轮总复习 • 数学 • 新高考
返回导航
题组三 考题再现 5.(2019·江苏,5 分)函数 y= 7+6x-x2的定义域是____[_-__1_,7_]_______.
[解析] 要使函数有意义,则 7+6x-x2>0,解得-1≤x≤7,则函数的定义域是 [-1,7].
第二章 函数、导数及其应用
高考一轮总复习 • 数学 • 新高考
[答案] (1)①是映射,也是函数 ②不是映射,更不是函数 ③不是映射,更不是函数 ④是映射,但不是函数 (3)不同函数①②;同一函数③
返回导航
第二章 函数、导数及其应用
高考一轮总复习 • 数学 • 新高考
返回导航
1.映射与函数的含义 (1)映射只要求第一个集合A中的每个元素在第二个集合B中有且只有一个元素与 之对应;至于B中的元素有无原象、有几个原象却无所谓. (2)函数是特殊的映射:当映射f:A→B中的A,B为非空数集时,且每个象都有 原象,即称为函数. 2.判断两个函数是否相同的方法 (1)构成函数的三要素中,定义域和对应法则相同,则值域一定相同. (2)两个函数当且仅当定义域和对应法则相同时,才是相同函数.
f2:
x
x≤1
y
1
1<x<2 2
x≥2 3
返回导航
f3:
第二章 函数、导数及其应用
高考一轮总复习 • 数学 • 新高考
返回导航
[解析] (1)①是映射,也是函数; ②不是映射,更不是函数,因为从A到B的对应为“一对多”; ③当x=0时,与其对应的y值不存在.故不是映射,更不是函数; ④是映射,但不是函数,因为集合A不是数集. (2)A图象不满足函数的定义域,不正确;B、C满足函数的定义域以及函数的值 域,正确;D不满足函数的定义,故选B、C. (3)①中f1的定义域为{x|x≠0},f2的定义域为R,f3的定义域为{x|x≠0},故不是 同一函数; ②中f1的定义域为R,f2的定义域为{x|x≥0},f3的定义域为{x|x≠0},故不是同 一函数; ③中f1,f2,f3的定义域相同,对应法则也相同,故是同一函数.
第二章 第一节 函数及其表示

A. 0,
5 2
C. -
1 2
,2
B.[-1,4] D.[-5,5]
(2)已知函数y=f(x2-1)的定义域为[- 3, 3],则函数y=f(x)的定义域为
.
答案 (1)C (2)[-1,2]
解析 (1)∵函数y=f(x)的定义域为[-2,3],
∴-2≤2x-1≤3,即- 1 ≤x≤2,
2
即函数y=f(2x-1)的定义域为
x2
D.f(x)=x,g(x)=
x
教材研读 栏目索引
4.函数f(x)= 2x -1+ 1 的定义域为 ( C )
x-2
A.[0,2)
B.(2,+∞)
C.[0,2)∪(2,+∞) D.(-∞,2)∪(2,+∞)
教材研读 栏目索引
5.已知f
1 2
x-1=2x-5,且f(a)=6,则a等于
(
A
)
A. 7 B.- 7
|
1 2
a
N*
,B=
b
|
b
1 n
,n
N*
,对应关系f:a→b,b=
1
;
a
③A={x|x≥0},B=R,对应关系f:x→y,y2=x,x∈A,y∈B;
④A={x|x是平面α内的矩形},B={y|y是平面α内的圆},对应关系f:每一个矩形都
对应它的外接圆.
其中是从A到B的映射的为 ( B )
A.①③ C.①④
考点二 函数的定义域
命题方向一 具体函数的定义域 考法一 已知函数解析式,求函数定义域 典例2 (1)函数f(x)= x 1+lg(6-3x)的定义域为 ( C ) A.(-∞,2) B.(2,+∞) C.[-1,2) D.[-1,2] (2)(多选)若函数y=x2-4x-4的定义域为[0,m],值域为[-8,-4],则实数m的值可能为
人教B版高中数学必修一 《函数及其表示方法》函数的概念与性质PPT(第2课时函数的表示方法)

3.已知两个函数 f(x)和 g(x)的定义域和值域都是集合{1,2,3}, 其函数对应关系如下表:
x
1
2
3
f(x)
2
3
1
x
1
2
3
g(x)
3
2
1
则方程 g(f(x))=x 的解集为________.
解析:当 x=1 时,f(1)=2,g(f(1))=2,不符合题意; 当 x=2 时,f(2)=3,g(f(2))=1,不符合题意; 当 x=3 时,f(3)=1,g(f(3))=3,符合题意. 综上,方程 g(f(x))=x 的解集为{3}.
函数图像的作法及应用 作出下列函数的图像并求出其值域. (1)y=2x+1,x∈[0,2]; (2)y=2x,x∈[2,+∞); (3)y=x2+2x,x∈[-2,2].
【解】 (1)列表:
x
0
1 2
1
3 2
2
y
1
2
3
4
5
当 x∈[0,2]时,图像是直线的一部分,观察图像可知,其值域
为[1,5].
函数 f(x)的图像如图所示,则 f(x)的定义域是________,值 域是________.
答案:[-1,0)∪(0,2] [-1,1)
函数的三种表示方法 某商场新进了 10 台彩电,每台售价 3 000 元,试求售 出台数 x(x 为正整数)与收款数 y 之间的函数关系,分别用列表 法、图像法、解析法表示出来.
2.下表表示函数 y=f(x),则 f(x)>x 的整数解的集合是________.
x
0<x<5 5≤x<10 10≤x<15 15≤x<
函数的概念及其表示
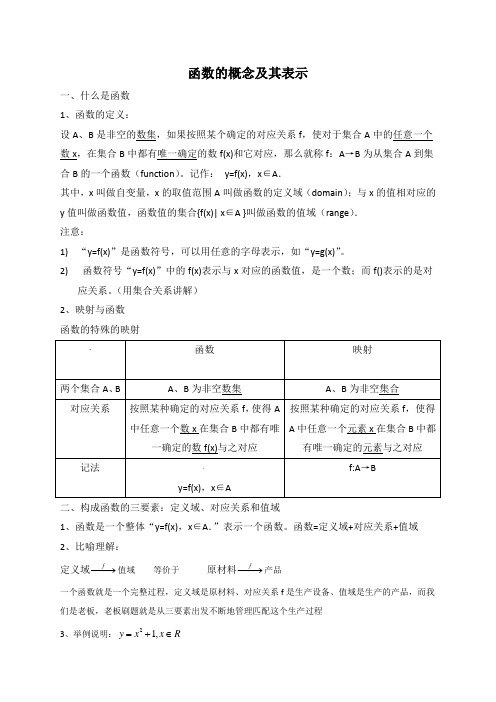
函数的概念及其表示一、什么是函数1、函数的定义: 设A 、B 是非空的数集,如果按照某个确定的对应关系f ,使对于集合A 中的任意一个数x ,在集合B 中都有唯一确定的数f(x)和它对应,那么就称f :A →B 为从集合A 到集合B 的一个函数(function )。
记作: y=f(x),x ∈A .其中,x 叫做自变量,x 的取值范围A 叫做函数的定义域(domain );与x 的值相对应的y 值叫做函数值,函数值的集合{f(x)| x ∈A }叫做函数的值域(range ).注意:1) “y=f(x)”是函数符号,可以用任意的字母表示,如“y=g(x)”。
2) 函数符号“y=f(x)”中的f(x)表示与x 对应的函数值,是一个数;而f()表示的是对应关系。
(用集合关系讲解)2、映射与函数函数的特殊的映射二、构成函数的三要素:定义域、对应关系和值域1、函数是一个整体“y=f(x),x ∈A .”表示一个函数。
函数=定义域+对应关系+值域2、比喻理解:定义域f −−→值域 等价于 原材料f −−→产品 一个函数就是一个完整过程,定义域是原材料、对应关系f 是生产设备、值域是生产的产品,而我们是老板,老板刷题就是从三要素出发不断地管理匹配这个生产过程3、举例说明:21,y x x R =+∈问:定义域值域是对应关系是三、求函数定义域.主要题型:偶次方被开方数为非负;分式的分母不为零;零次幂的底数不为零;对数真数大于零;指数对数的底数大于零且不等于1例题讲解:1、1()f x x x =-2、1()11f x x=+ 3、()f x =4、2()ln(1)f x x =- 5、()1f x x =- 四、求函数解析式1、函数的三种表达方法解析式法+图像法+列表法 因此我们可以看出解析式是函数的表达方式之一,也是我们学习过程中接触最多的。
2、函数解析式求法1) 配凑法\由已知条件(())()f g x F x =,可以将()F x 改写成关于()g x 的表达式,然后以x 替代()g x 例题:已知2222(1))3x f x x ++=-,求()f x 解析式 2) 待定系数法如已知函数类型(如一次函数、二次函数)可用待定系数法例题:已知()f x 是一次函数,且满足3(1)()29f x f x x +-=+,求函数()f x 的解析式3) 换元法若已知(())f g x 的解析式,可用换元法 例题:已知2222(1))3x f x x ++=-,求()f x 解析式 4) 解方程组法已知关于()f x 与1()f x 或者()f x 与()f x 的表达式,可根据条件构造出另外一个等式,组成方程组求解例题:已知()f x +21()f x =3x ,则求()f x 的解析式。
人教数学B版必修一《函数及其表示方法》函数的概念与性质PPT课件(第2课时函数的表示方法)

(4)函数 f(x)=x-+x1+,3,x≤x>1,1 是分段函数.(3)× (4)√
栏目导航
x2+1,x≤1,
2.设函数 f(x)=2x,x>1,
则 f(f(3))=( )
A.15
B.3
2
13
C.3
D. 9
D [∵f(3)=23≤1,
∴f(f(3))=232+1=193.]
栏目导航
20
1.若集合A={x|0≤x≤2},B={y|0≤y≤3},则给出的下列图形 表示为定义在A上的函数图像的是( )
A
B
C
D
栏目导航
21
(2)由下表给出函数y=f(x),则f(f(1))等于( )
x12345
y45321
A.1
B.2
C.4
D.5
(1)D (2)B [(1)A中的对应不满足函数的存在性,即存在x∈A,
44
栏目导航
45
1.函数有三种常用的表示方法,可以适时的选择,以最佳的方式 表示函数,解析式后不注明定义域即可视为该函数的定义域为使此解 析式有意义的实数集 R 或 R 的子集.
2.作函数图像必须要让作出的图像反映出图像的伸展方向,与 x 轴、y 轴有无交点,图像有无对称性,并标明特殊点.
栏目导航
栏目导航
37
[解] (1)列表
x2345 …
y
1
2 3
1 2
2 5
…
当 x∈[2,+∞)时,图像是反比例函数 y=2x的一部分,观察图像
可知其值域为(0,1].
栏目导航
(2)设票价为y元,里程为x公里,定义域为(0,20]. 由题意得函数的解析式如下:
函数的表示法

函数的定义 设A、B是非空的数集, 如果按照某都有唯一确定的数 f (x)与 之对应, 那么就把对应关系 f 叫作定义在集合A上的函数.
记作 f:A→B,或 y=f (x), x∈A.
其中x叫做自变量, x的取值范围A叫做函数的定义域, 与x的值相对应的 y [或 f (x)]值叫做函数值, 函数值的集 合{y |y=f (x), x∈A}叫做函数的值域.
二、例题与练习:
1.作函数的图像
x, x 0, 例1.请画出下面函数的图像:y x x, x 0.
解: 图像为第一和第二象限的角平分线,如图, y
1 o
1 2
x
x 4, 2 例2.已知函数 f ( x) x 2 x, x 2,
f f (5) f (3) 3 4 1.
( x 1) 2 , x 0, 练习1.已知函数 f ( x ) x 0. x, (2)画出函数的图像. (1)求 f f f 1 的值;
2.求函数的解析式 例3.国内跨省市之间邮寄信函,每封信函的质量和对应的邮资 如表.画出图像,并写出函数的解析式.
§2.2函数的表示法
一、函数的表示:
把函数的两个变量之间的函数关系, 用一个等式来表示, (1)解析法: 这个等式叫做函数的解析表达式,简称解析式.
函数的表示法 (2)列表法: 列出表格来表示两个变量的函数关系. (3)图象法:用函数的图象表示两个变量之间的函数关系.
(1)函数关系清楚. 解析法的优点:(2)给自变量一个值,可求它的函数值. (3)便于研究函数的性质. 列表法的优点:不必计算,查表可得到自变量与函数的对应值. 图象法的优点:直观形象地表示出函数值随自变量的变化规律.
(二)函数定义域值域及表示

函数及其表示【学习重点】 函数的定义域的求法以及函数的表示方法 【学习难点】 函数值域的求法 一、函数的概念设A 、B 是非空的数集,如果按照某个确定的对应关系f ,使对于集合A 中的任意一个数x ,在集合B 中都有唯一确定的数f(x)和它对应,那么就称f :A →B 为从集合A 到集合B 的一个函数.记作: y=f(x),x ∈A .其中,x 叫做自变量,x 的取值范围A 叫做函数的定义域;与x 的值相对应的y 值叫做函数值,函数值的集合{f(x)| x ∈A }叫做函数的值域.注意:如果只给出解析式y=f(x),而没有指明它的定义域,则函数的定义域即是指能使这个式子有意义的实数的集合; 函数的定义域、值域要写成集合或区间的形式.构成函数的三要素:定义域、对应关系和值域 再注意:1)构成函数三个要素是定义域、对应关系和值域.由于值域是由定义域和对应关系决定的,所以,如果两个函数的定义域和对应关系完全一致,即称这两个函数相等(或为同一函数)2)两个函数相等当且仅当它们的定义域和对应关系完全一致,而与表示自变量和函数值的字母无关。
相同函数的判断方法:①表达式相同;②定义域一致 (两点必须同时具备)例1 判断下列各组中的两个函数是否是同一函数?为什么?1.3)5)(3(1+-+=x x x y52-=x y2.111-+=x x y )1)(1(2-+=x x y3.x x f =)( 2)(x x g = 4.x x f =)( 33)(x x F = 5.21)52()(-=x x f 52)(2-=x x f二、区间的概念及表示法设,a b 是两个实数,且a b <,满足a x b ≤≤的实数x 的集合叫做闭区间,记做[,]a b ;满足a x b <<的实数x 的集合叫做开区间,记做(,)a b ;满足a x b ≤<,或a x b <≤的实数x 的集合叫做半开半闭区间,分别记做[,)a b ,(,]a b ;满足,,,x a x a x b x b ≥>≤<的实数x 的集合分别记做[,),(,),(,],(,)a a b b +∞+∞-∞-∞.注意:对于集合{|}x a x b <<与区间(,)a b ,前者a 可以大于或等于b ,而后者必须a b <. 三、求函数的定义域时,一般遵循以下原则: ①()f x 是整式时,定义域是全体实数.②()f x 是分式函数时,定义域是使分母不为零的一切实数.③()f x 是偶次根式时,定义域是使被开方式为非负值时的实数的集合.④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1.⑤tan y x =中,()2x k k Z ππ≠+∈.⑥零(负)指数幂的底数不能为零.⑦若()f x 是由有限个基本初等函数的四则运算而合成的函数时,则其定义域一般是各基本初等函数的定义域的交集.⑧对于求复合函数定义域问题,一般步骤是:若已知()f x 的定义域为[,]a b ,其复合函数[()]f g x 的定义域应由不等式()a g x b ≤≤解出.⑨对于含字母参数的函数,求其定义域,根据问题具体情况需对字母参数进行分类讨论.⑩由实际问题确定的函数,其定义域除使函数有意义外,还要符合问题的实际意义. 例2 求下列函数的定义域:⑪y =⑫y =(3)xx x x f -+=0)1()( (4)g(x)=211+-++x x例3 求复合函数求定义域记住两句话:地位相同范围相同,定义域是关于x 的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
教学过程
一、课堂导入
函数的概念、表示方法、分段函数是近几年高考的热点;常和对数、指数函数的性质等相结合考查,有时也会命制新定义问题;题型以选择题和填空题为主,与其他知识点交汇则以解答题的形式出现。
二、复习预习
映射与函数:以考查概念与运算为主,部分涉及新定义运算;定义域、值域、解析式是考查的重点,而且比较稳定,有时结合其它知识点(一本部分内容为背景),分段函数较多、花样翻新;
三、知识讲解
考点1函数与映射的概念
考点2 函数的定义域、值域
在函数()
=,x A
y f x
∈中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y值叫做函数值,函数值{()|}
∈的集合叫做函数的值域
f x x A
考点3 函数的表示方法与分段函数
表示函数的常用方法有:解析法、图象法和列表法。
若函数在其定义域的不同子集上,因对应关系不同而分别用几个不同的式子来表示,这种函数称为分段函数。
分段函数的定义域等于各段函数的定义域的并集,其值域等于各段函数的值域的并集,分段函数虽由几个部分组成,但它表示的是个函数。
四、例题精析
考点1函数与映射的概念
例1对于实数x,y ,定义运算x*y=ax y(xy 0)x by(xy 0)
+⎧⎨+⎩><,已知1*2=4,-1*1=2,则下列运算结果为
______.(填写所有正确结果的序号)
②
③
④
【规范解答】∵1*2=a+2=4,-1*1=-1+b=2,得a=2,b=3.
∴x*y=2x y(xy 0)x 3y(xy 0)
+⎧⎨+⎩><
②
③
×
④
=
3×
【总结与反思】函数与映射的区别:函数是特殊的映射,二者区别在于映射定义中的两个集合是非空集合,可以不是数集,而函数中的两个集合必须是非空数集。
考点2 函数的定义域、值域
例2求函数()
-=2lg x 2x f x ;
(2)已知函数f(2x )的定义域是[-1,1],求f(x)的定义域;
(3)求下列函数的值域.
①y=x 2+2x,x ∈[0,3],
②y=log 3x+log x 3-1,
③.-=2x 1y 2
【规范解答】(1)要使该函数有意义,
需要⎧-⎪⎨-⎪⎩2
2x 2x 09x 0>,>则有:⎧⎨-⎩x 0x 23x 3<或>,<<解得:-3<x <0
或2<x <3,所以所求函数的定义域为 (-3,0)∪(2,3).
(2)∵f(2x )的定义域为[-1,1],即-1≤x ≤1,12∴≤≤x 22,故f(x)的定义域为[1
,22].
(3)①y=(x+1)2-1在[0,3]上的图象如图所示
,
由图象知:0≤y ≤32+2×3=15,
所以函数y=x 2+2x ,x ∈[0,3]的值域为[0,15].
②=+-331y log x 1log x
,定义域为(0,1)∪(1,+∞), 当0<x <1
时,,≤-=-y 13 当x >1
时,,≥=y 11 综上可知,其值域为(-∞,-3]∪[1,+∞).
③因为x 2-1≥-1,又y=2x 在R 上为增函数,
∴-=2x 1
y 2≥2-1=12
. 故值域为[12,+∞). 【总结与反思】求抽象函数的定义域:①若已知函数f(x)的定义域为[a,b ],其复合函数f(g(x))的定义域由不等式a ≤g(x)≤b 求出.②若已知函数f(g(x))的定义域为[a,b ],则f(x)的定义域为g(x)在x ∈[a,b ]时的值域.
考点3 函数的表示方法与分段函数
例3我国是水资源相对匮乏的国家,为鼓励节约用水,某市打算制定一项水费措施,规定每季度每人用水不超过5吨时,每吨水费的价格(基本消费价)为1.3元,若超过5吨而不超过6吨时,超过部分的水费加收200%,若超过6吨而不超过7吨时,超过部分的水费加收400%,如果某人本季度实际用水量为x(x≤7)吨,试计算本季度他应缴纳的水费.
【规范解答】设y表示本季度应缴纳的水费(元),当0<x≤5时,y=1.3x;当5<x≤6时,应将x分成两部分:5与(x-5)分别计算,第一部分为基本消费1.3×5,第二部分由基本消费与加价消费组成,即
1.3×(x-5)+1.3(x-5)×200%=3.9x-19.5,
此时y=1.3×5+3.9x-19.5=3.9x-13,
当6<x≤7时,同理y=6.5x-28.6
综上可知:
1.3,05
3.913,56
6.528.6,67
x x
y x x
x x
<≤⎧
⎪
=-<≤
⎨
⎪-<≤
⎩
.
【总结与反思】计算本季度他应缴纳的水费,应看他的用水量x在何范围内,不同的范围,缴纳的水费不同;可采用分段函数来表示.
课程小结
1、求具体函数y=f(x)的定义域
2、求抽象函数的定义域
3、求简单函数值域的方法
(1)观察法;(2)图象观察法;(3)单调性法;(4)分离常数法;(5)均值不等式法;(6)换元法.
4、分段函数及实际应用题。
