成都市东湖中学九上数学反比例函数面积问题导练
成都市东湖中学九上数学位似导练

成都市东湖中学九上数学位似导练一.选择题1.在平面直角坐标系中,已知点E(﹣4,2),F(﹣2,﹣2),以原点O为位似中心,相似比为,把△EFO缩小,则点E的对应点E′的坐标是()3.如图,△ABC与△A1B1C1为位似图形,点O是它们的位似中心,位似比是1:2,已知△ABC的面积为3,那么△A1B1C1的面积是_________.4.关于对位似图形的表述,下列命题正确的是_________.(只填序号)①相似图形一定是位似图形,位似图形一定是相似图形;②位似图形一定有位似中心;③如果两个图形是相似图形,且每组对应点的连线所在的直线都经过同一个点,那么,这两个图形是位似图形;④位似图形上任意两点与位似中心的距离之比等于位似比.三、解答题1、如图,在平面直角坐标系中,有两点A(6,3),B(6,0).以原点O为位似中心,相似比为1/3 ,把线段AB缩小,观察对应点之间坐标的变化,你有什么发现?位似变换后A,B的对应点为A ' (,),B'(,);A"(,),B"(,).2、如图,△ABC三个顶点坐标分别为A(2,3),B(2,1),C(6,2),以点O为位似中心,相似比为2,将△ABC放大,观察对应顶点坐标的变化,你有什么发现?位似变换后A,B,C的对应点为A '(,),B ' (,),C ' (,);A"(,),B"(,),C"(,).归纳:在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于或.3 、如图,四边形ABCD的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),画出它的一个以原点O为位似中心,相似比为1/2 的位似图形.4. 如图表示△AOB和把它缩小后得到的△COD,求它们的相似比.5. 如图,△ABC三个顶点坐标分别为A(2,-2),B(4,-5),C(5,-2),以原点O为位似中心,将这个三角形放大为原来的2倍.解:A'(,), B ' (,),C ' (,),A"(,),B"(,),C"(,)6:如果四边形ABCD的坐标分别为A(-6,6),B(-8,2),C(-4,0),D(-2,4),写出以原点为位似中心,相似比为(1/2)的一个图形的对应点的坐标。
成都市东湖中学九上数学《二次函数》专题————二次函数与反比例函数综合导练

成都市东湖中学九上数学《二次函数》专题————二次函数与反比例函数综合导练1.如图,已知抛物线y =(3-m)x2+2(m -3)x +4m -m2的顶点A 在双曲线y =3 x上,直线y =mx +b 经过点A ,与y 轴交于点B ,与x 轴交于点C . (1)求直线AB 的解析式;(2)将直线AB 绕点O 顺时针旋转90°,与x 轴交于点D ,与y 轴交与点E ,求sin ∠BDE 的值; (3)过点B 作x 轴的平行线与双曲线交于点F ,点M 在直线BF 上,且到抛物线的对称轴的距离为6.若点N 在直线BF 上,直接写出使得∠AMB +∠ANB =45°的点N 的坐标.2.如图,抛物线y =ax2+bx (a >0)与双曲线y =kx相交于点A ,B ,已知点B 的坐标为(-2,-2),点A 在第一象限内,且tan ∠AOx =4.过点A 作直线AC ∥x 轴,交抛物线于另一点C . (1)求双曲线和抛物线的解析式;(2)计算△ABC 的面积;(3)在抛物线上是否存在点D ,使△ABD 的面积等于△ABC 的面积?若存在,直接写出点D 的坐标;若不存在,请说明理由.3.如图,已知二次函数y =ax2+2x +c (a >0)图象的顶点M 在反比例函数y =3 x的图象上,且与x 轴相交于A 、B 两点.(1)若二次函数图象的对称轴为x =-12,试求a 、c 的值; (2)在(1)的条件下,求线段AB 的长;(3)若二次函数图象的对称轴与x 轴的交点为N ,当NO +MN 取最小值时,试求二次函数的解析式.4.如图,正比例函数和反比例函数的图象都经过点 A ( 3 , 3) ,把直线 OA 向下平移后,与反比例函数的图象交于点B(6,m),与x 轴、y 轴分别交于C 、D 两点。
(1)求 m 的值;( 2 )求过 A 、B 、D 三点的抛物线的解析式;( 3 )若点E 是抛物线上的一个动点,是否存在点 E ,使四边形 OECD 的面积S 1 ,是四边形OACD 面积S 的32?若存在,求点 E 的坐标;若不存在,请说明理由.5.如图,抛物线y=ax 2+bx (a 0)与双曲线y =xk相交于点A ,B . 已知点B 的坐标为(-2,-2),点A 在第一象限内,且tan ∠AOx =4. 过点A 作直线AC ∥x 轴,交抛物线于另一点C .(1)求双曲线和抛物线的解析式; (2)计算△ABC 的面积;(3)在抛物线上是否存在点D ,使△ABD 的面积等于△ABC 的面积.若存在,请你写出点D 的坐标;若不存在,请你说明理由.5.如图,二次函数y =ax2+bx (a >0)与反比例函数y =kx的图象相交于A ,B 两点,且点A 的坐标为(1,4),点B 在第三象限,△AOB 的面积为3. (1)求二次函数的表达式;(2)过点A 作x 轴的平行线,交二次函数y =ax2+bx 的图象于另一点C ,连接CO ,在坐标平面内求点P ,使△POC ∽△AOB (点P 与点A 对应).6.如图,二次函数y=ax2+bx(a>0)的图象与反比例函数y=kx的图象相交于A,B两点,且点A的坐标为(1,4),点B在第三象限.(1)求该二次函数的表达式;(2)设二次函数图象与x轴的另一个交点为D,E点为线段OD上的动点(与O,D不重合),过E点作EF∥OB,交BD于F,连接BE.①设OE的长为m,△BEF的面积为S,求S关于m的函数关系式;②当△BEF为等腰三角形时,求点E的坐标.。
成都市东湖中学九上数学反比例函数复习导学二

成都市东湖中学九上数学反比例函数复习导学二一次函数与反比例函数综合例1. 如图,在直角坐标平面内,函数m y x=(0x >,m 是常数)的图象经过(14)A ,,()B a b ,,其中1a >.过点A 作x 轴垂线,垂足为C ,过点B 作y 轴垂线,垂足为D ,连结AD ,DC ,CB .(1)若ABD △的面积为4,求点B 的坐标;(2)求证:DC AB ∥;(3)当AD BC =时,求直线AB 的函数解析式.练1、如图,已知A (-4,2)、B (n ,-4)是一次函数y =kx +b 的图象与反比例函数m y x =的图象的两个交点. (1) 求此反比例函数和一次函数的解析式;(2) 根据图象写出使一次函数的值小于反比例函数的值的x 的取值范围.例2.如图,已知直线12y x =与双曲线(0)k y k x=>交于A B ,两点,且点A 的横坐标为4. (1)求k 的值; (2)若双曲线(0)k y k x=>上一点C 的纵坐标为8,求AOC △的面积; (3)过原点O 的另一条直线l 交双曲线(0)k y k x =>于P Q ,两点(P 点在第一象限),若由点A B P Q ,,,为顶点组成的四边形面积为24,求点P 的坐标.练2.两个反比例函数k y x =和1y x=在第一象限内的图象如图所示,点P 在k y x =的图象上,PC ⊥x 轴于点C ,交1y x =的图象于点A ,PD ⊥y 轴于点D ,交1y x=的图象于点B ,当点P 在k y x =的图象上运动时,以下结论: ①△ODB 与△OCA 的面积相等;②四边形PAOB 的面积不会发生变化;③PA 与PB 始终相等;④当点A 是PC 的中点时,点B 一定是PD 的中点.其中一定正确的是 (把你认为正确结论的序号都填上,少填或错填不给分)例3.若一次函数y =2x -1和反比例函数y =2k x的图象都经过点(1,1). (1)求反比例函数的解析式;(2)已知点A 在第三象限,且同时在两个函数的图象上,求点A 的坐标;(3)利用(2)的结果,若点B 的坐标为(2,0),且以点A 、O 、B 、P 为顶点的四边形是平行四边形,请你直接写出点P 的坐标.练3.如图,点A (m ,m +1),B (m +3,m -1)都在反比例函数xk y 的图象上. (1)求m ,k 的值;(2)如果M 为x 轴上一点,N 为y 轴上一点, 以点A ,B ,M ,N 为顶点的四边形是平行四边形,试求直线MN 的函数表达式.反比例与三角形例4.已知:等腰三角形OAB 在直角坐标系中的位置如图,点A 的坐标为(-),点B 的坐 标为(-6,0).(1)若三角形OAB 关于y 轴的轴对称图形是三角形O A B '',请直接写出A 、B 的对称点A 'B '、的坐标;(2)若将三角形OAB 沿x 轴向右平移a 个单位,此时点A 恰好落在反比例函数y =的图像上,求a 的值;(3)若三角形OAB 绕点O 按逆时针方向旋转α度(090α<<).①当α=30 时点B 恰好落在反比例函数k y x=的图像上,求k 的值. ②问点A 、B 能否同时落在①中的反比例函数的图像上,若能,求出α的值;若不能,请说明理由.练4.如图①,△OAB 中,A (0,2),B (4,0),将△AOB 向右平移m 个单位,得到△O′A′B′.(1)当m=4时,如图②.若反比例函数y=的图象经过点A′,一次函数y=ax+b 的图象经过A′、B′两点.求反比例函数及一次函数的表达式;(2)若反比例函数y=的图象经过点A′及A′B′的中点M ,求m 的值.。
成都市东湖中学九上数学反比例函数面积问题专项导学

成都市东湖中学九上数学反比例函数面积问题专项导学一、问题探究1、已知点P 是双曲线上任意一点,过点P 作x 轴的垂线PA ,y 轴的垂线PB,垂足分别为A,B.矩形OAPB的面积会随P 点的移动而发生改变吗?若不变,请求出其面积;若改变,试说明理由。
2、K 的几何意义: ①、过双曲线)0(≠=k x k y 上一点P(x,y)分别作x 轴,y 轴的垂线,垂足分别为A 、B ,则 S 矩形OAPB=OA·AP=|x| ·|y|=|k|②、则垂足为轴的垂线作过有上任意一点是双曲线设,,)1(:,)0(),(A x P k xk y n m P ≠= ||21||||2121k n m AP OA S OAP =∙=⋅⋅=∆ 二、经典例题1.如图,点P 是正比例函数y=x 与反比例函数y=在第一象限内的交点,PA ⊥OP 交x 轴于点A ,△POA的面积为2,求k 的值.2.如图,矩形AOBC的面积为4,反比例函数的图象的一支经过矩形对角线的交点P,求该反比例函数的解析式。
3.如图,在平面直角坐标系中直线y=x﹣2与y轴相交于点A,与反比例函数在第一象限内的图象相交于点B(m,2).(1)求反比例函数的关系式;(2)将直线y=x﹣2向上平移后与反比例函数图象在第一象限内交于点C,且△ABC的面积为18,求平移后的直线的函数关系式.4.如图,已知正比例函数y=2x 和反比例函数的图象交于点A (m ,﹣2).(1)求反比例函数的解析式;(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x 的取值范围;(3)若双曲线上点C (2,n )沿OA 方向平移个单位长度得到点B ,判断四边形OABC 的形状并证明你的结论.【问题解决】1.如图,已知四边形ABCD 是平行四边形,BC =2AB ,A ,B 两点的坐标分别是(-1,0),(0,2),C ,D 两点在反比例函数)0(<=x xk y 的图象上,求k 的值.2.若反比例函数过面积为9的正方形AMON的顶点A,且过点A的直线y2=mx﹣n的图象与反比例函数的另一交点为B(﹣1,a)(1)求出反比例函数与一次函数的解析式;(2)求△AOB的面积.3.如图,反比例函数图象在第一象限的分支上有一点C(1,3),过点C的直线y=kx+b〔k<0〕与x 轴交于点A.(1)求反比例函数的解析式;(2)当直线与反比例函数的图象在第一象限内的另一交点的横坐标为3时,求△COD的面积.4.如图,点P(4,3)是双曲线y=上一点,过点P作x轴、y轴的垂线,分别交x轴、y轴于A、B两点,交双曲线y=(k2>0)于E、F两点.(1)k1=_________,四边形PAOB的面积S=_________;(2)试判断AB与EF的位置关系,并说明理由.。
成都市东湖 中学九上数学反比例函数复习 专项练习1

成都市东湖 中学九上数学反比例函数复习 专项练习1一、选择题(每小题3分,共30分) 1、反比例函数y =xn 5+图象经过点(2,3),则n 的值是( ). A 、-2 B 、-1 C 、0 D 、12、若反比例函数y =x k(k ≠0)的图象经过点(-1,2),则这个函数的图象一定经过点( ). A 、(2,-1) B 、(-21,2) C 、(-2,-1) D 、(21,2)3、(08双柏县)已知甲、乙两地相距s (km ),汽车从甲地匀速行驶到乙地,则汽车行驶的时间t (h )与行驶速度v (km/h )的函数关系图象大致是( )4、若y 与x 成正比例,x 与z 成反比例,则y 与z 之间的关系是().A 、成正比例B 、成反比例 C、不成正比例也不成反比例 D 、无法确定 5、一次函数y =kx -k ,y 随x 的增大而减小,那么反比例函数y =xk满足( ). A 、当x >0时,y >0 B 、在每个象限内,y 随x 的增大而减小 C 、图象分布在第一、三象限 D 、图象分布在第二、四象限6、如图,点P 是x 轴正半轴上一个动点,过点P 作x 轴的垂线PQ 交双曲线y =x1于点Q ,连结OQ ,点P 沿x 轴正方向运动时, Rt △QOP 的面积( ).A 、逐渐增大B 、逐渐减小C 、保持不变D 、无法确定7、在一个可以改变容积的密闭容器内,装有一定质量m 的某种气体,当改变容积V 时,气体的密度ρ也随之改变.ρ与V 在一定范围内满足ρ=Vm,它的图象如图所示,则该气体的质量m 为( ). A 、1.4kg B 、5kg C 、6.4kg D 、7kg8、若A (-3,y 1),B (-2,y 2),C (-1,y 3)三点都在函数y =-x1 的图象上,则y 1,y 2,y 3的大小关系是( ).A 、y 1>y 2>y 3B 、y 1<y 2<y 3C 、y 1=y 2=y 3D 、y 1<y 3<y 2 9、已知反比例函数y =xm21-的图象上有A (x 1,y 1)、B (x 2,y 2)两点,当x 1<x 2<0时,y 1<y 2,则m 的取值范围是( ).A 、m <0B 、m >0C 、m <21 D 、m >21 10、如图,一次函数与反比例函数的图象相交于A 、B 两点,则图中使反比例函数的值小于一次函数的值的x 的取值范围 是( ).A 、x <-1B 、x >2A .B .C . .C 、-1<x <0或x >2D 、x <-1或0<x <2 二、填空题(每小题3分,共30分)11.某种灯的使用寿命为1000小时,它的可使用天数y 与平均每天使用的小时数x 之间的函数关系式为 . 12、已知反比例函数xky =的图象分布在第二、四象限,则在一次函数b kx y +=中,y 随x 的增大而 (填“增大”或“减小”或“不变”). 13、若反比例函数y =xb 3-和一次函数y =3x +b 的图象有两个交点,且有一个交点的纵坐标为6,则b = .14、反比例函数y =(m +2)xm2-10的图象分布在第二、四象限内,则m 的值为 .15、有一面积为S 的梯形,其上底是下底长的31,若下底长为x ,高为y ,则y 与x 的函数关系是 .16、如图,点M 是反比例函数y =xa(a ≠0)的图象上一点, 过M 点作x 轴、y 轴的平行线,若S 阴影=5,则此反比例函数解析 式为 .17、使函数y =(2m 2-7m -9)xm2-9m +19是反比例函数,且图象在每个象限内y 随x 的增大而减小,则可列方程(不等式组)为 .18、过双曲线y =xk(k ≠0)上任意一点引x 轴和y 轴的垂线,所得长方形的面积为______.19. 如图,直线y =kx(k >0)与双曲线xy 4=交于A (x 1,y 1), B (x 2,y 2)两点,则2x 1y 2-7x 2y 1=___________.20、如图,长方形AOCB 的两边OC 、OA 分别位于x 轴、y 轴上,点B 的坐标为B (-320,5),D 是AB 边上的一点, 将△ADO 沿直线OD 翻折,使A 点恰好落在对角线OB 上的点E 处,若点E 在一反比例函数的图象上,那么该函数的解析 式是 .三、解答题(共60分)21、如图,P 是反比例函数图象上的一点,且点P 到x 轴的距离为3,到y 轴的距离为2,求这个反比例函数的解析式.22、已知Rt△ABC 的斜边AB 在平面直角坐标系的x 轴上,点C (1,3)在反比例函数y = k x的图象上,且sin∠BAC = 35.(1)求k 的值和边AC 的长;(2)求点B 的坐标.23、如图,已知反比例函数y =-x8与一次函数y =kx +b 的图象交于A 、B 两点,且点A 的横坐标和点B的纵坐标都是-2. 求:(1)一次函数的解析式; (2)△AOB 的面积.24、如图,一次函数y =ax +b 的图象与反比例函数y =xk的图象交于M 、N 两点. (1)求反比例函数与一次函数的解析式;(2)根据图象写出使反比例函数的值大于一次函数的值的x 的取值范围.25、(12分)如图, 已知反比例函数y =xk的图象与一次函数y =a x +b 的图象交于M (2,m )和N (-1,-4)两点.(1)求这两个函数的解析式;(2)求△MON 的面积; (3)请判断点P (4,1)是否在这个反比例函数的图象上, 并说明理由.26、如图,在平面直角坐标系xOy 中,一次函数y =kx +b (k ≠0)的图象与反比例函数y =xm(m ≠0)的图象交于二、四象限内的A 、B 两点,与x 轴交于C 点,点B 的坐标为(6,n ),线段OA =5,E 为x 轴负半轴上一点,且s i n ∠AOE =45.(1)求该反比例函数和一次函数;(2)求△AOC 的面积.27、如图,一次函数b x y +=的图象经过点B (1-,0),且与反比例函数xky =(k 为不等于0的常数)的图象在第一象限交于点A (1,n ).求:(1)一次函数和反比例函数的解析式;(2)当61≤≤x 时,反比例函数y 的取值范围.。
九年级数学上册 第1章 反比例函数与面积问题习题课件 (新版)湘教版

4.如图,在平面直角坐标系中,函数 y=xk(x>0,常数 k>0)的图 象经过点 A(1,2)和点 B,过点 B 作 y 轴的垂线,垂足为点 C,若△ABC 的面积为 2,求点 B 的坐标.
解:根据题意知 k=2,设 B 的坐标为(x0,y0),x0·y0=2,S△ABC =12·x0·(2-y0)=x0-12x0y0=2,∴x0=3,则 y0=23,∴B(3,23)
CABD
=2(xB-
xA)
=
2
+12
(
4 a
+
4 2a
)(2a
-a)
=
5,
S△
AOB
=
SODBA-S△OBD=5-2=3
5
6.如图,点 B 为 x 轴正半轴上一点,点 A 为双曲线 y=4x(x>0) 上一点,且 AO=AB,过 B 作 BC⊥x 轴交双曲线于 C 点,求 S△ABC.
解:过点 A 作 AD⊥x 轴交 x 轴于点 D,∵ AO=AB,∴D 为 OB 中点,设 A(x0,y0),则 B(2x0, 0),C(2x0,y20),SOACB=S△OAD+S 梯形 ADBC=2+12(y0 +y20)(2x0-x0)=2+34x0y0=2+3=5,S△ABC=SOACB -S△AOB=5-2S△AOD=5-4=1
4
5.如图,点 A,B 在反比例函数 y=kx的图象上,且点 A,B 的横 坐标分别为 a,2a(a>0),AC⊥x 轴于点 C,且△AOC 的面积为 2.
(1)求反比例函数的表达式.
(2)求△AOB 的面积.
解:(1)根据题意知 k=4,∴反比例函数的表达式
为 y=4x (2)过 B 作 BD⊥x 轴交 x 轴于点 D,S 四边形 ODBA=S△AOC+S 梯形
成都市东湖中学九上数学反比例函数的应用 导学
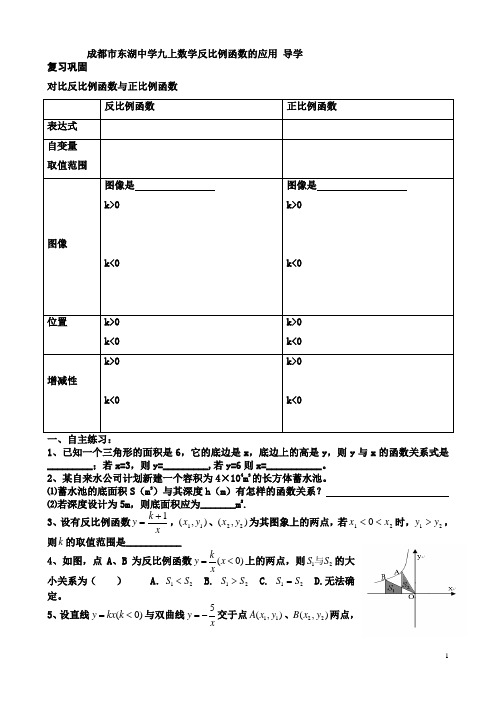
成都市东湖中学九上数学反比例函数的应用 导学复习巩固对比反比例函数与正比例函数1、已知一个三角形的面积是6,它的底边是x ,底边上的高是y ,则y 与x 的函数关系式是_________;若x=3,则y=_________,若y=6则x=___________。
2、某自来水公司计划新建一个容积为4×104m 3的长方体蓄水池。
⑴蓄水池的底面积S (m 3)与其深度h (m )有怎样的函数关系? ⑵若深度设计为5m ,则底面积应为_______m 2.3、设有反比例函数y k x=+1,(,)x y 11、(,)x y 22为其图象上的两点,若x x 120<<时,y y 12>,则k 的取值范围是___________4、如图,点A 、B 为反比例函数(0)ky x x=<上的两点,则12S S 与的大小关系为( ) A .12S S < B. 12S S > C. 12S S = D.无法确定。
5、设直线(0)y kx k =<与双曲线5y x=-交于点11(,)A x y 、22(,)B x y 两点,则12213x y x y -的值为___________二、合作学习,共同探索1、小明将一篇24000字的社会调查报告录入电脑,打印成文。
⑴如果小明以每分钟120字的速度录入,他需要多长时间才能完成?⑵完成录入的时间t (min )与录入文字的速度v (字/min )有怎样的函数关系? ⑶小明希望能在3小时内完成录入任务,那么他每分钟至少应录入多少个字?三、巩固练习:1.京沈高速公路全长658km ,汽车沿京沈高速公路从沈阳驶往北京,则汽车行完全程所需时间t (h )与行驶的平均速度v (km/h )之间的函数关系式为2.完成某项任务可获得500元报酬,考虑由x 人完成这项任务,试写出人均报酬y (元)与人数x (人)之间的函数关系式3.一定质量的氧气,它的密度ρ(kg/m 3)是它的体积V (m 3)的反比例函数,当V =10时,ρ=1.43,(1)求ρ与V 的函数关系式;(2)求当V =2时氧气的密度ρ4.小林家离工作单位的距离为3600米,他每天骑自行车上班时的速度为v (米/分),所需时间为t (分)(1)则速度v 与时间t 之间有怎样的函数关系?(2)若小林到单位用15分钟,那么他骑车的平均速度是多少?(2)如果小林骑车的速度最快为300米/分,那他至少需要几分钟到达单位?5.学校锅炉旁建有一个储煤库,开学初购进一批煤,现在知道:按每天用煤0.6吨计算,一学期(按150天计算)刚好用完.若每天的耗煤量为x 吨,那么这批煤能维持y 天 (1)则y 与x 之间有怎样的函数关系? (2)画出函数图象.(3)若每天节约0.1吨,则这批煤能维持多少天?6.某气球内充满了一定质量的气体,当温度不变时,气球内气体的气压P (千帕)是气体体积V (立方米)的反比例函数,其图像如图所示(千帕是一种压强单位) (1)写出这个函数的解析式;(2)当气球的体积是0.8立方米时,气球内的气压是多少千帕?(3)当气球内的气压大于144千帕时,气球将爆炸,为了安全起见,气球的体积应不小于多少立方米?四、课后练习一、选择题1.某厂现有800吨煤,这些煤能烧的天数y 与平均每天烧的吨数x 之间的函数关系是( )A .x y 300=(x >0)B .xy 300=(x ≥0) C .y =300x (x ≥0) D .y =300x (x >0)2.已知甲、乙两地相s (千米),汽车从甲地匀速行驶到达乙地,如果汽车每小时耗油量为a (升),那么从甲地到乙地汽车的总耗油量y (升)与汽车的行驶速度v (千米/时)的函数图象大致是( )3.在一个可以改变体积的密闭容器内装有一定质量的二氧化碳,当改变容器的体积时,气体的密度也会随之改变,密度ρ(单位:kg/m 3)是体积V (单位:m 3)的反比例函数,它的图6.象如图3所示,当310m V =时,气体的密度是( )A .5kg/m 3B .2kg/m 3C .100kg/m 3D ,1kg/m 34.物理学知识告诉我们,一个物体所受到的压强P 与所受压力F 及受力面积S 之间的计算公式为SFP =. 当一个物体所受压力为定值时,那么该物体所受压强P 与受力面积S 之间的关系用图象表示大致为( )6.我们知道,溶液的酸碱性由PH 确定,当PH >7时,溶液呈碱性;当PH <7时,溶液呈酸性.若将给定的HCL 溶液加水稀释,那么在下列图象中,能反映HCL 溶液的PH 与所加水的体积(V )的变化关系的是( )二、解答题如图,李老师设计了一个探究杠杆平衡条件的实验:在一个自制类似天平的仪器的左边固定托盘A 中放置一个重物,在右边的活动托盘B (可左右移动)中放置一定质量的砝码,使得仪器左右平衡,改变活动托盘B 与点O 的距离x (cm ),观察活动托盘B 中砝码的质量y (g )的变化情况.实验数据记录如下表:(1)把上表中(x ,y )的各组对应值作为点的坐标,在坐标系中描出相应的点,用平滑曲线连接这些点; (2)观察所画的图象,猜测y 与x 之间的函数关系,求出函数关系式并加以验证; (3)当砝码的质量为24g 时,活动托盘B 与点O 的距离是多少cm ? (4)当活动托盘B 往左移动时,应往活动托盘B 中添加还是减少砝码?B C。
成都市九上数学反比例函数图象和性质导练

成都市东湖中学反比例函数图象和性质导练一、选择题1.对于反比例函数2y x=,下列说法不正确...的是 ( ) A .点(21)--,在它的图象上 B .它的图象在第一、三象限C .当0x >时,y 随x 的增大而增大D .当0x <时,y 随x 的增大而减小 2.在反比例函数12my x-=的图象上有两点A ()11,x y ,B ()22,x y ,当120x x <<时,有12y y <,则m 的取值范围是 ( )A .0m < B.0m > C.12m <D.12m > 3.如果点(3,-4)在反比例函数ky x=的图象上,那么下列各点中,在此图象上的是( )A.(3,4)B. (-2,-6)C.(-2,6)D.(-3,-4) 4. 如图,函数11y x =-和函数22y x=的图象相交于点M (2,m ),N (-1,n ),若12y y >,则x 的取值范围是 ( ) A .102x x <-<<或 B .12x x <->或C .1002x x -<<<<或D .102x x -<<>或5.如图:等腰直角三角形ABC 位于第一象限,AB=AC=2,直角顶点A 在直线y =x 上,其中A 点的横坐标为1,且两条直角边AB 、AC 分别平行于x 轴、y 轴,若双曲线ky x=(k ≠0)与ABC ∆有交点,则k 的取值范围是 ( )A .12k <<B .13k ≤≤C .14k ≤≤D .14k <≤二、填空题6. 点(231)P m -,在反比例函数1y x=的图象上,则m = . 7.老师给出了一个函数,甲、乙、丙三位同学分别指出了这个函数的一个性质,甲:第一象限内有它的图象;乙:第三象限内有它的图象;丙:在每个象限内,y 随x 的增大而减小.请你写一个满足上述性质的函数解析式_________________.8. 若点A(m ,-2)在反比例函数4y x=的图像上,则当函数值y ≥-2时,自变量x 的取值范围是___________.9.如图,在反比例函数2y x=(0x >)的图象上,有点1234P P P P ,,,,它们的横坐标依次为1,2,3,4.分别过这些点作x 轴与y 轴的垂线,图中所构成的阴影部分的面积从左到右依次为123S S S ,,,则 .10.如图,已知双曲线ky x=(0x >)经过矩形OABC 的边AB BC ,的中点F E ,,且四边形OEBF 的面积为2,则k = .11.已知反比例函数y = - n-3x 的图像具有以下特征:在同一象限内,y 随x 增大而增大,(1)求n 的取值范围. (2)点(2,a )、(-1,b)、(-2,c )都在这个反比例函数图像上,比较a 、b 、c 的大小.12.已知反比例函数xy m=(m ≠0)的图像经过点A 、B ,点A 的坐标为(1,3),点B 到x 轴的距离为1,点C 坐标为(2,0).(1)求次反比例函数的关系式; (2)求直线BC 的函数关系式.2y x =xy OP 1 P 2P 3P 4 12 34(第9题)第9题图123S S S ++=13.已知反比例函数 y = kx 与一次函数y=mx+b 的图像交于P(-2,1)和Q (1,n )两点.(1) 求k 、n 的值;(2) 求一次函数y=mx+b 的解析式. (3) 求△POQ 的面积.14.如图,已知A(-4,2)、B(n ,-4)是一次函数y kx b =+的图象与反比例函数my x=的图象的两个交点.(1) 求此反比例函数和一次函数的解析式;(2) 根据图象写出使一次函数的值小于反比例函数的值 的x 的取值范围.15.如图,在平面直角坐标系xOy中,直线y=2x+n与x轴、y轴分别交于点A、B,与双曲线4y=x在第一象限交于点C(1,m)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
成都市东湖中学九上数学反比例函数面积问题导练1.在反比例函数的图象上有一点P(x,y),过P点作PA⊥x轴于A点,PB⊥y
轴于B点,且矩形AOBP的面积为4,则该反比例函数的解析式为_________.
2.若正方形OABC的顶点B和正方形ADEF的顶点E都在函数的
图象上.若正方形OABC的面积为1,则k的值为_________;点E的坐标为
_________.
3.如图,A、B是双曲线上的点,A、B两点的横坐标分别是a、
2a,线段AB的延长线交x轴于点C,若S△AOC=12.则k=_________.
4.如图,两个反比例函数y=和y=﹣的图象分别是l1和l2.设点P在l1上,
PC⊥x轴,垂足为C,交l2于点A,PD⊥y轴,垂足为D,交l2于点B,则△PAB
的面积为_________.
5.在一双曲线的分支(如图)上有A、B两点,且它们的横坐标分别为
(﹣4,﹣3),过这两点分别作坐标轴的垂线段,阴影部分面积为3,则函数解析
式为_________.
6.如图是反比例函数和在第一象限内的图象,在上取点M分别
作两坐标轴的垂线交于点A、B,连接OA、OB,则图中阴影部分的面积
为_________.
7.如图,双曲线y=(k>0)经过矩形OABC的边BC的中点E,交AB
于点D.若梯形ODBC的面积为3,则k=_________.
轴的垂线,垂足为M,已知△OAM的面积为1.
(1)求反比例函数的解析式;
(2)如图,点B为反比例函数在第三象限图象上的点,过B点作x轴的垂线,垂足为N,求证:△OAM≌△OBN.
9.如图,直线y=x与双曲线y=相交于A、B两点,BC⊥x轴于
点C(﹣4,0).
(1)求A、B两点的坐标及双曲线的解析式;
(2)若经过点A的直线与x轴的正半轴交于点D,与y轴的正半轴
交于点E,且△AOE的面积为10,求CD的长.
(1)求反比例函数的解析式;
(2)若以OA为边的菱形OABC的对角线OB在x轴上,求菱形OABC的面积.
11.如图,反比例函数y1=(k<0)的图象经过点A(﹣,m),连结AO并延长交双曲线于另一点D,
过A作AB⊥x轴于点B,过D作DE⊥y轴交AB延长线于点E,且△AED的面积为4.
(1)求m与k的值;
(2)若过A点的直线y2=ax+b与x轴正半轴交于C点,且∠ACO=30°,求直线解析式;
(3)当y1>y2时,请直接写出自变量x的取值范围.
12.如图,矩形OABC的顶点A、C分别在x轴和y轴上,点
B的坐标为(2,3).双曲线y=(x>0)的图象经过BC的中
点D,且与AB交于点E,连接DE.
(1)求k的值及点E的坐标;
(2)若点F是OC边上一点,且△FBC∽△DEB,求直线FB
的解析式.
13.如图,一次函数y=kx+b与反比例函数y=的图象交于A(2,3),B(﹣3,n)两点.
(1)求一次函数与反比例函数的解析式;
(2)过点B作BC⊥x轴,垂足为C,连接AC,求△ABC的面积.。
