2015河北省考试说明拓展五 一次函数、反比例函数与问题解决
2015年河北中考数学总复习课件(第13课时_反比例函数)

第13课时┃ 反比例函数
考点4 反比例函数的应用
利用待定系数法确定反比例函数表达式: k ①根据两变量之间的反比例关系,设 y= ; x 求函数表达式的 方法步骤 ②代入图像上一个点的坐标,即 x,y 的一对对 应值,求出 k 的值; ③写出表达式 k2 反比例函数与一 求直线 y=k1x+b(k1≠0)和双曲线 y= (k2≠0) x 次函数的图像的 的交点坐标,解这两个函数表达式组成的方程 交点的求法 组即可
冀考解读 课前热身 考点聚焦 冀考探究
第13课时┃ 反比例函数
探究二 反比例函数的图像与性质
命题角度: 1.反比例函数的图像与性质的应用; 2.用反比例函数中 k 的几何意义解决问题.
例 2 已知 P1(x1,y1),P2(x2,y2),P3(x3,y3)是反比例函数 2 y= 的图像上的三点,且 x1<x2<0<x3,则 y1,y2,y3 的大小关 x 系是 ( C ) A.y3<y2<y1 B.y1<y2<y3 C.y2<y1<y3 D.y2<y3<y1
考点聚焦
冀考探究
第13课时┃ 反比例函数
课 前 热 身
1. 若 y=(a+1)xa2-2 是反比例函数, 则 a 的取值为 A.1 B.-1 C.±1 D.任意实数
解 析
( A )
a2-2=-1,且 a+1≠0,应选 A.
冀考解读
课前热身
考点聚焦
冀考探究
第13课时┃ 反比例函数
k 2.[2014· 常州] 已知反比例函数 y= 的图像经过点 P(-1, x 2),则这个函数的图像位于 ( D ) A.第二,三象限 B.第一,三象限 C.第三,四象限 D.第二,四象限 k-1 3. [2014· 哈尔滨] 在反比例函数 y= 的图像的每一条曲 x 线上, y 都随 x 的增大而减小, 则 k 的取值范围是 ( A ) A.k>1 B.k>0 C.k≥1 D.k<1
专题1--一次函数与反比例函数问题

B.x>2 D.x<-2或0<x<2
【变式训练3】如图,正比例函数 y1 k1x 的图像与反比例
函数
y2
k2 x
的图象相交于A、B
两点,其中点A
D
的横坐标
x 为2,当 y1>y2 时, 的取值范围是 ( )
A.x< 2或x>2
B. x< 2或0<x<2
C. 2<x<0或0<x<2
真题回顾
例 (2015•广东)如图-1,反比例函数y=k/x( k≠0,x>0)的图象与直线y=3x相交于点C,过直 线上点A(1,3)作AB⊥x轴于点B,交反比例函数 的图象于点D,且AB=3BD. (1)求k的值; (2)求点C的坐标; (3)在y轴上确定一点M,使点 M到C,D两点的距离之和d=MC+MD, 最小求点M的坐标.
∴m=﹣4,
∴y=﹣
(2)当x<0时,kx+b﹣ >0的解集是x<﹣4.
m x
【变式训练4】一次函数y=kx+b 与反比例函数 y= 图象相交于A(-1,4),B(2,n)两点, 直线AB交x轴于点D。 (1)求一次函数与反比例函数的表达式; (2)过点B 作BC⊥y轴,垂足为C,连接 AC交 x轴于点E,求△AED的面积S。
点
不 ①x的取值范围_x_≠_0____; ①x的取值范围_任__意__实__数;
同 ②图象是_双__曲__线_
②图象是_直__线____;
点 ③k>0时,y随的x增大 ③k>0时,y随的x增大
而_减__小(在每个象限
而_增__大_
内)
k<0时,y随的x增 大而增__大__减__小_
第二、四 象限
专题五 一次函数、反比例函数与实际应用
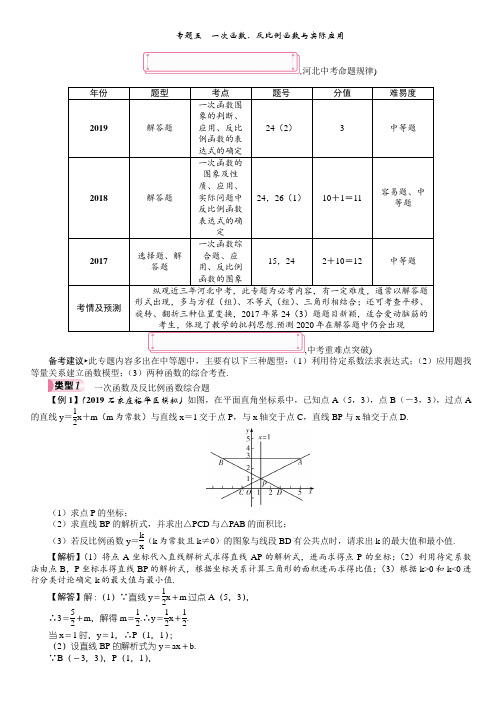
专题五 一次函数、反比例函数与实际应用,河北中考命题规律)年份 题型 考点 题号 分值 难易度2019 解答题 一次函数图象的判断、应用、反比例函数的表达式的确定24(2) 3 中等题2018 解答题 一次函数的图象及性质、应用、实际问题中反比例函数表达式的确定24,26(1) 10+1=11 容易题、中等题 2017 选择题、解答题 一次函数综合题、应用、反比例函数的图象15,24 2+10=12 中等题 考情及预测纵观近三年河北中考,此专题为必考内容,有一定难度,通常以解答题形式出现,多与方程(组)、不等式(组)、三角形相结合;还可考查平移、旋转、翻折三种位置变换,2017年第24(3)题题目新颖,适合爱动脑筋的考生,体现了教学的批判思想.预测2020年在解答题中仍会出现 ,中考重难点突破)备考建议►此专题内容多出在中等题中,主要有以下三种题型:(1)利用待定系数法求表达式;(2)应用题找等量关系建立函数模型;(3)两种函数的综合考查.一次函数及反比例函数综合题【例1】(2019·石家庄裕华区模拟)如图,在平面直角坐标系中,已知点A (5,3),点B (-3,3),过点A的直线y =12x +m (m 为常数)与直线x =1交于点P ,与x 轴交于点C ,直线BP 与x 轴交于点D.(1)求点P 的坐标;(2)求直线BP 的解析式,并求出△PCD 与△PAB 的面积比;(3)若反比例函数y =k x(k 为常数且k ≠0)的图象与线段BD 有公共点时,请求出k 的最大值和最小值. 【解析】(1)将点A 坐标代入直线解析式求得直线AP 的解析式,进而求得点P 的坐标;(2)利用待定系数法由点B ,P 坐标求得直线BP 的解析式,根据坐标关系计算三角形的面积进而求得比值;(3)根据k>0和k<0进行分类讨论确定k 的最大值与最小值.【解答】解:(1)∵直线y =12x +m 过点A (5,3), ∴3=52+m ,解得m =12.∴y =12x +12. 当x =1时,y =1,∴P (1,1);(2)设直线BP 的解析式为y =ax +b.∵B (-3,3),P (1,1),∴⎩⎪⎨⎪⎧3=-3a +b ,1=a +b.解得⎩⎨⎧a =-12,b =32. ∴直线BP 的解析式为y=-12x +32. 当y =0时,x =3,∴D (3,0).∵点C 在直线y =12x +12上, ∴当y =0时,x =-1,则C (-1,0).∴S △PCD S △PAB =12×4×112×8×2=14; (3)当k<0时,若反比例函数经过点B ,则k 的最小值为-9. 当k>0时,联立⎩⎨⎧y =-12x +32,y =k x, 整理,得x 2-3x +2k =0.令Δ=b 2-4ac =9-8k =0,解得k =98.∴k 的最大值为98. 1.(2019·邯郸一模)如图,直线l 1经过点A (6,0),且垂直于x 轴,直线l 2:y =kx +b (b>0)经过点B (-2,0),与l 1交于点C ,S △ABC =16.点M 是线段AC 上一点,直线MN ∥x 轴,交l 2于点N ,点D 是MN 的中点,双曲线y =m x(x>0)经过点D ,与l 1交于点E. (1)求l 2的解析式;(2)当点M 是AC 的中点时,求点E 的坐标;(3)当MD =1时,求m 的值.解:(1)由题意,得AB =8.∵S △ABC =16,即12×8×AC =16,∴AC =4. ∴C (6,4).把B (-2,0),C (6,4)分别代入y =kx +b ,得⎩⎪⎨⎪⎧-2k +b =0,6k +b =4.解得⎩⎪⎨⎪⎧k =12,b =1.∴l 2的解析式为y =12x +1; (2)∵点M 是AC 的中点,∴M (6,2).∵MN ∥x 轴,∴点N 的纵坐标为2.把y =2代入y =12x +1,得x =2.∴N (2,2). ∵点D 是MN 的中点,∴D (4,2).把D (4,2)代入y =m x,得m =8. ∴双曲线的解析式为y =8x(x>0). 当x =6时,y =43,∴E ⎝⎛⎭⎫6,43; (3)设点M (6,n ),当MD =1时,D (5,n ),N (4,n ).把N (4,n )代入y =12x +1,得n =3. ∴D (5,3).∴m =15.一次函数的实际应用【例2】(2019·唐山路南区二模)某公司在甲、乙仓库共存放某种原料450 t .如果运出甲仓库所存原料的60%、乙仓库所存原料的40%,那么乙仓库剩余的原料比甲仓库剩余的原料多30 t .(1)求甲、乙两仓库分别存放原料多少吨;(2)现公司需将300 t 原料运往工厂,从甲、乙两仓库到工厂的运价分别为120元/t 和100元/t .经协商,从甲仓库到工厂的运价可优惠a 元/t (10≤a ≤30),从乙仓库到工厂的运价不变.设从甲仓库运m t 原料到工厂,请求出总运费W 关于m 的函数解析式(不要求写出m 的取值范围);(3)在(2)的条件下,请根据函数的性质说明:随着m 的增大,W 的变化情况.【解析】(1)根据甲、乙两仓库原料运出前后的关系,可得二元一次方程组,求解即可;(2)根据甲、乙的运费与运价的关系,可得函数解析式;(3)根据一次函数的性质,首先确定a 的取值,即要分类讨论,进而得出W 的变化情况.【解答】解:(1)设甲仓库存放原料x t ,乙仓库存放原料y t .根据题意,得⎩⎪⎨⎪⎧x +y =450,(1-40%)y -(1-60%)x =30.解得⎩⎪⎨⎪⎧x =240,y =210. 答:甲仓库存放原料240 t ,乙仓库存放原料210 t ;(2)由于从甲仓库运m t 原料到工厂,则从乙仓库运(300-m ) t 原料到工厂,根据题意,得W =(120-a )m +100(300-m )=(20-a )m +30 000;(3)①当10≤a<20时,20-a>0,此时W 随着m 的增大而增大;②当a =20时,20-a =0,W 是定值30 000,此时W 不随m 的变化而变化;③当20<a ≤30时,20-a<0,此时W 随着m 的增大而减小.2.(2019·新疆中考)某水果店以每千克8元的价格购进苹果若干千克,销售了部分苹果后,余下的苹果每千克降价4元销售,全部售完.销售金额y (元)与销售量x (kg )之间的关系如图所示.请根据图象提供的信息完成下列问题:(1)降价前苹果的销售单价是 元/kg ;(2)求降价后销售金额y (元)与销售量x (kg )之间的函数解析式,并写出自变量的取值范围;(3)该水果店这次销售苹果盈利了多少元?解:(1)16;(2)由题意,得降价后y =640+(16-4)(x -40)=12x +160.当y =760时,x =50,∴自变量的取值范围是40<x ≤50;(3)760-50×8=360(元).∴该水果店这次销售苹果盈利了360元.反比例函数与其他函数综合应用【例3】某药品研究所开发一种抗菌新药,经多年动物实验,首次用于临床人体试验,测得成人服药后血液中药物浓度y (μg /mL )与服药时间x (h )之间的函数关系如图所示(当4<x ≤10时,y 与x 成反比例).(1)根据图象分别求出血液中药物浓度上升和下降阶段y 与x 之间的函数关系式;(2)问血液中药物浓度不低于4 μg /mL 的持续时间为多少小时?【解析】(1)分别利用正比例函数以及反比例函数表达式求法得出即可;(2)由y =4分别求出相应的x 的值,进而得出答案.【解答】解:(1)由图象可知,当0≤x ≤4时,y 与x 成正比例关系,设y =kx.当x =4时,y =8,∴4k =8,解得k =2.∴y =2x (0≤x ≤4).当4<x ≤10时,y 与x 成反比例关系,设y =m x . 当x =4时,y =8,∴m =4×8=32.∴y =32x(4<x ≤10). ∴y =⎩⎪⎨⎪⎧2x (0≤x ≤4),32x(4<x ≤10); (2)血液中药物浓度不低于4 μg /mL ,即y ≥4.∴2x ≥4且32x≥4,解得2≤x ≤8. ∵8-2=6(h ),∴血液中药物浓度不低于4 μg /mL 的持续时间为6 h .,3.石家庄某公司将农副产品运往北京市场进行销售,记汽车行驶时间为t h ,平均速度为v km /h (汽车行驶速度不超过100 km /h ).根据经验,v ,t 的一组对应值如下表:v/(km /h ) 75 80 85 90 95t/h 4.00 3.75 3.53 3.33 3.16(1(2)汽车上午7:30从石家庄出发,能否在上午10:00之前到达北京市场?请说明理由;(3)若汽车到达北京市场的行驶时间t 满足3.5≤t ≤4,求平均速度v 的取值范围.解:(1)根据表格中的数据,可知v =k t. ∵v =75时,t =4,∴k =75×4=300.∴v 关于t 的函数表达式为v =300t(t ≥3); (2)不能.理由:从上午7:30到上午10:00经过的时间为2.5 h .当t =2.5时,v =3002.5=120. ∵120>100,∴汽车上午7:30从石家庄出发,不能在上午10:00之前到达北京市场;(3)∵3.5≤t ≤4,∴平均速度v 的取值范围是75≤v ≤6007. 运动型问题【例4】(2019·石家庄桥西区模拟)如图1,在直角坐标系中,一次函数的图象l 1与y 轴交于点A (0,2),与一次函数y =x -3的图象l 2交于点E (m ,-5).(1)求m 的值及l 1的表达式;(2)直线l 1与x 轴交于点B ,直线l 2与y 轴交于点C ,求四边形OBEC 的面积;(3)如图2,已知矩形MNPQ ,PQ =2,NP =1,M (a ,1),矩形MNPQ 的边PQ 在x 轴上平移,若矩形MNPQ 与直线l 1或l 2有交点,直接写出a 的取值范围.【解析】(1)把点E 的坐标代入l 2,即可求出m 的值,根据点E 和点A 的坐标可求出直线l 1的表达式;(2)连接OE ,根据点B ,C 的坐标可得OB ,OC 的长,点E 纵、横坐标的绝对值分别为△OBE 和△OCE 的高,先求出这两个三角形的面积,它们的和即为四边形OBEC 的面积;(3)当矩形与l 1有交点时,临界情况是相交于顶点,分别为点Q 和点N ,根据已知条件和l 1的表达式可求出点Q 和点N 的横坐标,结合点M 的坐标,可求出a 的取值范围;同理,当矩形与l 2有交点时,也可求出a 的取值范围.【解答】解:(1)∵点E (m ,-5)在一次函数y =x -3的图象上,∴m -3=-5,解得m =-2.∴E (-2,-5).设直线l 1的表达式为y =kx +b.∵直线l 1过点A (0,2),E (-2,-5),∴⎩⎪⎨⎪⎧b =2,-2k +b =-5.解得⎩⎪⎨⎪⎧b =2,k =72. ∴直线l 1的表达式为y =72x +2; (2)连接OE.∵l 1:y =72x +2,∴y =0时,x =-47.∴B ⎝⎛⎭⎫-47,0. ∵l 2:y =x -3,∴x =0时,y =-3.∴C (0,-3).∴S 四边形OBEC =S △OBE +S △OCE=12×47×5+12×2×3=317; (3)-47≤a ≤127或3≤a ≤6. 4.如图,在平面直角坐标系中,四边形OABC 的顶点O 是坐标原点,点A 在第一象限,点C 在第四象限,,点B 在x 轴的正半轴上,∠OAB =90°且OA =AB ,OB =6,OC =5.(1)求点A 和点B 的坐标;(2)点P 是线段OB 上的一个动点(点P 不与点O ,B 重合),以每秒1个单位长度的速度由点O 向点B 运动,过点P 的直线a 与y 轴平行,直线a 交边OA 或边AB 于点Q ,交边OC 或边BC 于点R ,设点P 运动时间为t s ,线段QR 的长度为m ,已知t =4时,直线a 恰好过点C.①当0<t <3时,求m 关于t 的函数关系式;②点P 出发时,点E 也从点B 出发,以每秒1个单位长度的速度向点O 运动,点P 停止时点E 也停止.设△QRE 的面积为S ,求S 与t 的函数关系式;③直接写出②中S 的最大值是 .解:(1)由题意知△OAB 是等腰直角三角形.∵OB =6,∴A (3,3),B (6,0);(2)∵A (3,3),B (6,0),∴直线OA 的解析式为y =x ,直线AB 的解析式为y =-x +6.∵当t =4时,直线a 恰好过点C ,OC =5,∴C (4,-3).∴直线OC 的解析式为y =-34x ,直线BC 的解析式为y =32x -9. ①当0<t <3时,Q (t ,t ),R ⎝⎛⎭⎫t ,-34t , ∴m =t +34t =74t ; ②当0<t <3时,S =12PE·QR =12(6-2t )·74t =-74t 2+214t ; 当3<t <4时,S =12PE·QR =12(2t -6)·⎝⎛⎭⎫-t +6+34t =-14t 2+274t -18; 当4≤t <6时,S =12PE·QR =12(2t -6)·⎝⎛⎭⎫-t +6-32t +9=-52t 2+452t -45; ③458.[当0<t <3时,t =32时,S 的最大值为6316; 当3<t ≤4时,∵S =-14t 2+274t -18=-14⎝⎛⎭⎫t -2722+14×2724-18,∴t =4时,S 的值最大,最大值为5;当4≤t <6时,S =-52t 2+452t -45=-52⎝⎛⎭⎫t -922+458,∴t =92时,S 的最大值为458.综上所述,S 的最大值为458.] 请完成限时训练A 本P A 72~A 73,选做B 本P B 41。
一次函数与反比例函数综合应用教案

一次函数与反比例函数综合应用教案一、教学目标1. 让学生掌握一次函数和反比例函数的基本概念和性质。
2. 培养学生运用一次函数和反比例函数解决实际问题的能力。
3. 引导学生通过合作交流,提高解决问题的策略和思维能力。
二、教学内容1. 一次函数的基本概念和性质。
2. 反比例函数的基本概念和性质。
3. 一次函数和反比例函数的综合应用。
三、教学重点与难点1. 教学重点:一次函数和反比例函数的基本概念、性质和综合应用。
2. 教学难点:一次函数和反比例函数的综合应用。
四、教学方法1. 采用问题驱动法,引导学生主动探究一次函数和反比例函数的性质。
2. 利用案例分析法,让学生通过实际问题体会一次函数和反比例函数的应用价值。
3. 采用合作交流法,培养学生团队协作和沟通能力。
五、教学过程1. 导入新课:通过生活实例引入一次函数和反比例函数的概念。
2. 自主学习:让学生自主探究一次函数和反比例函数的性质。
3. 案例分析:分析实际问题,引导学生运用一次函数和反比例函数解决问题。
4. 合作交流:分组讨论,让学生分享解题策略和心得。
5. 总结提升:总结一次函数和反比例函数的性质及应用,提高学生解决问题的能力。
6. 课后作业:布置相关练习题,巩固所学知识。
六、教学活动设计1. 活动一:引入概念通过展示实际生活中的线性关系图片,如直线轨道上列车的运动,引导学生思考线性关系的表现形式。
引导学生提出一次函数的表达式,并解释其含义。
2. 活动二:探索性质学生通过绘制一次函数图像,观察并总结其在坐标系中的性质。
通过实际例子,让学生理解一次函数的斜率和截距对图像的影响。
3. 活动三:反比例函数的引入引导学生从比例关系出发,思考反比例函数的概念。
通过实际问题,如在固定面积内,距离与面积的关系,引入反比例函数。
七、教学评价设计1. 评价目标:学生能理解并应用一次函数和反比例函数解决实际问题。
通过设计具有挑战性的问题,如购物预算问题,让学生应用所学的函数知识。
一次函数和反比例函数综合题

一次函数和反比例函数综合题一次函数和反比例函数综合题一次函数和反比例函数是数学中常见的两种函数形式。
它们在实际应用中具有广泛的应用,能够帮助我们分析和解决很多问题。
在这篇文档中,我们将通过几个实际问题来介绍一次函数和反比例函数,并且阐述它们在问题求解中的作用。
一次函数(即线性函数)的一般形式为y = kx + b,其中k和b分别代表斜率和截距。
一次函数的图像是一条直线,通过给定的两个点,我们就可以确定唯一一条直线。
一次函数在直线上的特点使得它在很多实际问题中都起到了重要作用。
反比例函数的一般形式为y = k/x,其中k是一个非零实数。
反比例函数的图像是一个拋物线,其与x轴和y 轴都有渐进线。
若要确定一条反比例函数的图像,我们需要已知一对坐标点。
反比例函数在实际生活中也能够很好地解决问题。
首先,我们来看一个一次函数的应用问题。
问题1:某校体育场的露天电视屏幕宽度为10米。
如果离电视屏幕距离为30米,站在距离电视屏幕10米处,该同学把电视屏幕的宽度误看为5米,请问该同学距离屏幕实际上有多远?解析:设该同学离电视屏幕的实际距离为x,则有一次函数关系式10/30 = 5/x。
解出x可得x = 15(米)。
所以该同学距离电视屏幕实际上是15米。
接下来,我们来看一个反比例函数的应用问题。
问题2:一个车间有6台机器,可以在20小时内完成一项任务。
现在该车间购买了2台新机器,那么完成同样任务需要多少小时?解析:设新的完成任务所需小时数为x,则有反比例函数关系式6/20 = 8/x。
解出x可得x = 40(小时)。
所以完成同样任务现在需要40小时。
通过以上两个问题的分析,我们可以看出一次函数和反比例函数在解决实际问题中的作用。
一次函数可以用来建立两个变量之间的线性关系,而反比例函数用来建立两个变量之间的反比例关系,这样我们就能够通过已知条件确定未知量的值,解决问题。
另外,我们还可以将一次函数和反比例函数结合起来进行分析。
考点05 反比例函数的图像和性质(解析版)

考点五反比例函数的图像和性质知识点整合一、反比例函数的概念1.反比例函数的概念一般地,函数ky x=(k 是常数,k ≠0)叫做反比例函数.反比例函数的解析式也可以写成1y kx -=的形式.自变量x 的取值范围是x ≠0的一切实数,函数的取值范围也是一切非零实数.2.反比例函数ky x=(k 是常数,k ≠0)中x ,y 的取值范围反比例函数ky x=(k 是常数,k ≠0)的自变量x 的取值范围是不等于0的任意实数,函数值y 的取值范围也是非零实数.二、反比例函数的图象和性质1.反比例函数的图象与性质(1)图象:反比例函数的图象是双曲线,它有两个分支,这两个分支分别位于第一、三象限,或第二、四象限.由于反比例函数中自变量x ≠0,函数y ≠0,所以,它的图象与x 轴、y 轴都没有交点,即双曲线的两个分支无限接近坐标轴,但永远达不到坐标轴.(2)性质:当k >0时,函数图象的两个分支分别在第一、三象限,在每个象限内,y 随x 的增大而减小.当k <0时,函数图象的两个分支分别在第二、四象限,在每个象限内,y 随x 的增大而增大.表达式ky x=(k 是常数,k ≠0)kk >0k <0大致图象所在象限第一、三象限第二、四象限增减性在每个象限内,y随x的增大而减小在每个象限内,y随x的增大而增大2.反比例函数图象的对称性反比例函数的图象既是轴对称图形,又是中心对称图形,其对称轴为直线y=x和y=-x,对称中心为原点.3.注意(1)画反比例函数图象应多取一些点,描点越多,图象越准确,连线时,要注意用平滑的曲线连接各点.(2)随着|x|的增大,双曲线逐渐向坐标轴靠近,但永远不与坐标轴相交,因为反比例函数kyx=中x≠0且y≠0.(3)反比例函数的图象不是连续的,因此在谈到反比例函数的增减性时,都是在各自象限内的增减情况.当k>0时,在每一象限(第一、三象限)内y随x的增大而减小,但不能笼统地说当k>0时,y随x的增大而减小.同样,当k<0时,也不能笼统地说y随x 的增大而增大.三、反比例函数解析式的确定1.待定系数法确定解析式的方法仍是待定系数法,由于在反比例函数kyx=中,只有一个待定系数,因此只需要一对对应值或图象上的一个点的坐标,即可求出k的值,从而确定其解析式.2.待定系数法求反比例函数解析式的一般步骤(1)设反比例函数解析式为kyx=(k≠0);(2)把已知一对x,y的值代入解析式,得到一个关于待定系数k的方程;(3)解这个方程求出待定系数k;(4)将所求得的待定系数k的值代回所设的函数解析式.四、反比例函数中|k|的几何意义1.反比例函数图象中有关图形的面积2.涉及三角形的面积型当一次函数与反比例函数结合时,可通过面积作和或作差的形式来求解.(1)正比例函数与一次函数所围成的三角形面积.如图①,S △ABC =2S △ACO =|k |;(2)如图②,已知一次函数与反比例函数ky x=交于A 、B 两点,且一次函数与x 轴交于点C ,则S △AOB =S △AOC +S △BOC =1||2A OC y ⋅+1||2B OC y ⋅=1(||||)2A B OC y y ⋅+;(3)如图③,已知反比例函数ky x=的图象上的两点,其坐标分别为()A A x y ,,()B B x y ,,C 为AB 延长线与x 轴的交点,则S △AOB =S △AOC –S △BOC =1||2A OC y ⋅–1||2B OC y ⋅=1(||||)2A B OC y y ⋅-.五、反比例函数与一次函数的综合1.涉及自变量取值范围型当一次函数11y k x b =+与反比例函数22k y x=相交时,联立两个解析式,构造方程组,然后求出交点坐标.针对12y y >时自变量x 的取值范围,只需观察一次函数的图象高于反比例函数图象的部分所对应的x 的范围.例如,如下图,当12y y >时,x 的取值范围为A x x >或0B x x <<;同理,当12y y <时,x 的取值范围为0A x x <<或B x x <.2.求一次函数与反比例函数的交点坐标(1)从图象上看,一次函数与反比例函数的交点由k 值的符号来决定.①k 值同号,两个函数必有两个交点;②k 值异号,两个函数可能无交点,可能有一个交点,也可能有两个交点;(2)从计算上看,一次函数与反比例函数的交点主要取决于两函数所组成的方程组的解的情况.考向一反比例函数的定义1.反比例函数的表达式中,等号左边是函数值y ,等号右边是关于自变量x 的分式,分子是不为零的常数k ,分母不能是多项式,只能是x 的一次单项式.2.反比例函数的一般形式的结构特征:①k ≠0;②以分式形式呈现;③在分母中x 的指数为-1典例引领变式拓展故答案为:2.考向二反比例函数的图象和性质当k>0时,函数的图象在第一、三象限,在每个象限内,曲线从左向右下降,也就是在每个象限内,y随x的增大而减小.当k<0时,函数的图象在第二、四象限,在每个象限内,曲线从左向右上升,也就是在每个象限内,y随x的增大而增大.双曲线是由两个分支组成的,一般不说两个分支经过第一、三象限(或第二、四象限),而说图象的两个分支分别在第一、三象限(或第二、四象限).典例引领根据图象可知,114x x>+的解集是-正确的有②③;故选:B .【点睛】本题考查了反比例函数的性质,平移的性质,反比例函数图象与几何变换,掌握性质,数形结合是解题的关键.2.如图,点(1,2)A 和点(,)B a b 是反比例函数右侧,则下列说法中,不正确的是(A .该反比例函数解析式B .矩形OCBD 的面积为C .该反比例函数的另一个分支在第三象限,且【详解】解:根据题意,10k ->,解得1k <,∴0k =满足题意,故选:D .变式拓展二、填空题三、解答题把上表中的坐标系中描出这些点,并用光滑的曲线连接起来,得到如图所示的(1)请在该平面直角坐标系中作出(2)观察函数图象,并结合表中的数据:①猜测1y与x之间的函数关系,并求②求2y关于x的函数表达式;(2)①观察表格可知,1y 是x 设1k y x=,把()30,10代入得:1030k =,∴300k =,∴612x ≤≤.考向三反比例函数解析式的确定1.反比例函数的解析式k y x=(k ≠0)中,只有一个待定系数k ,确定了k 值,也就确定了反比例函数,因此要确定反比例函数的解析式,只需给出一对x ,y 的对应值或图象上一个点的坐标,代入k y x=中即可.2.确定点是否在反比例函数图象上的方法:(1)把点的横坐标代入解析式,求出y 的值,若所求值等于点的纵坐标,则点在图象上;若所求值不等于点的纵坐标,则点不在图象上.(2)把点的横、纵坐标相乘,若乘积等于k ,则点在图象上,若乘积不等于k ,则点不在图象上.典例引领【答案】30【分析】此题主要考查了平移的性质和反比例函数图象上点的坐标特征,题关键.利用平行四边形的面积公式得出得出k 的值.【详解】∵将该函数图像向上平移x 【答案】52【分析】本题主要考查了矩形的性质及待定系数法求反比例函数解析式,根据矩形的边与y 轴平行,()1,B m ,D【答案】8 yx =【分析】本题主要考查了求反比例函数解析式、正方形的性质等知识点,确定点是解题的关键.先根据坐标与图形得到A【答案】5 yx =-【分析】本题考查反比例函数图像的性质,键.变式拓展【答案】28【分析】利用反比例函数图像上的坐标特点,即可得出答案.【详解】解:∵ABCD 是矩形,∴90DAB ABC ∠∠==【答案】24a <<【分析】本题考查利用待定系数法求反比例函数解析式,及解不等式.先求出双曲线解析式,由题意可用长.再由线段BC 与双曲线有交点且与点考向四反比例函数中k的几何意义三角形的面积与k的关系(1)因为反比例函数kyx=中的k有正负之分,所以在利用解析式求矩形或三角形的面积时,都应加上绝对值符号.(2)若三角形的面积为12|k|,满足条件的三角形的三个顶点分别为原点,反比例函数图象上一点及过此点向坐标轴所作垂线的垂足.典例引领A .4-B .6【答案】C 【分析】本题考查反比例函数与一次函数的交点问题,题的关键.利用APC 与PBD 相似即可解决问题.【详解】解:PC x ⊥ 轴,PD ⊥PDB PCA ∴∠=∠,PD x 轴,BPD PAC ∴∠=∠,APC PBD ∴ ∽,∴AC PC PD BD=.二、填空题【答案】-3【分析】本题考查的是反比例函数系数k 的几何意义,的面积是是解答此题的关键.作AD OB ⊥OA =12OB ,然后通过证得AOD BOA ∽何意义即可求得k 的值.∵Rt OAB 中,30ABO ∠=︒,∴OA =12OB ,∵90ADO OAB ∠∠==︒,AOD BOA ∠∠=∴AOD BOA ∽,∴214AOD S OA S OB ⎛⎫== ⎪⎝⎭ ,【答案】5-【分析】此题主要考查了反比例函数的图象,比例函数的图象,理解反比例函数比例系数的几何意义是解决问题的关键.连接AB y ∥轴,得ABC 和AB y ∥轴,ABC ∴ 和AOB ∆关于AB 边上的高相等,52ABC AOB S S ∆∆∴==,根据反比例函数比例系数的几何意义得:变式拓展(1)用含m 的代数式表示(2)若3OMN S =△,则【答案】24m k =90OAB ∠=︒,∴N 点的横坐标为m ,反比例函数()0k y x x=>的图象过点N ,∴N 点的纵坐标为4m , OME OAN S S =△△,OMN OME OAN MEAN MEAN S S S S S=+-=△△△梯形梯形,3OMN S =△,三、解答题【答案】(2,4)C 或(8,1)C 【分析】本题考查了反比例函数的图象与性质,形的判定与性质;由反比例函数的对称性得四边形设点8,C m m ⎛⎫ ⎪⎝⎭,分别过点∵点A 、C 在反比例函数∴1842AOE COF S S ∆∆==⨯=,当04m <<时,则AOE S ∆∴6ACFE AOC S S ∆==梯形,k=【答案】6【分析】本题考查了反比例函数⊥轴,垂足为点E,连接等.作AE x到三角形AOB的面积,两个面积之和为⊥轴,垂足为点【详解】解:作AE x,AE x⊥轴,AB AC=∴=,BE CE,=5OC OB(1)求k和m的値;(2)当8x≥时,求函数值【答案】(1)10k=,m(2)5 04y<≤.考向五反比例函数与一次函数的综合反比例函数与一次函数综合的主要题型:(1)利用k值与图象的位置的关系,综合确定系数符号或图象位置;(2)已知直线与双曲线表达式求交点坐标;(3)用待定系数法确定直线与双曲线的表达式;(4)应用函数图象性质比较一次函数值与反比例函数值的大小等.解题时,一定要灵活运用一次函数与反比例函数的知识,并结合图象分析、解答问题.典例引领(1)若2k =,4b =-,则(2)若CE DE =,则b 与【答案】12k +【分析】本题考查了一次函数和反比例函数的交点问题,系是解此题的关键.【答案】12【分析】本题主要考查了反比例函数的综合应用,解析式,解题的关键是数形结合,熟练掌握相关的性质.过点⊥轴于点E,过点CB作BE x()DE=---=,证明AD∥132联立43y x y x =+⎧⎪⎨=-⎪⎩,解得:1131x y =-⎧⎨=⎩,2113x y =-⎧⎨=⎩,∴()3,1A -,()1,3B -,二、解答题(1)求反比例函数与一次函数的函数表达式;(2)连接OA OB ,,求OAB 的面积;(3)请结合图象直接写出不等式m kx b x+<【答案】(1)6y x =,y =x +1(2)52AOB S =对于1y x =+,当0y =时,=1x -;当0x =∴()1,0C -,()0,1D ∴1,OC =1,OD =∴111112*********AOB S =⨯⨯+⨯⨯+⨯⨯=+ (3)解:由图象可知:不等式m kx b x+<的解集为:(1)求反比例函数和一次函数的解析式;(2)设D 为线段AC 上的一个动点(不包括图象于点E ,当CDE 的面积最大时,求点【答案】(1)反比例函数解析式为y =(2)点E 坐标为()2,3-.变式拓展(1)求一次函数和反比例函数的解析式;(2)求AOB 的面积;(3)观察图象,直接写出不等式【答案】(1)y x =--(2)6(3)<4x -或02x <<【分析】(1)先把点A 代入反比例函数解析式,即可求出(2)先求出直线y =-(3)观察函数图象即可求得不等式的解集.【详解】(1)解:∵(A(1)求一次函数和反比例函数的关系式;(2)若点E 是点C 关于x 轴的对称点,求【答案】(1)一次函数解析式1y x 4=-(2)32ABE S =△【分析】(1)利用点A 的坐标,代入可求出反比例函数解析式,进而求出点待定系数法可求出一次函数的解析式;当点P在BC上运动时,则PB∵2sin ==2PH B PB ,即PH =∴(1132822y DB PH =⋅=⨯⋅()304;x x ⎧≤≤由图像可得,函数图像有最大值为(3)解:根据函数图像可得:当【点睛】本题主要考查了函数图像与性质、求函数解析式、画函数图像、三角形面积、运用函数图像解不等式等知识点,求得函数解析式以及数形结合思想是解题的关键.(1)求反比例函数和一次函数的解析式;的面积;(2)求ABO(1)求a ,k 的值.(2)利用图像信息,直接写出不等式1102k x x+-≥的解集(3)如图2,直线CD 过点A ,与反比例函数图像交于点C ,与x 轴交于点,OA OC ,求OAC 的面积.【答案】(1)4a =,12k =;(2)4x ≥(1)求一次函数和反比例函数的解析式;(2)在y轴上取一点N,当(3)将直线1y向下平移2围.根据函数图象可得:当11.如图,在平面直角坐标系例函数2myx=(m为常数,且(1)求反比例函数与一次函数的解析式.(1)求反比例函数的解析式;(2)点C在这个反比例函数图象上,坐标.【答案】(1)8 yx =(2)()4,2 C90∠=∠=∠=ABO BOE AEO∴四边形ABOE是矩形,∴==,OB AE2OE AB==45,∠=︒ADO∴ 是等腰直角三角形,AED∴==,DE AE4。
《反比例函数》突破提高类型五 反比例函数与一次函数结合求不等式解集与面积

类型五、反比例函数与一次函数结合求不等式解集与面积【解惑】如图,在平面直角坐标系xOy 中,一次函数1y kx b =+与反比例函数2(0)ny n x =>交于点()2,1A --,()1,B m .(1)求1y ,2y 对应的函数表达式; (2)求AOB 的面积; (3)直接写出不等式nkx b x+≥的解集. 方法:1.求(1)代入即可;2.(2)先求得直线AB 与y 轴的交点C 为()0,1,然后根据割补AOB AOC BOC S S S =+△△△求得即可;3.(3)观察图形,先找出一次函数与反比例函数的交点,一次函数的值大于反比例函数的值,说明一次函数在反比例函数上面的部分,然后再看横坐标范围即可.【融会贯通】1.如图,直线1y k x b =+与双曲线2k y x =交于A 、B 两点,其横坐标分别为1和5,则不等式21kk x b x+<的解集是( ).A .15x <<B .5x >或01x <<C .5x >或1x <D .15x ≤≤2.如图,直线y kx =与双曲线3y x -=在同一坐标系中如图所示,则不等式3kx x-<的解集为( )A .01x <<B .1x <-C .1x <-或01x <<D .10x -<<或1x >3.如图,一次函数111y k x b =+的图象与反比例函数22k y x=的图象相交于点()5,A m ,()1,B n -两点,当12y y >时,则自变量x 的取值范围是______.【知不足】1.如图,小明同学利用计算机软件绘制函数22x y x =+,122y x =-+,根据学习函数的经验,可以知道21222x x x ≥-++的解集是( )A .4x ≤-或2x ≥B .42x -≤<-或22x -<≤C .42x -≤<-或2x ≥D .4x ≤-或42x -≤<-2.已知一次函数1(0)y kx b k =+<与反比例函数()20my m x=≠的图象交于点A (-1,yA )和点B (3,yB )两点,当y 1>y 2时,实数x 的取值范围是( ) A .x <-1或0<x <3 B .-1<x <0或0<x <3 C .-1<x <0或x >3D .0<x <33. 如图,一次函数11(0)y k x b k =+≠与反比例函数22(0)k y k x=≠的图象交于点()2,3A ,(),1B a -,则不等式 xk b x k 21≥+ 的解集是___________.4.如图,一次函数1y k x b =+的图象与反比例函数2k y x=的图象相交于点()3,1A 、()1,B n -两点.(1)分别求出一次函数和反比例函数的解析式; (2)根据图象,请你直接写出满足条件:21k k x b x+≥的x 的取值范围. 【一览众山小】1.如图,直线y kx =与双曲线3y x =-在同一坐标系中如图所示,则不等式3kx x>-的解集为( )A .01x <<B .1x <-C .1x <-或01x <<D .10x -<<或1x >2.如图,正比例函数11y k x =的图像与反比例函数22k y x=的图像相交于A 、B 两点,点A 的横坐标为2,当120y y <<时,x 取值范围是( )A .02x <<或2x >B .02x <<C .2x <-D .20x -<<3.如图,一次函数3y x =-+的图象与反比例函数()0ky k x =≠在第一象限内的图象交于()1,A a 和B 两点,与x 轴交于点C .(1)求反比例函数的解析式; (2)求出另一个交点B 的坐标;(3)根据图象直接写出当0x >时,不等式3kx x-+<的解集. 4.如图,直线3y kx =+与x 轴、y 轴分别交于点B 、C ,与反比例函数my x=交于点A 、D ,过D 作DE x ⊥轴于E ,连接OA ,OD ,若()2,A n -,:1:2OAB ODE S S =△△.(1)求点B 的坐标,并求出反比例函数的表达式; (2)求点D 的坐标; (3)直接写出关于x 不等式:3mkx x>-的解集为______.5.如图,一次函数()0y ax b a =+≠的图像与反比例函数()0ky k x=≠的图像交于()2,M m ,()1,4N --两点.(1)求反比例函数的解析式及m 的值; (2)观察图像,直接写出不等式kax b x<+的解集. 【温故为师】1.已知一次函数(0)y ax b a =+≠的图象与反比例函数(0)ky k x=≠的图象相交于点(3,2)A -,(2,)B n .(1)求一次函数和反比例函数的表达式,并在图中画出这个一次函数的图象;(2)根据函数图象,直接写出不等式kax b x+<的解集;(3)若这个一次函数的图象与y 轴交于点C ,点D 是点C 关于x 轴的对称点,连接AD ,BD ,求△ABD 的面积.2.如图,一次函数1y kx b =+与反比例函数2my x=的图像交于()1,A n -、()3,2B -两点.(1)求一次函数与反比例函数的解析式.(2)根据图像,请直接写出一次函数值1y 大于反比例函数值2y 时x 的取值范围.3.如图,直线(0)y kx b k =+≠与双曲线my x=(m ≠0)相交于A (1,2),B (-2,-1)两点,(1)若111222333(,),(,),(,)A x y A x y A x y 为双曲线上的三点,且1230x x x <<<,则123,,y y y 的大小关系为 ; (2)观察图象,请直接写mkx b x+>时,x 的取值范围为 ; (3)分别连接OA 、OB ,求△OAB 的面积.4.如图,在平面直角坐标系中,P 是坐标原点,反比例函数1ky x=的图象与正比例函数22y x =的图象交于A ,B 两点,点C 在x 轴正半轴上,AC AO =,ACO △的面积为8.(1)求k 的值和B 点的坐标;(2)根据图象直接写出12y y >时x 的取值范围.5.如图,在平面直角坐标系中,直线11y k x b =+与双曲线2y =2k x相交于A (-2,3),B (m ,-2)两点,(1)求1y ,2y 对应的函数表达式;(2)根据函数图像,直接写出关于x 的不等式1+k x b <2k x的解集; (3)过点B 作BP //x 轴交y 轴于点P ,在x 轴上是否存在点Q ,使得△ ABQ 的面积等于△ABP 的面积的一半,若存在求出Q 点的坐标.6.如图,一次函数y =kx +b 与反比例函数6(0)y x x=>的图像交于A (m ,6),B (n ,3)两点.(1)求一次函数的解析式; (2)根据图像直接写出60kx b x+-<时x 的取值范围; (3)若M 是x 轴上一点,且△MOB 和△AOB 的面积相等,求点M 坐标. 7.如图,直线12y x =-+与x 轴交于点B ,与y 轴交于点A ,与反比例函数()20ky k x=<的图象交于点()2,C m -,D ,连接OD ,OC .(1)求反比例函数的解析式; (2)求COD △的面积;(3)直接写出当x 取什么值时,12y y >. 8.如图,一次函数y =kx +b (k ≠0)与反比例函数y =mx(m ≠0)的图象在第一象限内交于A (1,6),B (3,n )两点.请解答下列问题:(1)求这两个函数的表达式;(2)根据图象直接写出kx +b ﹣mx>0的x 的取值范围. 9.如图,直线y x m =+与双曲线ky x=相交于()21A ,、B 两点.(1)求m 及k 的值;(2)不解关于x 、y 的方程组,,y x m k y x =+⎧⎪⎨=⎪⎩直接写出点B 的坐标;(3)直接写出0kx m x--> 的取值范围. 10.如图,已知一次函数1y kx b =+的图象与x 轴相交于点A ,与反比例函数2c y x =的图象相交于()1,5B -、5,2C d ⎛⎫ ⎪⎝⎭两点.(1)求k 、b 的值,并直接写出当12y y ≤时x 的取值范围;(2)点(),P m n 是线段AB 上的一个动点,过点P 作x 轴的平行线与函数2cy x=的图象相交于点D .求PAD 的面积S 关于n 的函数解析式11.已知:正比例函数y x =的图像与反比例函数ky x=的图像有一个交点的纵坐标是2,(1)当3x =-时,求反比例函数ky x=的值; (2)当32x -<<时,反比例函数ky x=的取值范围是______; (3)当正比例函数值大于反比例函数值时,x 的取值范围是______.12.如图,已知反比例函数ky x=的图象与一次函数y x b =-+的图象交于点()1,4A ,点()4,B n .(1)求n 和b 的值; (2)观察图像,不等式kx b x>-+的解集为________.答案与解析1.如图,直线1y k x b =+与双曲线2k y x=交于A 、B 两点,其横坐标分别为1和5,则不等式21k k x b x+<的解集是( ).2.如图,直线y kx =与双曲线y x =在同一坐标系中如图所示,则不等式kx x<的解集为( )A .01x <<B .1x <-3.如图,一次函数111y k x b =+的图象与反比例函数22y x=的图象相交于点()5,A m ,()1,B n -两点,当12y y >时,则自变量x 的取值范围是______.【答案】10x -<<或5x >【详解】由图像知,当10x -<<或5x >时,一次函数在反比例函数上方,即12y y >,【知不足】1.如图,小明同学利用计算机软件绘制函数22x y x =+,122y x =-+,根据学习函数的经验,可以知道21222x x x ≥-++的解集是( )A .4x ≤-或2x ≥B .42x -≤<-或22x -<≤2.已知一次函数1(0)y kx b k =+<与反比例函数()20y m x=≠的图象交于点A (-1,yA )和点B (3,yB )两点,当y 1>y 2时,实数x 的取值范围是( ) A .x <-1或0<x <3 B .-1<x <0或0<x <3 C .-1<x <0或x >3 D .0<x <3【答案】A 【详解】解:依照题意画出函数图象,如图所示.观察函数图象,可知:当x <﹣1或0<x <3时,一次函数图象在反比例函数图象上方,∴当y 1>y 2,实数x 的取值范围为x <﹣1或0<x <3.4. 如图,一次函数11(0)y k x b k =+≠与反比例函数22(0)k y k x=≠的图象交于点()2,3A ,(),1B a -,则不等式xk b x k 21≥+ 的解集是___________.2kb x,只需要一次函数的图象在反比例函),(6,B --4.如图,一次函数1y k x b =+的图象与反比例函数2ky x=的图象相交于点()3,1A 、()1,B n -两点.(1)分别求出一次函数和反比例函数的解析式; (2)根据图象,请你直接写出满足条件:21k k x b +≥的x 的取值范围.10x -≤<或3x ≥.【一览众山小】1.如图,直线y kx =与双曲线3y x =-在同一坐标系中如图所示,则不等式3kx x>-的解集为( )A .01x <<B .1x <-x 把3y =代入3y x=-得=1x -,∴()1,3A -,再把()1,3-代入直线y kx =得,3k =-,解得3k =-,∴3y x =-,联立方程组33y xy x =-⎧⎪⎨=-⎪⎩,解得13x y =-⎧⎨=⎩或13x y =⎧⎨=-⎩, 32.如图,正比例函数11y k x =的图像与反比例函数22y x=的图像相交于A 、B 两点,点A 的横坐标为2,当120y y <<时,x 取值范围是( )A .02x <<或2x >B .02x <<C .2x <-D .20x -<<【答案】C 【详解】解:正比例函数与反比例函数的图象均关于原点对称,点A 的横坐标为2,∴点B 的横坐标为2-,由函数图象可知,当<2x -时,反比例函数图象在正比例函数的图象的上方,且位于y 轴负半轴,∴当120y y <<时,x 取值范围是<2x -,3.如图,一次函数3y x =-+的图象与反比例函数()0ky k x=≠在第一象限内的图象交于()1,A a 和B 两点,与x 轴交于点C .(1)求反比例函数的解析式; (2)求出另一个交点B 的坐标;(3)根据图象直接写出当0x >时,不等式3kx-+<的解集. 4.如图,直线3y kx =+与x 轴、y 轴分别交于点B 、C ,与反比例函数y x=交于点A 、D ,过D 作DE x ⊥轴于E ,连接OA ,OD ,若()2,A n -,:1:2OAB ODE S S =△△.(1)求点B 的坐标,并求出反比例函数的表达式; (2)求点D 的坐标;(3)直接写出关于x 不等式:3mkx >-的解集为______.1=2AOB S =3DOE S ,∵反比例函数图像位于二、四象限,∴,∴反比例函数的表达5.如图,一次函数()0y ax b a =+≠的图像与反比例函数()0y k x=≠的图像交于()2,M m ,()1,4N --两点.(1)求反比例函数的解析式及m 的值;(2)观察图像,直接写出不等式kax b <+的解集..点x【温故为师】1.已知一次函数(0)y ax b a =+≠的图象与反比例函数(0)ky k x=≠的图象相交于点(3,2)A -,(2,)B n .(1)求一次函数和反比例函数的表达式,并在图中画出这个一次函数的图象;(2)根据函数图象,直接写出不等式kax b x+<的解集; (3)若这个一次函数的图象与y 轴交于点C ,点D 是点C 关于x 轴的对称点,连接AD ,BD ,x∴反比例函数的表达式为6y x=-,612ABD ACD BCD S S S CD =+=2.如图,一次函数1y kx b =+与反比例函数2y x=的图像交于()1,A n -、()3,2B -两点.(1)求一次函数与反比例函数的解析式.y 大于反比例函数值y 时x 的取值范围.3.如图,直线(0)y kx b k =+≠与双曲线y x=(m ≠0)相交于A (1,2),B (-2,-1)两点,(1)若111222333(,),(,),(,)A x y A x y A x y 为双曲线上的三点,且1230x x x <<<,则123,,y y y 的大小关系为 ;(2)观察图象,请直接写mkx b x+>时,x 的取值范围为 ;减小,10x x <<于反比例函数的图象上方,kx b +得:与x 轴的交点为点C ,当0y =时,10x +=,解得=1x -,即(1,0),1C OC -=,1131211222OABOACOBCSSS=+=⨯⨯+⨯⨯= 4.如图,在平面直角坐标系中,P 是坐标原点,反比例函数1ky x=的图象与正比例函数22y x =的图象交于A ,B 两点,点C 在x 轴正半轴上,AC AO =,ACO △的面积为8.(1)求k 的值和B 点的坐标;y y >时x 的取值范围.【答案】(1)8,(2,4)k B =--(2)<2x -或02x <<(1)如图,过点A 作AD OC ⊥于点D ,AC AO =,CD DO ∴=,11184222AODACDAOCSSS k ∴===⨯==,又该反比例函数图象在第一、三象限,即0k >, 8=,由题意得,方程组2y x=⎧⎪⎨,又点5.如图,在平面直角坐标系中,直线11y k x b =+与双曲线2y =2x相交于A (-2,3),B (m ,-2)两点,(1)求1y ,2y 对应的函数表达式;(2)根据函数图像,直接写出关于x 的不等式1+k x b <2k x的解集; (3)过点B 作BP //x 轴交y 轴于点P ,在x 轴上是否存在点Q ,使得△ ABQ 的面积等于△ABP222226.如图,一次函数y=kx+b与反比例函数6(0)y xx=>的图像交于A(m,6),B(n,3)两点.(1)求一次函数的解析式;(2)根据图像直接写出6kx bx+-<时x的取值范围;当y =0时,0=-3x +9,解得:x =3,∴P (3,0)∵点A 到x轴的距离为6,点B 到x 轴的距离为3,∴AOB AOP BOP S S S ∆∆∆=-=1193633222⨯⨯-⨯⨯=,197.如图,直线12y x =-+与x 轴交于点B ,与y 轴交于点A ,与反比例函数()20y k x=<的图象交于点()2,C m -,D ,连接OD ,OC .(1)求反比例函数的解析式; (2)求COD △的面积;x 取什么值时,y y >.(2)解:过D 作DN OB ⊥于N ,过C 作CM OB ⊥于M ,设(),D a b ,∴2b a =-+,8-=b a ,∴82--+=a a,∴2280a a --=,∴12a =-,24a =,∴14b =,22b =-,∴()2,4C -,()4,2D -,4CM =2y x =-+()0,2A ()2,0B 2OB =CODCOBBODSSS=+,8.如图,一次函数y =kx +b (k ≠0)与反比例函数y =mx(m ≠0)的图象在第一象限内交于A (1,6),B (3,n )两点.请解答下列问题:(1)求这两个函数的表达式; (2)根据图象直接写出kx +b ﹣m>0的x 的取值范围.9.如图,直线y x m =+与双曲线y x=相交于()21A ,、B 两点.(1)求m 及k 的值;(2)不解关于x 、y 的方程组,,y x m k y x =+⎧⎪⎨=⎪⎩直接写出点B 的坐标;(3)直接写出0kx m x--> 的取值范围.【答案】(1)12m k =-=,(2)()12B --,(3)02x <<或1x <-【详解】(1)将点A (2,1)的坐10.如图,已知一次函数1y kx b =+的图象与x轴相交于点A ,与反比例函数2y x=的图象相交于()1,5B -、5,2C d ⎛⎫⎪⎝⎭两点.(1)求k 、b 的值,并直接写出当12y y ≤时x 的取值范围;(2)点(),P m n 是线段AB 上的一个动点,过点P 作x 轴的平行线与函数2cy x=的图象相交于PADS=)解:点5c ∴=-,5,2C d ⎛⎫ ⎪⎝⎭两个点的坐标代入1y ,(,)P m n 在线段,PD x ∥轴及点在反比例函数图象上,5,n n ⎫-⎪⎭,532n n -∴=+21344PAD S n n =++PAD ∴的面积析式为PAD S =-11.已知:正比例函数y x =的图像与反比例函数y x=的图像有一个交点的纵坐标是2,(1)当3x =-时,求反比例函数ky x =的值; (2)当32x -<<时,反比例函数ky x=的取值范围是______;x ,点,A 点在反比例函数3-时,y 的增大而减小,当3=-时,的增大而减小,当解:A 、B 两点关于原点对称性,,当正比例函数值大于反比例函数值时,正比例函数的图像位于反的取值范围是12.如图,已知反比例函数y x=的图象与一次函数y x b =-+的图象交于点()1,4A ,点()4,B n .(1)求n 和b 的值; (2)观察图像,不等式kx b >-+的解集为________.。
一次函数和反比例函数及解答
2015年初中一次函数和反比例函数的练习题及解答一.填空题(共5小题)1.(2014秋•嘉祥县校级期末)如果函数y=(k﹣3)+kx+1是二次函数,那么k的值一定是.2.(2013秋•东海县校级月考)函数的图象是抛物线,则m=.3.(2014•武汉模拟)直线y=mx+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示,那么不等式mx+n<ax2+bx+c<0的解集是.4.(2011•河池)如图是二次函数y1=ax2+bx+c(a≠0)和一次函数y2=mx+n(m≠0)的图象,当y2>y1,x的取值范围是.5.(2011•沙县校级质检)如图,⊙O的半径为2.C1是函数y=x2的图象,C2是函数y=﹣x2的图象,则阴影部分的面积是.二.解答题(共8小题)6.(2014•仙桃)反比例函数y=在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数y=的图象于点M,△AOM的面积为3.(1)求反比例函数的解析式;(2)设点B的坐标为(t,0),其中t>1.若以AB为一边的正方形有一个顶点在反比例函数y=的图象上,求t的值.7.(2014•自贡)如图,一次函数y=kx+b与反比例函数的图象交于A(m,6),B(3,n)两点.(1)求一次函数的解析式;(2)根据图象直接写出的x的取值范围;(3)求△AOB的面积.8.(2014•南充)如图,一次函数y1=kx+b的图象与反比例函数y2=的图象相交于点A(2,5)和点B,与y轴相交于点C(0,7).(1)求这两个函数的解析式;(2)当x取何值时,y1<y2.9.(2014•天水模拟)如图,已知A (﹣4,n),B (2,﹣4)是一次函数y=kx+b的图象和反比例函数的图象的两个交点;(1)求反比例函数和一次函数的解析式;(2)求直线AB与x轴的交点C的坐标及△AOB的面积;(3)求不等式的解集(请直接写出答案).10.(2014•淮北模拟)如图,已知A(﹣4,2)、B(n,﹣4)是一次函数y=kx+b的图象与反比例函数的图象的两个交点.(1)求此反比例函数和一次函数的解析式;(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围.11.(2014•永川区校级模拟)如图,已知反比例函数y=的图象经过点A(1,﹣3),一次函数y=kx+b的图象经过点A与点C(0,﹣4),且与反比例函数的图象相交于另一点B(3,n).(1)试确定这两个函数的解析式;(2)求△AOB的面积;(3)根据图形直接写出反比例函数值大于一次函数值时自变量的取值范围.12.(2014•市中区一模)如图,反比例函数(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=.(1)求k的值;(2)将线段AB沿x轴正方向平移到线段DC的位置,反比例函数(x>0)的图象恰好经过DC的中点E,求直线AE的函数表达式;(3)若直线AE与x轴交于点M、与y轴交于点N,请你探索线段AN与线段ME的大小关系,写出你的结论并说明理由.13.(2014•黄冈模拟)如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(8,4).过点D(0,6)和E(12,0)的直线分别与AB,BC交于点M,N.(1)求直线DE的解析式和点M的坐标;(2)若反比例函数(x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上;(3)若反比例函数(x>0)的图象与△MNB有公共点,请直接写出m的取值范围.2015年04月07日467044198的初中数学组卷参考答案与试题解析一.填空题(共5小题)1.(2014秋•嘉祥县校级期末)如果函数y=(k﹣3)+kx+1是二次函数,那么k的值一定是0.2.(2013秋•东海县校级月考)函数的图象是抛物线,则m=﹣1.3.(2014•武汉模拟)直线y=mx+n和抛物线y=ax2+bx+c在同一坐标系中的位置如图所示,那么不等式mx+n<ax2+bx+c<0的解集是1<x<2.;根据4.(2011•河池)如图是二次函数y1=ax2+bx+c(a≠0)和一次函数y2=mx+n(m≠0)的图象,当y2>y1,x的取值范围是﹣2<x<1.5.(2011•沙县校级质检)如图,⊙O的半径为2.C1是函数y=x2的图象,C2是函数y=﹣x2的图象,则阴影部分的面积是2π.π×2二.解答题(共8小题)6.(2014•仙桃)反比例函数y=在第一象限的图象如图所示,过点A(1,0)作x轴的垂线,交反比例函数y=的图象于点M,△AOM的面积为3.(1)求反比例函数的解析式;(2)设点B的坐标为(t,0),其中t>1.若以AB为一边的正方形有一个顶点在反比例函数y=的图象上,求t的值.|k|=3;的图象上,根据正方形的性质得∴|k|=3;得的图象上时,7.(2014•自贡)如图,一次函数y=kx+b与反比例函数的图象交于A(m,6),B(3,n)两点.(1)求一次函数的解析式;(2)根据图象直接写出的x的取值范围;(3)求△AOB的面积.)代入时,××8.(2014•南充)如图,一次函数y1=kx+b的图象与反比例函数y2=的图象相交于点A(2,5)和点B,与y轴相交于点C(0,7).(1)求这两个函数的解析式;(2)当x取何值时,y1<y2.,.,,9.(2014•天水模拟)如图,已知A (﹣4,n),B (2,﹣4)是一次函数y=kx+b的图象和反比例函数的图象的两个交点;(1)求反比例函数和一次函数的解析式;(2)求直线AB与x轴的交点C的坐标及△AOB的面积;(3)求不等式的解集(请直接写出答案).,运用y=.∴×2+10.(2014•淮北模拟)如图,已知A(﹣4,2)、B(n,﹣4)是一次函数y=kx+b的图象与反比例函数的图象的两个交点.(1)求此反比例函数和一次函数的解析式;(2)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围.求出﹣求出得;得﹣,11.(2014•永川区校级模拟)如图,已知反比例函数y=的图象经过点A(1,﹣3),一次函数y=kx+b的图象经过点A与点C(0,﹣4),且与反比例函数的图象相交于另一点B(3,n).(1)试确定这两个函数的解析式;(2)求△AOB的面积;(3)根据图形直接写出反比例函数值大于一次函数值时自变量的取值范围.)∵∴即(又∵∴12.(2014•市中区一模)如图,反比例函数(x>0)的图象经过线段OA的端点A,O为原点,作AB⊥x轴于点B,点B的坐标为(2,0),tan∠AOB=.(1)求k的值;(2)将线段AB沿x轴正方向平移到线段DC的位置,反比例函数(x>0)的图象恰好经过DC的中点E,求直线AE的函数表达式;(3)若直线AE与x轴交于点M、与y轴交于点N,请你探索线段AN与线段ME的大小关系,写出你的结论并说明理由.,∴=的纵坐标为在双曲线),解得,∴,AN=…EC=13.(2014•黄冈模拟)如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(8,4).过点D(0,6)和E(12,0)的直线分别与AB,BC交于点M,N.(1)求直线DE的解析式和点M的坐标;(2)若反比例函数(x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上;(3)若反比例函数(x>0)的图象与△MNB有公共点,请直接写出m的取值范围.∴,x+6x+6)∵;x+6((。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
k 2 1 6、在下图中,反比例函数 y 的图象大致是( x
)
2、平面直角坐标系中有六个点:A(1,5) ,B(-3,
5 5 )C(-5,-1) ,D(-2, )E(3, 3 2
A. B.
C.
D.
5 5 ) ,F( ,2) .其中有五个点在同一反比例函数图象上,不在这个反比例函数图象上的点是 3 2
( ) A.点 C B.点 D C.点 E D.点 F
7、如图,把直线 y= -2x 向上平移后得到直线 AB,直线 AB 经过 点(m,n)且 2m n 6 ,则直线 AB 的解析式是( ) A . y 2 x 3 D. y 2 x 6 8、 已知某函数图象关于直线 x=1 对称, 其中一部分图象如图所示, 点 A( x1 , y1 ) 和点 B( x2 , y2 ) 在函数图象上,且 1 x1 x2 0 ,则 y1与y2 的大小关系为( ) B . y 2 x 6 C . y 2 x 3
BA,则△AOB 的面积为 。 2、近视眼镜的度数 y 与镜片焦距 x 成反比,已知 400 度近视眼镜镜片 的焦距为 0.25 米,则眼镜度数 y 与镜片焦距 x 之间函数关系式为 。 3、随着海拔的升高,大气压强下降,空气中的含氧量也随之下降,即含氧量 y 与大气压强 x 成
河北省考试说明 拓展五 一次函数、反比例函数与问题解决 第 1 页
正比例函数关系 ,当 x=36(kPa)时,y=108 (g/m3),y 与 x 的函数关系为 4、如图,正比例函数与反比例函数的图象相交于 A、B 两点,点 A (2,1) ,分别以 A、B 为圆心的圆与 x 轴相切,则图中两个阴影部分 面积的和为 。 5、如图,已知函数 y=3x+b 和 y=ax-3 的图象相交于点 P(-2,-5) ,则 根据图象可得不等式 3x+b>ax-3 的解集是 。 6、已知点 P(x,y)位于第二象限,并且 y≤x+4,y 为整数, 写出一个符合上述条件的点 P 的坐标 。 7、如图 A、B 是双曲线 y
正整数 ) 依次为 x 轴正半轴上的点,已知 x1=a ( 0<a<1 ) , △ A1B1A2, △ A2B2A3, △ A3B3A4, … △AnBnAn+1 分别是以 B1,B2,B3 …Bn 为顶点的等腰三角形。 ( 1)写出 B2,Bn 的坐标 (2)求 x2,x3(用含 a 的代数式表示) ,分析图中各等腰三角形底边长度之间的关系, 写出你认为成立的两个结论 (3)当 a(0<a<1)变化时,在上述所有的等腰三角形中,是否存在直角三角形?若 存在,求出相应的 a 值;若不存在,请说明理由。
k 的一个分 x
支上两点, 且点 B (a, b) 在点 A 的右侧, 则 b 的取值范围是 。
8、如图,矩形 ABCD 的边 AB 在 x 轴上,AB 的中点与原点重合 AB=2, AD=1,过定点 Q(0,2)和动点 P(a,0)的直线与矩形 ABCD 的边有公 共点,则 a 的取值范围是 。 三、解答: 1、如图在直角坐标系中,△ABC 的 A、B、C 三点坐标为 A(7,1) ,B(8,2) ,C(9,0) (1)请在图中画出△ABC 的一个以点 P(12,0)为位似中心,相似比为 3 的位似图形(要求与 △ABC 同在点 P 的一侧) (2)求线段 BC 对应线段 B C 所在直线解析式。
6、某地区一种商品的需求量 y1(单位:万件) 、供应量 y2(单位:万件)与价格 x(单位:元/ 件) 分别近似满足下列函数关系式: y1=-x+60, y2=2x-36, 需求量为 0 时, 即停止供应, 当 y1=y2 时,该商品的价格称为稳定价格,需求量称为稳定需求量。 (1)求该商品的稳定价格与稳定需求量; (2)价格在什么范围,该商品的需求量低于供应量? (3)当需求量高于供应量时,政府常通过对供应方提供价格补贴来提高 供货价格,以提高供应量,现若要使稳定需求量增加 4 万件,政府应对每 件商品提供多少元补贴,才能使供应量等于需求量?
2 x
6 (x>0)的图象于点 C, x
河北省考试说明
拓展五 一次函数、反比例函数与问题解决 第 2 页
4、我国铁路第六次大提速,在甲、乙两城市之间开通了动车组高速列车,已知每隔 1h 有一列速 度相同的动车组列车从甲城开往乙城。如图所示,OA 是第一列动车组列车离开甲城的路程 s(单 位在:km)与运行时间 t(单位:h)的函数图象,BC 是一列从乙城开往甲城的普通快车距甲城的路 程 s(单位:km)与运行时间 t(单位:h)的函数图象。请根据图中信息,解答下列问题: (1)点 B 的横坐标 0.5 的意义是普通快车发车时间比第一列动车组列车发车时间_____h,点 B 的纵坐标 300 的意义是_____; (2)请你在原图中直接画出第二列动车组列车离开甲城的路程 s(单位:km)与时间 t(单位:h)的 函数图象; (3)若普通快车的速度为 100km/h, ①求 BC 的解析式,并写出自变量 t 的取值范围; ②求第二列动车组列车出发后多长时间与普通列车相遇; ③直接写出这列普通列车在行驶途中与迎面而来的相邻两列动车组 列车相遇的间隔时间。
A、 B、 C、 D、 10、有一本书,每 20 页厚 1mm,设从第 1 页到第 x 页的厚度为 ymm,则( A. y
)
1 x 20
B. y 20 x
C. y
1 x 20
D. y
20 x
二、填空: 1、如图,点 A 为反比例函数 y
1 图象一点,点 B 在 x 轴上,且 OA= x
河北题解决 第 3 页
7、如图,点 B1(1,y1) ,B2(2,y2)B3(3,y3)…Bn(n,yn)(n 是正整数)依次为一
次函数 y=
1 1 x+ 的图像上的点,点 A1(x1,0), A2(x2,0), A3(x3,0), …An(xn,0) (n 是 4 12
a 1(a b) 3、定义新运算: a b = a ,则函数 y 3 x 的图象大致是( (a b且b 0) b
)
A. y1 y2 B. y1 y2C. y1 y2 D。无法确定
9、如图是王老师早晨出门散步时离家的距离(y)时间(x) 之间的函数图象,若用黑点表示王老师家的位置,则王老 师散步行走的路线可能是( )
4、一名考生步行前往考场,10 分钟走了总路程的
1 ,估计不能 4
准时到达,于是他改乘出租车赶往,他的行程与时间关系如图所 示(假定总路程为 1) ,则他到达考场所花时间比一直步行提前了 ( ) A.20 分钟 B.22 分钟 C.24 分钟 D.26 分钟 5、在平面直角坐标系 xOy 中,点 P 在由直线 y x 3 ,直线 y 4 和直线 x 1 所围成的区域 内或其边界上,点 Q 在 x 轴上,若点 R 的坐标为 R (2, 2) ,则 QP+QR 的最小值为( A. 17 B. 5 2 C. 3 5 D.4 )
Y B4 B3 B2 B1 Bn
O
A1
1 A2
2
A3 3 A4
4
x A5 An n An+1
河北省考试说明
拓展五 一次函数、反比例函数与问题解决 第 4 页
。 2、如图,已知直线 y
3 x 1 与 x 轴、y 轴分别交于点 A、B,以线段 AB 为直角边在第一象 3
限内作等腰 Rt△ABC,∠BAC=90°,且点 P(1,a)为坐标系中的一个动点, (1)求三角形 ABC 的面积。 (2)要使得△ABC 和△ABP 的面积相等,求实数 a 的值。
5、工业园区某消毒液工厂,今年 4 月份以前,每天的产量与销售量均为 500 箱,进入 4 月份后, 每天的产量保持不变,市场需求量不断增加,如图 1 是四月前后一段时期库存量 y(箱)与生产 时间 t(月份)之间的函数图像。 (1)四月份的平均日销售量为多少箱? (2)该厂什么时候开始出现供不应求的现象,此时日销售量为多少箱? (3)为满足市场需求,该厂打算在投资不超过 135 万元的情况下,购买 5 台新设备,使扩大生 产规模后的日产量不低于四月份的平均日销售量,现有 A、B 两种型 号的设备可供选择,其价格与两种设备的日产量如下表: 请问:有哪几种购买设备的方案?若为了使日产量最大,应选择哪种 方案?
' '
3、如图,在平面直角坐标系中,A 为 y 轴正半轴上一点, 过 A 作 x 轴的平行线,交函数 y (x<0)的图象于点 B,交函数 y 过 C 作 y 轴的平行线交 BO 的延长线于点 D, (1)如果点 A 的坐标为(0,2) ,求线段 AB 与线段 CA 的 长度之比; (2)如果点 A 的坐标为(0,a)求线段 AB 与 CA 的长度之 比; (3)对于动点 A,求四边形 AODC 的面积。
