20秋启东九年级数学上徐州(JS)作业11
合集下载
20秋 启东九年级数学上(R)作业11
第2题
‹#›
返回目录
3.在一个边长为 2 的正方形中挖去一个边长为
x(0<x<2)的小正方形,如果设剩余部分的面积为 y,
那么 y 关于 x 的函数解析式是( B )
A.y=x2
B.y=4-x2
C.y=x2-4
D.y=4-2x
第3题
‹#›
返回目录
4.某公司的年生产利润原来是 a 万元,经过连
续两年的增长达到了 y 万元,如果每年增长的百分
题号 PPT页码 题号 PPT页码
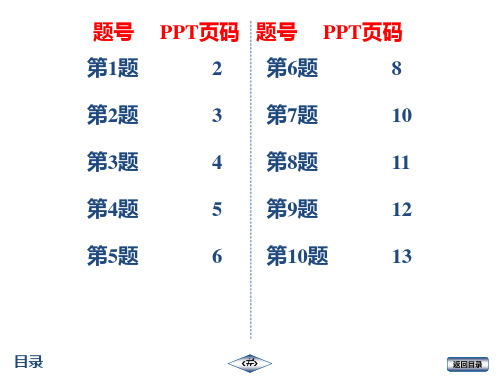
第1题
2 第6题
8
第2题
3 第7题
10
第3题
4 第8题
11
第4题
5 第9题
12
第5题
6 第10题
13
目录
‹#›
返回目录
1.n 个球队进行单循环比赛(参加比赛的任何一
个球队都与其他所有的球队各赛一场),总的比赛场
数为 y,则有( D ) A.y=2n
B.y=n2
C.y=n(n-1)
第7题
‹#›
返回目录
8.二次函数 y=3x2-x-4 的二次项系数与常数
项的和是( B )
A.1
B.-1
C.7
D.-6
第8题
‹#›
返回目录
9.若关于 x 的函数 y=(2-a)x2-x 是二次函数,
则 a 的取值范围是( B )
A.a≠0
B.a≠2
C.a<2
D.a>2
第9题
‹#›
返回目录
10.有一人患了流感,经过两轮传染后共有m 人患了流感,假设每轮传染恰好每一个人传染n个 人,则m与n之间的函数关系式为_m__=__n_2+__2_n__+__1_.
20秋 启东作业九年级数学上(BS)作业11
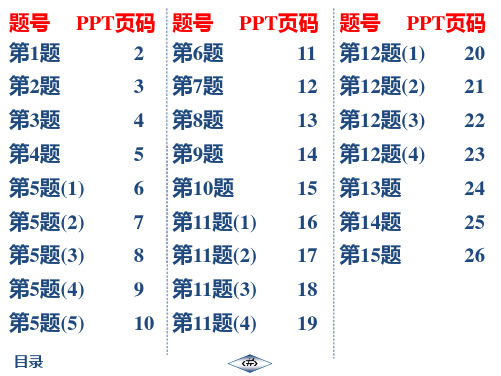
第12题(1)
‹#›
返回目录
12.用配方法解下列方程: (2)x2-12x=4; 解:∵x2-12x=4, ∴x2-12x+36=4+36,即(x-6)2=40, 开方,得 x-6=±2 10, ∴x1=6+2 10,x2=6-2 10.
第12题(2)
‹#›
返回目录
12.用配方法解下列方程: (3)x2+x+1=7x+3; 解:x2+x+1=7x+3, 移项,得 x2-6x=2, 配方,得(x-3)2=11, 开方,得 x-3=± 11, ∴x1=3+ 11,x2=3- 11.
第11题(1)
‹#›
返回目录
11.用直接开平方法解下列方程: (2)(x-1)(x+1)=1; 解:x2-1=1,x2=2,∴x1= 2,x2=- 2.
第11题(2)
‹#›
返回目录
11.用直接开平方法解下列方程:
(3)(2x-1)2=( 2-1)2;
解:2x-1=±(
2-1),∴x1= 22,x2=2-2
第14题
‹#›
返回目录
15.已知 x2+y2-4x+6y+13=0,求 x2-6xy +9y2 的值.
解:x2+y2-4x+6y+13=0, x2-4x+4+y2+6y+9=0, (x-2)2+(y+3)2=0, 解得 x=2,y=-3, ∴ x2 - 6xy + 9y2 = (x - 3y)2 = [2 - 3×( - 3)]2 = 121.
第9题
‹#›
返回目录
10.(2018·顺义区模拟)把方程 x2-3=2x 用配方 法化为(x+m)2=n 的形式,则 m=___-__1_____,n= ___4___.
第10题
‹#›
返回目录
20秋启东九年级数学上徐州(JS)作业9

解:因为 1200×10=12000<20000,所以人数超过 10 人.
设该公司参加旅游的人数为 x,依题意,得 x[1200-20(x-10)]=20000, 解得 x1=20,x2=50. 当 x=20 时,1200-20(20-10)=1200-200=1000 >800; 当 x=50 时,1200-20(50-10)=1200-800=400 <800,不合题意,舍去.
答:该公司参加旅游的人数为 20.
第3题
‹#›
返回目录
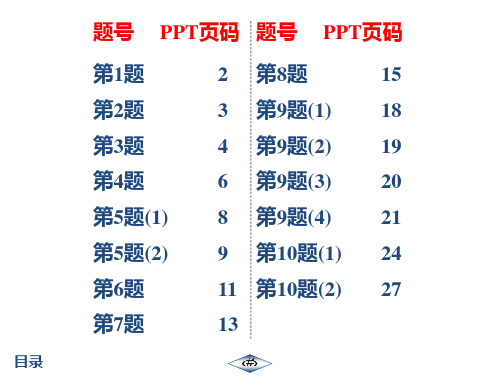
第1题
‹#›
返回目录
解:设每箱降价 x 元,则每天可售出(200+40x) 箱,
依题意,得(12-x)(200+40x)=2800, 整理,得 x2-7x+10=0, 解得 x1=2,x2=5. ∵尽可能多地减少库存,增加利润,∴x=5. 答:每箱应降价 5 元.
第1题
‹#›
返回目录
2.某水果店销售某种水果的成本价是 5 元/千 克,在销售中发现,当这种水果的价格定为 7 元/千 克时,每天可以卖出 160 千克,在此基础上,这种 水果的单价每提高 1 元,该水果店每天就会少卖出 20 千克,设这种水果的单价为 x 元(x>7).
(2)若该水果店一天销售这种水果所获得的利润 是 420 元,为了让利于顾客,单价应定为多少元?
第2题(2)
‹#›
返回目录
解:由题意知(x-5)[160-20(x-7)]=420, 整理得 x2-20x+96=0. 解得 x1=8,x2=12. 因为让利于顾客,所以 x=8 符合题意. 答:单价应定为 8 元.
(1)请用含 x 的代数式表示:每千克水果的利润 为_x_-__5__元,每天的销售量是_1_6_0_-__2_0_(_x_-__7_)_千克;
20秋启东九年级数学上徐州(JS)作业10

第3题
图放大
‹#›
返回目录
第3题
图还原
‹#›
返回目录
解:设经过 t s,△PBQ 的面积等于 10 cm2,则 PB=(6-t)cm,BQ=4t cm.
根据题意,得12×4t(6-t)=10, 整理,得 t2-6t+5=0,解得 t1=1,t2=5. ∵BQ=4t≤8,∴t=1.
答:经过 1 秒钟,△PBQ 的面积等于 10 cm2.
第3题
‹#›
返回目录
题号 PPT页码
第1题
2
第2题
4
第3题
7
目录
‹#›
1.一个直角三角形的面积为 24 cm2,两直角边 长的和为 14 cm,求该直角三角形的两直角边的长.直角边长为 x cm,则另
一直角边长为(14-x) cm.根据题意,得
12x(14-x)=24,整理,得 x2-14x+48=0, 解得 x1=6,x2=8. 当 x=6 cm 时,另一直角边长为 8 cm;
答:25 s 后,P,Q 间的距离为 4 2 cm.
第2题
‹#›
返回目录
3.如图,在△ABC 中,∠B=90°,BC=8 cm, AB=6 cm.点 P 从点 A 开始沿 AB 边向点 B 以 1 cm s 的速度移动,点 Q 从点 B 开始沿 BC 边向点 C 以 4 cm
s 的速度移动.如果点 P,Q 分别从点 A,B 同时出 发,经过几秒钟,△PBQ 的面积等于 10 cm2?
当 x=8 cm 时,另一直角边长为 6 cm. 答:这个直角三角形的两直角边长分别为 6 cm,
8 cm.
第1题
‹#›
返回目录
2.如图,在 Rt△ABC 中,∠B=90°,AB=6 cm,BC=3 cm,点 P 从点 A 开始沿 AB 向点 B 以 1 cm/s 的速度移动,点 Q 从点 B 开始沿 BC 向点 C 以 2 cm/s 的速度移动.如果点 P,Q 分别从 A,B 同时 出发,几秒钟后,P,Q 间的距离为 4 2 cm?
20秋 启东作业九年级数学上(BS)作业15

第9题(1)
‹#›
返回目录
9.用因式分解法解下列方程: (2)(2018·梧州)2x2-4x-30=0; 解:x2-2x-15=0, (x-5)(x+3)=0, ∴x1=5,x2=-3.
第9题(2)
‹#›
返回目录
9.用因式分解法解下列方程: (3)x(x-1)=4x+6; 解:x2-x=4x+6, x2-5x-6=0, (x-6)(x+1)=0, ∴x1=6,x2=-1.
根据题意得,x(10-x)=24, 解得 x1=4,x2=6, 当 x=4 时,10-x=6, 当 x=6 时,10-x=4<6,不合题意,舍去. 答:边 AB 的长为 4 米.
第10题
‹#›
返回目录
11.阅读材料:解方程(x2-1)2-5(x2-1)+4=0 的过程如下:
设 x2-1=y,则原方程可化为 y2-5y+4=0①, 解得 y1=1,y2=4.
解:设 x=a+b,则原方程可化为 x2-7x+10 =0,
解得 x1=2,x2=5, 即 a+b=2 或 a+b=5,由斜边 c=4,舍去 a +b=2,
第11题(2)
‹#›
返回目录
∴Rt△ABC 的周长为 4+5=9. 由勾股定理得 a2+b2=42, 则(a+b)2-2ab=16, 解得 ab=92, 因此,Rt△ABC 的面积为12ab=94.
A.(x+5)(x-6) B.(x-5)(x+6) C.(x+5)(x+6) D.(x-5)(x-6)
第2题
‹#›
返回目录
3.(2019·峄城区期末)方程 2(x-3)=3x(x-3)的 根是_x_1=__3_,__x_2_=__23_.
第3题
‹#›
返回目录
20秋 启东作业九年级数学上(BS)作业14

第11题
‹#›
返回目录
12ቤተ መጻሕፍቲ ባይዱ(2019·海淀区期末)已知方程 x2+2x+k-4 =0 有实数根.
(1)求 k 的取值范围; 解:Δ=22-4(k-4)≥0, 解得 k≤5.
第12题(1)
‹#›
返回目录
12.(2019·海淀区期末)已知方程 x2+2x+k-4 =0 有实数根.
(2)若 k 是该方程的一个根,求 2k2+6k-5 的值. 解:把 x=k 代入方程得 k2+2k+k-4=0,即 k2+3k=4, 所以 2k2+6k-5=2(k2+3k)-5=2×4-5=3.
(1)经多少秒时足球的高度为 20 米? 解:足球高度为 20 米,即 h=20, 将 h=20 代入公式得 20t-5t2=20, 解得 t1=t2=2, ∴t=2.
第14题(1)
‹#›
返回目录
14.(2019·富阳区期末)把一个足球按垂直于地 面的方向向上踢,t(秒)后该足球的高度 h(米)适用公 式 h=20t-5t2.
∵Δ=(-8)2-4×1×10=24>0,
∴方程有两个不相等的实数根.
第5题(4)
‹#›
返回目录
6.(2018·河南)下列一元二次方程中,有两个不
相等的实数根的是( B )
A.x2+6x+9=0 B.x2=x
C.x2+3=2x
D.(x-1)2+1=0
第6题
‹#›
返回目录
7.(2018·包头)已知关于 x 的一元二次方程 x2+
A.不存在实数根 B.有两个不相等的实数根 C.有一个根是 x=-1 D.有两个相等的实数根
第8题
‹#›
返回目录
9.(2018·南通)若关于 x 的一元二次方程12x2- 2mx-4m+1=0 有两个相等的实数根,则(m-2)2-
20秋 启东作业九年级数学上(BS)作业56
阿基米德发现了杠杆平衡,后来人们把它归纳为
“杠杆原理”,即:阻力×阻力臂=动力×动力
臂.小伟欲用撬棍撬动一块大石头,已知阻力和阻
力臂分别是 1200 N 和 0.5 m,则动力 F(单位:N)关
于动力臂 l(单位:m)的函数解析式正确的是( B )
A.F=12l00
B.F=60l 0
C.F=50l 0
第9题(3)
‹#›
返回目录
(4)如果每小时排水量是 5 m3,那么排完水池中 的水需要多少小时?
解:当 V=5 时,t=458=9.6,即如果每小时排 水量是 5 m3,那么排完水池中的水需要 9.6 h.
第9题(4)
‹#›
返回目录
10.(2019·鄂尔多斯)教室里的饮水机接通电源 就进入自动程序,开机加热时每分钟上升 10 ℃,加 热到 100 ℃停止加热,水温开始下降,此时水温 y(℃) 与开机后用时 x(min)成反比例关系,直至水温降至 30 ℃,饮水机关机,饮水机关机后即刻自动开机, 重复上述自动程序.若在水温为 30 ℃时接通电源, 水温 y(℃)与时间 x(min)的关系如图所示.
待334 min.
第10题(2)
‹#›
返回目录
第8题
‹#›
返回目录
9.如图是某一蓄水池的每小时排水量 V(m3)与 排完水池中的水所用的时间 t(h)之间的函数关系图 象.
第9题
图放大
‹#›
返回目录
第9题
图还原
‹#›
返回目录
(1)请你根据图象提供的信息求出此蓄水池的蓄 水量;
解:由图象可知 4×12=48,因此蓄水池的蓄水 量 48 m3.
计算公式为 p=FS,其中 p 是压强,F 是压力,S 是
20秋启东九年级数学上徐州(JS)作业29

题号 PPT页码
第1题
2
第2题
3第3题4Fra bibliotek第4题
5
第5题
6
第6题
7
目录
‹#›
1.方差是表示一组数据的( D )
A.变化范围
B.平均水平
C.数据个数
D.波动大小
第1题
‹#›
返回目录
2.有一组数据:1,2,3,6,这组数据的方差
是( C )
A.2.5
B.3
C.3.5
D.4
第2题
‹#›
返回目录
3.有 31 位学生参加学校举行的“最强大脑”
智力游戏比赛,比赛结束后根据每个学生的最后得
分计算出中位数、平均数、众数和方差,如果去掉
一个最高分和一个最低分,则一定不发生变化的是
(A) A.中位数
B.平均数
C.众数
D.方差
第3题
‹#›
返回目录
4.老师对甲、乙两人的五次数学测验成绩进行
统计,得出两人五次测验成绩的平均分均为 90 分,
方差分别是 s2甲=51,s2乙=12,则成绩比较稳定的是
甲
55
119 191 115
乙
55
121 110 115
要从甲、乙两班选一个班的部分学生外出参加
比赛,应选哪个班?
第6题
‹#›
返回目录
解:不能确定选哪个班. 当要求参加比赛的人数较多时,可以选乙班, 因为乙班的优秀学生较多,且较稳定,整体成绩可 能较高; 当要求参加比赛人数较少时,应选甲班,因为 两班平均成绩相同,但甲班学生成绩差异大且达到 优秀的学生较少,说明有少数学生的成绩较高.
第6题
‹#›
返回目录
第1题
2
第2题
3第3题4Fra bibliotek第4题
5
第5题
6
第6题
7
目录
‹#›
1.方差是表示一组数据的( D )
A.变化范围
B.平均水平
C.数据个数
D.波动大小
第1题
‹#›
返回目录
2.有一组数据:1,2,3,6,这组数据的方差
是( C )
A.2.5
B.3
C.3.5
D.4
第2题
‹#›
返回目录
3.有 31 位学生参加学校举行的“最强大脑”
智力游戏比赛,比赛结束后根据每个学生的最后得
分计算出中位数、平均数、众数和方差,如果去掉
一个最高分和一个最低分,则一定不发生变化的是
(A) A.中位数
B.平均数
C.众数
D.方差
第3题
‹#›
返回目录
4.老师对甲、乙两人的五次数学测验成绩进行
统计,得出两人五次测验成绩的平均分均为 90 分,
方差分别是 s2甲=51,s2乙=12,则成绩比较稳定的是
甲
55
119 191 115
乙
55
121 110 115
要从甲、乙两班选一个班的部分学生外出参加
比赛,应选哪个班?
第6题
‹#›
返回目录
解:不能确定选哪个班. 当要求参加比赛的人数较多时,可以选乙班, 因为乙班的优秀学生较多,且较稳定,整体成绩可 能较高; 当要求参加比赛人数较少时,应选甲班,因为 两班平均成绩相同,但甲班学生成绩差异大且达到 优秀的学生较少,说明有少数学生的成绩较高.
第6题
‹#›
返回目录
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第7题
‹#›
返回目录
8.在平面直角坐标内,⊙O 的半径是 5,圆心 O 的坐标为(-1,-4),试判断点 P(3,-1)与⊙O 的位置关系.
解:∵圆心 O 的坐标为(-1,-4),点 P 的坐 标为(3,-1),
∴OP= (3+1)2+(-1+4)2=5. ∵⊙O 的半径是 5, ∴点 P 在⊙O 上.
第4题
‹#›
返回目录
5.过圆内的一点(非圆心)有_且__只__有__一___条半径.
第5题
‹#›
返回目录
6.平面内到定点 P 的距离等于 4 cm 的所有点 构成的图形是一个___圆_____.
第6题
‹#›
返回目录
7.在同一平面内,⊙O 的直径为 2 cm,点 P 到圆心 O 的距离是 3 cm,则点 P 与⊙O 的位置关系 是_点__P_在__⊙__O__外__.
第9题(2)
‹#›
返回目录
OP 的长是( C )
A.12 cm
B.5 cm
C.6 cm
D.4 cm
第2题
‹#›
返回目录
3.已知⊙O 的半径为 2,点 P 在⊙O 内,则 OP
的长可能是( A ) A.1
B.2
C.3
D.4
第3题
‹#›
返回目录
4.到圆心的距离不大于半径的点的集合是
(D) A.圆的外部
B.圆的内部
C.圆
D.圆的内部和圆
第9题(1)
‹#›
返回目录
9.如图,已知点 P,Q,且 PQ=4 cm. (2)在所画图中,到点 P 的距离等于 2 cm,且到 点 Q 的距离等于 3 cm 的点有几个?请在图中将它们 表示出来.
第9题(2)
‹#›
返回目录
解:到点 P 的距离等于 2 cm,且到点 Q 的距离 等于 3 cm 的点有 2 个,如答图中点 C,D.
题号 PPT页码 题号 PPT页码
第1题 第2题 第3题 第4题 第5题
2 第6题
7
3 第7题
8
4 第8题
9
5 第9题(1) 10
6 第9题(2) 13
目录
‹#›
1.以点 O 为圆心,可以作几个圆( D )
A.只能 1 个
B.2 个
C.3 个
D.无数个
第1题
‹#›
返回目录
2.已知⊙O 的半径为 6 cm,点 P 在⊙O 上,则
第8题
‹#›
返回目录
9.如图,已知点 P,Q,且 PQ=4 cm. (1)画出下列图形:到点 P 的距离等于 2 cm 的点 的集合;到点 Q 的距离等于 3 cm 的点的集合.
第9题(1)
图放大
‹#›
返回目录
第9题(1)
图还原
‹#›
返回目录
解:如答图,到点 P 的距离等于 2 cm 的点的集 合为图中的⊙P;到点 Q 的距离等于 3 cm 的点的集 合为图中的⊙Q.
