四位超前进位加法器原理
超前进位加法器的设计原理_概述及解释说明

超前进位加法器的设计原理概述及解释说明1. 引言1.1 概述超前进位加法器是一种用于在数字电路中进行二进制数的加法运算的特殊电路。
相较于传统的二进制加法器,超前进位加法器通过预先计算进位,从而实现更快速的运算。
本文旨在对超前进位加法器的设计原理进行概述和解释说明。
1.2 文章结构本文分为五个主要部分,分别是引言、超前进位加法器的设计原理、实现步骤和流程、优势与应用范围以及结论。
首先介绍引言部分,接下来详细解释超前进位加法器的设计原理,然后说明实现步骤和流程。
之后介绍该加法器的优势及其应用范围,并最后得出结论。
1.3 目的本文旨在向读者阐明超前进位加法器的设计原理并提供相关解释说明。
对于数字电路领域的研究者和工程师而言,了解超前进位加法器背后的原理可以帮助他们更好地应用这一技术,并且展示其在优势与应用范围方面所具备的潜力。
2. 超前进位加法器的设计原理2.1 超前进位加法器的定义和背景超前进位加法器是一种常用于数字电路中的加法器,用来实现两个二进制数的相加操作。
与传统的普通进位加法器不同,超前进位加法器在进行计算时能够提前计算并预测进位信号,从而减少计算时间并提高加法运算速度。
2.2 原理解释超前进位加法器采用了两级运算的方式,利用了先行进位预测的思想,以优化传统加法器的运算效率。
其基本原理如下:- 首先,对于每一位(bit)进行相应位置的逻辑门电路设计。
- 然后,在相邻位之间引入前导输入(Generate input)和进位输出(Carry output),这样可以使得下一级可以预测到当前级别产生的所有可能进位。
- 通过与门、或门和异或门等逻辑门之间巧妙的组合连接,实现了高速、低功耗的超前进位运算。
超前进位加法器主要依靠已知最高有效输入块(G代表Generate, P代表Propagate, C代表Carry In) 确定其对应输出(S代表Sum, C代表Carry Out),并将这些信息传递给下一级加法器。
用Verilog HDL语言编写的四位超前进位加法器

——Verilog HDL语言
四位超前进位加法器的进位是并 行同时产生的,能够极大的减 少加法器由进位引起的延时。 增加了逻辑器件,但有效的减 少的延迟。进位是由ALU部件超 前算出,本位是由四个不含进 位的加法器算出。
Verilog HDL代码如下: module jiafaqi_4(x,y,c0,c4,f); //四位超前进位加法器 input [4:1]x; //四位x值 input [4:1]y; //四位y值 output [4:1]f; //四位加和f input c0; //上一的级进位 output c4; //向下一级的进位 wire [3:1]c; //超前进位 wire [4:1]p; wire [4:1]g; wire [4:1]cd; assign p=x|y; assign g=x&y;
module jiafaqi_1(x,y,c0,f); //一位加法器模块 input x; input y; input c0; output f; assign f=(x^y)^c0; endmodule //该一位加法器只有本位输出,不含向下一级 的进位输出,进位输出是由顶层模块的并 行超前进位提供
// 在BASYS2开发板上的管脚配置 NET "c4" LOC = N5; NET "c0" LOC = A7; NET "x[1]" LOC = P11; NET "x[2]" LOC = L3; NET "x[3]" LOC = K3; NET "x[4]" LOC = B4; NET "y[1]" LOC = G3; NET "y[2]" LOC = F3; NET "y[3]" LOC = E2; NET "y[4]" LOC = N3; NET "f[1]" LOC = M5; NET "f[2]" LOC = M11; NET "f[3]" LOC = P7; NET "f[4]" LOC = P6;
超前进位的原理及应用

超前进位的原理及应用1. 什么是超前进位?超前进位是一种计算机算法,用于在数值加法中处理进位的问题。
通常,在进行加法计算时,我们需要将每个位上的数值相加,如果相加的结果超过了该位所能表示的最大值,就会发生进位。
而超前进位的算法可以在发生进位之前就预先计算出进位的结果,并将其应用到后续的计算中。
2. 超前进位的原理超前进位的原理主要是基于二进制数的加法规则。
在二进制加法中,同一位上的两个数相加,可能会有以下四种情况:•0 + 0 = 0•0 + 1 = 1• 1 + 0 = 1• 1 + 1 = 0,进位为1根据这些规则,我们可以发现,只有当两个数都为1时才会发生进位。
因此,可以通过逻辑电路来实现超前进位的计算。
超前进位的计算过程如下:1.首先,将需要相加的两个数的每一位输入到超前进位的电路中。
2.对于每一位,进行逻辑判断,如果两个输入数都为1,则表示该位要发生进位,输出1;否则,输出0。
3.将这些进位输出和相加的结果相加,即可得到最终的计算结果。
3. 超前进位的应用超前进位算法在计算机的运算器中有广泛的应用。
它可以提高加法运算的效率,减少进位的延迟时间,从而提高运算速度。
在实际应用中,超前进位算法可以用于优化处理器的设计。
处理器中的加法器单元通常会采用超前进位的策略,以提高运算速度。
超前进位还可以用于高速缓存控制器等需要进行快速计算的电路中。
除了在硬件电路中的应用,超前进位算法也可以应用于软件算法中。
例如,一些高性能的计算库会使用超前进位算法来优化大整数的加法运算,以提高计算速度。
4. 超前进位的优势超前进位算法相比于传统的进位处理算法,具有以下几个优势:•提高运算速度:超前进位算法可以减少进位的延迟时间,从而加快计算速度。
•降低功耗:由于减少了进位的发生次数,超前进位算法可以降低功耗,使得计算更加节能。
•简化电路设计:超前进位算法可以简化电路设计,减少逻辑门的数量,降低成本。
5. 总结超前进位是一种用于处理进位问题的算法,它可以在进行加法计算时提前计算出进位的结果,并应用到后续的计算中。
数字电路课程设计之超前进位加法器
reg
Cin;
wire[3:0] S;
wire
Cout;
carry_look_add CAL (.A(A),.B(B),.Cin(Cin),.Cout(Cout),.S(S)); initial begin
#10 A=4'd0;B=4'd0;Cin=0; #10 A=4'd11;B=4'd1;Cin=0; #10 A=4'd10;B=4'd12;Cin=0; #10 A=4'd11;B=4'd4;Cin=0; #100 $stop; end endmodule
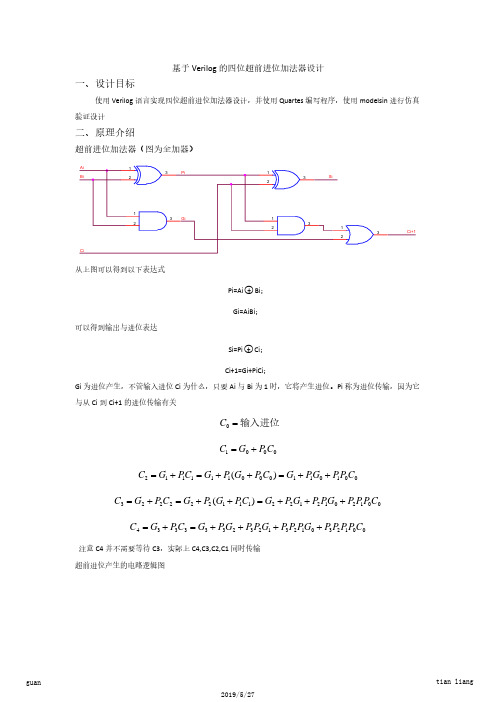
Pi=Ai○+ Bi;
可以得到输出与进位表达
Gi=AiBi;
Si=Pi○+ Ci;
Ci+1=Gi+PiCi; Gi 为进位产生,不管输入进位 Ci 为什么,只要 Ai 与 Bi 为 1 时,它将产生进位。Pi 称为进位传输,因为它 与从 Ci 到 Ci+1 的进位传输有关
C0 = 输入进位
C1 = G0 + P0C0
Half_Add H3(.a(A[2]),.b(B[2]),.s(v6),.c(v5));
Half_Add H4(.a(A[3]),.b(B[3]),.s(v8),.c(v7));
carry_look
CL1(.C0(Cin),.P0(v2),.G0(v1),.P1(v4),.G1(v3),.P2(v6),.G2(v5),.P3(v8),.G3(v7),.C1(o1),.C2(o2),.C3(o3),.C4(Cout));
注意 C4 并不需要等待 C3,实际上 C4,C3,C2,C1 同时传输 超前进位产生的电路逻辑图
计算机组成原理课程设计—超前进位加法器的设计资料

沈阳航空航天大学课程设计报告课程设计名称:计算机组成原理课程设计课程设计题目:超前进位加法器的设计院(系):计算机学院专业:班级:学号:姓名:指导教师:完成日期:沈阳航空航天大学课程设计报告目录第1章总体设计方案 (1)1.1设计原理 (1)1.2设计思路 (2)1.3设计环境 (3)第2章详细设计方案 (4)2.1顶层方案图的设计与实现 (4)2.1.1创建顶层图形设计文件 (4)2.1.2器件的选择与引脚锁定 (5)2.1.3编译、综合、适配 (7)2.2功能模块的设计与实现 (7)2.2四位超前进位加法器模块的设计与实现 (7)2.3仿真调试 (9)第3章编程下载与硬件测试 (11)3.1编程下载 (11)3.2硬件测试及结果分析 (11)参考文献 (13)附录(程序清单或电路原理图) (14)第1章总体设计方案1.1设计原理八位超前进位加法器,可以由2个四位超前进位加法器构成。
由第一个四位超前进位加法器的进位输出作为第二个超前进位加法器的进位输入即可实现八位超前进位加法器的设计。
超前进位产生电路是根据各位进位的形成条件来实现的。
只要满足下述条件,就可形成进位C1、C2、C3、C4。
所以:第一位的进位C1=X1*Y1+(X1+Y1)*C0第二位的进位C2=X2*Y2+(X2+Y2)*X1*Y1+(X2+Y2)(X1+Y1)C0第三位的进位C3=X3*Y3+(X3+Y3)X2*Y2+(X3+Y3)*(X2+Y2)*X1*Y1+(X3+Y3)(X2+Y2)(X1+Y1)*C0第四位的进位C4=X4*Y4+(X4+Y4)*X3*Y3+(X4+Y4)*(X3+Y3) * X2*Y2+(X4+Y4)(X3+Y3)(X2+Y2)*X1*Y1+(X4+Y4)(X3+Y3)(X2+Y2)(X1+Y1)*C0 下面引入进位传递函数Pi和进位产生函数Gi的概念。
它们定义为:Pi=Xi+YiGi=Xi*YiP1的意义是:当X1和Y1中有一个为1时,若有进位输入,则本位向高位传递此进位。
4位超前进位加法器原理

4位超前进位加法器原理
4位超前进位加法器是一种用于进行4位二进制数相加的电路,能够进行四位二进制数的相加,若两个4位二进制数相加结果超过4位,则可以产生一个进位。
其原理如下:
1. 输入:两个四位二进制数A和B以及一个进位输入Cin。
2. 输出:一个四位的和S和一个进位输出Cout。
3. 首先,对于每一位相加,可以使用一个全加器。
4. 对于最低位的相加,输入为A0、B0和Cin,输出为S0和
C0(即第一位的进位)。
5. 对于其他位的相加(A1+B1、C0+A2+B2、C1+A3+B3),
输入为A1、B1、C0,输出为S1和C1(即第二位的进位)。
6. 最后,输出为四位和S3和一个进位输出Cout,Cout等于最
高位相加的进位。
7. 这样,就能够实现4位超前进位加法器,并且能够处理进位的情况。
总之,4位超前进位加法器通过使用多个全加器来实现四位二
进制数的相加,并且能够产生进位。
四位超前进位加法器原理
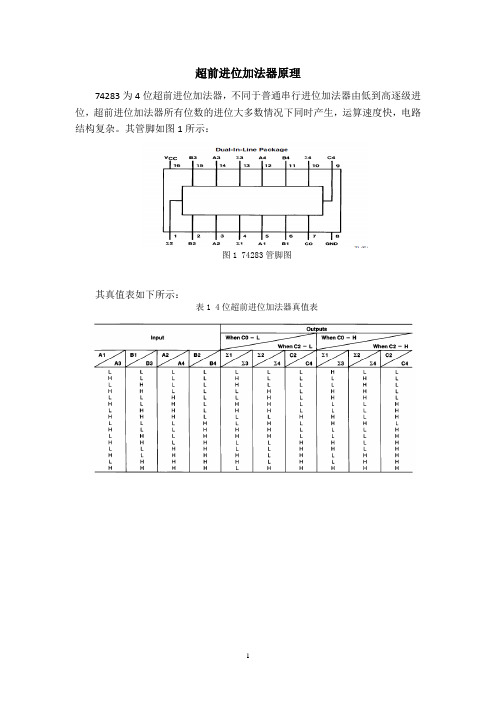
超前进位加法器原理74283为4位超前进位加法器,不同于普通串行进位加法器由低到高逐级进位,超前进位加法器所有位数的进位大多数情况下同时产生,运算速度快,电路结构复杂。
其管脚如图1所示:图1 74283管脚图其真值表如下所示:表1 4位超前进位加法器真值表由全加器的真值表可得Si 和Ci的逻辑表达式:定义两个中间变量Gi 和Pi:当Ai =Bi=1时,Gi=1,由Ci的表达式可得Ci=1,即产生进位,所以Gi称为产生量变。
若Pi =1,则Ai·Bi=0,Ci=Ci-1,即Pi=1时,低位的进位能传送到高位的进位输出端,故Pi称为传输变量,这两个变量都与进位信号无关。
将Gi 和Pi代入Si和Ci得:进而可得各位进位信号的逻辑表达如下:根据逻辑表达式做出电路图如下:逻辑功能图中有2输入异或门,2输入与门,3输入与门,4输入与门,2输入或门,3输入或门,4输入或门,其转化成CMOS晶体管图如下:电路网表如下:*xor 2.subckt xor2 a b c d fmxorpa 1 a vdd vdd pmos l=2 w=8 mxorpb f d 1 vdd pmos l=2 w=8 mxorpc 2 b vdd vdd pmos l=2 w=8 mxorpd f c 2 vdd pmos l=2 w=8 mxorna f a 3 0 nmos l=2 w=4 mxornb 3 b 0 0 nmos l=2 w=4 mxornc f c 4 0 nmos l=2 w=4 mxornd 4 d 0 0 nmos l=2 w=4.ends xor2*and2.subckt and2 a b fmandpa f a vdd vdd pmos l=2 w=4 mandpb f b vdd vdd pmos l=2 w=4 mandna f a 1 0 nmos l=2 w=4 mandnb 1 b 0 0 nmos l=2 w=4.ends and2*and3.subckt and3 a b c fmandpa f a vdd vdd pmos l=2 w=4 mandpb f b vdd vdd pmos l=2 w=4 mandpc f c vdd vdd pmos l=2 w=4 mandna f a 1 0 nmos l=2 w=6 mandnb 1 b 2 0 nmos l=2 w=6 mandnc 2 c 0 0 nmos l=2 w=6.ends and3*and4.subckt and4 a b c d fmandpa f a vdd vdd pmos l=2 w=4 mandpb f b vdd vdd pmos l=2 w=4 mandpc f c vdd vdd pmos l=2 w=4 mandpd f d vdd vdd pmos l=2 w=4 mandna f a 1 0 nmos l=2 w=8 mandnb 1 b 2 0 nmos l=2 w=8 mandnc 2 c 3 0 nmos l=2 w=8 mandnd 3 d 0 0 nmos l=2 w=8.ends and4*or2.subckt or2 a b fmorpa 1 a vdd vdd pmos l=2 w=8 morpb f b 1 vdd pmos l=2 w=8mna f a 0 0 nmos l=2 w=4mnb f b 0 0 nmos l=2 w=4.ends or2*or3.subckt or3 a b c fmorpa 1 a vdd vdd pmos l=2 w=12 morpb 2 b 1 vdd pmos l=2 w=12 morpc f c 2 vdd pmos l=2 w=12mna f a 0 0 nmos l=2 w=4mnb f b 0 0 nmos l=2 w=4mnc f c 0 0 nmos l=2 w=4.ends or3*or4.subckt or4 a b c d fmorpa 1 a vdd vdd pmos l=2 w=16 morpb 2 b 1 vdd pmos l=2 w=16 morpc 3 c 2 vdd pmos l=2 w=16 morpd f d 3 vdd pmos l=2 w=16mna f a 0 0 nmos l=2 w=4mnb f b 0 0 nmos l=2 w=4mnc f c 0 0 nmos l=2 w=4mnd f d 0 0 nmos l=2 w=4.ends or4*not.subckt not a fmnotpa f a vdd vdd pmos l=2 w=4 mnotna f a 0 0 nmos l=2 w=2.ends not *反相器*or21.subckt or21 a b fxor2 a b 1 or2xnot 1 f not.ends or21 *2输入或门*or31.subckt or31 a b c fxor3 a b c 1 or3xnot 1 f not.ends or31 *3输入或门*or41.subckt or41 a b c d fxor4 a b c d 1 or4xnot 1 f not.ends or41 *4输入或门*xor21.subckt xor21 a b fxm a A5 notxn b B5 notxxor a b A5 B5 f xor2.ends xor21 * 2输入异或门*and21.subckt and21 a b fxand2 a b 1 and2xnot 1 f not.ends and21 *2输入与门*and31.subckt and31 a b c fxand3 a b c 1 and3xnot 1 f not.ends and31 *3输入与门*and41.subckt and41 a b c d fxand4 a b c d 1 and4xnot 1 f not.ends and41 *4输入与门xxor211 a1 b1 p1 xor21xxor212 a2 b2 p2 xor21xxor213 a3 b3 p3 xor21xxor214 a4 b4 p4 xor21xand211 a1 b1 g1 and21xand212 a2 b2 g2 and21xand213 a3 b3 g3 and21xand214 p1 c0 m0 and21xor211 m0 g1 c1 or21 *进位C1xand311 p2 p1 c0 m1 and31xand215 p2 g1 m2 and21xor312 g2 m1 m2 c2 or31 *进位C2xand411 p3 p2 p1 c0 m3 and41xand313 p3 p2 g1 m4 and31xand216 p3 g2 m5 and21xor412 m3 m4 m5 g3 c3 or41 *进位C3xxor215 p1 c0 s1 xor21 *输出s1xxor216 p2 c1 s2 xor21 *输出s2xxor217 p3 c2 s3 xor21 *输出s3xxor218 p4 c3 s4 xor21 *输出s4.include "c:\lib\130nm_bulk.l"tt.opt scale=0.05u.global vdd gndvdd vdd 0 1.2va1 a1 0 pulse 1.2 1.2 20n 1f 1f 30n 100nva2 a2 0 pulse 0 0 20n 1f 1f 30n 100nva3 a3 0 pulse 0 0 20n 1f 1f 30n 100nva4 a4 0 pulse 0 0 20n 1f 1f 30n 100nvb1 b1 0 pulse 1.2 1.2 20n 1f 1f 30n 100n vb2 b2 0 pulse 1.2 1.2 20 1f 1f 30n 100nvb3 b3 0 pulse 0 0 20n 1f 1f 30n 100nvb4 b4 0 pulse 1.2 1.2 20n 1f 1f 30n 100nvc0 c0 0 pulse 0 0 4n 1f 1f 0n 100n.tran 1n 100n.plot tran v(s1).plot tran v(s2).plot tran v(s3).plot tran v(s4).end。
超前进位加法器公式

超前进位加法器公式
超前进位加法器是一种数字电路,用于执行加法运算。
它在执行加法时可以提前产生进位信号,从而加快运算速度。
其公式可以通过逻辑门电路来表示。
一般来说,超前进位加法器的公式可以分为两部分,和的计算和进位的计算。
对于和的计算部分,我们可以使用异或门来实现。
假设我们有两个输入A和B,它们分别代表要相加的两个数的对应位,然后我
们使用一个异或门来计算它们的和,即S = A ⊕ B。
这部分公式表示了加法的结果。
接下来是进位的计算部分。
进位的计算涉及到两个方面,一是当前位的进位,二是下一位的进位。
我们可以使用与门和或门来实现这一部分。
假设我们有两个输入A和B,它们分别代表要相加的
两个数的对应位,然后我们使用一个与门来计算它们的进位,即C = A ∧ B。
这部分公式表示了当前位的进位。
然后,我们使用一个或门来计算下一位的进位,即P = A ∧ B。
这部分公式表示了下一位的进位。
综合起来,超前进位加法器的公式可以表示为,S = A ⊕ B,C
= A ∧ B,P = A ∧ B。
这些公式描述了超前进位加法器的运算原理和逻辑电路结构。
通过合理的设计和布线,我们可以将这些公式转化为实际的电路,从而实现超前进位加法器的功能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
超前进位加法器原理
74283为4位超前进位加法器,不同于普通串行进位加法器由低到高逐级进位,超前进位加法器所有位数的进位大多数情况下同时产生,运算速度快,电路结构复杂。
其管脚如图1所示:
图1 74283管脚图
其真值表如下所示:
表1 4位超前进位加法器真值表
由全加器的真值表可得S
i 和C
i
的逻辑表达式:
定义两个中间变量G
i 和P
i
:
当A
i =B
i
=1时,G
i
=1,由C
i
的表达式可得C
i
=1,即产生进位,所以G
i
称为产生量变。
若P
i =1,则A
i
·B
i
=0,C
i
=C
i-1
,即P
i
=1时,低位的进位能传
送到高位的进位输出端,故P
i
称为传输变量,这两个变量都与进位信号无关。
将G
i 和P
i
代入S
i
和C
i
得:
进而可得各位进位信号的逻辑表达如下:
根据逻辑表达式做出电路图如下:
逻辑功能图中有2输入异或门,2输入与门,3输入与门,4输入与门,2输入或门,3输入或门,4输入或门,其转化成CMOS晶体管图如下:
电路网表如下:
*xor 2
.subckt xor2 a b c d f
mxorpa 1 a vdd vdd pmos l=2 w=8 mxorpb f d 1 vdd pmos l=2 w=8 mxorpc 2 b vdd vdd pmos l=2 w=8 mxorpd f c 2 vdd pmos l=2 w=8 mxorna f a 3 0 nmos l=2 w=4 mxornb 3 b 0 0 nmos l=2 w=4 mxornc f c 4 0 nmos l=2 w=4 mxornd 4 d 0 0 nmos l=2 w=4
.ends xor2
*and2
.subckt and2 a b f
mandpa f a vdd vdd pmos l=2 w=4 mandpb f b vdd vdd pmos l=2 w=4 mandna f a 1 0 nmos l=2 w=4 mandnb 1 b 0 0 nmos l=2 w=4
.ends and2
*and3
.subckt and3 a b c f
mandpa f a vdd vdd pmos l=2 w=4 mandpb f b vdd vdd pmos l=2 w=4 mandpc f c vdd vdd pmos l=2 w=4 mandna f a 1 0 nmos l=2 w=6 mandnb 1 b 2 0 nmos l=2 w=6 mandnc 2 c 0 0 nmos l=2 w=6
.ends and3
*and4
.subckt and4 a b c d f
mandpa f a vdd vdd pmos l=2 w=4 mandpb f b vdd vdd pmos l=2 w=4 mandpc f c vdd vdd pmos l=2 w=4 mandpd f d vdd vdd pmos l=2 w=4 mandna f a 1 0 nmos l=2 w=8 mandnb 1 b 2 0 nmos l=2 w=8 mandnc 2 c 3 0 nmos l=2 w=8 mandnd 3 d 0 0 nmos l=2 w=8
.ends and4
*or2
.subckt or2 a b f
morpa 1 a vdd vdd pmos l=2 w=8 morpb f b 1 vdd pmos l=2 w=8
mna f a 0 0 nmos l=2 w=4
mnb f b 0 0 nmos l=2 w=4
.ends or2
*or3
.subckt or3 a b c f
morpa 1 a vdd vdd pmos l=2 w=12 morpb 2 b 1 vdd pmos l=2 w=12 morpc f c 2 vdd pmos l=2 w=12
mna f a 0 0 nmos l=2 w=4
mnb f b 0 0 nmos l=2 w=4
mnc f c 0 0 nmos l=2 w=4
.ends or3
*or4
.subckt or4 a b c d f
morpa 1 a vdd vdd pmos l=2 w=16 morpb 2 b 1 vdd pmos l=2 w=16 morpc 3 c 2 vdd pmos l=2 w=16 morpd f d 3 vdd pmos l=2 w=16
mna f a 0 0 nmos l=2 w=4
mnb f b 0 0 nmos l=2 w=4
mnc f c 0 0 nmos l=2 w=4
mnd f d 0 0 nmos l=2 w=4
.ends or4
*not
.subckt not a f
mnotpa f a vdd vdd pmos l=2 w=4 mnotna f a 0 0 nmos l=2 w=2
.ends not *反相器
*or21
.subckt or21 a b f
xor2 a b 1 or2
xnot 1 f not
.ends or21 *2输入或门
*or31
.subckt or31 a b c f
xor3 a b c 1 or3
xnot 1 f not
.ends or31 *3输入或门
*or41
.subckt or41 a b c d f
xor4 a b c d 1 or4
xnot 1 f not
.ends or41 *4输入或门
*xor21
.subckt xor21 a b f
xm a A5 not
xn b B5 not
xxor a b A5 B5 f xor2
.ends xor21 * 2输入异或门
*and21
.subckt and21 a b f
xand2 a b 1 and2
xnot 1 f not
.ends and21 *2输入与门
*and31
.subckt and31 a b c f
xand3 a b c 1 and3
xnot 1 f not
.ends and31 *3输入与门
*and41
.subckt and41 a b c d f
xand4 a b c d 1 and4
xnot 1 f not
.ends and41 *4输入与门
xxor211 a1 b1 p1 xor21
xxor212 a2 b2 p2 xor21
xxor213 a3 b3 p3 xor21
xxor214 a4 b4 p4 xor21
xand211 a1 b1 g1 and21
xand212 a2 b2 g2 and21
xand213 a3 b3 g3 and21
xand214 p1 c0 m0 and21
xor211 m0 g1 c1 or21 *进位C1
xand311 p2 p1 c0 m1 and31
xand215 p2 g1 m2 and21
xor312 g2 m1 m2 c2 or31 *进位C2
xand411 p3 p2 p1 c0 m3 and41
xand313 p3 p2 g1 m4 and31
xand216 p3 g2 m5 and21
xor412 m3 m4 m5 g3 c3 or41 *进位C3
xxor215 p1 c0 s1 xor21 *输出s1
xxor216 p2 c1 s2 xor21 *输出s2
xxor217 p3 c2 s3 xor21 *输出s3
xxor218 p4 c3 s4 xor21 *输出s4
.include "c:\lib\130nm_bulk.l"tt
.opt scale=0.05u
.global vdd gnd
vdd vdd 0 1.2
va1 a1 0 pulse 1.2 1.2 20n 1f 1f 30n 100n
va2 a2 0 pulse 0 0 20n 1f 1f 30n 100n
va3 a3 0 pulse 0 0 20n 1f 1f 30n 100n
va4 a4 0 pulse 0 0 20n 1f 1f 30n 100n
vb1 b1 0 pulse 1.2 1.2 20n 1f 1f 30n 100n vb2 b2 0 pulse 1.2 1.2 20 1f 1f 30n 100n
vb3 b3 0 pulse 0 0 20n 1f 1f 30n 100n
vb4 b4 0 pulse 1.2 1.2 20n 1f 1f 30n 100n
vc0 c0 0 pulse 0 0 4n 1f 1f 0n 100n
.tran 1n 100n
.plot tran v(s1)
.plot tran v(s2)
.plot tran v(s3)
.plot tran v(s4)
.end。
