平面简谐波的波函数(知识题课)
合集下载
10-02 平面简谐波的波函数(26)
t x y = A cos[ 2π ( − ) + ϕ ] T λ
(1)
10 – 2 平面简谐波的波函数 确定初相角： 确定初相角：∵t
第十章 波动
=0 x=0
O
∂y y = 0, v = >0 ∂t
π ∴ϕ = − 2
A
(2)
y ω
于是有： 于是有： (3)
10 – 2 平面简谐波的波函数 2.求 t = 1 . 0 s 波形图； 求 波形图； 由(3)式令 t = 1 . 0 s 式令
x = 0 .5 m 处质点的振动规律并做图 ； t x π y = (1.0m)cos[2 π( − )− ] 2.0s 2.0m 2 x = 0 .5 m 处质点的振动方程： 处质点的振动方程：
于是有： 于是有：
3 4
O
y = (1.0m) cos[(π s )t − π ]
y
1.0 2 0 -1.0*1 2 *
x x ∆ ϕ = −ω = − 2 π u λ
10 – 2 平面简谐波的波函数
第十章 波动
波线上各点的简谐运动图
10 – 2 平面简谐波的波函数
第十章 波动
2.令 t 一定：波函数 令 一定：波函数y=y(x)，描述 t 时刻距原点 ， 不同处x 轴上所有质点谐振动的位移分布情况。 不同处 轴上所有质点谐振动的位移分布情况。 时刻波线上各质点相对其平衡位置的位移， 表示 t 时刻波线上各质点相对其平衡位置的位移， 即此刻的波形图： 即此刻的波形图：
10 – 2 平面简谐波的波函数
第十章 波动
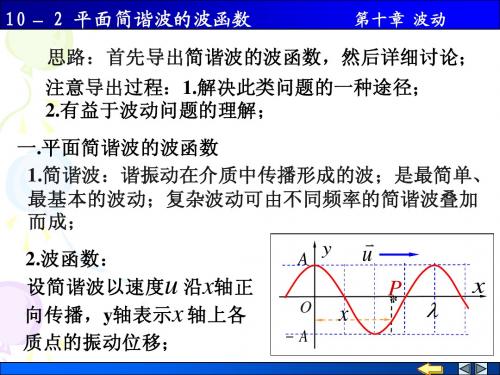
思路：首先导出简谐波的波函数，然后详细讨论； 思路：首先导出简谐波的波函数，然后详细讨论； 简谐波的波函数 注意导出过程： 解决此类问题的一种途径 解决此类问题的一种途径； 注意导出过程：1.解决此类问题的一种途径； 导出过程 2.有益于波动问题的理解； 有益于波动问题的理解； 有益于波动问题的理解 一.平面简谐波的波函数 平面简谐波的波函数 1.简谐波：谐振动在介质中传播形成的波；是最简单、 简谐波： 简谐波 谐振动在介质中传播形成的波；是最简单、 最基本的波动； 最基本的波动；复杂波动可由不同频率的简谐波叠加 而成； 而成； 2.波函数： 波函数： 波函数 设简谐波以速度u 沿x轴正 向传播， 轴表示 向传播，y轴表示x 轴上各 质点的振动位移； 质点的振动位移；
2平面简谐波的波函数
具有一般意义，即为沿 x 轴正方向传播的
平面简谐波的波函数，又称波动方程。
2、平面简谐波的波函数
波动
利用 2π 2πν 和 uT
T
波动方程的几种不同形式：
y
A
cos
t
x u
A
cos2π
t T
x
A cost
2πx
2、平面简谐波的波函数
波动
由波函数： y
A
cos[ (t
x)
]
2、平面简谐波的波函数
波动
3、x 、t 都变
方程表示在不同时刻各质元的位移， 即不同时刻的波形，体现了波的传播。
yu
O
x
2、平面简谐波的波函数
波动
4、沿 x轴负向传播的波动方程
y
u
A
设 O 点振动方程为：
P
x
yO
Acost
O
A
x
P 点振动比O点超前了Δt x u
故P点的振动方程（波动方程）为：
Байду номын сангаас
y(x,t) y(x,t T ) （波具有时间周期性）
2、平面简谐波的波函数
波动
2、t 一定，x 变化
y
y Acost 2πx
o
x
令 t C（定值）
则
y
A
cos
2πx
表示t 时刻波传播方向上各质元的位移, 即t
时刻的波形图（y — x的关系）
y(x , t) y(x,t)（波具有空间周期性）
2、平面简谐波的波函数
波动
一、平面简谐波的波函数
波函数：用以描述波在传播过程中空间x轴 上各质元振动的位移 y 随时间 t 变化的表达式。
平面简谐波的波函数，又称波动方程。
2、平面简谐波的波函数
波动
利用 2π 2πν 和 uT
T
波动方程的几种不同形式：
y
A
cos
t
x u
A
cos2π
t T
x
A cost
2πx
2、平面简谐波的波函数
波动
由波函数： y
A
cos[ (t
x)
]
2、平面简谐波的波函数
波动
3、x 、t 都变
方程表示在不同时刻各质元的位移， 即不同时刻的波形，体现了波的传播。
yu
O
x
2、平面简谐波的波函数
波动
4、沿 x轴负向传播的波动方程
y
u
A
设 O 点振动方程为：
P
x
yO
Acost
O
A
x
P 点振动比O点超前了Δt x u
故P点的振动方程（波动方程）为：
Байду номын сангаас
y(x,t) y(x,t T ) （波具有时间周期性）
2、平面简谐波的波函数
波动
2、t 一定，x 变化
y
y Acost 2πx
o
x
令 t C（定值）
则
y
A
cos
2πx
表示t 时刻波传播方向上各质元的位移, 即t
时刻的波形图（y — x的关系）
y(x , t) y(x,t)（波具有空间周期性）
2、平面简谐波的波函数
波动
一、平面简谐波的波函数
波函数：用以描述波在传播过程中空间x轴 上各质元振动的位移 y 随时间 t 变化的表达式。
10-2平面简谐波的波函数
x
O
x
A
理学院 物理系
大学物理
§10-2 平面简谐波的波函数
yO Acost
yO表示质点O在 t时刻离开平衡位置的距离.
考察波线上P点(坐标x), P点比O点的振
动t 落Δ后t 时刻t 的ux,位P移点，在由t此时得刻的位移是O点在
y A
u
P
x
O
x
A
理学院 物理系
大学物理
§10-2 平面简谐波的波函数
y
u
A
P
x
O
x
A
理学院 物理系
大学物理
§10-2 平面简谐波的波函数
故P点的振动方程（波动方程）为：
y
yo
(t
t)
A cos[ (t
x) u
]
对波动方程的各种形式，应着重从
物理意义上去理解从形式上看：波动是波形的传播.
理学院 物理系
大学物理
§10-2 平面简谐波的波函数
大学物理 §§1100--22 平平面简面谐波简的谐波函波数 的波函数
一 平面简谐波的波函数
波函数：用以描述波在传播过程中空间各点 x 的振
动 y 随时间 t 变化的表达式。 y Acos[(t x) ]
u
设有一平面简谐波沿 x轴正方向传播，
波速为u，坐标原点 O处质点的振动方程为
y A
u
P
uu
Acos[(t x ) ( x0 )]
理学u院 物理u系
大学物理
§10-2 平面简谐波的波函数
例4 一平面简谐波以速度 u 20 m s-1 沿直线传播，波线上点 A 的简谐运动方 程
yA 3102 cos(4 π t); ( y, t单位分别为m，s).
6-2平面简谐波的波函数
各质点相对平 衡位置的位移
波线上各质点 平衡位置
1
各种不同的简谐波
合成 分解
复杂波
简谐波 1 简谐波 2
合成
复杂波
2
波源的振动方程
y A cos( t ) o 0
距波源为 x 处质点 P 的振动方程
x P 点的振动比振源落后一段时间 t u A cos[ ( t t ) ] P点的振动方程 y p 0
波函数的物理意义:
1. 当 x 固定时， 波函数表示该点的简谐运动方程.
d A cos t 例 x＝d（常数）时 y d 0 u
波函数变为距离波源为 d 处的质点的振动方程。
（波具有时间的周期性） y ( x , t ) y ( x , t T )
x t 0 u
在 x 处的质点在时刻 t 的相位
( u 0) x ut
即给定的相的位置随时间而改变，它的移动速度为
dx u dt
说明，波速 u也是相的传 播速度－又称为相速度.
7
波函数 二
x y A cos t W 0 u
波数等于在2π的长度内 含有“完整波”的数目。
y x v A sin[ ( t ) ] 0 t u 2 y x 2 a 2 A cos[ ( t ) ] 0 t u
6
波函数
相速度
x y A cos t W 0 u
y A cos( t )
——振动方程是时间 t 的函 数，描写一个质元的位移。
y
o
y f (t)
§12-2平面简谐波的波函数
x2 − x1 −1 u= = 250 cm ⋅ s t 2 − t1
轴正方向传播， 例2 一平面简谐波沿 O x 轴正方向传播，已知振 幅 A = 1.0m T = 2 . 0 s λ = 2.0m .在 t = 0 时坐 标原点处的质点位于平衡位置沿 O y 轴正方向运 动 .求 1）波函数 解:写出波函数的标准式
振动向右传播 滞后的时间
x ∆t = u
t 时刻点 P 的运动
=
t-x/u时刻点 的运动 时刻点O 时刻点
P点振动方程
yP
t
= yO
t−x u
x = A cos[ω (t − ) + ϕ0 ] u
点选取的任意性，得波函数即上式。 由P点选取的任意性，得波函数即上式。 太原理工大学物理系
方法之二
相位落后法
8m 5m 9m
−2
λ = 10 m
C B o A D 点 C 的相位比点 A 超前 AC −2 yC = 3 × 10 cos[4 π t + 2 π ]
x
点的坐标x＝ 带入波函数 将D点的坐标 ＝9m带入波函数 点的坐标
−2
λ 13 −2 = 3 × 10 cos[4 π t + π] 5
t 9 y D = 3 ×10 cos[2 π( − )](m) 0.5 10
12§12-2 平面简谐波的波函数 介质中任一质点（ 介质中任一质点（坐标为 x）相对其平衡位置的 ） 位移（ 位移（坐标为 y）随时间的变化关系，即 y ( x, t ) ）随时间的变化关系， 称为波函数. 称为波函数.
y = y ( x, t )
各质点相对平 衡位置的位移 衡位置的位移 波线上各质点 平衡位置 平衡位置
10-2-平面简谐波的波函数
-1
u
8m C B 5m 9m D
oA
x
1
第五版
为坐标原点， (1) 以 A 为坐标原点，写出波动方程 )
A = 3 ×10−2 m T = 0.5 s ϕ = 0
λ = uT = 10 m
t x y = A cos[ 2π ( − ) + ϕ ] T λ t x −2 y = (3 × 10 m ) cos 2 π ( − ) 0 .5 s 10 m
λ = 10 m
xC − xD
λ
− 22 = −2π = 4.4π 10
9m
u
8m C B 5m
λ = 10 m
波沿 x 轴正向传播
第十章 波动
14
物理学
1010-2 平面简谐波的波函数
第五版
轴正方向传播， 例1 一平面简谐波沿 Ox 轴正方向传播， 已知振幅 A = 1.0 m， = 2 .0 s， = 2.0 m. 在 t = 0 T λ 时坐标原点处的质点在平衡位置沿 Oy 轴正向 ( )波动方程； ) 波形图； 运动. 运动 求： 1)波动方程；(2)t = 1 . 0 s波形图； (3) x = 0.5 m 处质点的振动规律并作图 处质点的振动规律并作图. ) 解 (1) 写出波动方程的标准式 )
1010-2 平面简谐波的波函数
第五版
点 D 的相位落后于点 A AD −2 ] y D = (3 ×10 m)cos[(4πt ) − 2π λ 9 −2 = (3 × 10 m ) cos[( 4 π t ) − π ] 5
λ = 10 m
u y A = (3 × 10 m ) cos(= 10sm )t λ 4π 8m 5m 9m
物理学
u
8m C B 5m 9m D
oA
x
1
第五版
为坐标原点， (1) 以 A 为坐标原点，写出波动方程 )
A = 3 ×10−2 m T = 0.5 s ϕ = 0
λ = uT = 10 m
t x y = A cos[ 2π ( − ) + ϕ ] T λ t x −2 y = (3 × 10 m ) cos 2 π ( − ) 0 .5 s 10 m
λ = 10 m
xC − xD
λ
− 22 = −2π = 4.4π 10
9m
u
8m C B 5m
λ = 10 m
波沿 x 轴正向传播
第十章 波动
14
物理学
1010-2 平面简谐波的波函数
第五版
轴正方向传播， 例1 一平面简谐波沿 Ox 轴正方向传播， 已知振幅 A = 1.0 m， = 2 .0 s， = 2.0 m. 在 t = 0 T λ 时坐标原点处的质点在平衡位置沿 Oy 轴正向 ( )波动方程； ) 波形图； 运动. 运动 求： 1)波动方程；(2)t = 1 . 0 s波形图； (3) x = 0.5 m 处质点的振动规律并作图 处质点的振动规律并作图. ) 解 (1) 写出波动方程的标准式 )
1010-2 平面简谐波的波函数
第五版
点 D 的相位落后于点 A AD −2 ] y D = (3 ×10 m)cos[(4πt ) − 2π λ 9 −2 = (3 × 10 m ) cos[( 4 π t ) − π ] 5
λ = 10 m
u y A = (3 × 10 m ) cos(= 10sm )t λ 4π 8m 5m 9m
物理学
10-02 平面简谐波的波函数
波程差
∆x21 = x2 − x1
∆ϕ = 2π ∆x
∆ϕ12 = ϕ1 −ϕ2 = 2π
x2 − x1
λ
= 2π
∆x21
λ
λ
10 – 2 平面简谐波的波函数
第十章 机械波
x t x y = A cos[ω (t − ) + ϕ ] = A cos[2 π( − ) + ϕ ] u T λ
3. 若x和t两个都变化时，波方程就表示了波线上 两个都变化时， 和 两个都变化时 所有质点在各个不同时刻的位移分布情况。 所有质点在各个不同时刻的位移分布情况。 形象地说， 形象地说，在这个波动方程中包括了无数个不 同时刻的波形。随着t的增加波的表达式就描述 同时刻的波形。随着 的增加波的表达式就描述 波形沿传播方向的运动情况。 了波形沿传播方向的运动情况。
y = y ( x, t )
各质点相对平 衡位置的位移 衡位置的位移
波线上各质点 平衡位置 平衡位置
10 – 2 平面简谐波的波函数
第十章 机械波
3. 平面简谐波的波方程 （1）导出波方程的思路 ） 已知波源的振动方程，当振动传到各质元时， ◆ 已知波源的振动方程，当振动传到各质元时，各 质元都以相同的振幅、 频率来重复波源的振动。 质元都以相同的振幅、 频率来重复波源的振动。 波源的振动状态以某一速度先后传播到各个质元， ◆ 波源的振动状态以某一速度先后传播到各个质元， 沿波的传播方向上的各质元振动的相位依次落后。 沿波的传播方向上的各质元振动的相位依次落后。 （2）导出波方程步骤 ） 选定坐标并明确波的传播方向。 ◆ 选定坐标并明确波的传播方向。 给出波的传播方向上某点(参考点 波源)的振动方 参考点、 ◆ 给出波的传播方向上某点 参考点、波源 的振动方 程。 比较位于x处的任一点和参考点相位的超前和落后 ◆ 比较位于 处的任一点和参考点相位的超前和落后 关系，由参考点的振动表达式即可得出波的表达式。 关系，由参考点的振动表达式即可得出波的表达式。
§12-2平面简谐波的波函数
将沿x轴正方向传播的平面简谐波式(1)分别对x和t
求二阶偏导数，有
2 y x2
－
A 2
u2
cos[(t
x) u
0 ]
比较可得
2 y t 2
A2
cos[(t
x) u
0 ]
推广到x2 y2三维u空12 间，t2 2y则——2平 面 波1波动2的微分方P34程，12.12式
u 2 t 2
其中 2
2
y(t，x) y(t t，x x)
太原理工大学物理系
A cos[ (t
x) u
0
]
A cos{[(t
t)
x
x] u
0}
即 t x 0 u
x ut
说明：x处质点的振动状态是以速度u向前传播的，
经过t时间向前传播了x=ut 的距离。整个波形
也就以速度u向前传播。可见，波速就是振动状态 的传播速度，也就是波形的传播速度。
C
BA
Dx
（2）若以B点为坐标原点，写出波动方程
（3）分别求出 B、C ，C、D 两质点间的相位差
太原理工大学物理系
解 u 20m / s 4 2 / s 10m
（1） A 点振动方程 yA 0.03cos 4 t (m)
以A点位原点，波动方程为
y 0.03cos 4 (t x )
所示，试求：（1）波的周期和圆频率；（2）写出 该平面简谐波的表达式。
解：（1）由图知：
A 0.1m ， 2 m
A
在t=0到t=1s时间内，波形向x轴正方向移动了
λ/4，即
t 1s
x 0.5m
4
由 x ut 得 u=0.5m/s
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
*
太原理工大学物理系
例3 若一平面简谐波在均匀介质中以速度u传播，
已知a点的振动表达式为 y A(t 。 2)
(1)试写出如图所示的坐标系中的波动方程。
解：(a)波向x轴正向传播，
x
xa 4
波动方程为
y
Acos[(t
2
)
2
(x
xa
)]
Acos(t 2 x )
太原理工大学物理系
（2）b点的振动表达式.
y/m
1.0
o
2.0
-1.0
太原理工大学物理系
x/m
3） x 0.处5m质点的振动规律并做图 .
y 1.0cos[2 π( t x ) π] 2.0 2.0 2
x 0.处5m质点的振动方程
y 1.0cos[πt π]
y
y/m
3
1.0
3*
4O
2
0
2*
1.0
4 *
2.0
*
t /s
1 -1.0*1
例5 一平面简谐波沿轴正向传播，其振幅为A，频率
为 ，波速为u，设 时t′ 刻的波形曲线如图。
求：（1）原点处质点振动方程
y/m
A
o
-A
u
t
x/m
太原理工大学物理系
解 （1）设o点振动方程
由图：在 t=t´时刻，o点位移为零，振动速度小于
零，所以在t=ቤተ መጻሕፍቲ ባይዱ´时刻o点的相位等于/2
t 0
2
0
2
t
A
y0 0, v 0
0
π 2
y 1.0 cos[2π( t x ) ](m)
2.0 2.0 2
太原理工大学物理系
2）求t 1.波0s形图. y 1.0 cos[2 π( t x ) π ] 2.0 2.0 2 t 1.0s 时的波形方程
y 1.0 cos[ π π x] 2
0.5
与标准形式比较得
1m
1 2HZ
T
u 2m/s
太原理工大学物理系
求：(2)写出t=4.2s时刻各波峰位置的坐标表达式，并 求出此时离坐标原点最近的那个波峰的位置；
解 波动方程为 y Acos (4t 2x)
波峰位置即y=A处 由cos (4t 2x) 1
得 (4t 2x) 2k (k 0,1,2)
x k 2t
当t 4.2s时， x (k 8.4)m
此时离坐标原点最近的那个波峰的位置在 x=-0.4m处。
太原理工大学物理系
(3)求t=4.2s时离坐标原点最近的那个波峰通过坐标原
点的时刻t。
解 该波峰由原点传播到x=-0.4m所需要的时间
t x 0.4 0.2st 4s
u 2
习题类型
1）已知波函数，求波长、频率、波速。 2）已知某点振动状态，求波函数、某点
的振动方程。 3）由图形求波函数。
太原理工大学物理系
例1 已知一平面简谐波的方程为
y Acos (4t 2x) (SI)
求：(1)求该波的波长，频率和波速u的值；
解：这是一列向x轴负向传播的波,将波方程变成
y Acos2 ( t x)
u
y
t=4.2s
t=4s
-0.4m O
x
太原理工大学物理系
例2 一平面简谐波沿 O x 轴正方向传播，已知振
幅 A 1.0m T 2.0.s在 2时.0坐m标原点t处的0 质点位
于平衡位置沿 O y 轴正方向运动 .求 1）波动方程
解:写出波动方程的标准式
y
Acos[2π( t T
x
)
0
]
O y t0 x0
太原理工大学物理系
所以
0
2
又
T 0.40 s 5s
u 0.08
波动方程 y 0.04cos[2 ( t x ) ]
5 0.4 2
（2）P处质点的振动方程为
y 0.04 cos[2 ( t 0.2 ) ]
5 0.4 2
0.04 cos(0.4 t 3 )
2
太原理工大学物理系
y/m
u
A
A
o
x/m
O
y
-A
太原理工大学物理系
x=0处振动方程为
y Acos[2 (t t) ]
2
（2）该波的波动方程
y
A cos[2
(t
t
x
u)
2
]
太原理工大学物理系
xb 2
b点的振动表达式
yb
A c os (t
2
2
)
A c ost
太原理工大学物理系
例4
如图所示为一平面简谐波t=0时刻的波形，求： （1）该波的波动方程； （2）P点处质点的振动方程。
解（1）对原点O处的质点 ym
t 0时
u 0.08ms1 p
y0 Acos0 0
O
0.02
xm
v0 A sin0 0 0.04