高等数学数学分析题解选
数学分析参考书

数学分析参考书1.《微积分学教程》菲赫金哥尔茨人民教育出版社推荐理由:经典的数学分析的百科全书, 论述严谨, 内容全面, 例题丰富, 对希望全面掌握数学分析理论的学生是一本较好的参考书。
2.《数学分析》华东师大数学系高等教育出版社推荐理由:本书是教育部推荐的优秀教材,内容安排自然合理,读者容易接受,选学内容加了“*”适合多层次的需求;读者可以通过附录1和附录2了解微积分的发展线索记实数理论。
3.《数学分析》北大数学系方企勤、沈燮昌、廖可人等高等教育出版社推荐理由:本书阐述细致,引进概念注意讲清实际背景,定理证明、公式推演作了必要的分析,并提出一些值得思考的问题;通过大量不同类型例题,介绍解题基本方法和特殊技巧。
全书还配有习题集一册,其中有不少难度较大的题目。
适合要求进一步提高数学分析素养的同学。
4. 《数学分析》李成章黄玉民科学出版社推荐理由:总体内容与华东师大教材相仿. 书中有大量的习题可作为补充练习题.5. 《数学分析》陈纪修等高等教育出版社推荐理由:书中对三角级数阐述的较为详细,可供参考.6. 《数学分析习题精解》吴良森等高等教育出版社推荐理由:书中题型丰富,可供较为优秀的学生选7. 《数学分析习题课讲义》谢惠民等高等教育出版社推荐理由:李大潜院士是这样评价此书的“它的着眼点,不像现在充斥市面的各种各样的习题解答那样,消极地为读者提供一些习题的解答,而是引导学生理解课程内容,启发学生深入思考,扩大学生知识视野,力求使学生达到举一反三,由小见大,由表及里的境界,较快的高等数学的思想方法,迈进高等数学的广阔天地。
对于学生,这是一本富有启发性且颇有新意的辅导读物。
”8. 《数学分析中的典型问题与方法》裴礼文高等教育出版社推荐理由:本书收录了大量的研究生数学分析入学试题,前苏联高校竞赛题。
选题具有很强的典型性,灵活性,启发性,趣味性和综合性,对培养学生的能力极为有益。
8. 《Calculus(微积分)》Howard Anton, Irl Bivens, Stephen Davis郭镜明改编高等教育出版社推荐理由:本书为高等教育出版社“世界优秀教材中国版”系列教材之一。
高数面试题目及答案解析

高数面试题目及答案解析一、选择题1. 下列哪个函数在其定义域上是连续的?A. f(x) = 1/2xB. f(x) = |x|C. f(x) = 1/xD. f(x) = √x答案解析:选项A对于所有实数x都是连续的,因此答案选A。
2. 函数f(x) = 2x^3 - 3x^2 + 5的导数为下列哪个?A. f'(x) = 6x^2 - 6xB. f'(x) = 2x^2 - 3xC. f'(x) = 6x^2 - 3xD. f'(x) = 6x - 3答案解析:计算f(x)的导数,得到f'(x) = 6x^2 - 6x + 0,因此答案选A。
3. 函数f(x) = e^x的反函数为下列哪个?A. f^(-1)(x) = ln(x)B. f^(-1)(x) = log(x)C. f^(-1)(x) = e^xD. f^(-1)(x) = x答案解析:e^x的反函数为ln(x),因此答案选A。
二、填空题1. 设函数f(x) = x^2 + 2x,则f(-1)的值为________。
答案解析:将x替换为-1,得到f(-1) = (-1)^2 + 2(-1) = 1 - 2 = -1,因此答案为-1。
2. 设函数f(x) = a^x,其中a为正常数,若f(2) = 8,则a的值为________。
答案解析:将x替换为2,得到f(2) = a^2 = 8,解得a = 2,因此答案为2。
三、解答题1. 求函数f(x) = 3x^2 - 2x + 1的极值点。
答案解析:对于一元二次函数f(x) = ax^2 + bx + c,其极值点的横坐标x = -b/2a。
对于f(x) = 3x^2 - 2x + 1,a = 3,b = -2,c = 1,将值代入公式得到x = -(-2)/(2*3) = 1/3。
将x = 1/3代入函数f(x)中,得到纵坐标f(1/3) = 3(1/3)^2 - 2(1/3) + 1 = 4/3。
高等教育出版社样书目录(数学类)
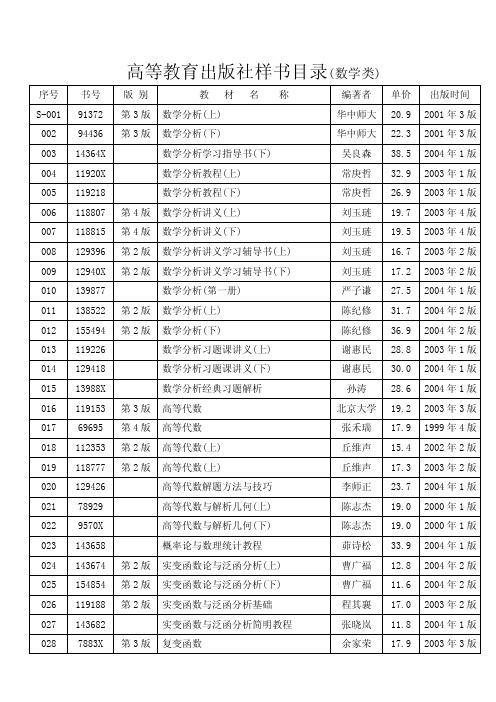
同济大学 10.1 2001 年 2 版
重温微积分
齐民生 39.6 2004 年 1 版
第 2 版 微积分(上)
同济大学 24.9 2003 年 2 版
第 2 版 微积分(下)
同济大学 23.1 2003 年 2 版
微积分学习辅导与习题选解
同济大学 28.4 2004 年 1 版
第 2 版 微积分学简明教程(上)
余家荣 17.9
出版时间 2001 年 3 版 2001 年 3 版 2004 年 1 版 2003 年 1 版 2003 年 1 版 2003 年 4 版 2003 年 4 版 2003 年 2 版 2003 年 2 版 2004 年 1 版 2004 年 2 版 2004 年 2 版 2003 年 1 版 2004 年 1 版 2004 年 1 版 2003 年 3 版 1999 年 4 版 2002 年 2 版 2003 年 2 版 2004 年 1 版 2000 年 1 版 2000 年 1 版 2004 年 1 版 2004 年 2 版 2004 年 2 版 2003 年 2 版 2004 年 1 版 2003 年 3 版
高等教育出版社样书目录(数学类)
版别
教材名 称
编著者 单价 出版时间
第4版 第3版
概率论与数理统计教程 概率论与数理统计教程学习辅导与习题 选解
概率论与数理统计
沈恒范 沈恒范 盛骤
20.6 2003 年 4 版 17.6 2003 年 1 版 19.3 2001 年 3 版
概率论与数理统计习题全解指南
第 2 版 数学史概论
李文林 21.0 2002 年 2 版
大学文科高等数学(第一册)
姚孟臣 11.9 1997 年 1 版
本科高等数学教材推荐书目

本科高等数学教材推荐书目随着数学的发展,本科高等数学教材的选择变得越来越重要。
一本好的教材可以帮助学生更好地理解和应用数学知识,提高他们的学习效果。
下面是几本推荐的本科高等数学教材:1.《高等数学》(第七版)- 同济大学数学系作者:郭庆林、钱泳帆出版社:高等教育出版社2.《高等数学》(第六版)- 北京大学数学系作者:李建国、杜应奎出版社:高等教育出版社3.《高等数学》(上、下册)- 李建国版作者:李建国出版社:清华大学出版社4.《数学分析教程》(第二版) - 同济大学数学系作者:赵毅、李涛出版社:高等教育出版社5.《数学分析习题课程辅导》- 黄春来、郑晨编著出版社:高等教育出版社这些教材在本科高等数学教学中都有着很高的声誉和影响力。
它们以其全面、系统和详细的内容介绍、清晰易懂的表达方式以及丰富的例题和习题而闻名。
以下简要介绍每本教材的特点:《高等数学》(第七版)是同济大学数学系推荐使用的教材,由郭庆林教授和钱泳帆教授合著。
它以全面、详尽而又具有一定难度的内容,适合那些希望深入学习高等数学的学生。
《高等数学》(第六版)是北京大学数学系所编写的教材,被广大数学专业及相关专业的学生所使用。
该教材在内容上既保留了高等数学的经典部分,又增加了许多前沿的数学知识。
《高等数学》(上、下册)是李建国教授编写的教材,由清华大学出版社出版。
它以理论与实际相结合的方式,能够帮助学生更好地理解高等数学的概念与方法。
《数学分析教程》是由同济大学数学系赵毅教授和李涛教授合著的教材,该教材系统地介绍了数学分析的基本概念、定理和方法,并包含大量的例题和习题,有助于学生巩固所学知识。
《数学分析习题课程辅导》则侧重于提供一系列与教材对应的习题以供学生练习,由黄春来教授和郑晨编著,适合那些希望加强数学分析习题应用能力的学生。
总之,选择一本适合自己的本科高等数学教材是非常重要的。
这些推荐的教材都具备了全面、详细和易懂的特点,可以帮助学生更好地掌握数学知识,提高学习成效。
高等数学求极限的常用方法(附例题和详解)

高等数学求极限的常用方法(附例题和详解)高等数学中求极限是一项重要的数学技巧,它在数学分析、微积分和其他数学领域中都有广泛应用。
本文将介绍一些常用的求极限的方法,并给出相应的例题和详解。
一、直接代入法直接代入法是求极限的最基本方法之一。
当函数在某一点连续时,可以直接将该点代入函数中来求极限。
例题1:求函数f(x) = x^2在x=2处的极限。
解:直接将x=2代入函数中,得到f(2) = 2^2 = 4。
因此,f(x)在x=2处的极限为4。
二、夹逼法夹逼法(也称为夹挤准则)是求解一些复杂极限的常用方法。
它基于一个简单的想法:如果函数g(x)和h(x)在某一点p附近夹住函数f(x),并且g(x)和h(x)的极限都相等,那么f(x)的极限也等于这个相等的极限。
例题2:求极限lim(x→∞) [(x+1)/x]。
解:我们可以用夹逼法来求解这个极限。
首先,我们可以注意到1 ≤ [(x+1)/x] ≤ [x/x] = 1(其中[x]表示取整函数)。
因此,我们可以将极限表达式两侧夹逼:lim(x→∞) 1 ≤ lim(x→∞) [(x+1)/x] ≤ lim(x→∞) 1。
根据夹逼准则,当lim(x→∞) 1 = 1时,极限lim(x→∞) [(x+1)/x]存在且等于1。
三、极限的四则运算法则在求解复杂函数的极限时,可以利用极限的四则运算法则。
该法则规定,如果函数f(x)和g(x)在某点p处的极限存在,则函数h(x) = f(x) ± g(x)、h'(x) = f(x) * g(x)、和h''(x) = f(x) / g(x)在点p的极限也存在,并满足相应的运算法则。
例题3:求极限lim(x→0) (sinx/x)。
解:我们可以利用极限的四则运算法则来求解这个极限。
首先,观察到当x→0时,分子sinx和分母x都趋向于0,因此这个极限是一个未定式。
根据极限的四则运算法则,我们可以将lim(x→0) (sinx/x)转化为lim(x→0) sinx / lim(x→0) x。
2024年考研高等数学一计算机辅助数学分析历年真题

2024年考研高等数学一计算机辅助数学分析历年真题高等数学一是考研数学的重要科目之一,其内容覆盖了大量的数学分析知识。
为了更好地备考2024年考研高等数学一,我们可以借助计算机辅助来进行数学分析的学习和练习。
以下是2024年考研高等数学一计算机辅助数学分析历年真题,通过这些历年真题的训练,我们可以更好地了解考研数学分析的考点和解题方法,提升我们的解题能力和应试水平。
一、选择题1.设函数f(x)在区间[a,b]上连续,且f(x)≠0,则函数f(x)的零点个数最多是()。
A. 0B. 1C. 2D. 32.曲线y=ln(x2-2x+2)的拐点的个数为()。
A. 0B. 1C. 2D. 3二、填空题1.设函数f(x)=x3-3x2-9x+5,则f(x)在区间[-1,2]上的最大值为____。
2.设函数f(x)为偶函数,且在区间(-∞,0)上是减函数,那么在区间(0,+∞)上f(x)的单调性为____。
三、解答题1.证明:对于任意的实数x,当x≥1时,有x3≥x2。
解:由已知条件可得,对于任意的实数x,当x≥1时,有x-1≥0。
同时,我们可以得到以下不等式关系:x^3 - x^2 = x^2(x-1) ≥ 0所以,当x≥1时,有x3≥x2成立。
2.已知函数f(x)=x2+px+q,其中p,q为常数,且对于任意的实数x,都有f(x)≥0。
求p和q的取值范围。
解:由题目已知条件可得,Δ = p^2 - 4q ≤ 0解得,p^2 ≤ 4q根据函数f(x)≥0的条件,我们还有:Δ = p^2 - 4q ≥ 0解得,p^2 ≥ 4q综合以上两个不等式,可以得到:p^2 ≥ 4q ≥ p^2即,p^2 = 4q所以,p^2 = 4q,p和q的取值范围为:p^2 ≥ 4q。
通过以上数学分析的历年真题训练,相信大家对2024年考研高等数学一的计算机辅助数学分析有了更深入的了解。
为了更好地备考,我们可以通过大量的练习题提高解题能力和应试水平。
高等数学辅导教材推荐

高等数学辅导教材推荐高等数学是大学阶段的重要学科之一,对于理工科、经济学等专业的学生来说,它是必修课程。
好的辅导教材可以帮助学生更好地理解和掌握高等数学的概念和方法。
本文将为大家推荐几本适合高等数学辅导的教材。
一、《高等数学(上、下册)》(同济大学版)同济大学出版社的《高等数学》是一套经典的高等数学教材。
该教材从基础概念出发,逐步深入,内容结构合理,逻辑严谨。
它既包含了数学原理的讲解,又涵盖了大量的例题和习题,可以帮助学生巩固所学知识。
该教材通俗易懂,注重培养学生的实际运算能力,是高等数学学习的首选教材之一。
二、《高等数学导学与习题解析》(高等教育出版社)《高等数学导学与习题解析》是高等教育出版社出版的一本辅导教材。
该教材以导学方式呈现知识点,每个知识点都附带大量习题。
通过讲解和解题过程的详细分析,学生可以更清晰地理解和掌握数学概念和方法。
该教材注重思维方法的培养,凸显数学的应用,对于理解高等数学的思维逻辑起到了积极的辅助作用。
三、《高等数学分析习题解法详解》(清华大学出版社)清华大学出版社的《高等数学分析习题解法详解》是一本专门针对高等数学分析课程的辅导教材。
它选取了一些经典的高等数学分析习题,详细解析了解题的方法和技巧。
该教材旨在帮助学生更好地理解和运用高等数学分析的基本概念,强化学生的问题解决能力。
它的解题思路独特,注重方法的总结和推广,对于数学分析课程的学习具有较高的参考价值。
四、《高等数学习题精选与解析》(人民邮电出版社)《高等数学习题精选与解析》是人民邮电出版社出版的一本高等数学辅导教材。
该教材以习题为主线,选取了一些典型的难题,通过详细解析和分析,帮助学生理解习题的解题技巧和思路。
该教材的解析过程详细,习题数量较多,对于提高学生的解题能力和应对考试有一定的帮助。
以上是本文为大家推荐的几本适合高等数学辅导的教材。
需要强调的是,教材只是辅助学习的工具,学生在选择教材时应根据个人的学习特点和需求来进行选择。
新编高等数学教材习题答案

新编高等数学教材习题答案一、实数与复数1. 实数答案:实数是包括有理数和无理数在内的数的集合。
有理数包括整数、分数和循环小数,可以表示为有限位数或无限循环的小数。
无理数是不能表示为有限小数或无循环小数的数,例如根号2、圆周率π等。
2. 复数答案:复数是由实数和虚数共同构成的数。
其中,实数部分和虚数部分分别用a和b表示,复数可以写为a + bi的形式,其中i是虚数单位,满足i^2 = -1。
复数可以表示为有限位数或无限循环的小数。
二、极限和连续函数1. 极限答案:极限是数列或函数在某一点或趋向于某一点时的趋近情况。
数列的极限指数列中的数字当n趋近于无穷大时的极限值。
函数的极限指当自变量趋近于某一值时,函数的值趋近于某一值。
在数学中,使用极限来研究数列和函数的性质及其变化趋势。
2. 连续函数答案:连续函数是指在定义域内的每一点,函数值都与极限值相等。
也就是说,如果一个函数在某一点处的函数值等于该点的极限值,那么该函数在这一点处是连续的。
连续函数在数学分析和应用中具有重要的作用,能够描述物理现象、经济模型等实际问题。
三、微分与积分1. 微分答案:微分是导数的另一种称呼。
导数可以理解为函数在某一点的瞬时变化率,描述了函数曲线在该点处的切线斜率。
通过求导可以得到函数的导函数,导函数可以描述函数的变化趋势、极值点等重要信息。
微分在数学和物理学中具有广泛的应用,例如在求速度、加速度等问题时经常用到微分的概念。
2. 积分答案:积分是导数的逆运算。
它是确定在给定区间上函数与坐标轴之间的面积或曲线长度的过程。
积分可以看作是对函数的求和操作,通过求积分可以反推得到函数的原函数。
积分在数学、物理、经济等领域广泛应用,例如在求曲线下的面积、质量、功等问题中都需要用到积分。
【篇幅较短,可再根据文章长度要求进行补充和扩展】。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
φ(θ) ∈ (0, π) 满足 cot φ(θ) = e−(u ∫ dr
−π+α
2 2 + t2 + 1 2w )
√ 2 sin θ, 则
∫ ∫∫
dudwdt
π
α
∫ dθ
√ 2 −r 2 2r e sin φ dφ
= = = = =
√ ∫ α ∫ π 2π dθ sin φ dφ 4 −π+α φ(θ ) √ ∫ α 2π (1 + cos φ(θ)) dθ 4 −π+α √ √ ∫ α ( 2π 2 sin θ ) 1+ √ dθ 4 −π+α 1 + 2 sin2 θ √ ( ∫ 2 ) 3 2π ds √ π−2 ds 4 1 − s2 0 √ ( 2π 2) √ 1 π − 2 arcsin = 2π arcsin √ . 4 3 6
4
ytdwdw: 数学分析高等数学题选解
证明: {cos n|n = 1, 2, . . .} 在 [−1, 1] 中稠密. 证明: 考虑 E = {ein |n = 1, 2, 3, . . .}. 记 F 为 E 在 C 中的闭包. 只要证明 { } F = S 1 = eiθ |θ ∈ [0, 2π) . 否则 U ≡ S 1 \ F 非空. 此时, 容易依次证明以下结论: (1) 对于 eiθ ∈ U , 存在最大的 β 和最小的 α 使得 eiθ ∈ Iθ ≡ {eit |α < t < β } ⊆ U 成立. 了解一点拓扑的会知道 U 是 S 1 中的相对开集. 了解一点实变函数的知 道 Iθ 就是开集 U 的“构成区间”. (2) 对于 eiθ ∈ U , Iθ 的弧长 ℓθ ∈ (0, 1). (3) 对于 eiθ , eiβ ∈ U , Iθ 和 Iβ 要么重合, 要么不想交. (4) ℓθ (eiθ ∈ U ) 的最大值可以取到. 否则有 θ1 , θ2 , . . . 使得 ℓθ1 < ℓθ2 < ℓθ3 < . . .. 从而 Iθ1 , Iθ2 , Iθ3 , . . . 两两不同, 进而由 (3) 知他们两两不交. 注意到 S 1 中只 能放下有限个弧长不小于 ℓθ1 的这种构成区间, 我们就会得到矛盾. 所以相应的最 大值一定取到. (5) ei F ≡ {ei z |z ∈ F } ⊆ F . 从而 ei U ⊇ U , 进而 e−i U ⊆ U . (6) 设 θ 使得 Iθ 的弧长达到最大. 考虑 e−i Iθ , e−2i Iθ , e−3i Iθ , . . .. 则其中必有 两个会相交. 若相交则必定重合, 否则与弧长最大的假设矛盾. 而其中的两个集合 e−mi Iθ 和 e−ni Iθ (m ̸= n) 重合的充要条件是 m − n 为 2π 的整数倍. 这与 π 为无 理数矛盾. 因此, F = S 1 . 所以 E 在 S 1 中稠密. 从而 {cos n|n = 1, 2, . . .} 在 [−1, 1] 中 稠密. 类似地可以证明 {sin n|n = 1, 2, . . .}, {cos(2n + 1)|n = 1, 2, . . .} 等都在 [−1, 1] 中稠密. 本题有很多其他的证明方法.
0,
因此, g 可导但导数在 0 点不连续. 进一步, |g (x)| ≤ 16, |g ′ (x)| ≤ 9, ∀ x ∈ [−4, 4].
特别, 注意到 g 在 0 点以外有连续的两阶导数, 可见 ( ) ( ) g ′ x + 21 − g ′ 21 n n Mn ≡ sup x 0<|x|≤1 ( ) ( ) ( ( g ′ x + 21 − g ′ 21 g′ x + n n = max sup , sup 1 x <|x|≤1 0<|x|≤ n1 2 +1 2n+1 ( ) ( 1) ≤ max sup g ′′ x + n , 18 · 2n+1 < +∞. 1 2 0<|x|≤ n+1
φ(θ )
1
ytdwdw: 数学分析高等数学题选解
问题: 导函数在一点可导, 是否意味着导函数在该点的某个领域内连续. 反例: 令 g (x) = 则 g ′ (x) = { {
1 x2 sin x ,
如果 x ̸= 0, 如果 x = 0. 如果 x ̸= 0, 如果 x = 0.
0,
1 1 2x sin x − cos x ,
a
∀ x ∈ (a, b)
x= c
与 f ′ (x) − µ(f (x) − f (a)) 恒正矛盾. 证毕.
3
ytdwdw: 数学分析高等数学题选解
证明: cos n2 发散. 证明: 给一个不太漂亮的证明. 假设已经证明 {cos(2n + 1)|n = 1, 2, 3, . . .} 的 导集为 [−1, 1], 这一点不难证明. 现 在, 反 设 cos n2 收 敛, 则 | cos n2 |, | sin n2 | 均 收 敛, 设 极 限 为 α, β . 则 α2 + β 2 = 1. 由和角公式, cos(n + 1)2 = cos(n2 + 2n + 1) = cos n2 cos(2n + 1) − sin n2 sin(2n + 1). 所以 |(1 − cos(2n + 1)) cos n2 + cos(n + 1)2 − cos n2 | = | sin n2 sin(2n + 1)|. 由于当 n → ∞ 时, |(1 − cos(2n + 1)) cos n2 + cos(n + 1)2 − cos n2 | = |(1 − cos(2n + 1)) cos n2 + o(1)| = |(1 − cos(2n + 1)) cos n2 | + o(1) = (α + o(1))(1 − cos(2n + 1)) + o(1) = α(1 − cos(2n + 1)) + o(1), | sin n2 sin(2n + 1)| = (β + o(1))| sin(2n + 1)| = β | sin(2n + 1)| + o(1), 可得 α(1 − cos(2n + 1)) = β | sin(2n + 1)| + o(1), n → ∞.
数学分析高等数学题选解
本文内容主要是本人截止 2012年 2 月前在网上解答 的一些数学分析和高等数学题.
ytdwdw: 数学分析高等数学题选解
计算:
∫
+∞
∫ dt
t
+∞
∫ dw
+∞
e−(u
2
2 +t2 + 1 2w )
du.
−∞
w
解: 记 Ω = {(u, w, t)| − ∞ < t ≤ w ≤ u < +∞}, 做广义球面坐标变换 cos θ sin φ, u=r √ w = 2r sin θ sin φ, t = r cos φ. 设 α ∈ (0, π ) 满足 sin α = 2 原积分 = ∫ =
利用 {cos(2n + 1)|n = 1, 2, 3, . . .} 的导集为 [−1, 1], 对任何 s ∈ [−1, 1], 对上式在 √ 子列意义上求极限可得: α(1 − s) = β 1 − s2 . 取 s = −1 得 α = 0, 再取 s = 0 得 β = 0, 与 α2 + β 2 = 1 矛盾. 所以原数列 cos n2 发散.
5
2
1 2n
) x
− g′
(
1 2n
) )
考虑 f (x) = 则可证 f ′ (x) =
∞ ∑ n=0 ∞ ∑ n=0
1 2n (M
( 1) g x+ n , 2 n + 1) ( 1) g′ x + n , 2 n + 1) 1 g ′′ (1) , 2n∈ [−1, 1], x ∈ [−1, 1],
f ′′ (0) =
∞ ∑ n=0
2n (M
n
+ 1)
但 f ′ 在 − 21 n 这些点上不连续.
2
ytdwdw: 数学分析高等数学题选解
问题: 设 µ > 0, f (x) 在 [a, b] 上连续, 在 (a, b) 内可导, c ∈ (a, b) 且 f ′ (c) = 0. 求证: ∃ ξ ∈ (a, b) 使得 f ′ (ξ ) = µ(f (ξ ) − f (a)). 证明: 给大家一把牛刀—Darboux 定理. 今后此类问题用不着灵机一动. ∫ x ( )′ 由于 f (x) − µ(f (t) − f (a)) dt = f ′ (x) − µ(f (x) − f (a)), 因此由 Darboux 定理, f ′ (x) − µ(f (x) − f (a)) 在 (a, b) 内满足介值性. 于是若结论不成立, 则 f ′ (x) − µ(f (x) − f (a)) 在 (a, b) 内恒正或恒负. 不妨设 f ′ (x) − µ(f (x) − f (a)) 恒正, 则 ( )′ ( ) e−µx (f (x) − f (a)) = e−µx f ′ (x) − µ(f (x) − f (a)) > 0, 所以 e−µx (f (x) − f (a)) > e−µa (f (a) − f (a)) = 0, 即 f (x) − f (a) > 0, 所以 ( ) f ′ (x) − µ(f (x) − f (a)) ∀ x ∈ (a, b]. = −µ(f (c) − f (a)) < 0. ∀ x ∈ (a, b].
