上证指数的有序聚类分析
上证指数的运行规律及趋势分析

上证指数的运行规律及趋势分析作者:郭博瑞来源:《市场周刊·市场版》2017年第03期摘要:在对金融证券市场深入研究的基础上,本文从斐波那契序列出发,探讨上证指数运行规律,提出上证指数的“彼得定律”,据此做出上证指数正运行在第Ⅸ波的推论,并对第Ⅸ波高低点的时间及点位做出预测。
关键词:上证指数;斐波那契数列;运行规律;未来趋势上证指数是以上海证券交易所挂牌上市的全部股票为计算范围,以发行量为权数的加权综合股价指数,是国内外普遍采用的反映中国股市总体走势的统计指标。
它的基日定为1990年12月19日。
目前,对证券市场波动性特征的研究已经成为金融研究者关注的对象。
从上证指数历史走势看,高低点位置疏密不一,极难发现周期性规律。
但是,研究上证指数高低点分布规律是一个很有意义的难题,这对研究上证指数运行规律及中国证券市场的发展具有积极作用。
作者通过观察、分析和研究,发现上证指数波段高低点的分布规律与斐波那契数列存有联系。
一、斐波那契数列斐波那契数列,又称黄金分割数列,指这样一个数列:0、1、1、2、3、5、8、13、21、34、…这是一个线性递推数列。
它有如下一些特点:1、从第三项起,数列中任一数字都是由前两个数字之和构成;2、前一数字与后一数字之比,趋近于一固定常数,即0.618;3、后一数字与前一数字之比例,趋近于 1.618;在数学上,斐波那契数列被以递归的方法定义:F(0)=0,F(1)=1,F(n)=F(n-1)+F(n-2)(n≥2,n∈N*)。
依次可得:F(2)=1,F(3)=2,F(4)=3,F(5)=5,F (6)=8,F(7)=13,F(8)=21,F(9)=34,F(10)=55,F(11)=89,…二、上证指数中的“彼得定律”按上证指数月线运行走势,进行波段划分,见图1:图中数字波依次命名为:第Ⅰ波、第Ⅱ波、第Ⅲ波、第Ⅳ波、第Ⅴ波、第Ⅵ波、第Ⅶ波、第Ⅷ波。
每波由升浪和跌浪两部分组成(第Ⅱ波除外)。
聚类分析在股票投资分析中的应用

总资产利润率是净利润与平均资产总额的比值。 可以在一定程度上 反映上市公司实际整体盈利能力。 净资产利润率是净利润与平均净资产
之间的比值, 可以在一定程度上反映股东投资报酬大小。 主营业务收益
率实际上就是主要业务利润与主营业务收入的比值, 主营业务就是上市
公司主要利润来源以及发展方向。 如果具有越大的主营业务收益率, 就
选取数据指标的时候尽可能在不重复的时候, 选择时间跨度最小的、 增
加样本量比较多的指标。 基本数据来源区间 114 家基本股票样本, 并且适当的把不完整数据样本剔
除, 给出每只股票的净资产、 收益、 经营现金流、 净资产收益、 主营收
入增长率以及利润增长率等相关指标数据, 并以此分析和研究股票的投
关键词: 聚类分析; 股票; 投资分析; 应用
前言 现阶段, 社会在信息爆炸时代发展, 在此过程中会出现相应的不确 定因素, 需要合理利用数据分析的方式来分析数据, 保证能够从数据中 提取有效的信息。 股票市场是市场经济发展的重要部分, 并且逐渐朝着 规范化和成熟化方向发展。 但是, 股市变化莫测、 涨跌无常, 想要在股 市中得到一定的回报, 成为股市发展中的成功者, 需要充分研究和分析 上市公司的发展前景、 历史业绩等相关财务情况, 合理判断上市公司股 票价值。 1.聚类分析概述 聚类实际上就是把抽象或者物理对象进行集合分类, 形成由类似对 象构成多个类的过程。 通过聚类形成的簇是数据对象组合, 相比较同簇 中对象具有很高相似度, 但是相比较其他簇中的对象就存在很大差异。 利用描述对象的实际属性值来计算相异度[1] 。 在应用的时候, 能够适当 的把簇中数据当作整体进行分析。 聚类分析是经过众多领域研究得到 的, 主要包括统计学、 数据挖掘、 机器学习以及生物学。 聚类分析实际 上就是在相应给定的数据集合对象中, 适当的分为不同簇的集合, 也就 是说在某空间中规定了数据库中能够得到有限的例子集合或者得到有限 的取样点集合。 聚类的主要目的就是把相关数据信息聚集成类, 使得类 间具有最小的相似性, 而类内具有最大相似性。 聚类分析属于统计学中 的分支之一, 已经被大量运用到众多领域中, 并且可以在很多应用中使 用不同分析技术, 例如, 模式识别、 数据分析、 空间数据库技术以及图 像处理技术等。 利用聚类分析的方式来准确的识别稀疏区域和密集区 域, 并且能够在分析过程中找到全局布局方式以及相关数据间存在的联 系。 在实际运用的过程中, 聚类分析技术可以在不同的众多消费者中找 到具有一定特征的消费群体。 此外, 还能够对不同群体的消费模式进行 分析和研究, 以便于为企业在决策营销策略的时候提供保障和依据。 例 如, 聚类分析应用到网络信息中, 可以在一定程度上识别和分析不同种 类文档, 找到数据隐藏的模式。 聚类分析方法基本特征: 分析方式十分直观、 简单。 聚类分析一般 都是使用在研究性分析方面, 可以从多方面理解聚类分析结果, 最后在 众多结果中找到最符合实际情况的, 以此来进行后续分析以及主观判 断。 不管实际数据中是否具有不同种类的区别, 在进行聚类分析以后都 可以适当得到各种类别。 研究人员选择的聚类变量实际上就是聚类分析 的解, 删除或者增加变量, 都有可能会对最后的结果造成一定影响。 相 关研究人员在应用聚类分析的时候, 需要密切注意相关因素, 对于聚类 结果存在比较大影响的就是特殊变量和异常值[2] 。 2.聚类指标的选取利用 依据上市公司基本发展情况, 支持股票长期发展的主要因素就是成 长能力和盈利能力, 同时也是判断上市公司是否具有一定投资价值的基 本保障, 业绩良好的公司具有相对比较高的扩张能力。 适当的选出每股 收益, 主营收入以及净资产收益率等三个因素与股票息息相关, 以此来 判断影响股票发展的收益。 2.1 公司潜力指标
上证指数的有序聚类分析

20 0 8年 6月
重庆 文 理 学 院学 报 ( 自然 科 学版 )
Ju o m ̄ o h nq n nvri f f n ce c s( a rl c n eE io ) fC o g i U i s yo l a dS i e N t a S i c dt n g e t A s n u e i
} [ 稿 日期 ]0 8— 3— 5 收 20 0 0 [ 作者 简 介 ] 春 华 (9 3一) 女 , 杨 17 , 四川 自贡 人 , 师 , 士 讲 硕
2 6
维普资讯
其
P 中 ,
, .
一
1 {2i } i, 2+1 … , , i 3—1 … { , } ii K+1 … , } , n
m
1
就是使 e P nK) ( ( , )达 到最 小 的一 种分 法 .
第 3步 :
an ri
l I< 。 < 2
an ri
<t K≤
类分 析 .
本文建 立 金融 时间序 列 的有序 聚类 分 析 , 2 0 对 0 7年 上证 指 数进 行 实 证分 析 . 序 聚 类分 析 有 精 有 确最优 解方 法 : 费歇算 法 . 1 算 法分析 第 1 : 义类 的直径 . 步 定 设 变量 的某一 归 类是 ,川 , , }i … , ≤J, 其均值 向量是 :
的AI R MA和对误 差项 进行 拟合等 .
最 常用 的 时间序 列分析 除 了用上述 的 回归模 型 外 , 用得 较多 的是 对 时 间序 列进 行分 割 . 间序 列 时 分 割是 将长度 为 n的时 间序 列分 为 k , 段 对各 段分 别使 用不 同 的模型 进行 描 述 . 如何 准确 对 时 间序 列 进 行分 割才 能取得 所需 的效 果 , 要进行 分 析. 需 聚类分 析是把 一组 物理 或抽 象对象 按照 相似 性归 为各类 , 也称 为 “ 指导 分类 ” 它是 将 整个 目标 无 . 数据 分成 多个 不 同的组 , 得 每个 组 内 的数据 尽 可能 相 似 , 使 而不 同组 中的数 据 具有 明显 的 差别 . 常用 的 聚类分 析不 太适合 金 融时 间的 聚类 分析 . 我们 考 虑到金 融 时间序 列 的时 间先 后 的顺 序 , 建立 有序 聚
聚类分析和因子分析在股票投资中的应用
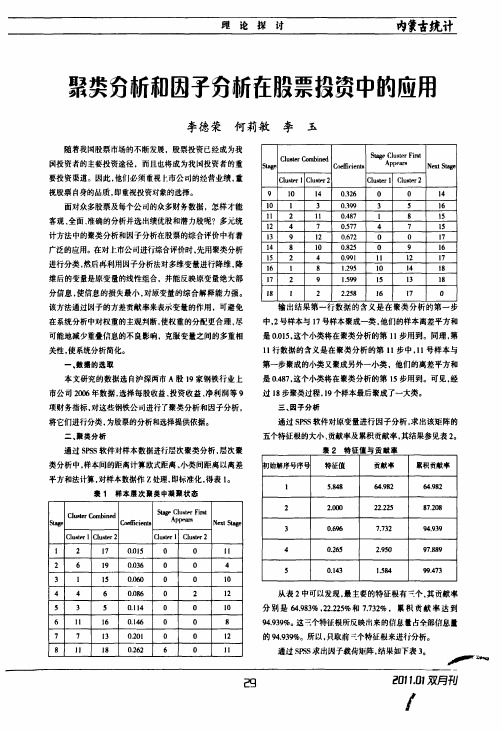
理论探讨内蒙吉统计聚类穷析和因子分析在股票投资中的应用李德荣何莉敏李玉随着我国股票市场的不断发展,股票投资已经成为我国投资者的主要投资途径,而且也将成为我困投资者的重要投资渠道。
因此.他们必须重视上市公司的经营业绩.重视股票自身的晶质,即重视投资对象的选择。
面对众多股票及每个公司的众多财务数据,怎样才能客观、全面、准确的分析并选出绩优股和潜力股呢?多元统计方法中的聚类分析和因子分析在股票的综合评价中有着广泛的应用。
在对上市公司进行综合评价时.先用聚类分析进行分类.然后再利用因子分析法对多维变量进行降维。
降维后的变量是原变量的线性组合.并能反映原变量绝大部分信息,使信息的损失最小,对原变量的综合解释能力强。
该方法通过因子的方差贡献率来表示变量的作用。
可避免在系统分析中对权重的主观判断.使权重的分配更合理,尽可能地减少重叠信息的不良影响,克服变量之间的多重相关性.使系统分析简化。
一、数据的选取本文研究的数据选自沪深两市A 股19家钢铁行业上市公司2006年数据.选择每股收益。
投资收益。
净利润等9项财务指标.对这些钢铁公司进行了聚类分析和因子分析,将它们进行分类。
为股票的分析和选择提供依据。
二、聚类分析通过SPSS 软件对样本数据进行层次聚类分析,层次聚类分析中,样本间的距离计算欧式距离、小类间距离以离差平方和法计算。
对样本数据作z 处理.即标准化.得表l 。
裘1样本屡次聚类中凝聚状态Clus te r C om bi n edStage C l u s t er Fi rstSt a g eC oe ffi c i ent sA ppear sN ext StageClus te r l C l u s t er 2Clus te r IC l u s t er 2I 2170.015O O I l26190.0360O 43l150.0600010446O .086O 2125350.1140O 106l l 160.14600877130.20I O 0128JJJ 80.2626l IC l u s t er C o m bi ne dSt age C l u s t er Fi rstStageCoef f i ei e nt sA ppear sN ext StageC l u s t er lC l u s t er 2C l u s t er lC l u s t er 29l O 140.3260O1410l 30.39935161l 2l l 0.48781512470.5774715139120.6720O 17148i 00.825O91615240.99l l I 12171681.295l O 141817291.5991513181822.2581617输出结果第一行数据的含义是在聚类分析的第一步中,2号样本与17号样本聚成一类,他们的样本离差平方和是0.015.这个小类将在聚类分析的第l l 步用到。
聚类分析在证券市场分析中的应用

山东交通学院毕业生毕业论文(设计)题目:聚类分析在证券市场分析中的应用摘要本文随机选取了40家在沪深上市的山东省的公司企业,选择每股收益、每股净资产、主营收入增长率、主营利润增长率和净资产收益率5项指标评价体系。
通过系统聚类分析方法对这40家公司企业的股票进行聚类分析,以此对股票的收益性、成长性等方面进行分析,帮助投资者准确地把握股票的总体特性以及预测股票的成长能力,使投资者及时做出最佳的投资决策,进而获得可观的投资回报。
最后在聚类分析的基础上,对聚类分析结果采用means方法进行检验,以此来进一步验证分析结果的可靠性和可信性。
此研究表明聚类分析方法在证券市场投资分析中具有有效性和实用性。
关键词:聚类分析,证券市场投资,means方法,投资回报AbstractIn this paper, we randomly selected 40 companies in Shandong province which were listed in Shanghai and Shenzhen stock market, and we choice the five indicators evaluation system that are the earnings of per share, the net assets of per share, the growth rate of the main business revenue, the growth rate of the main business profit and the yield of the net assets. In order to help investors to accurately grasp the overall features of the stock and the growth ability of the stock, we effectively use the method of the system clustering analysis to analyze the stock`s profitability, growth, etc, which were mentioned above the stocks of the 40 companies. Above all, this can help investors to make the best investment decisions, and get considerable returns in a timely manner. Finally, in order to further verify the reliability and credibility of analysis results, we use means methods to test the results of cluster analysis. The study shows that the method of clustering analysis has validity and practicability in the securities market investment analysis.Key words: Clustering analysis, Stock market investment, Means method,Return on investment目录1.绪论 (1)1.1论文研究的背景及意义 (1)1.2 聚类分析在证券市场分析中的应用价值 (2)1.3 聚类分析在证券市场分析中应用的优点 (2)1.4 聚类分析在证券市场分析中应用的当前状况 (2)1.5本文的研究内容及内容结构 (3)1.5.1 研究内容 (3)1.5.2 内容结构 (3)2.聚类分析 (4)2.1聚类分析的基本思想 (4)2.2聚类分析的方法 (4)2.3系统聚类法的基本思想和基本步骤 (5)2.3.1样本间距离的度量 (6)2.3.2类间距离的度量 (8)2.4 系统聚类分析方法的比较 (9)2.5系统聚类法中类个数的确定问题 (10)3.聚类分析在证券市场分析中的应用 (12)3.1 聚类分析在证券市场分析中应用时的指标评价体系的选择 (12)3.1.1盈利能力指标 (12)3.1.2成长能力指标 (12)3.1.3扩张能力指标 (13)3.2实证研究 (14)3.2.1原始样本数据标准化 (15)SPSS软件对样本公司股票进行聚类分析 (17)3.2.2用 19.03.2.3分类个数的确定 (22)3.2.4聚类结果 (24)3.2.5对聚类结果进行检验 (25)3.2.6结果分析 (26)4.总结和展望 (29)总结 (30)1.绪论1.1论文研究的背景及意义改革开放以来,随着我国市场经济的迅速、健康发展,国民的金融意识和投资意愿日益增强,而作为市场经济的重要组成部分——证券市场,正渐渐地走向成熟,越来越多的投资者把目光投向了股票,历史已经证明,股票不仅在过去是一种已经给投资者提供了可观的长期收益,并且在将来也会是提供良好机遇的投J西格尔,资媒介。
上证指数历史规律总结

上证指数历史规律总结上证指数历史规律总结前言作为一名资深的创作者,我一直对上证指数的历史规律感兴趣。
通过对过去几十年的数据进行分析和总结,我发现了一些有趣的规律和趋势。
在本文中,我将对这些规律进行归纳总结,并分享给读者。
正文1. 季节性影响•春季行情:每年春季都有一波较大的行情,这与资金活跃和资金需求增加有关。
•夏季调整:在春季行情过后,往往会迎来一段相对较长的调整期,这是由于市场回调和投资者集体观望造成的。
•秋季反弹:在夏季调整之后,往往会有一波反弹行情,投资者信心逐渐恢复,市场情绪也会有所改善。
•冬季震荡:在秋季反弹之后,市场常常进入一个震荡的状态,这是市场寻找方向和筑底的过程。
2. 周期性波动•短期波动:上证指数的短期波动受到各种因素的影响,如政策变动、经济数据、利率等。
这种波动往往是短暂的,投资者需保持耐心和谨慎。
•中期波动:上证指数的中期波动一般以几个月至一年为周期,可以根据市场热点和行业轮动进行分析和预测。
•长期趋势:尽管上证指数存在周期性波动,但从长期来看,指数一般呈现出上涨的趋势。
这与中国经济的长期增长和资本市场的发展密切相关。
3. 技术指标应用•移动平均线:通过计算一段时间内的平均价格,可以把过去一段时间内的价格趋势反映出来,帮助判断指数的走势。
•相对强弱指标(RSI):通过计算一段时间内的上涨幅度和下跌幅度之比,可以判断市场的超买超卖情况,辅助投资决策。
•成交量指标:成交量是市场活跃程度的指标,高成交量多伴随着市场行情的变化。
通过观察成交量的变化,可以判断市场的态势。
结尾上证指数的历史规律总结表明,市场的行情和波动是受多种因素影响的。
投资者在进行投资决策时,需要结合季节性影响、周期性波动以及技术指标的应用进行综合考虑。
同时,投资要有长远的眼光,遵循定投和分散投资的原则,以平滑风险、实现长期稳定的投资收益。
综上所述,上证指数的历史规律总结表明市场的变化是有规律可寻的。
在投资过程中,投资者应该注重以下几点:1.监测季节性影响:了解春季行情、夏季调整、秋季反弹和冬季震荡等季节性的市场变化规律,合理把握投资时机。
聚类分析和因子分析在股票投资中的作用

聚类分析和因子分析在股票投资中的应用摘要:随着我国股票市场的迅速发展和逐步完善,股票的投资特点和前景越来越受到投资者的追捧。
理性的投资者,将会更加重视上市公司的经营业绩和股票的内在价值。
但如何对股票的价值进行评价在实践中是个难点,对此进行探讨十分必要。
本文运用聚类分析对影响上市公司股票业绩的变量进行分类,运用因子分析模型得出决定股票业绩的公因子,并进行了比较。
关键词:聚类分析因子分析SPSS 股票投资分析1研究目的与方法1.1研究目的及意义随着我国股票市场的不断发展,股票投资已经成为我国投资者的主要投资途径,而且也将成为我国投资者的重要投资渠道。
因此,他们必须重视上市公司的经营业绩,重视股票自身的品质,即重视投资对象的选择。
面对众多股票及各个公司的财务数据,怎样才能客观、全面、准确的分析并选出绩优股和潜力股呢?本文选择30家上市公司作为研究对象,进行业绩评价。
目的是对上市公司财务分析的基础上,探索各上市公司的投资价值,为投资者提供一定的决策指导和理论参考。
1.2研究方法多元统计分析方法中的聚类分析和因子分析在股票的综合评价中有着广泛的应用。
本文采用的分析方法是因子分析和聚类分析。
在对上市公司进行综合评价时,先用聚类分析进行分类,然后再利用因子分析法对多维变量进行降维,降维后的变量是原变量的线性组合,并能反映原变量绝大部分信息,使信息的损失最小,对原变量的综合解释能力强。
该方法通过因子的方差贡献率来表示变量的作用,可避免在系统分析中对权重的主观判断,使权重的分配更合理,尽可能地减少重叠信息的不良影响,克服变量之间的多重相关性,使系统分析简化。
2文献综述2.1国外研究Serpil(2006)将主成分分析法和判别分析法结合起来,用来对早期综合预警模型的估计。
April Kerby, James Lawrence运用多元统计方法中的主成分分析和判别分析来作为选择好或不好股票的依据,另外,他认为这也是处理多变量高维复杂财经数据的一种方法。
中国证券市场阶段划分的有序聚类

方,计算结果被定义为年波动性的日贡献:
Sdt =(100
△rt )2 △准t
其中:分母表示在 r 变化过程中观测值之间日期时间流
逝的作用。如果每天都要新的数据产生,则△准t=1,坌t,但是 在周末或节假日不产生数据,则△准t=∈(1,7)。
2012. 7 下旬·71·□
□财会月刊·全国优秀经济期刊
策 可 能 会 出 现 暂 时 的 (或 有 条 件 的) 稳 定(Crotty,1994;
Dymski,1994)。Dymsk(i 1992)认为在平静时期,金融市场中行
为的特点可以刻画为新凯恩斯主义的信息不对称下的决策;
而动荡时期金融市场中的行为更适合用后凯恩斯主义的基础
不确定性下的决策进行分析。因此,在对金融市场经济现象进
本文运用有序样品聚类分析法,采用市场不确定性、股票 错误定价和盈余管理数据对证券市场进行阶段分类,讨论在 不同阶段三者的关系,并分析不同市场阶段合适的主导理 论—— —信息不对称理论还是行为财务理论。
一、理论分析与变量的衡量 1. 简单理论分析。现实世界中存在不确定性,必然会影 响到投资者的信息处理。Glickman(1994)认为在存在基础不 确定的条件下,个体对客观事实的理解会影响预期。对客观事 实的理解就涉及到个体处理客观信息时存在的有限理性,因
此,不确定性必然与有限理性相关。事实上,早在 20 世纪 30
年代,全球经历了经济大萧条以后,Keynes(1936)就认为股
价“泡沫”反映了投资者的非理性行为。由此推理,可以认为不
确定性影响投资者的非理性行为从而影响股价。
关于盈余管理对股价的影响,也有众多的学者在进行研
究。Myers 和 Majlu(f 1984)研究表明,如果投资者掌握的关于
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 实证分析
用中国人民银行网站提供的金融股票交易统计数据 ,采取 2007年的上证指数 A 股的最低综合股
价指数进行实证分析. 原始数据见表 1. 由于一般的统计分析软件没有有序聚类分析的实现 ,故使用
matlab7. 0软件编程实现.
表 1 原始数据
时间 1月
2月
3月
4月
5月
6月
7月
8月
9月 10月 11月 12月
i =1
Байду номын сангаас
j =1
j=1
e ( P ( n, K) ) + eA ( P ( n, K) ) .
∑ 其中 ,
x
=
1 n
n i =1
xi 是均值向量 ;
eA
( P ( n,
K) ) 叫作类间平方和 ,是反映各类之间的差异的. 当
n,
K
固定时 , ST 为一个常数. 显然 ,当 e ( P ( n, K) ) 越小 , eA ( P ( n, K) ) 越大 ,分类越合理. 因此 ,最优分法也
表 3 最小误差函数 e ( P ( i, j) )
2
3
4
5
3
3 594. 7 (2)
4
18 686 (4)
3 594. 7 (4)
5 2. 432 5e + 005 (4)
18 686 (5)
3 594. 7 (5)
6 2. 535e + 005 (4) 1. 240 7e + 005 (5) 18 686 (6) 3 594. 7 (6)
在金融市场分析中 ,技术分析和基本面分析是两大分析方法. 进行技术分析的人士认为 : ( 1)市场
行为包含一切信息 ; (2)价格呈趋势运动 ; (3)历史会重演. 对于金融时间序列研究的主要方法是建立
合适的回归预测模型. 文献 [ 1 ]对金融时间序列建立 ARCH 模型. 文献 [ 2 ]对金融时间序列建立相关
2008年 6月 第 27卷 第 3期
重庆文理学院学报 (自然科学版 ) Journal of Chongqing University of A rts and Sciences (Natural Science Edition)
Jun1, 2008 Vol127 No13
上证指数的有序聚类分析
K
∑ e ( P ( n, K) ) = D ( ij, ij+1 - 1) . j =1
考虑到总离差平方和 :
n
K
K
∑ ∑ ∑ ST >
( xi - x) ′( xi - x) ′=
D ( ij , ij+1 - 1) +
( ij+1 - ij ) ( xij, ij+1 - 1 - ′ x ) ( xij, ij+1 - 1 - x ) =
最低价 2 753. 12 2 668. 33 2 861. 18 3 359. 73 4 029. 90 3 570. 80 3 739. 50 4 494. 21 5 275. 70 5 734. 09 5 015. 93 5 034. 41
j
∑ 第 1步 :计算直径 D ( i, j) = ( xl - xij ) ′( xl - xij ) ,得到所有的直径的计算结果列于表 2. l=i
表 4 上证指数分类情况表 分类
(1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12) (1, 2, 3, 4, 5, 6, 7) , (8, 9, 10, 11, 12) (1, 2, 3, 4, 5, 6, 7) , (8) , (9, 10, 11, 12) (1, 2, 3, 4, 5) , (6, 7) , (8) , (9, 10, 11, 12 ) (1, 2, 3, 4, 5) , (6, 7) , (8) , (9, 10) , (11, 12) (1, 2, 3, 4, 5) , (6, 7) , (8) , (9) , (10) , (11, 12) (1, 2, 3, 4) , (5) , (6, 7) , (8) , (9) , (10) , (11, 12) (1, 2, 3) , (4) , (5) , (6, 7) , (8) , (9) , (10) , (11, 12) (1, 2, 3) , (4) , (5) , (6) , (7) , (8) , (9) , (10) , (11, 12) (1, 2) , (3) , (4) , (5) , (6) , (7) , (8) , (9) , (10) , (11, 12) (1) , (2) , (3) , (4) , (5) , (6) , (7) , (8) , (9) , (10) , (11, 12)
m in e ( P ( 3, 2) ) = m in { D ( 1, j - 1) + D ( j, 3) } = m in{ D ( 1, 1) + D ( 2, 3) , D ( 1, 2) + D ( 3, 3) } 2≤j≤3 = m in{ 0 + 18 686, 3 594. 7 + 0} = 3 594. 7 ( 2) ,
于是 ,又得到第 K - 1类 Gk - 1 = { 1, 2, …, jK - 1}. 由类似方法依次得到分类. 可见 ,求最优解只要计算
出 { D ( i, j) , 1 ≤ i ≤ j ≤ n} 和 { e ( P ( i, j) , 1 ≤ i ≤ n, 1 ≤ j ≤ n} , 并进行适当的判断即可 . [ 4, 5 ]
为记号简单 ,变量 xi 就用下标 i来表示. 设将 n个有序变量分成 K类 ,某一分法为 :
3 [收稿日期 ]2008 - 03 - 05 [作者简介 ]杨春华 (1973 - ) ,女 ,四川自贡人 ,讲师 ,硕士.
26
P ( n, K) : { i1 = 1, i1 + 1, …, i2 - 1} { i2 , i2 + 1, …, i3 - 1} …{ iK , iK + 1, …, n} . 其中 , i1 = 1 < i2 < … < iK ≤ n. 定义这一类的误差函数为 :
7 2. 590 5e + 005 (4)
……
……
1. 265 4e + 005 (5) ……
32 916 (6) ……
17 825 (6) ……
6
……
……
……
……
……
3 594. 7 (7) ……
…… ……
第 3步 :进行分类. 例如 ,我们现在想分为 3类 ,即 k = 3. 由数据知道 , e ( P ( 12, 3) ) = 1. 069 8e + 006,相应的首次分
数据分成多个不同的组 ,使得每个组内的数据尽可能相似 ,而不同组中的数据具有明显的差别. 常用
的聚类分析不太适合金融时间的聚类分析. 我们考虑到金融时间序列的时间先后的顺序 ,建立有序聚
类分析.
本文建立金融时间序列的有序聚类分析 ,对 2007年上证指数进行实证分析. 有序聚类分析有精
确最优解方法 :费歇算法.
就是使 e ( P ( n, K) ) 达到最小的一种分法.
第 3步 : m in e ( P ( n, K) ) 的递推公式为 : i1 = 1 < i2 < … < iK≤n
m in e ( P ( n, K) ) = m in {
m in
e ( P ( j - 1, K - 1) ) + D ( j, n) }.
表 2 直径 D ij
1
2
3
4
5
……
2
3 594. 7
……
3
18 686
18 596
……
4
2. 876 5e + 005 2. 545 9e + 005 1. 242 8e + 005
……
5
1. 289 9e + 006 1. 108 2e + 006 6. 878 6e + 005 2. 245 6e + 005
杨春华 ,刘润智
(重庆文理学院 数学与计算机科学系 ,重庆 永川 402160)
[摘 要 ]本文利用多元统计分析的聚类分析法对 2007年的上证指数 A 股的最低综合股价指 数进行实证分析 ;根据金融时间序列的顺序关系进行有序聚类分析 ,将 2007年的上证指数 A 股的最低综合股价指数进行实证分析 ,并认为分为 2类或 3类较好. [关键词 ]上证指数 ;聚类分析 ;有序聚类分析 [中图分类号 ]O212 [文献标识码 ]A [文章编号 ]1673 - 8012 (2008) 03 - 0026 - 04
从而得到 1, 2, 3分为 2类是分类方法 {1, 2} , { 3} (括号内的数字代表分类达到最小的最后一类的始
27
编号 ). 其次 ,计算 m in{ e ( P ( i, j) ) , 4 ≤ i ≤ 12, 3 ≤ j ≤ 11} .
根据算法 (1)计算得到最小误差函数 e ( P ( i, j) ) ,结果列于表 3,括号内的数字含义同上.
的 AR IMA 和对误差项进行拟合等.
最常用的时间序列分析除了用上述的回归模型外 ,用得较多的是对时间序列进行分割. 时间序列
分割是将长度为 n的时间序列分为 k段 ,对各段分别使用不同的模型进行描述. 如何准确对时间序列
进行分割才能取得所需的效果 ,需要进行分析.
聚类分析是把一组物理或抽象对象按照相似性归为各类 ,也称为“无指导分类 ”. 它是将整个目标
……
