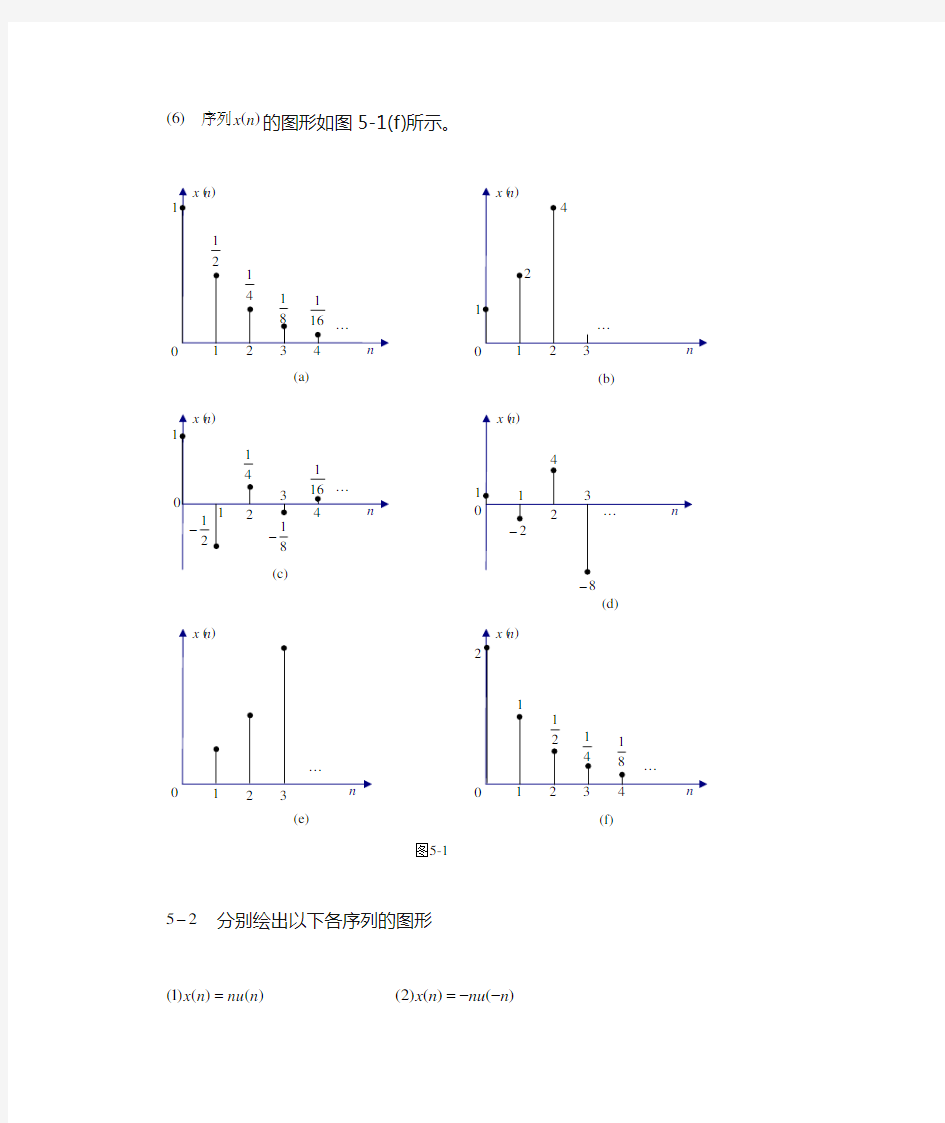
信号与系统课后习题与解答第七章

15- 分别绘出以下各序列的图形

)()21

()()1(n u n x n = )(2)()2(n u n x n =

)()2

()()3(n u n x n -= )()2()()4(n u n x n -=

)1(2)()5(1-=-n u n x n )()2

()()6(1n u n x n -=

解

)()1(n x 序列的图形如图5-1(a)所示。 )()2(n x 序列的图形如图5-1(b)所示。 )()3(n x 序列的图形如图5-1(c)所示。 )()4(n x 序列的图形如图5-1(d)所示。 )()5(n x 序列的图形如图5-1(e)所示。

(b)

图5-1

(a)

(f)

(e)

(d)

25- 分别绘出以下各序列的图形

)()()1(n nu n x = )()()2(n nu n x --= )(2)()3(n u n x n -= )()2

()()4(n u n x n --=

)()21()()5(n u n x n --= )1()2

()()6(1+=+n u n x n

解

)

　序列的图形如图5-２(b)所示。

(

)2(n

　序列的图形如图5-２(c)所示。

)

)3(n

(

　序列的图形如图5-２(d)所示。)4(n

(

)

)5(n

　序列的图形如图5-２(e)所示。

(

)

　序列的图形如图5-２(f)所示。

(

)

)6(n

(b)

图5-2

(c)

(f)

(e)

(d)

-(a)

35- 分别绘出以下各序列的图形

sin()()1(π

n n x =

)510cos()()2(π

π-=n n x

)

sin()65()()3(π

n n x n =

解

)()1(n x 序列的图形如图5-３(a)所示。 )()2(n x 序列的图形如图5-３(b)所示。 )()3(n x 序列的图形如图5-３(c)所示。

图5-3

(a)

45- 判断以下各序列是否是周期性的，如果是周期性的，试确定其周期。 )8

73sin()()1(π

π-=n A n x

()()2(π-=n

e n x j

解

)1(因为

3147322==πππw 是有理数，所以)(n x 是周期性的，且周期为14。 )2(因为

πππ168

122==w

为无理数，所以)(n x 是非周期性的。 55- 列出图45-所示系统的差分方程，已知边界条件0)1(=-y 。分别求以下

输入序列时的输出)(n y ，并绘出其图形（用逐次迭代方法求）。

图5-4

)()()1(n n x δ= )()()2(n u n x =

)5()()()3(--=n u n u n x

解：

由图45-可写出该系统的差分方程为

)()1(3

)(n x n y n y =--

即)1(3

)()(-+=n y n x n y

)1(当)()(n n x δ=时， 103

1)1(31)0()0(=?+=-+

=y y δ

)

()31

()()3

()1(31)()(...

(31310)1(31)2()2(311310)0(31)1()1(2

n u n y n y n n y y y y y n n ==-+

==?+=+==?+=+=所以δδδ 其图形如图)(55a -所示

(b)

图5-5

(a)

(c)

)2(当)()(n u n x =时，

)31(310311)1(31)0()0(0

-==?+=-+=y u y 2

)31(3341311)0(31)1()1(1

-==?+=+=y u y 2

)31(3134311)1(31)2()2(2

-==?+=+=y u y …

)31(3)1(31)()(n

n y n u n y -=-+= 所以 )(2)31(3)(n u n y n

其图形如图)(55b -所示

)3(当)5()()(--=n u n u n x 时，

)31(3)1(31)0()0(0

-=-+=y u y 2

)31(3)0(31)1()1(1

-=+=y u y 2

)31(3)1(31)2()2(2

-=+=y u y 2

)31(3)2(31)3()3(3

-=+=y u y 2)31(3)3(31)4()4(4

-=+=y u y 543121

312131)4(310)5(=?=+=y y

63121

)5(310)6(=+=y y

n n y 3

121

)(= )5(≥n

所以 )5(3121

)]5()(][)31(2123[)(-+---=n u n u n u n y n n

其图形如图)(55c -所示

65- 列出图65-所示系统的差分方程，已知边界条件0)1(=-y 并限定当0

图5-6

解由图65-可写出该系统的差分方程为

)1()1(31

)(-=--n x n y n y

即)1()1(31

)(-+-=n x n y n y

若)()(n n x δ=，则有

000)1()1(31

)0(=+=-+-=

δy y 110)0()0(31

)1(=+=+=δy y

310131)1()1(31)2(=+?=+=δy y

2)31(03131)2()2(31)3(=+?=+=δy y

32)3

1(0)31(31)3()3(31)4(=+?=+=δy y

…

1)3

()1()1(31)(-=-+-=n n n y n y δ

所以 )1()31

()(1-=-n u n y n

与题)1(55-比较，此题中的序列)(n y 的第一个非零值位于1=n ，而题)1(55-中的)(n y 的第一个非零值位于0=n 。题)1(55-中的)(n y 向右移一个单位即可得到此题中的)(n y 。

75- 在题55-中，若限定当0>n 时，全部0)(=n y ，以0)1(=y 为边界条件，

求当)()(n n x δ=时的响应)(n y ，这时，可以得到一个左边序列，试解释为什么会出现这种结果。

解题55-中的差分方程为)1(3

)()(-+

=n y n x n y ① 若限定当0>n 时，全部0)(=n y ，则迭代时分别令,...2,1,0,1--=n 。将①改写为)(3)(3)1(n x n y n y -=- 则有

000)1(3)1(3)0(=-=-=δy y 330)0(3)0(3)1(-=-=-=-δy y

23)1(3)1(3)2(-=---=-δy y 33)2(3)2(3)3(-=---=-δy y …

n n y --=3)(

所以 )1(3)(---=-n u n y n

)(n y 是个左边序列。之所以得到一个左边序列，是因为限定了当0

>n 时，0)(=n y ，即)(n y 的非零值只可能出现在0

85- 列出图75-所示系统的差分方程，指出其阶次。

图5-7

解图75-所示系统的差分方程为 )1()()1()(1010-+=-+n x a n x a n y b n y b 此为一阶差分方程。

95- 列出图85-所示系统的差分方程，指出其阶次。

图5-8

解图85-所示系统的差分方程为

)1()()2()1()(1021-+=----n x a n x a n y b n y b n y 此为二阶差分方程。

105- 已知描述系统的差分方程表示式为 ∑=-=7

0)()(r r r n x b n y

试绘出此离散系统的方框图。如果)()(,0)1(n n x y δ==-，试求)(n y ，指出此时

)(n y 有何特点，这种特点与系统的结构有何关系。

解此离散系统的方框图如图95-所示若)()(n n x δ=，则

∑=-=7

0)()(r r r n b n y δ

即0)0(b y =，1)1(b y =，2)2(b y =，3)3(b y =

4)4(b y =，5)5(b y =，6)6(b y =，7)7(b y =

而当0n 时，0)(=n y

此时)(n y 是有限长序列，且在非零值区间内的值为)7,...,0(=r b r ，即正好是各前向支路的增益。)(n y 的这一特点确决于系统在结构上只有前向支路，没有反馈支路的特点。 115- 解差分方程

)1( 1)0(,0)1(2

)(==--y n y n y

)2( 2

)0(,0)1(2)(==--y n y n y

)3( 1)1(,0)1(3)(==-+y n y n y )4( 1)0(,0)1(3

)(==-+

y n y n y 解 )1(特征方程为 02

=-α

求得特征根 2

=α

于是齐次解 n C n y )2

()(?=

因而 n n y )2

()(=

)2(特征方程为 02=-α 求得特征根 2=α 于是齐次解 n C n y 2)(?=

将21)0(=

y 代入上式，得2

1=C 因而 122)2

()(-=?=n n n y

)3(特征方程为 03=+α

求得特征根 3-=α 于是齐次解 n C n y )3()(-?=

将1)1(=y 代入上式，得3

-=C

因而 1)3()3(2

)(--=-?-=n n n y

)4(特征方程为 03

=+α

求得特征根 32

-=α

于是齐次解 n C n y )3

()(-?=

将1)0(=y 代入上式，得1=C

因而 n n y )3

()(-=

125- 解差分方程

)1( 1)2(,2)1(,0)2(2)1(3)(=-=-=-+-+y y n y n y n y )2( 1)1()0(,0)2()1(2)(=-==-+-+y y n y n y n y

)3( 2)1(,1)0(,0)2()(===-+y y n y n y

解 )1(特征方程为 0232=++αα 求得特征根 2,121-=-=αα 于是齐次解 n n C C n y )2()1()(21-+-= 将1)2(,2)1(=-=-y y 代入上式，得方程组

???

?=+=--141221212

1C C C C 解得 12,421-==C C 因而 n n n y )2(12)1(4)(---=

)2(特征方程为 0122=++αα

求得特征根 1,21-=α

于是齐次解 n C n C n y )1)(()(21-+= 将1)2(,2)1(=-=-y y 代入上式，得方程组

?=-?+-=1)1()(1

212C C C 解得 1,221==C C

因而 n n n y )1)(12()(-+=

)3(特征方程为 012=+α

求得特征根 j j -==21,αα

于是齐次解 2

121)()(ππ

n j

n j n n e

C e

C j C j C n y -+=-+=

s i n ()2c o s (π

πn n +=

将2)1(,1)0(==y y 代入上式，得方程组

?=-=+21

21j C j C C C 解得 j C j C +=-=

,2121 因而 )()(2

1)(2

ππππ

n j

j e

n y ----+=

sin()2cos(

ππn n += 135- 解差分方程

0)3(12)2(16)1(7)(=---+--n y n y n y n y

5)3(,3)2(,1)1(-=-=-=y y y 解特征方程为 01216723=-+-ααα 求得特征根 2,33,21==αα

于是齐次解 n n C n C C n y 2)(3)(321?++?= 将5)3(,3)2(,1)1(-=-=-=y y y 代入上式，得方程组

??-=++-=++-=?++5

)3(8273)2(4912)(3321321321C C C C C C C C C 求得 1,1,1321-=-==C C C 因而 n n n n y 2)1(3)(+-=

145- 解差分方程n n y n y +--=)1(5)(。已知边界条件0)1(=-y 。

解特征方程为 05=+α 求得特征根 5-=α 于是齐次解 n h C n y )5()(-= 令特解 21)(D n D n y p += 将)(n y p 代入原方程，有

n D n D D n D =+-++])1([52121 比较上式两边得 36

5,6121==

D D 则全解 36

61)5()()()(++-=+=n C n y n y n y n p h

将0)1(=-y 代入上式，得 36

-=C

因而 ]56)5[(361

)(1++-=+n n y n

155- 解差分方程21(2)(-=-+n n y n y 。已知1)0(=y 。

解特征方程为 02=+α 求得特征根 2-=α 于是齐次解 n h C n y )2()(-= 令特解 21)(D n D n y p += 将)(n y p 代入原方程，有

22)1(22121-=+-++n D n D D n D

比较上式两边得 9

,3121-==D D

则全解 9

31)2()()()(-+-=+=n C n y n y n y n p h

将1)0(=y 代入上式，得 9

因而 ]43)2(13[9

)(-+-=n n y n

165- 解差分方程

n n y n y n y 3)2()1(2)(=-+-+ 已知0)0(,0)1(==-y y 解特征方程为 0122=++αα

求得特征根 12,1-=α

于是齐次解 n C n C n y )1()()(21-?+= 令特解 n p D n y 3)(1= 将)(n y p 代入原方程，有

n n n n D D D 3332321111=++-- 比较上式两边得 16

91=

D 则全解 n n p h C n C n y n y n y 316

)1)(()()()(21?+-+=+=

将0)0(,0)1(==-y y 代入上式，得方程组

???

=+=?+-?+-016903

1169)1()(221C C C 求得 16

,4321-=-=C C

因而 n n n n y 316

)1)(16943()(----=

175- 解差分方程

n n y n y sin )2()(=-+

已知0)2(,0)1(=-=-y y 。解特征方程为 012=+α 求得特征根 j j -==21,αα

于是齐次解 2

121)()(ππ

n j

n j n

C e C j C j C n y -+=-+=

令特解 jn jn p e D e D n y -+=21)( 将)(n y p 代入原方程，有

jn n j n j jn jn e j

e j e D e D e D e D ------=

+++2121)2(2)2(121

比较上式两边得 1c o s 4)(2)1(221j

j j j je e e e j e j D -=+-=+-=--- 1cos 4)(2)1(222j

j j j je e e e j e j D --=+=+= 则全解 jn j jn j n j

n j e je e je e

C e C n y ---+-++=1

cos 41cos 4)(2

1ππ

将0)2(,0)1(=-=-y y 代入上式，得方程组

???

????

=+-+--=+-++--0

1cos 41cos 401

cos 41cos 42121j

j je je jC jC j j jC jC 解得 1t a n 4

21-==C C

因而 )2

c o s ()1(t a n 21c o s 1t a n 21s i n 21)2c o s ()1(t a n 21]c o s 1s i n 1c o s [s i n 1c o s 21)

1s i n (1c o s 21)2c o s ()1(t a n 21]

[1c o s 4)(1t a n 41)()1()1(22

ππππ

n n n n n n n n e e j e e n y n j n j n j n j +?+=++=++-=--++-=+-+- 185- 解差分方程n n y n y =--)1()(，已知0)1(=-y 。

)1( 用迭代法逐次求出数值解，归纳一个闭式解答（对于0≥n ）。 )2( 分别求齐次解与特解，讨论此题应如何假设特解函数式。

解 )1( n n y n y +-=)1()( 令 ,...,2,1,0=n 有

)0(2

)

1()(...

410464)3()4(24

36333)2()3(23

23212)1()2(22

11101)0()1(2100000)1()0(≥+=

=+=+=?==+=+=?=

=+=+=?=

=+=+=?==+=+-=n n n n y y y y y y y y y y y

)2( 易知齐次解 C C n y n h =?=)1()(

特解应设为 n D n D n y p 221)(+= 将)(n y p 代入原方程，有

n n D n D n D n D =----+)1()1(221221 比较上式两边，得 2

21==D D 因而 n n C n y 2

121)(2++

= 将0)1(=-y 代入上式，得 0=C 因而 )0)......(1(2

2121)(2≥+=+=

n n n n n n y 195- 如果上题185-中的方程式改为3)1()(n n y n y =--，重复回答上

题所问。

解齐次解依然为 C n y h =)(

特解设为 n D n D n D n D n y p 1223344)(+++= 将)(n y p 代入原方程，有

312233*********)1()1()1()1(n n D n D n D n D n D n D n D n D =--------+++

比较上式两边，得 0,41

,21,411234====

D D D D 因而全解 2344

2141)(n n n C n y +++=

将0)1(=-y 代入上式，得 0=C

因而 2222

2234]2

)1([)1(41)1(4

1412141)(+=+=++=++=

n n n n n n n n n n n y

205- 某系统的输入输出关系可由二阶常系数线性差分方程描述，如

果相应于输入为)()(n u n x =的响应为

)(]10)5(32[)(n u n y n n ++=

)1( 若系统起始为静止的，试决定此二阶差分方程。 )2( 若激励为)]10()([2)(--=n u n u n x ，求响应)(n y 。

解 )1( 由题意可知，

)2()1()()

2(10)1(7)(210-+-+=-+--n x b n x b n x b n y n y n y

引入算子E ，有 )(10

7)(2

120n x E E b E b E b n y +-++= 当)()(n u n x =，即)(1

)(n E E

n x δ-=

时， ①

)

(45125252324)

(512525232414)

107)(2102102102102102

1022120n u b b b b b b b b b n E E b b b E E b b b E E b b b n E E E E b E b E b n y n n ??

? ??++++++-++=????????????-+++--+++-++=-?+-++=δδ

又

)()10532()(n u n y n n +?+= ②

比较式①和②，有

???

??=++-=++=++40

3243652521

0210210b b b b b b b b b 从而 111,85,14210=-==b b b 因此此二阶差分方程为

)2(111)1(85)(14)2(10)1(7)(-+--=-+--n x n x n x n y n y n y （2）由线性时不变系统的特性可知：当输入)10()(1-=n u n x 时，输出为 )10(]10532[)(10101-+?+=--n u n y n n 当输入)(2)(2n u n x =时，输出为

)(]10532[2)(2)(2n u n y n y n n +?+== 因此当)]10()([2)(--=n u n u n x 时，输出为

{}

)10(]10532[)(]10532[2)(1010-+?+-+?+=--n u n u n y n n n n

5-28 以下各序列是系统的单位样值响应h (n ),试分别讨论各系统的因果性与稳定性。 (1) )(n δ (2) )5(-n δ (3) )4(+n δ (4) )(2n u

(5) )3(n u - (6) )(2n u n (7) )(3n u n - (8) [])5()(2--n u n u n (9) )(5.0n u n (10) )(5.0n u n -

信号与系统课后答案.doc

1-1 （2）∞<<-∞=-t e t f t ,)( （3）)()sin()(t t t f επ= （4）)(sin )(t t f ε= （5）)(sin )(t r t f = （7）)(2)(k t f k ε= （10）)(])1(1[)(k k f k ε-+= 1-3 1-5 判别下列各序列是否为周期性的。如果是，确定其周期。（2）)6 3cos()443cos()(2π πππ+++=k k k f （5）)sin(2cos 3)(5t t t f π+= ：

1-9 已知信号的波形如图1-11所示，分别画出 )(t f和 dt t df)( 的波形。解：由图1-11知，) 3(t f-的波形如图1-12(a)所示（) 3(t f-波形是由对) 2 3(t f- 的波形展宽为原来的两倍而得）。将) 3(t f-的波形反转而得到)3 (+ t f的波形，如图1-12(b)所示。再将)3 (+ t f的波形右移3个单位，就得到了)(t f，如图1-12(c)所示。dt t df)(的波形如图1-12(d)所示。 1-23 设系统的初始状态为)0(x，激励为)(? f，各系统的全响应)(? y与激励和初始状态的关系如下，试分析各系统是否是线性的。（1）?+ =-t t dx x xf x e t y ) ( sin )0( )(（2）?+ =t dx x f x t f t y ) ( )0( )( )( （3）?+ =t dx x f t x t y ) ( ])0( sin[ )(（4）)2 ( ) ( )0( )5.0( ) (- + =k f k f x k y k （5）∑=+ = k j j f kx k y ) ( )0( ) (

信号与系统课后习题与解答第七章

15- 分别绘出以下各序列的图形 )()21 ()()1(n u n x n = )(2)()2(n u n x n = )()2 1 ()()3(n u n x n -= )()2()()4(n u n x n -= )1(2)()5(1-=-n u n x n )()2 1 ()()6(1n u n x n -= 解 )()1(n x 序列的图形如图5-1(a)所示。 )()2(n x 序列的图形如图5-1(b)所示。 )()3(n x 序列的图形如图5-1(c)所示。 )()4(n x 序列的图形如图5-1(d)所示。 )()5(n x 序列的图形如图5-1(e)所示。

(b) 图5-1 (a) (f) (e) (d) 25- 分别绘出以下各序列的图形 )()()1(n nu n x = )()()2(n nu n x --= )(2)()3(n u n x n -= )()2 1 ()()4(n u n x n --= )()21()()5(n u n x n --= )1()2 1 ()()6(1+=+n u n x n 解

) 　序列的图形如图5-２(b)所示。 x ( )2(n 　序列的图形如图5-２(c)所示。 x ) )3(n ( x 　序列的图形如图5-２(d)所示。)4(n ( ) )5(n 　序列的图形如图5-２(e)所示。 x ( ) x 　序列的图形如图5-２(f)所示。 ( ) )6(n

(b) 图5-2 (c) (f) (e) (d) 8 -(a) 35- 分别绘出以下各序列的图形 )5 sin()()1(π n n x = )510cos()()2(π π-=n n x ) 5 sin()65()()3(π n n x n =

信号与系统试题附答案99484

信科0801《信号与系统》复习参考练习题一、单项选择题：

14、已知连续时间信号,) 2(100)2(50sin )(--=t t t f 则信号t t f 410cos ·)(所占有的频带宽度为（） A ．400rad ／s B 。200 rad ／s C 。100 rad ／s D 。50 rad ／s

15、已知信号)(t f 如下图（a ）所示，其反转右移的信号f 1(t) 是（） 16、已知信号)(1t f 如下图所示，其表达式是（） A 、ε（t ）＋2ε(t －2)－ε(t －3) B 、ε(t －1)＋ε(t －2)－2ε(t －3) C 、ε(t)＋ε(t －2)－ε(t －3) D 、ε(t －1)＋ε(t －2)－ε(t －3) 17、如图所示：f （t ）为原始信号，f 1(t)为变换信号，则f 1(t)的表达式是（） A 、f(－t+1) B 、f(t+1) C 、f(－2t+1) D 、f(－t/2+1)

18、若系统的冲激响应为h(t),输入信号为f(t),系统的零状态响应是（） 19。信号)2(4sin 3)2(4cos 2)(++-=t t t f π π 与冲激函数)2(-t δ之积为（） A 、2 B 、2)2(-t δ C 、3)2(-t δ D 、5)2(-t δ ，则该系统是（）＞－系统的系统函数．已知2]Re[,6 51)(LTI 202s s s s s H +++= A 、因果不稳定系统 B 、非因果稳定系统 C 、因果稳定系统 D 、非因果不稳定系统 21、线性时不变系统的冲激响应曲线如图所示，该系统微分方程的特征根是（） A 、常数 B 、实数 C 、复数 D 、实数+复数 22、线性时不变系统零状态响应曲线如图所示，则系统的输入应当是（） A 、阶跃信号 B 、正弦信号 C 、冲激信号 D 、斜升信号

信号与系统期末考试试题(有答案的)

信号与系统期末考试试题一、选择题（共10题，每题3分，共30分，每题给出四个答案，其中只有一个正确的） 1、卷积f 1(k+5)*f 2(k-3) 等于。（A ）f 1(k)*f 2(k) （B ）f 1(k)*f 2(k-8)（C ）f 1(k)*f 2(k+8)（D ）f 1(k+3)*f 2(k-3) 2、积分 dt t t ? ∞ ∞ --+)21()2(δ等于。（A ）1.25（B ）2.5（C ）3（D ）5 3、序列f(k)=-u(-k)的z 变换等于。（A ） 1-z z （B ）-1-z z （C ）11-z （D ）1 1--z 4、若y(t)=f(t)*h(t),则f(2t)*h(2t)等于。（A ） )2(41t y （B ）)2(21t y （C ）)4(41t y （D ）)4(2 1 t y 5、已知一个线性时不变系统的阶跃相应g(t)=2e -2t u(t)+)(t δ,当输入f(t)=3e —t u(t)时，系统的零状态响应y f (t)等于（A ）(-9e -t +12e -2t )u(t) （B ）(3-9e -t +12e -2t )u(t) （C ）)(t δ+(-6e -t +8e -2t )u(t) （D ）3)(t δ +(-9e -t +12e -2t )u(t) 6、连续周期信号的频谱具有（A ）连续性、周期性（B ）连续性、收敛性（C ）离散性、周期性（D ）离散性、收敛性 7、周期序列2)455.1(0 +k COS π的周期N 等于（A ） 1（B ）2（C ）3（D ）4 8、序列和 ()∑∞ -∞ =-k k 1δ等于（A ）1 (B) ∞ (C) ()1-k u (D) ()1-k ku 9、单边拉普拉斯变换()s e s s s F 22 12-+= 的愿函数等于 ()()t tu A ()()2-t tu B ()()()t u t C 2- ()()()22--t u t D 10、信号()()23-=-t u te t f t 的单边拉氏变换()s F 等于 ()A ()()()232372+++-s e s s ()() 2 23+-s e B s

信号与系统试题附答案

信号与系统》复习参考练习题一、单项选择题：

14、已知连续时间信号,) 2(100) 2(50sin )(--= t t t f 则信号t t f 410cos ·)(所占有的频带宽度为（） A ．400rad ／s B 。200 rad ／s C 。100 rad ／s D 。50 rad ／s

f如下图（a）所示，其反转右移的信号f1(t) 是（） 15、已知信号)(t f如下图所示，其表达式是（） 16、已知信号)(1t A、ε（t）＋2ε(t－2)－ε(t－3) B、ε(t－1)＋ε(t－2)－2ε(t－3) C、ε(t)＋ε(t－2)－ε(t－3) D、ε(t－1)＋ε(t－2)－ε(t－3) 17、如图所示：f（t）为原始信号，f1(t)为变换信号，则f1(t)的表达式是（） A、f(－t+1) B、f(t+1) C、f(－2t+1) D、f(－t/2+1) 18、若系统的冲激响应为h(t),输入信号为f(t),系统的零状态响应是（）

19。信号)2(4 sin 3)2(4 cos 2)(++-=t t t f π π 与冲激函数)2(-t δ之积为（） A 、2 B 、2)2(-t δ C 、3)2(-t δ D 、5)2(-t δ ，则该系统是（）＞－系统的系统函数．已知2]Re[,6 51 )(LTI 202s s s s s H +++= A 、因果不稳定系统 B 、非因果稳定系统 C 、因果稳定系统 D 、非因果不稳定系统 21、线性时不变系统的冲激响应曲线如图所示，该系统微分方程的特征根是（） A 、常数 B 、实数 C 、复数 D 、实数+复数 22、线性时不变系统零状态响应曲线如图所示，则系统的输入应当是（） A 、阶跃信号 B 、正弦信号 C 、冲激信号 D 、斜升信号 23. 积分 ?∞ ∞ -dt t t f )()(δ的结果为( ) A )0(f B )(t f C.)()(t t f δ D.)()0(t f δ 24. 卷积)()()(t t f t δδ**的结果为( ) A.)(t δ B.)2(t δ C. )(t f D.)2(t f

信号与系统课后习题与解答第三章

3-1 求图3-1所示对称周期矩形信号的傅利叶级数（三角形式和指数形式）。图3-1 解由图3-1可知，)(t f 为奇函数，因而00==a a n 2 1120 11201)cos(2)sin(242,)sin()(4T T T n t n T n E dt t n E T T dt t n t f T b ωωωπωω-== = =?? 所以，三角形式的傅利叶级数（FS ）为 T t t t E t f πωωωωπ2,)5sin(51)3sin(31)sin(2)(1111=?? ? ???+++= Λ 指数形式的傅利叶级数（FS ）的系数为??? ??±±=-±±==-=ΛΛ,3,1,0,,4,2,0, 021n n jE n jb F n n π 所以，指数形式的傅利叶级数为 T e jE e jE e jE e jE t f t j t j t j t j π ωπππ π ωωωω2,33)(11111= ++- + -=--Λ 3-2 周期矩形信号如图3-2所示。若：

图3-2 2 T -2- 重复频率kHz f 5= 脉宽 s μτ20= 幅度 V E 10= 求直流分量大小以及基波、二次和三次谐波的有效值。解对于图3-2所示的周期矩形信号，其指数形式的傅利叶级数（FS ）的系数 ?? ? ??=??? ??== = =??--22 sin 12,)(1112212211τωττωππωτ τ ωωn Sa T E n n E dt Ee T T dt e t f T F t jn T T t jn n 则的指数形式的傅利叶级数（FS ）为 ∑∑∞ -∞ =∞ -∞ =?? ? ? ?== n t jn n t jn n e n Sa T E e F t f 112 )(1ωωτωτ 其直流分量为T E n Sa T E F n ττωτ=?? ? ??=→2lim 100 基波分量的幅度为??? ? ? ?= +-2sin 2111τωπE F F 二次谐波分量的幅度为??? ? ? ?= +-22sin 122τωπE F F 三次谐波分量的幅度为??? ? ? ?=+-23sin 32133τωπE F F 由所给参数kHz f 5=可得

信号与系统习题答案

《信号与系统》复习题 1．已知f(t)如图所示，求f(-3t-2)。 2．已知f(t)，为求f(t0-at)，应按下列哪种运算求得正确结果？（t0和a 都为正值） 3．已知f(5-2t)的波形如图，试画出f(t)的波形。解题思路：f(5-2t)?????→?=倍展宽乘22/1a f(5-2×2t)= f(5-t) ??→?反转f(5+t)??→?5 右移 f(5+t-5)= f(t) 4．计算下列函数值。（1） dt t t u t t )2(0 0--?+∞ ∞-）（δ （2） dt t t u t t )2(0 --?+∞ ∞-）（δ （3） dt t t e t ?+∞ ∞ --++）（2)(δ

5．已知离散系统框图，写出差分方程。解：2个延迟单元为二阶系统，设左边延迟单元输入为x(k) 左○ ∑:x(k)=f(k)-a 0*x(k-2)- a 1*x(k-1)→ x(k)+ a 1*x(k-1)+ a 0*x(k-2)=f(k) (1) 右○ ∑: y(k)= b 2*x(k)- b 0*x(k-2) (2) 为消去x(k)，将y(k)按（1）式移位。 a 1*y(k-1)= b 2* a 1*x(k-1)+ b 0* a 1*x(k-3) (3) a 0*y(k-2)= b 2* a 0*x(k-2)-b 0* a 0*x(k-4) (4) (2)、（3）、（4）三式相加：y(k)+ a 1*y(k-1)+ a 0*y(k-2)= b 2*[x(k)+ a 1*x(k-1)+a 0*x(k-2)]- b 0*[x(k-2)+a 1*x(k-3)+a 0*x(k-4)] ∴ y(k)+ a 1*y(k-1)+ a 0*y(k-2)= b 2*f(k)- b 0*f(k-2)═>差分方程 6．绘出下列系统的仿真框图。 )()()()()(10012 2t e dt d b t e b t r a t r dt d a t r dt d +=++ 7．判断下列系统是否为线性系统。（2） 8．求下列微分方程描述的系统冲激响应和阶跃响应。 )(2)(3)(t e dt d t r t r dt d =+

信号与系统试题附答案精选范文

信科0801《信号与系统》复习参考练习题一、单项选择题 (2分1题，只有一个正确选项，共20题，40分) 1、已知连续时间信号,)2(100)2(50sin )(--= t t t f 则信号t t f 410cos ·)(所占有的频带宽度为（C ） A ．400rad ／s B 。200 rad ／s C 。100 rad ／s D 。50 rad ／s 2、已知信号)(t f 如下图（a ）所示，其反转右移的信号f 1(t) 是（ D ） 3、已知信号)(1t f 如下图所示，其表达式是（ B ） A 、ε（t ）＋2ε(t －2)－ε(t －3) B 、ε(t －1)＋ε(t －2)－2ε(t －3) C 、ε(t)＋ε(t －2)－ε(t －3) D 、ε(t －1)＋ε(t －2)－ε(t －3) 4、如图所示：f （t ）为原始信号，f 1(t)为变换信号，则f 1(t)的表达式是（ D ） A 、f(－t+1) B 、f(t+1) C 、f(－2t+1) D 、f(－t/2+1) 5、若系统的冲激响应为h(t),输入信号为f(t),系统的零状态响应是（ C ）

6。信号)2(4sin 3)2(4cos 2)(++-=t t t f π π与冲激函数)2(-t δ之积为（ B ） A 、2 B 、2)2(-t δ C 、3)2(-t δ D 、5)2(-t δ 7线性时不变系统的冲激响应曲线如图所示，该系统微分方程的特征根是（ B ） A 、常数 B 、实数 C 、复数 ? D 、实数+复数 8、线性时不变系统零状态响应曲线如图所示，则系统的输入应当是（ A ） A 、阶跃信号 B 、正弦信号? C 、冲激信号 ? D 、斜升信号

(完整版)信号与系统习题答案.docx

《信号与系统》复习题 1．已知 f(t) 如图所示，求f(-3t-2) 。 2．已知 f(t) ，为求 f(t0-at) ，应按下列哪种运算求得正确结果？（t0 和 a 都为正值）

3．已知 f(5-2t) 的波形如图，试画出f(t) 的波形。解题思路：f(5-2t)乘a 1 / 2展宽 2倍f(5-2 × 2t)= f(5-t)

反转右移 5 f(5+t) f(5+t-5)= f(t) 4．计算下列函数值。（ 1）（ 2）（ t ） t 0 )dt t 0 u(t 2 （t t 0）u(t 2t 0 )dt （ 3） (e t t ) （t 2）dt 5．已知离散系统框图，写出差分方程。解： 2 个延迟单元为二阶系统，设左边延迟单元输入为 x(k) ∑ 0 1 1) → 左○ :x(k)=f(k)-a *x(k-2)- a*x(k- x(k)+ a 1*x(k-1)+ a 0*x(k-2)=f(k) (1) ∑ y(k)= b 2*x(k)- b 0*x(k-2) (2) 右○ : 为消去 x(k) ，将 y(k) 按（ 1）式移位。 a 1*y(k-1)= b 2 * a 1*x(k-1)+ b * a 1*x(k-3) (3) a 0*y(k-2)= b 2 * a 0*x(k-2)-b 0* a 0*x(k-4) (4) (2) 、（ 3）、（ 4）三式相加： y(k)+ a 1*y(k-1)+ a 0*y(k-2)= b *[x(k)+ a 1 *x(k-1)+a *x(k-2)]- b *[x(k-2)+a 1*x(k-3)+a *x(k-4)] 2 0 0 0 ∴ y(k)+ a 1 *y(k-1)+ a *y(k-2)= b 2 *f(k)- b *f(k-2) ═ >差分方程

信号与系统试题附答案

信科0８01《信号与系统》复习参考练习题一、单项选择题（2分1题,只有一个正确选项,共20题,４０分) １、已知连续时间信号则信号所占有得频带宽度为(C) A.400rａd／ｓB。200 raｄ/ｓC。1０0 ｒad／s D。50 rad/s 2、已知信号如下图(a）所示,其反转右移得信号f1(t) 就是( Ｄ) ３、已知信号如下图所示,其表达式就是(B) Ａ、ε(t)＋２ε（t－2)-ε(t-３）B、ε(t－1)＋ε(ｔ－2）-2ε(t-3) Ｃ、ε（t)＋ε(ｔ－２)-ε(ｔ-３) D、ε（t-1)+ε(t-２)－ε(t-3） 4、如图所示:ｆ(t)为原始信号,f1（t)为变换信号，则f1(t)得表达式就是( D )

A、f（－t+１) B、ｆ(t＋1）?Ｃ、f（-２t＋1）Ｄ、 f(－t/2+1) ５、若系统得冲激响应为h(t),输入信号为f(t）,系统得零状态响应就是( Ｃ) ?6。信号与冲激函数之积为( B ) A、2 B、２ C、３ D、５ 7线性时不变系统得冲激响应曲线如图所示,该系统微分方程得特征根就是（ B ） A、常数Ｂ、实数Ｃ、复数 D、实数+复数 8、线性时不变系统零状态响应曲线如图所示,则系统得输入应当就是( A ) A、阶跃信号Ｂ、正弦信号Ｃ、冲激信号 D、斜升信号 9、积分得结果为( A)?A B C、D、 10卷积得结果为( Ｃ）?Ａ、B、Ｃ、D、１１零输入响应就是( B )?Ａ、全部自由响应B、部分自由响应?Ｃ、部分零状态响应Ｄ、全响应与强迫响应之差? 1２号〔ε(ｔ)－ε(ｔ-２)〕得拉氏变换得收敛域为( C ) A、Re［s］>０ B、Ｒe[ｓ]>２ C、全S平面 D、不存在 13知连续系统二阶微分方程得零输入响应得形式为，则其2个特征根为( A ）?Ａ。-1,－２B。－1，2 C。１,-2 D。1,2 14数就是( Ａ) A.奇函数B。偶函数C。非奇非偶函数Ｄ。奇谐函数１5期矩形脉冲序列得频谱得谱线包络线为(Ｂ)

信号与系统西安邮电习题答案

第一次 1.1 画出下列各个信号的波形[式中()()r t t t ε=为斜升函数] 知识要点：本题主要考查阶跃函数和单位阶跃序列的性质，包括()t ε和()k ε的波形特性以及它们与普通函数结合时的波形变化特性。解题方法：①首先考虑各信号中普通函数的波形特点，再考虑与()t ε或()k ε结合时的变化情况； ②若()t f 只是普通信号与阶跃信号相乘，则可利用()t ε或()k ε的性质直接画出 0>t 或0≥k 部分的普通函数的波形； ③若()t f 是普通函数与阶跃信号组合成的复合信号，则需要考虑普通函数值域及其对应的区间。 (1) ()()()t t t f εsin = 解：正弦信号周期ππ ω π 21 22== = T 1 -1 2ππ t () f t (2) ()()sin f t t επ= 解：()0 sin 0 1 sin 0 t f t t ππ?，

正弦信号周期22== π π T 10-1-1 -212 -1 -2 12 1 () f t t t () sin t π (3) ()()cos f t r t = 解：()0 cost 0 cos cos 0f t t t ?，正弦信号周期221 T π π= = 1 0-1t () cos t π 2π π -2π -1 () f t 0 t π 2π π -2π -

(4) ()()k k k f ε)12(+= -1 -2 1 2 k 3 13 5() f k …… …… (5) ()()()1 11k f k k ε+??=+-? ? -2 -4 1 2 k 3 12 () f k …… …… 4 5 -1 -3 1.2 画出下列各信号的波形[式中()()r t t t ε=为斜升函数] 知识要点：本题主要考查阶跃函数和单位阶跃序列的性质，包括()t ε和()k ε的波形特性以及它们与普通函数结合时的波形变化特性。解题方法：①首先考虑各信号中普通函数的波形特点，再考虑与()t ε或()k ε结合时的变化情况； ②若()t f 只是普通信号与阶跃信号相乘，则可利用()t ε或()k ε的性质直接画出 0>t 或0≥k 部分的普通函数的波形；

信号与系统复习题及答案

1．系统的激励是)t (e ，响应为)t (r ，若满足dt ) t (de )t (r = ，则该系统为线性、时不变、因果。（是否线性、时不变、因果？） 2．求积分dt )t ()t (212-+?∞ ∞-δ的值为 5 。 3．当信号是脉冲信号f(t)时，其低频分量主要影响脉冲的顶部，其高频分量主要影响脉冲的跳变沿。 4．若信号f(t)的最高频率是2kHz ，则t)f(2的乃奎斯特抽样频率为 8kHz 。 5．信号在通过线性系统不产生失真，必须在信号的全部频带内，要求系统幅频特性为一常数相频特性为_一过原点的直线（群时延）。 6．系统阶跃响应的上升时间和系统的截止频率成反比。 7．若信号的3s F(s)= (s+4)(s+2) ，求该信号的=)j (F ωj 3(j +4)(j +2)ωωω。 8．为使LTI 连续系统是稳定的，其系统函数)s (H 的极点必须在S 平面的左半平面。 9．已知信号的频谱函数是）） 00(()j (F ωωδωωδω--+=，则其时间信号f(t)为 01 sin()t j ωπ 。 10．若信号f(t)的2 11 )s (s )s (F +-=，则其初始值=+)(f 0 1 。二、判断下列说法的正误，正确请在括号里打“√”，错误请打“×”。（每小题2分，共10分） 1.单位冲激函数总是满足)()(t t -=δδ （ √ ） 2.满足绝对可积条件∞

信号与系统课后习题答案—第1章

第1章习题答案 1－1 题1－1图所示信号中，哪些是连续信号？哪些是离散信号？哪些是周期信号？哪些是非周期信号？哪些是有始信号？解： ① 连续信号：图（a ）、（c ）、（d ）； ② 离散信号：图（b ）； ③ 周期信号：图（d ）； ④ 非周期信号：图（a ）、（b ）、（c ）； ⑤有始信号：图（a ）、（b ）、（c ）。 1－2 已知某系统的输入f(t)与输出y(t)的关系为y(t)=|f(t)|，试判定该系统是否为线性时不变系统。解：设T 为此系统的运算子，由已知条件可知： y(t)=T[f(t)]=|f(t)|，以下分别判定此系统的线性和时不变性。 ① 线性 1）可加性不失一般性，设f(t)=f 1(t)+f 2(t)，则 y 1(t)=T[f 1(t)]=|f 1(t)|，y 2(t)=T[f 2(t)]=|f 2(t)|，y(t)=T[f(t)]=T[f 1(t)+f 2(t)]=|f 1(t)+f 2(t)|，而 |f 1(t)|＋|f 2(t)|≠|f 1(t)+f 2(t)| 即在f 1(t)→y 1(t)、f 2(t)→y 2(t)前提下，不存在f 1(t)＋f 2(t)→y 1(t)＋y 2(t)，因此系统不具备可加性。由此，即足以判定此系统为一非线性系统，而不需在判定系统是否具备齐次性特性。 2）齐次性由已知条件，y(t)=T[f(t)]=|f(t)|，则T[af(t)]=|af(t)|≠a|f(t)|=ay(t) （其中a 为任一常数）即在f(t)→y(t)前提下，不存在af(t)→ay(t),此系统不具备齐次性，由此亦可判定此系统为一非线性系统。 ② 时不变特性由已知条件y(t)=T[f(t)]=|f(t)|，则y(t-t 0)=T[f(t-t 0)]=|f(t-t 0)|，即由f(t)→y(t)，可推出f(t-t 0)→y(t-t 0)，因此，此系统具备时不变特性。依据上述①、②两点，可判定此系统为一非线性时不变系统。 1－3 判定下列方程所表示系统的性质： )()()]([)()(3)(2)(2)()()2()()(3)(2)()()()()() (2''''''''0t f t y t y d t f t y t ty t y c t f t f t y t y t y b dx x f dt t df t y a t =+=++-+=+++=? 解：（a ）① 线性 1）可加性由 ?+=t dx x f dt t df t y 0)()()(可得?????→+=→+=??t t t y t f dx x f dt t df t y t y t f dx x f dt t df t y 01122011111)()()()()()()()()()(即即则 ???+++=+++=+t t t dx x f x f t f t f dt d dx x f dt t df dx x f dt t df t y t y 0212102201121)]()([)]()([)()()()()()( 即在)()()()()()()()(21212211t y t y t f t f t y t f t y t f ＋＋前提下，有、→→→，因此系统具备可加性。 2）齐次性由)()(t y t f →即?+=t dx x f dt t df t y 0)()()(，设a 为任一常数，可得 )(])()([)()()]([)]([000t ay dx x f dt t df a dx x f a dt t df a dx x af t af dt d t t t =+=+=+??? 即)()(t ay t af →，因此，此系统亦具备齐次性。由上述1）、2）两点，可判定此系统为一线性系统。

奥本海姆《信号与系统(第二版)》习题参考答案

Charpt 1 1.21—(a),(b),(c) 一连续时间信号x(t)如图original所示，请画出下列信号并给予标注：a）x(t-1) b）x(2-t) c）x(2t+1) d）x(4-t/2) e）[x(t)=x(-t)]u(t) f）x(t)[δ(t+3/2)-δ(t-3/2)] (d),(e),(f)

1.22 一离散时间信号x[n]如图original所示，请画出下列信号并给予标注。 a)x[n-4] b)x[3-n] c)x[3n] e)x[n]u[3-n] f)x[n-2]δ[n-2]

1.23 确定并画出图original信号的奇部和偶部，并给予标注。

1.25 判定下列连续时间信号的周期性，若是周期的，确定它的基波周期。 a) x(t)=3cos(4t+π/3) T=2π/4=π/2; b) x(t)=e ) 1(-t j π T=2π/π=2; c) x(t)=[cos(2t-π/3)]2 x(t)=1/2+cos[(cos(4t-2π/3))]/2, so T=2π/4=π/2; d) x(t)=E v {cos(4πt)u(t)} 定义x(0)=1/2,则T=1/2; e) E v {sin(4πt)u(t)} 非周期 f ）x(t)= ∑∞ -∞ =--n n t e )2(

假设其周期为T 则 ∑∞ -∞ =--n n t e ) 2(= ∑∞ -∞ =+--n T n t e ) 22(= ∑∞ -∞ =---n T n t e )) 2(2(= ∑ ∞ -∞ =--n n t e ) 2( 所以T=1/2(最小正周期)； 1.26 判定下列离散时间信号的周期性；若是周期的，确定他们的基波周期。 (a) x[n]=sin(6π/7+1) N=7 (b) x[n]=cos(n/8-π) 不是周期信号（c ）x[n]=cos(πn 2 /8) 假设其周期为N ，则8/8/)(22n N n ππ=+＋πk 2 所以易得N=8 （d ）x[n]=)4 cos( )2 cos(n n π π N=8 (e) x[n]=)6 2 cos( 2)8 sin( )4 cos(2π π π π + -+n n n N=16 1.31 在本题中将要说明线性时不变性质的最重要的结果之一，即一旦知道了一个线性系统或线性时不变系统对某单一输入的响应或者对若干个输入的响应，就能直接计算出对许多其他输入信号的响应。（a ）考虑一个LTI 系统它对（a ）的信号x1（t ）的响应y1（t ）示于（b ）,确定并画出该系统对于图（c ）的信号x2（t ）的响应。（b ）确定并画出（a ）中的系统对于（d ）的信号x3（t ）的响应。

信号与系统复习题含答案完整版

信号与系统复习题含答案 HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】

（C ）) (t δ+(-6e -t +8e -2t )u(t) （D ）3) (t δ +(-9e -t +12e -2t )u(t) 6、连续周期信号的频谱具有（A ）连续性、周期性（B ）连续性、收敛性（C ）离散性、周期性（D ）离散性、收敛性 7、周期序列2)455.1(0+k COS π的周期N 等于 (A) 1 （B ）2 （C ）3 （D ） 4 8、序列和() ∑∞ -∞=-k k 1δ等于（A ）1 (B) ∞ (C) ()1-k u (D) ()1-k ku 9、单边拉普拉斯变换 ()s e s s s F 2212-+= 的愿函数等于 10、信号 ()()23-=-t u te t f t 的单边拉氏变换()s F 等于二、填空题（共9小题，每空3分，共30分） 1、卷积和[（） k+1 u(k+1)]*)1(k -δ=______________________ __ 2、单边z 变换F(z)= 12-z z 的原序列 f(k)=______________________ 3、已知函数f(t)的单边拉普拉斯变换 F(s)=1+s s ，则函数y(t)=3e -2t ·f(3t)的单边拉普拉斯变换 Y(s)=_________________________ 4、频谱函数F(j ω)=2u(1-ω)的傅里叶逆变换 f(t)=__________________ 5、单边拉普拉斯变换 s s s s s F +++= 221 3)(的原函数 f(t)=__________________________ 6、已知某离散系统的差分方程为 ) 1(2)()2()1()(2-+=----k f k f k y k y k y ，则系统的单位序列响应 h(k)=_______________________ 7、已知信号f(t)的单边拉氏变换是F(s),则信号 ? -=2 )()(t dx x f t y 的单边拉氏变换 Y(s)=______________________________ 8、描述某连续系统方程为该系统的冲激响应h(t)= 9、写出拉氏变换的结果()=t u 66 ，=k t 22 三（8分）已知信号 ()()()???? ?><==?./1,0,/1,1s rad s rad jw F j F t f ωωω设有函数()(), dt t df t s = 求? ?? ??2ωs 的傅里叶逆变换。四、（10分）如图所示信号 ()t f ，其傅里叶变换 ()()[]t f jw F F =，求（1） ()0F （2） ()?∞ ∞-dw jw F 五、（12）分别求出像函数()25232 +-= z z z z F 在下列三种收敛域下所对应的序列（1）2?z （2） 5 .0?z （3）2 5.0??z 六、（10分）某LTI 系统的系统函数 ()1222 ++= s s s s H ，已知初始状态 ()(),20,00=='=--y y 激励()(),t u t f =求该系统的完全响应。试题三一、单项选择题(在每小题的四个备选答案中，选出一个正确答案，并将正确答案的序号填在题干的括号内。每小题3分，共30分) 1.设：如图—1所示信号。则：信号f(t)的数学表示式为( )。 (A)f(t)=t ε(t)-t ε(t-1) (B)f(t)=t ε(t)-(t-1)ε(t-1) (C)f(t)=(1-t)ε(t)-(t-1)ε(t-1) (D)f(t)=(1+t)ε(t)-(t+1)ε(t+1) 2.设：两信号f 1(t)和f 2(t)如图—2。则：f 1(t)与f 2(t)间变换关系为( )。 (A)f 2(t)=f 1(2 1t+3) (B)f 2(t)=f 1(3+2t) (C)f 2(t)=f 1(5+2t) (D)f 2(t)=f 1(5+2 1t) 3.已知：f(t)=SgN(t)的傅里叶变换为F(j ω)=ω j 2, 则：F 1(j ω)=j πSgN(ω)的傅里叶反变换f 1(t)为( )。 (A)f 1(t)=t 1 (B)f 1(t)=-t 2 (C)f 1(t)=-t 1 (D)f 1(t)=t 2 4.周期性非正弦连续时间信号的频谱，其特点为( )。 (A)频谱是连续的，收敛的 (B)频谱是离散的，谐波的，周期的 (C)频谱是离散的，谐波的，收敛的 (D)频谱是连续的，周期的 5.设：二端口网络N 可用A 参数矩阵{a ij }表示，其出端与入端特性阻抗为Z c2、Z c1，后接载Z L ，电源? U s 的频率为ωs ，内阻抗为Z s 。则：特性阻抗Z c1、Z c2仅与 ( )有关。 (A){a ij }，Z L (B){a ij },Z L ,Z s (C){a ij },ωs , *U s (D){a ij } 6.设：f(t)?F(j ω) 则：f 1(t)=f(at+b) ?F 1(j ω)为( ) (A)F 1(j ω)=aF(j a ω)e -jb ω (B)F 1(j ω)=a 1 F(j a ω)e -jb ω

信号与系统课后习题与解答第一章

1-1 分别判断图1-1所示各波形是连续时间信号还是离散时间信号，若是离散时间信号是否为数字信号？图1-1 图1-2

解信号分类如下： ??? ?? ? ????--???--））（散（例见图数字：幅值、时间均离））（连续（例见图抽样：时间离散，幅值离散））（连续（例见图量化：幅值离散，时间））（续（例见图模拟：幅值、时间均连连续信号d 21c 21b 21a 21图1-1所示信号分别为（a ）连续信号（模拟信号）；（b ）连续（量化）信号；（c ）离散信号，数字信号；（d ）离散信号；（e ）离散信号，数字信号；（f ）离散信号，数字信号。 1-2 分别判断下列各函数式属于何种信号？（重复1-1题所示问）（1）)sin(t e at ω-；（2）nT e -；（3）)cos(πn ；（4）为任意值）（00)sin(ωωn ；（5）2 21??? ??。解由1-1题的分析可知：（1）连续信号；（2）离散信号；（3）离散信号，数字信号；（4）离散信号；（5）离散信号。 1-3 分别求下列各周期信号的周期T ：（1）)30t (cos )10t (cos -；（2）j10t e ；（3）2)]8t (5sin [；（4）[]为整数）（n )T nT t (u )nT t (u )1(0 n n ∑∞ =-----。解判断一个包含有多个不同频率分量的复合信号是否为一个周期信号，需要考察各分量信号的周期是否存在公倍数，若存在，则该复合信号的周期极为此公倍数；若不存在，则该复合信号为非周期信号。（1）对于分量cos (10t )其周期5T 1π=；对于分量cos (30t )，其周期15 T 2π=。由于 5π

信号与系统课后习题答案汇总

第一章习题参考解答 1.1 绘出下列函数波形草图。 (1) | |3)(t e t x -= (2) ()? ???<≥=02021)(n n n x n n (3) )(2sin )(t t t x επ= (5) )]4()([4cos )(--=-t t t e t x t εεπ (7) t t t t x 2 cos )]2()([)(π δδ--= (9) )2()1(2)()(-+--=t t t t x εεε )5- (11) )]1()1([)(--+=t t dt d t x εε (12) )()5()(n n n x --+-=εε (13) ?∞--= t d t x ττδ)1()( (14) )()(n n n x --=ε 1.2 确定下列信号的能量和功率，并指出是能量信号还是功率信号，或两者均不是。 (1) | |3)(t e t x -= 解能量有限信号。信号能量为： (2) ()?????<≥=0 2 021)(n n n x n n 解能量有限信号。信号能量为： (3) t t x π2sin )(= 解功率有限信号。周期信号在(∞-∞,)区间上的平均功率等于在一个周期内的平均功率，t π2sin 的周期为1。 (4) n n x 4 sin )(π = 解功率有限信号。n 4 sin π 是周期序列，周期为8。 (5) )(2sin )(t t t x επ= 解功率有限信号。由题(3)知，在),(∞-∞区间上t π2sin 的功率为1/2，因此)(2sin t t επ在),(∞-∞区间上的功率为1/4。如果考察)(2sin t t επ在),0(∞区间上的功率，其功率为1/2。 (6) )(4 sin )(n n n x επ = 解功率有限信号。由题(4)知，在),(∞-∞区间上n 4 sin π 的功率为1/2，因此)(4 sin n n επ 在),(∞-∞区间上的功率为1/4。如果考察)(4 sin n n επ 在),0(∞区间上的功率，其功率为1/2。 (7) t e t x -=3)( 解非功率、非能量信号。考虑其功率：上式分子分母对T 求导后取极限得∞→P 。 (8) )(3)(t e t x t ε-= 解能量信号。信号能量为： 1.3 已知)(t x 的波形如题图1.3所示，试画出下列函数的波形。 (3) )2(t x (4) ( x (5) )(t x - (6) )2(+-t x 1 1 -1/ 2 0 1 1 -2 -1 0 1 2 3 4

信号与系统试题库史上最全内含答案)

信号与系统考试方式：闭卷考试题型：1、简答题（5个小题），占30分；计算题（7个大题），占70分。一、简答题： 1．dt t df t f x e t y t ) ()()0()(+=-其中x(0)是初始状态，为全响应，为激励，)()(t y t f 试回答该系统是否是线性的？[答案：非线性] 2．)()(sin )('t f t ty t y =+试判断该微分方程表示的系统是线性的还是非线性的，是时变的还是非时变的？[答案：线性时变的] 3．已知有限频带信号)(t f 的最高频率为100Hz ，若对)3(*)2(t f t f 进行时域取样，求最小取样频率s f =？[答案：400s f Hz =] 4．简述无失真传输的理想条件。[答案：系统的幅频特性为一常数，而相频特性为通过原点的直线] 5．求[]?∞ ∞ --+dt t t e t )()('2δδ的值。[答案：3] 6．已知)()(ωj F t f ?，求信号)52(-t f 的傅立叶变换。 [答案：521(25)()22 j f t e F j ωω --?] 7．已知)(t f 的波形图如图所示，画出)2()2(t t f --ε的波形。

[答案： ] 8．已知线性时不变系统，当输入)()()(3t e e t x t t ε--+=时，其零状态响应为 )()22()(4t e e t y t t ε--+=，求系统的频率响应。[答案：()) 4)(2(52)3(++++ωωωωj j j j ] 9．求象函数2 ) 1(3 2)(++=s s s F ,的初值)0(+f 和终值)(∞f 。 [答案：)0(+f =2，0)(=∞f ] 10．若LTI 离散系统的阶跃响应为)(k g ，求其单位序列响应。其中：)()2 1 ()(k k g k ε=。 [答案：1111 ()()(1)()()()(1)()()(1)222 k k k h k g k g k k k k k εεδε-=--=--=--] 11．已知()1 1 , 0,1,20 , k f k else ==??? ，()2 1 , 0,1,2,3 0 , k k f k else -==??? 设()()()12f k f k f k =*，求()3?f =。[答案：3] 12．描述某离散系统的差分方程为()()()122()y k y k y k f k +---= 求该系统的单位序列响应()h k 。[答案：21()[(2)]()33 k h k k ε=-+] 13．已知函数()f t 的单边拉普拉斯变换为()1 s F s s =+，求函数()()233t y t e f t -=的单边拉普拉斯变换。[答案：()2 5 Y s s s = ++] 14．已知()()12f t f t 、的波形如下图，求()()()12f t f t f t =*（可直接画出图形）