指数函数3
指数函数(3)

2 y( x) 0
y( x)的值域为 2,0] [
记住下列重要结记.
1. f ( x)与 f ( x)增减性相反.
1 2. f ( x)恒为正或恒为负时,函数f ( x)与 增减性相反. f ( x)
3.函数f ( x)与f ( x) k增减性相同.
4.当k 0, f ( x)与kf ( x)的增减性相同, k 0时, f ( x)与kf ( x)增减性相反.
10 10 例6:讨论函数f(x)= x x 10 10
x
x
的奇偶性
和单调性
解:(1)函数的定义域为R ∵f(-x)=
10 10 x x 10 10
x
x
=-
10 10 x x 10 10
x
x
=-f(x) ∴ f(x)在R上是奇函数
(2)解法一:设x1,x2∈R,且x1<x2
f ( x) f ( x)
f ( x)
的值域.
与函数f ( x)单调性相同;
与函数f ( x)的单调性相反.
例题讲解
1 例1.求函数y 3 的定义域 9 1 1 2 x 1 2 x 1 解:3 0 3 化同底 9 9 2 x1 2 利用指数函数的性质
3 x 1
3
3
x
f (a 2) 3
ax a x
a2
,3
x x
a 2
18
x
3 2
a
又 y ( x) 3 4
x
y ( x) (3 ) 4 2 4
(2) 函数y( x)的定义域为[0,1] 令t 2 , x [0,1],函数t在区间[0,1]单调递增.
3. 指数函数图像

当0 x 1 时,y 0 ;当x 1 时,y 0 , 故选B
4.翻折变化:
1 y f x 去掉y 轴左边图,保 留y 轴右 边图 y f x 将y 轴右边的图像翻折到左边去
① f x ex f x = e x
② f x = e x f x 2 = e x-2
指数函数的图象
知识点
1.当 当0a
1 a
时, 底数a 越大,图象在x 1 时,底数a 越小,图象在x
0
时越接近y 轴,在x 0 0 时越接近x 轴,在x
时越接近x 轴 0 时越接近y 轴
2.平移变换:左加右减
1 f x 向左平移a 个单位 f x a 2 f x 向上平移 a个单位 f x a 3 f x 向右平 移 a个单位 f x a 4 f x 向下平移a个单位 f x a
解析:① 有界性:由函数的定义域得x 0 , A错; 当x 0 时,y 0 ,B错;
② 指数爆炸,当x , y 0 ,D错
例7 函数y x3 x 2 x 的图象大致是
解析:① 奇偶性:f x x3 x 2 x f x ,故函数为奇函数,C错; ② 有界性:令y 0 ,则 x3 x 2 x 0
D. a b 1 d c
例2 已知1 n m 0 ,则指数函数① y mx ,
② y nx 的图象为
例3 已知函数y ax b a 0且 a 1 的图象经过
第二、三、四象限,则有
A. 0 a 1 ,b 1
第三章 3 3.1 指数函数的图像和性质

[典例 2] 求下列函数的定义域和值域. (1)y=2
1 x4
2 -|x| ;(2)y=( ) ; 3
(3)y=4x+2x+1+1.
[解析] (1)由 x-4≠0 得 x≠4. ∴定义域为{x|x≠4}
1 1 又 ≠0,∴2 x4 ≠1. x-4 1 x4
∴y=2
的值域为{y|y>0 且 y≠1}
北师大版数学 ·必修1
返回导航
上页
下页
3.比较下列各组数的大小. (1)3 2,0.3 2,2 2,0.2 2; (2)1.7-0.3 与 1.9-0.3; (3)21.1 与 31.2.
解析:(1)构造四个指数函数,分别为 y=3x,y=0.3x,y=2x, y=0.2x,它们在第一象限内,图像由下至上,依次是 y=0.2x, y=0.3x,y=2x,y=3x,如图,由于 x= 2>0, 所以 0.2 2<0.3 2<2 2<3 2.
北师大版数学 ·必修1
返回导航
上页
下页
3 3.1
指数函数
指数函数的图像和性质
北师大版数学 ·必修1
返回导航
上页
下页
考 纲 定 位 1.理解指数函数的概念. 2.掌握指数函数的定义域、值域. 3.掌握指数函数的性质.
重 难 突 破 重点:指数函数的图像与性质. 难点:与二次函数、幂函数等相结合的问题.
又∵2.1 和 2.2 的底数不同,指数相同,可以用幂函数的单调性. ∵y=x 在(0,+∞)上是增函数,且 2.1<2.2, ∴2.1 <2.1 <2.2 .
1 3 2 3 2 3 2 3
北师大版数学 ·必修1
返回导航
上页
14指数函数3(教学案)

1 2
本节内容个人掌握情况反思:
2
学习要点及自主学习导引
1. 若函数 y 2 x1 m 的图象不经过第一象限,则 m 的取值范围是 _______ 。 x 2.解方程 4 2x 1 8 0
y
3.如图为指数函数 (1) y a x , (2) y b x , (3) y c x , (4) y d x , 则 a, b, c, d 与 1 的大小关系为
典例探究
a b
c d
O
x
思想方法总结
例1、 已知函数 y f ( x) 是奇函数,则当 x 0 时, f ( x) 3 x 1 ,求
当 x 0 时 y f ( x) 的解析式。
例 2、已知 2 x
2
x
1 4
x2
, 求函数 yΒιβλιοθήκη 2 x 2 x 的值域1
例 3、 (1)求.函数 y=( ) x
1 2
2
2 x 2
的递增区间。
(2)求.函数 y 36x 12 6x 5 的单调区间。
例 4、已知定义域为 R 的函数 f ( x) (Ⅰ)求 a , b 的值;
2 x b 是奇函数。 2 x 1 a
(Ⅱ)若对任意的 t R ,不等式 f (t 2 2t ) f (2t 2 k ) 0 恒成立,求
k 的范围;
课堂练习: 1、已知函数 f ( x)
自我纠错
a x 1 (a 0, a 1) ax 1
(1)求 f ( x ) 的定义域和值域; (2)讨论 f ( x ) 的单调性。
2、若 a2x+ ·ax- ≤0(a>0 且 a≠1) ,求 y=2a2x-3·ax+4 的值 域.
高中数学第三章指数运算与指数函数3指数函数第1课时指数函数的概念图象和性质课件北师大版必修第一册

知识点2 指数函数的图象和性质
1.指数函数的图象和性质
图象和性质
图象
a>1
0<a<1
图象和
性质
a>1
0<a<1
(1)定义域:R
(2)值域:(0,+∞)
(3)过定点(0,1),即x=0时,y=1
性质
(4)当x<0时,0<y<1;
(4)当x<0时,y>1;
当x>0时,y>1
当x>0时,0<y<1
(5)在R上是增函数
f(x)=kag(x)+b(k,a,b均为常数,且k≠0,a>0,且a≠1).若g(m)=0,则f(x)的图象过定
点(m,k+b).即令指数等于0,解出相应的x,y,则点(x,y)为所求定点.
角度2画指数型函数的图象
【例3】 画出下列函数的图象,并说明它们是由函数f(x)=2x的图象经过怎
样的变换得到的.
变式探究
比较下面两个数的大小:
(a-1)1.3与(a-1)2.4(a>1,且a≠2).
解∵a>1,且a≠2,∴a-1>0,且a-1≠1.
若a-1>1,即a>2,则y=(a-1)x是增函数,∴(a-1)1.3<(a-1)2.4.若0<a-1<1,即1<a<2,
则y=(a-1)x是减函数,∴(a-1)1.3>(a-1)2.4.
变式探究
本例中函数改为f(x)=5·a3x-2+4,其他条件不变,求点P的坐标.
解令 3x-2=0,得
2
x= ,此时
3
2
f( )=5×a0+4=9,故函数
2.1.2指数函数及其性质(3)

太原市新希望双语学校高一年级第一学期数学学科练习题2.1.2-3课题:指数函数(3) 责任编辑人:赵晶晶 校对人:杨鹏飞 日期:班级: 姓名:一、选择题:1.已知函数()⎪⎩⎪⎨⎧≤⎪⎭⎫ ⎝⎛>=,0,21,0,21x x x x f x 则()()=-4f f ( ) A.-4 B.41- C.4 D. 6 2.函数()()21025--+-=x x y 的定义域是 ( ) A.{}2,5≠≠x x x B.{}2>x x C.{}5>x x D.{}552><<x x x 或 3.若a a 23122121-+⎪⎭⎫ ⎝⎛<⎪⎭⎫ ⎝⎛,则实数a 的取值范围是 ( )A.()+∞,1B.⎪⎭⎫ ⎝⎛+∞,21C.()1,∞-D.⎪⎭⎫ ⎝⎛∞-21, 4.设函数(),1,1,2,13≥<⎩⎨⎧-=x x x x f x 则满足()()()a f a f f 2=的a 的取值范围是 ( ) A.⎥⎦⎤⎢⎣⎡1,32 B.[]1,0 C.⎪⎭⎫⎢⎣⎡+∞,32D.[)+∞,1二、填空题:5.不等式12193-+<x x 的解集为 . 6.方程81323=-x ,则=x .7.方程803322=--+x x ,则=x .8.()=⋅-+⎪⎭⎫ ⎝⎛63430321687 . 9.已知()()x x a a a a -+++>++12126464,则x 的取值范围为 .三、解答题:10.(1)解不等式22112≤⎪⎭⎫ ⎝⎛-x ;(2)若43+->x x a a (0>a 且1≠a )求x 的取值范围.11.设10≤≤x ,求10264+⋅-=--x x y 的最大值和最小值.(选做题)已知定义域为R 的函数()x f 满足()()()y f x f y x f ⋅=+,当0>x 时,()1>x f . ⑴求()0f ;⑵证明:()()()y f x f y x f =-; ⑶判定()x f 的单调性.。
高中数学指数运算与指数函数3指数函数课件

提示:本题有两处错误,一是a>0,不能保证f(x)=ax在R上是增函
数;二是不等式的解集没有写成集合的形式.
正解:设 f(x)=ax(a>0,且 a≠1).
-
- +
当 a>1 时,f(x)在 R 上是增函数,由
当0<a<1时,原不等式⇔-3x<x+4⇔x>-1,
故当a>1时,实数x的取值范围是{x|x<-1},
当0<a<1时,实数x的取值范围是{x|x>-1}.
3.已知a>0,比较aπ与a3的大小.
解:设f(x)=ax,易知π>3.
当a>1时,函数f(x)在R上是增函数,则aπ>a3;
当a=1时,函数f(x)=1是常数,则aπ=a3;
x的取值范围.
解:因为0<a<1,所以y=ax在R上是减函数,
又a-3x>ax+4,所以-3x<x+4,得x>-1,
故实数x的取值范围是{x|x>-1}.
2.若把本例(2)中的“a>1”换为“a>0,且a≠1”,其他条件不变,求
实数x的取值范围.
解:当a>1时,原不等式⇔-3x>x+4⇔x<-1,
下到上相应的底数由小变大.
【变式训练2】 如图,若0<a<1,则函数y=ax与y=(a-1)x2的图象
可能是(
)
解析:因为0<a<1,所以a-1<0,因此y=(a-1)x2的图象开口向下.
答案:D
探究三 利用指数函数比较大小
【例3】 比较下列各组数的大小:
常用函数图像
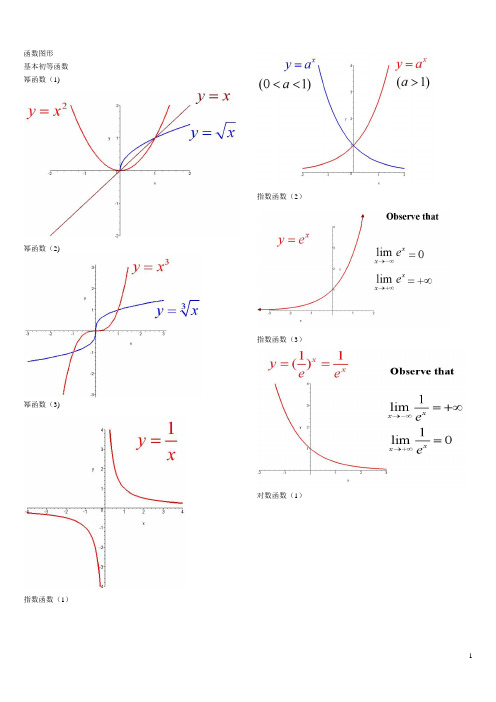
函数图形基本初等函数幂函数(1)幂函数(2)幂函数(3)指数函数(1)指数函数(2)指数函数(3)对数函数(1)三角函数(3)对数函数(2)三角函数(4)三角函数(1)三角函数(5)三角函数(2)反三角函数(1)反三角函数(2)反三角函数(3)反三角函数(4)反三角函数(5)反三角函数(6)反三角函数(7)反三角函数(8)双曲函数(1)双曲函数(2)双曲函数(3)双曲函数(4)双曲函数(5)双曲函数(6)双曲函数(7)反双曲函数(1)反双曲函数(2)反双曲函数(3)反双曲函数(4)反双曲函数(5)反双曲函数(6)y=sin(1/x) (1)y=sin(1/x) (2)y=sin(1/x) (3) y=sin(1/x) (4)y = [1/x](1) y = [1/x](2) y=21/xy=21/x (2)y=xsin(1/x)y=arctan(1/x) y=e1/xy=sinx (x->∞)绝对值函数 y = |x|符号函数 y = sgnx取整函数 y= [x]极限的几何解释(1)极限的几何解释 (2)极限的几何解释 (3)极限的性质 (1) (局部保号性)极限的性质 (2) (局部保号性)极限的性质 (3) (不等式性质)极限的性质 (4) (局部有界性)极限的性质 (5) (局部有界性)两个重要极限y=sinx/x (1)y=sinx/x (2)limsinx/x的一般形式y=(1+1/x)^x (1)y=(1+1/x)^x (2)lim(1+1/x)^x 的一般形式(1) lim(1+1/x)^x 的一般形式(2) lim(1+1/x)^x 的一般形式(3) e的值(1)等价无穷小 (x->0)sinx 等价于xarcsinx 等价于xtanx 等价于xarctanx 等价于x1-cosx 等价于x^2/2sinx 等价于x数列的极限的几何解释海涅定理渐近线水平渐近线铅直渐近线y=(x+1)/(x-1)y=sinx/x (x->∞)夹逼定理(1)夹逼定理(2)数列的夹逼性(1)数列的夹逼性(2)pi 是派的意思(如果你没有切换到公式版本) ^是次方的意思,$是公式的标记符,切换到公式版(安装mathplayer)就看不到$了。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3 期后的本利和为y a1 r ,
3
x 期后的本利和为y a1 r , x N ,
x
即本利和 y 随存期x 变化的函数关系式为
2将 a 1000元, r 2.25%, x 5 代入上式, 得 5 y 1000 1 2.25% 1000 1.02255 1117 68元. .
后的本利和. 复利是把前一期的利息 和本金加在一起作本金再计算 ,
下一期利息的一种计算 利息方法 .
解 1已知本金为a 元, 利率为r, 则 1期后的本利和为y a a r a1 r ,
2 期后的本利和为y a1 r a1 r r a1 r ,
(精确到0.001) ?
在例 5中, 请借助计算器解答下列问题 :
作业
P55
3
2 . 2 . .进一步体会指数函数是现代科技、生 活中具有广泛用途的重要数学模型; 2.进一步体会从具体到抽象、从特殊到 一般的思维过程; 3.进一步体会归纳----总结的一般方法; 4.进一步学习使用计算器进行计算。
自学指导
1.什么叫做复利? 2.例4、例5中都体现了一种什么样的思维过 程?它们用的方法有什么共同之处?你能够 总结吗?
即5 期后的本利和约为 111768元. .
y a1 r , x N .
x
分层训练
一必做题
1.用清水漂洗衣服,若每次能洗去污垢 的3/4,写出存留污垢y与漂洗次数x的函 数关系式,若要使存留的污垢不超过原 1 来的 2 ,则至少要漂洗几次?
16
思考题 :
1第几期后本利和超过本金的1.5 倍 ? 2要使10 期后本利和翻一番, 利率应为多少 ?
一般地, 经过 x 年, 剩留量 y 0.84
x
x 0 .
例5 某种储蓄按复利计算利 , 若本金为a元, 每期利 息 率为r , 设存期是 x, 本利和 (本金加上利息 为 y 元 . )
1写出本利和y 随存期x变化的函数关系式 : 2如果存入本金1000元, 每期利率为 .25%, 试计算5期 2
例 4 某种放射性物质不断变 化为其他物质 每经 , 过一年, 这 种物质剩留的质量是原 来的84% .写出 这种物质的剩留量关于 时间的函数关系式 .
解 设该物质最初的质量为 , 经过 x年剩留量为y. 1
经过1 年, 剩留量 y 1 0.84 0.84 ;
1
经过2 年, 剩留量 y 0.84 0.84 0.842 ;
