汽车动力学建模
新能源汽车智能驾驶系统的车辆动力学建模与仿真

新能源汽车智能驾驶系统的车辆动力学建模与仿真近年来,新能源汽车的发展取得了显著的进展。
随着技术的不断创新,新能源汽车智能驾驶系统逐渐成为了新能源汽车的核心竞争力之一。
而车辆动力学建模与仿真则是实现智能驾驶系统的重要环节。
本文将探讨新能源汽车智能驾驶系统的车辆动力学建模与仿真技术。
一、新能源汽车智能驾驶系统概述新能源汽车智能驾驶系统是将人工智能、传感器、控制算法等技术应用于汽车驾驶过程中,实现车辆自主感知、决策和控制的系统。
它可以通过感知周围环境、分析车辆状态和道路信息等实现自动驾驶、避障、自动停车等功能,提高驾驶安全性和舒适性。
二、车辆动力学建模与仿真的重要性车辆动力学建模与仿真是新能源汽车智能驾驶系统的核心技术之一。
通过建立准确的车辆动力学模型,可以模拟车辆在不同道路条件下的行驶状态,包括车辆加速度、速度、转向等。
基于动力学模型进行仿真可以帮助开发人员更好地理解车辆行为和特性,优化系统算法,提升驾驶性能。
三、车辆动力学建模的方法与技术1. 基于物理模型的建模方法基于物理模型的车辆动力学建模是一种传统的方法。
它通过分析车辆的结构、动力系统、悬挂系统等,建立车辆动力学方程,并结合实际测试数据对模型进行参数修正。
这种方法可以较准确地描述车辆的动力学行为,但需要大量的实验测试数据和复杂的数学计算。
2. 基于数据驱动的建模方法基于数据驱动的建模方法是一种基于大量实际数据进行模型建立的方法。
通过采集车辆行驶数据,使用数据挖掘和机器学习算法分析数据特征,建立车辆动力学模型。
这种方法可以在一定程度上降低建模的难度,但需要大量的数据样本和较强的数据处理能力。
四、车辆动力学仿真的工具与平台针对车辆动力学仿真,目前有多种仿真工具和平台可供选择。
例如,CarSim、ADAMS、Simulink等。
这些工具提供了丰富的车辆模型库和仿真环境,可以方便地进行车辆动力学建模和仿真。
开发人员可以根据具体需求选择适合的工具和平台进行仿真实验。
汽车构造中的车辆动力学建模与仿真

汽车构造中的车辆动力学建模与仿真车辆动力学是研究汽车运动学和力学性能的重要领域,它对汽车设计、性能评估以及优化具有重要意义。
随着计算机仿真技术的快速发展,车辆动力学的建模与仿真成为了研究的热点,并且在汽车工程领域得到了广泛应用。
本文将介绍汽车构造中的车辆动力学建模与仿真技术,以及其在汽车设计和性能评估中的应用。
一、车辆动力学基础在深入了解车辆动力学建模与仿真之前,我们先来了解一下车辆动力学的基础知识。
车辆动力学主要包括车辆运动学和车辆力学两个方面。
1. 车辆运动学车辆运动学研究车辆的运动状态和轨迹,包括车辆的速度、加速度、位置等。
常见的车辆运动学参数有车速、加速度、转向角等。
在车辆动力学建模与仿真中,需要准确地描述车辆的运动学特性,以便进行仿真分析和性能评估。
2. 车辆力学车辆力学研究车辆在运动中受到的力和力矩,并分析车辆受力情况对车辆运动的影响。
常见的力学参数有车辆的质量、弹簧刚度、减振器阻尼等。
在车辆动力学建模与仿真中,需要将车辆的力学特性进行建模,以便进行力学仿真和性能评估。
二、车辆动力学建模车辆动力学建模是指根据车辆的运动学和力学特性,利用数学模型对车辆的运动进行描述。
常用的车辆动力学建模方法包括物理建模方法和系统辨识方法。
1. 物理建模方法物理建模方法是将车辆运动学和力学原理应用于车辆动力学建模中。
通过考虑车辆的质量分布、惯性矩阵以及受力情况等因素,建立车辆的数学模型。
常见的物理建模方法有刚体动力学模型、多体动力学模型等。
2. 系统辨识方法系统辨识方法是通过对车辆的输入和输出进行实验测量,然后利用辨识算法对车辆的动力学模型进行识别和估计。
常见的系统辨识方法有参数辨识方法和非参数辨识方法等。
三、车辆动力学仿真车辆动力学仿真是指利用计算机技术对车辆的运动进行模拟和仿真。
通过车辆动力学建模和仿真,可以对车辆的运动性能进行分析和评估。
1. 仿真平台在进行车辆动力学仿真时,需要选择合适的仿真平台。
汽车动力学建模及控制方法研究

汽车动力学建模及控制方法研究1. 引言在现代社会中, 汽车已经成为人们日常生活中不可或缺的交通工具。
为了提高汽车行驶的安全性和性能,汽车动力学建模及控制方法的研究显得尤为重要。
本文旨在探讨汽车动力学建模及控制方法的研究现状和未来发展趋势。
2. 汽车动力学建模方法在汽车动力学建模中,常用的方法包括理论建模和仿真建模。
理论建模基于物理学原理和数学模型,通过推导方程来描述汽车在运动中的动力学性能。
仿真建模则是利用计算机进行模拟,根据实际的车辆参数和运动状态进行建模和仿真分析。
这两种方法在汽车动力学研究中是相辅相成的。
3. 汽车动力学控制方法在汽车动力学控制方面,目前较为常用的方法包括传统PID控制和模型预测控制(MPC)。
传统PID控制方法通过测量车辆状态和目标状态之间的误差,并计算出相应的控制信号来调节汽车的运动状态。
而MPC方法则是基于预测模型来进行控制,通过对车辆的状态和约束条件进行预测,计算出最优控制信号以使车辆按照预期的轨迹行驶。
4. 汽车动力学建模与控制方法的研究进展随着计算机技术和模拟仿真技术的发展,汽车动力学建模和控制方法的研究取得了显著进展。
在动力学建模方面,越来越多的基于物理学原理的数学模型被提出和改进,并成功应用于真实的车辆控制系统中。
针对不同类型的车辆(如传统燃油车、电动车、混合动力车等),研究者们也在动力学建模方法上进行了不同的探索。
在动力学控制方面,传统PID控制方法在实际车辆应用中取得了较好的效果。
然而,PID控制方法在处理非线性、时变性以及不确定性问题时存在局限性。
因此,在近年来,MPC方法被广泛应用于汽车动力学控制领域,并取得了较好的控制性能。
MPC方法通过建立系统的动力学模型,并考虑约束条件的影响,能够在多变环境下实现更好的控制效果。
5. 汽车动力学建模与控制方法的挑战与展望虽然汽车动力学建模与控制方法取得了一定的进展,但仍然存在一些挑战需要解决。
首先,实际车辆存在非线性、时变性和不确定性,因此建模方法需要更准确地描述车辆的动力学特性。
车辆动力学(4)-齿轮机构建模
二、行星齿轮机构模型
(6)外啮合双星行星排
两个互相啮 合的行星轮, 这两个行星轮 分别与两个不 同的中心轮啮 合。
二、行星齿轮机构模型
(7)内啮合双星行星排
两个互相啮 合的行星轮, 这两个行星轮 分别与两个不 同的中心轮啮 合。
J*
J1
J2 i2
Je
k2,c2 J L
ML
J2 2
L
Me e
k1,c1 J *
k2* ,c2*
J
* L
M
* L
Je
k2*
k2 i2
c2*
c2 i2
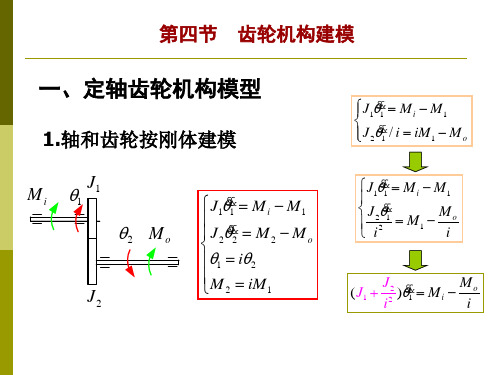
一、定轴齿轮机构模型
3. 轮齿和轴均按弹性体建模
θ1
J1
M1
r1
e km
θ2
M2
J2
r2
cm
J11 M1 Fd r1
2)当量原则:能量不变
① 质量的动能保持相等:1 Jω2 const 2
② 弹性环节的变形势能保持相等: 1 k 2 const
2
③ 散耗能量保持相等: 1 cω2 const 2
J
J i2
K
K i2
c
c i2
一、定轴齿轮机构模型
2.齿轮按刚体、轴按弹性体建模
Me e
k1,c1 J1 1
如何转化?
熟悉的定轴齿轮传动
如果整个行星机构以转速 nc转动 此时行星架转速为
nc nc 0
k zr zs
行星排特性参数
固定行星架
整车动力学模型的建立与优化方法研究

整车动力学模型的建立与优化方法研究整车动力学模型是指通过对汽车整体结构、动力系统、传动系统等各个部分进行建模和仿真,来分析和优化整车性能的一种方法。
建立和优化整车动力学模型对于提高汽车性能、降低燃料消耗和减少排放具有重要意义。
本文将从动力学模型的建立和优化方法两个方面进行探讨。
首先,动力学模型的建立是整车设计和优化的基础。
建立整车动力学模型需要考虑到车辆在不同工况下的运动学和动力学特性。
其中,运动学特性包括车辆的加速度、速度和位移等;动力学特性则包括车辆的加速度、力和扭矩等。
为了准确地描述车辆在运动中的行为,需要综合考虑车辆的转向、制动、加速等各种因素。
在建立整车动力学模型时,可以采用多种方法。
一种常用的方法是基于物理原理的建模方法。
这种方法利用牛顿力学和运动学等基本原理,通过建立汽车动力学方程和约束方程来描述车辆的运动状态。
另一种方法是基于试验数据的建模方法。
这种方法通过对车辆在实际行驶中的数据进行采集和分析,然后利用数学模型对数据进行处理,得到模型参数。
这两种方法可以结合使用,通过不断调整模型参数,逐步优化整车动力学模型的准确性和可靠性。
其次,优化整车动力学模型是提高汽车性能的关键。
在优化整车动力学模型时,需要考虑各种约束条件和目标函数。
约束条件包括车辆的动力系统、传动系统和悬挂系统等各个部分的性能指标。
目标函数则包括提高车辆的操控性、减少能量消耗和降低排放等方面的指标。
通过调整不同参数,可以改变整车的性能和特性,进而实现优化目标。
为了有效地优化整车动力学模型,可以采用多种方法。
一种是基于多目标优化的方法。
这种方法通过设置多个相互独立的优化目标,将整车动力学模型转化为一个多维优化问题。
然后利用多目标优化算法对模型进行求解,得到一组最优解。
另一种方法是基于遗传算法的方法。
这种方法通过模拟生物进化过程,不断优化整车动力学模型的参数,以获得最佳的性能表现。
此外,还可以利用仿真软件进行优化,利用虚拟试验来评估和优化整车性能。
新能源汽车的动力学建模与优化控制

新能源汽车的动力学建模与优化控制随着全球对环境问题的日益关注,新能源车已成为汽车领域的热门话题。
而新能源汽车的核心技术之一便是动力学建模与优化控制。
本文将着眼于此,对新能源汽车的动力学建模与优化控制进行探讨。
一、动力学建模动力学建模是指将车辆的物理特性转化为数学模型,以便在模型中进行动力学仿真与预测。
在新能源汽车发展初期,常常采用传统的机械模型进行建模,而现在则更多地应用基于控制理论的系统动力学建模。
在新能源汽车的动力学建模方面,电池模型是最为关键的一个环节。
电池模型的精确程度会极大地影响到对新能源汽车性能参数的预测与优化控制。
当前应用较为广泛的电池模型包括电化学-热力学模型、累积电量模型以及RC网络模型等。
此外,在新能源汽车动力学建模中,还需要考虑车辆动力匹配和电机控制系统的问题。
有一些研究将IC与EM共同看作混合动力总体的动力源,建立了复杂的混合动力系统数学模型,并针对不同使用条件进行了优化设计。
二、优化控制新能源汽车的优化控制是指通过控制系统实现对整车性能的优化,从而达到提高效率、降低能耗、增加续航里程等多个目的。
当前新能源汽车的优化控制方法主要包括以下几种:1. 能量管理策略控制能量管理策略控制是指通过对车辆电池状态进行实时监测与预测,根据动力需求对车辆进行节能控制。
目前应用较多的策略控制方法包括基于最大化续航里程的电池剩余能量控制和基于最大化效率的功率控制。
2. 智能化驾驶控制智能化驾驶控制旨在通过车辆与环境信息的获取与分析,实现自主化的驾驶。
该控制方法主要包括自适应巡航控制、自动泊车控制和车道保持控制等多种技术手段。
3. 车辆动力输出控制车辆动力输出控制是指通过对车辆的电机控制系统进行优化,以实现对动力输出轻重适度控制,提高车辆的驾驶稳定性。
该控制方法主要包括电机RMS电流控制、自适应前馈控制和预测控制等。
三、问题和挑战在新能源汽车的动力学建模和优化控制方面,仍然存在一些问题和挑战。
新能源汽车车辆运动控制系统的动力学建模

新能源汽车车辆运动控制系统的动力学建模新能源汽车是近年来受到广泛关注的新兴产业,其具有环保、节能、高效等优点,受到相关部门和社会的重视和支持。
为了更好地实现新能源汽车的高效运行和控制,车辆动力学建模成为了迫切需要研究的领域。
一、新能源汽车的发展现状随着环境污染加剧和传统燃油资源逐渐枯竭,人们对新能源汽车的需求日益增加。
目前,电动汽车、混合动力汽车等新能源汽车开始逐渐普及,但其在动力系统设计、车辆运动控制等方面还存在着一些挑战。
因此,研究具有重要意义。
二、新能源汽车车辆运动控制系统的概念与特点车辆运动控制是指通过控制车辆动力系统、传动系统等部件,实现车辆在运行过程中的加速、减速、转向等动作。
新能源汽车车辆运动控制系统相比传统内燃机车辆控制系统具有以下特点:1. 电力输出特性不同:新能源汽车动力系统采用电动机作为动力源,其输出特性与传统内燃机不同,需要针对性的控制策略。
2. 能量管理复杂:电池管理是新能源汽车的核心问题之一,需要合理管理车载电池的能量,实现最佳性能和续航里程。
3. 内部结构复杂:新能源汽车动力系统由电池、电机、控制器等多个部件构成,需要各部件之间的协调工作才能保证车辆有效运行。
三、新能源汽车车辆运动控制系统的动力学建模方法车辆运动控制系统的动力学建模是实现车辆精确控制的关键。
在新能源汽车中,动力学建模一般基于电动机模型和车辆整体动力学模型。
主要方法有:1. 电动机模型的建立:电动机是新能源汽车的动力源,通过建立电动机的控制模型,可以实现对电动汽车输出扭矩和转速的控制。
2. 车辆整体动力学模型的建立:车辆整体动力学模型主要包括车辆的运动学模型和动力学模型。
通过建立车辆整体动力学模型,可以实现对车辆的运动学和动力学性能进行准确控制。
3. 控制策略的设计:基于电动机模型和车辆整体动力学模型,设计合理的控制策略是实现新能源汽车车辆运动控制的关键。
常用的控制策略有PID控制、模糊控制、神经网络控制等。
汽车车辆动力学的建模与仿真

汽车车辆动力学的建模与仿真汽车车辆动力学是指研究汽车在行驶过程中受到的各种力的作用及其对车辆运动的影响的学科。
在现代汽车工业中,为了更好地设计汽车、提高汽车性能和安全性,建模与仿真技术成为了不可或缺的工具。
本文将重点讨论汽车车辆动力学的建模与仿真,以及其在汽车工程领域的应用。
汽车车辆动力学建模是指通过数学、物理等方法描述汽车在运动中受到的各种力和力矩的作用,将汽车系统简化为一系列数学模型。
这些模型可以用来研究汽车在不同路况、驾驶方式下的运动特性,如加速度、速度、转向和悬挂系统的响应等。
建模通常包括车辆动力学、车辆悬挂、车辆转向、车辆稳定性等方面的内容。
通过建模,工程师可以更好地了解汽车在不同情况下的运动规律,为汽车设计和优化提供依据。
在建模的基础上,仿真技术则是将建立的数学模型转化为计算机模型,并进行仿真计算。
通过仿真,工程师可以模拟汽车在不同条件下的运动状态,如加速、制动、转向等,评估汽车性能、安全性和稳定性。
仿真技术还可以用来研究汽车系统的优化设计,提高汽车的性能和安全性。
通过不断调整模型参数和条件,工程师可以找到最佳的解决方案,为汽车设计和制造提供参考。
汽车车辆动力学的建模与仿真在汽车工程领域有着广泛的应用。
首先,它可以帮助工程师更好地了解汽车在不同工况下的运动特性,评估汽车的性能和安全性。
其次,建模与仿真可以帮助设计师优化汽车结构和系统,提高汽车的动力性、操控性和燃油效率。
最后,建模与仿真还可以用来研究汽车的碰撞安全、行驶稳定性、轮胎抓地力等关键问题,为汽车的主动安全和 passagive安全提供支持。
总的来说,汽车车辆动力学的建模与仿真是汽车工程领域的重要技术手段,可以帮助工程师更好地理解汽车的运动规律,优化汽车的设计和性能。
随着计算机技术的不断发展,建模与仿真技术将在未来得到更广泛的应用,为汽车工程师提供更强大的工具来设计、研发和测试新型汽车。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.1 仿真平台核心模型车辆模型作为一个仿真平台软件部分的核心,不仅要考虑仿真平台的应用范围对模型精度的要求,而且也要考虑仿真平台的软硬件性能对模型复杂程度的限制。
因此找到一个适合于应用范围并且匹配于软硬件要求的车辆模型,是一个仿真平台能否具有合理性和实施性的关键。
鉴于本仿真平台将应用于ESP控制系统,并且兼容ABS,TCS的开发,因此,车辆模型必须能够反应这些电子控制系统的控制变量以及它们的敏感变量,能够反应这些控制系统的控制效果。
ESP的控制变量涉及到车辆的横向稳定性,不考虑横向自由度的车辆模型是不能满足要求的。
比如2自由度1/4车辆模型或7自由度1/2车辆模型,都只适应于不考虑横向稳定性的情况。
因此,平台选用了15自由度的整车模型,示意如图2.1。
图2.1 车辆模型自由度示意图15个自由度包括:整车前进方向,侧向,垂直方向的线运动,俯仰,横摆,侧倾6个自由度,每个车轮转动,垂直2个自由度共8个自由度以及转向轮转向角度1个自由度。
根据这样的自由度分布,并且按照模型模块化的要求,将整车模型分成了如下的模块:悬架以上结构动力学模块,悬架模块,轮胎模块,转向系统模块,液压制动系统模块,动力系统模块(发动机模块,传动系统模块),驾驶员行为模块,控制系统软ECU模块等。
整个整车模型是一个典型的混杂系统。
混杂系统(Hybrid System)是指连续时间系统(Continuous Time System)和离散事件系统(Discrete Event System)并存并交换信息的一种动态系统。
通常的混杂系统是分层次表示的,低层次代表的是物理设备及下位控制器,使用微分方程表示的动力学系统;而高层次代表的是控制策略及上位控制器,是用接近自然语言的高级语言描述的控制逻辑系统[19]。
控制系统软ECU 模块就属于这样的离散事件系统。
在MATLAB 的环境下,利用Simulink 搭建连续系统模型,利用Stateflow 搭建离散事件系统模型,仿真平台可以运行在三种不同的仿真方式下,它们分别是:normal 方式,accelerate 方式,xPC 方式。
为了适应于这样的多仿真方式要求,在不同的仿真方式下,对模型分别进行了必要的适应性改造。
2.1.1 整车动力学模型构建整车的自由度以及坐标设置如图2.1所示,模型中共包括15个自由度,沿前进方向运动自由度X ,速度为u ;侧向运动自由度Y ,速度为v ;悬置以上结构垂直运动自由度Z ;侧顷运动自由度ϕ,速度为ϕ∙;横摆运动自由度Yaw ,速度为Yaw ∙;俯仰运动自由度为θ,速度为θ∙;左前,右前,左后,右后轮垂直运动自由度11,12,21,22Z Z Z Z 和旋转自由度11,12,21,22ωωωω;以及前轮转向角自由度δ。
由这15个系统构成的整车运动微分方程如下所示:悬置以上6自由度的微分方程为: 车辆前进方向:00111211122122()()cos ()sin aw s s aw x x y y x x m u vY m D m e Y F F F F F F θϕδδ⋅∙∙∙∙∙∙-++=+-+++(2.1)车辆侧向:00111211122122()()sin ()cos aw s s aw x x y y y y m v uY m e m D Y F F F F F F ϕθδδ⋅∙∙∙∙∙∙+-+=+++++(2.2)车辆垂直方向:111221220s s s s s m Z F F F F ∙∙++++=(2.3)车辆横摆:11112111222122111211122122()cos ()sin 2()()sin ()cos 2()z aw x x y y x x x x y y y y B I Y F F F F B F F a F F F F b F F δδδδ∙∙⎡⎤=-+--++⎣⎦⎡⎤-+++++⎣⎦-+(2.4)车辆俯仰:011122122()0y s aw s s s s J m D u vY F a F a F b F b θ∙∙∙∙+---++=(2.5)车辆侧倾:01111121121222222()11112222x s aw s s s s J m e v uY F B F B F B F B ϕ∙∙∙∙+-+-+-=(2.6)轮胎垂直方向自由度以及转动自由度微分方程:111s11b111m Z -F +K Z =0∙∙(2.7)112121120s b m Z F K Z ∙∙-+= (2.8)221212210s b m Z F K Z ∙∙-+= (2.9)222222220s b m Z F K Z ∙∙-+= (2.10)1111111111x F J F R P T ω∙=--+ (2.11)1211211212x F J F R P T ω∙=--+ (2.12)21221221x J F R P ω∙=-- (2.13)22222222x J F R P ω∙=--(2.14)2.1.2 整车力分析模型的构建整车动力学微分方程中出现的悬架力11122122,,,s s s s F F F F 、轮胎纵、侧向力11,12,21,22,11,12,21,22x x x x y y y y F F F F F F F F ,需用建立这些力与整车运动的15个自由度的关系,才能使得整个微分方程组形成一个可解算的整体。
悬架力可利用下列各式计算:11111111111111()()22s F K Z Z a B C Z Z a B θϕθϕ∙∙∙∙=--++--+ (2.15)12112111111111()()22s F K Z Z a B C Z Z a B θϕθϕ∙∙∙∙=---+--- (2.16)21221222212211()()22s F K Z Z b B C Z Z b B θϕθϕ∙∙∙∙=-+++-++ (2.17)22222222222211()()22s F K Z Z b B C Z Z b B θϕθϕ∙∙∙∙=-+-+-+-(2.18)轮胎纵、侧向力11,12,21,22,11,12,21,22x x x x y y y y F F F F F F F F ,需要利用轮胎模型进行计算,而轮胎纵、侧向力,是车辆在运动过程中受到的最重要的外力,决定了车辆的响应结果,轮胎的力学特性对汽车的操纵稳定性、舒适性、动力性和制动安全性起着极其重要的作用。
因此,车辆性能的定量分析与研究及先进的底盘控制系统的设计开发,在很大程度上依赖于车辆动力学模型和轮胎力学模型的研究。
开发平台的有效性同样需要建立合理的轮胎动力学模型。
现代轮胎是一个复杂的粘性结构体,具有明显的非线性特性,历来的轮胎建模,主要分为基于实测数据和基于物理机理两大流派。
物理机理的建模,就是通过对轮胎结构和形变机制的数学描述,建立剪切力和回正力矩与相应参数的函数关系。
而基于实测数据的轮胎建模,是通过对大量的轮胎力特性的实验数据进行回归分析,将轮胎力特性通过含有拟合参数的公式有效的表达出来。
目前在轮胎力学分析方面使用较为广泛的是基于实测数据的经验公式的代表——魔术公式MF (Magic Formula )[20],MF 源于二十世纪八十年代中期V olvo 公司和荷兰Delft 大学的联合研究,H.B.Pacejka 和E.Bakker 等人为此做出了非常突出的贡献。
由于本仿真开发平台将用于对华晨中华车ESP 的开发工作,而华晨方面提供了基于89版Magic Formula 轮胎模型的轮胎参数,因此根据已有的数据条件,我们选用具有拟合精度高,表达式比较统一的魔术公式轮胎模型。
虽然魔术公式有计算量较大这个缺点,但经过测试,本试验台的硬件条件完全能满足魔术公式实时计算的要求。
另外,由于魔术公式轮胎模型计算的是轮胎稳态特性,因此适用于低输入频率下的操纵稳定性研究,而对于高输入频率下的响应,则具有局限性,这也是本仿真平台在改进过程中所需要注意和完善的问题。
轮胎坐标如图2.2所示。
图2.2 轮胎坐标系Magic Formula 轮胎模型,一般公式如下:[]{}()sin arctan ()(1)arctan(())h h vy x D C B x S E E B x S S =+-+++ (2.19)式中,D 为峰值因子,C 为形状因子,B 为刚度因子,E 为曲率因子,h S 为横向补偿量,v S 为纵向补偿量,本文忽略了外倾角的影响。
对于侧向力,x 表示侧偏角,()y x 表示轮胎侧向力,MF 中各因子的表达如下:21234679101213sin[2arctan(/)]h v C a D a P a Pa P a B CDE a P a S a p a S a p a ==+==+=+=+ (2.20)华晨中华车基于此模型的各参数如表2.1 所示:表2.1 MF 侧向力-侧偏角系数0a 1a 2a 3a 4a 6a 7a 9a 10a 12a 13a1.65 -34 1250 3036 12.8 -0.021 0.7739 0.01344 0.00371 1.21356 6.26206对于纵向力,x 表示滑移率,()y x 表示轮胎纵向力,MF 中各因子的表达如下:5021223426789100b Ph v C b D b P b P b P b P B CDe E b P b P b S b p b S ==++==++=+= (2.21)华晨中华车基于此轮胎模型的各参数如表2.2 所示。
表2.2 MF 纵向力-滑移率系数0b1b2b3b4b5b6b7b8b9b10b2.37272-9.4614901302760.08860.00402-0.06151.20.0299-0.176制动/驱动和转向联合工况下的侧向力和纵向力满足附着椭圆,从MF 中得到的侧向力和纵向力,在联合工况下需要进行修正:(),()tan ,11y xx y Fx y x Fy y x σσσσλασσσλλ=====++(2.22)式中λ——滑移率α——侧偏角车轮沿轮胎平面的速度分量为(以左前轮为例)11cos(V α= (2.23)定义滑移率如下,制动为负,驱动为正11111R V V ωλ-=(制动) (2.24)111111R V r ωλω-=(驱动) (2.25)式中1α——左前轮侧偏角载荷的单位为kN ,侧偏角的单位为度,滑移率按百分比计。
这个轮胎模型的纵向特性,侧偏特性如图2.3所示。
图2.3 轮胎力学特性同时,魔术公式也可以计算回正力矩,但因为回正力矩的主要作用在于通过方向盘为驾驶员提供一个反馈力矩,即通常所说的“路感”,它对车辆运动的影响并不大,因此本仿真平台中忽略回正力矩的影响。
